2. 北京机电工程研究所,北京 100074
2. Beijing Electro-mechanical Engineering Institute, Beijing 100074, China
目标关联是数据融合过程的重要步骤,其本质是确定传感器量测与目标源之间的对应关系。根据应用场景的不同,又可以分为量测与目标的关联和量测与量测的关联。前者的任务是将新获得的量测信息与已有目标进行对应,后者关心的是将对同一目标群的多个量测进行一一对应。本文的研究任务是如何对异视角下同一目标群的多个量测进行目标关联。
国外针对航迹起始比较成熟的量测−量测关联方法主要有3类:基于启发式规则的方法[1],基于逻辑规则的方法[2]和基于Hough变换的方法[3-4]。前两者利用的都是目标运动的机动限制条件,仅适用于噪声虚警和杂波较少的环境。后者适应性更强但需要知道目标轨道的参数信息,并且在参数域运行聚类方法的计算量较大。
按照关联因子的不同,目标关联主要可分为基于位置信息和基于属性信息两大类[5],由于异视角对属性特征的影响较大,早期关联算法大多是基于位置信息的。一些经典的多目标关联算法,如最近邻算法(NN)、概率数据关联算法(PDA)、多假设跟踪算法(MHT)等。近年来,很多学者在此基础上做了很多改进。赵健[6]研究的基于点模式匹配算法可以处理目标群的刚体或非刚体形变,对基于位置的关联效果有很大提升。Zeng等[7]提出了一种舰船编队特征与舰船属性特征相结合的目标关联算法,该算法同时考虑了目标的属性特征和舰船编队形状特征进行证据合成,充分利用了两者的互补性,但受形状描述及目标识别算法的影响,关联正确率不高。刘铮等[8]针对多源数据多特征融合的应用场景,提出基于多模型估计方法对同类型目标进行初步筛选,再基于多特征最大联合概率分布对目标精细关联的方案,有效提高了弱小目标关联的准确性。王继阳等[9]提出了一种基于目标属性特征的多假设关联算法,仅仅使用目标的属性特征作为关联依据,该算法适用于基于低时间分辨率的遥感图像关联。如何单纯依靠属性特征完成关联任务,目前鲜见较为成熟的解决方案。唐宏美[10]详细研究了从坐标变换、全局结构、谱特征到拓扑特征的多种位置关联算法,得出拓扑特征具有最强的适应性和最高准确率的结论。此外,也有少量综合位置和属性信息的目标关联方法。汤守波等[11]在目标运动状态信息可用的情况下,采用原始的状态滤波的方法形成多条可能航迹,而后利用属性信息的相似性对关联结果进行修正。孙寒涛[12]利用灰色系统理论和系统聚类分析方法判断目标间的相似程度。对于不确定的集合再次进行方位数据关联,有效弥补了单一方法的缺陷。
总体来说,以上方案的主要思路都是基于目标的位置信息,对目标群运动过程建立适当的模型,根据这些运动参量计算出航迹量测的匹配度,进而对关联关系的判断[13]。这些算法并没有充分利用目标的属性信息。随着无人机信息采集技术的发展,目标关联可以利用的信息越来越丰富。区别于传统的天基、地基传感器,以无人机编队为载体的各种传感器可以提供多视角、近距离的各种目标特征信息。综合利用目标在时空和属性上的特征,能够有效提高关联的准确率。与传统目标关联算法相比,本文算法具有以下优势:
1)借助姿态及位置传感器,无人机成像平台提供的目标空间信息,能够对二维图像特征进行一定的优化。
2)算法同时考虑了目标群的位置特征和属性特征,具有更好的抗干扰能力和准确性。
3)基于D-S证据理论的融合框架具有很好的扩展能力,可以根据应用场景的不同使用不同的目标群特征。
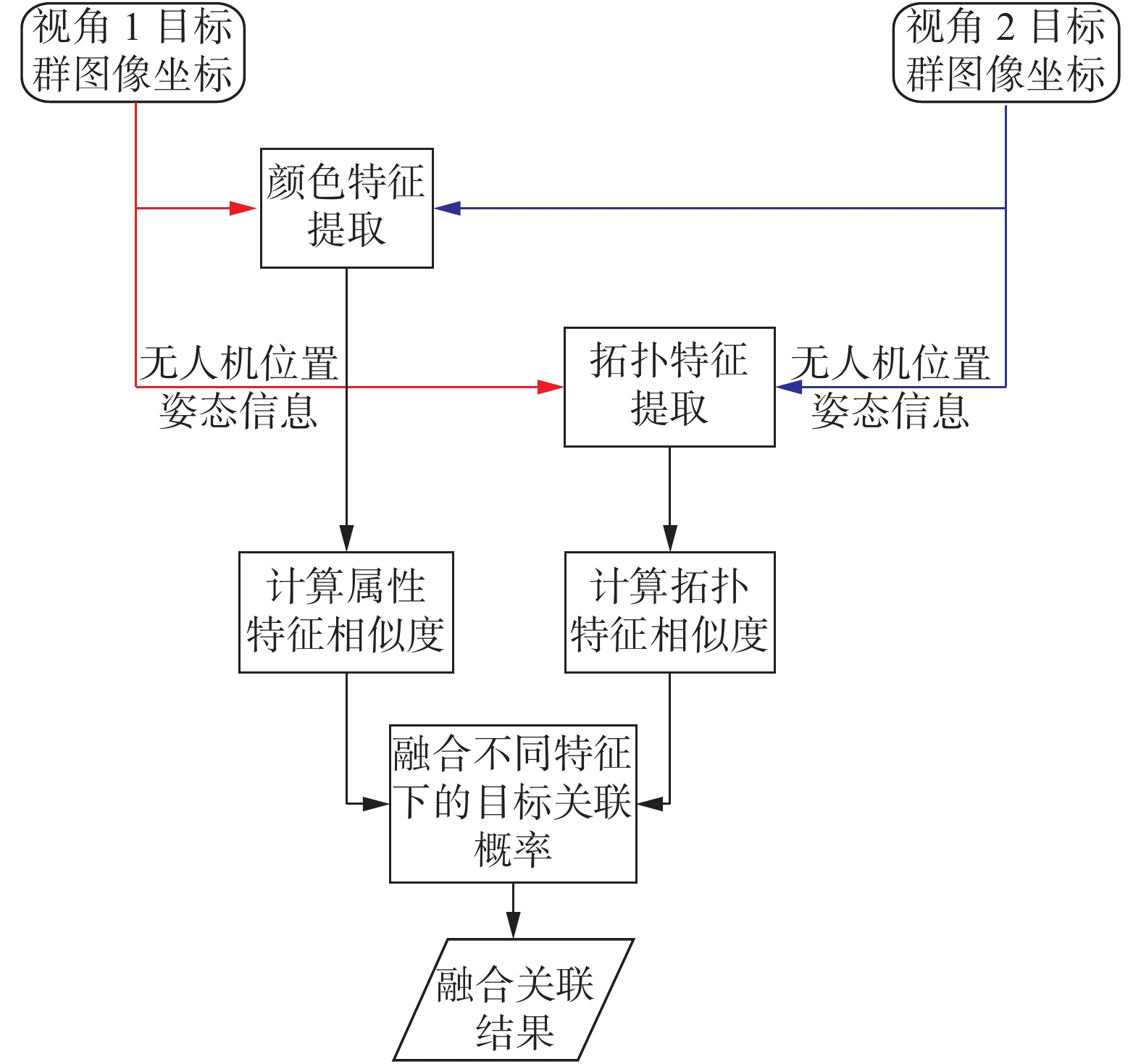
1 算法基本框架本文整体算法框架如图1所示,目标检测模块获得目标群位置后,将目标区域子图像送入属性特征提取模块,获得目标的颜色特征并计算不同视角下的特征相似度。与此同时,将目标群的位置分布及无人机姿态信息等送入拓扑特征提取模块,获得目标的位置信息特征及对应的相似度。利用D-S证据理论融合不同特征下的关联概率分配结果并输出最终关联结果。
|
Download:
|
| 图 1 本文算法流程图 Fig. 1 Flow chart of the proposed method | |
目标的属性特征包括目标的颜色、纹理、形状等,这些属性特征大多受视角变换影响较大,因此传统目标关联算法很少利用其属性特征。无人机编队因其自带姿态位置传感器,能够在一定程度上修正视角对观测结果的影响,使得属性特征的引入具有可行性。
本文算法主要使用了目标的颜色特征,为减小视角变化对目标颜色特征的影响,使用以下步骤提取目标的颜色特征。
1)去除背景干扰。由于目标检测给出的目标框往往带有一定的背景区域,这些背景不属于目标的信息,在统计目标的颜色特征时应当预先剔除。本文使用基于自适应阈值的泛洪填充算法计算背景区域。具体步骤如下:①计算宽w高h的跟踪框内每个像素对应的像素梯度,按升序进行排序得到w×h长度的一维数组S;②计算目标边缘的梯度阈值;③从跟踪框的矩形边缘开始向中心进行遍历,将梯度小于阈值的像素点标记为背景,直到遇到大于边缘阈值的像素停止遍历。标记为背景的像素不参与颜色统计。
2)二维透视变换消除视角畸变。由于无人机多为高空侦查,地面目标可近似为二维物体,使用二维透视变换将目标的前下视图像矫正为正下视图可以消除视角倾斜带来的影响。具体方案为使用无人机的姿态及相机内参确定投影矩阵,将图像上的目标像素分别投影到地平面上,然后将地平面上的虚拟目标等比例缩放获得目标的俯视图[14]。
3)统计目标颜色直方图并计算频率直方图。本文采用RGB或HSV颜色空间,将每种颜色分量按照0~255分为10个区间,统计每个区间的像素点数目,并除以目标像素点总数。这个30维的颜色频率分布直方图即为属性特征向量。
4)计算两目标区域的颜色特征相似度并进行关联概率分配。本文采用余弦距离计算颜色特征向量的相似度。相似度取值范围为0~1,数值越大相似度越高。为方便后续进行特征融合,两视角不同量测之间的关联概率需要满足∑Pij=1,Pij表示视角1中的量测i与视角2中的量测j对应同一目标的概率。
2.2 拓扑特征提取子模块目标的拓扑特征指的是目标在目标群中的几何位置信息,与单纯的坐标信息不同,拓扑特征综合考虑了参考目标与其他目标之间的相对位置关系。由于当前技术条件下无人机的位置传感器精度不足,基于坐标相对关系的拓扑特征往往更加准确稳定。
由于不同无人机视角不同,为获得同一坐标系下的几何位置分布,需要使用无人机的姿态参数将目标群图像坐标转换为地理坐标。具体算法步骤如下:
1)将目标的二维图像坐标转化为三维地理坐标。转换过程需先把成像坐标系转换为导航坐标系,再将导航坐标系变为地理坐标系。坐标系转化公式如下:
| $\begin{array}{c} \left[ \begin{array}{c} {{X}} \\ Y \\ Z \\ \end{array} \right] = {{{T}}^{ - 1}}\left[ \begin{array}{c} {X_c} \\ {Y_c} \\ {Z_c} \\ \end{array} \right]{{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos\; \gamma }&{\sin\; \gamma } \\ 0&{ - \sin\; \gamma }&{\cos\; \gamma } \end{array}} \right]* \\ \left[ {\begin{array}{*{20}{c}} {\cos\; \theta }&{\sin\; \theta }&0 \\ { - \sin\; \theta }&{\cos\; \theta }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos\; \varphi }&0&{ - \sin\; \varphi } \\ 0&1&0 \\ {\sin\; \varphi }&0&{\cos\; \varphi } \end{array}} \right] \\ \end{array} $ |
式中:(X,Y,Z)为目标在地理坐标系下的坐标;(θ,φ,γ)分别为无人机的俯仰角、航向角、滚动角。
2)计算目标的拓扑描述子。由于无人机编队覆盖范围有限,目标群分布范围可近似看做同一高度分布,只需要提取目标的二维拓扑特征。以视角中某一目标为原点建立极坐标系,将其余目标按照极角分为12个区间,每个区间为π/6弧度的扇形区域。统计每个区间中目标的极径之和,作为这一区间的特征值。这个12维特征向量即为当前参考目标的拓扑描述子。
3)根据描述子计算目标之间的拓扑特征相似度。本文使用改进的曼哈顿距离计算拓扑描述子的相似度,具体步骤如下。①将两目标的拓扑描述子按位相减,获得12维的差值;②以3为滑动窗口宽度,对12维差值非零部分做均值滤波,消除观测角度误差带来的影响;③对滤波后的差值绝对值求和为S,最终相似度Similarity计算方式如下,A、B分别为两视角下某观测的拓扑描述子,函数f为均值滤波操作。
| $\begin{array}{*{20}{c}} {{\rm{Similarity}} = 1{\rm{ - }}\dfrac{{{S}}}{{{\rm{sum}}}}} \\ {{{S}} = \displaystyle\sum\limits_{i = 1}^{12} {{\rm{abs}}(f(A(i) - B(i)))} } \\ {{\rm{s}}{\rm{um}} = \max \left(\displaystyle\sum\limits_{i = 1}^{12} {{\rm{abs}}(A(i))} ,\displaystyle\sum\limits_{j = 1}^{12} {{\rm{abs}}(B(j))} \right)} \end{array}$ |
4)根据拓扑相似度进行关联概率分配。设两视角下分别有M和N个目标,由以上步骤可获得M×N维的相似度矩阵Ms。在矩阵中寻找最大元素Msij,若Msij≥ɛ(ɛ=0.7),则量测i与量测j关联,然后从相似矩阵中划掉i、j对应的行和列,得到降阶的相似矩阵,在降阶矩阵中再找最大元素,重复上述过程,直到所有元素均小于阈值为止。
2.3 D-S证据理论特征融合模块基于颜色特征和拓扑特征均可获得一个M×N维的关联概率矩阵,使用D-S证据理论融合两个矩阵可获得更加可靠的关联结果。
本文在基于属性特征和拓扑特征的关联概率矩阵上运行证据融合过程,视角1中每个量测分别有8个关联概率与视角2中目标对应,加上全集和空集,每个量测的关联概率向量为10维。合成规则如下:
θ为假设空间,mass函数是一个在假设空间上的基本概率分配函数m,满足:
| $m( \text{Ø} ) = 0,\;\sum\limits_{A \subseteq \theta } {m(A)} = 1$ |
对任意A属于θ,θ上的两个mass函数m1,m2的Dempster合成规则为
| $\begin{array}{*{20}{c}} {{m_1} \oplus {m_2}(A) = \dfrac{1}{K}\displaystyle\sum\limits_{B \cap C = A} {{m_1}(B) \cdot {m_2}(C),B,C \subseteq \theta ,} } \\ {K = 1 - \displaystyle\sum\limits_{B \cap C = \text{Ø} } {{m_1}(B) \cdot {m_2}(C)} } \end{array}$ |
对任意A属于θ,θ上的n个mass函数m1,m2,…,mn的Dempster合成规则为
| $\begin{array}{*{20}{c}} {{m_1} \oplus {m_2} \oplus \cdots \oplus {m_n}(A) = } \\ {\dfrac{1}{K}\displaystyle\sum\limits_{{A_1} \cap {A_2} \cdots {A_n} = A} {{m_1}({A_1}) \cdot {m_2}({A_2}) \cdot \; \cdots \; \cdot {m_n}({A_n})} } \\ {\begin{array}{*{20}{c}} {{A_1},{A_2}, \cdots ,{A_n} \subseteq \theta ,} \\ {K = 1 - \displaystyle\sum {{m_1}({A_1}) \cdot {m_2}({A_2}) \cdot \; \cdots \; \cdot {m_n}({A_n})} } \end{array}} \end{array}$ |
本文的实验图像是基于两架无人机在不同视角下同时采集获得的可见光图像,图2为原图,分辨率3000×4000,图3为目标群的位置分布情况,关联目标为车辆,每幅图像带有相应的拍摄坐标及飞行姿态数据。在两个视角中分别选取8个和9个车辆目标作为识别目标,分别编号为101~109,201~208。正确对应关系如表1所示。

|
Download:
|
| 图 2 两视角下无人机拍摄原图 Fig. 2 Original picture taken by UAV | |

|
Download:
|
| 图 3 两个视角下的目标分布 Fig. 3 Target distribution from two perspectives | |
| 表 1 两视角不同目标与量测的对应关系 Tab.1 Corresponding relationship between different targets and measurement from two perspectives |
两视角目标区域图片裁剪如表2所示,视角2拍摄位置离地更高,故同一目标的量测更小。
| 表 2 目标区域裁剪子图像 Tab.2 Sub image cut from target area |
基于自适应阈值的泛洪填充算法处理后的目标图像如表3所示,预处理将背景像素统一标记为黑色。
| 表 3 消除背景后的目标图像 Tab.3 Target area without background pixels |
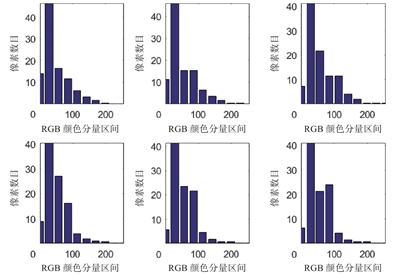
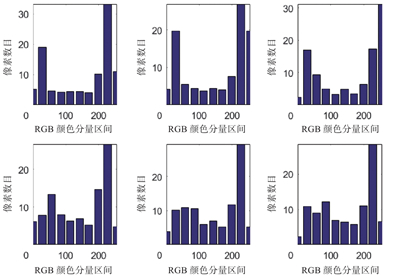
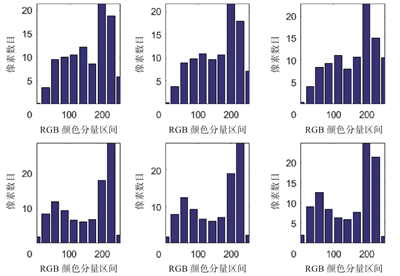
表4是以RGB颜色分量计算的部分目标频率分布直方图,可以看出,不同颜色的目标颜色特征向量有很大的不同。
| 表 4 部分目标的颜色特征向量 Tab.4 Color feature vector of some targets |
基于颜色特征向量计算的相似度矩阵如式(1)所示。取阈值ɛ=0.7,关联概率分配结果如表5所示。显然属于同一目标的两个量测关联概率较大,相似度一般在0.8以上,满足D-S据理论对证据有效性的要求,然而,仅仅使用颜色对目标量测进行关联决策存在较大的误差,需要其他特征的辅助判别。
| ${\rm{simi}}{\rm{larity}} = \left[ {\begin{array}{*{20}{c}} {0.754}&{0.367}&{0.825}&{0.766}&{0.970}&{0.427}&{0.388}&{0.425} \\ {0.308}&{0.965}&{0.455}&{0.408}&{0.429}&{0.450}&{0.592}&{0.535} \\ {0.786}&{0.488}&{0.837}&{0.758}&{0.939}&{0.409}&{0.347}&{0.387} \\ {0.750}&{0.341}&{0.879}&{0.934}&{0.811}&{0.799}&{0.593}&{0.688} \\ {0.492}&{0.244}&{0.633}&{0.566}&{0.861}&{0.355}&{0.402}&{0.471} \\ {0.611}&{0.334}&{0.758}&{0.834}&{0.612}&{0.863}&{0.649}&{0.731} \\ {0.311}&{0.529}&{0.531}&{0.539}&{0.482}&{0.588}&{0.934}&{0.749} \\ {0.385}&{0.724}&{0.606}&{0.605}&{0.546}&{0.669}&{0.751}&{0.927} \\ {0.347}&{0.609}&{0.571}&{0.582}&{0.519}&{0.621}&{0.834}&{0.884} \end{array}} \right]$ | (1) |
| 表 5 基于颜色特征的关联概率分配结果 Tab.5 Association probability assignment results based on color features |
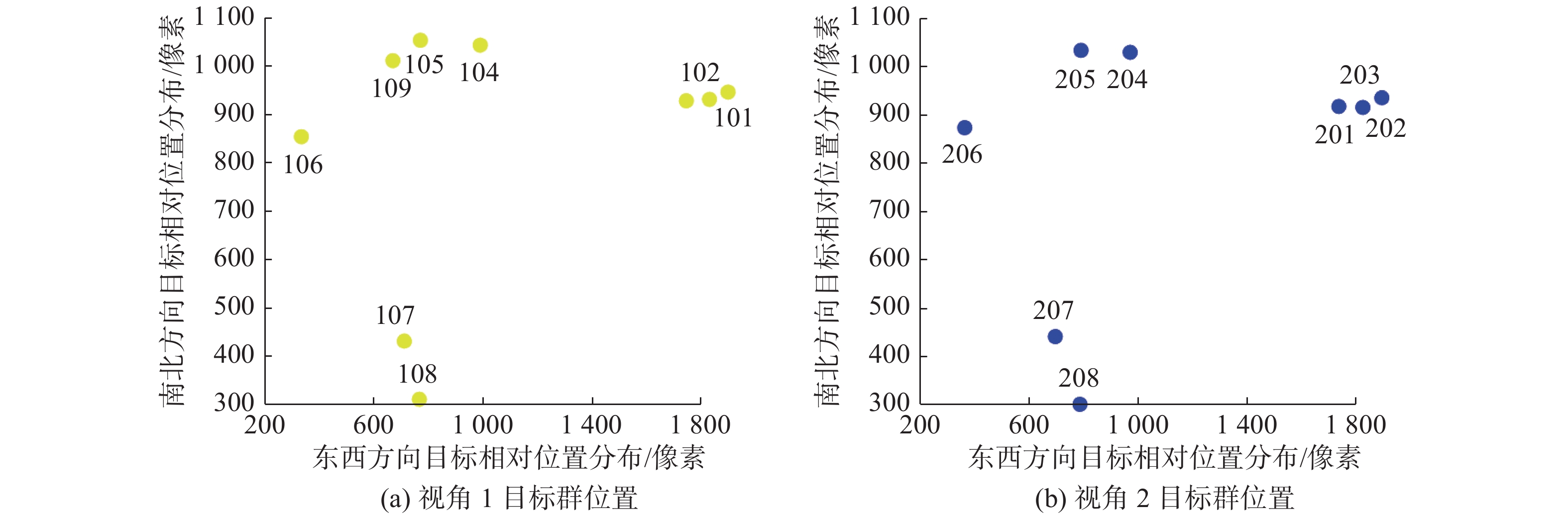
将目标坐标从图像坐标系统一到地理坐标后,两视角的目标群位置分布如图4所示。
|
Download:
|
| 图 4 目标群位置分布示意图 Fig. 4 Location distribution of target group | |
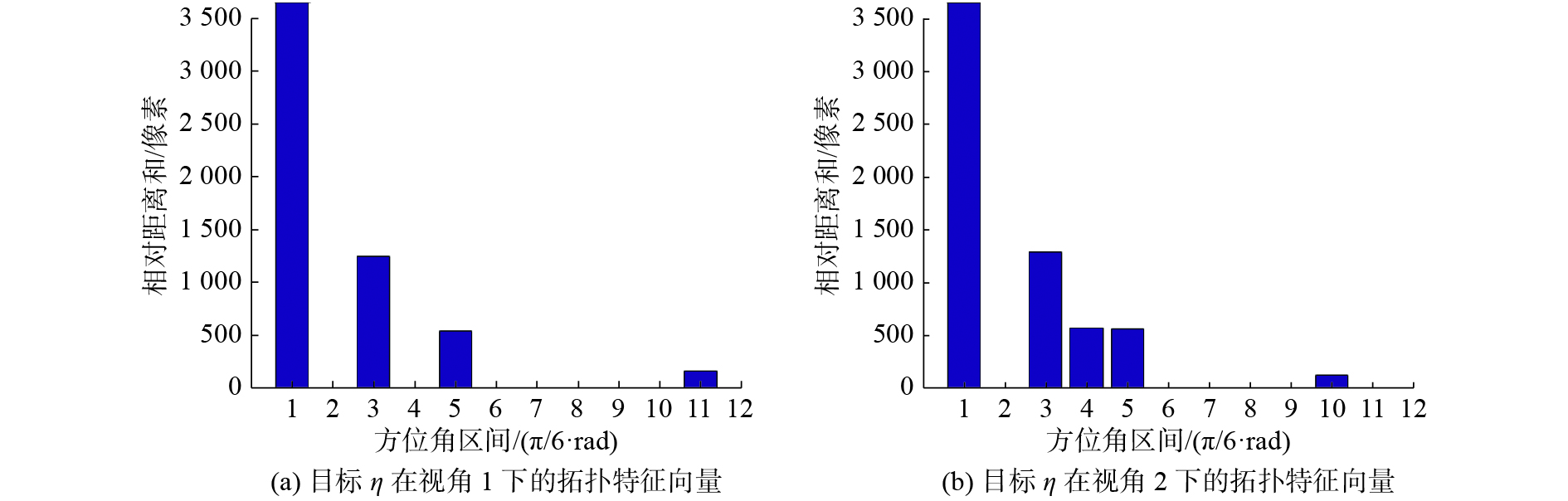
以7号目标为例,其在视角1和视角2量测的拓扑描述子如图5所示。
|
Download:
|
| 图 5 目标7在视角1及视角2下的拓扑特征向量 Fig. 5 Topological characteristics of target 7 from different perspectives | |
基于拓扑特征向量计算的相似度矩阵如式(2),同一目标的拓扑特征相似度都在0.9以上。
| ${\rm{simi}}{\rm{larity}} = \left[ {\begin{array}{*{20}{c}} {0.905}&{0.968}&{0.934}&{0.381}&{0.312}&{0.807}&{0.126}&{0.175} \\ {0.833}&{0.908}&{0.874}&{0.130}&{0.072}&{0.758}&{0.082}&{0.129} \\ {0.864}&{0.939}&{0.906}&{0.353}&{0.287}&{0.784}&{0.096}&{0.144} \\ {0.452}&{0.788}&{0.436}&{0.951}&{0.842}&{0.659}&{0.132}&{0.386} \\ {0.330}&{0.739}&{0.317}&{0.899}&{0.972}&{0.533}&{0.130}&{0.380} \\ {0.214}&{0.635}&{0.193}&{0.635}&{0.736}&{0.959}&{0.678}&{0.678} \\ {0.159}&{0.692}&{0.303}&{0.522}&{0.603}&{0.862}&{0.943}&{0.978} \\ {0.153}&{0.304}&{0.311}&{0.257}&{0.220}&{0.811}&{0.884}&{0.941} \\ {0.313}&{0.726}&{0.286}&{0.839}&{0.937}&{0.546}&{0.204}&{0.373} \end{array}} \right]$ | (2) |
取阈值ɛ=0.85,拓扑特征的关联概率分配结果如表6所示。
| 表 6 基于拓扑特征的关联概率分配结果 Tab.6 Distribution results of association probability based on topological features |
使用D-S证据理论融合颜色特征和拓扑特征的关联概率后,综合关联概率如表7所示(Pij表示量测i和量测j的关联概率)。
| 表 7 融合拓扑特征和颜色特征的关联概率分配结果 Tab.7 Association probability assignment result based on the topological feature and color feature |
根据关联概率矩阵进行量测分配,所有量测对应关系均分配正确,其中量测109不与视角2中任何一个目标对应,与事实一致。目标7和目标8颜色接近,并且在两视角下的拓扑结构接近,因此对应的量测关联概率也较为接近。对比单独使用颜色特征和拓扑特征的关联概率,显然融合概率矩阵更加准确可靠,其中大部分目标能给出清晰的判定结果。
3.4 关联算法优劣势对比考虑到关联算法应用场景的不同,本文没有进行对比实验,通过总结不同文献的关联思想,归纳出适用于无人机平台的3类基础算法,并与本文算法进行优劣势对比。
算法1 基于全局结构的位置关联算法。以目标的绝对位置或相对位置(相对目标群重心或地图指定参考点)为关联依据的一类算法。相关特征有点对特征、谱特征、拓扑特征等,对传感器精度要求较高。
算法2 基于属性特征的数据关联算法。依据使用传感器的不同,关联可以使用的属性特征主要有目标面积、周长、长宽比、形状特征链表、偏心率、电磁特性、红外成像提供的温度特征等。受应用环境、传感器性能不足、电磁干扰等因素的影响,单一属性特征往往很不可靠,视角变换带来的畸变因素更加限制了属性特征的使用。
算法3 基于目标运动信息的关联算法。以目标速度、加速度、航迹等因素作为关联依据的算法,适用于长时关联,但需要对目标的稳定跟踪,关联时间较长。
以上3种算法与本文算法优缺点如表8所示。
| 表 8 本文算法与常用算法的效果对比 Tab.8 Effect comparison between the algorithm in this paper and the classical algorithm |
此外,目前也有一些算法融合了不同类型特征,如基于电子与光学传感器多特征综合的关联算法。然而,由于受到视角差异的干扰,这类算法在无人机平台上效果较差。对近距离无人机探测任务来说,引入无人机提供的位置姿态信息对属性信息修正是有效而必要的措施。
4 结束语本文提出了一种基于无人机编队平台的多特征融合目标关联算法,通过融合目标的颜色和位置信息,对两视角下的目标量测取得了较好的关联结果。研究发现,无人机平台提供的位置姿态信息能够对目标的颜色和拓扑特征起到一定的优化效果。
实验证明了利用多特征融合改进关联结果的可行性,由于证据理论中基本概率分配的独立性,新型有效特征的引入必然对关联结果有一定的改进。由于时间关系,本文仅使用了颜色和拓扑两种特征,对于其他应用场景,可以在本框架的基础上使用其他特征,如目标面积、纹理等。在国防领域,对于搭载红外传感器和雷达的无人侦察机,本文可使用的基础特征有更多的选择,可以预见,通过综合不同传感器获得的目标特征信息,关联结果的准确性能够得到极大的提升。
| [1] |
VAN KEUK G. Sequential track extraction[J]. IEEE Transactions on aerospace and electronic systems, 1998, 34(4): 1135-1148. DOI:10.1109/7.722699 ( 0) 0)
|
| [2] |
BAR-SHALOM Y, FORTMANN T E. Tracking and data association[M]. New York: Academic Press, 1988.
( 0) 0)
|
| [3] |
CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the Hough transform. III. Detection performance with binary integration[J]. IEEE transactions on aerospace and electronic systems, 1994, 30(1): 116-125. DOI:10.1109/7.250412 ( 0) 0)
|
| [4] |
CHEN Ji, LEUNG H, LO T, et al. A modified probabilistic data association filter in a real clutter environment[J]. IEEE transactions on aerospace and electronic systems, 1996, 32(1): 300-313. DOI:10.1109/7.481270 ( 0) 0)
|
| [5] |
曾昊. 基于星载异类传感器的舰船编队目标数据关联方法研究[D]. 合肥: 国防科技大学, 2008. ZENG Hao. Data association research about targets among ship formation based on heterogeneous spaceborne reconnaissance sensors[D]. Hefei: National University of Defense Technology, 2018. (  0) 0)
|
| [6] |
赵健. 点模式匹配算法研究[D]. 合肥: 国防科技大学, 2012. ZHAO Jian. The research on point pattern matching[D]. Hefei: National University of Defense Technology, 2012. (  0) 0)
|
| [7] |
ZENG Hao, WANG Zhuang. A ships data association algorithm based on the ships formation structure and ships attribute information[C]//2008 9th International Conference on Signal Processing. Beijing, China: IEEE, 2008: 2837−2841.
( 0) 0)
|
| [8] |
刘铮, 毛宏霞, 戴聪明, 等. 基于多源数据多特征融合的弱小目标关联研究[J]. 红外与激光工程, 2019, 48(5): 0526001. LIU Zheng, MAO Hongxia, DAI Congming, et al. Dim and small target association based on multi-source data and multi-feature fusion[J]. Infrared and laser engineering, 2019, 48(5): 0526001. (  0) 0)
|
| [9] |
王继阳, 陆军, 粟毅. 一种基于目标属性特征的多假设关联算法[J]. 计算机仿真, 2005, 22(1): 76-79, 83. WANG Jiyang, LU Jun, SU Yi. A multiple hypothesis association algorithm based on targets’ attribute data[J]. Computer simulation, 2005, 22(1): 76-79, 83. DOI:10.3969/j.issn.1006-9348.2005.01.023 (  0) 0)
|
| [10] |
唐宏美. 基于电子与光学传感器的目标关联技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. TANG Hongmei. Research on technology of target association based on electronic sensor and optical sensor[D]. Harbin: Harbin Institute of Technology, 2013. (  0) 0)
|
| [11] |
汤亚波, 徐守时. 基于D-S证据理论的多源遥感图像目标数据联合关联算法[J]. 中国科学技术大学学报, 2006, 36(5): 466-471. TANG Yabo, XU Shoushi. A united target data association algorithm based on D-S theory and multiple remote sensing images[J]. Journal of University of Science and Technology of China, 2006, 36(5): 466-471. DOI:10.3969/j.issn.0253-2778.2006.05.002 (  0) 0)
|
| [12] |
孙寒涛. 基于状态和属性的多目标联合关联算法[J]. 应用科技, 2020, 47(3): 74-79. SUN Hantao. Multi-objective joint association algorithm based on state and attribute[J]. Applied science and technology, 2020, 47(3): 74-79. (  0) 0)
|
| [13] |
李文超, 邹焕新, 雷琳, 等. 目标数据关联技术综述[J]. 计算机仿真, 2014, 31(3): 1-5, 10. LI Wenchao, ZOU Huanxin, LEI Lin, et al. A survey of target data association[J]. Computer simulation, 2014, 31(3): 1-5, 10. DOI:10.3969/j.issn.1006-9348.2014.03.001 (  0) 0)
|
| [14] |
代勤, 王延杰, 韩广良. 基于改进Hough变换和透视变换的透视图像矫正[J]. 液晶与显示, 2012, 27(4): 552-556. DAI Qin, WANG Yanjie, HAN Guangliang. Perspective image rectification based on improved Hough transformation and perspective transformation[J]. Chinese journal of liquid crystals and displays, 2012, 27(4): 552-556. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15