2. 西安长庆科技工程有限责任公司,陕西 西安 710018
2. Xi’an Changqing Technology Engineering Co., Ltd., Xi’an 710018, China
随着现代生产对精密装配、无夹具协作以及柔性软排线等复杂任务的要求不断提高,双臂冗余度机器人以其高精度、高灵活性、手动单元与自动单元交互平稳且安全等特点,拓宽了诸如3C产品装配等既需要机器人的重复工作能力,又需要人的熟练技能的行业,相较于单臂机器人在操作能力及控制等方面的局限性,拥有双臂协调作业及良好人机协作功能的双臂冗余度机器人呈现出明显的优势,并且依托冗余自由度带来的自运动特性,使其在面临关节限制、避障、获取最小力矩等问题上拥有更大的优势。因此,针对双臂冗余度机器人协调运动系统的研究越来越受重视,同时也是机器人技术发展到一定程度亟需解决的问题[1]。
目前针对双臂冗余度机器人协调运动问题的研究主要包括双臂间约束关系分析、双臂协同工作时的避碰问题、轨迹生成方法等。文献[2]中提出了一种通过在控制过程中建立物体和机器人动态模型来保证运动所需约束关系的动态协调方法;文献[3]对冗余度机器人进行运动学优化,设计了一种分层递阶控制结构,仿真和实验显示出了协调控制策略的有效性;文献[1]通过引入相对位姿变量与绝对位姿变量构建协调运动的雅可比矩阵,并提出一种基于冗余度机械臂自运动特性的双臂机器人避障算法,通过仿真验证了算法的有效性;文献[4]提出一种双树随机树搜索算法bi-RRT,通过调整末端姿态结合关节自运动来生成目标树,在单臂七自由度机器人达点运动规划中取得了良好的实验效果。
虽然到目前为止,有很多关于多机器人协调运动规划问题的研究,但主要是针对运动学约束和路径规划,而关于冗余度机器人的研究则多体现为避障算法和轨迹规划,关注冗余度机器人高灵活性并在协调运动规划时考虑运动性能的研究并不多见,为此,本文拟从运动学角度通过双臂冗余度机器人的运动灵活性分析开展两种协调运动方式的研究。
本文以ABB公司的双臂冗余度机器人YuMi为研究对象,采用运动灵活性指标可操作度分析机器人在工作空间中的运动能力,提出一种双臂可操作度指标,并求得其在双臂协调工作空间中的分布范围;建立双臂紧协调运动坐标系[5],推导协调运动矩阵描述,利用MATLAB进行紧协调仿真;以电机转子和轴承的松协调装配为例,推导协调运动学约束方程及相应的运动控制规律,通过仿真和实验验证本文所建立运动学模型的正确性。
1 建立机器人运动学模型区别于其他工业机器人,YuMi第一个连杆关节轴线与基座在笛卡尔空间中的位置关系不是常规的相互垂直,而是呈空间交错状态,这种结构可以有效地消除机器人连杆1与连杆3的奇异状态,并且扩大双臂协调作业空间。下面根据YuMi的结构尺寸建立运动学模型,推导正向运动学的方程。
YuMi机器人结构简图如图1所示。以右臂为研究对象建立机器人连杆坐标系,其结构尺寸及参数如图2和表1所示,所得连杆坐标系见图3。
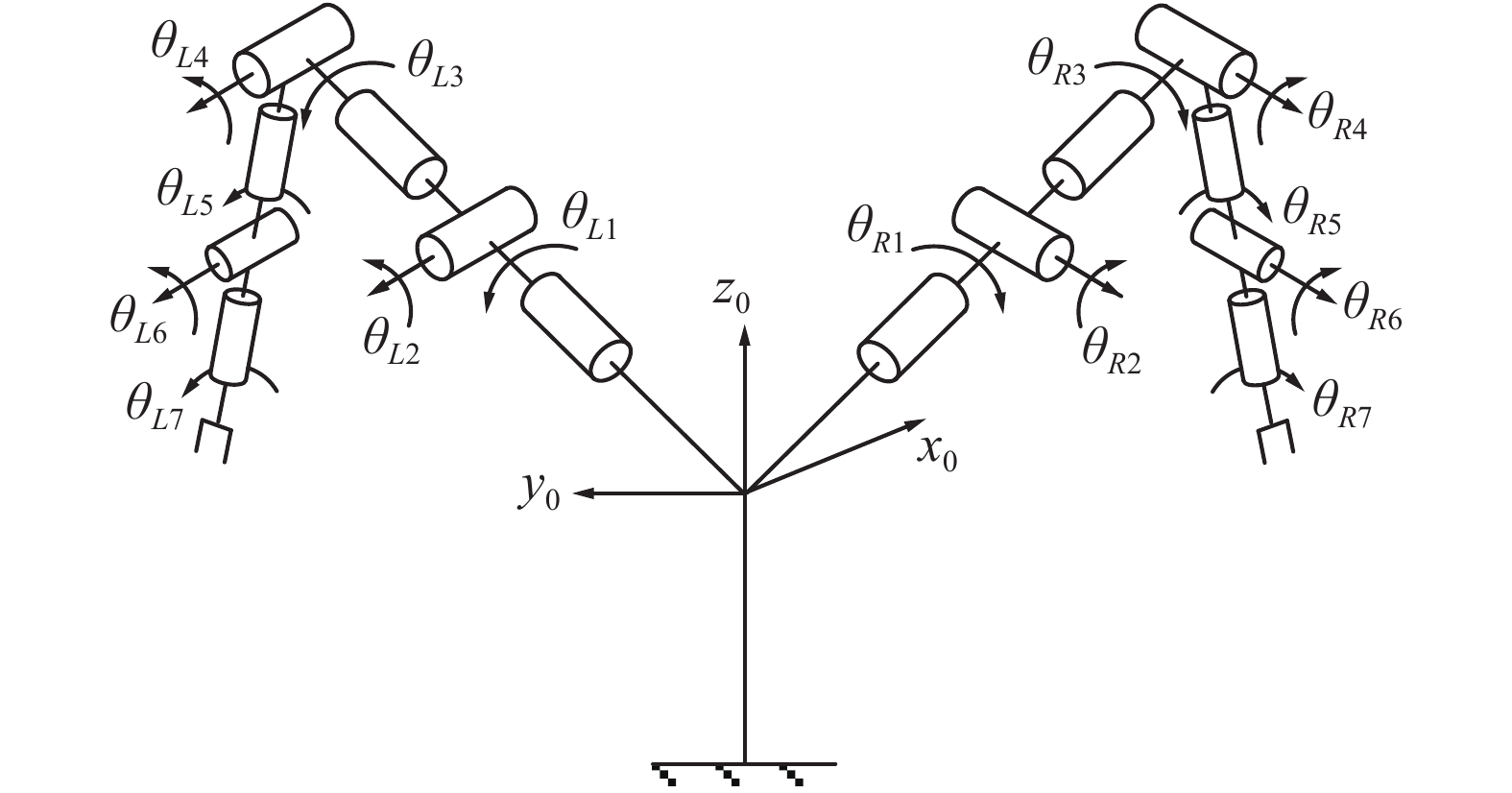
|
Download:
|
| 图 1 YuMi机器人结构简图 Fig. 1 Structure sketch of the YuMi robot | |

|
Download:
|
| 图 2 YuMi机器人结构尺寸图 Fig. 2 Structure size chart of the YuMi robot | |
| 表 1 YuMi机器人连杆参数 Tab.1 Link parameters of the YuMi robot |

|
Download:
|
| 图 3 YuMi机器人连杆坐标系 Fig. 3 Link coordinate system of the YuMi robot | |
连杆变换通式为
| $ {}_{\;\;\;\;i}^{i-1}{{T}}=\left[\begin{array}{cccc}{c\theta }_{i}& {-s\theta }_{i}& 0& {a}_{i-1}\\ {s\theta }_{i}c{\alpha }_{i-1}& {c\theta }_{i}c{\alpha }_{i-1}& -s{\alpha }_{i-1}& {-d}_{i}s{\alpha }_{i-1}\\ {s\theta }_{i}s{\alpha }_{i-1}& {c\theta }_{i}s{\alpha }_{i-1}& c{\alpha }_{i-1}& {d}_{i}c{\alpha }_{i-1}\\ 0& 0& 0& 1\end{array}\right] $ |
正向运动学方程可以表示为
| $ {}_{n}^{0}{{T}}={}_{1}^{0}{{T}}\left({q}_{1}\right){}_{2}^{1}{{T}}\left({q}_{2}\right)\cdots {}_{\;\;\;\;\;n}^{n-1}{{T}}\left({q}_{n}\right)=\left[\begin{array}{cccc}{n}_{x}& {o}_{x}& {a}_{x}& {p}_{x}\\ {n}_{y}& {o}_{y}& {a}_{y}& {p}_{y}\\ {n}_{z}& {o}_{z}& {a}_{z}& {p}_{z}\\ 0& 0& 0& 1\end{array}\right] $ |
文献[6]研究表明YuMi相较于LBR iiwa(KUKA公司7自由度机器人)由于构型偏置而引起了工作空间在某一方向上增加而在另一方向上减小的情况,并评价YuMi的构型使得性能指标降低,但从协调作业角度考虑,这种构型通过削弱双臂协调作业以外的工作空间提升了双臂在其交互工作空间中的协调作业能力。
在协调运动实际应用中,如何在双臂交互的工作空间中选取灵活性较高的区域进行任务规划成为一个难题,现有的运动灵活性指标以Salisbury和Craig[7]定义的条件数以及Yoshikawa[8]提出的可操作度、可操作度椭球研究最为成熟,以此为基础还衍生出了基于任务的可操作度、基于任务的方向可操作度、基于条件数约束的方向可操作度等性能指标[9-11],此类指标强调依赖于某一特定任务对机器人进行灵活性分析,但双臂协作的任务具有多样性,使得上述指标在双臂协作应用上通用化程度较低且运算复杂,因此本文针对双臂协调作业提出一种通用化双臂可操作度指标,期望实现通过对双臂可操作度分析获得机器人系统灵活性较高的工作空间,并以此为基础进行运动规划,这种方法适用于不依赖某一特定任务要求的工艺情况,将机器人灵活性与运动规划分开考虑。
首先根据双臂工作空间云点图计算出各采样点的可操作度,以双臂各取N个采样点的工作空间为例,解得可操作度
| $ e=\frac{\max\left({M}_{L\left(R\right)}\right)-\min\left({M}_{L\left(R\right)}\right)}{n} $ |
对各区间中的采样点依次赋加权值i,i为该区间可操作度的概括描述,随可操作度的数值增大而增大,其数量与区间个数保持一致,然后计算一个机械臂在另一个机械臂工作空间中的可操作度,取两次计算结果权值的均值作为描述双臂协调运动的性能指标。
取采样点N=30000,解得双臂可操作度范围
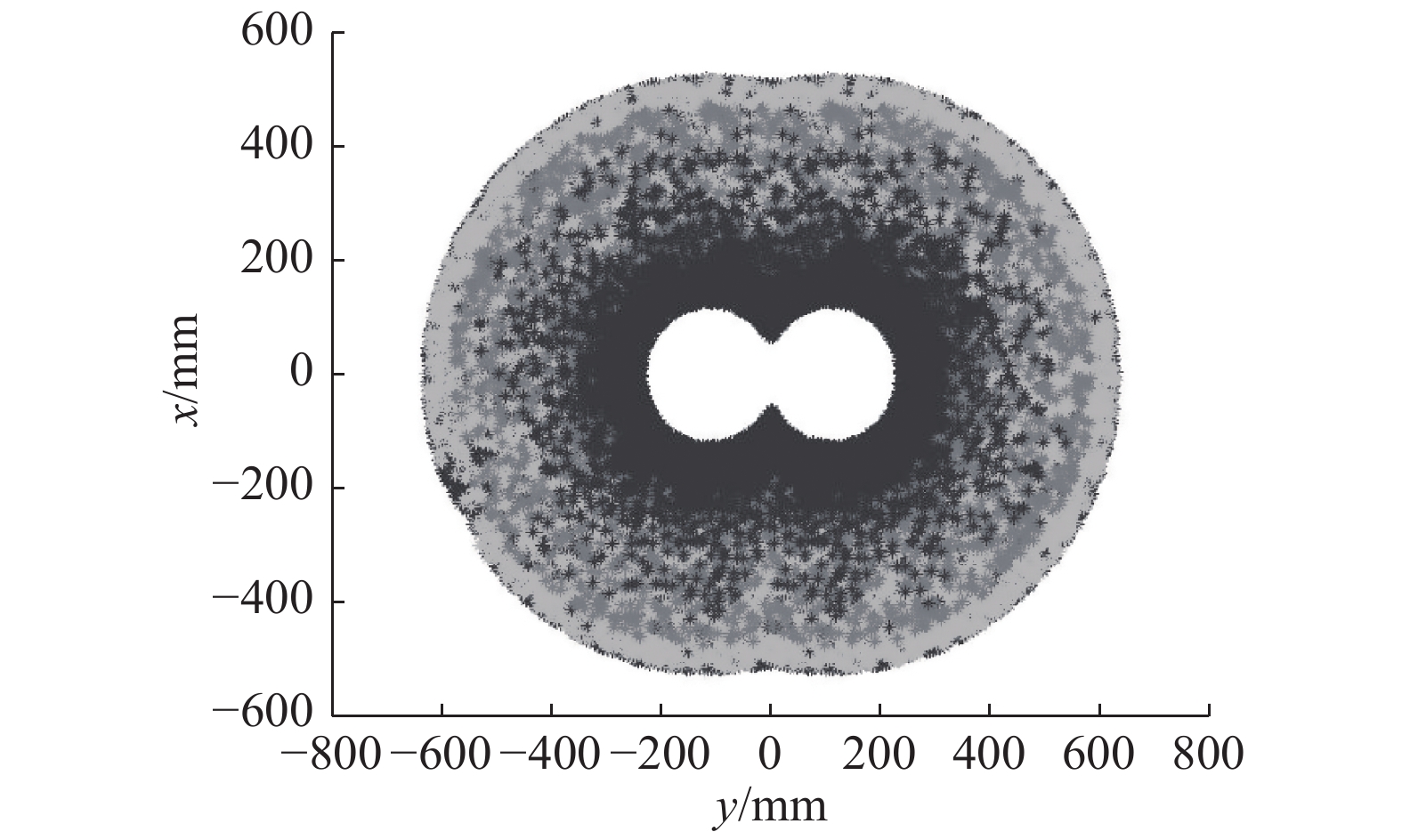
|
Download:
|
| 图 4 双臂可操作度x-y截面分布 Fig. 4 Dual-arm manipulability x-y cross section distribution | |
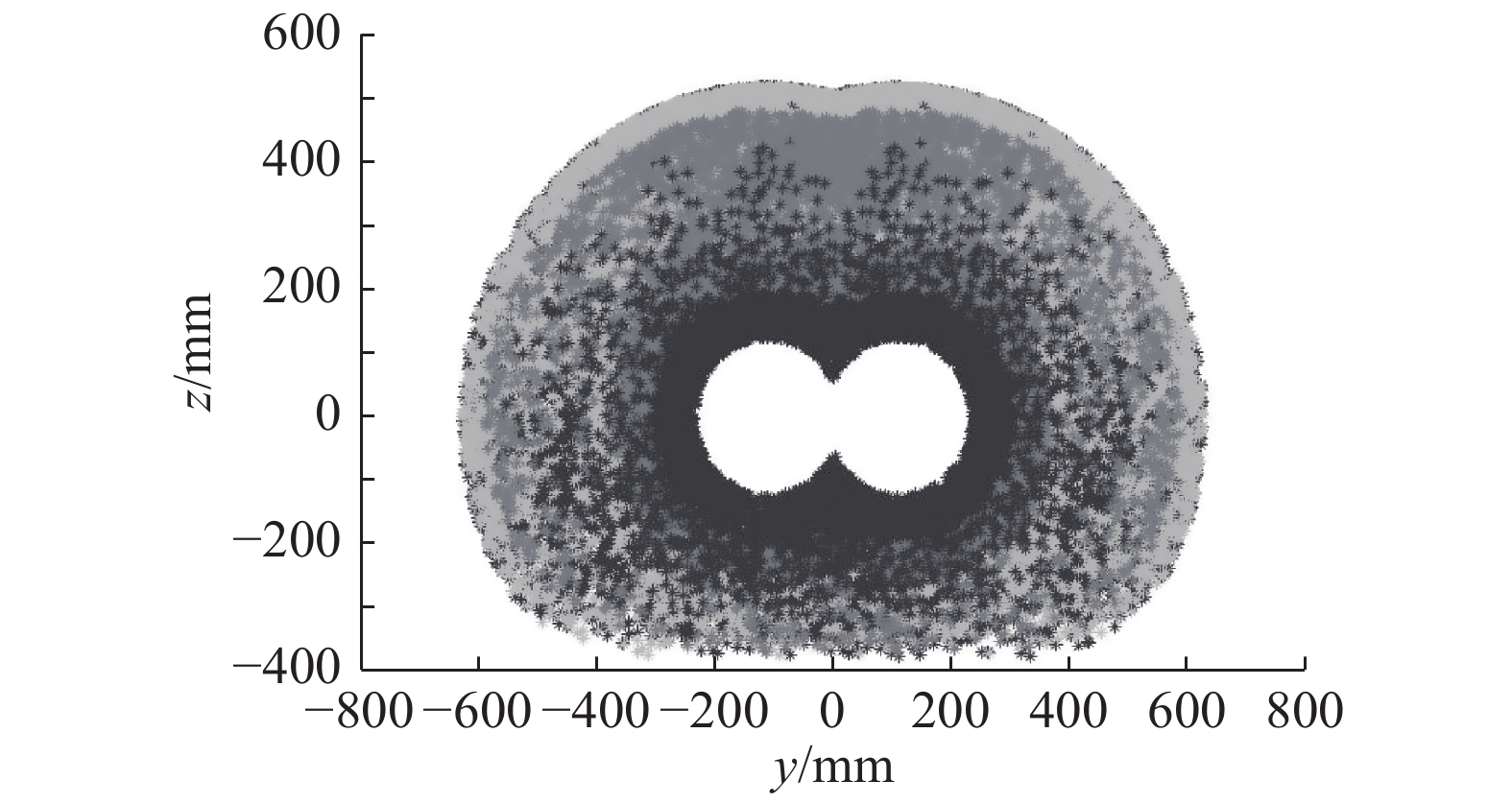
|
Download:
|
| 图 5 双臂可操作度y-z截面分布 Fig. 5 Dual-arm manipulability y-z cross section distribution | |
图4和5中灰度值越小代表可操作度越低,即双臂协调运动灵活性越低[12],通过可操作度在工作空间中的分布情况可知,工作范围在250~500区域的双臂协调作业可操作度较高,因此在进行运动规划时,应当尽量保证工作区域在250~500的范围内,而靠近工作空间边界的部分无法实现双臂协调,机器人运动灵活性最差。显然上述双臂可操作度指标仅反映双臂在工作空间中的运动能力,而不考虑具体方向或速度的约束,但是由于其计算的简便性以及对双臂协调运动灵活性的有效反映,可以作为诸如轴孔装配、示教选点以及确定复杂工艺作业区域等任务的运动灵活性指标。
3 双臂协调运动规划双臂机器人的协调运动问题分为松协调和紧协调。松协调是指双臂在工作空间中执行彼此无关的作业任务,要求各机械臂末端执行器与工件在某些点位上有约束关系,如位置、时间、速度、姿态等,双臂与工件形成的运动链为开链;而紧协调是指双臂在工作空间中执行同一作业任务,要求各机械臂末端执行器与工件之间相对位姿保持不变,双臂之间形成完整闭环运动链[13]。
3.1 电机转子与轴承松协调装配双臂机器人松协调运动的核心在于根据具体工艺要求推导运动学约束关系以及对应的主从协调运动控制规律。首先求得双臂协调的相对位姿关系,在已知主臂运动轨迹的情况下,设定从臂的末端执行器配合时的位置和速度,并进一步求得双臂机器人之间的加速度关系,最后设定相应的运动参数,即可实现基于工艺要求的双臂机器人松协调作业。本文以电机转子与轴承的松协调装配为例,进行双臂机器人的松协调运动研究。
3.1.1 位置、姿态和关节速度约束关系双臂末端执行器的线速度
| $ \left[\begin{array}{c}{{v}}\\ {{w}}\end{array}\right]={{J}}\left({{q}}\right)\dot{{{q}}} $ | (1) |
令:
| $ {{J}}\left({{q}}\right)={\left[\begin{array}{cc}{{{J}}}_{v}\left({{q}}\right)& {{{J}}}_{w}\left({{q}}\right)\end{array}\right]}^{\rm{T}} $ | (2) |
则:
| $ {{{J}}}_{v}\left({{q}}\right)\dot{{{q}}}={{v}} ,\; {{{J}}}_{w}\left({{q}}\right)\dot{{{q}}}={{w}} $ | (3) |
如图6所示,以左臂和右臂各持轴承与转子进行装配。假定运动过程中,末端手爪与各工件之间没有相对运动,
| $ {{p}}\left({{{q}}}^{l}\right)+{{R}}_{0}^{n}\left({{{q}}}^{l}\right){{r}}-{{p}}\left({{{q}}}^{r}\right)=0 $ | (4) |
式中:
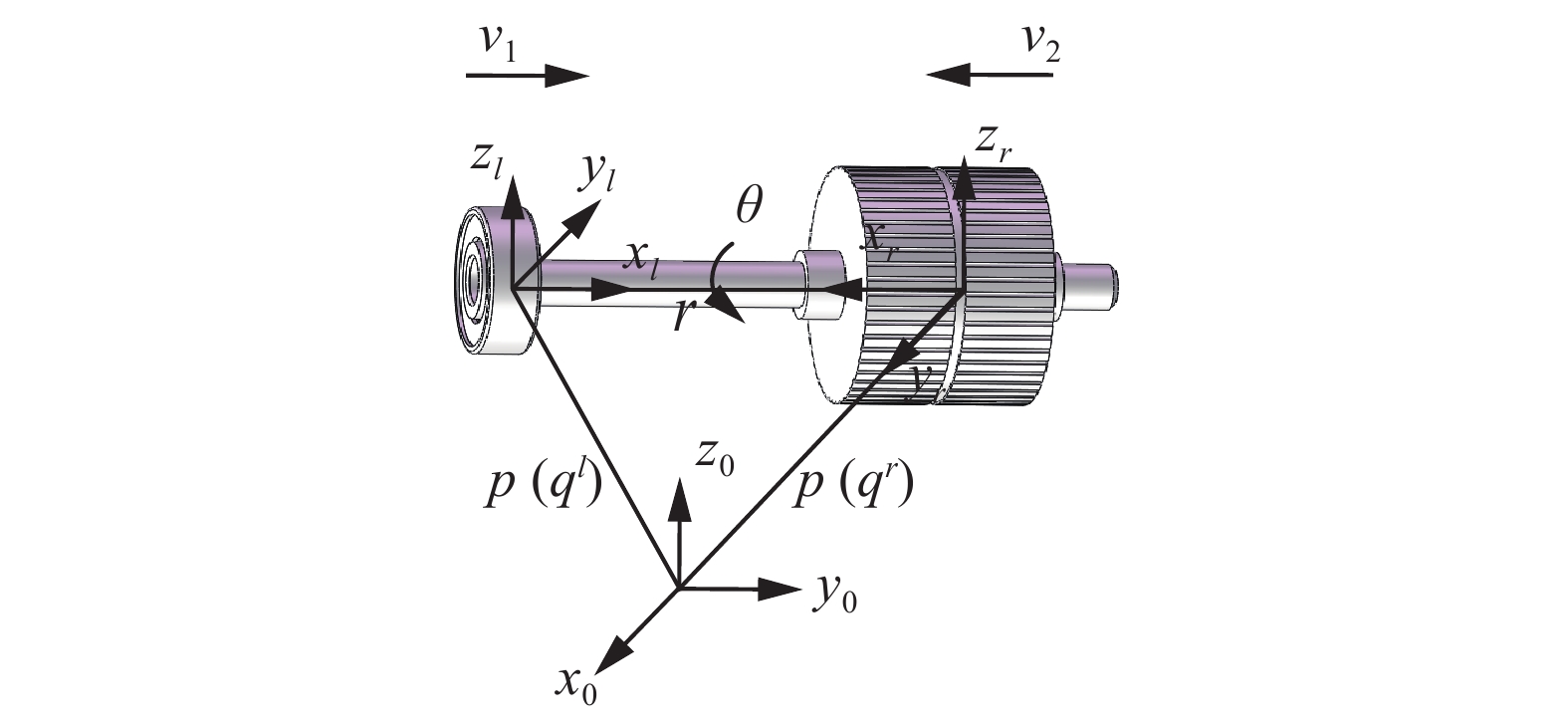
|
Download:
|
| 图 6 双臂转子与轴承装配示意 Fig. 6 Sketch map for rotor and bearing of dual-arm | |
双臂之间的姿态约束为
| $ {{{R}}}_{0}^{n}\left({{{q}}}^{r}\right)={{{R}}}_{0}^{n}\left({{{q}}}^{l}\right){{R}}\left({x}_{l},\theta \right) $ | (5) |
式中:
| $ {{R}}\left({x}_{l},\theta \right)=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -{\rm{cos}}\;\theta & -{\rm{sin}}\;\theta \\ 0& -{\rm{sin}}\;\theta & {\rm{cos}}\;\theta \end{array}\right] $ | (6) |
| $ {}_{n}^{0}{{T}}\left({{{q}}}^{j}\right)=\left[\begin{array}{cc}{{{R}}}_{0}^{n}\left({{{q}}}^{j}\right)& {{p}}\left({{{q}}}^{j}\right)\\ 0& 1\end{array}\right] $ | (7) |
式中:j=l,r,分别表示左臂与右臂。
对式(4)求导,得到末端执行器的线速度约束为
| $ \left[{{{J}}}_{v}\left({{{q}}}^{l}\right)+{{L}}\left({{{q}}}^{l}\right)\right]\dot{{{{q}}}^{l}}+{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right)\dot{{{r}}}-{{{J}}}_{v}\left({{{q}}}^{r}\right)\dot{{{{q}}}^{r}}=0 $ | (8) |
其中,
| $ {{L}}\left({{{q}}}^{l}\right)=\partial \left[{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right){{r}}\right]/\partial {{{q}}}^{l} $ | (9) |
由式(5),得到末端执行器角速度约束为
| $ {{{w}}}_{1}={{{w}}}_{2}+{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right){\left[\begin{array}{ccc}1& 0& 0\end{array}\right]}^{\rm{T}}\dot{\theta } $ | (10) |
其中,
| $ {{{J}}}_{w}\left({{{q}}}^{l}\right)\dot{{{{q}}}^{l}}={{{J}}}_{w}\left({{{q}}}^{r}\right)\dot{{{{q}}}^{r}}+\dot{\theta }{{n}}\left({{{q}}}^{l}\right) $ | (11) |
其中
结合式(8)和式(11),得:
| $ \dot{{{{q}}}^{r}}={{{J}}}^{-1}\left({{{q}}}^{r}\right)\left\{{{{J}}}_{l}\left({{{q}}}^{l}\right)\dot{{{{q}}}^{l}}+{\left[{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right)\dot{{{r}}}-\dot{\theta }{{n}}\left({{{q}}}^{l}\right)\right]}^{\rm{T}}\right\} $ | (12) |
式中
由于从臂有冗余度,则式(12)变为
| $ \dot{{{{q}}}^{r}}={{{J}}}^{+}\left({{{q}}}^{r}\right)\left\{{{{J}}}_{l}\left({{{q}}}^{l}\right)\dot{{{{q}}}^{l}}+{\left[{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right)\dot{{{r}}}-\dot{\theta }{{n}}\left({{{q}}}^{l}\right)\right]}^{\rm{T}}\right\} $ | (13) |
其中,
假定
| $ \begin{split} \ddot{{{{q}}}^{r}}=&{{{J}}}^{+}\left({{{q}}}^{r}\right)\left\{{{{J}}}_{l}\left({{{q}}}^{l}\right)\ddot{{{{q}}}^{l}}+{\left[{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right)\ddot{{{r}}}-\ddot{\theta }{{n}}\left({{{q}}}^{l}\right)\right]}^{\rm{T}}\right\}+\\ &\dot{{G}}\left({{{q}}}^{l},{{{q}}}^{r}\right)\dot{{{{q}}}^{l}}+\dot{{H}}\left({{{q}}}^{l},{{{q}}}^{r}\right){\left(\dot{{{r}}}-\dot{\theta }\right)}^{\rm{T}} \end{split}$ | (14) |
式中
| $ {{G}}\left({{{q}}}^{l},{{{q}}}^{r}\right)={{{J}}}^{+}\left({{{q}}}^{r}\right){{{J}}}_{l}\left({{{q}}}^{l}\right) $ |
| $ {{H}}\left({{{q}}}^{l},{{{q}}}^{r}\right)={{{J}}}^{+}\left({{{q}}}^{r}\right)\left[\begin{array}{cc}{{{R}}}_{0}^{n}\left({{{q}}}^{l}\right)& 0\\ 0& {{n}}\left({{{q}}}^{l}\right)\end{array}\right] $ |
进一步可得:
| $ \begin{split} \ddot{{{{q}}}^{r}}=&\left[\begin{array}{cc}{{G}}\left({{{q}}}^{l},{{{q}}}^{r}\right) {{H}}\left({{{q}}}^{l},{{{q}}}^{r}\right)\end{array}\right]{\left[\begin{array}{ccc}\ddot{{{{q}}}^{l}} \ddot{{{r}}} \ddot{\theta }\end{array}\right]}^{\rm{T}}+\\ &\left[\begin{array}{cc}\dot{{{G}}}\left({{{q}}}^{l},{{{q}}}^{r}\right) \dot{{{H}}}\left({{{q}}}^{l},{{{q}}}^{r}\right)\end{array}\right]{\left[\begin{array}{ccc}\dot{{{{q}}}^{l}} \dot{{{r}}} \dot{\theta }\end{array}\right]}^{\rm{T}} \end{split}$ | (15) |
在已知
双臂协调运动在满足运动学约束方程式(13)时,即可实现松协调装配,但由于YuMi双臂冗余的特性,即便给定主臂运动轨迹,其关节速度仍有无穷多解,因此需要引入某些性能指标(最小范数解或路径最短等)来获取主臂的唯一关节运动,然后通过式(13)确定从臂的协调运动。结合双臂灵活性分析,选取作业点灵活性较高的区域进行协调装配,不仅可以完成装配要求,而且还能根据不同需求改善机器人的操作性能。
3.2 紧协调运动规划在进行紧协调运动的两个机械臂之间存在强耦合关系,除了需要考虑运动学约束关系之外,还有动力学控制问题以及协调运动误差模型分析[14],本文仅研究紧协调运动的运动学约束关系。紧协调运动过程中要求各臂与工件之间相对位姿保持不变,其中从臂末端执行器的运动轨迹完全取决于工件的期望运动轨迹,因此紧协调运动规划的实现首先要分析双臂协调运动闭环运动链并推导运动学约束关系。
3.2.1 建立双臂协调运动坐标系YuMi机器人左右臂与基座、末端执行器及工件之间的相对位姿关系如图7所示。

|
Download:
|
| 图 7 双臂协调运动坐标系 Fig. 7 Coordinated motion coordinate system of the dual arm | |
在6自由度机器人主从协调运动规划[8]的基础上推导双臂主从式协调运动的矩阵描述如下:
| $ {}_{{{R}}0}^{{{W}}}{{T}}{}_{{{R}}7}^{{{R}}0}{{T}}{}_{{{R}}{{E}}}^{{{R}}7}{{T}}={}_{{{L}}0}^{{{W}}}{{T}}{}_{{{L}}7}^{{{L}}0}{{T}}{}_{{{L}}{{E}}}^{{{L}}7}{{T}}{}_{{{G}}}^{{{L}}{{E}}}{{T}}{}_{{{Y}}}^{{{G}}}{{T}} $ | (16) |
式中:
在基坐标系中给定以工件上的某点Y为起点的一系列轨迹点的位姿,用
| $ {}_{{{L}}0}^{{{W}}}{{T}}{}_{{{L}}7}^{{{L}}0}{{T}}{}_{{{L}}{{E}}}^{{{L}}7}{{T}}{}_{{{G}}}^{{{L}}{{E}}}{{T}}{}_{{{Y}}}^{{{G}}}{{T}}={}_{{{Y}}}^{{{W}}}{{T}} $ |
末端连杆相对于基坐标系的变化关系为
| $ {}_{{{L}}7}^{{{L}}0}{{T}}={{}_{{{L}}0}^{{{W}}}{{T}}}^{-1}{}_{{{Y}}}^{{{W}}}{{T}}{{}_{{{Y}}}^{{{G}}}{{T}}}^{-1}{{}_{{{G}}}^{{{L}}{{E}}}{{T}}}^{-1}{{}_{{{L}}{{E}}}^{{{L}}7}{{T}}}^{-1} $ |
在工件坐标系中对任务进行路径规划,通过右臂末端执行器到路径点的约束矩阵
| $ {}_{{{G}}}^{{{R}}0}{{T}}{}_{{{Y}}}^{{{G}}}{{T}}{}_{{{R}}{{E}}}^{{{Y}}}{{T}}={}_{{{R}}7}^{{{R}}0}{{T}}{}_{{{R}}{{E}}}^{{{R}}7}{{T}} $ | (17) |
将
| $ {}_{{{R}}7}^{{{R}}0}{{T}}={}_{{{L}}0}^{{{R}}0}{{T}}{}_{{{G}}}^{{{L}}0}{{T}}{}_{{{Y}}}^{{{G}}}{{T}}{}_{{{R}}{{E}}}^{{{Y}}}{{T}}{{}_{{{R}}{{E}}}^{{{R}}7}{{T}}}^{-1} $ |
最后进行逆运动学解算即可得到右臂运动过程中7个对应关节角度的变化。
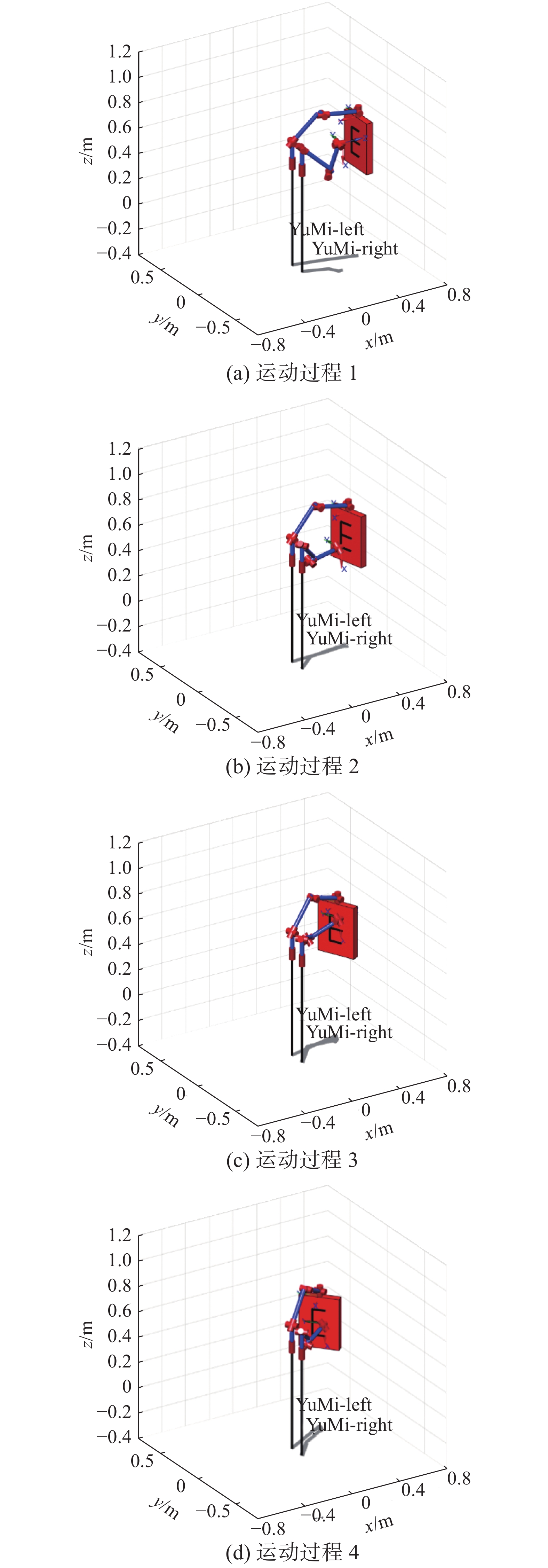
4 仿真与实验 4.1 双臂紧协调字母绘制仿真基于前文双臂运动性能分析以及紧协调运动学约束关系推导,设计双臂协调完成字母“E”绘制的任务,要求双臂末端执行器与工件之间始终保持相对位姿约束。以MATLAB Robotics Toolbox工具箱[15]为仿真平台,逆运动学解算采用工具箱自带的迭代数值解法,通过前文对双臂可操作性的分析,将工件放置在X=450 mm的平面内进行仿真,任务要求左臂夹持工件,运动轨迹为绕基坐标系Z轴的一条变姿态空间曲线,右臂在工件表面进行字母绘制。双臂协调运动过程如图8所示,左右臂末端连杆Z轴时刻保持与工件表面的相互垂直关系,可以看出机器人在双臂可操作度较高的区间中协调完成字母绘制能够取得良好的效果,基于同一种逆解算法,还可以通过设置不同关节坐标初始值的隐含控制实现不同位形的双臂协调仿真。
|
Download:
|
| 图 8 双臂紧协调运动过程 Fig. 8 Dual-arm tight coordination motion process | |
双臂松协调装配电机转子与轴承实验平台如图9所示。该实验平台主要是由1零件定位机构、2YuMi机器人、3输送线、4零件放置托盘、5步进电机转子、6深沟球轴承组成,同样设定工件放置在X=450 mm的平面内进行装配,左臂为主臂抓取电机转子,右臂为从臂抓取轴承,双臂末端执行器在装配过程中姿态保持不变,装配过程如图10所示。

|
Download:
|
| 图 9 双臂协调装配实验平台 Fig. 9 Experimental platform for coordinated assembly of dual-arm | |

|
Download:
|
| 图 10 双臂机器人装配电机转子与轴承实验 Fig. 10 Motor rotor and bearing mating experiment of dual-arm robot | |
实验结果表明,YuMi机器人在双臂灵活性较高的工作空间同时满足松协调运动学约束关系的条件下,能够顺利地进行电机转子与轴承的装配。
5 结束语本文采用D-H法,根据YuMi的结构尺寸参数建立了机器人的运动学模型,提出了一种计算简便但能有效反映双臂运动灵活性分布空间的运动性能指标,分析得出了能够改善双臂机器人协调运动操作性能的工作空间,采用主从式协调运动规划方法,分别推导出了双臂机器人松协调装配电机转子与轴承以及紧协调的运动学约束关系,通过实验和仿真验证了运动灵活性指标以及协调运动策略的有效性。本研究为此类双臂冗余度机器人协调运动规划以及工业现场实际应用提供一定的参考和借鉴。
本文仅考虑在双臂灵活性较高的工作空间中进行协调作业的运动学约束问题,没有考虑动力学协调以及运动灵活性指标对不同任务的具体影响,下一步的研究主要集中在双臂冗余度机器人协调运动接触力/力矩、力/位姿的动态问题上。
| [1] |
申浩宇, 吴洪涛, 陈柏, 等. 冗余度双臂机器人协调避障算法[J]. 农业机械学报, 2015, 46(9): 356-361. SHEN Haoyu, WU Hongtao, CHEN Bai, et al. Obstacle avoidance algorithm for coordinated motion of redundant dual-arm robot[J]. Transactions of the Chinese society for agricultural machinery, 2015, 46(9): 356-361. DOI:10.6041/j.issn.1000-1298.2015.09.052 (  0) 0)
|
| [2] |
TAVASOLI A, EGHTESAD M, JAFARIAN H. Two-time scale control and observer design for trajectory tracking of two cooperating robot manipulators moving a flexible beam[J]. Robotics and autonomous systems, 2009, 57(2): 212-221. DOI:10.1016/j.robot.2008.04.003 ( 0) 0)
|
| [3] |
周军, 丁希仑, 陆震. 冗余度双臂机器人轴孔装配的三维动态仿真与实验[J]. 机器人, 2006, 28(4): 422-427. ZHOU Jun, DING Xilun, LU Zhen. 3-D dynamic simulation and experiment for shaft and hole mating of redundant dual-arm robot[J]. Robot, 2006, 28(4): 422-427. DOI:10.3321/j.issn:1002-0446.2006.04.012 (  0) 0)
|
| [4] |
谢碧云, 赵京, 刘宇. 基于快速扩展随机树的7R机械臂避障达点运动规划[J]. 机械工程学报, 2012, 48(3): 63-69. XIE Biyun, ZHAO Jing, LIU Yu. Motion planning of reaching point movements for 7R robotic manipulators in obstacle environment based on rapidly-exploring random tree algorithm[J]. Journal of mechanical engineering, 2012, 48(3): 63-69. DOI:10.3901/JME.2012.03.063 (  0) 0)
|
| [5] |
赵娜, 岳建锋, 李亮玉, 等. 双机器人主从协调焊接的路径规划算法[J]. 焊接学报, 2015, 36(3): 67-70. ZHAO Na, YUE Jianfeng, LI Liangyu, et al. Path planning algorithm for leader-follower of two-robot coordinate welding[J]. Transactions of the China welding institution, 2015, 36(3): 67-70. (  0) 0)
|
| [6] |
田勇, 王洪光, 潘新安, 等. 协作机器人的构型分析研究[J]. 智能系统学报, 2019, 14(2): 217-223. TIAN Yong, WANG Hongguang, PAN Xin’an, et al. Research on configuration analysis of collaborative robots[J]. CAAI transactions on intelligent systems, 2019, 14(2): 217-223. (  0) 0)
|
| [7] |
SALISBURY J K, CRAIG J J. Articulated hands: force control and kinematic issues[J]. The international journal of robotics research, 1982, 1(1): 4-17. DOI:10.1177/027836498200100102 ( 0) 0)
|
| [8] |
YOSHIKAWA T. Manipulability of robotic mechanisms[J]. The international journal of robotics research, 1985, 4(2): 3-9. DOI:10.1177/027836498500400201 ( 0) 0)
|
| [9] |
LEE S. Dual redundant arm configuration optimization with task-oriented dual arm manipulability[J]. IEEE transactions on robotics and automation, 1989, 5(1): 78-97. DOI:10.1109/70.88020 ( 0) 0)
|
| [10] |
姚建初, 丁希仑, 战强, 等. 冗余度机器人基于任务的方向可操作度研究[J]. 机器人, 2000, 22(6): 501-505. YAO Jianchu, DING Xilun, ZHAN Qiang, et al. On task-based directional manipulability measure of redundant robot[J]. Robot, 2000, 22(6): 501-505. DOI:10.3321/j.issn:1002-0446.2000.06.012 (  0) 0)
|
| [11] |
谢碧云, 赵京. 基于条件数约束的方向可操作度[J]. 机械工程学报, 2010, 46(23): 8-15. XIE Biyun, ZHAO Jing. Directional manipulability constrained by the condition number[J]. Journal of mechanical engineering, 2010, 46(23): 8-15. DOI:10.3901/JME.2010.23.008 (  0) 0)
|
| [12] |
胡明伟, 王洪光, 潘新安, 等. 一种协作型机器人运动性能分析与仿真[J]. 智能系统学报, 2017, 12(1): 75-81. HU Mingwei, WANG Hongguang, PAN Xin’an, et al. Analysis and simulation on kinematics performance of a collaborative robot[J]. CAAI transactions on intelligent systems, 2017, 12(1): 75-81. (  0) 0)
|
| [13] |
杜晔. 双机械臂协同运动规划方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018. DU Ye. Research on coordinated motion planning of dual manipulator[D]. Harbin: Harbin Institute of Technology, 2018. (  0) 0)
|
| [14] |
丁希仑. 拟人双臂机器人技术[M]. 北京: 科学出版社, 2011.
( 0) 0)
|
| [15] |
CORKE P. Robotics, vision and control: fundamental algorithms in MATLAB[M]. Berlin: Springer, 2011: 135−160.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


