随着基于位置的社交网络发展，一些基于位置服务的社交软件被广泛使用，如Foursquare、Gowalla、Yelp等，人们可以轻松地通过签到的形式分享他们的位置和记录生活。同时，用户大量的签到信息也为探索人们的行为规律提供了机遇。下一个兴趣点推荐已经成为基于位置的社交网络的重要任务。

然而，与传统的推荐系统(如音乐、视频和图书推荐等)不同，时空属性对于兴趣点推荐起着很强的约束性；并且，在兴趣点的签到信息中，用户并没有明确给出对兴趣点的喜爱或偏好。用户的隐式反馈信息以及地点签到信息存在稀疏性问题，因此下一个兴趣点的推荐极具挑战性。为了提高兴趣点的推荐效果，一些研究将序列信息^[1-2]、时空信息^[3-5]、社交关系^[6-8]以及签到兴趣点的上下文信息^[9-12]整合到模型中。本文主要利用签到信息中的序列信息、时间信息和空间信息进行下一个兴趣点推荐。

序列信息在下一个兴趣点推荐中扮演着重要角色。一些研究通过整合用户历史签到序列信息提升模型的效果，FPMC模型^[1]通过结合矩阵分解和马尔科夫链捕获用户连续签到兴趣点之间的序列影响。最近，一些研究采用RNN模型^[13]用于序列信息分析，基于循环神经网络(RNN)的方法能够更有效地捕捉序列数据之间的关系，因此在兴趣点推荐中得到了广泛应用，并成为当前主流的推荐模型。然而，RNN存在梯度爆炸和梯度消失的问题，不能学习到较长序列内远距离的依赖关系。为了解决这个问题，长短时记忆(LSTM)^[14]和门控循环单元(GRU)^[15]2种RNN变体被提出，使得循环神经网络能够学习到长序列内远距离的依赖问题。

空间信息是基于位置服务的基本属性^[16]，对兴趣点的推荐同样起着重要作用。一些研究表明^[17-18]，人们更倾向于访问距离用户当前位置较近的地点。这些模型通过将距离作为权重系数或者根据兴趣点之间的距离进行聚类进而推荐位置较近的兴趣点，限制了模型给用户推荐远距离的兴趣点。通过对实验数据集分析发现，在本文使用的Foursquare和CA数据集中,分别有24%和42%的相邻签到兴趣点之间的距离间隔大于10 km，这说明用户多数情况下偏好访问距离较近的兴趣点，但也有较大比例用户依然偏好访问距离较远的兴趣点。在现有的下一个兴趣点推荐模型中，大多数模型倾向于推荐较近的地点限制了模型的表现，使得模型并不会自适应用户需求和偏好的变化而进行推荐，这也意味着模型推荐的兴趣点列表是固定不变的。为了解决上述问题，模型需要用户提供其将要访问下一个兴趣点的距离间隔。这有两方面的好处：首先根据用户的距离间隔，能够给用户提供更灵活的推荐，如果当前的推荐列表用户不满意，用户可以有更多的灵活性去调整不同的距离间隔而得到不同的推荐列表，使用户能够与模型进行交互而不是只能得到固定推荐列表；其次，根据用户提供的距离间隔，能够分析出用户此时表现的偏好模式(即近距离偏好或者远距离偏好)，进而根据用户的偏好给出个性化的推荐列表。

时间信息在兴趣点推荐中也具有较大作用。用户偏好会随时间发生变化，用户在不同的时间间隔内会表现出不同的偏好。当用户要访问的下一个兴趣点的时间点与当前用户时间点的时间间隔较短时，模型应倾向于推荐用户较近的一些地点。同时，利用相邻时间间隔信息也能提供一些隐含的有价值信息。当用户从当前景点紧接着去附近的下一个景点时，不同的用户在这两个兴趣点通常有相似的访问时间间隔。因此利用用户在相邻兴趣点之间的转移时间间隔有利于进行兴趣点推荐。

由于RNN模型在序列建模中具有很好效果，本文采用RNN模型对序列信息建模，通过对RNN进行改进使其能够满足对用户变化的时空偏好信息进行下一个兴趣点推荐。现有模型通常将用户的整个签到序列作为RNN的输入用于下一个兴趣点推荐。而实际上，使用用户的整个签到记录并不一定适用于实际的应用场景，随着用户签到记录数量快速地增加，计算开销也随之增加。因此，本文仅根据最后一次会话信息用于下一个兴趣点推荐。为了对用户签到序列中用户变化的复杂时空偏好进行建模，本文分别建立时间转移矩阵和空间转移矩阵。时空转移矩阵由用户相邻签到兴趣点之间的时空间隔信息确定；为了进一步考虑用户的时间偏好，用户会话中的每个兴趣点与推荐兴趣点的时间间隔信息也被整合到模型中。本文通过同时考虑用户的两类时间信息(包括相邻兴趣点的时间间隔和会话中访问过的兴趣点与下一个兴趣点的时间间隔)、空间信息、签到序列信息和用户偏好给出个性化的下一个兴趣点推荐。

1 相关工作

传统兴趣点推荐通常采用协同过滤算法。矩阵分解^[19-20]是协同过滤最常用的方法，其目标是将“用户−兴趣点”隐式评分矩阵分解为2个低维矩阵，分别表示用户和兴趣点的潜在因子。然而，矩阵分解方法不适用于用户签到序列信息的建模。

序列信息和时空信息是下一个兴趣点推荐的最基本要素。为了提升下一个兴趣点的推荐效果，一些模型，如基于MC模型的方法^[21]、基于嵌入的方法^[22-23]和基于神经网络RNN的方法，通过整合序列信息和时空信息用于下一个兴趣点推荐。文献[1]提出了FPMC模型，该模型结合矩阵分解和马尔科夫链对用户偏好和序列信息建模。文献[21]是FPMC模型的扩展，通过结合用户的地理位置约束为用户推荐下一个兴趣点。文献[24]提出了POI2vec，该模型应用二叉树结构对附近的兴趣点进行聚类，进而为用户推荐下一个兴趣点。文献[17]提出了PRME-G，该模型利用嵌入的方法，通过度量嵌入的方法整合兴趣点的序列信息和地理位置信息进行下一个兴趣点推荐。文献[22]提出了一种嵌入学习方法(GE)用于兴趣点推荐，该方法利用二部图对POI推荐上下文中的一对上下文进行建模，并通过对4对嵌入模型(POI-POI、POI-Time、POI-Regin和POI-Word)进行统一优化。

然而，以上模型缺乏对用户连续签到的两个兴趣点之间的转移时空信息的考虑，并且时间信息和空间信息之间复杂的交互也被忽略。最近，序列信息和时空信息也被广泛地整合到RNN网络中。文献[25]提出了Distance2Pre模型，利用GRU模型首次整合用户不同地理距离偏好进行下一个兴趣点预测，提出线性和非线性方式整合用户距离偏好分数的2种结构模型。文献[4]通过对RNN改进，提出整合时空信息的RNN模型(ST-RNN)，然而它使用固定窗口的时空转化信息，缺乏对相邻的兴趣点之间的转移信息进行建模。文献[26]提出了改进的LSTM模型，该模型在LSTM模型中加入时间门和距离门，通过对相邻签到地点之间的时间间隔和距离间隔进行建模来提取用户长期和短期兴趣偏好。

以上模型都是将用户的历史签到记录作为RNN的输入，本文使用用户最后一次的会话信息作为RNN的输入。并且，上述模型都忽略了用户历史签到兴趣点与最终推荐的兴趣点的时间间隔信息。与本文工作最为相似是Distance2Pre模型，该模型通过对用户的不同距离偏好进行建模，但其忽略了用户偏好与时间之间的关联，这就意味着随着时间的改变，无论是之后的1个小时还是2天内，Distance2Pre将始终为用户预测相同的推荐列表。本文提出的模型与上述模型的不同之处体现在：1)模型只使用用户最后的会话作为RNN的输，具有更快的推荐速度；2)模型能够根据用户的查询条件以及用户的偏好变化情况进行自适应调整，为相同用户推荐变化的个性化的兴趣点推荐列表。

2 相关定义

令 $U = \{ {u_1},{u_2},\cdots ,{u_{|U|}}\}$ 表示所有用户组成的集合， $P = \{ {p_1},{p_2},\cdots ,{p_{|P|}}\}$ 和 $G = \{ {g_{{p_1}}},{g_{{p_2}}},\cdots ,{g_{|P|}}\}$ 分别表示兴趣点的集合及其对应兴趣点的地理坐标的集合，其中 ${\rm{|}}U{\rm{|}}$ 和 ${\rm{|}}P{\rm{|}}$ 分别表示用户数量和兴趣点数量。本文中用户和兴趣点的标识都用连续的整数编码，编码值从1开始。

定义1　兴趣点(POI)。兴趣点是具有唯一标识(编码)的地点，它包含经纬度信息。

定义2　历史签到序列。某一用户 $u$ 的历史签到序列表示为 $H_{{t_i}}^u = \{ p_{{t_1}}^u,p_{{t_2}}^u, \cdots ,p_{{t_i}}^u\} $ ，其中 $p_{{t_i}}^u$ 表示用户 $u$ 在 ${t_i}$ 时刻访问过兴趣点 $p$ 。

定义3　下一个兴趣点推荐。给定用户的历史签到记录 $H_{{t_i}}^u$ ，用户最后的签到位置信息 $p_{{t_i}}^u$ 以及查询条件 $Q = (\Delta d,{t_{i + 1}})$ ,其中 $\Delta d$ 表示用户访问下一个兴趣点的距离间隔。下一个兴趣点推荐目标是为用户推荐其在 ${t_{i + 1}}$ 时刻最有可能访问的TOP-K个兴趣点。

3 基于时空循环神经网络的兴趣点推荐模型 3.1 模型的输入信息

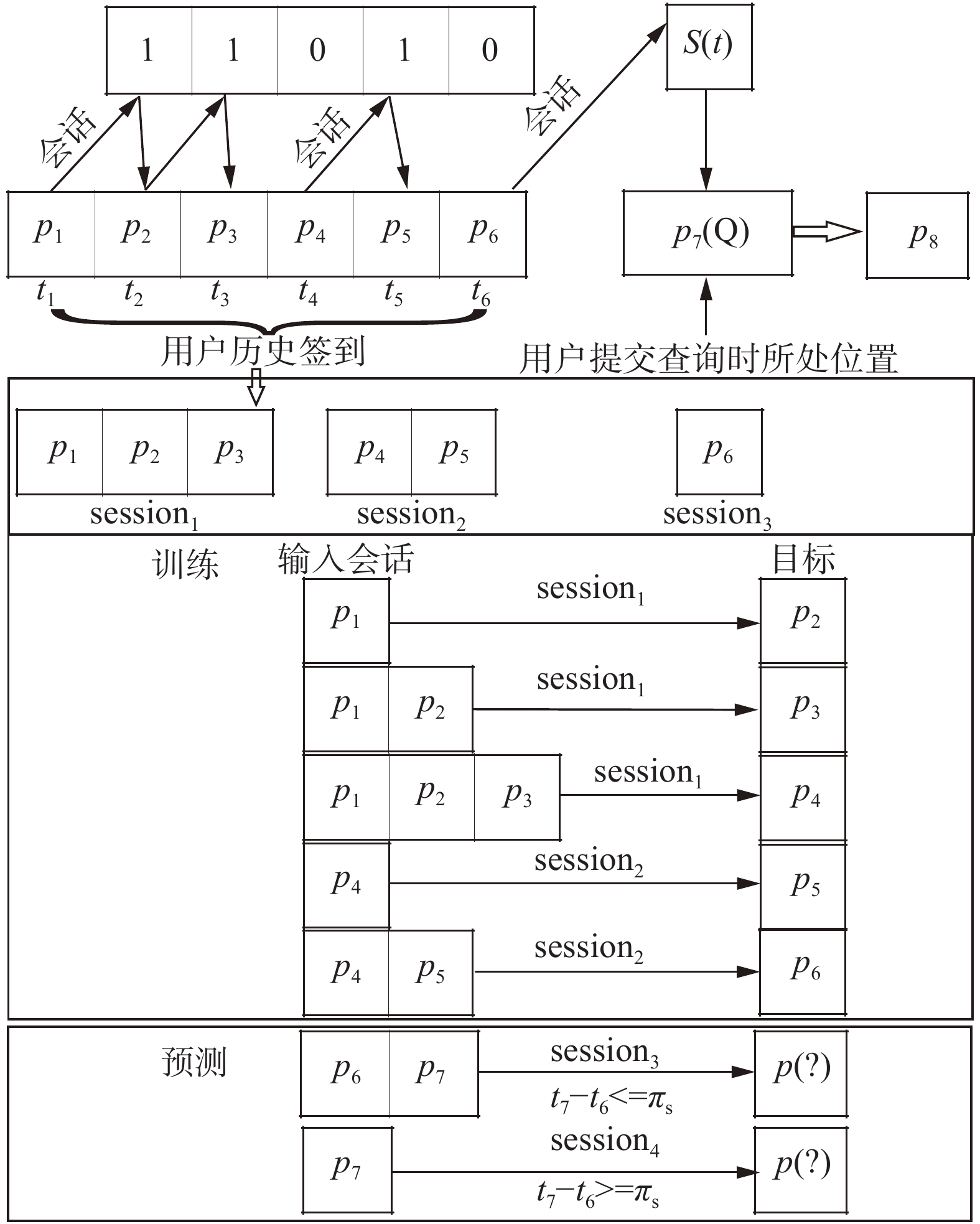
图1中 ${p_7}(Q)$ 表示用户在兴趣点 ${p_7}$ 发出的查询。 $S(t)$ 的取值为0或1，用于判断用户签到兴趣点是否属于同一个会话。 $S(t)$ 的值根据用户2个相邻签到兴趣点之间的时间差得到，如果用户在 ${t_i}$ 时刻签到与 ${t_{i - 1}}$ 时刻签到的差大于 ${{\pi}_s}$ ，即S(t)=0，表示用户在 ${t_i}$ 和 ${t_{i - 1}}$ 时刻的签到兴趣点不属于同一个会话。

用户的偏好是随时间变化的，同时用户所处地点也有可能发生变化，因此利用用户整个历史签到记录进行下一个兴趣点推荐并不一定合适。在下一个兴趣点推荐中，用户最近的签到地点通常对于下一个兴趣点的推荐具有较大影响，因此本文仅使用用户最后一次会话信息作为RNN的输入，用户的签到会话表示为相邻的签到兴趣点之间的最大间隔不超过 ${{\pi}_s}$ 的一段连续签到序列。从图1可以看出用户的历史签到记录被分成了多个会话，session₁和session₂是已完成会话，session₃是用户最后一次会话。图1中用户历史签到序列上面的0和1数值表示相邻的两个兴趣点之间是否属于一个会话。本文将用户的每一次签到记录作为训练目标，每个用户将会得到 $s - 1$ 训练序列， $s$ 为用户历史签到总数。下面举例说明模型的训练和推荐过程。如果一个用户在 ${t_3}$ 时刻之前已访问过 ${p_1}$ 、 ${p_2}$ 两个兴趣点，用户访问 ${p_1}$ 和 ${p_2}$ 之间的时间间隔小于 ${{\pi}_s}$ ，那么 ${p_1}$ 和 ${p_2}$ 属于同一个会话，假如用户在 ${t_3}$ ( ${t_3} - {t_2} \leqslant {{\pi} _s}$ )时刻在 ${p_3}$ 兴趣点提出一个查询 $Q$ ，此用户最后的会话信息{ ${p_1},{p_2},{p_3}$ }将会作为序列输入用于推荐，兴趣点 ${p_4}$ 将会作为目标兴趣点进行训练。假如用户在 ${t_4}$ ( ${t_4} - {t_3} > {{\text{π}} _s}$ )时刻在 ${p_4}$ 地点提出查询 $Q$ ，由于当前用户的会话信息不属于上一会话，模型将在 ${t_4}$ 时刻新建一个只包括当前用户查询位置的会话信息作为输入，用户下一个访问的兴趣点 ${p_5}$ 将会被作为训练目标。在模型的训练中，用户每次访问的下一个兴趣点被当成目标兴趣点，由于它的地理信息和签到时间是已知的，用户访问下一个兴趣点的时空间隔信息也可以通过计算得到。本文使用用户访问下一个兴趣点的时空信息作为用户的查询信息在模型中进行训练。通过大量用户历史签到数据集来学习，用户访问下一个兴趣点的远近距离偏好、长短时间偏好和时空信息的交互作用。

在模型的推荐过程中，模型根据用户的查询条件进行动态推荐，用户最后的一个会话信息被用于推荐。例如，当用户在 ${p_7}$ 地点提出查询时，模型将会根据用户在 ${p_7}$ 的签到时间判断是否上一个会话已结束，当用户的前一个会话结束时(即 $S(t) = 0$ )，用户最后一次签到的 ${p_7}$ 地点将作为一个新的会话用于推荐下一个兴趣点，当 $S(t) = 1$ ，说明 ${p_7}$ 地点的签到属于上一个会话信息，此时 ${p_6}$ 和 ${p_7}$ 将共同作为一个会话信息用于推荐下一个兴趣点。

3.2 序列建模

本文采用RNN模型对用户的签到序列信息进行建模。在RNN中，用户在 ${t_k}$ 时刻签到的隐藏层向量 ${{{h}}_{{t_k}}}$ 表示为

${{h}}_{{t_k}}^{} = f({{Mp}}_{{{{t}}_{{k}}}}^{{u}} + {{Ch}}_{{t_{k - 1}}}^{})$

(1)

式中： ${{p}}_{{{{t}}_{{k}}}}^{{u}}$ 表示对应兴趣点 $p$ 编码的低维向量； $f$ 表示激活函数； ${{M}}$ 、 ${{C}}$ 分别表示参数矩阵。

3.3 时空偏好建模

一些模型在对空间信息建模时，通常认为用户更倾向于访问位置较近的地点，通过利用空间距离作为参数控制用户的空间偏好。然而，这些模型无法对用户的远距离偏好的兴趣点进行推荐。传统的RNN模型对近距离和远距离的用户偏好建模存在困难，因此需要对RNN模型进行改进。本文通过设置2个空间转移矩阵 ${{{W}}_1}$ 、 ${{{W}}_2}$ 对用户的空间偏好进行建模， ${{{W}}_1}$ 用于捕获用户的短距离偏好， ${{{W}}_2}$ 用于捕获用户长距离偏好。为了能够让转移矩阵 ${{{W}}_1}$ 自然过渡到转移矩阵 ${{{W}}_2}$ ，设置了一个最大距离间隔 ${\pi _d}$ 。当兴趣点转换距离在最大距离间隔内时，用户的空间偏好转移矩阵由距离间隔对 ${{{W}}_1}$ 和 ${{{W}}_2}$ 转移矩阵进行加权计算得到。当兴趣点转换距离在最大距离间隔外时，用户表现出远距离的偏好，此时 ${{{W}}_2}$ 将作为空间转移矩阵。在训练时，用户访问下一个兴趣点的转换距离( $\Delta d$ )由用户历史签到兴趣点相邻的下一个签到兴趣点的距离相减得到，即

$\Delta {d_k} = h\left(g_{k + 1}^{u,{p_{k + 1}}} - g_k^{u,{p_k}}\right)$

式中： $\Delta {d_k}$ 表示相邻兴趣点的距离间隔； $g_k^{u,{p_k}}$ 表示用户 $u$ 在 $k$ 时刻访问的兴趣点 $p$ 的经纬度坐标； $h$ 表示 ${\rm{Harversine}}$ 公式，用于计算经纬度坐标之间的距离。根据用户签到兴趣点的转换距离，兴趣点的空间转移矩阵可表示为

${{{D}}_{\Delta {d_k}}} = \left\{ {\begin{split} &{\dfrac{{({{\pi} _d} - \Delta {d_k}){{{W}}_1}}}{{{{\text{π}} _d}}} + \dfrac{{\Delta {d_k}{{{W}}_2}}}{{{{\text{π}} _d}}},}\quad{\Delta {d_k} < {{\pi} _d}} \\ &{{{{W}}_2},\quad }{\Delta {d_k} \geqslant {{\pi} _d}} \end{split}} \right.$

得到用户的空间转移矩阵 ${{{D}}_{\Delta {d_k}}}$ 后，用 ${{{D}}_{\Delta {d_k}}}$ 替代式(1)中的 ${{M}}$ 矩阵，因此考虑用户空间偏好的RNN公式可以表示为

$h_{{t_k}}^{} = f({{{D}}_{\Delta {d_k}}} \cdot {{p}}_{{{{t}}_{{k}}}}^{{u}} + {{Ch}}_{{t_{k - 1}}}^{})$

同理，为了考虑用户的时间偏好，本文也设置两个时间转移矩阵 ${{{W}}_3}$ 、 ${{{W}}_4}$ 和最大时间间隔 ${{\text{π}} _t}$ 来捕获用户的短时间偏好和长时间偏好。两个相邻签到兴趣点之间的时间间隔由用户历史签到兴趣点与相邻的下一个兴趣点的签到时间差得到，表示为

$\Delta {t_k} = t_{k + 1}^{u,{p_{k + 1}}} - t_k^{u,{p_k}}$

式中： $\Delta {t_k}$ 为相邻签到兴趣点之间的时间间隔，min； $t_k^{u,{p_k}}$ 表示用户 $u$ 在 $k$ 时刻访问兴趣点 $p$ 的时间点。因此用户的时间转移矩阵可表示为

${{{T}}_{\Delta {t_k}}} = \left\{ {\begin{split} &{\dfrac{{({{\pi} _t} - \Delta {t_k}){{{W}}_3}}}{{{{\pi} _t}}} + \dfrac{{\Delta {t_k}{{{W}}_4}}}{{{{\pi} _t}}}{\rm{,}}}\quad{\Delta {t_k} < {{\pi} _t}}\\ &{{{{W}}_4}{\rm{,}}}\quad{\Delta {t_k} \geqslant {{\pi} _t}} \end{split}} \right.$

为了同时考虑用户的时间转移偏好和距离转移偏好，本文使用时间转移矩阵和空间转移矩阵乘积的形式作为用户的时空偏好转移矩阵。因此RNN公式可以改写为

${{h}}_{{t_k}}^{} = f({{{T}}_{\Delta {t_k}}} \cdot {{{D}}_{\Delta {d_k}}} \cdot {{p}}_{{{{t}}_{{k}}}}^{{u}} + {{Ch}}_{{t_{k - 1}}}^{})$

为了更充分利用签到序列中的时间信息，本文进一步提取用户签到序列中的每个兴趣点与推荐兴趣点的时间间隔 $\Delta {a_{{t_k}}}$ ：

$ \Delta {a_{{t_k}}} = t_{i + 1}^{u,{p_{i + 1}}} - t_k^{u,{p_k}} $

式中： $k \in {\rm{ }}\{ {\rm{ }}1,2, \cdots ,i{\rm{ }}\} {\rm{ }} $ ； $t_{i + 1}^{u,{p_{i + 1}}}$ 表示用户将要访问的下一个兴趣点的时刻； $t_k^{u,{p_k}}$ 表示用户在 ${t_k}$ 时刻访问兴趣点 ${p_k}$ 的签到时间。这里对 $\Delta {a_{{t_k}}}$ 进行分段表示，时间间隔为20 min，分成等间距的145段，每段用对应的连续整数表示。例如：当 $0 \leqslant \Delta {{{a}}_{{{{t}}_{{k}}}}} < 20$ min时，其分段数值编号为0，当 $\Delta {{{a}}_{{{{t}}_{{k}}}}} \geqslant 2\;880$ min时，其数值编号为144。之后通过嵌入层得到对应的嵌入向量 $\Delta {{{a}}_{{{{t}}_{{k}}}}}$ ，因此整合时间信息 $\Delta {{{a}}_{{{{t}}_{{k}}}}}$ 的循环神经网络可进一步表示为

$ {{h}}_{{t}_{k}}^{}=f({{{T}}}_{\Delta {t}_{k}}\cdot {{{D}}}_{\Delta {d}_{k}}\cdot ({{{p}}}_{{{{t}}}_{{{k}}}}^{{{u}}}+\Delta {{{a}}}_{{{{t}}}_{{{k}}}})+{{C}}{{{h}}}_{{t}_{k-1}}^{})$

最后，将用户签到序列信息和用户偏好作为用户访问下一个兴趣点的最终推荐向量，表示为

${{h}}_{{t_i}}^u = {{{h}}_{{t_i}}} + {{u}}$

式中： ${{{h}}_{{t_i}}}$ 表示RNN网络最终的输出向量； ${{u}}$ 表示用户的嵌入向量； ${{h}}_{{t_i}}^u$ 表示 ${t_i}$ 时刻用户将要访问的下一个兴趣点对应的偏好向量。

3.4 模型推荐

受矩阵分解的启发，用户对下一个兴趣点的偏好可由偏好向量 ${{h}}_{{t_i}}^u$ 与兴趣点 $p$ 对应的向量 ${{p}}$ 的内积来表示。向量的内积越大表示用户越倾向于访问此兴趣点，即

${x_p} = {{h}}_{{t_i}}^u \otimes {{p}}$

本文将兴趣点推荐问题看成分类问题，根据用户访问每个兴趣点的偏好分数 ${x_p}$ ,利用softmax函数计算用户访问每个兴趣点的概率：

${y_{{p_m}}} = \frac{{{\rm{exp}}({x_{{p_m}}})}}{{\displaystyle\sum\limits_{n = 1}^N {\rm{e}} {\rm{xp}}({x_{{p_n}}})}},\quad m \in 1,2, \cdots ,N$

式中： $N$ 表示兴趣点的总数； $m$ 表示兴趣点的唯一标识； ${y_{{p_m}}}$ 表示用户将会访问标识为 $m$ 的兴趣点的概率。

4 模型实验及结果 4.1 实验设置

1）数据集

本文使用2个公开数据集，即Foursquare和CA数据集。2个数据集中，用户的每次签到记录都包括4个属性：用户ID、兴趣点ID、签到时间和GPS位置。Foursquare数据集^[27]，包括用户在Foursquare应用软件上2010年8月—2011年1月在新加坡的352850条签到记录；CA数据集包括生活在美国加利福尼亚州的4163名使用者的483813个签到信息、121142个不同的兴趣点。遵循常用的下一个兴趣点预处理方式^{[21, 26, 28]}，在这2个数据集中，移除了少于5次签到信息的用户以及少于5个用户访问的兴趣点。数据预处理结果如表1所示。本文选择用户历史签到数据集的最后一次签到记录作为测试集，其余作为训练集，以前的大多数工作^{[9, 25, 29]}也都采用这种方法对数据集进行分割。

2）参数设置

实验中，SST-RNN模型采用PyTorch编程实现，设置用户向量、兴趣点向量和时间间隔向量的嵌入维度为20，隐藏层神经元个数为20。向量嵌入过程是通过PyTorch提供的“nn.Embedding”嵌入查找表的方法实现。时间转移矩阵和空间转移矩阵的大小为R^20x20， ${{\pi} _s}$ 为8 h。在Foursquare数据集中，最优的参数值为 ${{\pi} _t}$ =24 h， ${{\pi} _d}$ =14 km，在CA数据集中，最优的参数值为 ${{\pi} _t}$ =16 h， ${{\pi} _d}$ =12 km，参数的确定将在之后的“参数分析”部分进行说明。学习率设置为0.001，激活函数选择ReLU。本文使用交叉熵损失函数和BPTT算法进行误差的计算和误差的反向传播，使用SGD优化器对参数进行优化。

3）评价方法

选用两个常用的度量标准Accuracy@K(ACC@K)和MAP作为实验评价指标。ACC@K是推荐系统中常用衡量推荐效果好坏的指标，对于用户的一次推荐，如果用户访问的下一个兴趣点出现在推荐列表中，则认为预测正确，其值为1，否则为0。ACC@K的值是取所有测试实例的平均值，值越高表示模型的推荐效果越好。MAP是衡量推荐列表中兴趣点排名的标准，如果用户访问下一个兴趣点在推荐列表的位置越靠前，MAP的得分就会越高。

4）对比模型

本文使用基线算法和最新的算法进行对比，对比模型中的所有用户和兴趣点的向量维度均为20。对比模型的参数设置采用原论文默认的参数，实验结果是模型训练迭代100次中的最优结果。

①BPR^[29]：利用矩阵分解算法和BPR损失对“用户−兴趣点”的隐式反馈矩阵进行优化。作为基线模型，BPR认为用户对交互过的兴趣点偏好大于未交互的兴趣点。

②RNN：通过标准的循环神经网络结构对用户历史访问兴趣点的时序信息建模。作为基线模型，RNN只使用最后一次会话信息作为输入。

③GRU^[15]：RNN的最新变体，通过2个门控单元控制信息的流动，能够处理长序列依赖问题，解决RNN存在的梯度消失和梯度爆炸问题。作为基线模型，该模型使用用户的全部历史签到记录作为输入。

④FPMC-LR^[21]：利用个性化马尔科夫链对用户签到序列建模，结合用户的地理位置限制进行下一个兴趣点推荐。

⑤PRME-G^[17]：利用度量嵌入的方法对用户序列信息建模，将空间距离作为权重控制用户的距离偏好。

⑥POI2Vec^[24]：该模型使用二叉树将距离相近的兴趣点聚为一类。为了增强兴趣点的空间影响，一个兴趣点可以分配到多个类中。

⑦Distance2Pre^[25]：利用GRU模型根据用户签到历史序列信息和距离偏好进行推荐。提出了Distance (linear)和Distance (non-linear)两种模型，本文使用效果表现最好的Distance (non-linear)模型，其默认的隐藏层神经元个数为20。

⑧SST-RNN：本文提出的模型，通过改进RNN模型使其能够对用户访问下一个兴趣点的远近距离偏好和长短时间偏好建模，根据用户的会话信息进行个性化的下一个兴趣点推荐。

4.2 实验结果和分析 4.2.1 实验结果

Foursquare和CA数据集在不同模型的实验结果如表2、3所示，其中Improvement表示本文提出的模型相对于对比模型中的最好性能提升的效果，模型提升效果的计算公式为

$I=\frac{R-C}{C}\times100{\text{%}}$

式中：R表示SST-RNN模型的实验结果；C表示最好的对比模型实验结果。

4.2.2 实验结果分析

首先，比较BPR和GRU这2个基线算法，它们只用到单一的信息进行推荐，表现效果较差。BPR利用用户的偏好进行推荐，而GRU模型使用用户历史签到的序列信息。从2个数据集的实验结果可以看出，GRU模型的表现优于使用BPR损失的矩阵分解算法，说明在下一个兴趣点推荐中，序列信息比用户偏好更重要。BPR模型更适合一般的兴趣点推荐，然而GRU更适合于下一个兴趣点推荐。

其次，从两个数据集上的实验结果可以看出整合兴趣点的地理位置信息和序列信息的FPMC-LR、PRME-G、POI2Vec、Distance2Pre和SST-RNN模型优于BPR和GRU算法。反映出序列信息和地理位置信息是下一个兴趣点推荐的重要指标，同时整合序列信息和地理位置信息通常能提高下一个兴趣点推荐的准确率。POI2Vec模型优于PRME-G和FPMC-LR模型，说明用户在访问下一个兴趣点中更倾向于访问较近的兴趣点。PRME-G在两个数据集的表现均优于FPMC-LR模型。

下面比较RNN、GRU、Distance2Pre、SST-RNN，它们都是基于循环神经网络的模型。GRU是最新RNN的变体，通过门控单元控制信息流动，解决了RNN存在的梯度消失和梯度爆炸问题。标准的RNN模型使用用户最后的会话信息用于推荐，而GRU使用用户的整个历史签到信息。通过实验结果可以看出，相比于GRU模型，RNN模型在两个数据集上的表现有极大的提升，表明用户访问下一个兴趣点的行为主要受当前用户所在环境的影响，使用整个用户的签到记录可能导致增加更多的干扰信息以及无法捕获用户变化的偏好。通过Distance2Pre、SST-RNN与其他模型对比，可以看出Distance2Pre和SST-RNN优于其他比较算法。其原因是：其他模型更倾向于给用户推荐近距离的地点，从而限制模型给用户推荐较远的地点，而且这些模型也忽略用户访问下一个兴趣点的不同距离偏好。Distance2Pre使用GRU模型根据用户对空间距离的偏好进行建模，通过在GRU隐藏层上应用一层全连接神经网络对用户的不同距离偏好进行建模，提升了模型的推荐效果，说明用户访问下一个兴趣点受不同距离偏好的影响。可以看出，结合用户时空偏好和序列信息的SST-RNN模型在各个评价标准中均表现出最优的结果，显著优于其他所有比较的模型。这是因为SST-RNN能够对用户访问下一个兴趣点的远近距离偏好和长短时间偏好进行建模，充分利用时间信息、序列信息和用户偏好进行个性化的下一个兴趣点推荐。

4.2.3 参数分析

本文的SST-RNN模型中的参数主要包括神经元个数、会话长度 ( ${{\pi} _s}$ )、控制用户访问下一个兴趣点的远近距离偏好( ${{\pi} _d}$ )和长短时间偏好( ${{\pi} _t}$ )4个参数变量。为了保持模型对比的公平性，本文设置神经元个数与之前提到的基于GRU对比模型的算法保持一致，神经元个数设置为20。 ${{\pi} _s}$ 参数用于控制输入的会话信息，较长的2个相邻兴趣点时间间隔将导致2个兴趣点之间的序列依赖性降低^[21]。本文首先在2个数据集上测试 ${{\pi} _s}$ =6 h、 ${{\pi} _s} $ =8 h、 ${{\pi} _s} $ =10 h模型的效果，发现在2个数据集上 ${\pi _s}$ 的取值对于模型的表现有很微弱的影响，因此本文固定会话长度 ${{\pi}_s}$ =8 h。主要探索用户访问下一个兴趣点的远近距离偏好 ${{\pi} _d}$ 和长短时间偏好( ${{\pi}_t}$ )的影响。由于 ${{\pi}_t}$ 和 ${{\pi} _d}$ 参数取值之间相互影响，找出最优的参数值将需要大量的计算。本文首先随机初始化一些 ${{\pi}_d}$ ={6，8，10，12，14}km和 ${{\pi} _t}$ ={8，16，24，32，40} h的参数组合，当 ${{\pi} _d}$ =10 km， ${{\pi}_t}$ =8 h，时，模型在2个数据集中表现较好。为了进一步探索较优的参数值，本文首先固定 ${{\pi} _t}$ =8 h，探索最优的 ${{\pi} _d}$ 取值，实验结果如表4所示。找到最优的 ${{\pi} _d}$ 参数值后，再固定 ${{\pi} _d}$ 的值，之后找出最优 ${{\pi} _t}$ 参数值，实验结果如表5所示。最终得到的较优的 ${{\pi} _t}$ 和 ${{\pi} _d}$ 参数将作为2个数据集上最终的实验参数设置。实验中，ACC@5和MAP指标被选为评价标准，。

从表4、5的实验结果可以看出：当 ${{\pi} _d}$ =14 km, ${{\text{π}}_t}$ =24 h时，模型在Foursquare数据集上表现最好；当 ${{\pi} _d}$ =12 km, ${{\pi} _t}$ =16 h时，模型在CA数据集上表现最好。

5 结束语

本文研究了下一个兴趣点推荐的问题，提出了一种新的基于会话的时空循环神经网络模型，该模型能够同时考虑序列信息、两类时间信息、空间信息以及用户偏好进行个性化的下一个兴趣点推荐。为了解决用户不同的时空偏好问题，本文对RNN神经网络进行改进，提出利用时空转移矩阵对用户不同的时空偏好进行建模，使RNN模型能够捕获用户签到行为的时空信息。通过在真实的数据集上对模型进行性能测试，结果表明，提出的模型显著优于当前主流相关模型。下一步工作将探索更丰富的数据集，进一步结合用户基本属性、地点基本属性来解决兴趣点推荐中出现的冷启动问题，并且整合其他辅助的信息(如图像、用户评分和文本评论等)作更精确的下一个兴趣点推荐。