2. 辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105
2. School of business administration, Liaoning Technical University, Huludao 125105, China
人工智能是面向人的,具备类人能力的实体或方法。人的最基本能力就是对事物的选择能力。人能通过各种渠道获得知识,而这些知识的主要应用就是人面对问题时的选择。因此人工智能的最基本操作就是模仿人对问题做出选择。人的选择过程是宏观到微观的过程,先选择关心的方面,再选择具体的定性定量特征,这是从内涵到外延的过程。目前人工智能的三大主流学派及大数据和深度学习等都是基于数据的研究。即首先从大数据的处理开始,再进行数据归类分析各类别之间的关系抽象为范围,再根据范围关系抽象为因素,最终用因素定义概念,完成外延到内涵的建立。因此人对样本的选择过程与现有人工智能样本选择过程是相反的。
关于人工智能的处理过程、理念及模型等有一些研究:知识驱动的智能生态网络研究[1];基于功能模型和层次分析法的智能方案构建[2];基于深度确定性的智能车汇流模型[3];多智能体情绪仿真模型[4];小波智能模型时序预测[5];智能电网可靠性模型预测[6];智能化云制造系统[7];智能网联环境下的车辆跟驰模型[8];智能制造成熟度评估模型[9];智能模型与自主智能系统[10];智能网联车环境下的数据转发模型[11];机制主义人工智能理论[12];人工智能的概念、方法、机遇[13];人工智能与科学方法创新[14]。这些研究各有所长,解决的问题也各不相同。但正如莫拉维克悖论[15]所述,高级的人类思维需要数据较少;反而人类的基本行为需要大量数据描述。这其实并不矛盾,高级思维涉及的因素很多;而基本行为则很少。人在分析问题时首先关注因素而不是数据;但人工智能方法需要大量数据。
为解决莫拉维克悖论提出的问题,论文基于因素空间理论[16-18]和作者的相关研究[19-26]对人的基本选择行为在人工智能框架下予以实现。最终建立了人工智能样本选择策略网络模型。
1 莫拉维克悖论20世纪80年代,由H.莫拉维克等人提出了一种现象:像逻辑演绎这样高级理性思维只需要相对很少的计算能力,而实现感知、运动等低等级智能活动却需要耗费巨大的计算资源,即莫拉维克悖论。
这也许成为人工智能发展的一个方向。目前普遍认为人工智能应涉及大数据智能理论;跨媒体感知;人机协同智能、群体智能、个体控制与优化、机器学习、类脑智能和量子智能等。但现有人工智能基础普遍基于大数据分析抽象形成数学模型,进而模拟人受外界刺激后的响应。当然这是当下较为有效的方法。也形成了三大人工智能流派,即结构模拟(人工神经网络)[27-29]、功能模拟(物理符号系统)[30-33]和行为模拟(感知动作系统)[34-35]。这些研究更加倾向于以数据为基础的分析,但这并不是人脑真正的问题处理方式。正如莫拉维克悖论所说,人脑擅长对于逻辑、理念及感情方面的处理;而具体的定量数值处理则不擅长。例如:别人送了一些苹果,你要选择一个吃掉。你首先会根据自己的经验来选择因素从而判断选择哪个苹果,从苹果的颜色、大小、形状等方面进行判断。无论这次选择是否令你满意,其经验都会留在大脑中。相反一般不会有人拿着色谱、直尺等去对每一个苹果进行测量,再通过复杂的数学方法选择。高度抽象和演绎行为的多数信息来源于人的直观感受,比如视觉、听觉、触觉、味觉等。这些不提供具体信息,而只是客观事物在某些因素的表象。人通过事前表象和事后效果来判断是否完成目标,并形成对应关系。因此作者认为人对事物的理解首先是因素层面的理解与运算,如果难以确定才会使用因素的相进行模糊或精确分析。
汪培庄教授提出的因素空间也对莫拉维克悖论提出了相同的观点:1)只要找到描述因素,高级理性思维活动都是简单的;2)低级本能活动之所以困难,是因为人们不知道使用何种因素描述它们;3)因素由人输给机器,输给因素越多,机器就越聪明。根据莫拉维克悖论,基于数据的人工智能方法很难完成对人脑智能的模拟;同时受大数据获得条件限制也难以完成。
2 人的选择等同于比较人的思维、感情及逻辑推理基本是对少量样本进行的。人们从古至今都是在少量样本组成的样本空间中选择。不同在于由于信息及大数据技术的发展,选择的样本空间越来越大。因此从以前的信息不对称变成了选择综合症。实际上人脑对大样本空间有自己的处理策略。人脑将大样本空间细化,形成样本数量大致相同的子样本空间来处理,当然这和个人的记忆和处理能力有关。通常的,人脑在子样本空间中选择最好的样本保留,这样多个子样本空间就得到了各自最好的样本组成下一轮样本空间进一步选择。该策略也应用于各大电商平台的购物车策略。过程中人脑基本使用因素及其相之间的推理和运算,这种运算适合于人脑,且处理速度相当快。
在样本空间中选择最好样本的具体过程则是比较,更为具体的是两两比较,类似于冒泡法,由于人脑并不擅长并行处理。那么回到莫拉维克悖论,这时样本空间中的样本已经很少,同时也基本符合人脑根据经验、逻辑和推理得到的结果。在只能选择一个样本时,人脑将使用类似冒泡法进行比较。这时考虑苹果需要装入方形礼盒,而礼盒的尺寸是固定的,那么要具体考虑苹果的尺寸和形状因素的具体相。形状因素的相尽可能方正;尺寸因素的相尽量适合。对于尺寸的相可使用模糊和精确测量,当然这取决于样本数。可通过测量找到小于礼盒尺寸且又最接近礼盒尺寸的苹果放入礼盒。
因此可以说,人的思维、推理和判断过程是一个选择比较过程,过程中样本数量是较少的,不需要大数据支持;通过选择适合的因素、因素概念相(如较大、红色)和因素量化相(如10 cm)来最终选择适合的样本。但这刚好与基于大数据的人工智能策略相反。
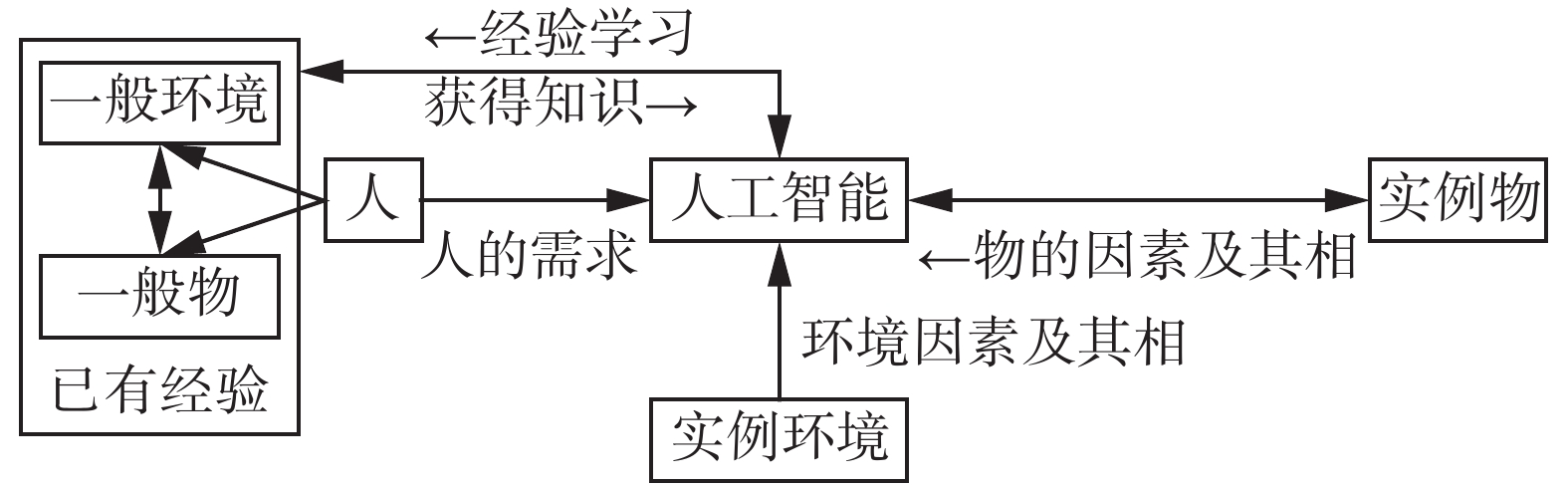
3 人工智能样本选择策略人工智能选择是人工智能理论实现的方式之一。人工智能目标是使机器代替人进行工作,而人最基本的工作就是样本选择。因此从莫拉维克悖论来看人工智能完成样本选择应无需大数据支持,但现状却相反。这里作者提出一种基于莫拉维克悖论和因素空间理论的人工智能样本选择策略。以人工智能系统本身为主体,将人、物和环境作为辅助系统,考虑选择因素、因素概念相和因素量化相,在环境系统中按照人的要求对物(样本)进行选择。图1为研究对象的关系图。
|
Download:
|
| 图 1 研究对象关系图 Fig. 1 Relationship of research objects | |
解释图1中符号含义。人工智能:代替人具有类人智能的实体或程序,其中包括信息接收、处理和存储的一系列子结构,但这里并不关心该结构。人:指自然人,用于为人工智能提供需求、以往积累的经验及可能的推理和理智策略等。一般环境:经验积累过程中出现的环境。一般物:经验积累过程中出现的物。实例环境:人工智能具体实施选择实例物时的环境。实例物:人工智能具体实施选择的物。图中关系有人对一般环境和一般物的以往处理过程和结果形成的人已有经验;人向人工智能提出工作需求;实例环境提供人工智能可感知的因素及其相;实例物提供人工智能可感知的因素及其相;人工智能对实例物进行选择。
图1的研究对象中心是人工智能系统,而不是人。更为重要的是该人工智能系统并不基于大数据,而是人的已有经验。这些经验往往不是具体的或模糊的数值,而是如上所述的因素及其相之间的逻辑推理和运算,结果形成了对应关系结构。这些操作在作为智能科学数学基础的因素空间理论中已有研究。该结构可定义为具体个人的喜好和偏向。选择具体对象时,根据这些偏好及对应的实例环境选择实例物。继续苹果的例子,考虑因素为尺寸∧颜色(∧表示合取[17]),相f(尺寸)={大,中,小}和f(颜色)={红,绿,黄},f(尺寸∧颜色)={大红,中红,小红,大绿,中绿,小绿,大黄,中黄,小黄}。人甲偏好可能是大红;而乙则偏好小黄。那么他们挑选苹果时选择的因素是尺寸∧颜色,这是第1次因素选择。选择的相分别是大红和小黄,这是第二次因素概念相选择;苹果需要装入礼盒考虑尺寸因素,度量礼盒(实例环境)尺寸和苹果尺寸(实例物)选择苹果,这是第三次因素量化相选择。对人而言,再复杂的选择都可通过这三步完成。目前各种方法论和数学方法等都是帮助人完成这三次选择的,同样也可帮助人工智能完成实例物的选择。
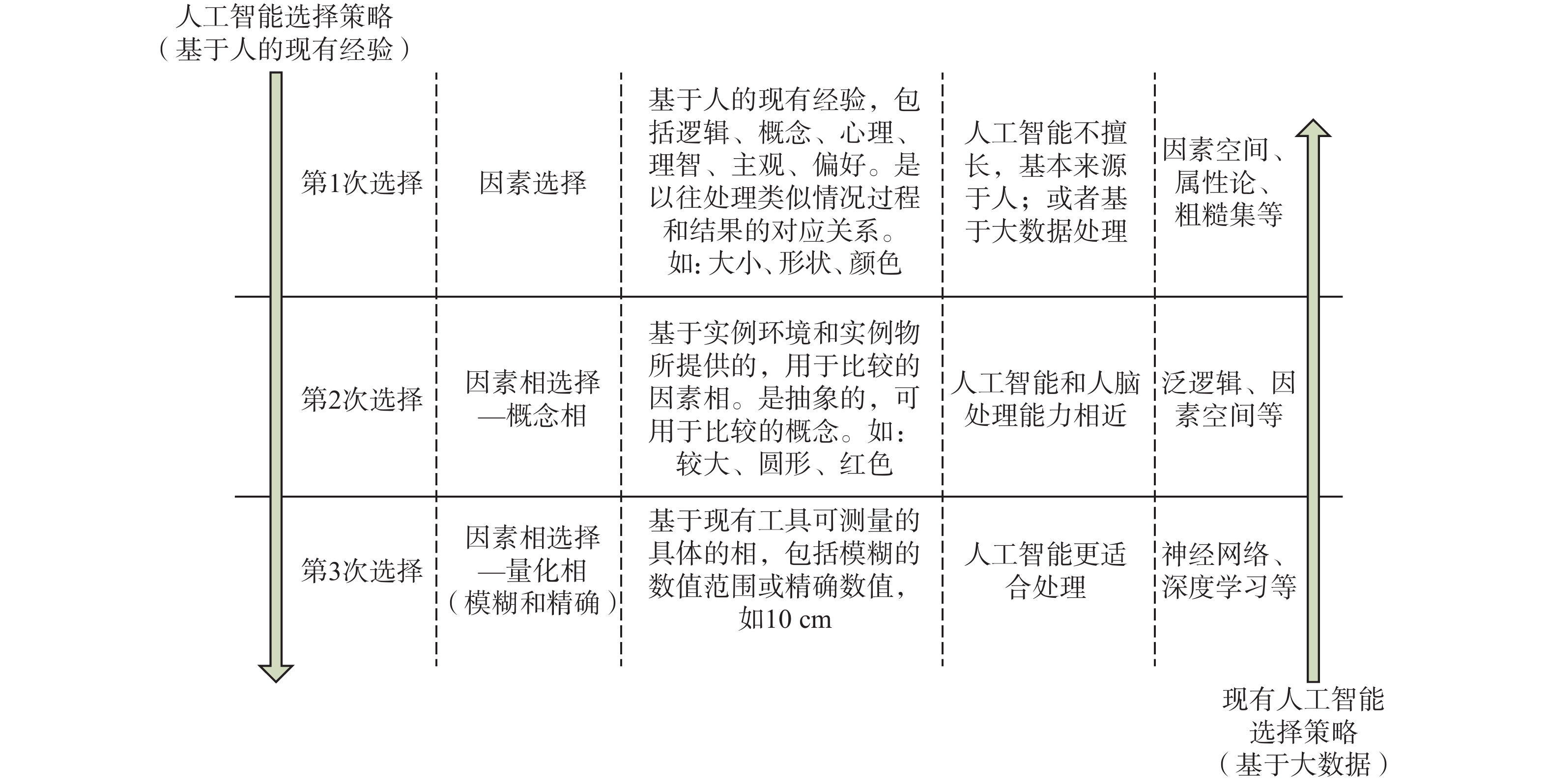
图2给出了类人的人工智能样本选择策略过程。这种策略分成3次选择实例物。第一次选择基于人的经验,是人工智能对人的学习结果。是基于实例环境和实例物所提供的可比较因素而非数据条件下完成的因素选择。其特点是速度快且少数据,人的因素选择往往是一瞬间。当人深思熟虑时,可能面临的是多因素、多样本,且需要后两次选择参与。但对因素的选择不会花费太长时间,当了解人偏好和需求时人工智能也是如此。第2次选择是对第一次选择得到因素的相的选择,包括概念相和量化相。参考人的目的和偏好,比较不同实例物(样本空间)相同因素的不同概念相,进行实例物选择。第3次选择是更为具体的对因素量化相的测量。这时因素量化相可以是模糊范围或精确数值,比较实例环境与各实例物的匹配性,从而选择实例物。通过这3次选择逐渐减少样本数量,最终选择适合的实例物。
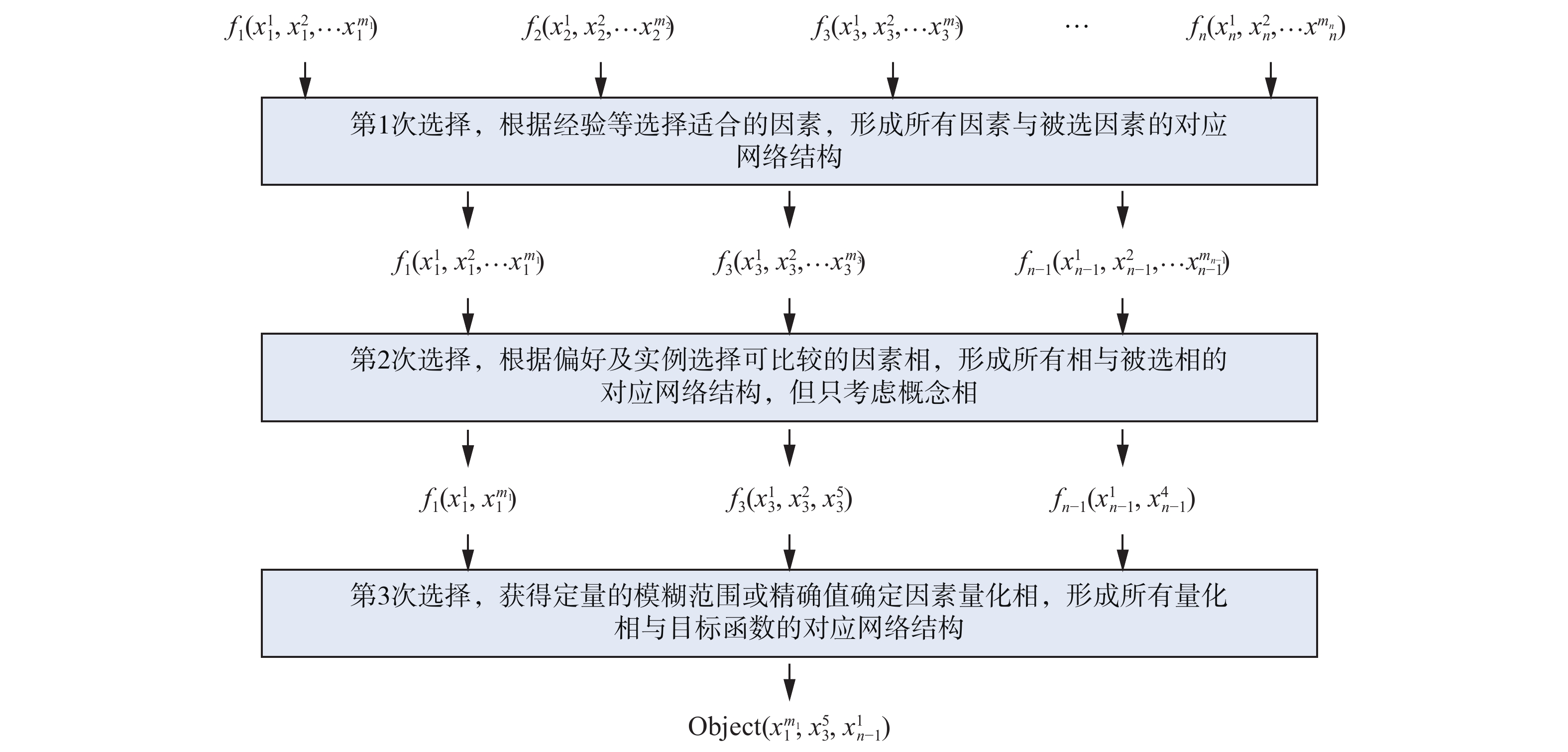
图3给出了最终得到的人工智能样本选择策略网络结构。其中,f代表因素,共n个;x代表某因素下的因素相,共m个;
|
Download:
|
| 图 2 人工智能样本选择策略层次 Fig. 2 Strategy level of artificial intelligence sample selection | |
|
Download:
|
| 图 3 人工智能样本选择策略网络模型 Fig. 3 Strategy network model of artificial intelligence sample selection | |
使用上述策略,分析一道智力题,如图4所示。

|
Download:
|
| 图 4 图形选择 Fig. 4 Graph selection | |
第1次因素选择:f={颜色,形状,内线条数,内线条交叉,内线溢出}。第2次因素概念相选择:f(颜色)={黑},f(形状)={正方形,圆形}。第3次因素量化相选择:f(内线条数)={1,2},f(内线条交叉)={0,1},f(内线溢出)={0,2}。那么这5个图形的特征如表1所示。
| 表 1 5个图形的特征 Tab.1 Characteristics of five graphs |
Object={a,b,c,d,e}。Object(颜色)={a,b,c,d,e}/f(颜色)={a,b,c,d,e};Object(颜色,形状)={a,b,c,d,e}/f(形状)={a,c}+ {b,d,e};Object(颜色,形状,内线条数)= ({a,c}+ {b,d,e})/f(内线条数)={a,c}+ {b}+{d,e};Object(颜色,形状,内线条数, 内线条交叉)= ({a,c}+ {b}+{d,e})/f(内线条交叉)={a,c}+ {b}+{d,e};Object(颜色,形状,内线条数, 内线条交叉, 内线溢出)= ({a,c}+ {b}+{d,e})/f(内线溢出)={a,c}+ {b}+{d,e}。从该过程来看,b是区别于其他图像的选项,因此最终选择b图。同时也可了解到图a和c可以归为一类;d和e可以归为一类。如果再增加因素内线交叉角度,则a和c,d和e可进一步区分。但这时也进一步增大了b与他们的区别。也有类似的决定度等相关概念可区分对象[17]。
综上,实例分析过程基本是因素及因素相的运算,最后才涉及具体的数据统计和测量。这是人对样本的选择过程,也是人工智能样本选择应具备的策略。当然例子是简单的,大规模分析需实现图3中3次网络结构,组成人工智能样本选择策略网络。基于目前情况,第1、2次选择可通过因素空间理论实现,第3次可通过现有神经网络实现。因此我们得到实现人工智能的基础是学习人思维的本质。人思维的本质是依靠因素进行大规模的样本筛选从而确定关注点,再根据因素的定性相(概念相)选择喜好样本,最后才是根据因素的定量相(量化相)获得匹配最好的样本。从该角度分析,目前的人工智能面向大数据的驱动可能是背道而驰,大数据驱动的人工智能只能显示表象,冗余和虚假信息对结果有很大影响。这部分研究有待进一步展开。
5 结论论文提出了一种人工智能样本选择策略。主要结论如下:
1)利用因素空间思想论述了莫拉维克悖论的合理性。认为人对事物的理解首先是因素层面的理解与运算,如果难以确定才会使用因素相进行模糊或精确分析。
2)人的选择过程就是比较过程。人的思维、推理和判断过程是选择比较过程,样本数量是较少的,不需大数据支持;通过选择适合的因素、因素概念相和因素量化相来选择适合样本。
3)建立了人工智能样本选择策略。首先给出了研究对象中人、机、环境及人工智能系统之间的关系。建立了人工智能样本选择策略结构,3次选择分别对应了因素、因素概念相和因素量化相选择。给出了3次选择的特点、基础和方法。最终建立人工智能样本选择策略网络模型,模型中3次选择对应于3种网络结构。
4)通过实例演示了人工智能样本选择策略。过程中基本是因素及因素相的运算,最后才涉及具体的数据统计和测量。该策略是人对样本的选择过程,也是人工智能样本选择应具备的策略。
| [1] |
雷凯, 黄硕康, 方俊杰, 等. 智能生态网络: 知识驱动的未来价值互联网基础设施[J]. 应用科学学报, 2020, 38(1): 152-172. LEI Kai, HUANG Shuokang, FANG Junjie, et al. Intelligent Eco Networking (IEN): knowledge-driven and value-oriented future internet infrastructure[J]. Journal of applied sciences, 2020, 38(1): 152-172. DOI:10.3969/j.issn.0255-8297.2020.01.012 (  0) 0)
|
| [2] |
武春龙, 朱天明, 张鹏, 等. 基于功能模型和层次分析法的智能产品服务系统概念方案构建[J]. 中国机械工程, 2020, 31(n): 853-864. WU Chunlong, ZHU Tianming, ZHANG Peng, et al. Conceptual scheme construction of smart pss based on functional model and AHP[J]. China mechanical engineering, 2020, 31(n): 853-864. (  0) 0)
|
| [3] |
吴思凡, 杜煜, 徐世杰, 等. 基于深度确定性策略梯度的智能车汇流模型[J]. 计算机工程, 2020, 46(1): 87-92. WU Sifan, DU Yu, XU Shijie, et al. Traffic merging model for intelligent vehicle based on deep deterministic policy gradient[J]. Computer engineering, 2020, 46(1): 87-92. (  0) 0)
|
| [4] |
刘翠娟, 刘箴, 柴艳杰, 等. 人群应急疏散中一种多智能体情绪感染仿真模型[J]. 计算机辅助设计与图形学学报, 2020, 32(4): 660-670. LIU Cuijuan, LIU Zhen, CHAI Yanjie, et al. A multi-agent emotional contagion model in crowd emergency evacuation[J]. Journal of computer-aided design & computer graphics, 2020, 32(4): 660-670. (  0) 0)
|
| [5] |
郭健, 陈健, 胡杨. 基于小波智能模型的地铁车站基坑变形时序预测分析[J]. 岩土力学, 2020(S1): 299-304. GUO Jian,CHEN Jian,HU Yang. Time series prediction for deformation of the metro foundation pit based on wavelet intelligence model[J]. Rock and soil mechanics, 2020(S1): 299-304. (  0) 0)
|
| [6] |
孙伟, 余浩, 杨建平, 等. 智能电网可靠性需求约束下无线发射功率模型预测控制[J]. 电力系统自动化, 2020, 44(2): 185-193. SUN Wei, YU Hao, YANG Jianping, et al. Model predictive control of wireless transmit power constrained by reliability requirement of smart grid[J]. Automation of electric power systems, 2020, 44(2): 185-193. (  0) 0)
|
| [7] |
李伯虎, 柴旭东, 侯宝存, 等. 云制造系统3.0——一种“智能+”时代的新智能制造系统[J]. 计算机集成制造系统, 2019, 25(12): 2997-3012. LI Bohu, CHAI Xudong, HOU Baocun, et al. Cloud manufacturing system 3.0——new intelligent manufacturing system in era of “Intelligence +”[J]. Computer integrated manufacturing systems, 2019, 25(12): 2997-3012. (  0) 0)
|
| [8] |
李林恒, 甘婧, 曲栩, 等. 智能网联环境下基于安全势场理论的车辆跟驰模型[J]. 中国公路学报, 2019, 32(12): 76-87. LI Linheng, GAN Jing, QU Xu, et al. Car-following model based on safety potential field theory under connected and automated vehicle environment[J]. China journal of highway and transport, 2019, 32(12): 76-87. (  0) 0)
|
| [9] |
肖吉军, 郑颖琦, 徐洁萍. 基于AHP与DHNN的智能制造成熟度评估模型研究[J]. 系统科学学报, 2020, 28(2): 105-110. XIAO Jijun, ZHENG Yingqi, XU Jieping. Research on intelligent manufacturing maturity evaluation model based on AHP and DHNN[J]. Chinese journal of systems science, 2020, 28(2): 105-110. (  0) 0)
|
| [10] |
吴飞, 段书凯, 何斌, 等. 健壮人工智能模型与自主智能系统[J]. 中国科学基金, 2019, 33(6): 651-655. WU Fei, DUAN Shukai, HE Bin, et al. Robust artificial intelligence and autonomous intelligent system[J]. Bulletin of national natural science foundation of China, 2019, 33(6): 651-655. (  0) 0)
|
| [11] |
毕俊蕾, 朱宗强, 李致远. 智能网联车环境下基于路段评分的数据转发模型[J]. 数据采集与处理, 2019, 34(6): 1030-1038. BI Junlei, ZHU Zongqiang, LI Zhiyuan. Road section scoring-based data forwarding model for intelligent connected vehicles[J]. Journal of data acquisition & processing, 2019, 34(6): 1030-1038. (  0) 0)
|
| [12] |
钟义信. 机制主义人工智能理论——一种通用的人工智能理论[J]. 智能系统学报, 2018, 13(1): 2-18. ZHONG Yixin. Mechanism-based artificial intelligence theory: a universal theory of artifical intelligence[J]. CAAI transactions on intelligent systems, 2018, 13(1): 2-18. (  0) 0)
|
| [13] |
钟义信. 人工智能: 概念·方法·机遇[J]. 科学通报, 2017, 62(22): 2473-2479. ZHONG Yixin. Artificial intelligence: concept, approach and opportunity[J]. Chinese Science Bulletin, 2017, 62(22): 2473-2479. DOI:10.1360/N972016-01315 (  0) 0)
|
| [14] |
钟义信. 人工智能的突破与科学方法的创新[J]. 模式识别与人工智能, 2012, 25(3): 456-461. ZHONG Yixin. Breakthroughs in artificial intelligence and innovation in methodology[J]. Pattern recognition and artificial intelligence, 2012, 25(3): 456-461. DOI:10.3969/j.issn.1003-6059.2012.03.014 (  0) 0)
|
| [15] |
马立伟. 深度学习驱动的领域专用架构[J]. 中国科学: 信息科学, 2019, 49(3): 334-341. MA Liwei. Domain-specific architectures driven by deep learning[J]. Scientia sinica informationis, 2019, 49(3): 334-341. DOI:10.1360/N112018-00278 (  0) 0)
|
| [16] |
汪培庄. 因素空间理论——机制主义人工智能理论的数学基础[J]. 智能系统学报, 2018, 13(1): 37-54. WANG Peizhuang. Factor space-mathematical basis of mechanism based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 37-54. (  0) 0)
|
| [17] |
汪培庄. 因素空间与数据科学[J]. 辽宁工程技术大学学报(自然科学版), 2015, 34(2): 273-280. WANG Peizhuang. Factor spaces and data science[J]. Journal of Liaoning Technical University (Natural Science Edition), 2015, 34(2): 273-280. DOI:10.11956/j.issn.1008-0562.2015.02.026 (  0) 0)
|
| [18] |
汪培庄, 郭嗣琮, 包研科, 等. 因素空间中的因素分析法[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(7): 865-870. WANG Peizhuang, GUO Sicong, BAO Yanke, et al. Causality analysis in factor spaces[J]. Journal of Liaoning Technical University (Natural Science Edition), 2014, 33(7): 865-870. (  0) 0)
|
| [19] |
崔铁军, 李莎莎. 安全科学中的故障信息转换定律[J/OL]. 智能系统学报. [2020-02-14].http://kns.cnki.net/kcms/detail/23.1538.TP.20191205.1008.002.html. CUI Tiejun, LI Shasha. The conversion law of fault information in Safety Science[J/OL]. CAAI transactions on intelligent systems. [2019-12-29]. http://kns.cnki.net/kcms/detail/23.1538.TP.20191205.1008.002.html. (  0) 0)
|
| [20] |
崔铁军, 汪培庄. 空间故障树与因素空间融合的智能可靠性分析方法[J]. 智能系统学报, 2019, 14(5): 853-864. CUI Tiejun, WANG Peizhuang. Intelligent reliability analysis method based on space fault tree and factor space[J]. CAAI transactions on intelligent systems, 2019, 14(5): 853-864. (  0) 0)
|
| [21] |
崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J]. 安全与环境学报, 2019, 19(2): 399-405. CUI Tiejun, LI Shasha. Revision of the space fault tree and the space fault network system[J]. Journal of safety and environment, 2019, 19(2): 399-405. (  0) 0)
|
| [22] |
崔铁军, 李莎莎, 韩光, 等. 基于信息增益的SFT中故障影响因素降维方法研究[J]. 安全与环境学报, 2018, 18(5): 1686-1691. CUI Tiejun, LI Shasha, HAN Guang, et al. On the dimensional reduction method for the fault-affecting factors based on the information gain[J]. Journal of safety and environment, 2018, 18(5): 1686-1691. (  0) 0)
|
| [23] |
崔铁军, 李莎莎, 王来贵. 完备与不完备背景关系中蕴含的系统功能结构分析[J]. 计算机科学, 2017, 44(3): 268-273, 306. CUI Tiejun, LI Shasha, WANG Laigui. System function structure analysis in complete and incomplete background relationship[J]. Computer science, 2017, 44(3): 268-273, 306. DOI:10.11896/j.issn.1002-137X.2017.03.055 (  0) 0)
|
| [24] |
崔铁军, 汪培庄, 马云东. 01SFT中的系统因素结构反分析方法研究[J]. 系统工程理论与实践, 2016, 36(8): 2152-2160. CUI Tiejun, WANG Peizhuang, MA Yundong. Inward analysis of system factor structure in 01 space fault tree[J]. Systems engineering-theory & practice, 2016, 36(8): 2152-2160. DOI:10.12011/1000-6788(2016)08-2152-09 (  0) 0)
|
| [25] |
崔铁军, 马云东. 基于因素空间中属性圆对象分类的相似度研究及应用[J]. 模糊系统与数学, 2015, 29(6): 56-63. CUI Teijun, MA Yundong. Research on the similarity of object classification of attribute circular and application based on factors space[J]. Fuzzy systems and mathematics, 2015, 29(6): 56-63. (  0) 0)
|
| [26] |
崔铁军, 马云东. 基于因素空间的煤矿安全情况区分方法的研究[J]. 系统工程理论与实践, 2015, 35(11): 2891-2897. CUI Tiejun, MA Yundong. Research on the classification method about coal mine safety situation based on the factor space[J]. Systems engineering-theory & practice, 2015, 35(11): 2891-2897. DOI:10.12011/1000-6788(2015)11-2891 (  0) 0)
|
| [27] |
MCCULLOCH W S, PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. The bulletin of mathematical biophysics, 1943, 5(4): 115-133. DOI:10.1007/BF02478259 ( 0) 0)
|
| [28] |
ROSENBLATT F. The perceptron: a probabilistic model for information storage and organization in the brain[J]. Psychological review, 1958, 65(6): 386-408. DOI:10.1037/h0042519 ( 0) 0)
|
| [29] |
HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the national academy of sciences of the United States of America, 1982, 79(8): 2554-2558. DOI:10.1073/pnas.79.8.2554 ( 0) 0)
|
| [30] |
MCCARTHY J, MINSKY M L, ROCHESTER N, et al. A proposal for the Dartmouth summer research project on artificial intelligence[R]. Dartmouth: Dartmouth College, 1955.
( 0) 0)
|
| [31] |
SIMON H A. The sciences of the artificial[M]. Cambridge, MA, USA: MIT Press, 1969.
( 0) 0)
|
| [32] |
NEWELL A. Physical symbol systems[J]. Cognitive science, 1980, 4(2): 135-183. DOI:10.1207/s15516709cog0402_2 ( 0) 0)
|
| [33] |
TURING A M. Computing machinery and intelligence[J]. Mind, 1950, 59: 433-460. ( 0) 0)
|
| [34] |
BROOKS R A. Elephant cannot play chess[J]. Autonomous Robert, 1990, 6: 3015. ( 0) 0)
|
| [35] |
BROOKS R A. Engineering approach to building complete, intelligent beings[C]//Proceedings of SPIE 1002, Intelligent Robots and Computer Vision VII. Boston, USA, 1989: 618−625.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16



