音乐词曲匹配度评估是针对音乐的词曲匹配程度给出的一个客观评估。随着智能音乐研究发展，越来越多智能音乐作品产生，随之而来的便是对生成的音乐作品评价问题。

目前对音乐作品的评价方式主要包括以下几种方式：1）基于互动的评价方式，这种评价方式一般依赖于听者对一般音乐的反馈，通过收集听者对生成音乐作品的反应，如心跳、脉搏和皮肤电导，如评估分数、偏好或生理信号等；然后使用收集到的信息来评估生成的音乐作品。由于音乐作品的主观性，这种交互式评价方法被广泛使用。文献[1]根据用户对音乐流派的选择，使用马尔可夫链和歌词数据库创建歌词，而音乐则由旋律和该流派的3个伴奏之一组成。而词曲的组合则通过人工的方式由用户来决定。2）在基于交互评价的基础之上，通过与音乐家合作获得专业反馈。文献[2]通过选择专业人士和非专业人士若干，综合评价为两方评价均分的加权求和。3）基于规则的评价方法，使用显式的评价规则对生成的音乐作品进行评价。评价规则是根据个人的创作经验或音乐理论，综合考虑节奏、词组、音阶、和弦等音乐要素而制定的。如文献[3]中采用了音乐理论中考虑跳跃和间隔的一些评价规则对音乐作品进行评价。这种方式对于创作特定音乐流派的音乐作品是有效果的。4）基于学习的评价方法，文献[4]利用神经网络构建了音乐情感分类及评估模型。

本文采用的是基于学习的评价方式，随着自然语言处理技术的发展和应用，通过算法模型对音乐词曲进行情感分析的准确性逐渐增加。然而对旋律或歌词进行单独的情感分析是不准确的，主要包含两点：1）缺少旋律衬托的歌词无法确定作曲者要突出的内容，从而对情感的分析是不准确的；2）在没有旋律背景下的歌词，容易忽略歌词中的节奏感，而节奏感在音乐中，对情感表达是非常重要的。而现有的评价方式却未充分考虑上述问题。

因此本文尝试综合考虑词曲的情感和词曲间的节奏关系来给出一个尽量准确且客观的智能评估。而要学习到词曲间的情感和节奏特征，则需要研究设计合理的音乐表达形式，才能从中学习到情感及节奏上的特征，因此本文将主要从音乐数据表达形式研究及算法模型设计两个方面进行阐述。

1 音乐数据表达形式

要从音乐数据中能学习到词曲之间的情感关系和节奏关系，则需要研究并构建情感、节奏正反例音乐样本，音乐反例构建的好坏决定了模型是否可以通过正反例之间的差异挖掘到词曲之间匹配的特征关系。若反例无法充分将不匹配的关键因素表达出来，则难以通过词曲匹配算法区分当前音乐词曲是否匹配。

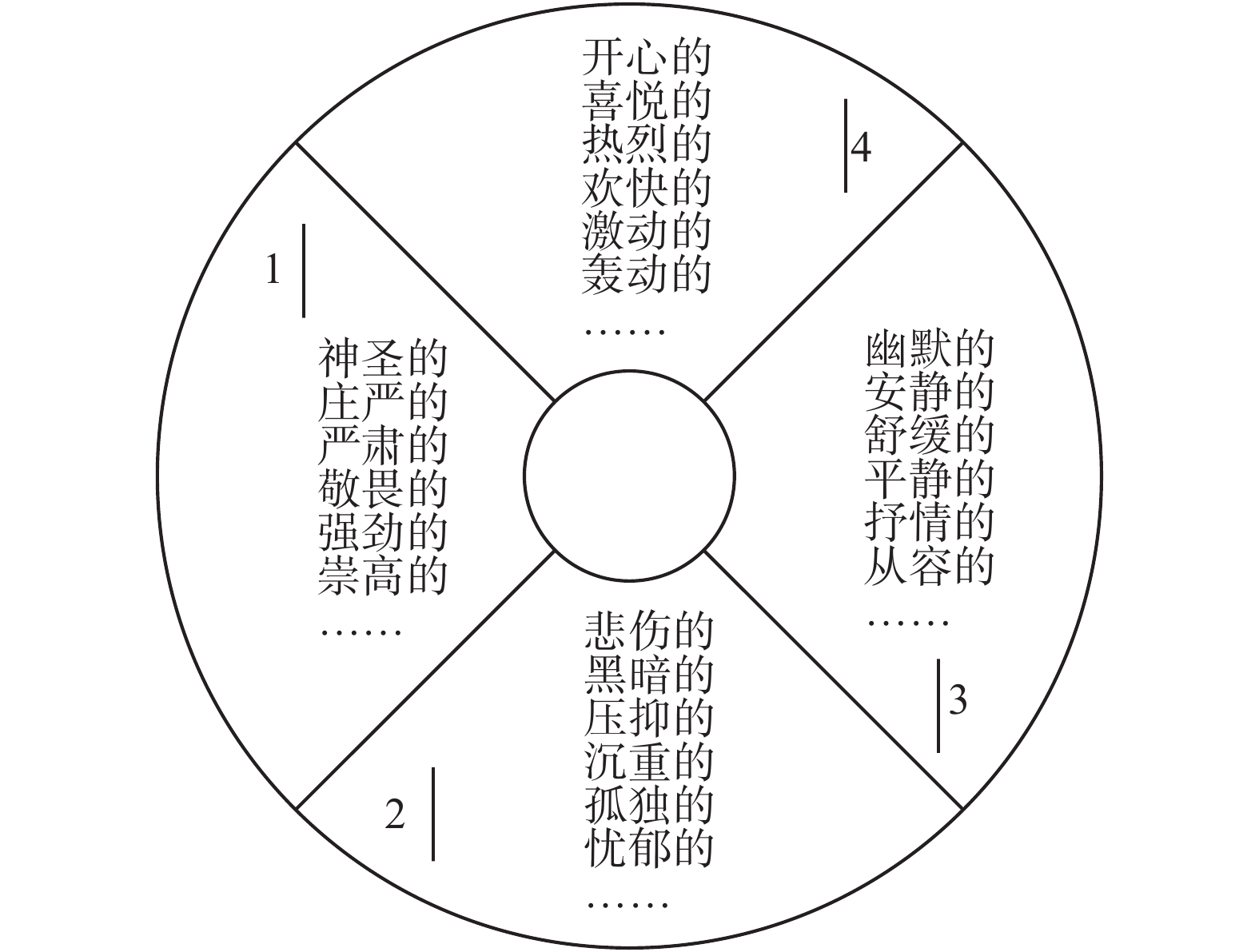
1.1 音乐情感反例构建

由于本文是基于序列模型进行词曲匹配度评估，是基于音乐序列的分析，所以在音乐情感模型上，采用离散的音乐情感模型，提出了简化的Hevner^[5]情感分类模型，并结合国人的审美标准，对关键词进行适当修改。如图1所示，建立了音乐情感模型，从情感角度将音乐分成四大类。相邻类别具有一定的情感相似性，情感可以在相邻类别上转换。相对两个情感类别表达情感内涵相反。

基于提出的CZH音乐情感模型。对公开的词曲同步音乐数据集^[6]根据情感进行划分。在情感标定的过程中，尽可能使得每一类情感音乐都具有鲜明的情感表达，即当听欢快的音乐时，能很容易区分该音乐为欢快的音乐，而不会模棱两可。该做法的目的旨在为后续构建音乐情感反例打下基础。基于此基准，一共标定1 275首乐曲。如表1所示。

进一步，本文在歌词数相当的情况，将情感表达相反的两种情感音乐，进行词曲交换，作为音乐情感反例。如图2为音乐情感反例。图中两个片段分别来自音乐剧《悲惨世界》中的《On my own》以及欢快的音乐《Boogie Down》构建的反例。

可以发现，其实在进行情感音乐词曲交换后，反例音乐一方面是由于情感不一致，而导致不匹配。但更具体的体现为歌词和旋律的整体节奏产生了不一致。这种不一致，使得词曲原先相互呼应的情感关系被破坏，从而导致词曲不匹配。换句话说，情感很大程度上还是通过节奏表现出来的。比如存在一些音乐，歌词在没有旋律的情况下，仅理解歌词含义，可能表达的是悲伤的情感，但是结合旋律以后，会发现其实这首音乐听起来是欢快的。仔细探究，便会发现其实歌词中，通过大量的有节奏性的重复操作，使得整首歌的节奏感很强，因此不会透露出悲伤的情绪。

1.2 音乐节奏反例构建

对于一首音乐，节奏至关重要。其中歌词和旋律常在节奏上，如发音的音调上；或者是对于短且快的旋律片段常对应发音可以较短的歌词，而不是复杂的歌词；在相同的旋律片段下，对应的歌词也具有足够的相似性，即在节奏上与歌词保持一致等。本文通过歌词乱序的方法将原有的节奏联系打破，从而实现节奏反例构建。

而要对歌词进行乱序操作，就必须确定乱序的粒度，即以歌词片段、以单词或者以词块为最小粒度进行乱序。以《on my own》歌曲为例，如图3~5所示为3种乱序方式。

首先对于以词块为最小粒度的乱序会存在破坏基本单词结构，比如连续唱出词块ing。这样的歌词序列是不合理的，因此不应通过该方式进行乱序操作。其次对于以单词为最小粒度的乱序，这种方式相对词块方式更加合理，这种方式会破坏句子语意。同时表达了节奏上的不匹配和语意上不匹配。所以可以作为打乱的最小粒度。最后对于以歌词片段为最小粒度的乱序，片段长度设定为尽可能包含一个句子的长度，因此该乱序方式，最大程度地保留了语意上的特征。同时表达了节奏上的不匹配。其构建算法流程如下：

算法1　 音乐歌词乱序算法

输入　 m首输入音乐的输入歌词 $ {L^{\left( i \right)}},i \in \left( {0,{\rm{}}m} \right),$ ${L^{\left( i \right)}} =$ $ \left\{ {L_0^{\left( i \right)},L_1^{\left( i \right)},L_2^{\left( i \right)}, \cdots ,L_n^{\left( i \right)}} \right\} $ ，乱序方式 ${\rm{ shuffle\_level}} \in $ {WORD，SENTENCE}。

参数　输入音乐歌词长度 $ n = {\rm{len}}\left( L \right)$ ，歌曲片段长度 $ l = {\rm{len}}\left( {L_n^{\left( i \right)}} \right)$ ，随机种子seed。

输出　乱序后的音乐歌词。

流程　对整体的迭代次数 $ i = 0,1, 2,\cdots ,m$ ：

1）生成随机数seed，作为当前歌曲乱序的随机种子。

2）根据乱序标志符shuffle_level决定对当前音乐样本进行词级别还是片段级别乱序。

3）对于单首音乐片段个数，循环次数 $j = 0,1,$ $2,\cdots,{\rm{length}}$ ：

① if shuffle_level=SENTENCE：

a.要交换音乐歌词片段的索引：

$ k = {\rm{int}}\left( {{\rm{ramdom}}\left( {{\rm{seed}}} \right){\rm{*}}\left( {j + 1} \right)} \right) $

b. 交换两个音乐片段：

$ {\rm{swap}}\left( {L_j^{\left( i \right)},L_k^{\left( i \right)}} \right) \quad\quad\quad\quad\quad\quad\quad $

② if shuffle_level=WORD：

$ \;\;\;\;\;\;\;\;{\rm{ for \;{\textit{v}} \;in \;range}}\left( l \right) : \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad $

a. 此片段要交换单词的索引：

$ k = {\rm{int}}\left( {{\rm{ramdom}}\left( {\rm{seed}} \right){\rm{*}}\left( {v + 1} \right)} \right) $

b. 交换此片段中的两个单词：

$ {\rm{swap}}\left( {L_j^{\left( i \right)}\left( v \right),L_j^{\left( i \right)}\left( k \right)} \right)\quad\quad\quad\quad $

1.3 音乐反例构建结果

基于已情感标定的1 275首正例音乐，并利用上述两种音乐反例构建方法，随机选择其中一部分的音乐用于音乐反例构建。随机选择主要是为了避免模型在特定样本中学到过多额外的特征，使得泛化性能降低。如表2所示，其中音乐情感反例为1 184首，音乐节奏反例为1 175首，共计2 359首反例音乐。

1.4 音乐歌词及旋律表达形式

由于本文使用的是英文的音乐数据集，而英文是表音的，在音乐中，单词的后缀发音等对音乐本身的节奏是有影响的。因此对于音乐中的歌词，为了更好地捕捉歌词的含义及发音。采用分布式形式表示^[7]，同时将单词拆分为更小的词块(word piece)，考虑单词编码和词块编码，充分提取英文歌词中发音的特征，即：

$ {{{v}}_{{\rm{lyrics}}}} = {{{v}}_{{\rm{word}}}}||{{{v}}_{{\rm{piece}}}} $

式中：v_word为词向量，v_piece为词块向量。拼接得到歌词向量。如对于单词womon，由词块 ${\rm{ wom,on}}$ 组成，则： $ {{v}}_{{\rm{lyrics}}}^{\left\langle j \right\rangle }{\rm{}} = {{{v}}_{{\rm{wom}}}} + {{{v}}_{{\rm{womon}}}}$ ，其中 $ {{v}}_{{\rm{lyrics}}}^{\left\langle j \right\rangle }$ 表示音乐片段中第j个词块；对于音乐旋律，将音符转换为音高、音长、休止时长来进行表征，则在第j个词块对应的音符编码向量表示为 $ {{v}}_{{\rm{melody}}}^{\left\langle j \right\rangle } = \left\{ {{\rm{pitch,duration,rest}}} \right\}$ 。

如表3所示，为旋律编码结果。

1.5 音乐切分方法

本文将用于训练的单曲划分为多个片段，采用滑动窗口的方法对音乐进行切分，假设音乐长度N=10，每个窗口长短为l=4，窗口移动步长s=l/2=2，则切分效果如图6。

通过设置合理的窗口大小，能尽可能保证每个片段的语意完整，且每个音乐片段长度固定。本文中将窗口大小l设定为20。算法流程如下：

算法2　 音乐切分算法

输入　音乐 $ S = M\mathop \cup L$ ，且 ${\rm{len}}\left( S \right) = N$ 。

参数　窗口大小l，移动步长s=l/2。

输出　切分后的词曲片段数组 $ M,L $ 。

流程如下：

1）计算循环次数(乐曲片段数)n：

$ n = \left\{ {\begin{array}{*{20}{l}} {\left\lfloor {\dfrac{{N - l - 1}}{s}} \right\rfloor ,}&{\left( {N - l - 1} \right){\rm{MOD}}s = 0}\\ {\left\lfloor {\dfrac{{N - l - 1}}{s} + 1} \right\rfloor ,}&{\left( {N - l - 1} \right){\rm{MOD}}s, \ne 0} \end{array}} \right. $

式中： $\left\lfloor {\;} \right\rfloor $ 表向下取整，MOD表取余。

2）对于整体循环次数 $ i = 0,1,2,\cdots,n$ ：

①计算单个片段范围：

start=i·s，end=start+l；

②构造旋律片段样本：

${M_i} = M\left[ {{\rm{start}},{\rm{end}}} \right]$ ；

③构造旋律片段样本：

${L_i} = L\left[ {{\rm{start}},{\rm{end}}} \right]$ ；

3）重新构建 $M $ 、 $L$ ：

$ \begin{array}{l} M = \left\{ {{M_0},{M_1}, \cdots ,{M_n}} \right\}{M_i}\epsilon M\\ L = \left\{ {{L_0},{L_1}, \cdots ,{L_n}} \right\}{L_i} \epsilon L \end{array} $

2 词曲匹配度评估算法

通过数据处理，得到了用于训练词曲匹配算法模型的样本数据。本节综合考虑音乐词曲情感及节奏特征，提出基于序列模型^[8]的词曲匹配度智能评估算法。

2.1 算法原理及框图

第一章中提到，对旋律或歌词进行单独的情感分析是不准确的，主要包含两点：1）缺少旋律衬托的歌词无法确定作曲者要突出的内容，从而对情感的分析是不准确的；2）在没有旋律背景下的歌词，容易忽略歌词中的节奏感，而节奏感在音乐中，对情感表达是非常重要的，正如本文提出的观点：情感很大程度上还是通过音乐节奏表现出来的。因此本节设计的算法，将情感和节奏两者综合考虑，设计得到词曲匹配算法模型如图7。结合模型框图，给出算法定义如下：

给定输入音乐S=M∪L，其中输入旋律 $ M = \left\{ {{M_0},{M_1},{\rm{}}{\rm{}} \cdots {\rm{}},{\rm{}}{M_n}} \right\}$ 包含n个旋律片段，每个输入旋律片段包含l个音符，即M_i= $ \{ M_i^{\left\langle 0 \right\rangle },M_i^{\left\langle 1 \right\rangle },\cdots ,M_i^{\left\langle l \right\rangle }\} $ ，同理对于输入歌词 $ L = \left\{ {{L_0},{L_1},{\rm{}} \cdots ,{\rm{}}{\rm{}}{L_n}} \right\}$ 包含n个歌词片段，每个歌词片段包含l个词块，即 $ {L_i} = \left\{ {L_i^{\left\langle 0 \right\rangle },L_i^{\left\langle 1 \right\rangle },\cdots ,} \right.$ $\left. {L_i^{\left\langle l \right\rangle }} \right\}$ 。音乐词曲匹配算法通过歌词编码器和旋律编码器，对输入旋律片段M_i、输入歌词片段L_i中对应的词块 $ L_i^{\left\langle j \right\rangle }$ 和音符 $ M_i^{\left\langle j \right\rangle }$ 进行同步编码，并将编码结果通过词曲匹配解码器解析、判断当前词曲匹配度，并在解过程中，保存更新词曲特征匹配关系的状态信息，实现音乐片段的词曲匹配判断，综合输入音乐的n个词曲片段匹配程度，判断当前输入音乐词曲匹配程度。

基于词曲匹配算法框架，算法计算流程如下：

算法3　 词曲匹配算法

输入　旋律M包含n个旋律片段，每个片段包含l个音符， ${{M}}_i^{\left\langle j \right\rangle }$ 表示第i个输入旋律片段中的第j个音符的向量表示， ${{M}}_i^{\left\langle j \right\rangle } = \left\{ {{\rm{norm}}\left( {{\rm{pitch}}} \right),{\rm{}}{\rm{duration}},} \right.$ rest}；歌词L包含n个歌词片段，每个片段包含l个词块， ${{L}}_i^{\left\langle j \right\rangle }$ 表示第i个输入歌词片段中的第j个歌词的向量表示为：v_lyrics=v_word+v_piece，其中v_word为歌词词向量，v_piece为歌词词块向量；

模型参数如表4所示。

输出　输入词曲的匹配程度

流程如下：

1）令 $ X_i^{\left\langle j \right\rangle } = M_i^{\left\langle j \right\rangle }$ ，通过循环神经网络，即通过式(1)~(6)，对输入旋律进行编码，同理，令 $ X_i^{\left\langle j \right\rangle } = L_i^{\left\langle j \right\rangle }$ ，对输入歌词进行编码。

${\cal T}_f^{\left\langle i \right\rangle } = \sigma \left( {{W_f}\left[ {{a^{i - 1}},{\rm{}}X_i^{\left\langle j \right\rangle }} \right] + {b_f}} \right)$

(1)

${\cal T}_u^{\left\langle i \right\rangle } = \sigma \left( {{W_u}\left[ {{a^{i - 1}},{\rm{}}X_i^{\left\langle j \right\rangle }} \right] + {b_u}} \right)$

(2)

${\hat c^{\left\langle i \right\rangle }} = \tanh \left( {{W_C}\left[ {{a^{i - 1}},{\rm{}}X_i^{\left\langle j \right\rangle }} \right] + {b_C}} \right)$

(3)

${c^{\left\langle i \right\rangle }} = {\cal T}_f^{\left\langle i \right\rangle } \circ {c^{\left\langle {i - 1} \right\rangle }} + {\cal T}_u^{\left\langle i \right\rangle } \circ {\hat c^{\left\langle i \right\rangle }}$

(4)

${\cal T}_o^{\left\langle i \right\rangle } = \sigma \left( {{W_o}\left[ {{a^{i - 1}},{\rm{}}X_i^{\left\langle j \right\rangle }} \right] + {b_o}} \right)$

(5)

$\begin{split}&\;\\[-1pt] &{\rm{cod}}{{\rm{e}}^{\left\langle j \right\rangle }} = {a^{\left\langle i \right\rangle }} = {\cal T}_o^{\left\langle i \right\rangle } \circ \tanh \left( {{c^{\left\langle i \right\rangle }}} \right)\end{split}$

(6)

式中“◦”表示前后量之间对应元素相乘。

对于输入旋律片段M_i的第j个时间步 $ M_i^{\left\langle j \right\rangle }$ 以及输入歌词片段L_i的第j个时间步 $ L_i^{\left\langle j \right\rangle }$ 。可计算得到第j个时间步的旋律编码向量和歌词编码向量。

$ {\rm{{\rm{code}}}}_{{\rm{note}}}^{\left\langle j \right\rangle } = {f_{{\rm{LSTM}}}}\left( {M_i^{\left\langle j \right\rangle }} \right) $

(7)

$ {\rm{{\rm{code}}}}_{{\rm{lyrics}}}^{\left\langle j \right\rangle } = {f_{{\rm{LSTM}}}}\left( {L_i^{\left\langle j \right\rangle }} \right) $

(8)

式中： ${\rm{{\rm{code}}}}_{{\rm{note}}}^{\left\langle j \right\rangle }$ 表示第j个音符的编码向量，为旋律编码器输出； ${\rm{{\rm{code}}}}_{{\rm{lyrics}}}^{\left\langle j \right\rangle }$ 表示第j个歌词的编码向量，为歌词编码器输出。

2）如式(7)~(8)，将第j个时间步的旋律编码向量 > $ {\rm{code}}_{{\rm{note}}}^{\left\langle j \right\rangle }$ 和歌词编码向量 $ {\rm{code}}_{ {\rm{lyrics}}}^{\left\langle j \right\rangle }$ 进行拼接：

$ {\rm{cod}}{{\rm{e}}^{\left\langle j \right\rangle }} = \left[ {\begin{array}{*{20}{c}} {{\rm{code}}_{{\rm{note}}}^{\left\langle j \right\rangle }}\\ {{\rm{code}}_{{\rm{lyrics}}}^{\left\langle j \right\rangle }} \end{array}} \right] $

3）将当前输入歌词及旋律片段中l个同步音符及词块编码完成后，作为词曲匹配解码器输入，通过双向LSTM计算得到两个隐藏状态编码，该状态保存了词曲间的情感关系和节奏关系摘要：

$ {c_{{\rm{head}}}},{c_{{\rm{tail}}}} = {f_{{\rm{Bi - LSTM}}}}\left( {{\rm{cod}}{{\rm{e}}^{\left\langle 0 \right\rangle }}, {\rm{cod}}{{\rm{e}}^{\left\langle 1 \right\rangle }},\cdots ,{\rm{cod}}{{\rm{e}}^{\left\langle l \right\rangle }}} \right) $

4）将正反向状态编码拼接，作为全连接层输入。

$ {{c}} = \left[ {\begin{array}{*{20}{c}} {{c_{{\rm{head}}}}}\\ {{c_{{\rm{tail}}}}} \end{array}} \right] $

(9)

解码器通过全连接层对词曲情感特征和节奏特征输入，判断词曲是否匹配，即求解：

$ {p_i} = {\rm{}}P{\rm{(}}{y_i}{\rm{|}}c) = {\rm{sigmoid}}\left( {{W_m}c + {b_m}} \right) $

因此给出目标函数：

$ {\cal L} = - \frac{1}{m}\mathop \sum \limits_{i = 1}^m \left[ {{y_i}\log\left( {{p_i}} \right) + \left( {1 - {y_i}} \right)\log \left( {1 - {p_i}} \right)} \right] $

式中m表示音乐片段个数。

5）重复步骤1）至步骤4），直至当前音乐m个词曲片段判断完成。

2.2 实验过程及结果

本节主要对算法模型实现及结果进行阐述，模型参数同表4。其中两个编码器隐藏单元个数均设置为64，因此解码器输入为128维向量，解码器隐藏单元个数与输入保持一致，经过全连接层及sigmoid得到匹配概率值。算法模型使用零值初始化旋律编码器和歌词编码器的隐藏状态。

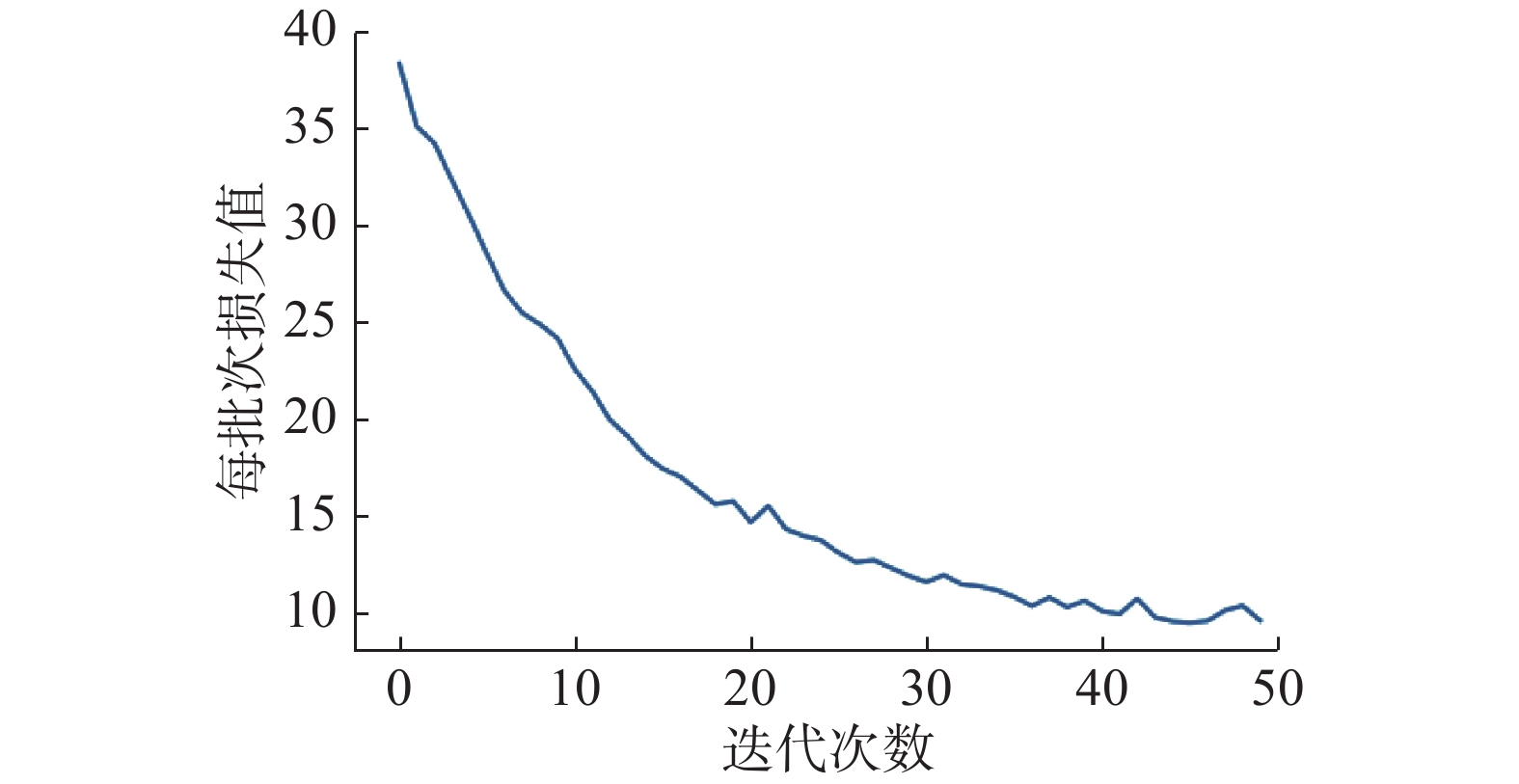
训练过程使用学习率为0.01的Adam^[10]优化器计算并更新反向传播梯度，并基于式(9)损失函数完成迭代训练。迭代过程损失变化如图8所示。

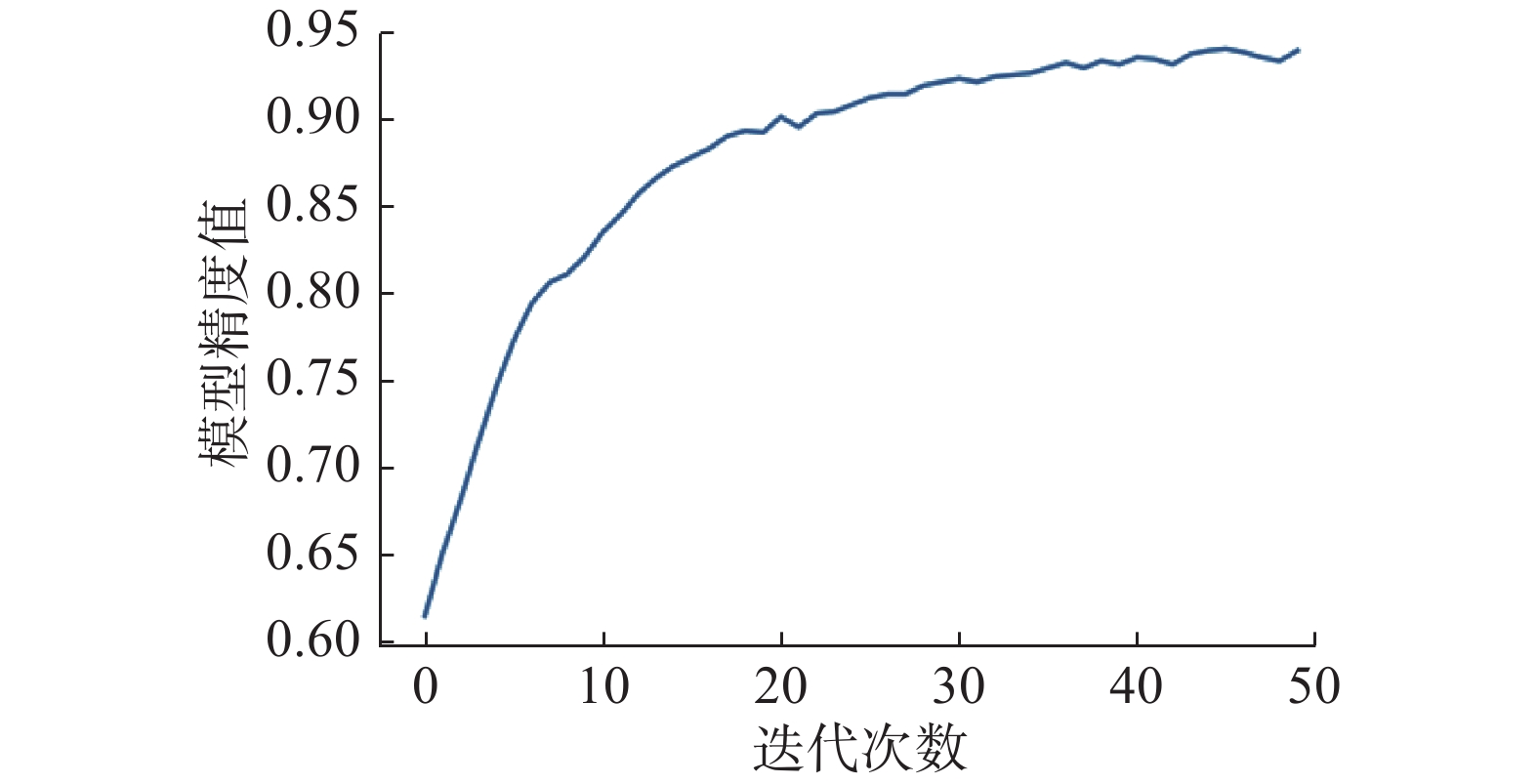
图8中，每批次损失值为批量样本损失之和，每个批次样本片段数64；迭代过程精确度变化如图9所示。

可以发现，模型在迭代过程中是收敛的，在训练集上的精度达到了94.0%，通过实验，在测试集上的精度达到85.9%。

表5为词曲匹配结果，包含了当前词曲名称、最终匹配程度，以及当前音乐在算法模型中被切分为多少个片段和匹配了多少个片段。同时，展示了每个片段的匹配结果。图中展示的音乐为歌曲《I feel lonely》，在单看旋律时，旋律体现较为欢快的情感；单看歌词时，歌词则体现悲伤的情感，但是歌词结合旋律可以发现，该歌曲的节奏感很强，因此整体节奏是吻合的，是一首词曲匹配的音乐。若不将情感和节奏同时考虑，单纯通过情感维度，会认为该乐曲的词曲不匹配。利用本文提出的词曲匹配模型对该首音乐进行词曲评价，可以发现当前音乐18个词曲片段中，有效匹配的片段数为16个，最终词曲匹配得分为0.89，说明算法模型可以综合考虑情感和节奏两个因素，给出一个合理的评价。

进一步的，随机选择一首音乐，当对音乐打乱时，由于词曲间节奏不一致和歌词押韵被打破，因此词曲匹配度将降低。可以发现通过模型计算后，在当前音乐16个片段中，有效匹配的片段数仅为1个，且最终匹配得分仅为0.062 5。

3 结束语

针对情感匹配模型在评价词曲匹配度时存在评价准确度低的缺陷，本文提出综合考虑词曲情感和词曲间节奏关系，进一步提出了基于序列模型的词曲匹配度智能评估算法。仿真结果表明，综合考虑音乐词曲间情感和节奏特征的音乐词曲匹配算法模型，能给音乐作品做出更加准确的智能评估。