2. 江南大学 物联网技术应用教育部工程研究中心,江苏 无锡 214122
2. Engineering Research Center of Internet of Things Technology Applications Ministry of Education, Jiangnan University, Wuxi 214122, China
聚类旨在根据数据点之间的相似性将其划分到不同的簇,使簇内相似度最大,簇间相似度最小[1]。传统聚类方法如K-means算法和模糊聚类算法,缺乏处理复杂数据结构的能力,当样本空间非凸时,易陷入局部最优。近年来,谱聚类算法因其可在任意形状空间内进行聚类,并收敛到全局最优,在非凸数据集表现出良好聚类性能,在人脸识别、社区检测、图像分割等领域有着广泛的应用[2]。
谱聚类将聚类问题转化为图分割问题[3],通过寻找最优子图对数据点进行划分。但现存的多数谱聚类算法在处理大规模数据集时,涉及相似度矩阵构造和对应的拉普拉斯矩阵分解,往往需要高昂的时空开销,高计算成本成为制约其在大规模场景应用中的瓶颈[4]。为实现对大规模数据的高效聚类分析,提升谱聚类算法的扩展性,大量研究方法被提出。Nyström扩展作为一种近似低秩矩阵的有效方法,利用抽样技术,减少特征分解复杂度[5]。针对抽样策略的选择,Zhan等[6]设计了一种自适应的Nyström采样方法,通过多次遍历并更新抽样概率,选取更有意义的样本点,以较小的抽样集获得理想的聚类效果。考虑到高斯核参数调整问题,Yang等[7]提出一种基于层次二部图的谱聚类算法,通过金字塔结构式的多层锚点构造层次二部图降低计算复杂度,此外采用无参数邻接分配策略构造相似度矩阵,避免参数调优过程。蔡登等[8-9]提出基于地标表示的研究,择取具有代表性的数据点作为地标点,通过地标点的稀疏线性组合近似构造图相似度矩阵,从而有效降低谱嵌入的计算复杂度,该算法一定程度上解决了矩阵存储开销问题,但其随机采样确定地标点的方式会造成聚类结果的不稳定,故而地标点的选取为算法的关键。叶茂等[10]利用由近似奇异向量的长度计算的抽样概率来进行抽样,以保证聚类结果的稳定性和精度。Zhang等[11]提出一种基于增量视角的抽样框架,每一个要抽样的点是由先前选定的地标点决定,在地标点之间建立显式关系。但这些改进的方法在择取地标点时都忽略了节点的拓扑属性,其可有效描述亲和图整体结构特性,对于捕捉高维数据空间的拓扑信息有着重要意义。故邓思雨等[12]将PageRank分值作为样本信息量的度量指标,Rafailid等[13]提出一种基于地标选择的快速谱聚类算法,根据加权PageRank算法选择亲和图中最重要的节点作为地标点。Liu等[14]将数据点视为web页面,数据点之间的距离类似为链路间的权重,采用PageRank算法评估数据点的重要性,选择代表点。该方法能够区分球状和非球状的簇,且减少噪声点的负面影响。以上这些改进的谱聚类算法虽然降低了计算复杂度,仍然需要对矩阵进行特征分解。Jia等[15]设计了一种无需特征分解的大规模近似Ncut谱聚类算法,一方面通过对数据点的采样推断数据集的全局特征,减少归一化切割的空间需求,另一方面利用近似加权核k-均值优化Ncut的目标函数,避免拉普拉斯矩阵的直接特征分解。Tian等[16]证明了自编码器和谱聚类之间的相似性,利用栈式自编码器代替特征分解,有效降低计算复杂度。Banijamali等[17]提出将深层结构与地标表示相结合,实现快速且准确的聚类。但上述提及的谱聚类算法均使用传统基于欧氏距离度量方案,并不能完全反映数据复杂的空间分布特性。光俊叶等[18]提出融合欧氏距离和Kendall Tau距离的谱聚类方法,充分利用不同相似性度量从不同角度获取数据信息的优势,全面反映底层结构信息。
本文在地标点采样[8-9]的理论基础上,采用基于网页质量的PageRank算法计算节点的重要性,作为抽样策略依据代替随机抽样,选取代表点作为地标点,通过稀疏表示近似获得图相似度矩阵,以降低存储开销。同时为全面反映数据底层结构信息,将欧氏距离与Kendall Tau距离两种度量方案融合,用局部标准差代替特定的缩放尺度,构造融合多度量方式的自适应相似度矩阵,以提高聚类精度。此外,用栈式自编码器代替特征分解,在联合学习框架中进行嵌入表示学习和聚类,避免微调环节覆盖之前所得最优参数,从而进一步提高聚类精度。
1 相关算法理论 1.1 基于QPR的地标选择PageRank算法采用平均分配思想,将节点权重划分给入链节点,忽略节点质量存在差异性,改进后的加权PageRank算法通过传入链路权重
| $\begin{array}{l} {{Q} } (a) = \dfrac{{{\rm{PR}} (a)}}{{\Bigg(\displaystyle \sum\limits_{b \in {{B}} (a)} {{\rm{PR}} (b)\Bigg)\Bigg/{\rm{MPR}} (a)} }} \\ {\rm{MPR}} (a) = \mathop {\max }\limits_{b \in {{B}} (a)} {\rm{PR}} (b) \end{array} $ | (1) |
式中:
| $\begin{array}{c} {\rm{PR}} (a) = d\displaystyle \sum\limits_{b \in {\rm{B}} (a)} {{\rm{PR}} (b)\Pr (b \to a) + \frac{{(1 - d)}}{n}} \\ \Pr (b \to a) = {\rm{Q} } (a)/\displaystyle \sum\limits_{c \in {\rm{F}} (b)} {{\rm{Q} } (c)} \end{array} $ | (2) |
式中:
| $\dfrac{{{\rm{PR}} {{(a)}_{{\rm{iter}} - 1}} - {\rm{PR}} {{(a)}_{{\rm{iter}}}}}}{{{\rm{PR}} {{(a)}_{{\rm{iter}}}}}} \leqslant \beta $ | (3) |
该式表示上一次迭代与当前迭代之间的归一化差值,其中,
相似度矩阵的构造是谱聚类算法的一个重要步骤,而高斯核函数是构造相似度矩阵最常用的度量方法之一。给定数据集
| ${A_{ij}} = \left\{ \begin{array}{l} \exp \Bigg(\dfrac{{ - {\rho ^2}({x_i},{x_j})}}{{2{\sigma ^2}}}\Bigg),\;\;\;i \ne j \\ 0,\;\;\;i = j \end{array} \right.$ |
式中:
| ${A_{ij}} = \left\{ \begin{array}{l} \exp \Bigg(\dfrac{{ - {\rho ^2}({x_i},{x_j})}}{{2{\sigma _i}{\sigma _j}}}\Bigg),\;\;\;i \ne j \\ 0,\;\;\;i = j \end{array} \right.$ |
特定的缩放参数
| ${A_{ij}} = \left\{ \begin{array}{l} \exp \Bigg(\dfrac{{ - {\rho ^2}({x_i},{x_j})}}{{2{\sigma _{{\rm{std}}\_i}}{\sigma _{{\rm{std}}\_j}}}}\Bigg),\;\;\;i \ne j \\ 0,\;\;\;i = j \end{array} \right.$ | (4) |
由1.2节可以看出谱聚类算法中所构造的相似度矩阵维度为
| ${\hat x_i} = \displaystyle \sum\limits_{j = 1}^p {{Z_{ji}}{y_j}} $ |
式中:
| ${Z_{ji}} = \left\{ \begin{array}{l} \dfrac{{{A_{ji}}}}{{\displaystyle \sum\limits_{m \in {\rm{KNN}}({x_i})} {{A_{mi}}} }},\;\;\;j \in {\rm{KNN}}({x_i})\\ 0,\;\;\;j \notin {\rm{KNN}}({x_i}) \end{array} \right.$ | (5) |
式中:
| $ {\rm{KT}}({L_1},{L_2}) = \left| {\{ (i,j):i<j,(({L_{i1}}<{L_{j1}}) \wedge ({L_{i2}}<{L_{j2}})){\rm{or}}(({L_{i1}}>{L_{j1}}) \wedge ({L_{i2}}>{L_{j2}}))\} } \right| $ | (6) |
式中:
若将欧氏距离及Kendall Tau距离两种度量方式融合,生成增强的相似度矩阵,能在反映点对之间地理相似性的同时考虑点之间的拓扑逻辑相似性。将点
| ${\rho _2}({x_i},{x_j}) = {\rm{KT}} ({{\rm{List}} _i},{{\rm{List}} _j})$ |
从度量融合的角度来看,大多数主流的思想都是通过线性组合多个亲和图来获得互补的相似信息[23],然而这个线性组合对分配给每个度量的权重很敏感,且来自多个亲和图的互补信息并非线性相关的。为探索两种距离度量方案相互融合的思想,综合考虑相邻点的几何分布和拓扑分布,受到联合训练算法的启发,采用基于消息传递理论和交叉扩散过程的融合方法。以完全相似矩阵作为初始状态矩阵,即对式(5)不考虑
| ${F_{ji}} = \frac{{{A_{ji}}}}{{\displaystyle \sum\limits_{m = 1}^p {{A_{mi}}} }}$ | (7) |
式(7)分别采用欧氏距离、Kendall Tau距离度量方法计算获得的完全相似矩阵表示为
| $\begin{array}{l} {{F}}_{h + 1}^{(1)} = {{{Z}}^{(1)}} \times {{F}}_h^{(2)} \times {({{{Z}}^{(1)}})^{\mathop{\rm T}\nolimits} }\\ {{F}}_{h + 1}^{(2)} = {{{Z}}^{(2)}} \times {{F}}_h^{(1)} \times {({{{Z}}^{(2)}})^{\rm{T}}} \end{array}$ | (8) |
式中:
| ${{Z}} = \dfrac{{{{F}}_h^{(1)} + {{F}}_h^{(2)}}}{2}$ | (9) |
从概率角度分析该交叉扩散过程,对于状态矩阵
在由式(9)获得稀疏表示矩阵
| ${{L}} = {{{D}}^{ - \frac{1}{2}}}{{\hat G}}{{{D}}^{ - \frac{1}{2}}} = {{{D}}^{ - \frac{1}{2}}}{{{\hat Z}}^{\rm{T}} }{{\hat Z}}{{{D}}^{ - \frac{1}{2}}}$ | (10) |
然后将
假定聚类任务为
| $J = {J_r} + \gamma {J_c}$ | (11) |
其中
对于训练所获得的嵌入特征表示,在文献[23]引入了由t-SNE衡量的软标签分布
| ${p_{ik}} = \dfrac{{{{(1 + {{\left\| {{h_i} - {m_j}} \right\|}^2})}^{ - 1}}}}{{\displaystyle \sum\limits_{j = 1}^K {{{(1 + {{\left\| {{h_i} - {m_j}} \right\|}^2})}^{ - 1}}} }},\quad j = 1,2, \cdots ,K$ | (12) |
式中
| ${J_c} = {\rm{KL}} ({{Q}}\parallel {{P}}) = \dfrac{1}{N}\displaystyle \sum\limits_i {\displaystyle \sum\limits_k {{q_{ik}}\lg \frac{{{q_{ik}}}}{{{p_{ik}}}}} } $ | (13) |
其中,辅助目标分布分量
| ${q_{ik}} = \dfrac{{p_{ik}^2/\displaystyle \sum\limits_{{i^{'}}} {{p_{{i^{'}}k}}} }}{{\displaystyle \sum\limits_{{k^{'}}} {\Bigg(p_{i{k^{'}}}^2/\displaystyle \sum\limits_{{i^{'}}} {{p_{{i^{'}}{k^{'}}}}\Bigg)} } }}$ | (14) |
最小化聚类损失目标函数
| ${J_r} =\displaystyle \sum\limits_{i = 1}^n {\left\| {{x_i} - {g_{{W'}}}({h_i})} \right\|_2^2} $ | (15) |
关于自编码器参数
| $\dfrac{{\partial {J_c}}}{{\partial {h_i}}} = 2\displaystyle \sum\limits_{j = 1}^K {{{(1 + {{\left\| {{h_i} - {\mu _j}} \right\|}^2})}^{ - 1}}({q_{ij}} - {p_{ij}})(} {h_i} - {\mu _j})$ |
| $\dfrac{{\partial {J_c}}}{{\partial {\mu _i}}} = 2\displaystyle \sum\limits_{j = 1}^K {{{(1 + {{\left\| {{h_i} - {\mu _j}} \right\|}^2})}^{ - 1}}({p_{ij}} - {q_{ij}})(} {h_i} - {\mu _j})$ |
将
| $W = W - \dfrac{\lambda }{m}\displaystyle \sum\limits_{i = 1}^m {\Bigg(\dfrac{{\partial {J_r}}}{{\partial W}}} + \gamma \frac{{\partial {J_c}}}{{\partial W}}\Bigg)$ | (16) |
| ${W'} = {W'} - \dfrac{\lambda }{m}\displaystyle \sum\limits_{i = 1}^m {\dfrac{{\partial {J_r}}}{{\partial {W'}}}} $ | (17) |
| ${\mu _j} = {\mu _j} - \dfrac{\lambda }{m}\displaystyle \sum\limits_{j = 1}^k {\dfrac{{\partial {J_r}}}{{\partial {\mu _j}}}} $ | (18) |
算法 结合度量融合和地标表示的自编码谱聚类算法
输入 输入数据X,聚类数目
输出 自编码器参数
1)根据式(1)、(2)计算节点PR值,当所有节点满足式(3)时,停止迭代,PR值降序排列,择取前
2)依据式(4)成对相似度计算,引入
3)将
4)通过式(10)构造拉普拉斯矩阵,将
5)对嵌入特征表示
6)若迭代次数大于
7)根据式(12)和式(14)计算
8)根据式(11)、(13)和(15)计算损失目标函数;
9)采用mini-batch随机梯度算法反向传播逐层训练网络,根据式(16)~(18)更新整个网络参数
10)根据软标签分布
首先,从
为证明本文算法适用于大规模数据集,选取如下5个数据集:MNIST、USPS、COIL100、CoverType和CIFAR10。这5个数据集包含不同类型的图像,如手写数字、英文字母表、物体图像和森林植被类等,样本数较大,可以有效验证本文算法在大规模数据集上的聚类性能。表1为相关数据集的具体信息。仿真实验硬件环境为Intel(R) Core(TM) i7-6700 CPU @3.40 GHz;16 GB RAM;操作系统:Windows7;编程语言:Python 3.5。
| 表 1 实验数据集描述 Tab.1 The description of experimental datasets |
本文算法与文献[8-9]基于地标表示的快速谱聚类算法LSC-R和LSC-K,未考虑地标点的基于自编码的谱聚类算法DEC[25]及GraEn[16]、文献[17]中自编码器与地标点结合的快速谱聚类算法SCAL-R及SCAL-K进行对比。LSC-R及SCAL-R是通过随机采样获取
为保证算法之间的公平对比,具体参数如下设置:文献[8-9]、[17]及本文算法涉及的地标点个数
为了比较这些算法性能,通过聚类结果和样本真实标签进行对比。采用聚类准确率(ACC)和标准化互信息(NMI)来作为度量指标进行评估比较。ACC和NMI这2种度量标准在[0,1]之间取值,值越大聚类性能越好。各种算法在5个大规模数据集的实验结果如表2、3所示。
| 表 2 不同数据集的准确率(ACC)的比较 Tab.2 Comparison of clustering accuracy (ACC) for different data sets |
| 表 3 不同数据集的标准化互信息(NMI)的比较 Tab.3 Comparison of normalized mutual information (NMI) for different data sets |
通过表2、3两种指标下的各种算法性能度量对比,可以看出本文提出的结合度量融合和地标表示的自编码谱聚类算法在MNIST、LetterRec、COIL100、CoverType及CIFAR10这5个大规模数据集上,相对于基于地标表示的快速谱聚类算法LSC-R和LSC-K,未考虑地标点的基于自编码的谱聚类算法DEC及GraEn,自编码器与地标点结合的快速谱聚类算法SCAL-R及SCAL-K,在ACC和NMI两种指标下均表现出了更为理想的聚类性能。同时,还可以得出如下结论:
1)本文算法在稀疏表示矩阵构造部分由于引入网页质量进行地标点择取,并进行度量融合计算点对相似度,在算法复杂度方面,相对于旨在提升谱聚类算法效率的LSC-R和LSC-K处于劣势。从运行时间上看,在MNIST数据集上,LSC-R及LSC-K算法仅需10 s左右,本文算法则需200~300 s的运行时间,但相对于DEC及GraEn,本文算法运行时间降低了1 000~2 000 s,有了很大的提升。且从表2中可以看出,就ACC,本文算法与LSC-K算法相比,在MNIST、LetterRec、COIL100、CoverType及CIFAR10F分别提升了17.42%、16.57%、34.47%、7.75%、10.89%,与随机抽样择取地标点的LSC-R算法相比,优势更大。同样地,从表3看出,本文算法NMI值也有了明显的提升。而与SCAL-R及SCAL-K算法相比,本文融合两种距离度量多角度描述数据集的结构信息,使其在ACC、NMI两种指标上均处于优势。
2)相比未考虑地标点的基于自编码的谱聚类算法DEC及GraEn,本文算法ACC和NMI也有了一定的提升,如与DEC算法对比,本文算法在LetterRec数据集上ACC、NMI分别提升了17.15%、5.84%。说明本文构造的结合度量融合和地标表示的相似度矩阵更全面地反映了数据之间的结构信息,且运行效率大大得到提升。
3)此外,间接可以看出,以LSC-R、LSC-K为代表的引入地标点算法与DEC、GraEn为代表的基于深度自编码算法相比,在MNIST、COIL100及CIFAR10这些维度相对较高的大规模数据集中,聚类性能处于劣势,但在LetterRec及CoverType维度较低的数据集上则处于优势,可见基于自编码器的算法对于高维数据集较为友好,地标点的择取有利于大规模数据集的聚类性能。
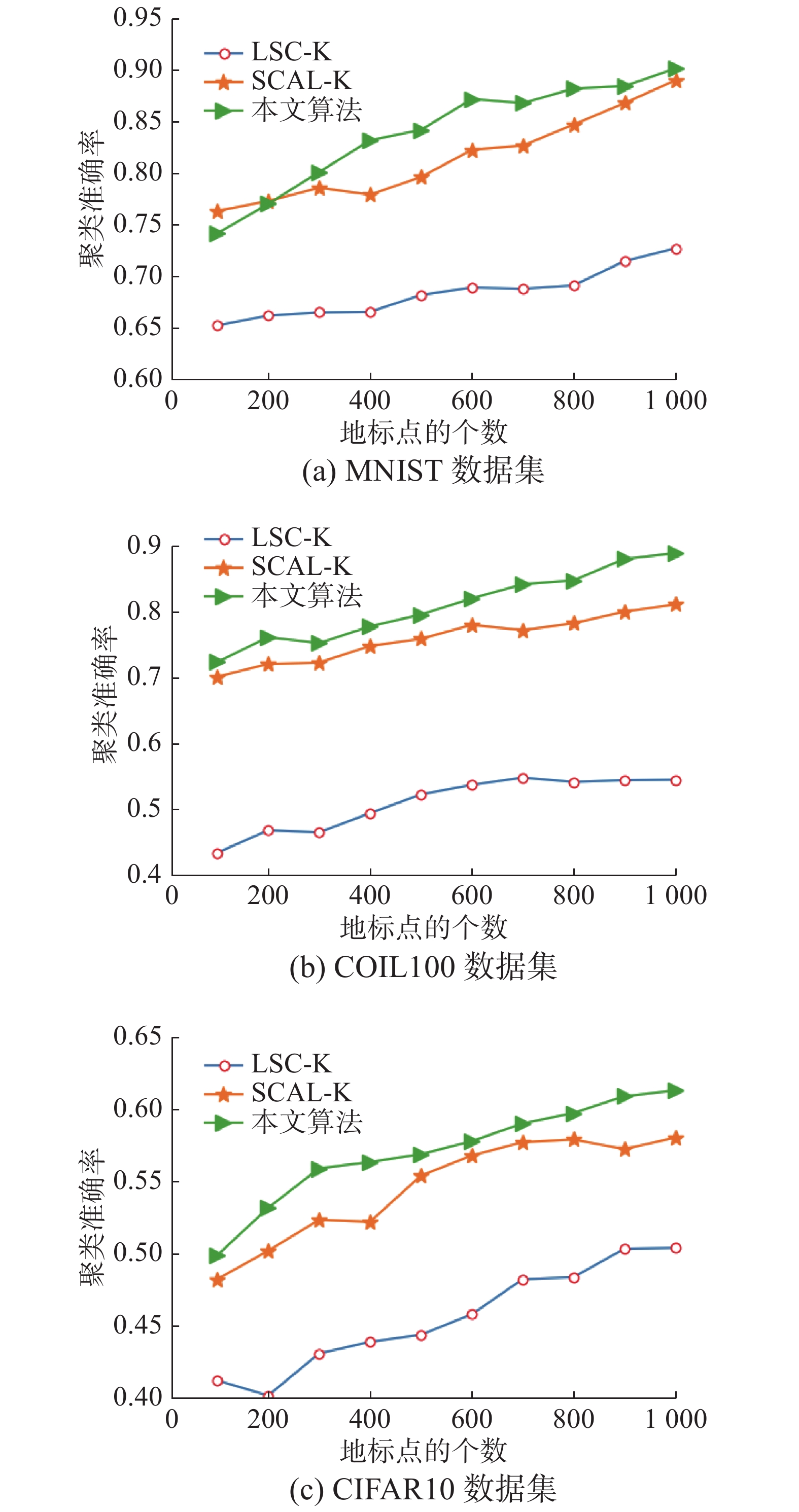
本文算法采用欧氏距离与Kendall Tau距离度量融合的方式,挖掘数据的真实分布,从上述结论1)可以看出算法性能会受到距离度量方式的影响。为深入分析,将本文算法稀疏表示矩阵构造部分,分别采用基于欧氏距离(SCE)与基于Kendall Tau距离(SCK)计算点对相似度,采用ACC和NMI两个指标与本文算法融合度量方案进行性能对比。表4显示3种算法在3个数据集上的算法性能。从表4可以看出,2种距离度量方式的融合一定程度上能更全面地反映数据之间的结构信息,从而获得更为理想的聚类性能。欧氏距离与Kendall Tau距离这两种度量方式的优劣,并不能准确地从数据中评判出来,但结合表2、3可以看出,基于本文算法的SCE和SCK算法在3个数据集上与其他几种算法相比,相对处于优势。特别是与SCAL_R及SCAL_K算法对应ACC和NMI对比可以得出,本文通过基于网页质量的PageRank算法择取地标点总体上要优于随机选择与k-means算法的方法,但也有低于这两种方法的情况出现,为深入分析,更改地标点个数
| 表 4 不同距离度量方案的算法性能对比 Tab.4 Performance comparision of algorithms with different distance measurement schemes |
|
Download:
|
| 图 1 不同数据集上3种算法的ACC比较 Fig. 1 Comparison of the ACCs of three algorithms on different datasets | |
|
Download:
|
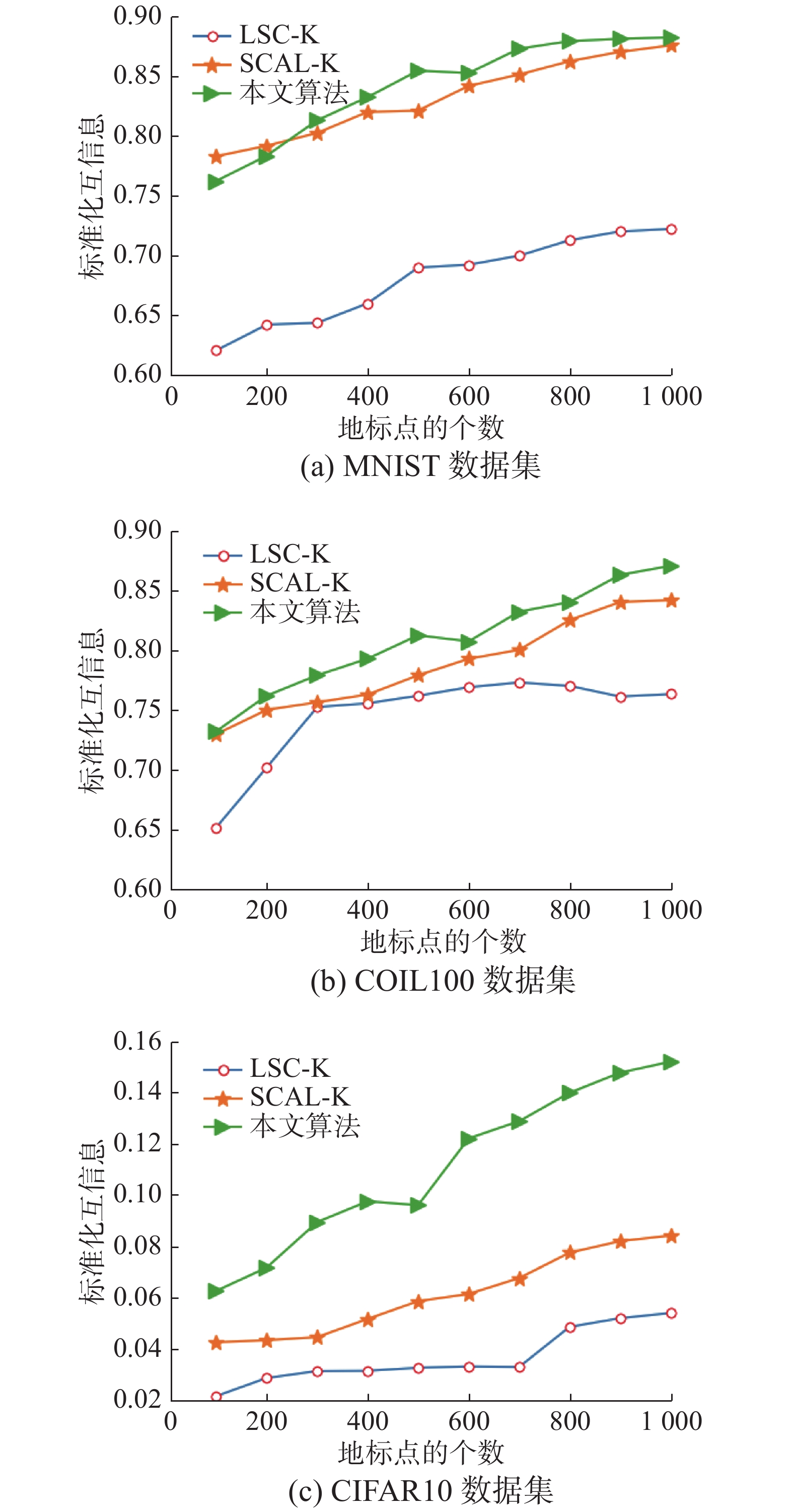
| 图 2 不同数据集上3种算法的NMI比较 Fig. 2 Comparison of the NMIs of three algorithms on different dataset | |
随着数据规模的增大,结构信息的复杂度提高,在聚类过程中往往会耗费大量时间,存在相似度矩阵存储开销大及矩阵分解复杂度高的问题,且聚类精度也会受到影响。为此,本文提出一种结合度量融合和地标表示的自编码谱聚类算法,通过引入节点相对质量概念作为地标点选择的依据,以地标点与其他样本点之间相似度构造图相似度矩阵,以降低存储开销。同时,融合欧氏距离与Kendall Tau距离作为相似度度量方式,充分挖掘数据底层结构信息,且以栈式自编码器代替拉普拉斯矩阵分解步骤,通过联合学习框架进一步提高聚类精度。实验表明在几种大规模数据集上本文算法具有较好的聚类性能,但由于本文算法聚类精度受地标点个数影响较大,且选取方式略微增加了算法复杂度,未来将致力于寻求更为有效的地标点选择方式,在保证聚类精度的同时进一步降低算法复杂度。
| [1] |
WANG Lijuan, DING Shifei, JIA Hongjie. An improvement of spectral clustering via message passing and density sensitive similarity[J]. IEEE access, 2019, 7: 101054-101062. DOI:10.1109/ACCESS.2019.2929948 ( 0) 0)
|
| [2] |
LI Xinning, ZHAO Xiaoxiao, CHU Derun, et al. An autoencoder-based spectral clustering algorithm[J]. Soft computing, 2020, 24(3): 1661-1671. DOI:10.1007/s00500-019-03994-5 ( 0) 0)
|
| [3] |
王一宾, 李田力, 程玉胜. 结合谱聚类的标记分布学习[J]. 智能系统学报, 2019, 14(5): 966-973. WANG Yibin, LI Tianli, CHENG Yusheng. Label distribution learning based on spectral clustering[J]. CAAI transactions on intelligent systems, 2019, 14(5): 966-973. DOI:10.11992/tis.201809019 (  0) 0)
|
| [4] |
赵晓晓, 周治平. 结合稀疏表示与约束传递的半监督谱聚类算法[J]. 智能系统学报, 2018, 13(5): 855-863. ZHAO Xiaoxiao, ZHOU Zhiping. A semi-supervised spectral clustering algorithm combined with sparse representation and constraint propagation[J]. CAAI transactions on intelligent systems, 2018, 13(5): 855-863. DOI:10.11992/tis.201703013 (  0) 0)
|
| [5] |
LANGONE R, SUYKENS J A K. Fast kernel spectral clustering[J]. Neurocomputing, 2017, 268: 27-33. DOI:10.1016/j.neucom.2016.12.085 ( 0) 0)
|
| [6] |
ZHAN Qiang, MAO Yu. Improved spectral clustering based on Nyström method[J]. Multimedia tools and applications, 2017, 76(19): 20149-20165. DOI:10.1007/s11042-017-4566-4 ( 0) 0)
|
| [7] |
YANG Xiaojun, YU Weizhong, WANG Rong, et al. Fast spectral clustering learning with hierarchical bipartite graph for large-scale data[J]. Pattern recognition letters, 2020, 130(2): 345-352. ( 0) 0)
|
| [8] |
CHEN Xinlei, CAI Deng. Large scale spectral clustering with landmark-based representation[C]//Proceedings of the 24th AAAI Conference on Artificial Intelligence. San Francisco, USA, 2011: 313−318.
( 0) 0)
|
| [9] |
CAI Deng, CHEN Xinlei. Large scale spectral clustering via landmark-based sparse representation[J]. IEEE trans cybern, 2015, 45(8): 1669-1680. DOI:10.1109/TCYB.2014.2358564 ( 0) 0)
|
| [10] |
叶茂, 刘文芬. 基于快速地标采样的大规模谱聚类算法[J]. 电子与信息学报, 2017, 39(2): 278-284. YE Mao, LIU Wenfen. Large scale spectral clustering based on fast landmark sampling[J]. Journal of electronics and information technology, 2017, 39(2): 278-284. (  0) 0)
|
| [11] |
ZHANG Xianchao, ZONG Linlin, YOU Quanzeng, et al. Sampling for Nyström extension-based spectral clustering: incremental perspective and novel analysis[J]. ACM transactions on knowledge discovery from data, 2016, 11(1): 1-25. ( 0) 0)
|
| [12] |
邓思宇, 刘福伦, 黄雨婷, 等. 基于PageRank的主动学习算法[J]. 智能系统学报, 2019, 14(3): 551-559. DENG Siyu, LIU Fulun, HUANG Yuting, et al. Active learning through PageRank[J]. CAAI transactions on intelligent systems, 2019, 14(3): 551-559. DOI:10.11992/tis.201804052 (  0) 0)
|
| [13] |
RAFAILID D, CONSTANTINOU E, MANOLOPOULOS Y. Landmark selection for spectral clustering based on weighted PageRank[J]. Future generation computer systems, 2017, 68: 465-472. DOI:10.1016/j.future.2016.03.006 ( 0) 0)
|
| [14] |
LIU Li, SUN Letian, CHEN Shiping, et al. K-PRSCAN: A clustering method based on PageRank[J]. Neurocomputing, 2016, 175: 65-80. DOI:10.1016/j.neucom.2015.10.020 ( 0) 0)
|
| [15] |
JIA Hongjie, DING Shifei, DU Mingjing, et al. Approximate normalized cuts without eigen-decomposition[J]. Information sciences, 2016, 374: 135-150. DOI:10.1016/j.ins.2016.09.032 ( 0) 0)
|
| [16] |
TIAN Fei, GAO Bin, CUI Qing, et al. Learning deep representations for graph clustering[C]//Proceedings of the 28th AAAI Conference on Artificial Intelligence. Québec, Canada, 2014: 1293−1299.
( 0) 0)
|
| [17] |
BANIJAMALI E, GHODSI A. Fast spectral clustering using autoencoders and landmarks[C]//Proceedings of International Conference Image Analysis and Recognition. Montreal, Canada, 2017: 380−388.
( 0) 0)
|
| [18] |
光俊叶, 邵伟, 孙亮, 等. 基于融合欧氏距离与Kendall Tau距离度量的谱聚类算法[J]. 控制理论与应用, 2017, 34(6): 783-789. GUANG Junye, SHAO Wei, SUN Liang, et al. Spectral clustering with mixed Euclidean and Kendall Tau metrics[J]. Control theory & applications, 2017, 34(6): 783-789. DOI:10.7641/CTA.2017.60606 (  0) 0)
|
| [19] |
WEI Kai, TIAN Pingfang, GU Jingguang, et al. RDF data assessment based on metrics and improved PageRank algorithm[C]//Proceedings of International Conference on Database Systems for Advanced Applications. Suzhou, China, 2017: 204−212.
( 0) 0)
|
| [20] |
谢娟英, 丁丽娟. 完全自适应的谱聚类算法[J]. 电子学报, 2019, 47(5): 1000-1008. XIE Juanying, DING Lijuan. The true self-adaptive spectral clustering algorithms[J]. Acta electronica sinica, 2019, 47(5): 1000-1008. DOI:10.3969/j.issn.0372-2112.2019.05.004 (  0) 0)
|
| [21] |
NG A Y, JORDAN M I, WEISS Y. On spectral clustering: analysis and an algorithm[C]//Proceedings of Neural Information Processing Systems 14, NIPS 2001. Vancouver, British Columbia, Canada, 2002: 849−856.
( 0) 0)
|
| [22] |
XIE Juanying, ZHOU Ying, DING Lijuan. Local standard deviation spectral clustering[C]// Proceedings of the 2018 IEEE International Conference on Big Data and Smart Computing (BigComp). Shanghai, China, 2018: 242−250.
( 0) 0)
|
| [23] |
WANG Bo, JIANG Jiayan, WANG Wei, et al. Unsupervised metric fusion by cross diffusion[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, Rhode Island, 2012: 2997−3004.
( 0) 0)
|
| [24] |
COIFMAN R R, LAFON S. Diffusion maps[J]. Applied and computational harmonic analysis, 2006, 21(1): 5-30. DOI:10.1016/j.acha.2006.04.006 ( 0) 0)
|
| [25] |
XIE Junyuan, GIRSHICK R B, FARHADI A. Unsupervised deep embedding for clustering analysis[C]//Proceedings of the 33nd International Conference on Machine Learning. New York, USA, 2016: 478−487.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


