受施工误差、测量误差及结构变形等因素影响，地铁隧道竣工后，建成的实际隧道与原始设计线路对应的理论隧道存在偏差。为了度量偏差，将整条隧道按相同距离间隔选取多个断面，计算出每个断面中关键点的侵限值，根据所有断面关键点侵限值大小即可判断隧道的偏差大小，进而判断原始设计线路方案是否满足行车要求。当隧道的偏差不满足要求时，需要调整原始设计线路，重新计算每个断面中关键点的侵限值。直至调整后的设计线路满足行车要求，才能进行列车轨道的铺设。但以上传统方法存在2个缺陷：

1)无法实时地计算每个断面关键点的侵限值。传统断面测量方法只测量每个断面特定10个点的坐标位置，结合设计线路方案便可计算出断面关键点的侵限值，然而，当设计线路方案进行了调整，原来测量的每个断面10个点的坐标位置会发生变化，需要重新测量每个断面的10个点坐标位置，才能计算出每个断面的偏差程度，而重新测量需要耗费大量的时间，测量工作完成后才能计算出每个断面关键点的侵限值。

2)根据测量值计算出的设备尺寸误差较大。传统计算设备尺寸的方法是基于轨检小车的轨距测量值^[1]，轨距测量值容易受人为因素的影响，导致测量数据不准确，进而使得设备尺寸的计算误差增大。

三维激光扫描技术获取隧道点云大数据的测量方式提高了侵限值计算的效率以及关键点坐标的准确度。三维激光扫描技术能够密集地、全面地对实际隧道进行数据采集^[2]，从而获取实际隧道点云大数据。与传统的基于断面10个关键点的测量方法相比，点云大数据能具体展示实际隧道细节信息。当设计线路发生变化时，能从点云大数据中快速、实时地抽取相应断面的关键点坐标；同时，点云大数据还具有很高的精度，这为侵限值及关键点坐标的计算提供了可靠的精度保证。

目前很多学者对点云大数据在隧道变形监测的应用做了大量研究。2008年，毕俊等^[3]率先将点云大数据应用于地铁隧道变形监测，从地铁隧道数据采集、三维模型建立、数据处理、成果输出等方面进行了分析，该方法的主要优点是可以一次快速、完整、全方位采集隧道内部的表面数据。随后，康志忠等^[4-5]、谢雄耀等^[6]、潘国荣等^[7]、张明智等^[8]对点云大数据在隧道形变监测中的应用做了一系列的研究。然而，隧道变形监测并未能充分发挥点云大数据高密度以及高精度的优势。

本文摒弃早期研究中的隧道多点测量^[9]，采用三维激光扫描的方式收集隧道数据，高精度的扫描仪能将误差控制在允许范围之内，完全满足隧道测量的精度要求。由于扫描收集到的点云大数据比较粗糙且有过多的冗余部分，需要对点云大数据进行进一步降噪以及分块处理，加快点云数据的查找过程。根据给定的设计线路参数，搭建设计路线对应的理论隧道模型，从而准确地找到理论线路对应的断面。根据设计线路参数建立的理论隧道模型以及点云大数据对应的实际隧道模型，便可计算隧道的侵限值。最后，本文采用深度神经网络学习设计路线与侵限值之间的函数关系，采用梯度下降方法求取函数的极值，从而得到最优线路参数，达到减小实际隧道与理论隧道偏差的目的。

1 点云大数据获取及处理 1.1 点云大数据的获取

地铁隧道建成后，需要建立实际隧道模型，从而在计算机中虚拟实际隧道。现有的方法是基于三维激光扫描的点云大数据建模，三维激光扫描能快速、高效地获取隧道内壁的坐标位置，所有的内壁坐标点构成隧道的点云大数据。点云大数据在三维空间中展现的是隧道内壁的三维坐标点。

扫描仪获得的点云坐标为扫描仪独立坐标系下的坐标，通过传感器及轨道设计线路等信息可得到地铁测量坐标系下的坐标，为得到点云在地铁测量坐标系下的坐标，需要标定扫描仪和轨道的相对位置关系^[10]。标定的过程实际上是获得扫描坐标系和地铁测量坐标系之间的旋转参数和平移参数的过程。获取地铁坐标系下的点云大数据基本流程如下：

1)建立地铁测量坐标系；

2)水平调整扫描仪，使得两个坐标系相对平行；

3)在隧道内壁放置扫描标志；

4)在地铁测量坐标系下测量标志中心坐标和扫描仪坐标；

5)扫描仪扫描隧道内壁，同时，得到扫描仪坐标系下的标志位置坐标；

6)将扫描仪下的点云坐标转换为地铁测量坐标系下的坐标；

7)获取地铁坐标系下的点云大数据。

1.2 点云分块处理

高密度的点云大数据降低了抽取特定点云数据的效率。在空间中给定平面，需要在所有点云大数据中抽取属于该平面的点云切片，抽取过程需要耗费大量计算资源以及时间，并且可能会导致计算机因运算内存不足而无法计算出结果。本文根据原始设计线路对点云大数据进行切分索引，从而将点云大数据切分成多个文件，并为这些文件加上对应索引，以便在搜索任意断面的点云数据时能够从文件名中快速找到相应的数据。点云分块具体步骤如下：

1)令 ${P_{{m_0}}}$ = ${P_s}$ ， ${P_{{m_1}}}$ = ${P_s}$ +0.01；

2)根据F(Ω₁,Ω₂)和 ${P_{{m_0}}}$ 、 ${P_{{m_1}}}$ 得到 ${P_s}$ 处曲线的法平面方程 ${s_{{P_{{m_0}}}}}$ 、 ${s_{{P_{{m_1}}}}}$ ；

3)从点云文件中找到介于 ${s_{{P_{{m_0}}}}}$ 、 ${s_{{P_{{m_1}}}}}$ 之间的点并存储到文件 ${\rm{fil}}{{\rm{e}}_{{m_0}}}$ 中去；

4)令 ${P_{{m_0}}}$ = ${P_{{m_1}}}$ ， ${P_{{m_1}}}$ = ${P_{{m_1}}}$ +0.01；

5)重复2)~4) 直到 ${m_0}$ >e。

其中s、 ${m_0}$ 、 ${m_1}$ 表示里程数值，Ω₁表示纵断面参数，Ω₂表示平面参数，F(Ω₁,Ω₂)表示直角坐标系中调线调坡的线路中心线方程， ${P_{{m_0}}}$ 表示F(Ω₁,Ω₂)上里程为 ${m_0}$ 的点， ${P_{{m_1}}}$ 表示F(Ω₁,Ω₂)上里程为 ${m_1}$ 的点，e表示F(Ω₁,Ω₂)的终点里程。

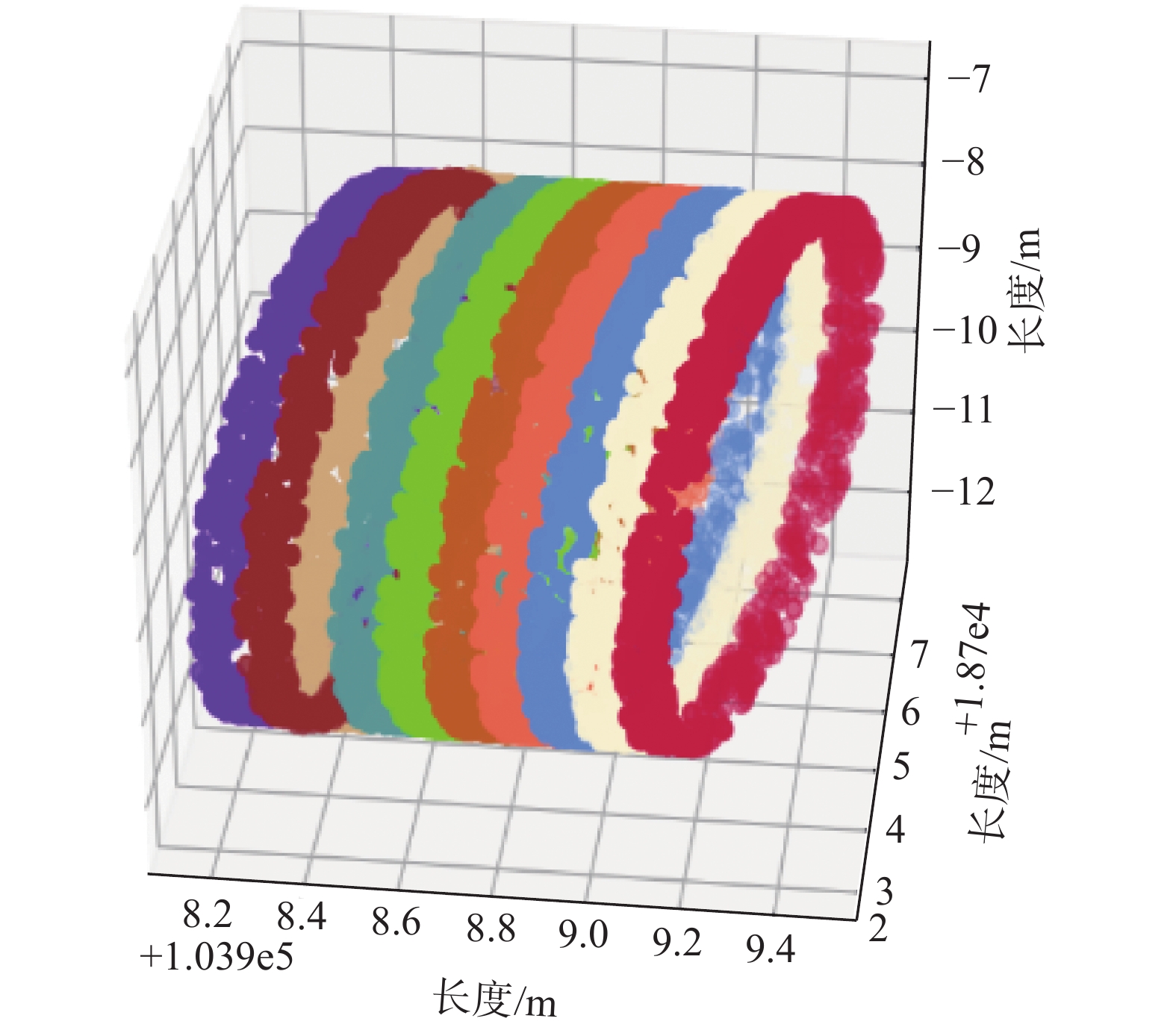
处理后的点云如图1所示，图中一种颜色表示一个文件中的点云数据。

1.3 点云去噪处理

通过三维激光扫描技术获取的点云大数据具有非接触测量、高密度、高精度、高效率、数字化采集、信息丰富等优点^{[11, 19, 22]}。然而，由于激光信号实际测量过程中会受到目标表面反射特性、大气折射等影响，收集到的点云大数据不可避免地会产生噪声。且隧道内壁常附着有电缆、电灯、管道等干扰设备，成为多余的噪声点云，导致模拟隧道与实际隧道不相符。因此，在应用点云数据前，需对原始点云大数据进行去噪处理。点云去噪的具体步骤如下：

1)令m=s+0.01；

2)根据最小二乘法在二维坐标系中拟合出实际的圆心O和半径R；

3)令m=m+0.01；

4)根据F(Ω₁,Ω₂)和 ${P_m}$ 得到 ${P_m}$ 处曲线的法平面方程 ${s_{{P_m}}}$ ；

5)将 ${\rm{fil}}{{\rm{e}}_m}$ 中的点投影到 ${s_{{P_m}}}$ 上，将平面中的所有点云映射到平面 ${s_{{P_m}}}$ 的二维坐标系中；

6)设二维坐标系中的点与点O距离为d，删除d> $R{\rm{ + }}$ 0.01与d< $R - $ 0.01的点，根据最小二乘法拟合出实际的圆心O和半径R；

7)重复4)~ 6)直到 $m$ >e。

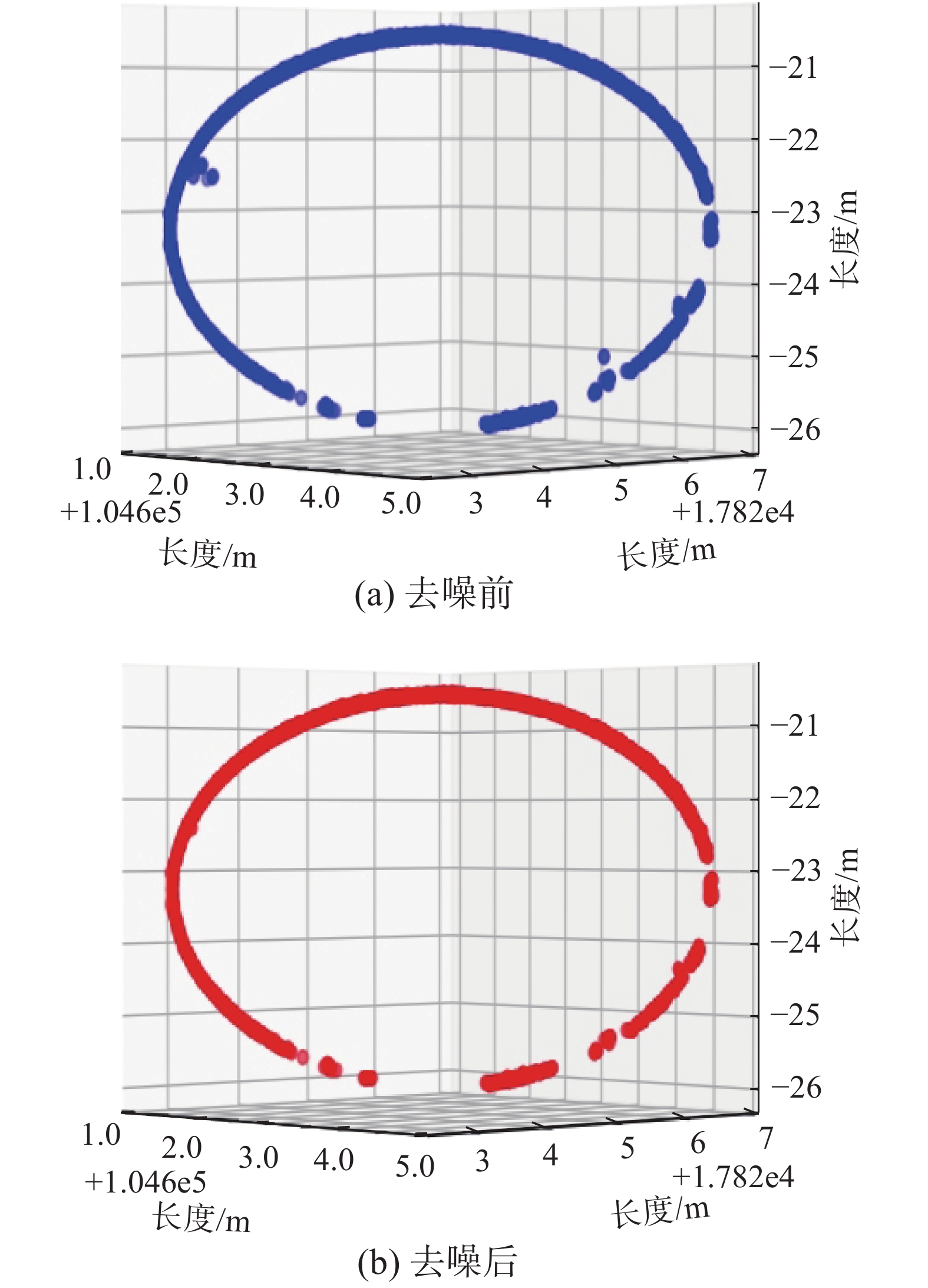
图2为去噪前后的对比图，其中蓝色的点云表示去噪之前的点云，红色的点云代表经过去噪算法处理之后的点云。从图中可以明显看出，使用去噪算法，能够将点云中处于半空中的噪点去除。

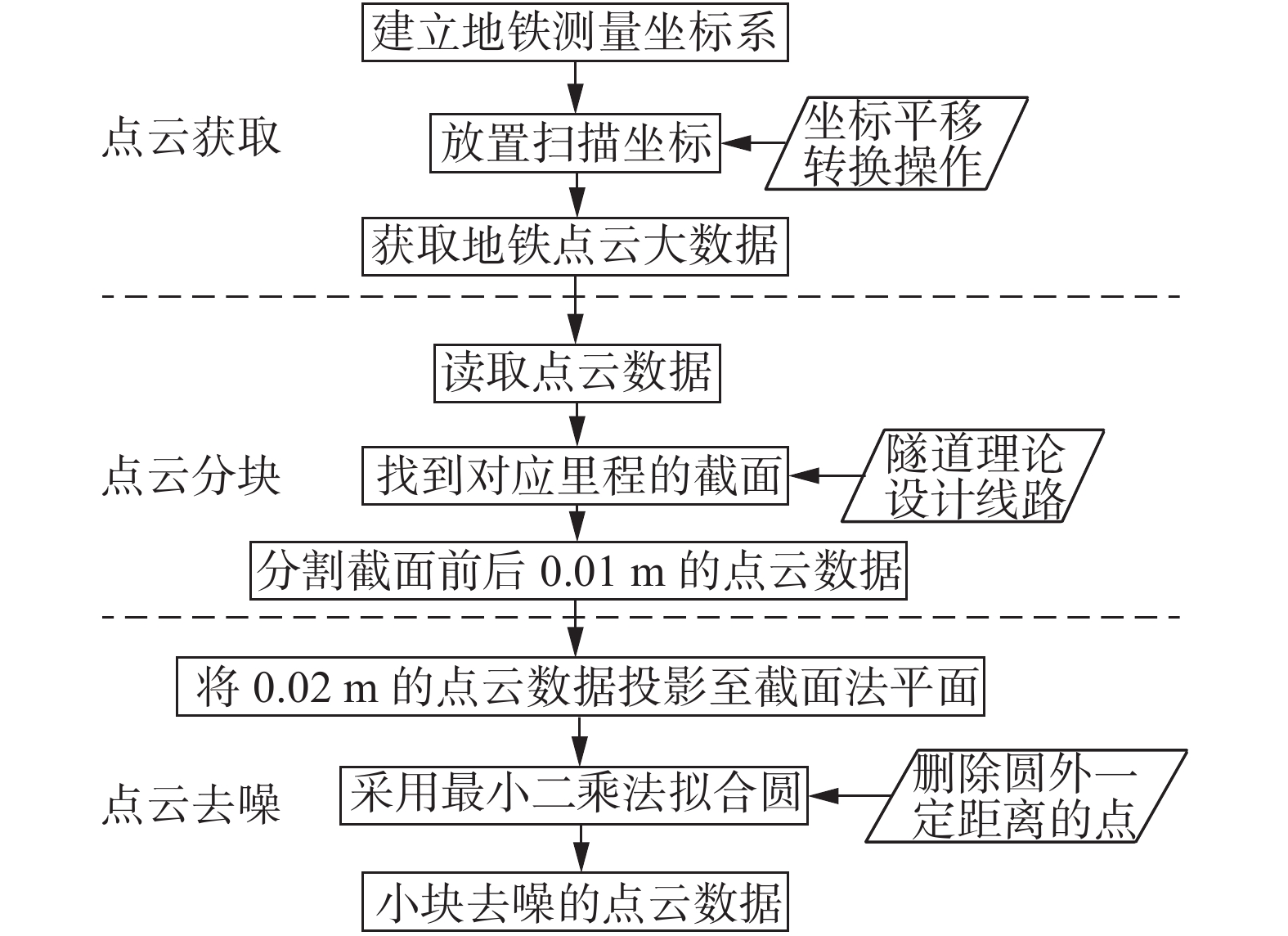
图3为点云处理流程图，介绍了点云的获取、分块以及去噪的过程。

2 建模与使用点云大数据

将设计线路进行优化求解的前提是建立合理可靠的数学模型，要求该模型能准确、形象地反应理论隧道情况，并具有普遍性和通用性^[20-21]。本文通过几何关系构建设计线路平纵断面二维图，利用设计线路中的交点坐标、缓和曲线长度、圆弧半径等参数构建平、纵断面模型，从而可以模拟理论隧道模型，准确获取任意里程的理论断面。结合上述经过处理的点云大数据，可获取同一里程对应的实际断面。对比同一里程的理论断面与实际断面，即可计算该里程关键点的侵限值。通过左下方关键点的侵限值，便可计算疏散平台尺寸。

2.1 平面建模

地铁线路的空间位置是用线路中心线在水平面及铅垂面的投影表示。线路在水平面上的投影为铁路线路的平面图。平面局部线路的构建方式如图4所示，点A到点C之间的直线、缓和曲线以及圆弧的实线部分构成了平面的局部线路图。点D、E为前缓和曲线与直线及圆弧的相交点，点F、G为后缓和曲线与直线及圆弧的相交点，点H为圆弧的圆心。

设∂为两直线的夹角，则∂可根据式（1）余弦定理计算：

$\partial = \arccos \left(\frac{{{b^2} - {a^2} - {c^2}}}{{ - 2ac}}\right)$

(1)

式中 $a$ 、 $b$ 、 $c$ 为线段BC、AC、AB的长度。

设直线AB、BC与X坐标轴的夹角分别为 ${\theta _{ab}}$ 、 ${\theta _{bc}}$ ，根据式(2)、(3)可计算出 ${\theta _{ab}}$ 、 ${\theta _{bc}}$ 。

${\theta _{ab}} = \arctan \left(\frac{{{y_b} - {y_a}}}{{{x_b} - {x_a}}}\right)$

(2)

$ {\theta _{bc}} = \arctan \left(\frac{{{y_b} - {y_c}}}{{{x_b} - {x_c}}}\right) $

(3)

已知前、后缓和曲线的长度以及圆弧半径分别为 ${l_{b1}}$ 、 ${l_{b2}}$ 、 ${r_{b}}$ ，根据对应的缓和曲线公式 $\;\beta {\rm{ = }}\dfrac{L}{{2R}}$ 可求出前、后缓和曲线的转角 $\;{\beta _{b1}}$ 、 $\;{\beta _{b2}}$ ，角度相减可求出圆弧的转角 $\;{\beta _R} = \partial - {\beta _{b1}} - {\beta _{b2}}$ ，根据公式 $x = L\left(1 - \dfrac{{{L^2}}}{{40{R^2}}}\right)$ 可求出前、后缓和曲线在相对坐标系下的横坐标 ${x_{l1}}$ 、 ${x_{l2}}$ ，根据公式 $y = \dfrac{{{x^2}}}{{6R}}$ 可求出前、后缓和曲线在相对坐标系下的纵坐标 ${y_{l1}}$ 、 ${y_{l2}}$ 。

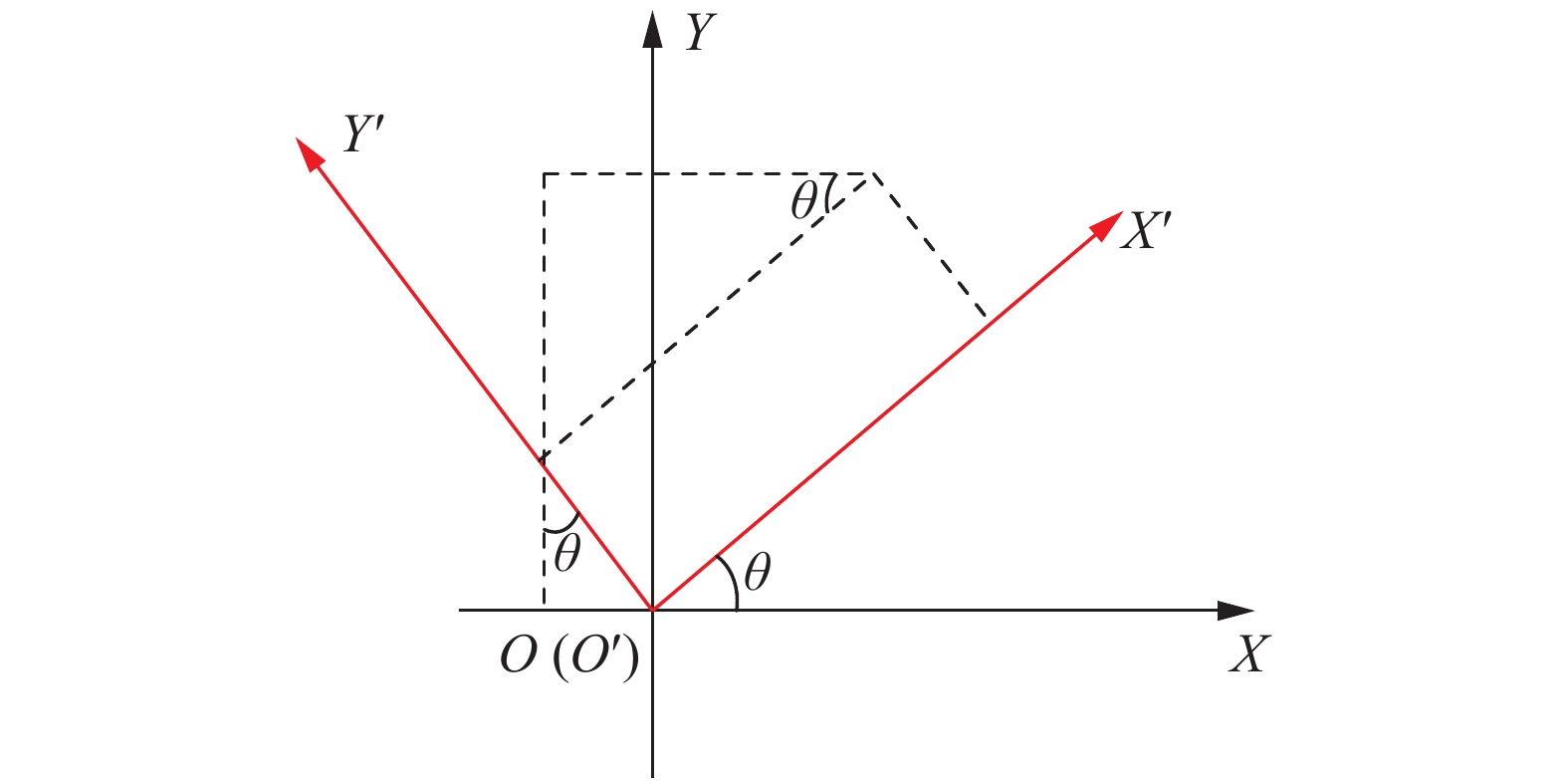
坐标轴变换如图5所示。

根据图中旋转平移的转换关系，可以得到以下公式：

$x = x'\cos (\theta ) + y'\sin (\theta ) + {x_0}$

(4)

$y = y'\cos (\theta ) - x'\sin (\theta ) + {y_0}$

(5)

设缓和曲线起始点D坐标为 $({x_D},{y_D})$ ，根据坐标轴转换式(4)、(5)，可以求出缓和曲线终点E坐标为 $({x_E},{y_E})$ ，同理可求得F、G点坐标分别为 $({x_F},{y_F})$ ， $({x_G},{y_G})$ ，将G点的坐标代入直线BC方程，从而可以根据推导的方程式求出未知数 ${x_D}$ 与 ${y_D}$ ，进而可求出E、F、G点的坐标 $({x_E},{y_E})$ 、 $({x_F},{y_F})$ 、 $({x_G},{y_G})$ 。

以上步骤求出了点D、E、F、G坐标，比较 $x$ 值的大小，即可判断给定的任意一点落在直线、圆弧还是缓和曲线区间。当 $x < {x_D}$ 时，给定的点在AB直线上，将 $x$ 代入AB直线的方程即可求出 $y$ 值。

当 ${x_D} < x < {x_E}$ 时，给定的点在DE前缓和曲线上，以D点为原点、AB为 $x$ 轴、AB的垂线为 $y$ 轴建立坐标系，根据式(6)、(7)：

$ x = L\left(1 - \frac{{{L^4}}}{{40{R^2}l_s^2}}\right) $

(6)

$ y = \frac{{{x^3}}}{{6RX}} $

(7)

可求出缓和曲线长度为L的相对坐标(其中X为 $L = {l_s}$ 时的坐标)，根据坐标的转换公式，即可求出前缓和曲线上任意一点的坐标值。

当 ${x_E} < x < {x_F}$ 时，给定的点在EF圆弧上，可以将 $x$ 代入BC直线的方程即可求出 $y$ 值。同理可以采用求前缓和曲线的方式求圆弧上任意一点的坐标值。

当 $x > {x_F}$ 时，给定的点在FG后缓和曲线上，求法同前缓和曲线，相对坐标系选G点为原点。即可求出后缓和曲线上任意一点的坐标值。

2.2 纵断面建模

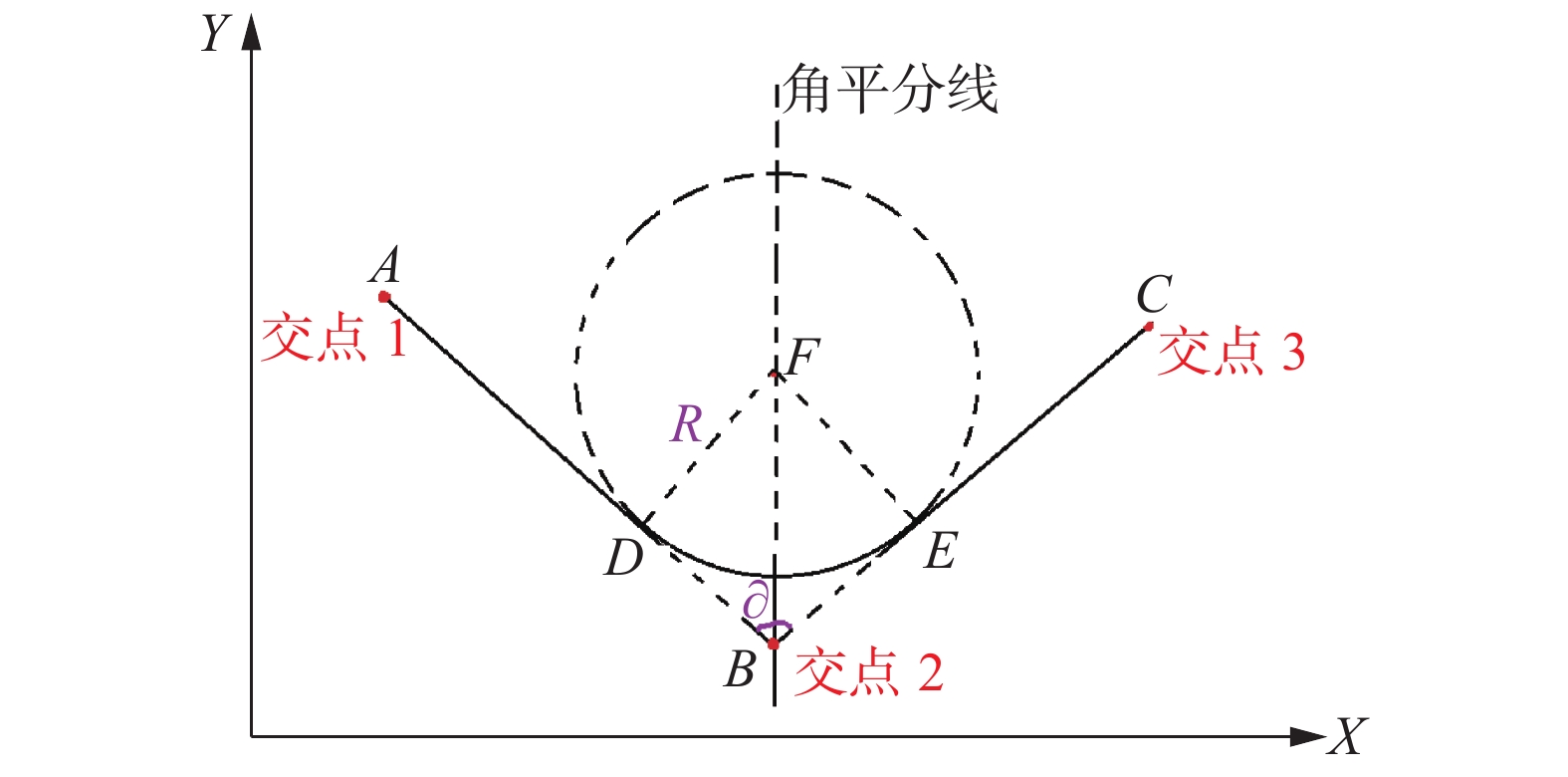
地铁的线路中心在竖直面上的投影，叫做铁路线路的纵断面图。纵断面局部线路的构建方式如图6所示，点A到点C之间的直线以及圆弧的实线部分构成了纵断面的局部线路图。点D、E为直线与圆弧的相交点，点F为圆弧的圆心。设∂为两直线的夹角 $\alpha {\rm{ = }}{\theta _{ab}} - \dfrac{\partial }{2} $ ，则∂根据式(1)计算，根据式(2)、(3)计算直线AB、BC与X坐标轴的夹角分为 ${\theta _{ab}}$ 、 ${\theta _{bc}}$ 。

实际中，BF 对应的直线为角平分线，即直线 AB 与 X 坐标轴的夹角为 $\alpha = {\theta _{ab}} - \dfrac{\partial }{2}$ ，从而可以根据式(8)求出 BF 对应的直线方程：

$y = (x - {x_B})\tan \alpha + {y_B}$

(8)

线段BF长度 ${l_{BF}}$ 可以根据正弦公式 $\sin \dfrac{\alpha }{2} = \dfrac{{{r_B}}}{{{l_{BF}}}}$ 来求出，进而可以根据式(9)、(10)计算出F点坐标：

${x_F} = {x_B} \pm \sin \left(\frac{{{\theta _{AB}} + {\theta _{BC}} - 180^\circ }}{2}\right)$

(9)

${y_F} = {y_B} \pm \cos \left(\frac{{{\theta _{AB}} + {\theta _{BC}} - 180^\circ }}{2}\right)$

(10)

得到圆的方程 ${(x - {x_F})^2} + {(y - {y_F})^2} = {r_B}^2$ ，将直线AB与BC的方程代入圆方程中，解方程组可以求出D点与E点的坐标 $({x_D},{y_D})$ 、 $({x_E},{y_E})$ 。

以上步骤求出了关键点D、E的坐标，比较 $x$ 值的大小，即可判断给定的任意一点落在直线上，还是圆弧上。当 $x < {x_D}$ 时，给定的点在AB直线上，将 $x$ 代入AB直线的方程即可求出 $y$ 值。当 ${x_D} < x < {x_E}$ 时，给定的点落在DE圆弧上，将 $x$ 代入圆的方程即可求出 $y$ 值。当 $x > {x_F}$ 时，给定的点落在BC直线上，将 $x$ 代入BC直线的方程即可求出 $y$ 值。

2.3 侵限值与疏散平台尺寸的计算

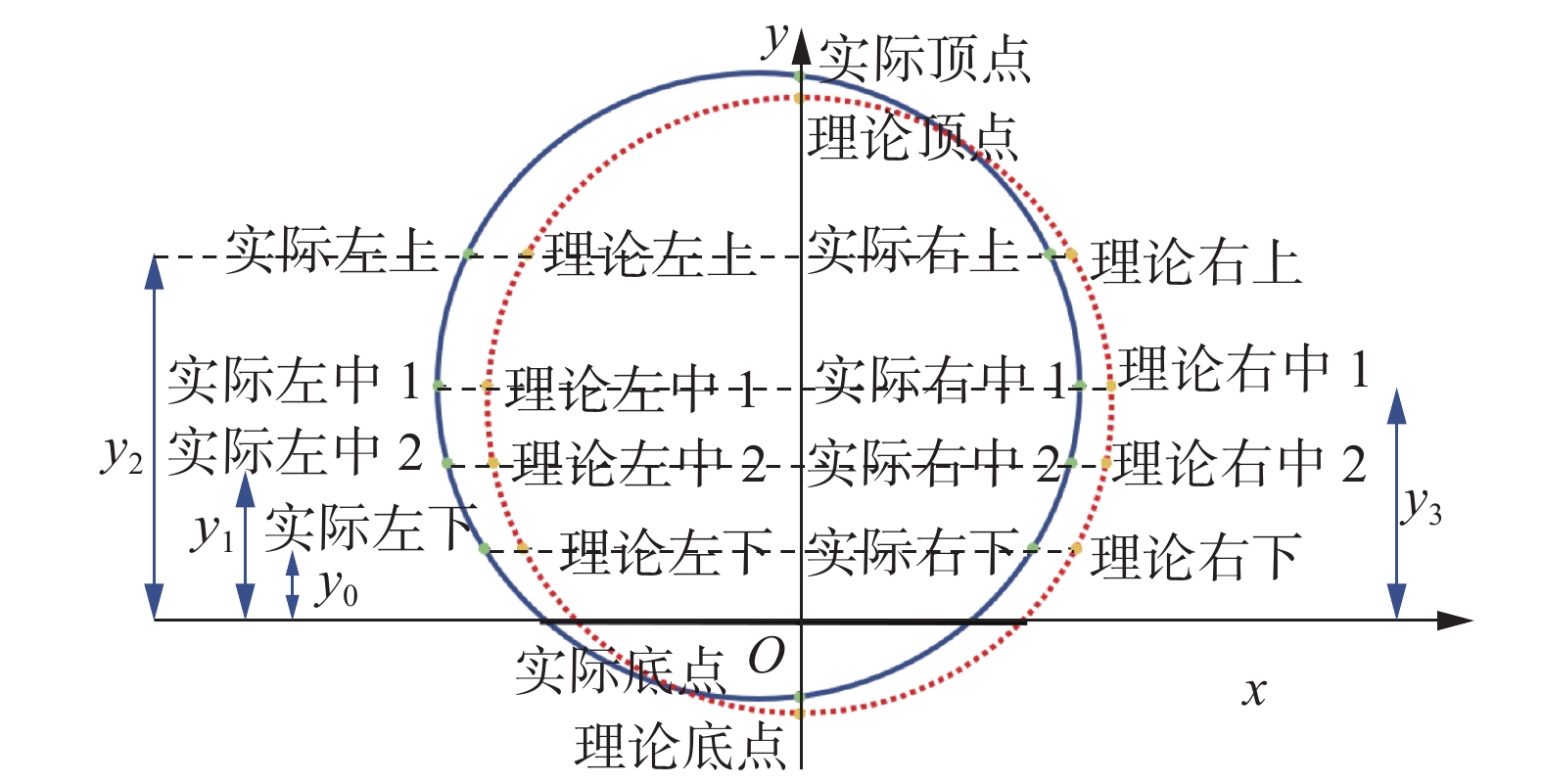
侵限值包括横向侵限值和纵向侵限值^[12]，横向侵限主要核实水平方向以检查线路中线与隧道壁之间的距离是否满足要求；纵向侵限主要核实竖直方向以检查线路中线与隧道壁之间的距离是否满足要求。通过平、纵断面建模可以确定线路中线，点云大数据可以确定隧道壁，对每个横断面测点的点云大数据与该测点的理论断面进行比较，核实横向与纵向是否侵限。通过计算出的左下侵限值，可以计算疏散平台尺寸。理论与实际的10个关键点如图7所示。

计算横向与纵向侵限值和疏散平台尺寸具体步骤如下：

1)以 ${P_{{m_0}}}$ 里程的轨道中心点为原点，建立直角坐标系，图7中虚线为理论断面；

2)根据F(Ω₁,Ω₂)求 ${P_{{m_0}}}$ 处的法平面方程 ${s_{{P_{{m_0}}}}}$ ；

3)点云大数据中找到 ${s_{{P_{{m_0}}}}}$ 平面小于0.01的点云，将所有点云投影至 ${s_{{P_{{m_0}}}}}$ 平面，图7中实线为实际断面；

4)两断面距离原点y₀、y₁、y₂、y₃处共有16个交点坐标，在x=0处求得4个交点坐标；

5)X_Theiretical–X_Real<0,即可判定该点横向侵限，并记录侵限值V₁，Y_{Real top}–Y_{Theoretical top}<0即可判定纵向顶点侵限，并记录侵限值V₂，Y_{Theoretical top}–Y_{Real top}<0即可判定纵向底点侵限，并记录侵限值V₃；

6)计算疏散平台的尺寸大小SV_i=612+V_i。

里程为–554的10个关键点的侵限值如表1。

3 深度神经网络模型

深度神经网络是一种常见的神经网络，它具有深度的网络层数，每个神经层之间完全连接。根据万有逼近定理^[13]，如果网络的隐藏层包含足够多的神经元，那么深度神经网络能以任意精度逼近任意连续函数。由于深度神经网络具有很强的表达能力^{[14, 24-26]}，因而可用于求取平纵断面参数与侵限值之间的关系。

3.1 神经网络构建 3.1.1 全连接神经网络模型的构建

深度神经网络是一种自上而下的监督学习模型^[15]，通过带标签的数据训练，误差自下向上传输，对网络中的参数进行微调。首先初始化所有网络层的权值和偏置，采用矩阵乘法得到第n−1层的结果，将第n−1层的输出作为第n层的输入，计算第n层，由此得到输出层的计算结果O，计算O与真实标签 $O'$ 的偏导，更新第n层的权值与偏置，计算第n层的偏导，继续更新第n−1层的权值与偏置，由此可以得到各层更新后的参数。

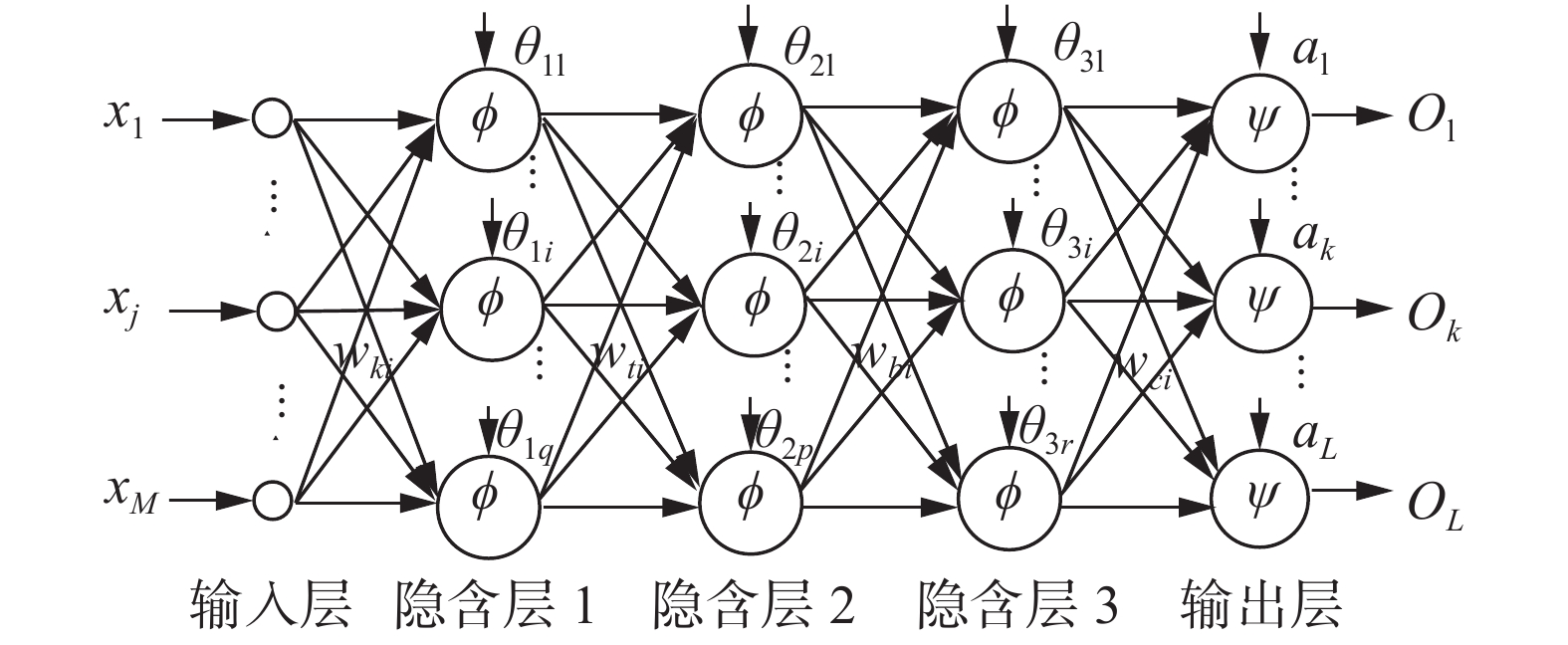
本文搭建的深度网络模型如图8所示。

图8参数设置具体如下：

输入层　向量x_j包含平纵断面参数，是29维的向量；

隐藏层1　32个神经元，激活函数为ReLU；

隐藏层2　64个神经元，激活函数为ReLU；

隐藏层3　128个神经元，激活函数为ReLU；

输出层　将隐含层3的输出结果经过线性变换，得到输出O_k。

3.1.2 卷积神经网络模型的构建

卷积神经网络（convolutional neural network, CNN）是深度学习领域具有代表性的神经网络，在图像处理以及其他领域取得了突破性的进展。其中的权值共享、池化等技术，克服了一般神经网络的过拟合问题，使得卷积神经网络在测试集上有着优秀的表现。本文结合地铁调线调坡中的问题，采用卷积神经网络学习设计线路与侵限值之间的函数关系，网络模型的搭建具体如下：

输入层　向量x_j包含平纵断面参数，是29维的向量；

卷积层1　1×3的卷积核，随机初始化参数；

池化层1　采样窗口为2×2，步长设置为1；

卷积层2　1×5的卷积核，随机初始化参数；

池化层2　采样窗口为3×3，步长设置为1；

全连接层　128个神经元，激活函数为ReLU；

回归层　采用实际侵限值与预测值的均方误差作为损失函数。

卷积神经网络结构如图9所示。

3.2 训练数据及方法

原始的设计线路参数是已知的，对每个参数设定可调节的范围，在设定的范围内随机生成100 000组线路参数，即可得到输入数据集。每组数据集对应一组线路参数，采用上述侵限值的计算方法，计算每组数据集对应的侵限值之和，即可得到输出数据集。将数据集的70%用于训练深度神经网络，余下的30%作为测试集进行测试。

在训练过程中，神经网络的线性输出与真实标签采用最小二乘法计算损失，误差BP优化器采用Adam优化器^[16]，初始学习率为0.1。为了减小过拟合，在训练中每层神经元drop out比率设置为0.25，当迭代次数达到设定值且损失值收敛后停止训练。

3.3 优化线路参数

当神经网络的损失值收敛后，说明神经网络通过权值以及偏置的更新能够逼近平纵断面参数与侵限值之间的函数关系。提取神经网络中最终的权值与偏置，将其设为常数，并且将设计线路参数设置为变量，采用梯度下降法^[23]求得最优线路参数。具体步骤如下：

1)提取神经网络参数 ${w_1}$ ~ ${w_4}$ 、 ${b_1}$ ~ ${b_4}$ ，将其设为常量；

2)将原始线路参数F(Ω₁,Ω₂)设置为变量；

3)定义侵限值为(((F(Ω₁,Ω₂) ${w_1}$ + ${b_1}$ ) ${w_2}$ + ${b_2}$ ) ${w_3}$ + ${b_3}$ ) ${w_4}$ + ${b_4}$ ；

4)反向求导；

5)更新线路参数，得到 $F'$ (Ω₁,Ω₂)；

6)重复步骤3)~ 5)，直至侵限值收敛，最终结果 $F'$ (Ω₁,Ω₂)即为最优结果。

4 实验结果

本文在时间上与效果上对比遗传算法以及人工调节的结果。在计算的准确性上，对比人工测量以及利用侵限值算出的疏散平台尺寸。

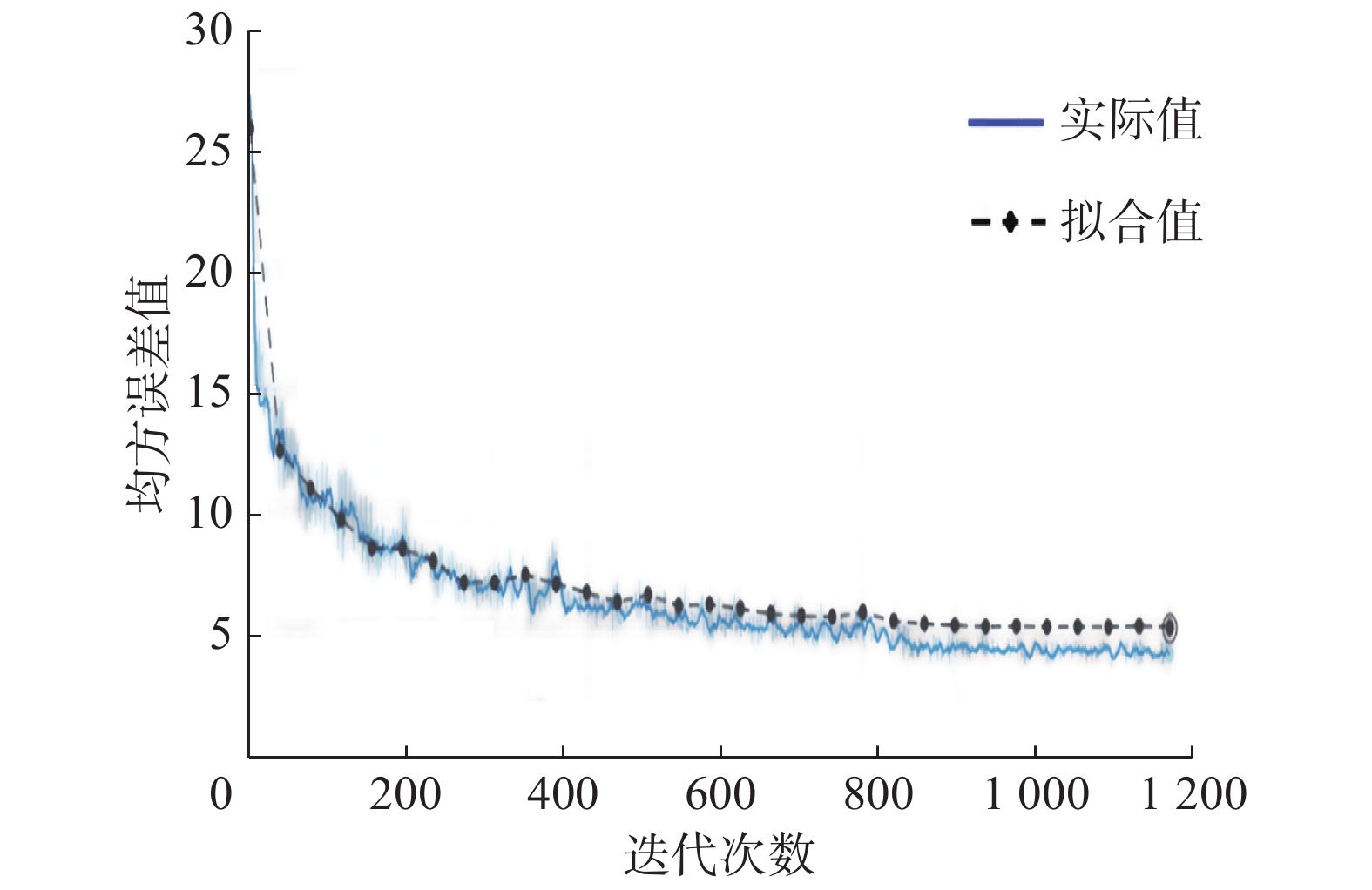
4.1 深度神经网络训练结果

深度神经网络模型构建完成后，将训练数据集输入模型中进行训练，如图10、11所示。

经过多次迭代后，全连接神经网络模型和CNN模型的损失值(输出值与真实标签的标准差)达到收敛，表示模型的训练过程已完成。随后，对已训练好的模型进行测试，测试集的损失值为8.86，略低于训练集的损失值，说明构建的模型已学习到线路参数与侵限值之间的关系。

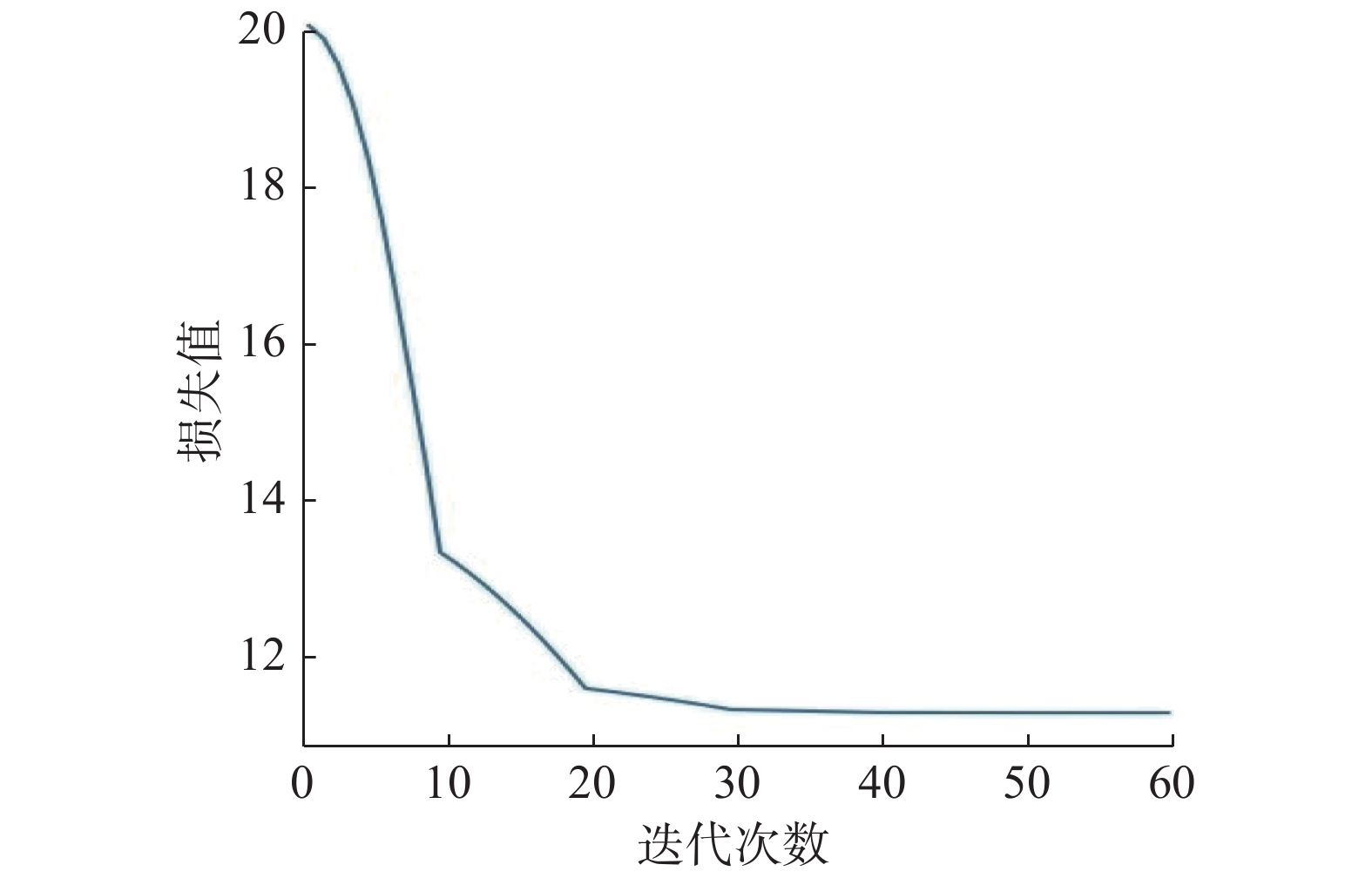
4.2 梯度下降结果

深度神经网络模型训练完成后，抽取模型的参数，构建以线路参数为未知数求取侵限值的表达式，采用上述的梯度下降算法求取最优线路参数。梯度下降损失函数收敛过程如图12所示，经过多次迭代后，损失值达到收敛，线路侵限值达到最小，即可获取最优的线路参数。

4.3 实验对比

遗传算法与深度神经网络模型的对比如表2所示，在结果、时间与计算资源方面，本文将深度神经网络模型与遗传算法进行了对比。从表中可以看出，深度神经网络模型在时间与计算资源的消耗上具有明显优势。但根据调整后侵限比较，神经网络的调节结果比遗传算法略差，而且，全连接神经网络模型与CNN模型在优化效果上差别不大，但综合计算时间和计算内存，全连接神经网络模型比CNN模型在优化地铁线路问题中显得更胜一筹。另外，图13对比了根据点云大数据算得的疏散平台尺寸与真实疏散平台尺寸。从图中可以看出，通过本文的方法计算出的尺寸与真实尺寸的偏差大多数在1~2 cm，最大偏差不超过3 cm。所有偏差值均在误差允许范围内，表明本文计算疏散平台尺寸方法具有可靠性。

5 结束语

本文结合点云大数据与线路参数计算侵限值，并使用深度神经网络模型学习线路参数与侵限值之间的函数关系。构建了以线路参数为自变量、侵限值为因变量的表达式，采用梯度下降算法求取最小侵限值对应的最优线路参数。虽然，实验结果显示深度神经网络模型最终优化效果略差于遗传算法，但深度模型比遗传算法需要更少的运行时间和计算机内存资源。本文的研究提供了一种高效的方法获取最优线路参数。未来的工作主要包含3个方面：

1)给定10个关键点的权重优先级，计算出合理的10个关键点权重值；

2)研究地铁隧道中包含的矩形、马蹄形等不同形状的隧道。

3)研究基于在线学习算法的智能地铁线路辅助系统，提升模型的实时预测能力。