2. 浙江大学 人工智能研究所,浙江 杭州 310027
2. Institute of Artificial Intelligence, Zhejiang University, Hangzhou 310027, China
自从AlexNet[1]在2012年的ImageNet Large Scale Visual Recognition Challenge(ILSVRC)[2]比赛中大放异彩之后,深度学习成为了大数据智能领域的一个研究热点。此后,神经网络的结构不断地更新,其规模也越来越大,但是从总体上来说,深度学习是一种有标注的大数据驱动下,拟合给定数据最优模型的学习方法。这种数据拟合的思想在解决单一任务中取得了较好性能,但是在不同数据集上应用相同模型时,或多或少的会对模型的超参数进行一定的改变。如何自动化地针对问题对模型进行适应性的改进仍是一个难题。
将深度学习模型应用于实际场景中,当采集到的数据与数据集的数据有较大的差别时,这种基于数据拟合的最优解方法可能会失效[3]。针对模型的对抗样本攻击也证明了这一点[4]。另一方面,真实世界的数据反映了复杂的社会现象,数据拟合的单纯方法难以刻画真实世界中商品竞拍和博弈对抗等行为。这样,盲目增加模型复杂度只会对数据集“过拟合”,而不会真正提升模型在现实世界中的表现。产生这种现象的一个重要原因是训练好的模型很难在实际使用中根据现实情况的差异做出调整。在这种情况下,对于复杂问题,机器学习不应只关注于求解数据拟合的最优解,而应该从博弈的角度出发,通过寻找问题的均衡解,找到不同场合下适用的求解方法。博弈论虽然是经济学的一个分支,但是自现代博弈论创立之初,其就与计算机科学产生了千丝万缕的联系,近年来更是与人工智能相结合,在围棋、德州扑克、星际争霸等游戏中战胜人类选手[5-8]。
1 深度学习中的最优解拟合 1.1 深度学习的数据拟合 1.1.1 从浅层学习到深度学习神经网络最初的研究可以追溯到20世纪50年代所提出的“感知机”模型[9],这是一种根据生物神经细胞信号传导过程而设计的学习模型。神经网络被普遍应用于机器学习等领域是在误差反向传播算法[10-12]被提出后,这一算法使得具有拟合非线性函数能力的“多层感知机”模型的参数可以通过反向传播算法进行优化。此后类似多层感知机的一系列浅层学习的机器学习算法被提出,包括支持向量机[13]和Boosting[14]等方法。浅层学习往往需要人工定义和构造特征,难以完成端到端的训练过程。
2006年,Hinton等[15]首次提出了深度学习的概念。深度学习是一种端到端学习(end-to-end learning)的机制,在给定输入数据后,可以自动提取其最具区别力的特征,挖掘数据内部的隐含关系。此后,深度学习在许多大规模数据上进行的实验都表现出了远超过浅层学习的效果,深度学习逐步成为当下人工智能的研究热点。
深度学习的基础仍然是人工神经网络,一个深度学习的模型由多个神经元叠加构成。对于单个神经元,其输入向量记为
| $f\left( a \right) = g({{{w}}^{\rm{T}}} \cdot {{a}}) = \mathop \sum \limits_{i = 1}^n g\left( {{w_i} \times {a_i}} \right)$ |
一个深度学习模型包含若干基本神经元,神经元之间的连接方式可以是简单的链式堆叠,也可以是有分支的有向无环图结构。
1.1.2 深度学习的参数优化深度学习中优化的参数主要是每个神经元链接权重大小。在深度学习的模型中,通过不同神经元的线性组合以及非线性激活函数输出预测结果,并计算预测结果与真实标签的误差,再将误差利用反向传播算法,对参数进行优化。此外,为了防止过拟合,在优化参数时常常会在误差项后对参数施以一定约束(如参数稀疏等)。记深度学习的神经网络模型为F,则第i个训练数据xi对应的预测输出结果为
| $\min (\mathop \sum \limits_{i = 1}^N {\rm{Loss}}\left( {F\left( {{x_i}} \right),{y_i}} \right)$ |
在进行参数优化的过程中,由于训练数据的规模通常较大,所以需要将训练数据分批计算损失函数,再将每一批数据的误差反向传播,应用梯度下降法[16]对参数进行优化。对于神经网络模型中的待优化参数w,在梯度下降的每一步中参数都会如下优化更新:
| ${{{w}}^{{\rm{new}}}} = {{w}} - \eta \times \frac{{\partial {\rm{loss}}}}{{\partial {{w}}}}$ |
式中:loss表示由一批训练数据计算所得误差;η表示学习率,是一个模型训练的超参数,表示根据每批训练数据进行优化的步长。
可以看出,即使利用梯度下降法,在模型参数较多和训练数据规模较大的情况下,深度学习的数据拟合是一个非常缓慢的过程,尤其是近年来神经网络的规模越来越大,例如在自然语言领域表现优秀的模型BERT,就有1.1×108~3.4×108个训练参数[17]。
1.2 深度学习中的超参数 1.2.1 深度学习模型的人工设计随着深度学习在各个领域大放异彩,人们提出了大量不同的深度学习模型。但是归根结底,深度学习模型可以优化的主要参数为神经元之间链接权重向量,除此之外神经元之间的连接方式均通过人工设计完成。目前最广泛使用的两种基本神经元网络结构有常用于计算机视觉的卷积神经网络和常用于自然语言处理的递归神经网络。在这基础之上的各种不同结构的模型都是针对某一种或某一类问题提出的,相比于最简单的多层感知机模型,这些模型能够减少可训练参数的数量,提升模型的效果。
除了模型结构的设计,模型大小也是需要人为调整的超参数,对单个神经元来说,就是神经元的可训练参数数量的多少,即
对于神经网络来说,神经元中激活函数的选择也可以认为是一个超参数。当然目前使用较为广泛的激活函数是线性整流函数(ReLU),其数学表达式为
| ${\rm{ReLU}}\left( x \right) = \max \left( {0,x} \right)$ |
在多数情况下,使用这一激活函数都能取得不错的效果。
此外还有一些特定模型中也包含一些针对自身结构特性而设定的超参数,例如卷积神经网络中卷积核的大小、卷积的步长等,模型的设计者通过增加这些与自身特性相关的超参数可以提高所设计模型的泛化能力,使其不止局限于单个问题的解决,对不同的问题通过调整超参数都能有较好的表现。就卷积网络来说,不同的卷积核大小可以提取粒度大小不一的局部特征。
以上这些超参数的人工选择除了需要根据经验进行设定外,往往还需要通过调整不同的超参数进行训练、验证的反复实验,根据实验结果选择效果最好的超参数作为最终的网络结构超参数。这是一个及其耗费时间和人力的过程。
最后,深度学习的模型在训练过程中也需要提供一些训练相关的参数,包括随机梯度下降法中每批数据的大小、训练数据全集遍历的次数以及学习率的大小。这些训练相关的超参数往往根据经验和硬件条件来选择。
1.2.2 深度学习超参调优的弊端深度学习中可以人为改变的超参数其实是非常多,在超参数调优的过程中,其实是在拟合训练数据集的基准数据,换用不同的数据集可能需要对超参数进行调整。如果每更新一批数据就要对超参数进行一次人为改变,那么深度学习模型的应用范围将会受到极大的限制,因为每次超参数调优都需要有一定的计算资源进行多次实验。一种简单的方法是不改变超参数直接在新的数据集上进行迁移学习,但是这样的效果要差于重新设计的模型。此外,面对越来越复杂的模型设计工作,人们也亟需一些超出惯常设计思路的模型来突破当前的瓶颈。
事实上从组合学的观点来看,在一幅图像中,稍微改变物体的方向、方位、遮挡情况所构成的场景数量其实是呈指数增长的。在训练时,数据的最优拟合的目标其实是平均情况,而现实情况更专注于模型的最坏情况[3]。例如在自动驾驶领域,为了保证汽车行驶的安全,就要保证车在最坏情况下仍然不会识别失败,否则将会导致严重的后果。博弈论的思想可以让模型更加注重最坏情况发生的情况,而不是“最优”的平均结果。
1.3 神经网络结构搜索 1.3.1 神经网络结构搜索思想随着深度学习的普及,模型设计的工作量和难度都有明显的增加,面对越来越复杂的任务,尤其是面对不同的任务需要使用类似模型结构的情况下,人们对自动化的模型设计和参数优化有了非常迫切的需求。这样的需求催生了自动化机器学习(auto machine learning, AutoML)领域的发展。自动化机器学习包括神经网络结构的搜索(neural network architecture search, NAS)、超参数优化(hyperparameter optimization)以及元学习(meta-learning)3个主要方面。其中超参数优化主要是选择机器学习模型中效果最好的超参数,元学习主要是找到针对特定问题最合适的机器学习模型或算法,神经网络结构搜索主要是针对特定的任务找到最合适的深度学习模型结构,在深度学习领域神经网络结构搜索其实包含了超参数优化以及元学习的任务。
神经网络结构搜索的一般搜索过程如图1所示[18]。图1利用搜索策略从搜索空间中选取一种神经网络结构,通过模型评价策略获得这个网络结构的效果,通过反馈这个结构效果的好坏,搜索策略可以继续搜索其他结构。最终得到效果较好的神经网络结构。对神经网络结构搜索的研究也主要集中于搜索空间、搜索策略和模型评价策略这3个领域[18]。

|
Download:
|
| 图 1 神经网络结构搜索流程 Fig. 1 Process of neural network architecture search | |
神经网络结构搜索中搜索空间指在搜索过程中所有可成为搜索对象的神经网络结构。可以想象,在对神经网络的连接方式不做任何限制的情况下,搜索空间的大小随着规模的增长是呈指数增长的。在有限的计算资源下进行搜索时,可能导致无法搜索较大规模的神经网络。同时,过于限制搜索空间的大小,可能并不能搜索出对效果有较大提升的神经网络模型。较为简单的神经网络搜索的搜索空间使用的是链式模型[19-21],即网络的每一层级依次链接,另一种较为复杂的搜索空间使用的是分支模型,即允许网络中存在跨层的跳跃链接,整个网络结构是一个有向无环图[22-24]。使用分支模型的效果明显优于使用链式模型,但是从搜索速度来说,链式模型的搜索空间更小,搜索时间更短。
搜索策略是根据模型评价反馈的结果不断遍历搜索空间的策略,搜索的过程面临着探索和利用的权衡,在利用的过程中,要快速找到效果较好的神经网络结构,在探索的过程中,要积极遍历搜索空间中更多的结构避免陷入局部最优解。常用的搜索策略主要有随机搜索、进化算法[25]、强化学习[18-19]等。
模型评估是对搜索得到的神经网络结构做一次性能评价,评价的结果可以指导搜索策略选择下一次的神经网络结构,当然如果性能评价是通过在训练集上做训练后,验证集上的表现来评估,这样一次完整的搜索过程可能需要几千个GPU日(GPU days)[18, 24]。如何在保证模型评价准确性的情况下,提升模型评估的效率是这一问题的研究重点。
1.3.3 神经网络结构搜索的优劣总体上神经网络结构搜索还处于起步阶段,距离真正的应用还有一段距离。但是这种自动化的模型结构设计能够极大程度的减少人力物力,让深度学习更广泛地应用于更多领域,而且相比人为设计,自动化的搜索能够显著提升网络的效果,甚至能够删除网络中的冗余部分,提升网络推理速度,使其更容易应用于前端芯片。
当然,神经网络结构搜索还存在一些问题,目前普遍的搜索方法都需要耗费大量的计算资源,这是导致神经网络结构搜索难以真正投入应用的关键问题。此外,从超参数优化的角度来讲,即使神经网络结构搜索能够自动化的选择最合理的超参数,但是本身搜索过程也是需要人为控制超参数的,这就会造成“高维”的超参数调优问题,距离真正的完全自动化还有一定的距离。
2 博弈论与深度学习 2.1 博弈的基本概念1944年冯·诺伊曼与奥斯卡·摩根斯特恩合著的《博弈论与经济行为》[26]出版,标志着现代博弈论思想登上了历史舞台。博弈论主要研究的是为博弈的参与者谋取最大利益,也就是“两害相权取其轻,两利相权取其重”。
博弈中,参与博弈的决策主体被称为玩家或参与者,这些参与者总能或多或少的获得一些与博弈相关的知识,这些知识被称为信息,如果并非所有的参与者都了解其他参与者所有可选的行动、每种局势下的收益等信息,这种博弈被称为不完全信息博弈,反之被称为完全信息博弈。博弈的参与者还需要遵守一定的规则,符合规则的行动方案被称为策略。
参与者采取了各自的行动之后的博弈状态被称为局势,而在不同的局势下,各个参与者所得到的利益或回报被称为博弈的收益。
博弈的稳定局势即为纳什均衡(Nash equilibrium)[27],其指参与者做出了这样一种策略组合,在该策略组合上,任何参与者单独改变策略,其收益都不会增加。
2.2 纳什均衡与纳什定理 2.2.1 纳什定理约翰纳什(John Forbes Nash Jr.)在提出纳什均衡的同时,还提出了纳什定理[27]。纳什定理指出:若参与者有限,每位参与者采取策略的集合有限,收益函数为实值函数,则博弈对抗必存在混合策略意义下的纳什均衡。所谓混合策略(mixed strategy)指参与者可以按照一定的概率来随机选择若干不同的行动,相应地,如果参与者能够确定地选择行为,这种策略被称为纯策略(pure strategy)。
纳什定理仅仅是一个存在性定理,但是这一定理为许多博弈论相关研究提供了理论基础。
2.2.2 均衡解与最优解在博弈论的观点中,所有博弈的参与者都是足够理性的,也就是他们都会采取使自己收益最大化的行动,这样做的最终结果就是导致博弈最终的局势总是稳定的,也就是最终总会达成纳什均衡的局势。但是,值得注意的是,均衡解并不是最优解,最优解关注的是平均利益的最大化,而均衡解是最有利于参与者的局势。
在博弈论的经典案例囚徒困境(prisoner’s dilemma)中,两名嫌犯都有认罪和沉默两种行为可以选择,对二人来说,最优解应当是两人同时保持沉默,导致警方仅能依靠已有的犯罪事实(缺乏口供)对两人轻判,但是对于两个嫌犯来说,认罪才是对自己最有利的行动,最终的结果就是两人同时认罪而得到应有的惩罚。
在大数据智能的视角下,假设训练数据是一批围棋的对弈棋谱,按照最优解的角度去拟合走子策略,拟合的结果必然是在这一批棋谱中胜率最高的位置优先落子而胜率较低的位置避免落子,但是棋局是变化的,当博弈对手的策略发生改变,这样的“最优解”没有任何意义,而此时真正需要找到的是达成均衡解的策略。
2.3 博弈视角下的大数据智能 2.3.1 博弈与人工智能人工智能起源于1956年的达特茅斯会议。在人工智能的发展历程中,与博弈论碰撞出了许多火花,一方面许多人工智能领域的问题,例如多智能体系统、广告推荐等,背后都蕴含着博弈的思想;另一方面,人工智能的许多算法提供了许多博弈策略的近似求解方法,例如在许多经典的博弈游戏中,利用计算机模拟采样可以求出近似的均衡解。人工智能与博弈论的交叉领域主要分为博弈策略求解和博弈规则设计两个方面。
首先,博弈论提供了一种实际问题的建模方法,同时纳什定理证明了博弈论解的存在性,那么为了求得博弈问题的均衡局势或者参与者的最优策略就可以采用人工智能的一些算法,最主要的是利用人工智能算法高效地搜索最优的策略[5-8]。
其次,在博弈中往往参与者会从自身利益最大化的角度出发去做出决策,这时很可能造成类似囚徒困境的两败俱伤的结果。如何设计博弈的规则来使得最终的均衡局势尽可能达到整体利益的最大化也是人工智能思想在博弈中的应用[28-29],这些规则设计往往计算量大,复杂度高,常见的利用人工智能算法来设计博弈规则的场景包括广告竞价、拍卖、供需匹配、名额分配等。
2.3.2 博弈与深度学习人工智能被提出时,神经网络就是人工智能的重要研究方向之一,而深度学习又是以神经网络为基础的,所以神经网络可以作为一种人工智能算法进行博弈的策略求解。
随着深度学习的发展,深度学习的算法背后也体现出了一些博弈的思想。比如生成对抗网络[30]的训练过程就像是一个博弈的过程。生成对抗网络是一种生成模型,它由生成器和判别器两个部分组成,生成器将随机生成的噪声数据转变为真实样本空间中的“真实”数据,而判别器用来判断生成器生成的数据是否真的符合真实数据的分布。在训练时,生成器能够根据判别器的判别结果提升自己生成的数据的“真实性”,而随着生成数据越来越接近真实样本,判别器也变得更加敏锐,识别的能力也会提升,最终的均衡局势是生成器完全模拟了真实样本数据的分布,判别器也就再也无法判定生成的数据是真是假了,此时的生成器就是一个训练好的生成模型。类似的思想还体现在基于策略的深度强化学习中,在基于行动者评论家的强化学习[31]中有根据环境做出决策的“行动者”和根据决策结果做出评估的“评论家”,两者协同决策的过程也是一个博弈的过程。
3 大数据智能下的均衡解 3.1 完全信息下的博弈 3.1.1 完全信息博弈的特点完全信息博弈实际上是可以获得博弈中的所有信息,在博弈的步骤比较少的情况下,比如井字棋等,很容易通过搜索算法获得博弈的最优策略,求出纳什均衡解。
但是往往我们面临的完全信息博弈是非常大规模的,所以在博弈的过程中,博弈者难以及时得知自己当前决策的利弊。如果可以估计当前行动对最终局势的影响,那么决策就是非常简单的过程了,即在完全信息博弈的过程中只需要根据经验判断或者模拟对手行为来计算每一步收益。在模拟的过程中,由于不需要猜测对手的行为,所以“完全信息”能够减少建模的难度。
3.1.2 围棋走子策略求解围棋是一种古老的棋类游戏,它起源于中国。围棋被认为是当前世界上最复杂的棋盘游戏之一,在博弈时,黑白双方轮流落子在棋盘上,最终通过所围的区域的大小决定胜负。围棋是一种完全信息博弈。由于简单的通过搜索算法不能在有限的时间内搜索出最优的走子策略,所以需要使用人工智能的方法来进行策略求解。AlphaGo Zero就是一个基于深度神经网络的人工智能围棋程序,它可以通过自博弈自我提升,近似拟合出一个较好的围棋走子策略[5]。最终AlphaGo Zero不但在棋力上超过人类选手,还在博弈过程中发现了许多人类围棋玩家常采用的经验策略。
围棋的博弈过程可以看作是一个马尔可夫决策过程,博弈时棋面可以认为是状态空间。给定一个棋面,可以继续走子的位置有限,因此选择可走子的位置就是当前状态下可以采取的动作集合。一旦走子之后,棋面发生改变,即以转移概率p=1的概率转换到下一状态,因为围棋总是在下棋的过程中逐步建立优势并最终取得胜利,所以回报的大小可以由当前的双方局势的优劣来决定。这样就将围棋博弈转换成了马尔科夫决策过程,而所求解的策略就是使得这个马尔科夫决策过程总回报的期望最大的策略。AlphaGo Zero就是在求取这样的策略。
AlphaGo Zero之所以能在自博弈的过程中提升自己的策略,是因为它使用了深度强化学习模型进行策略估计和策略提升。在深度强化学习中,有两个深度神经网络,一个是策略网络,一个是价值网络,这两个网络是同一个网络的两个分支,将棋面作为图像输入网络,经过卷积等操作,最后输出当前状态的收益以及在当前状态下应当采取的策略。
这里的策略网络并不是直接输出当前局势下的走子位置,而是输出几个预测位置,并按照策略网络的预测进行蒙特卡洛树搜索,将蒙特卡洛树搜索[32]所得策略作为最终的落子策略。蒙特卡洛树搜索是一种结合随机模拟和采样的最优决策方法,依靠快速的搜索效率和可靠的搜索结果,它被广泛应用于完全信息博弈中。蒙特卡洛树搜索的过程包括路径选择(selection)、节点扩展(expansion)、模拟实验(simulation)和反向传播(backpropagation) 4个步骤,通过这4个步骤的不断重复,确定不同行动的回报,并做出决策。在AlphaGo Zero中,蒙特卡洛最终模拟的结果还被反馈到了深度神经网络中,用于训练价值网络的参数。
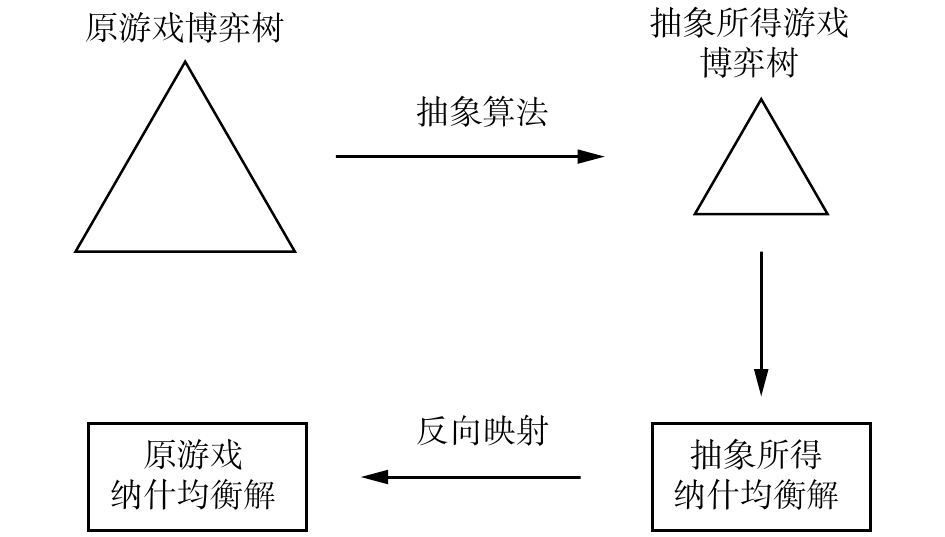
3.2 非完全信息下的博弈 3.2.1 非完全信息博弈的特点相对于完全信息的博弈,不完全信息下的博弈更加符合现实场景,能够指导人们对现实问题的科学决策。在非完全信息的纳什均衡求解中,对手采取的行动不一定是可见的,仅能根据部分已知的信息进行决策。非完全信息博弈树通常规模非常大,因为在中间状态下可能采取的行动一般有无穷多种,为了削减搜索空间,人们需要使用一些抽象算法对原有博弈问题进行压缩,即合并博弈树中的相似状态、压缩搜索层数以及剪枝等,最终得到一个相对简单的抽象问题,然后求解这个抽象问题的纳什均衡解,最后将所求解结果映射回原问题当中,于是得到原问题的纳什均衡解,如图2所示[33]。此外,强化学习越来越多地应用于非完全信息博弈的策略求解,在连续动态的环境中做出合理的决策正是强化学习的模型所擅长的内容[34]。
|
Download:
|
| 图 2 非完全信息博弈的策略求解 Fig. 2 Process of solving an incomplete information game | |
与棋类游戏在完全信息条件下进行不同,扑克游戏是一种非完全信息博弈。在扑克游戏中,每个玩家无法知道对手的手牌,这也使得求解博弈策略变得极为困难。比如在这种博弈过程中无法计算局势的收益,这导致了不能按照完全信息博弈方法来解决非完全信息博弈问题。2018年,智能体Libratus首次在双人德州扑克中击败人类选手[6],2019年,使用类似算法的Pluribus在多人德州扑克中也获得胜利[7]。
在德州扑克游戏中,先要对庞大的博弈树进行剪枝,形成一个抽象游戏。具体来说,需要将相近的状态节点进行合并,压缩博弈树的大小,此外还需要将每次下注的金额限制在几个固定数额上,从而减小行为空间的大小。
Pluribus和Libratus的训练不断通过自博弈过程来完成。这个自博弈过程中使用了虚拟遗憾值最小化算法[35]。所谓遗憾值指在过去几轮模拟博弈中,某一局势下采取其他策略与当前的策略带来的收益之差的累加。利用遗憾值就可以更新策略,使得智能体对所采取的新策略“遗憾”较少,也就收益更高。虽然扑克游戏的博弈过程比围棋所用时间短,但也无法立刻得知每一步博弈后的收益,所以需要通过“虚拟”方法来计算每一步行为的期望收益。一旦计算得到期望收益,就可以比较当前策略与其他策略的虚拟遗憾值,并根据遗憾值的大小来更新策略。
在实际游戏时,由于局势是不断动态变化的,仅仅依靠预训练所得策略难以完成决策,因此在博弈的过程中还需要不断根据局势来缩小博弈搜索空间,找到尽可能小的安全子博弈[36],进行细粒度的遍历搜索。
3.2.3 星际争霸的多智能体博弈求解星际争霸是一款即时战略游戏,游戏玩家需要在有限的地图视野下进行相互对抗。相比于棋牌游戏,星际争霸的操作更加复杂,对抗性更强。此外,由于对手行为的不确定性,星际争霸游戏并不存在理论上的最优解。2019年1月,星际争霸的人工智能模型AlphaStar首次战胜人类玩家,实现了智能体游戏博弈领域的重大突破。
考虑到星际争霸游戏的强对抗性,AlphaStar采取了从整体到个体的多智能体联合训练[37]模式。所谓“联合训练”是指在训练智能体的游戏过程中同时训练多个不同智能体游戏玩家。在群体训练过程中,智能体之间相互进行游戏对抗,在相互游戏的过程中不断提升。在这一过程中,一些表现突出的智能体被选中,作为种子选手,基于人类已有的对战数据,通过监督学习进一步的学习游戏经验。
在群体训练过程中,每一个个体都是单独进行优化的,针对个体的优化算法采用了深度强化学习,不断学习从多智能体联合训练以及人类对战数据中获得的经验,最终达到战胜人类玩家的目的。
4 结束语人工智能正在从感知智能向决策智能转变,从集中式结构向多智能体分布式结构演进。这些转变使得传统以数据拟合为核心的最优化方法正在走向以博弈对抗为核心的均衡解。本文从经典的深度学习模型出发,结合时下热门的神经网络结构搜索,简述了基于数据拟合的方法在解决一些人工智能问题时的缺陷,并进一步提出人工智能与博弈论结合,将是未来一个重要的研究方向。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Red Hook, USA, 2012: 1097–1105.
( 0) 0)
|
| [2] |
DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: a large-scale hierarchical image database[C]//Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami, USA, 2009: 248–255.
( 0) 0)
|
| [3] |
YUILLE A L, LIU Chenxi. Deep nets: what have they ever done for vision?[J]. arXiv: 1805.04025, 2018.
( 0) 0)
|
| [4] |
MOOSAVI-DEZFOOLI S M, FAWZI A, FAWZI O, et al. Universal adversarial perturbations[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 86–94.
( 0) 0)
|
| [5] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 ( 0) 0)
|
| [6] |
BROWN N, SANDHOLM T. Superhuman AI for heads-up no-limit poker: libratus beats top professionals[J]. Science, 2018, 359(6374): 418-424. DOI:10.1126/science.aao1733 ( 0) 0)
|
| [7] |
BLAIR A, SAFFIDINE A. AI surpasses humans at six-player poker[J]. Science, 2019, 365(6456): 864-865. DOI:10.1126/science.aay7774 ( 0) 0)
|
| [8] |
ARULKUMARAN K, CULLY A, TOGELIUS J. Alphastar: an evolutionary computation perspective[J]. arXiv: 1902.01724, 2019.
( 0) 0)
|
| [9] |
ROSENBLATT F. Principles of neurodynamics: perceptrons and the theory of brain mechanisms[R]. Washington: Spartan, 1961.
( 0) 0)
|
| [10] |
WERBOS P. New tools for prediction and analysis in the behavioral sciences[D]. Cambridge: Harvard University, 1974.
( 0) 0)
|
| [11] |
WERBOS P J. Backpropagation through time: what it does and how to do it[J]. Proceedings of the IEEE, 1990, 78(10): 1550-1560. DOI:10.1109/5.58337 ( 0) 0)
|
| [12] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 ( 0) 0)
|
| [13] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [14] |
FREUND Y, SCHAPIRE R E. Experiments with a new boosting algorithm[C]//Proceedings of the 13th International Conference on Machine Learning. Bari, Italy, 1996: 148–156.
( 0) 0)
|
| [15] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 ( 0) 0)
|
| [16] |
ROBBINS H, MONRO S. A stochastic approximation method[J]. The annals of mathematical statistics, 1951, 22(3): 400-407. DOI:10.1214/aoms/1177729586 ( 0) 0)
|
| [17] |
DEVLIN J, CHANG Mingwei, LEE K, et al. BERT: pre-training of deep bidirectional transformers for language understanding[J]. arXiv: 1810.04805, 2018.
( 0) 0)
|
| [18] |
ZOPH B, LE Q V. Neural architecture search with reinforcement learning[C]//Proceedings of 5th International Conference on Learning Representations. Toulon, France, 2017.
( 0) 0)
|
| [19] |
BAKER B, GUPTA O, NAIK N, et al. Designing neural network architectures using reinforcement learning[C]//Proceedings of International Conference on Learning Representations. Toulon, France, 2017.
( 0) 0)
|
| [20] |
CAI Han, CHEN Tianyao, ZHANG Weinan, et al. Efficient architecture search by network transformation[C]//Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA, 2018.
( 0) 0)
|
| [21] |
SUGANUMA M, SHIRAKAWA S, NAGAO T. A genetic programming approach to designing convolutional neural network architectures[C]//Proceedings of Genetic and Evolutionary Computation Conference. Berlin, Germany, 2017: 497–504.
( 0) 0)
|
| [22] |
CAI Han, YANG Jiacheng, ZHANG Weinan, et al. Path-level network transformation for efficient architecture search[C]//Proceedings of the 35th International Conference on Machine Learning. Stockholmsmässan, Stockholm, Sweden, 2018: 677–686.
( 0) 0)
|
| [23] |
ELSKEN T, METZEN J H, HUTTER F. Efficient multi-objective neural architecture search via lamarckian evolution[C]//Proceedings of 2019 International Conference on Learning Representations. New Orleans, USA, 2019.
( 0) 0)
|
| [24] |
ZOPH B, VASUDEVAN V, SHLENS J, et al. Learning transferable architectures for scalable image recognition[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018: 8697–8710.
( 0) 0)
|
| [25] |
REAL E, AGGARWAL A, HUANG Yanping, et al. Regularized evolution for image classifier architecture search[J]. AAAI technical track: machine learning, 2019, 33(1): 4780-4789. ( 0) 0)
|
| [26] |
VON NEUMANN J, MORGENSTERN O, KUHN H W, et al. Theory of games and economic behavior[M]. Princeton: Princeton University Press, 2007.
( 0) 0)
|
| [27] |
NASH JR J F. Equilibrium points in n-person games[J]. Proceedings of the national academy of sciences of the United States of America, 1950, 36(1): 48-49. DOI:10.1073/pnas.36.1.48 ( 0) 0)
|
| [28] |
TANG Pingzhong. Reinforcement mechanism design[C]//Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne, Australia, 2017: 5146–5150.
( 0) 0)
|
| [29] |
PÉROLAT J, LEIBO J Z, ZAMBALDI V, et al. A multi-agent reinforcement learning model of common-pool resource appropriation[C]//Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 3643–3652.
( 0) 0)
|
| [30] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Cambridge, USA, 2014: 2672–2680.
( 0) 0)
|
| [31] |
SUTTON R S, MCALLESTER D, SINGH S, et al. Policy gradient methods for reinforcement learning with function approximation[C]//Proceedings of the 12th International Conference on Neural Information Processing Systems. Cambridge, USA, 1999: 1057–1063.
( 0) 0)
|
| [32] |
KOCSIS L, SZEPESVÁRI C. Bandit based monte-carlo planning[C]//Proceedings of the 17th European Conference on Machine Learning. Berlin, Germany, 2006: 282–293.
( 0) 0)
|
| [33] |
SANDHOLM T. Solving imperfect-information games[J]. Science, 2015, 347(6218): 122-123. DOI:10.1126/science.aaa4614 ( 0) 0)
|
| [34] |
RACANIÈRE S, WEBER T, REICHERT D P, et al. Imagination-augmented agents for deep reinforcement learning[C]//Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 5690–5701.
( 0) 0)
|
| [35] |
ZINKEVICH M, JOHANSON M, BOWLING M, et al. Regret minimization in games with incomplete information[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. Red Hook, USA, 2007: 1729–1736.
( 0) 0)
|
| [36] |
BROWN N, SANDHOLM T. Safe and nested subgame solving for imperfect-information games[C]//Proceedings of the 31st Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 689–699.
( 0) 0)
|
| [37] |
VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature, 2019, 575(7782): 350-354. DOI:10.1038/s41586-019-1724-z ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


