2. 重庆邮电大学 计算机科学与技术学院,重庆 400065;
3. 重庆邮电大学 人工智能学院,重庆 400065
2. School of computer science and technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
3. College of Artificial Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
早在1997年,Zadeh教授[1]就提出了粒计算是模糊信息粒化、粗糙集理论和区间计算的超集,是粒数学的子集。粒计算[2-5]是一种新的模拟人类思维机制的方法论,在粒计算的“大伞”之下,包含了很多具体的模型,如:模糊集[6]、粗糙集[7]、商空间[8]、云模型[9]等。粒计算是研究基于多层次粒结构的思维方式、问题求解方法、信息处理模式的理论[10]。
基于粒计算理论,Yao[12]提出了序贯三支决策理论(sequential three-way decisions,S3WD)。从多粒度的角度来说[13-14],随着信息系统中属性或信息的增加,S3WD中等价类将逐渐变小。S3WD是一种利用粗糙近似空间的渐近式问题求解模型,本质上是粗糙粒结构,即通过由粗到细的切换粒度,实现问题的逐步求解。为了实现渐近式的最优尺度的选择和属性约简,文献[15]提出了一种局部规则提取方法,本质上运用了序贯三支决策的思想。在现实的决策分析中,S3WD为求解复杂问题提供了一种模拟人类的多粒度思维。从层次商空间结构(hierarchical quotient space structure,HQSS)[16-18]的角度来说,等价类将会随着粒度的细化逐渐细分成更细的等价类,这意味着在S3WD模型中,随着属性或信息的增加,一个目标概念可以通过不同粒度的知识进行描述。再者,由于较细粒度的知识空间上包含了更多的信息,所以在较细粒度的知识空间上可以更准确地刻画目标概念。但是,构建较细粒度的知识空间需要更多的代价以及在较细粒度上进行问题求解需要更多的时间消耗。
通过以上分析,在S3WD模型中,本文希望在约束条件下可以利用尽可能少的知识空间最大化降低问题的不确定性,从而对问题进行求解,并且针对不同的约束条件评价并选择不同的粗糙粒结构进行问题求解也是需要解决的问题。
基于这个思想,本文从知识距离的角度研究粗糙粒结构的评价模型(为了简单起见,本文仅考虑属性代价为约束条件下粗糙粒结构进行评价选择)。首先,基于前期工作中提出的知识距离框架进一步提出了一种粗糙近似空间距离并讨论了其相关性质。其次,基于提出的粗糙近似空间距离研究了层次粒结构对目标概念的刻画能力,并得到同一个粗糙粒结构中的两个知识空间的不确定性差异等于它们之间的知识距离的结论,并通过实例表验证了本文的评价模型的有效性。此外,本文的评价模型具有可扩展性,针对不同的粒结构设计合适的知识距离,可用于评价不同类型的粒结构,例如层次聚类、多尺度图像分割以及多粒度社区发现等问题。
1 基本概念一个信息系统是一个四元组,可表示为
定义1 粗糙集[7]。设一个信息系统
| $ \begin{array}{*{20}{c}} {\underline R (X) = \{ \left. {x \in U} \right|{[x]_R} \subseteq X\} }\\ {\overline R (X) = \{ \left. {x \in U} \right|{[x]_R} \cap X \ne \text{Ø} \} } \end{array} $ |
其中
本章中,仅从划分的角度,一个知识空间
| $ \begin{array}{*{20}{c}} {\text{POS}{_R}(X) = \underline R (X)}\\ {\text{BND}{_R}(X) = \overline R (X) - \underline R (X)}\\ {\text{NEG}{_R}(X) = U - \overline R (X)} \end{array} $ |
定义2 粒度度量[19-21]。假设
1)
2)
3)
则它是一个粒度度量。
定义3 距离度量[22]。假设
1)正定性:
2)对称性:
3)三角不等式:
则函数
定义4[23] 假设
| $\text{work}(P,Q) = \displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{c_{ij}}{f_{ij}}} } $ |
| $\begin{array}{*{20}{l}} {\text{s.t.}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;{f_{ij}} \geqslant 0;1 \leqslant i \leqslant n,1 \leqslant j \leqslant m} \end{array}$ | (1) |
| $\displaystyle\sum\limits_{j = 1}^m {{f_{ij}}} \leqslant {w_i};1 \leqslant i \leqslant n$ | (3) |
| $\displaystyle\sum\limits_{i = 1}^l {{f_{ij}}} \leqslant {w_j};1 \leqslant j \leqslant m$ | (4) |
| $\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{f_{ij}}} } = \min \Bigg\{ \displaystyle\sum\limits_{i = 1}^l {{w_i}} ,\displaystyle\sum\limits_{j = 1}^m {{w_j}} \Bigg\} $ | (5) |
式(1)限制流量传递过程为P到Q, 不能反向;式(2)限制从Pi运出去的总流量不能超过自身的总流量;式(3)限制Qj接收的总流量不能超过自身的总流量;式(4)限制总传递流量的上限是P和Q的流量的最小值。当这个运输问题解决时,这个最优的流量分配即可求得,即EMD被定义为由总流量归一化的结果:
| $\text{EMD}(P,Q) = \frac{{\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{c_{ij}}{f_{ij}}} } }}{{\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{f_{ij}}} } }}$ | (6) |
一般来说,式(5)中的
定理1[23-24] 如果
在粒计算中,信息粒化旨在建立基于外部世界的有效的并以用户为中心的概念,同时简化物理世界和虚拟世界的认识,可以高效地提供“实用”的非精确解。信息粒化首先需要研究信息粒、粒层和整个粒结构的表示,然后针对表示方法进行构建[11]。同一粒化准则对应一个知识空间,不同粒化准则对应多个知识空间,不同知识空间 (相邻两知识空间或跨知识空间) 中信息粒之间的相互关系构成一个结构,由此得到的多个知识空间及知识空间之间的关系称为粒的拓扑空间,简称为粒结构,如图1所示,为一个粒结构的整体示意图。

|
Download:
|
| 图 1 粒结构示意图 Fig. 1 Schematic diagram of granular structure | |
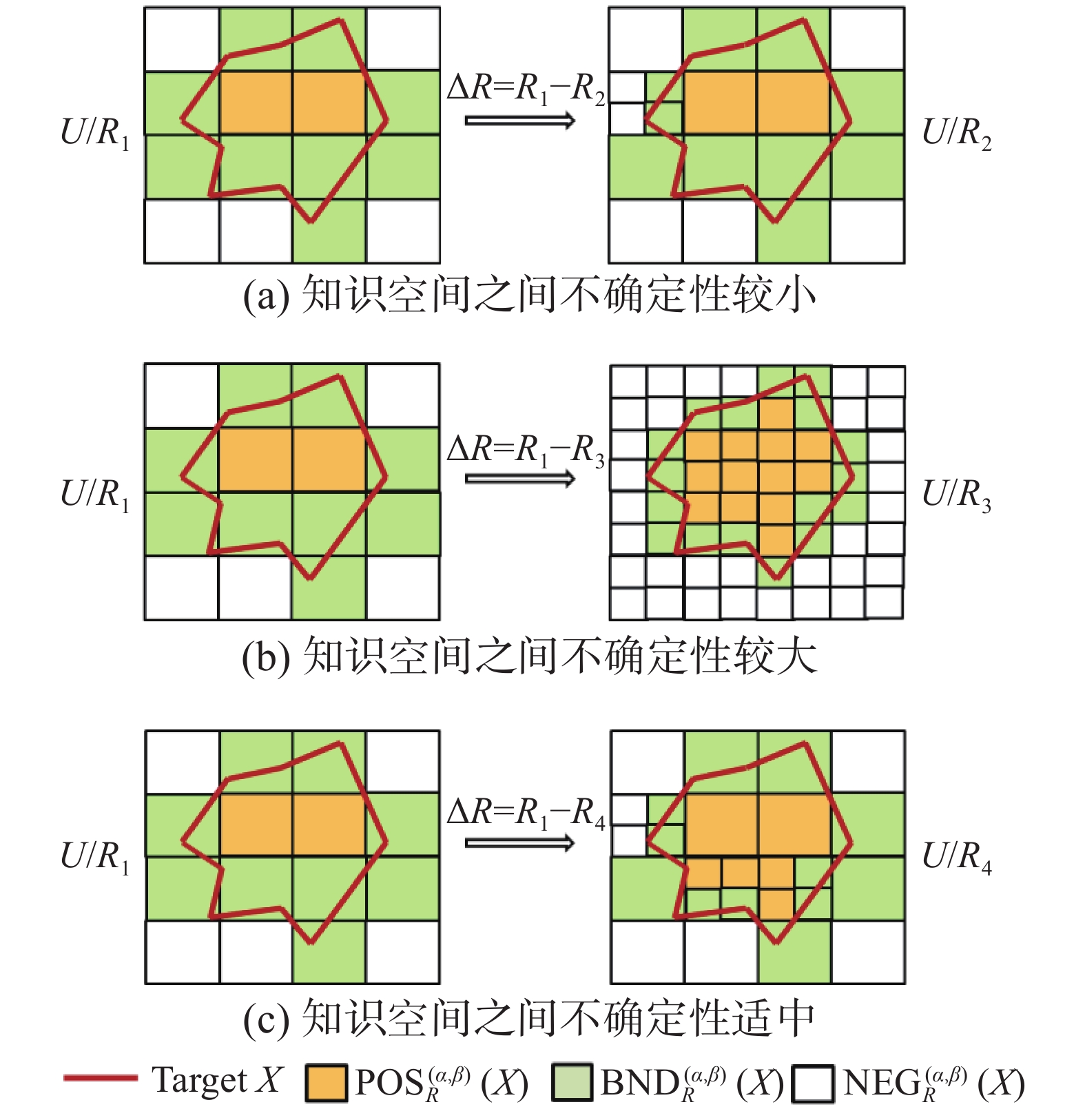
在S3WD模型中,随着粒度的细分,一方面,如果知识空间之间的不确定性差异太小,意味着新增加的属性对于不确定性的降低几乎没有贡献,因此原先在边界域的样本有可能仍然在边界域,无法对它们进行决策;另一方面,如果知识空间之间的不确定性差异太大,意味着获取新增加的属性需要很大的代价,因此有可能无法满足用户的时限约束条件。如图2所示,图2(a)和图2(b)分别表示了上面分析的两种情况,图2(c)表示两个知识空间之间不确定性差异适中的情况。
|
Download:
|
| 图 2 3种不同程度的知识空间细分情况 Fig. 2 Three different levels of knowledge spaces subdivision | |
从粒计算的角度来说,无论是信息熵还是知识粒度都无法刻画粒结构中知识空间之间的差异性。在粗糙集模型中,不确定性度量用于度量粗糙近似空间刻画目标概念的不确定性程度。虽然当前存在许多不确定性度量方法[25-29],但是这些方法仍然不够准确,即具有相同不确定性的两个知识空间不一定等价,它们的差异性如何刻画?为了解决这个问题,钱宇华[30-32]首次提出了基于邻域信息粒的知识距离,并建立了同一知识基中完备粒空间与不完备粒空间之间的关系。杨习贝[33-34]将知识距离应用到多粒度空间,通过知识距离代数格导出一个偏序关系,可用于描述多粒度空间中的层次结构。但是,当前的知识距离模型缺乏清晰的物理解释和理论背景,并且不具有扩展性。在前期工作中[35-36],本文基于EMD提出了一种知识距离框架(knowledge distance framework, KDF)并给出了知识距离的物理意义,在此基础上进一步构建了一种商空间知识距离(quotient space distance,QSD)。
定义5 知识距离框架[35]。假设
| $\text{KDF}({K_P},{K_Q}) = \frac{1}{{\left| U \right|}}\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{d_{ij}}{f_{ij}}} } $ | (7) |
由于对同一论域进行划分的不同知识空间的对象数是相同的,故
定义6 商空间知识距离[35]。设一个信息系统
| $\text{QSD}({U / {{R_1}}},{U / {{R_2}}}) = \frac{1}{{\left| U \right|}}\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {\frac{{\left| {{p_i} \oplus {q_j}} \right|}}{{\left| U \right|}}} } \left| {{p_i} \cap {q_j}} \right|$ |
式中
例1 设一个信息系统
| $\begin{array}{l} \text{QSD}({U / {{R_1}}},{U / {{R_2}}}) = \dfrac{1}{{\left| U \right|}}\displaystyle\sum\limits_{i = 1}^2 {\displaystyle\sum\limits_{j = 1}^3 {\dfrac{{\left| {{p_i} \oplus {q_j}} \right|}}{{\left| U \right|}}} } \left| {{p_i} \cap {q_j}} \right| =\\ \;\;\;\;\;\;\;\; \dfrac{{\dfrac{2}{9} \times 4 + \dfrac{5}{9} \times 2 + \dfrac{4}{9} \times 1 + \dfrac{1}{9} \times 2}}{9} = 0.296 \\ \end{array} $ |
通过多对多匹配计算,

|
Download:
|
| 图 3 两种类型的知识距离 Fig. 3 Two types of knowledge distance | |
为了反映不同知识空间对目标概念的刻画能力的差异性,本文基于知识距离框架进一步提出了一种粗糙近似空间距离。
定义7 模糊集合距离。假设
| $\delta (\widetilde A,\widetilde B) = \frac{{\displaystyle\sum\limits_{x \in \widetilde A \cup \widetilde B} {\mu (x)} - \displaystyle\sum\limits_{x \in \widetilde A \cap \widetilde B} {\mu (x)} }}{{\left| U \right|}}$ |
由定义7可知,无论
定理2 假设
证明 假设
| $\begin{array}{l} (\displaystyle\sum\limits_{x \in \widetilde A \cup \widetilde B} {\mu (x)} - \displaystyle\sum\limits_{x \in \widetilde A \cap \widetilde B} {\mu (x)} ) + (\displaystyle\sum\limits_{x \in \widetilde B \cup \widetilde C} {\mu (x)} - \displaystyle\sum\limits_{x \in \widetilde B \cap \widetilde C} {\mu (x)} ) \geqslant \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(\displaystyle\sum\limits_{x \in \widetilde A \cup \widetilde C} {\mu (x)} - \displaystyle\sum\limits_{x \in \widetilde A \cap \widetilde C} {\mu (x)} ) \\ \end{array} $ |
显然
| $\begin{array}{*{20}{l}} {\dfrac{{\displaystyle\sum\limits_{x \in \widetilde A \cup \widetilde B} {\mu \left( x \right)} - \displaystyle\sum\limits_{x \in \widetilde A \cap \widetilde B} {\mu \left( x \right)} }}{{\left| U \right|}} + \dfrac{{\displaystyle\sum\limits_{x \in \widetilde B \cup \widetilde C} {\mu \left( x \right)} - \displaystyle\sum\limits_{x \in \widetilde B \cap \widetilde C} {\mu \left( x \right)} }}{{\left| U \right|}}} \geqslant\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{ \dfrac{{\displaystyle\sum\limits_{x \in \widetilde A \cup \widetilde C} {\mu \left( x \right)} - \displaystyle\sum\limits_{x \in \widetilde A \cap \widetilde C} {\mu \left( x \right)} }}{{\left| U \right|}}} \end{array} $ |
则
| $\delta (\widetilde A,\widetilde B) + \delta (\widetilde B,\widetilde C) \geqslant \delta (\widetilde A,\widetilde C)$ |
因此,
例2 假设
定义8 设一个信息系统
| $\text{RASD}\left( {{U / {{R_1}}}(X),{U / {{R_2}(X)}}} \right) = \frac{{\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {{\delta _{ij}}{f_{ij}}} } }}{{\left| U \right|}}$ | (10) |
式中:
由于对同一论域进行划分的不同知识空间的对象数是相同的,即
定理3 假设
证明 假设
由定义7和定义8可知,无论
例3(续例1)
| $ \begin{array}{*{20}{l}} \;\;\;\;\;{\rm{RASD}}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\dfrac{{\displaystyle\sum\limits_{i = 1}^2 {\displaystyle\sum\limits_{j = 1}^3 {{\delta _{ij}}{f_{ij}}} } }}{{\left| U \right|}}\;\;}=\\ { \dfrac{{\dfrac{2}{9} \times 4 + \dfrac{2}{9} \times 2 + \dfrac{3}{9} \times 1 + \dfrac{1}{9} \times 2}}{9}}= {0.209} \end{array} $ |
定理4 设一个信息系统
证明 假设
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\text{RASD}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right)}=\\ { \dfrac{1}{{\left| U \right|}}\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{j = 1}^m {\dfrac{{(\displaystyle\sum\limits_{x \in \widetilde {{p_i}}} {\mu \left( x \right)} - \displaystyle\sum\limits_{x \in \widetilde {{q_j}}} {\mu \left( x \right)} )\displaystyle\sum\limits_{x \in \widetilde {{q_j}}} {\mu \left( x \right)} }}{{\left| U \right|}}} } } \end{array} $ |
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\text{RASD}\left( {{U / {{R_1}(X)}},{U /{{R_3}(X)}}} \right)}=\\ { \dfrac{1}{{\left| U \right|}}\displaystyle\sum\limits_{i = 1}^l {\displaystyle\sum\limits_{k = 1}^s {\dfrac{{(\displaystyle\sum\limits_{x \in \widetilde {{p_i}}} {\mu (x)} - \displaystyle\sum\limits_{x \in \widetilde {{r_k}}} {\mu (x)} )\displaystyle\sum\limits_{x \in \widetilde {{r_k}}} {\mu (x)} }}{{\left| U \right|}}} } } \end{array} $ |
由于
| $ \begin{array}{*{20}{l}} {\;\;\text{RASD}\left( {{U / {{R_1}}}(X),{U / {{R_2}(X)}}} \right)}= \end{array} $ |
| $ \begin{array}{*{20}{l}} { \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{{\mu _{{p_1}}}\left( {{\mu _{{q_1}}} + {\mu _{{q_2}}}} \right) - \left( {\mu _{{q_1}}^2 + \mu _{{q_2}}^2} \right)}}{{\left| U \right|}}} \end{array} $ |
| $\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\text{RASD}\left( {{U / {{R_1}}}(X),{U / {{R_3}(X)}}} \right)}=\\ { \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{{\mu _{{p_1}}}\left( {{\mu _{{r_1}}} + {\mu _{{r_2}}} + {\mu _{{r_3}}}} \right) - \left( {\mu _{{r_1}}^2 + \mu _{{r_2}}^2 + \mu _{{r_3}}^2} \right)}}{{\left| U \right|}}}=\\ {\;\;\;\;\;\;\;\;\;\; \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{2\left( {{\mu _{{r_1}}}{\mu _{{r_2}}} + {\mu _{{r_2}}}{\mu _{{r_3}}} + {\mu _{{r_1}}}{\mu _{{r_3}}}} \right)}}{{\left| U \right|}}。} \end{array} $ |
同理,
| $\begin{array}{l} \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{\left( {{\mu _{{q_1}}} - {\mu _{{r_1}}}} \right){\mu _{{r_1}}} + \left( {{\mu _{{q_1}}} - {\mu _{{r_2}}}} \right){\mu _{{r_2}}}}}{{\left| U \right|}}=\\ \;\;\;\;\dfrac{1}{{\left| U \right|}} \cdot \dfrac{{\left( {{\mu _{{q_1}}}{\mu _{{r_1}}} + {\mu _{{q_1}}}{\mu _{{r_2}}}} \right) - \left( {\mu _{{r_1}}^2 + \mu _{{r_2}}^2} \right)}}{{\left| U \right|}} \end{array} $ |
由于
| $ \begin{array}{*{20}{c}} {\text{RASD}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right) + \text{RASD}\left( {{U / {{R_2}}}(X),{U / {{R_3}(X)}}} \right)}=\\ { \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{2\left( {{\mu _{{r_1}}}{\mu _{{r_2}}} + {\mu _{{q_1}}}{\mu _{{q_2}}}} \right)}}{{\left| U \right|}}}=\\ { \dfrac{1}{{\left| U \right|}} \cdot \dfrac{{2\left( {{\mu _{{r_1}}}{\mu _{{r_2}}} + {\mu _{{r_1}}}{\mu _{{r_3}}} + {\mu _{{r_2}}}{\mu _{{r_3}}}} \right)}}{{\left| U \right|}}}= \\ { \text{RASD}\left( {{U / {{R_1}(X)}},{U / {{R_3}(X)}}} \right)} \end{array} $ |
由定理4可知,同一个粗糙粒结构中的两个粗糙近似空间的不确定性差异等于它们之间的知识距离。
例4 设一个信息系统
| $\text{RASD}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right) = \dfrac{{\dfrac{{1.3}}{5} \times 2.7 + \dfrac{{2.7}}{5} \times 1.3}}{9} = \dfrac{{10.6}}{{81}}$ |
类似地
| $ \begin{array}{*{20}{l}} \;{\text{RASD}\left( {{U / {{R_2}(X)}},{U / {{R_3}(X)}}} \right) = \dfrac{{5.9}}{{81}}}\\ {\text{RASD}\left( {{U / {{R_1}}}(X),{U / {{R_3}(X)}}} \right) = \dfrac{{16.5}}{{81}}} \end{array} $ |
因此
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\;\;\;\;\;{\text{RASD}\left( {{U / {{R_1}}},{U / {{R_3}}}} \right)}=\\ \;\;\;\;\text{RASD}\left( {U/{R_1}(X),U/{R_2}(X)} \right) + \\ \text{RASD}\left( {U/{R_2}(X),U/{R_3}(X)} \right)={ \dfrac{{16.5}}{{81}}} \end{array} $ |
在本文中,将一个信息系统中的最粗知识空间和最细知识空间分别表示为
推论1 设一个信息系统
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;{\rm RASD}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right)}=\\ {{\rm RASD}\left( {{U / {{R_1}(X)}},\omega } \right) -{\rm RASD}\left( {{U / {{R_2}}}(X),\omega } \right)} \end{array} $ |
推论2 设一个信息系统
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;\text{RASD}\left( {{U / {{R_1}(X)}},{U / {{R_2}(X)}}} \right)}=\\ {\text{RASD}\left( {{U / {{R_2}(X)}},\sigma } \right) - \text{RASD}\left( {{U / {{R_1}}}(X),\sigma } \right)} \end{array} $ |
定理5 设一个信息系统
证明 1)由定理3可知,
2)假设
| $ \text{RASD}\left( {{U / {{R_1}(X)}},\omega } \right) = \text{RASD}\left( {{U / {{R_2}(X)}},\omega } \right) $ |
3)由推论1可知,如果
定理6 设一个信息系统
证明 1)由定理3可知,
2)假设
| $ \text{RASD}\left( {{U / {{R_1}(X)}},\sigma } \right) = {\rm RASD}\left( {{U / {{R_2}(X)}},\sigma } \right) $ |
3)由推论1可知,如果
通过推论1和定理5可知,对于一个目标概念,粗糙粒结构中的任意两个粗糙近似空间的RASD等于它们之间的粒度度量差异。通过推论2和定理6可知,对于一个目标概念,粗糙粒结构中的任意两个粗糙近似空间的RASD等于它们之间的信息度量差异。结合定理4,本文以粗糙粒结构中的
在粗糙粒结构中,对不确定性问题进行求解时,通常希望在约束条件下可以利用尽可能少的知识空间使不确定性降低最大化。为了简单化,本文仅考虑约束条件为属性代价时的情形,通过第2节定义的粗糙知识距离以及在粗糙粒结构上得出的结论,提出了一种粗糙粒结构的评价模型。
定义9 知识距离序列。假设一个信息系统
基于定义9,本文提出了一种属性约束条件下的粗糙粒结构的评价模型,首先,本文在定义10中定义了一个评价参数
定义10 评价参数。假设一个信息系统S =
| $\lambda = \frac{{\displaystyle\sum\limits_{i = 1}^{\psi - 1} {{\Delta _i}} }}{\psi }$ | (11) |
其中,
| $\psi = \mathop {\max }\limits_{1 \leqslant k \leqslant \xi } \;k$ |
| $\begin{array}{*{20}{l}} {\text{s.t.}}{\;\;\;\;\;\;\;\;\;\;\;\;\text{T}{\text{C}_{\text{K}{\text{S}_k}}} \leqslant \text{T}{\text{C}_{\text{user}}}} \end{array}$ |
通过式(8)可知,
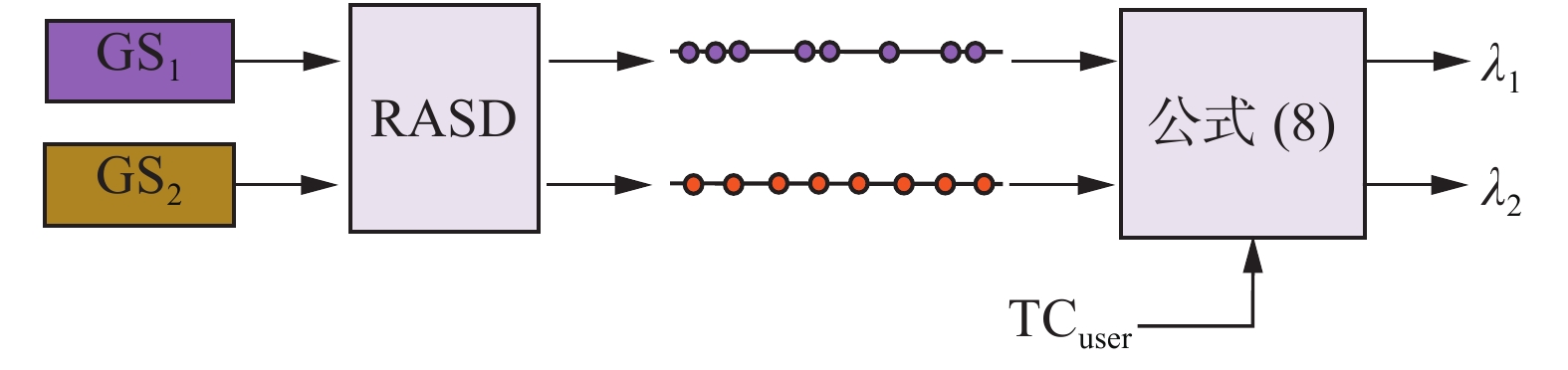
如图4所示,为整个粗糙粒结构评价模型的流程图。首先,通过粗糙近似空间距离计算出不同的粗糙粒结构对应的知识距离序列,然后,通过式(8)并结合不同的约束条件计算得到对应的评价参数,从而实现不同约束条件下的粗糙粒结构的评价和选择。
|
Download:
|
| 图 4 粗糙粒结构的评价模型 Fig. 4 Evaluation model of rough granular structure | |
例5 如图5所示,设一个信息系统S=
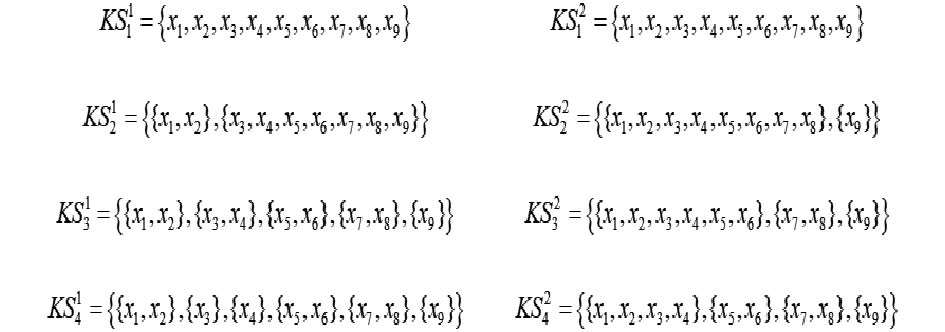
|
Download:
|
| 图 5 两个粗糙粒结构中的知识空间 Fig. 5 Knowledge spaces in two rough granular structures | |
通过式(7)可计算出
因此,
| $ {\lambda _1} = \dfrac{{\dfrac{{10}}{{81}}}}{{2 - 1}} = \dfrac{{10}}{{81}},\;{\lambda _2} = \dfrac{{\dfrac{5}{{81}} + \dfrac{{18}}{{81}}}}{{3 - 1}} = \dfrac{{23}}{{162}} $ |
此时,
因此,
同理,
| $ {\lambda _1} = \dfrac{{\dfrac{{10}}{{81}} + \dfrac{{25}}{{81}}}}{{3 - 1}} = \dfrac{{35}}{{162}},\;{\lambda _2} = \dfrac{{\dfrac{5}{{81}} + \dfrac{{18}}{{81}} + \dfrac{8}{{81}}}}{{4 - 1}} = \dfrac{{31}}{{243}} $ |
此时,
因此,
| $ {\lambda _1} = \dfrac{{\dfrac{{10}}{{81}} + \dfrac{{25}}{{81}} + \dfrac{3}{{81}}}}{{4 - 1}} = \dfrac{{38}}{{243}},\;{\lambda _2} = \dfrac{{\dfrac{5}{{81}} + \dfrac{{18}}{{81}} + \dfrac{8}{{81}}}}{{4 - 1}} = \dfrac{{31}}{{243}} $ |
此时,
因此,
不同的粒化机制可以形成不同的粒结构,在粗糙集的序贯三支决策模型中,通过不同的属性集添加顺序可形成不同的粗糙粒结构。如何建立对这些粗糙粒结构的评价方法是本文的主要研究内容。在前期工作的基础上,提出了一种粗糙近似空间距离,并利用该距离研究了粗糙粒结构的结构特征,得到了粗糙粒结构中的两个知识空间的不确定性差异等于它们之间知识距离的结论。利用该结论,本文建立了一种在属性代价约束条件下的粗糙粒结构的评价模型,解决了在不同约束条件下评价并选择不同粗糙粒结构的问题。由于本文采用的是基于EMD的知识距离框架,因此,本文的方法具有扩展性,可以针对不同类型的粒结构设计评价模型,例如,对不同层次聚类算法、多尺度图像分割算法以及多粒度社区发现算法的评价和选择。但是,本文的工作还处于初步阶段,仅研究了如何评价粗糙粒结构,并没有考虑粗糙粒结构的构建问题,并且只考虑了属性代价为约束条件,评价模型的目标函数还有待进一步改进,尤其如何根据不同的约束条件设计目标函数是下一步工作的主要目标。
| [1] |
ZADEH L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy sets and systems, 1997, 90(2): 111-127. DOI:10.1016/S0165-0114(97)00077-8 ( 0) 0)
|
| [2] |
PEDRYCZ W, SKOWRON A, KREINOVICH V. Handbook of granular computing[M]. Chichester: John Wiley & Sons, 2008: 719−740.
( 0) 0)
|
| [3] |
PEDRYCZ W, AL-HMOUZ R, MORFEQ A, et al. The design of free structure granular mappings: the use of the principle of justifiable granularity[J]. IEEE transactions on cybernetics, 2013, 43(6): 2105-2113. DOI:10.1109/TCYB.2013.2240384 ( 0) 0)
|
| [4] |
WANG Guoyin, YANG Jie, XU Ji. Granular computing: from granularity optimization to multi-granularity joint problem solving[J]. Granular computing, 2017, 2(3): 105-120. DOI:10.1007/s41066-016-0032-3 ( 0) 0)
|
| [5] |
YAO Yiyu. Perspectives of granular computing[C]//Proceedings of 2015 IEEE International Conference on Granular Computing. Beijing, China, 2005: 85−90.
( 0) 0)
|
| [6] |
ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [7] |
PAWLAK Z. Rough sets[J]. International journal of computer & information sciences, 1982, 11(5): 341-356. ( 0) 0)
|
| [8] |
张钹, 张铃. 问题求解理论及应用[M]. 北京: 清华大学出版社, 1990.
( 0) 0)
|
| [9] |
李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995(6): 15-20. LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and membership cloud generators[J]. Journal of computer research and development, 1995(6): 15-20. (  0) 0)
|
| [10] |
苗夺谦, 李德毅, 姚一豫, 等. 不确定性与粒计算[M]. 北京: 科学出版社, 2011.
( 0) 0)
|
| [11] |
徐计, 王国胤, 于洪. 基于粒计算的大数据处理[J]. 计算机学报, 2015(8): 1497-1517. XU Ji, WANG Guoyin, YU Hong. Review of big data processing based on granular computing[J]. Chinese journal of computers, 2015(8): 1497-1517. DOI:10.11897/SP.J.1016.2015.01497 (  0) 0)
|
| [12] |
YAO Yiyu. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341-353. DOI:10.1016/j.ins.2009.09.021 ( 0) 0)
|
| [13] |
QIAN Yuhua, LIANG Jiye, YAO Yiyu, et al. MGRS: a multi-granulation rough set[J]. Information sciences, 2010, 180(6): 949-970. DOI:10.1016/j.ins.2009.11.023 ( 0) 0)
|
| [14] |
QIAN Yuhua, LIANG Jiye, DANG Chuangyin. Incomplete multigranulation rough set[J]. IEEE transactions on systems, man, and cybernetics-part A: systems and humans, 2010, 40(2): 420-431. DOI:10.1109/TSMCA.2009.2035436 ( 0) 0)
|
| [15] |
QIAN Yuhua, CHENG Honghong, WANG Jieting, et al. Grouping granular structures in human granulation intelligence[J]. Information sciences, 2017, 382-383: 150-169. DOI:10.1016/j.ins.2016.11.024 ( 0) 0)
|
| [16] |
张钹, 张铃. 问题求解理论及应用[M]. 北京: 清华大学出版社, 1990.
( 0) 0)
|
| [17] |
ZHANG Ling, ZHANG Bo. The structure analysis of fuzzy sets[J]. International journal of approximate reasoning, 2005, 40(1/2): 92-108. ( 0) 0)
|
| [18] |
ZHANG Ling, ZHANG Bo. Fuzzy reasoning model under quotient space structure[J]. Information sciences, 2005, 173(4): 353-364. DOI:10.1016/j.ins.2005.03.005 ( 0) 0)
|
| [19] |
WIERMAN M J. Measuring uncertainty in rough set theory[J]. International journal of general systems, 1999, 28(4/5): 283-297. ( 0) 0)
|
| [20] |
LIANG Jiye, CHIN K S, DANG Chuangyin, et al. A new method for measuring uncertainty and fuzziness in rough set theory[J]. International journal of general systems, 2002, 31(4): 331-342. DOI:10.1080/0308107021000013635 ( 0) 0)
|
| [21] |
YAO Yiyu, ZHAO Liquan. A measurement theory view on the granularity of partitions[J]. Information sciences, 2012, 213: 1-13. DOI:10.1016/j.ins.2012.05.021 ( 0) 0)
|
| [22] |
LAWVERE F W. Metric spaces, generalized logic, and closed categories[J]. Rendiconti del seminario matematico e fisico di milano, 1973, 43(1): 135-166. DOI:10.1007/BF02924844 ( 0) 0)
|
| [23] |
RUBNER Y, GUIBAS L, TOMASI C. The earth mover's distance, multi-dimensional scaling, and color-based image retrieval[C]//Proceedings of the ARPA Image Understanding Workshop. 1997: 661−668.
( 0) 0)
|
| [24] |
RUBNER Y, TOMASI C, GUIBAS L J. The earth mover's distance as a metric for image retrieval[J]. International journal of computer vision, 2000, 40(2): 99-121. DOI:10.1023/A:1026543900054 ( 0) 0)
|
| [25] |
郭增晓, 米据生. 粗糙模糊集的模糊性度量[J]. 模糊系统与数学, 2005, 19(4): 135-140. GUO Zengxiao, MI Jusheng. An uncertainty measure in rough fuzzy sets[J]. Fuzzy systems and mathematics, 2005, 19(4): 135-140. DOI:10.3969/j.issn.1001-7402.2005.04.023 (  0) 0)
|
| [26] |
QIN Huani, LUO Darong. New uncertainty measure of rough fuzzy sets and entropy weight method for fuzzy-target decision-making tables[J]. Journal of applied mathematics, 2014, 2014: 487036. ( 0) 0)
|
| [27] |
HU J, PEDRYCZ W, WANG G. A roughness measure of fuzzy sets from the perspective of distance[J]. International journal of general systems, 2016, 45(3): 352-367. DOI:10.1080/03081079.2015.1086580 ( 0) 0)
|
| [28] |
SUN Bingzhen, MA Weimin. Uncertainty measure for general relation-based rough fuzzy set[J]. Kybernetes, 2013, 42(6): 979-992. DOI:10.1108/K-12-2012-0119 ( 0) 0)
|
| [29] |
DAI Jianhua, WANG Wentao, XU Qing. An uncertainty measure for incomplete decision tables and its applications[J]. IEEE transactions on cybernetics, 2013, 43(4): 1277-1289. DOI:10.1109/TSMCB.2012.2228480 ( 0) 0)
|
| [30] |
QIAN Y H, LIANG J Y, DANG C Y, et al. Knowledge granulation and knowledge distance in a knowledge base[J]. International journal of approximate reasoning, 2011, 19(2): 263-264. ( 0) 0)
|
| [31] |
QIAN Yuhau, LI Yebin, LIANG Jiye, et al. Fuzzy granular structure distance[J]. IEEE transactions on fuzzy systems, 2015, 23(6): 2245-2259. DOI:10.1109/TFUZZ.2015.2417893 ( 0) 0)
|
| [32] |
LIANG Jiye, LI Ru, QIAN Yuhau. Distance: a more comprehensible perspective for measures in rough set theory[J]. Knowledge-based systems, 2012, 27: 126-136. DOI:10.1016/j.knosys.2011.11.003 ( 0) 0)
|
| [33] |
YANG Xibei, QIAN Yuhua, YANG Jingyu. On characterizing hierarchies of granulation structures via distances[J]. Fundamenta informaticae, 2013, 123(3): 365-380. DOI:10.3233/FI-2012-816 ( 0) 0)
|
| [34] |
YANG Xibei, SONG Xiaoning, SHE Yanhong, et al. Hierarchy on multigranulation structures: a knowledge distance approach[J]. International journal of general systems, 2013, 42(7): 754-773. DOI:10.1080/03081079.2013.810625 ( 0) 0)
|
| [35] |
YANG Jie, WANG Guoyin, ZHANG Qinghua. Knowledge distance measure in multigranulation spaces of fuzzy equivalence relations[J]. Information sciences, 2018, 448-449: 18-35. DOI:10.1016/j.ins.2018.03.026 ( 0) 0)
|
| [36] |
YANG Jie, WANG Guoyin, LI Xukun. Multi-granularity similarity measure of cloud concept[C]//International Joint Conference on Rough Sets. Santiago, Chile, 2016: 318−330.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


