2. 大连交通大学 辽宁省隧道与地下结构工程技术研究中心,辽宁 大连 116028;
3. 辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105
2. Tunnel & Underground Structure Engineering Center of Liaoning, Dalian Jiaotong University, Dalian 116028 China;
3. School of Business Administration, Liaoning Technical University, Huludao 125105, China
系统发生故障的过程涉及因素很多,在相同因素作用下也可能经历不同的发展过程。这些过程各具特征,涉及的事件也是不同的。因此在研究SFEP时首先要解决过程的描述问题。作者在前期研究中提出了SFEP的概念[1-4]表示系统在不同因素、不同关系和不同事件情况下故障发生、发展和最终结果情况。进一步地,提出了空间故障网络(space fault network, SFN)来描述系统故障演化过程(SFEP)。
面对的另一个问题,SFEP的边界是演化过程的开始和结束。在SFEP表示为SFN后,起始于边缘事件,结束于最终事件,其间经历的事件称为过程事件,而各种事件之间的逻辑关系则用连接表示。SFN可通过两种方式研究,一是转换为空间故障树(space fault tree,SFT)[5-16],二是结构化表示。可证明最终事件发生概率分布可由边缘事件发生概率分布表示,因此获得SFEP边缘事件发生概率分布成为研究最终事件发生情况的关键。目前已有的事件发生概率分布计算方法有两种:一是经过大量实验,记录不同条件下的事件发生情况形成分布;二是通过相对较少的实验通过统计得到特征函数,最终得到概率分布。但这些实验的工作量仍然很大,难以满足实际研究要求。
对于少故障数据条件下的系统故障分析目前研究不多,主要包括:基于卷积网络的高速列车转向架故障辨识[17],改进SVDD算法的升降机轴承故障检测[18],改进AlexNet的滚动轴承变工况故障诊断[19],数控机床小样本可靠性建模[20]、栈式自编码网络的故障诊断方法研究[21]、小样本条件下化工设备可靠性预测[22]、指数正则化零空间鉴别分析的故障识别[23]、小样本数据下数控刀架可靠性研究[24]、小样本数据的数控机床MTBF评估[25]。这些方法和理论都是基于小样本或少数据情况下的研究方法。但这些方法缺乏系统层面的描述和研究,缺乏通用性方法研究。
本文在提出SFN基础上,从获得少量故障数据方面入手,考虑信息扩散思想,建立了少故障数据条件下SFEP最终事件发生概率分布计算方法。目的在于:在得到与准确结果精度可比条件下,大幅减少故障数据量;在获得少故障数据条件下,得到满足故障分析要求的事件发生概率分布。
1 SFEP和SFNSFEP描述了系统发生故障的过程。该过程中蕴含了众多事件,也蕴含了这些事件之间的关系。SFEP是在系统层面对系统故障过程进行描述,在系统层面抽象各种类型系统,并予以分析。最终达到对故障演化过程描述、分析、预测和干预的目的。SFEP就研究对象而言大体分为两个方面:一是人工系统;二是自然系统。虽然人工系统和自然系统的目的、发生、发展、结果、预测和控制措施不同,但在系统层面上都可表示为众多事件相互作用的过程。
为描述和分析SFEP,作者2018年提出了SFN理论,作为SFT理论的第三阶段。SFEP是众多事件及其逻辑关系组成的网络结构,同时网络中蕴含着事件间的各种逻辑关系和相互作用的联系。使用目前常规方法难以分析,如系统动力学[26]、符号有向图[27]、解释结构[28]、形式概念分析[29]等。因此在SFT前期研究基础上提出了SFN,将表示结构扩展为网络结构,来表示更具一般性的SFEP。SFN结构上由点和线段组成。点表示SFEP中的事件,箭头线段表示事件之间的关系。事件由对象、状态和逻辑关系组成。对象是作用的承受者和行为执行者。状态是对象的表象和体现。逻辑关系表示了原因事件导致该事件发生的逻辑关系。有时为了研究方便将事件分离成实体事件(对象和状态)和关系事件(逻辑关系),以表达演化过程中更为复杂的逻辑关系。
通过上述分析可知,SFN描述SFEP是通过网络实现的,则需要确定网络中的各种事件和边界。SFN包括3种事件:边缘事件、过程事件和最终事件、边缘事件是SFEP的起点;最终事件则是演化达到的最终状态;过程事件负责两者之间能量、物质和信息的传递。因此边缘事件和最终事件是SFEP的边界。事件之间的因果传递关系使用箭头线段表示称为连接,从原因事件指向结果事件。边缘事件是最基本的原因事件。连接蕴含了传递概率,代表原因事件导致结果事件的可能性。目前传递概率分为两种形式:一是延续性传递概率,认为原因事件在合理的情况下总有一定可能性导致结果事件发生;二是过滤性传递概率,认为原因事件发生概率只有大于传递概率才按照原因事件发生概率传递。这两种方式针对的问题不同,这里使用第一种方式。
如何获得基本原因事件,即边缘事件发生情况是另一个问题。在不同的基础数据条件下,获得原因事件发生情况的方法也不同。最基本的是只有发生概率或者元件故障概率,理想情况下获得事件发生概率分布[5]。发生概率是不考虑不同影响因素时得到的平均情况。实际上影响因素变化注定导致发生概率的变化,因此在SFT和SFN中使用事件发生概率或故障概率来表示不同因素值情况下的不同发生概率,称为概率分布。但在实际研究中发现获得完整的事件发生概率分布非常困难,给后期研究带来问题。
本文提出一种基于信息扩思想的少故障数据条件下事件发生概率分布确定方法。实际中获得系统运行条件因素范围内的故障或事故发生条件是简单的。例如:系统可能工作在0~50 ℃之间,数据统计的故障时间是0~100天。统计每一次故障或事故发生时系统运行时间和温度。将0~50 ℃和0~100天作为分布的2个因素,事件发生作为第3个因素,建立事件发生概率坐标系。0~50 ℃和0~100天组成了研究范围D。再将事件发生的温度和时间因素在D中对应位置的发生概率设为100%。得到了因素坐标系统的离散点,进而使用信息扩散思想得到事件发生概率分布。
2 边缘事件发生概率分布确定在得到离散事件发生情况的分布后,需将其转化为边缘事件发生概率分布,最后得到最终事件发生概率分布。离散事件发生的分布可表示为式(1):
| $P({x_1},{x_2}, \cdots ,{x_n}) = \left\{ {\begin{array}{*{20}{l}} {1(100{\text{%}} ),\quad{\text{发生}}}\\ {0,\quad{\text{不发生}}} \end{array}} \right.$ | (1) |
式中:x表示因素;n表示因素数量。
使用信息扩散概念将事件发生的离散点转化为以该点为中心的正态分布。将该点的发生概率1作为正态分布的最高点,对应的投影位置是各因素在D中的交点。并且将D范围都进行对该点的分布计算,参照正态分布形式,得到一个事件(mj)的事件发生概率分布,如式(2)所示:
| $\begin{array}{c} {P_{mj}}({x_1},{x_2}, \cdots ,{x_n})=\\ \exp \Bigg( - \dfrac{{{{\Bigg(\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - {x_{i0}})}^2}} \Bigg)}^{1/2}}}}{{2\tau }}\Bigg),\quad{x_1},{x_2}, \cdots ,{x_n} \in D \end{array}$ | (2) |
式中:
进一步地,在D中已经收集到了多个实际发生的事件并且记录了因素条件,那么这些事件组成了发生事件集合
| $\begin{array}{c} {P_M}({x_1},{x_2}, \cdots ,{x_n}) = \\ {\rm{max}}({P_{m_j}}({x_1}, {x_2}, \cdots ,{x_n})) = \\ {\rm{max}}\Bigg(\exp \Bigg( - \dfrac{{{{\Bigg(\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - {x_{i0}})}^2}} \Bigg)}^{1/2}}}}{{2\tau }}\Bigg)\Bigg),\\ {m_j} \in M; j = 1,2, \cdots ;J;{x_1},{x_2}, \cdots ,{x_n} \in D \\ \end{array} $ | (3) |
式(3)可研究在D区域内的各类事件发生概率分布。通过论述可知,SFEP起始于边缘事件,因此研究SFN最终事件发生概率分布只能从边缘事件开始。可用式(3)计算SFEP中边缘事件发生概率分布。这样只需记录少量该边缘事件的发生情况,就可确定该事件发生概率分布。
3 最终事件发生概率分布确定最终事件是由过程事件得到的,而所有过程事件是由多个边缘事件通过多次演化得到的。因此想要了解整个SFEP在得到边缘事件发生概率分布后还要分析由边缘事件到最终事件的演化过程。演化过程主要体现在事件间逻辑关系和传递概率,这里使用延续性传递概率。
首先分析事件间最基本的逻辑关系,即原因事件−连接−结果事件。针对同一最终事件,将涉及的所有关系组成关系组S。一般情况下,SFN有3种逻辑关系,与、或和传递蕴含在连接中。与关系和或关系分别表示多个原因事件同时或其一导致结果事件;传递则表示原因事件直接导致结果事件。当然根据柔性逻辑得到的事件发生逻辑关系有20种,这里只对上述3种进行讨论,关系组S如式(4)所示:
| $\begin{array}{l} S = \left\{ {{\rm{CE}} \to {\rm{RE}}|{p_{{\rm{RE}}}} = } \right.\coprod ({q_{{\rm{CE}} \to {\rm{RE}}}}{p_{{\rm{CE}}}})\;{\rm{or}}\\ {{p}_{{\rm RE}}}=\Pi ({{q}_{{\rm CE}\to {\rm RE}}}{{p}_{{\rm CE}}})\;{\rm{and}};\left. {{p}_{{\rm RE}}}=({{q}_{{\rm CE}\to {\rm RE}}}{{p}_{{\rm CE }}})\;{\rm{trans}} \right\} \end{array}$ | (4) |
式中:CE代表原因事件,包括边缘事件和过程事件;RE代表结果事件,包括过程事件和最终事件;
S相当于关系字典,记录了原因事件和结果事件之间的逻辑关系。将最终事件作为起点寻找其原因事件,再将该原因事件作为结果事件继续寻找原因事件,直到原因事件为边缘事件时停止。将这些关系从S中提出进行叠加,得到由边缘事件发生概率分布表示的最终事件发生概率分布解析式。
4 实例分析一个SFEP,用SFN表示如图1所示。
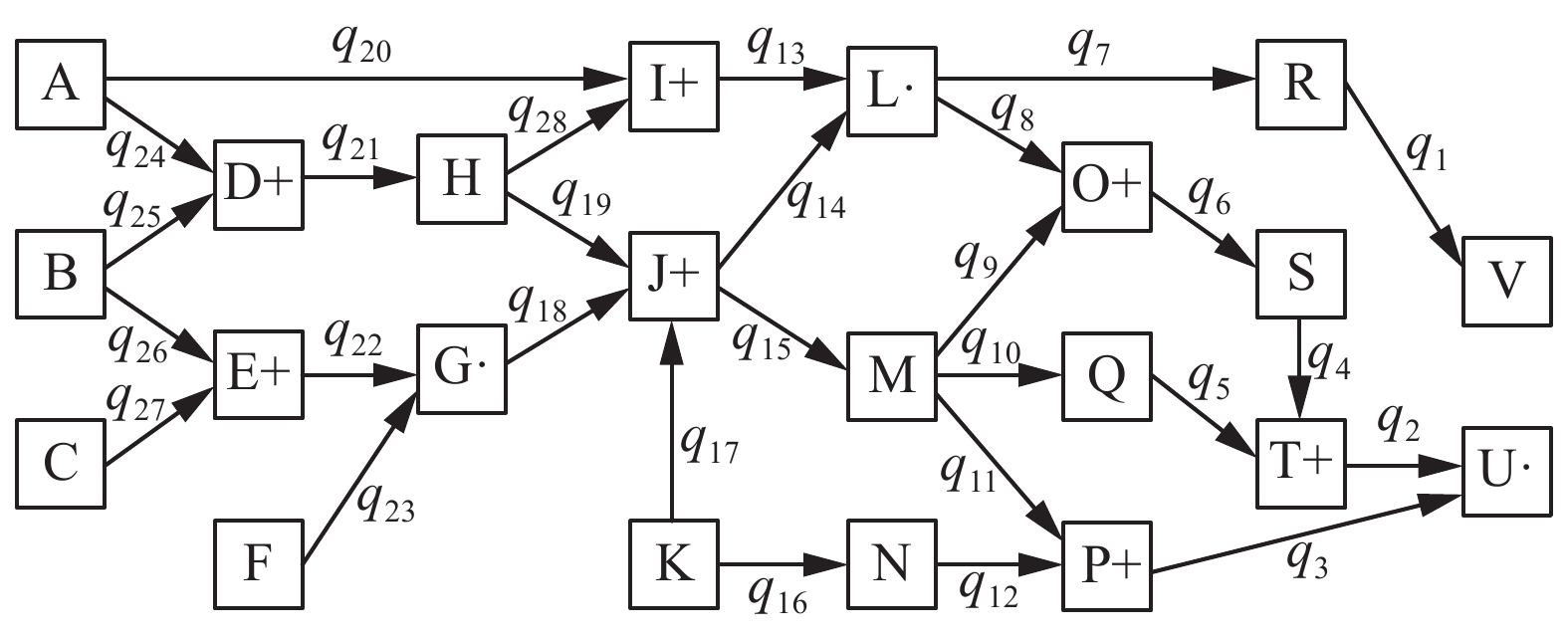
|
Download:
|
| 图 1 SFN网络图 Fig. 1 Network of SFN | |
图1中,包含了22个事件,其中事件A、B、C、F和K都是边缘事件,发生概率分布用pA、pB、pC、pF、pK表示;事件V和U是最终事件,发生概率分布用pV、pU表示;其余为过程事件。逻辑关系为28个,用28个传递概率表示。当有多个传递概率,即多个原因事件时,结果事件增加了逻辑关系标注。其中,·表示与关系,+表示或关系,传递关系不标出。从实际系统研究故障过程,事件发生可认为是系统中具体元件发生故障,因此事件发生概率分布可理解为元件故障概率分布。
根据前述过程,首先统计边缘事件在研究区域内的故障情况。研究区域D为0~50 ℃和0~100天。根据式(1)得到了各边缘事件在区域D中的发生情况,A发生30次、B发生50次、C发生100次、F发生70次、K发生25次。各事件发生情况如图2所示。图中红色位置即为事件发生(故障)位置,并对应了使用时间和使用温度因素。图中故障发生没有明确的分布特征,具有一定的随机性。但也有一些位置集中或稀疏,这些稀疏位置实际上对应了元件的更换状态,即新元件进入系统工作状态。进一步,根据式(2)和式(3)得到各事件发生概率分布(故障概率分布),如图3所示。调整系数τ=30。

|
Download:
|
| 图 2 各事件发生情况 Fig. 2 Occurrence situation of events | |

|
Download:
|
| 图 3 各事件发生概率分布 Fig. 3 Probability distribution of each event | |
图3中蓝色区域表示故障概率分布较低的区域,红色部分代表较高区域。由于各事件发生情况和数量的不同,导致在相同研究区域D内分布状态的不同。原则上能够得到的发生次数越多,调整系数τ越小,越接近实际情况。但也受限于实际故障数据统计情况。
根据式(4)得到的最终事件U和V的关系组,可最终叠加得到这两个事件的发生概率分布解析式,分别如式(5)和式(6)所示(MATLAB化简得到)。
| $ \begin{array}{c} {p_{\rm{U}}} = {q_2}(1 - (1 - {q_4}{q_6}(1 - (1 - {q_8}{q_{13}}(1 - (1 - {q_{20}}{p_{\rm{A}}})(1 - {q_{28}}{q_{21}}(1 - (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))){q_{14}}(1 - \\ (1 - {q_{19}}{q_{21}}(1 - (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))(1 - {q_{18}}{q_{23}}{p_{\rm{F}}}{q_{22}}(1 - (1 - {q_{26}}{p_{\rm{B}}})(1 - {q_{27}}{p_{\rm{C}}})))(1 - \\ {q_{17}}{p_{\rm{K}}})))(1 - {q_9}{q_{15}}(1 - (1 - {q_{19}}{q_{21}}(1 - (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))(1 - {q_{18}}{q_{23}}{p_{\rm{F}}}{q_{22}}(1 - (1 - {q_{26}}{p_{\rm{B}}})(1 - \\ {q_{27}}{p_{\rm{C}}})))(1 - {q_{17}}{p_{\rm{K}}})))))(1 - {q_5}{q_{10}}{q_{15}}(1 - (1 - {q_{19}}{q_{21}}(1 - (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))(1 - \\ {q_{18}}{q_{23}}{p_{\rm{F}}}{q_{22}}(1 - (1 - {q_{26}}{p_{\rm{B}}})(1 - {q_{27}}{p_{\rm{C}}})))(1 - {q_{17}}{p_{\rm{K}}})))){q_3}(1 - (1 - {q_{11}}{q_{15}}(1 - (1 - {q_{19}}{q_{21}}(1 - \\ (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))(1 - {q_{18}}{q_{23}}{p_{\rm{F}}}{q_{22}}(1 - (1 - {q_{26}}{p_{\rm{B}}})(1 - {q_{27}}{p_{\rm{C}}})))(1 - {q_{17}}{p_{\rm{K}}})))(1 - {q_{12}}{q_{16}}{p_{\rm{K}}})) \end{array} $ | (5) |
| $ \begin{array}{l} {p_{\rm{V}}} = {q_1}{q_7}{q_{13}}(1 - (1 - {q_{20}}{p_{\rm{A}}})(1 - {q_{28}}{q_{21}}(1 - (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}}))))q14(1 - (1 - {q_{19}}{q_{21}}(1 - \\ (1 - {q_{24}}{p_{\rm{A}}})(1 - {q_{25}}{p_{\rm{B}}})))(1 - {q_{18}}{q_{23}}{p_{\rm{F}}}{q_{22}}(1 - (1 - {q_{26}}{p_{\rm{B}}})(1 - {q_{27}}{p_{\rm{C}}})))(1 - {q_{17}}{p_{\rm{K}}})) \end{array} $ | (6) |
将图3中得到的各边缘事件发生概率分布分别带入式(5)和式(6),替换pA、pB、pC、pF、pK可得到pU和pV的分布,传递概率为0.1,如图4所示。
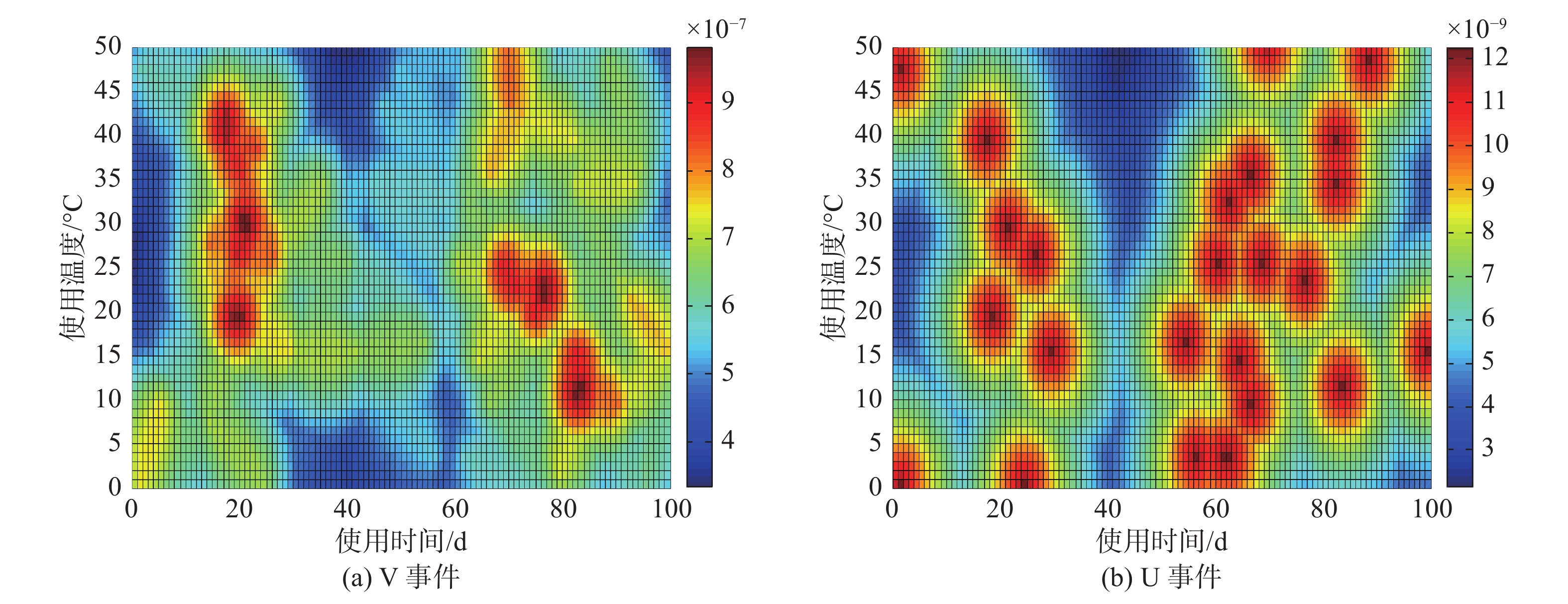
|
Download:
|
| 图 4 最终事件发生概率分布 Fig. 4 Probability distribution of target events | |
图4给出了得到的最终事件发生概率分布,图5给出了使用完整边缘事件发生概率分布得到的最终事件发生概率分布。对比二者,由于边缘事件数量、传递概率数值和演化结构是相同的,U和V最终事件概率数量级相同。图5可认为在研究范围D内是正确的分布状态。图5中故障概率低的分布区域,在图4中同样较低。图4中故障概率高的分布区域,在图5中都是高分布区域。因此给出的方法在一定程度上可以反映客观情况,但符合度取决于观察故障样本的数量。

|
Download:
|
| 图 5 完整的最终事件发生概率分布 Fig. 5 Complete probability distribution of target events | |
综上,实质上论文给出了一种在少故障数据条件下的SFEP最终事件发生概率分布计算方法。通情况下,对于所给实例研究区域,D={使用时间∈[0,100]天,使用温度∈[0,50]℃},需要对每一个因素整数值位置进行实验,得到元件故障次数和总实验次数,进而得到故障发生概率。这样的测试工作显然是不可取的,当然这是最原始的方法。也可以使用SFN中因素变化对元件故障概率影响表征的特征函数,进而得到在多因素影响下的元件故障概率分布,但这也需要相当数量实验确定特征函数。论文所提方法需要的故障数量少于上述方法几个数量级。当然故障数量越多,可越真实的反映实际情况。但通过实例分布可知,故障数量小于100时即可表现元件故障概率分布。从而叠加得到更为复杂的SFEP最终事件发生概率分布。而这种结果也与上述两种方法得到的结果类似,也表明了论文方法的效用。
5 结束语论文使用信息扩散思想,研究了少故障数据条件下的SFEP最终事件发生概率分布计算方法。研究了少故障数据条件下边缘事件发生概率分布确定方法。根据边缘事件发生的因素条件,对D内的该边缘事件的多次发生都生成正态分布,相同因素状态下取所有分布的最大值,得到该边缘事件在D中的发生概率分布。研究了少故障数据条件下最终事件发生概率分布确定方法。根据各边缘事件在D中的发生概率分布,按照SFN得到的关系组,叠加产生从边缘事件到最终事件的发生概率分布解析式。通过实例所得最终事件发生概率分布与以往结果对比说明方法的效用。所提方法在少故障数据条件下与真实结果在定性方面是可比的。可用于SFEP的SFN分析和应用。
| [1] |
崔铁军, 李莎莎, 朱宝岩. 空间故障网络及其与空间故障树的转换[J]. 计算机应用研究, 2019, 36(8): 2400-2403. CUI Tiejun, LI Shasha, ZHU Baoyan. Construction space fault network and recognition network structure characteristic[J]. Application research of computers, 2019, 36(8): 2400-2403. (  0) 0)
|
| [2] |
崔铁军, 李莎莎, 朱宝艳. 含有单向环的多向环网络结构及其故障概率计算[J]. 中国安全科学学报, 2018, 28(7): 19-24. CUI Tiejun, LI Shasha, ZHU Baoyan. Multidirectional ring network structure with one-way ring and its fault probability calculation[J]. China safety science journal, 2018, 28(7): 19-24. (  0) 0)
|
| [3] |
CUI Tiejun, LI Shasha. Research on complex structures in space fault network for fault data mining in system fault evolution process[J]. IEEE access, 2019, 7: 121881-121896. DOI:10.1109/ACCESS.2019.2937641 ( 0) 0)
|
| [4] |
崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J]. 安全与环境学报, 2019, 19(2): 399-405. CUI Tiejun, LI Shasha. Revision of the space fault tree and the space fault network system[J]. Journal of safety and environment, 2019, 19(2): 399-405. (  0) 0)
|
| [5] |
崔铁军. 空间故障树理论研究[D]. 阜新: 辽宁工程技术大学, 2015. CUI Tiejun. Research on space fault tree theory[D]. Fuxin: Liaoning Technology University, 2015. (  0) 0)
|
| [6] |
崔铁军, 马云东. 基于多维空间事故树的维持系统可靠性方法研究[J]. 系统科学与数学, 2014, 34(6): 682-692. CUI Teijun, MA Yundong. Research on the maintenance method of system reliability based on multi-dimensional space fault tree[J]. Journal of systems science and mathematical sciences, 2014, 34(6): 682-692. (  0) 0)
|
| [7] |
崔铁军, 马云东. 系统可靠性决策规则发掘方法研究[J]. 系统工程理论与实践, 2015, 35(12): 3210-3216. CUI Tiejun, MA Yundong. The method research on decision criterion discovery of system reliability[J]. Systems engineering—theory & practice, 2015, 35(12): 3210-3216. DOI:10.12011/1000-6788(2015)12-3210 (  0) 0)
|
| [8] |
崔铁军, 马云东. DSFT的建立及故障概率空间分布的确定[J]. 系统工程理论与实践, 2016, 36(4): 1081-1088. CUI Tiejun, MA Yundong. Discrete space fault tree construction and failure probability space distribution determination[J]. Systems engineering—theory & practice, 2016, 36(4): 1081-1088. DOI:10.12011/1000-6788(2016)04-1081-08 (  0) 0)
|
| [9] |
崔铁军, 马云东. DSFT中因素投影拟合法的不精确原因分析[J]. 系统工程理论与实践, 2016, 36(5): 1340-1345. CUI Tiejun, MA Yundong. Inaccurate reason analysis of the factors projection fitting method in DSFT[J]. Systems engineering—theory & practice, 2016, 36(5): 1340-1345. DOI:10.12011/1000-6788(2016)05-1340-06 (  0) 0)
|
| [10] |
LI Shasha, CUI Tiejun, LIU Jian. Study on the construction and application of cloudization space fault tree[J]. Cluster computing, 2019, 22(3): 5613-5633. DOI:10.1007/s10586-017-1398-y ( 0) 0)
|
| [11] |
CUI Tiejun, LI Shasha. Study on the construction and application of discrete space fault tree modified by fuzzy structured element[J]. Cluster computing, 2019, 22(3): 6563-6577. DOI:10.1007/s10586-018-2342-5 ( 0) 0)
|
| [12] |
崔铁军, 汪培庄, 马云东. 01SFT中的系统因素结构反分析方法研究[J]. 系统工程理论与实践, 2016, 36(8): 2152-2160. CUI Tiejun, WANG Peizhuang, MA Yundong. Inward analysis of system factor structure in 01 space fault tree[J]. Systems engineering—theory & practice, 2016, 36(8): 2152-2160. DOI:10.12011/1000-6788(2016)08-2152-09 (  0) 0)
|
| [13] |
CUI Tiejun, WANG Peizhuang, LI Shasha. The function structure analysis theory based on the factor space and space fault tree[J]. Cluster computing, 2017, 20(2): 1387-1399. DOI:10.1007/s10586-017-0835-2 ( 0) 0)
|
| [14] |
崔铁军, 马云东. 基于因素空间的煤矿安全情况区分方法的研究[J]. 系统工程理论与实践, 2015, 35(11): 2891-2897. CUI Tiejun, MA Yundong. Research on the classification method about coal mine safety situation based on the factor space[J]. Systems engineering—theory & practice, 2015, 35(11): 2891-2897. DOI:10.12011/1000-6788(2015)11-2891 (  0) 0)
|
| [15] |
CUI Tiejun, LI Shasha. Study on the relationship between system reliability and influencing factors under big data and multi-factors[J]. Cluster computing, 2019, 22(4): 10275-10297. DOI:10.1007/s10586-017-1278-5 ( 0) 0)
|
| [16] |
LI Shasha, CUI Tiejun, LIU Jian. Research on the clustering analysis and similarity in factor space[J]. International journal of computer systems science & engineering, 2018, 33(5): 397-404. ( 0) 0)
|
| [17] |
吴昀璞, 金炜东, 任俊箫. 基于孪生卷积网络的高速列车转向架故障辨识[J]. 系统仿真学报, 2019, 31(11): 2562-2568. WU Yunpu, JIN Weidong, REN Junxiao. Fault identification of high-speed train bogie based on Siamese convolutional neural network[J]. Journal of system simulation, 2019, 31(11): 2562-2568. (  0) 0)
|
| [18] |
刘俊辰, 唐文秀, 金剑桥, 等. 基于改进SVDD算法的升降机轴承故障检测研究[J]. 重庆理工大学学报(自然科学), 2019, 33(7): 66-73. LIU Junchen, TANG Wenxiu, JIN Jianqiao, et al. Bearing fault detection method of elevator based on improved SVDD algorithm[J]. Journal of chongqing university of technology (natural science edition), 2019, 33(7): 66-73. (  0) 0)
|
| [19] |
张青青. 基于改进AlexNet的滚动轴承变工况故障诊断研究[D]. 兰州: 兰州理工大学, 2019. ZHANG Qingqing. Research on fault diagnosis of rolling bearings under variable conditions based on improved AlexNet[D]. Lanzhou: Lanzhou University of Technology, 2019. (  0) 0)
|
| [20] |
姜京男. 基于工况因素聚类分析的数控机床小样本可靠性建模[D]. 长春: 吉林大学, 2019. JIANG Jinnan. Reliability modeling of NC machine tools with small samples based on clustering analysis of working conditions[D]. Changchun: Jilin University, 2019. (  0) 0)
|
| [21] |
吕菲亚. 基于栈式自编码网络的故障诊断方法研究[D]. 杭州: 浙江大学, 2019. LYU Feiya. Stacked autoencoder network based fault diagnosis[D]. Hangzhou: Zhejiang University, 2019. (  0) 0)
|
| [22] |
赵江平, 丁洁, 陈敬龙. 基于GM-SVR的小样本条件下化工设备可靠性预测[J]. 中国安全生产科学技术, 2019, 15(1): 145-150. ZHAO Jiangping, DING Jie, CHEN Jinglong. Reliability prediction of chemical equipment under small sample condition based on GM and SVR[J]. Journal of safety science and technology, 2019, 15(1): 145-150. (  0) 0)
|
| [23] |
吴迪, 林国汉, 胡慧, 等. 基于指数正则化零空间鉴别分析的故障识别[J]. 系统科学与数学, 2018, 38(10): 1128-1139. WU Di, LIN Guohan, HU Hui, et al. Fault recognition based on exponential regularized null space linear discriminant analysis[J]. Journal of systems science and mathematical sciences, 2018, 38(10): 1128-1139. (  0) 0)
|
| [24] |
王妍. 小样本数据下数控刀架可靠性研究及其应用[D]. 吉林: 东北电力大学, 2018. WANG Yan. Research and application of the reliability of CNC turret under small samples[D]. Jilin: Northeast Electric Power University, 2018. (  0) 0)
|
| [25] |
朱孟兵. 基于小样本数据的数控机床MTBF评估[D]. 沈阳: 东北大学, 2012. ZHU Mengbing. MTBF evaluation for CNC system based on small sample data[D]. Shenyang: Northeastern University, 2012. (  0) 0)
|
| [26] |
渠寒花, 张国斌, 何险峰. 气象灾害形式概念分析模型[J]. 计算机工程与设计, 2019, 40(2): 516-522. QU Hanhua, ZHANG Guobin, HE Xianfeng. Formal concept analysis model of meteorological disasters[J]. Computer engineering and design, 2019, 40(2): 516-522. (  0) 0)
|
| [27] |
胡钢, 徐翔, 过秀成. 基于解释结构模型的复杂网络节点重要性计算[J]. 浙江大学学报(工学版), 2018, 52(10): 1989-1997, 2022. HU Gang, XU Xiang, GUO Xiucheng. Importance calculation of complex network nodes based on interpretive structural modeling method[J]. Journal of Zhejiang University (engineering science edition), 2018, 52(10): 1989-1997, 2022. DOI:10.3785/j.issn.1008-973X.2018.10.019 (  0) 0)
|
| [28] |
张英, 李江涛. 基于系统动力学的数据化作战指挥模式分析[J]. 指挥控制与仿真, 2019, 41(2): 31-36. ZHANG Ying, LI Jiangtao. Analysis of data-based command based on system dynamics[J]. Command control & simulation, 2019, 41(2): 31-36. DOI:10.3969/j.issn.1673-3819.2019.02.006 (  0) 0)
|
| [29] |
聂银燕, 林晓焕. 基于SDG的压缩机故障诊断方法研究[J]. 微电子学与计算机, 2013, 30(3): 140-142. NIE Yinyan, LIN Xiaohuan. Research on the fault diagnosis of compressor based on the SDG method[J]. Microelectronics & computer, 2013, 30(3): 140-142. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15


