语言是思维的表达。智能决策是人们基于确定性与不确定性对立统一思维的一类不确定性决策，用自然语言或者把自然语言与数学语言相结合进行决策是智能决策的一个特点。集对分析作为处理事物确定性与不确定性关系的一种系统数学理论，把人们对事物的确定性与不确定性关系的辩证认识转换成一个具体的数学工具——联系数，使得集对分析自赵克勤于1989年提出以来^[1-4]，在不同领域得到广泛应用^[5-50]。其中有关不确定性决策方面的专著有2部^{[6, 13]}，在中国知网用主题词“集对分析−决策”查到的文献270多篇。从智能决策的角度看，这些应用大致分8个方面：1）纯自然语言智能决策^[51]，2）自然语言与数学混合智能决策^[52-53]，3）区间模糊决策和直觉模糊决策^[54-67]，4）应用赵森烽−克勤概率的风险决策与贝叶斯决策^[68-70]，5）借助偏联系数的前瞻性决策^[71-72]，6）集对分析粗糙决策^[13，73]，7）集对分析与马尔可夫链相结合的动态决策^[74]，8）集对分析与灰色、云模型等其他方法同异反综合集成智能决策^[75-76]等。集对分析在这8类不确定性决策中的主要应用途径是建立基于联系数的决策模型同时展开不确定性分析；常用的有二元联系数决策模型^{[4, 77]}、三元联系数决策模型^{[48, 78-79]}、四元联系数决策模型^[80-83]、五元联系数决策模型^[84-91]，六元以上联系数决策模型较为少见^{[74, 92-95]}，还有多维联系数模型^[96-98]，以及粗糙集对决策^[99]，累积前景理论与集对分析相结合的决策^[100]，基于偏联系数的系统演化趋势决策^[101]等。当然，理论上存在基于无穷多元联系数的决策模型，以便遍历决策空间中的任意一个决策点作出决策建议。本文试用文献资料法综述以上工作，但限于篇幅仅举3个应用实例，并在讨论中指出，基于集对分析的不确定性决策，是一种立足于全局的智能决策，其物理意义在于把蕴藏在决策系统中的信息能转换成智能。

1 集对分析及其联系数

由文献[1-2]可知，集对这个概念由赵克勤在解读集合论罗素悖论时给出，联系数是集对的特征函数，也是集对分析的主要数学工具，有不同的表达形式，决策中常用到二元、三元、四元、五元归一化联系数：

$u = a + bi$

$ u = a + bi + cj $

$ u = a + bi + cj + dk $

$u = a + bi + cj + dk + el$

式中：a、b、c、d、e统称为联系数 $u$ 的联系分量， $a,b,c,d,e \in [0,1]$ ，且对应上式分别有

$ a + b = 1, $

$a + b + c = 1,$

$a + b + c + d = 1,$

$a + b + c + d + e = 1,$

归一化约束。i、j、k、l是示性系数，表示相关联系分量的不确定性或确定性。

联系数是一种结构函数，具有不同的伴随函数，偏联系数是联系数的一种伴随函数，有偏正联系数、偏负联系数、全偏联系数、一阶至多阶偏联系数之分，研究表明，三元联系数有二阶全偏联系数。一个 $n$ 元联系数有 $n - 1$ 阶全偏联系数，一个联系数的全偏联系数指示出该联系数中各个联系分量在 $n - 1$ 层微观层次上的演化趋势，在用联系数建模的决策分析中有重要的现实意义^[101]。

2 集对分析的纯自然语言智能决策 2.1 纯自然语言智能决策特点

人类的自然语言是人类思维和智慧的表达。利用自然语言决策是一类常见的智能决策。这是因为，无论是普通人的日常决策，还是关键人物在紧要关头作重大决策，不少情况下很难用数字表示决策者的意见，使用定性的自然语言对事物进行评价和决策显得方便、快捷、明确。如指标值高或低、方案可行与不可行等。评价的语意可以是二等级语意，如“好坏”；也可以用三等级语意，如“好中差”；或四等级语意，如“优良中差”；或五等级语意，如“非常满意、很满意、满意、不满意、极不满意”；甚至更多级语意，如“极差、很差、差、一般、好、很好、极好”；或用“非常重要、很重要、重要、一般、差、很差、非常差”7等级语意， $ \cdots $ ，11等级语意“绝对好、很好、好、较好、中好、中等、中差、较差、差、很差、绝对差”等。我们把这一类只用自然语言表示的决策称为纯自然语言智能决策。

2.2 纯自然语言决策的集对分析原理与步骤

人类自然语言的一大特点是语意的模糊性，理解时的歧义性。因此，对纯自然语言决策问题，1）把自然语言用模糊数表示；2）把模糊数转换成联系数；3）建立基于联系数的决策模型；4）对模型作出计算；5）对计算结果作不确定性分析；6）根据计算和分析结果提出决策建议。

2.3 实例

本实例取自文献[51]。

例1　 已知作战仿真系统中生成了4套指挥方案 $S = \{ {S_1},{S_2},{S_3},{S_4}\} $ ，每个方案考虑指挥决策的时效性 ${Q_1}$ 、准确性 ${Q_2}$ 及可靠性 ${Q_3}$ 共3个属性。3名决策者 ${D_m}$ ( $m = $ 1,2,3)给出了用语言表示的决策矩阵，见表1。

已知3名决策者权重为 ${{{\lambda }}}= {(0.3,0.4,0.3)^{\rm{T}}}$ ，3名决策者给出的属性权重分别为

$ {{{w}}_1} = {(0.328,0.329,0.343)}, $

$ {{{w}}_2} = {(0.278,0.401,0.321)}, $

$ {{{w}}_3} = {(0.339,0.332,0.329)}, $

试选出最优方案。决策步骤如下：

1）把表1的语言变量用模糊数表示^[6]，得表2。

2）把表2中的模糊数转换成三元联系数，得表3。转换方法：直觉模糊数 $\left\langle {\mu ,\nu } \right\rangle $ ，转换为三元联系数 $u = a + bi + cj$ ，其中 $a = \mu $ ， $b = 1 - \mu - \nu $ ， $c = \nu $ 。

3）按照数(属性权重)与多项式(属性三元联系数)相乘的法则，计算每一个决策者关于方案的综合联系数。

第1位决策者的4个方案的综合联系数 $u_t^{(1)}$ ( $t$ =1，2，3，4)，分别为

$u_1^{(1)} = 0.603\;3 + 0.067\;15i + 0.329\;55j$

$u_2^{(1)} = 0.538\;8 + 0.049\;95i + 0.411\;25j$

$u_3^{(1)} = 0.565\;9 + 0.098\;5i + 0.335\;6j$

$ u_4^{(1)} = 0.603 + 0.165\;7i + 0.231\;3j。$

第2位决策者的4个方案的综合联系数分别为

$u_1^{(2)} = 0.652\;4 + 0.104\;3i + 0.243\;3j$

$u_2^{(2)} = 0.391\;4 + 0.167\;9i + 0.440\;7j$

$u_3^{(2)} = 0.577 + 0.047\;9i + 0.375\;11j$

$u_4^{(2)} = 0.519\;3 + 0.079\;9i + 0.400\;8j$

第3位决策者的4个方案的综合联系数分别为

$u_1^{(3)} = 0.668\;4 + 0.132\;9i + 0.197\;8j$

$u_2^{(3)} = 0.264\;8 + 0.050\;15i + 0.685\;05j$

$u_3^{(3)} = 0.533\;6 + 0.2i + 0.266\;4j$

$u_4^{(3)} = 0.598\;4 + 0.082\;85i + 0.318\;75j$

4）按照3位决策者各自的权重，计算决策群体关于每个方案的综合联系数 ${u_t}$ ( $t$ =1，2，3，4)，得到：

${u_1} = 0.642\;5 + 0.101\;7i + 0.255\;8j$

${u_2} = 0.397\;6 + 0.097\;3i + 0.505\;1j$

${u_3} = 0.560\;7 + 0.108\;7i + 0.330\;6j$

${u_4} = 0.568\;1 + 0.106\;5i + 0.325\;4j$

5）对每个方案的综合联系数 ${u_t} = {a_t} + $ ${b_t}i + {c_t}j$ ，按 ${e_t} = \dfrac{{{a_t}}}{{{a_t} + {c_t}}}$ ( $t$ =1，2，3，4)，也称为三元联系数的贴近度公式。计算得：

${e_1} = 0.715\;2,{e_2} = 0.440\;5$

${e_3} = 0.629\;1,{e_4} = 0.635\;8$

由此知，根据 ${e_t}$ 值的大小得到4个方案排序为 ${S_1} \succ {S_4} \succ {S_3} \succ {S_2}$ 。符号“ $ \succ $ ”表示“优于”。

6）计算每个方案综合联系数 $u = a + $ $bi + cj$ 的二阶全偏联系数 ${\partial ^{2 \pm }}u$ ，公式为 ${\partial ^{2 \pm }}u = {\partial ^{2 + }}u +$ $ {\partial ^{2 - }}u$ 。

其中，二阶偏正为 ${\partial ^{2 + }}u = \dfrac{{\dfrac{a}{{a + b}}}}{{\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}}}}$ ，二阶偏负为 ${\partial ^{2{\rm{ - }}}}u = \dfrac{{\dfrac{c}{{b + c}}}}{{\dfrac{b}{{a + b}} + \dfrac{c}{{b + c}}}}j$ ，并且取 $j = - 1$ ，得：

${\partial ^{2 \pm }}{u_1} = - 0.087\;5,{\partial ^{2 \pm }}{u_2} = 0.022\;5$

${\partial ^{2 \pm }}{u_3} = - 0.050\;6,{\partial ^{2 \pm }}{u_4} = - 0.053\;3$

由此知，根据 ${\partial ^{2 \pm }}{u_t}$ 值的大小得到4个方案排序为 ${S_2} \succ S_3 \succ {S_4} \succ {S_1}$ ，这个结果与按 ${e_t}$ 值的大小得到4个方案排序正好相反。

7）对每个方案的综合联系数作不确定性分析。分析情况见表4，为简便计，仅考虑 $i = - 1,i = 0,i = 1$ ( $j = - 1$ )3种情况时 ${u_t}$ ( $t$ =1，2，3，4)的值。

由表4看出，当方案 $S_3$ 的值为0.338 8( $i = 1,$ $j = - 1$ )时， $S_1$ 的值也可能是0.285( $i = - 1,j = - 1$ )， $S_4$ 的值也可能是0.242 7( $i = 0,j = - 1$ )， $S_2$ 的值也可能是−0.010 2( $i = 1,j = - 1$ )，或者 $S_2$ 的值为−0.107 5( $i = 0,j = - 1$ )，或者 $S_2$ 的值为−0.204 8( $i = - 1,$ $j = - 1$ )，此时，可以得到4个方案排序为 ${S_3} \succ {S_1} \succ $ ${S_4} \succ {S_2}$ 。

还可以看出，当方案 $S_4$ 的值为0.349 2( $i = 1,$ $j = - 1$ )， $S_3$ 值也可能为0.338 8( $i = 1,j = - 1$ )， $S_1$ 的值也可能是0.285( $i = - 1,j = - 1$ )， $S_2$ 的值也可能是−0.010 2( $i = 1,j = - 1$ )，或者 $S_2$ 值为−0.107 5( $i = 0,j = - 1$ )，或者 $S_2$ 值为−0.204 8( $i = - 1,j = - 1$ )，则得到4个方案排序为 ${S_4} \succ {S_3} \succ S_1 \succ {S_2}$ 。

综合以上可知，S₁、S₂、S₃、S₄ 4个方案都可以是最优方案，这一事实似乎看起来让人们难以理解，其实，上述计算和不确定性分析的价值恰恰在于指出了在哪些具体的条件下哪个方案最优，而这是最重要的，例如在忽略不计4个方案联系数中 $bi$ 的状态不确定性时有 ${S_1} \succ {S_4} \succ {S_3} \succ {S_2}$ ；仅考虑4个方案的三元状态联系数的二阶全偏联系数时有 ${S_2} \succ S_3 \succ {S_4} \succ {S_1}$ ；当计及4个方案的三元状态联系数中 $bi$ 的不确定性时有 ${S_3} \succ {S_1} \succ {S_4} \succ {S_2}$ ；或者有 ${S_4} \succ {S_3} \succ S_1 \succ {S_2}$ ；而不是如文献[51]的结论：无论不确定性条件如何变化，始终是方案 $S_1$ 最优。

3 基于集对分析的自然语言和数学语言混合不确定性智能决策 3.1 自然语言和数学语言混合决策

自然语言和数学语言混合的不确定性智能决策也简称混合智能决策，这也是一类常见的智能决策，基于集对分析的混合智能决策步骤总体上与基于集对分析的纯自然语言智能决策步骤相同，为节约篇幅，下面用一个实例^[52]说明具体决策步骤。

3.2 实例

例2　 电力系统黑启动是电力系统在出现大面积停电事故情况下的一种应急启动，作出应急启动的决策是一种带有诸多不确定性因素的多属性决策，通常由应急启动专家委员会根据电力系统的有关参数和专家经验，在若干个应急预案中筛选出最优黑启动方案和次优黑启动方案并付诸实施。原始数据见表5。

属性说明：需要选取最优启动方案(机组)，其中机组的额定容量和机组爬坡速率是效益型属性，机组启动需要的电能和变电站个数是成本型属性；对于机组所处状态，极热态比热态更容易启动，热态比温态更容易启动，温态比冷态更容易启动。当按“冷−热”次序依次赋“小−大”值时，该属性是效益型属性。

决策步骤如下：

1）把表5中的语言变量用区间数表示，按照“冷−热”语言变量在 $[0,1]$ 区间赋值，为简明起见，分别为：冷态 $ = [0.2,0.3]$ ，温态 $ = [0.4,0.5]$ ，热态 $ = [0.6,0.7]$ ，极热态 $ = [0.8,0.9]$ 。点实数也用区间数表示，如 $1 = [1,1],2 = [2,2]$ ， $0.9 = [0.9,0.9]$ 等，得表6。

2）把表6中的各区间数(属性值和权重)联系数化，转换为二元联系数，对区间数 ${p_{kt}} = [p_{kt}^ - ,p_{kt}^ + ]$ ( $k = 1,2, \cdots ,6$ ， $t = 1,2, \cdots ,5$ )，转换公式为 ${u_{kt}} = \dfrac{{p_{kt}^ + + p_{kt}^ - }}{2} + \dfrac{{p_{kt}^ + - p_{kt}^ - }}{2}i$ ，对权重区间数的转换方法类似，得表7。

3）把表7中的各数据作规范化处理(去量纲)，对于效益型属性值联系数，规范化处理后所得联系数 $u'{_{kt}}$ 为

$u'{_{kt}}$ = $\dfrac{{{u_{kt}}}}{{\mathop {\max }\limits_k {u_{kt}}}}$ ( $k = 1,2, \cdots ,6$ ， $t = 1,2, \cdots ,5$ )

对于成本型属性联系数，规范化后所得联系数 $u'_{kt}$ 为

$u{'_{kt}}$ = $\dfrac{{\mathop {\min }\limits_k {u_{kt}}}}{{{u_{kt}}}}$ ( $k = 1,2, \cdots ,6$ ， $t = 1,2, \cdots ,5$ ， ${u_{kt}} \ne 0$ )

6个候选方案的规范化属性值联系数见表8。

4）把表8中的各属性规范化联系数计入属性权重运用多项式乘法规则，并求和，用以下模型计算：

$ \begin{array}{c} {u_k} = \displaystyle\sum\limits_{t = 1}^n {w{'_t}u{'_{kt}}} = {A_{kt}} + {B_{kt}}i\\ \left( {k = 1,2, \cdots ,6,\;t = 1,2, \cdots ,5} \right) \end{array} $

式中： ${u_k}$ 表示方案的决策值联系数； $w{'_t}$ 表示用联系数表示的第 $t$ 个属性的权重； ${A_{kt}}$ 为方案决策值主值，根据决策值主值大小作出排序，得表9。

5）根据集对分析理论，把表9中的各方案决策值联系数还原成归一化三元决策联系数，并按 ${e_k} = \dfrac{{{a_k}}}{{{a_k} + {c_k}}}$ ( $k = 1,2, \cdots ,6$ )，计算每个方案的综合联系数 ${u_k}$ 的值，见表10。

根据表10可知，6个方案的排序为

${S_5} \succ {S_6} \succ {S_2} \succ S_3 \succ {S_1} \succ S_4$

6）利用例1中6）中的计算二阶全偏联系数公式，计算表10中的三元决策联系数的二阶全偏联系数 ${\partial ^{2 \pm }}{u_k}$ ，得表11。

根据表11可知，这时6个方案的排序为

${S_4} \succ S_1 \succ {S_3} \succ S_2 \succ {S_6} \succ {S_5}$

7）不确定性分析。

对表10中的各个方案的三元决策联系数计算 $i = 1,i = 0,i = - 1$ 时的值( $j$ =−1)，根据值的大小作出可能产生的排序，结果在表12中。

从表12看出，当 ${u_6} = 0.632\;1 + 0.064\;7i + 0.303\;2j$ 中的 $i = 1$ ，其他5个联系数中 $i = - 1$ 时，6个方案的排序为 ${S_6} \succ {S_5} \succ {S_2} \succ {S_3} \succ {S_1} \succ {S_4}$ 。

由此可知，在不同的条件下， ${S_4}$ 、 ${S_5}$ 、 ${S_6}$ 都有可能成为最优方案，在这里，重要的是指明在哪一个层次上，哪一些条件下哪个方案最优。

4 基于集对分析的区间数不确定性智能决策 4.1 区间数不确定性智能决策

区间数是一种最大、最小边界值确定，边界内取值不确定的实数。区间数可以客观地表示某些决策参数的边界范围确定，边界内取值不确定的智能决策问题。基于区间数不确定性智能决策分为属性值用区间数表示但属性权重是点实数，以及属性与属性权重都用区间数表示两类，这里给出属于后者的一个实例加以说明，因为后者包含前者。

4.2 实例

例3　 图书馆的空调系统选择问题。在该决策问题中，有5个备选方案S₁ 、S₂、S₃、S₄、S₅，有4个属性，分别是运营成本 ${Q_1}$ 、性能 ${Q_2}$ 、可维护性 ${Q_3}$ 、安全性 ${Q_4}$ ，其中 ${Q_2}$ 、 ${Q_3}$ 、 ${Q_4}$ 为打分值，其范围为1分(最差)到10分(最好)，且 ${Q_1}$ 为成本型属性，其他为效益型属性。该问题的原始区间数决策矩阵见表13。

各属性权重信息为不完全形式，其中 $0.7{w_1} \leqslant$ $ {w_2} \leqslant 0.8{w_1}$ ， ${w_3} - {w_2} \leqslant 0.1$ ， $0.2 \leqslant {w_4} \leqslant 0.3$ 。

这一实例引自文献[99]，该文献是利用MATLAB6.5软件求解二次线性规划问题得到的权重向量 ${{w}} = {(0.382\;8,0.306\;3,0.085\;7,0.225\;1)^{\rm{T}}}$ ，再利用TOPSIS方法计算各方案与正负理想点距离及其差异值，进而计算出每个方案与理想点的相对接近度，得到了5个方案的排序结果为： ${S_4} \succ {S_5} \succ {S_1} \succ $ ${S_3} \succ {S_2}$ 。

采用本文前2节的方法，决策过程如下：

1）对表13数据进行规范化处理，方法见参考文献[6]，得规范化区间数决策矩阵：

$\left[ {\begin{array}{*{20}{c}} {[0.609,0.712]}&{[0.8,1.0]}&{[0.3,0.5]}&{[0.6,0.8]} \\ {[0.737,0.894]}&{[0.4,0.6]}&{[0.3,0.5]}&{[0.4,0.6]} \\ {[0.808,1.000]}&{[0.4,0.6]}&{[0.7,0.9]}&{[0.5,0.7]} \\ {[0.764,0.933]}&{[0.7,0.9]}&{[0.8,1.0]}&{[0.7,0.9]} \\ {[0.700,0.840]}&{[0.6,0.8]}&{[0.5,0.7]}&{[0.8,1.0]} \end{array}} \right]$

2）用三元联系数表示用规范化处理得到的上述矩阵，例如化区间数[0.609，0.712]为0.609+0.103 $i$ +0.288 $j$ ，得到三元联系数表示的决策矩阵，见表14。

3）用区间数表示各属性权重得

${\tilde w_1} = [0.25,0.40]$ ， ${\tilde w_2} = [0.22,0.30]$ ， ${\tilde w_3} = [0.00,0.10]$ ， ${\tilde w_4} = [0.20,0.30]$ ，

4）把各属性权重区间数改写成三元联系数，得

${u_{{{\tilde w}_1}}} = 0.25 + 0.15i + 0.60j$

${u_{{{\tilde w}_2}}} = 0.22 + 0.08i + 0.70j$

${u_{{{\tilde w}_3}}} = 0.00 + 0.10i + 0.90j$

${u_{{{\tilde w}_4}}} = 0.20 + 0.10i + 0.70j$

5）按普通多项式相乘规则得到各属性加权联系数，见表15。

6）计算每个方案的综合联系数 ${u_t}$ ，并把得到的各方案的2次联系数化为一次幂的三元联系数，注意取 ${j^2} = 1$ ， $i$ 项、 $ij$ 项、 ${i^2}$ 项都归于 $i$ 项。

${u_1}$ =0.448 25+0.355 1 $i$ +1.727 4 $j$ + 0.635 $ij$ +0.071 45 ${i^2}$ +0.762 8 ${j^2} $

${u_2}$ =0.352 25+0.335 8 $i$ +1.466 7 $j$ + 0.692 1 $ij$ +0.079 55 ${i^2}$ +1.073 6 ${j^2}$

${u_3}$ =0.39+0.405 2 $i$ +1.892 8 $j$ + 0.647 2 $ij$ +0.084 8 $i^2$ +0.58 $j^2$

${u_4}$ =0.485+0.446 85 $i$ +2.217 15 $j$ + 0.589 45 $ij$ +0.081 35 $i^2$ +0.180 2 $j^2$

${u_5}$ =0.467+0.402 $i$ +1.934 $j$ + 0.614 $ij$ +0.077 $i^2$ +0.506 $j^2$

转化后为

$u{'_1}$ =1.211 05+1.061 55 $i$ +1.727 4 $j$

$u{'_2}$ =1.425 85+1.107 45 $i$ +1.466 7 $j$

$u{'_3}$ =0.97+1.137 2 $i$ +1.892 8 $j$

$u{'_4}$ =0.665 2+1.117 65 $i$ +2.217 15 $j$

$u{'_5}$ =0.973+1.093 $i$ +1.934 $j$

对这些三元联系数作归一(四舍五入保留4位小数)，得

$u'{'_1}$ =0.302 8+0.265 4 $i$ +0.431 8 $j$

$u'{'_2}$ =0.356 5+0.276 9 $i$ +0.366 6 $j$

$u'{'_3}$ =0.242 5+0.284 3 $i$ +0.473 2 $j$

$u'{'_4}$ =0.166 3+0.279 4 $i$ +0.554 3 $j$

$u'{'_5}$ =0.243 3+0.273 2 $i$ +0.483 5 $j$

7）按 ${e_t} = \dfrac{{{a_t}}}{{{a_t} + {c_t}}}$ ( $t$ =1，2，3，4，5)，计算每个方案的综合联系数 $u'{'_t}$ $ = {a_t} + {b_t}i + {c_t}j$ 的值，得：

${e_1} = {\rm{0}}{\rm{.412\;2}}$ ， ${e_2} = 0.4{\rm{93\;0}}$ ， ${e_3} = 0.{\rm{338\;8}}$ ， ${e_4} = 0.{\rm{230\;8}}$ ， ${e_{\rm{5}}} = {\rm{0}}{\rm{.334\;8}}$ 。

由此知，根据 ${e_t}$ 值的大小得到5个方案排序为 ${S_{\rm{2}}} \succ {S_{\rm{1}}} \succ {S_3} \succ {S_{\rm{5}}} \succ {S_4}$ 。

8）仿照例1的6）的方法，计算方案决策联系数的二阶全偏联系数 ${\partial ^{2 \pm }}{u_t}$ ( $t$ =1，2，3，4，5)，得：

${\partial ^{2 \pm }}u'{'_1} = 0.013\;3$

${\partial ^{2 \pm }}u'{'_2} = 0.000\;9$

${\partial ^{2 \pm }}u'{'_3} = 0.014\;4$

${\partial ^{2 \pm }}u'{'_4} = 0.012\;1$

${\partial ^{2 \pm }}u'{'_5} = 0.019\;0$

由此，根据决策联系数的二阶全偏联系数的值得到方案的排序为 ${S_5} \succ {S_3} \succ {S_1} \succ {S_4} \succ {S_2}$ 。

9）作方案的不确定性分析。仅考虑 $i = - 1,$ $i = 0,i = 1$ 这3种情况时 $u'{'_t}$ ( $t$ =1，2，3，4，5)的值( $j = - 1$ )。

从表16中看出，如果方案 ${S_1}$ 和 ${S_3}$ 取当 $i = 1$ 的情况，而方案 ${S_2}$ 和 ${S_4}$ 取 $i = 0$ 的情况，方案 ${S_5}$ 取 $i = - 1$ 的情况，5个方案的排序是 ${S_1}$ 、 ${S_3}$ 、 ${S_2}$ 、 ${S_4}$ 、 ${S_5}$ 。说明在不同条件下，最优方案也不同。

5 讨论

1)本文对两个三元联系数a+bi+cj作乘积运算采用普通的多项式乘法规则，在运算结果中出现了i、j项和 $i$ 的平方项(i²)以及j的平方项(j²)，根据集对分析原理，不确定性示性系数 $i$ 与任何数的乘积都具有不确定性，所以 $ij$ 项和 $i$ 的平方项(i²)并入bi项，j代表−1， $j$ 的平方项(j²)视为1，所以带j平方项(j²)的值计入a中。

2)决策总是在一定条件下做出。条件变化，决策也随之变化，简称为条件决策。条件决策的特点就是在决策的时候充分考虑条件的不确定性。

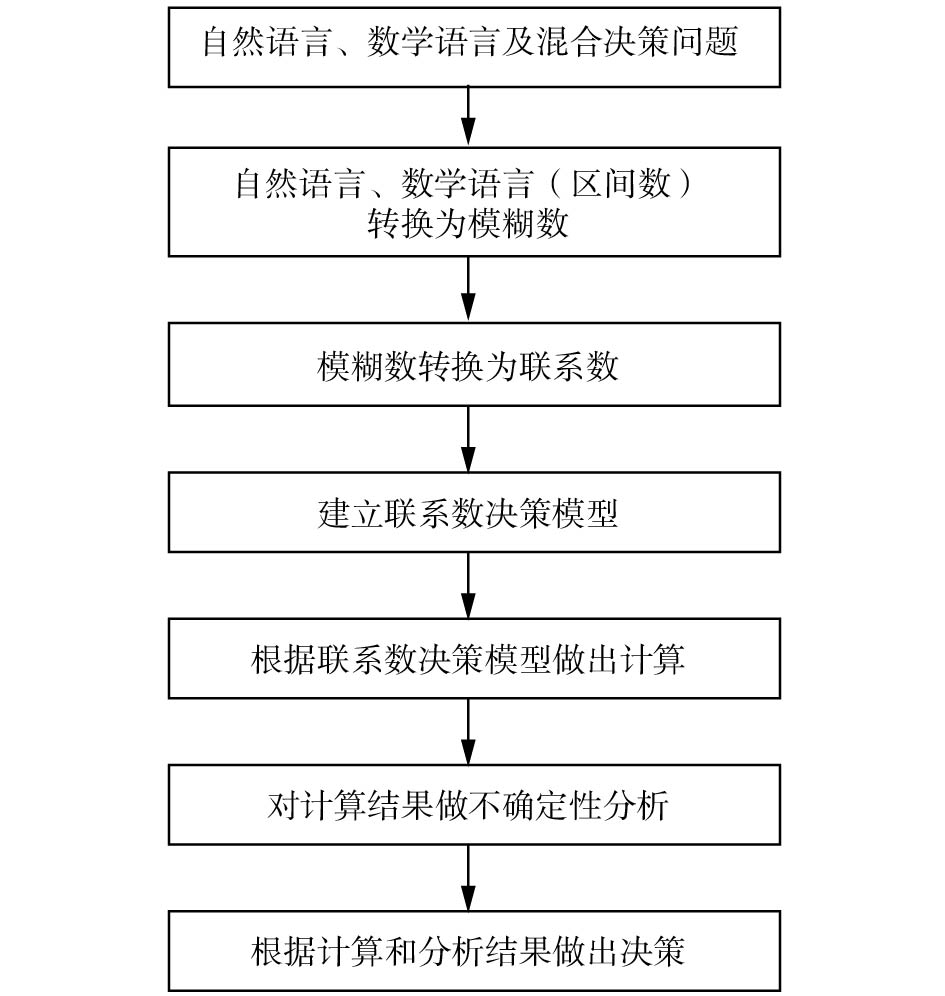
3)关于纯自然语言、自然语言与数学语言混合和区间数决策问题的决策程序。通过上述讨论，发现纯自然语言、自然语言与数学语言混合和区间数决策3种类型的决策模型具有统一的形式和统一的决策步骤，用框图表示如图1所示。

4)关于同异反集成决策。有二层意思，一是把“同异反”看作是“正常(同)，异常(异)”，反常(反)的代名词，由于决策环境通常处于开放状态，科学的决策就需要全方位地考虑到决策环境的“正常(同)，异常(异)”，反常(反)；二是在决策建模上，建同(同类型模型)异(不同类型模型)反(逆向模型)三类模型的组合模型，以提高决策的科学性与实用性,从效用的角度实现最优化决策。

5)在真实世界中，任何一个不确定性决策系统都是动态变化着的系统。为此，我们在文献[61]中提出既确定又有不确定性的D-U决策空间，D-U空间与虚实结合的复空间叠加，从而存在不同的层次，这样，即使在宏观层次上看来是静止的决策系统，在微观层次上依然处在变化之中，利用宏观层次上的状态联系数的偏联系数计算，可以判断出该决策系统在微观层次上的趋势，以便洞察秋毫、随机决策。

6)立足全局的智能决策。把前述的条件决策、同异反组合模型决策、基于不确定性的决策和基于层次的决策以及这些决策的算法统一性等内容加以归纳，可以看出基于集对分析的不确定性智能决策是一种立足全局的智能决策。其物理意义则在于把蕴藏在决策系统中的信息能转换成智能。因为从信息能的角度看，从给定的一组看上去处于静态的决策条件连同这组条件所在的决策环境在某个决策子空间中作出最优决策，实现既定目标，本质上实现了决策系统中的信息能向智能的转换。本文前面所综述的不确定性决策模型和阐述的决策步骤，就是在决策空间中把决策系统中的信息能转换成智能的过程，但转换机制需要深入研究。

6 结束语

集对分析用于决策研究已有众多文献，本文仅限于集对分析理论用于不确定性智能决策作一综述，基本思路是试图给出一种通用的决策模式，利用这种模式能给出一个不确定性智能决策问题在某个决策子空间的不确定性环境中，给出不同条件的决策建议，文中把这些条件归成3类：1）利用例1中 5）的贴近度公式，忽略不计不确定性得到方案排序；2）利用偏联系数规避宏观层次上的不确定性，得到各方案在微观层次上的演化趋势判断，3）经不确定性分析得到方案排序。同一批方案在上述不同条件下有不同的优劣排序，从而给出不同层次条件下的决策建议和立足于全局的决策建议。但由于决策问题的多样性，决策系统中的信息能转换成智能的具体途径和转换机制也具有多样性，这种多样性又决定了决策模型和决策算法的多样性；因此，这种立足全局的集对分析智能决策是一个需要作深入研究的课题。