2. 闽南师范大学 福建省粒计算及其应用重点实验室,福建 漳州 363000;
3. 闽南师范大学 信息与网络中心,福建 漳州 363000
2. Fujian Key Laboratory of Granular Computing and Application, Minnan Normal University, Zhangzhou 363000, China;
3. Information and Network Center, Minnan Normal University, Zhangzhou 363000, China
目标跟踪是计算机视觉领域研究的热点问题,大量文献对这一问题进行了详细的描述[1-2]。目标跟踪具有非常广泛的应用,如智能监控[3]、自动驾驶[4]、无人机[5]、机器人[6]等。运动目标跟踪通常是首先给定第一帧的初始位置,然后在后续的帧中精确定位目标位置。在实际跟踪场景中,由于快速运动、遮挡形变、运动模糊等因素影响,视觉跟踪仍然是一个挑战性的任务。因此,进一步提高视觉跟踪的精度和鲁棒性具有重要的研究意义。
过去几年,基于相关滤波和结合深度特征的目标跟踪取得了巨大的进展。深度跟踪方法采用的策略主要是在线微调预训练深度网络[7-8]或者利用线下预训练提取深度特征来表示跟踪的目标[9-10],这些方法取得了较好的跟踪精度。例如,宁欣等[11]基于判别式核相关滤波器提出自适应更新策略的目标跟踪新框架,有效判别快速运动和遮挡状态。Bertinetto等[12]提出的基于孪生全卷积网络的跟踪方法,通过离线训练卷积神经网络(convolutional neural networks, CNN)提取输入图像的高层卷积特征,然后用交叉相关的方法得到目标位置的响应。Guo等[13]提出动态的孪生网络跟踪方法,在孪生全卷积网络跟踪方法的基础上引入外观模型变换学习和背景抑制学习模块。Valmadre等[14]把相关滤波层当成是孪生网络的1层卷积层,实现了端到端的精确跟踪。Nam等[15]提出多域深度分类网络用于视觉跟踪,通过边界框回归和在线样本采集等技巧结合,取得很高的跟踪精度。Danelljan等[16]提出通过惩罚依赖于空间位置的相关滤波系数,减轻边界效应,减少损坏样本的影响;在连续空间域卷积的跟踪方法基础上,提出高效卷积运算跟踪方法[17],通过构造更小的卷积滤波核和使用矩阵分解来更有效地捕获目标表示。Huang等[18]提出提前终止策略,利用马尔可夫决策过程来学习智能体,通过智能体来决策终止策略,提升了深度跟踪速度。
然而,传统的深度相关滤波跟踪方法通常是初始化所有通道特征,由于各个通道之间存在强相关性,特征通道之间的冗余性不仅加剧了计算负载,还限制了模型学习更通用的表达。因此,需要对输入的特征空间进行选择。其次,这些方法提取的特征表示大部分都是采用预训练的高层深度特征,比如VGG网络的第4或第5层特征。一方面,预训练深度特征空间分辨率低,丢失大量运动目标的空间细节信息,在复杂背景和外观剧烈变化时,跟踪的目标容易发生漂移;另一方面,大部分深度跟踪方法和基于孪生网络的跟踪方法采用的模型都是计算像素级网络损失,忽略空间位置信息,丢失了像素间的固有关系。跟踪的目标很容易因为周围邻域的相似目标而发生错误匹配,导致跟踪失败。
针对上述问题,为了减少高层信息丢失,提高预训练深度特征对剧烈运动和低分辨率的鲁棒性。现提出区域损失函数的孪生网络目标跟踪(regional loss in siamese network for object tracking, RLST),用区域损失函数构建特征选择网络,通过目标感知特征和尺度特征选择,降低深度特征通道之间的冗余性,并减少高层信息丢失。首先,与传统的深度相关滤波跟踪方法类似,采用线下预训练的VGG-16模型对采样的图像块进行特征提取。为了减少池化降采样导致的空间分辨率低和高层信息丢失,只提取第4层卷积层的特征。各个通道的卷积特征构成初始的输入特征空间。其次,与已有的一些采用PCA、自编码网络降维的方法不同,采用迁移学习的思想,构建像素级损失函数和区域损失函数的特征选择网络,在线学习调整模型参数。通过引入区域损失函数,用反向传播的梯度对输入特征空间进行选择。反向传播得到的梯度能够很好地反映分类的显著性,通过这些梯度能够获得卷积滤波核的重要性,从而筛选出不同通道的卷积特征。此外,为了选择最有效的尺度估计,需要筛选出对尺度变化敏感的卷积滤波核。目标表示不是连续的,因此采用逼近的尺度估计方法,选择那些和采样对最接近的尺度。最后,对筛选后特征进行拼接,融入到孪生网络中。通过计算特征之间的互相关性,得到目标响应图,然后利用线性插值的方式得到原图大小,从而实现精确跟踪定位。RLST算法减少特征数量,降低需要更新计算的参数。
1 相关工作在本节中,主要介绍研究的相关基础工作,分别为VGG-Net和孪生网络。
1.1 VGG-NetVGG-Net由牛津大学的Visual Geometry Group和Google的DeepMind公司的研究员共同提出,探索CNN的深度及其性能之间的关系。通过反复堆叠3×3的小型卷积核和2×2的最大池化层,VGG-Net成功地构筑了16~19层深的CNN。VGG-16是一个具有16层的卷积神经网络,包括13个卷积层和3个全连接层。使用多个3×3卷积核的卷积层代替一个卷积核较大的卷积层,减少参数量的同时保留了同样的感受野,并且在一定程度上提升了神经网络的效果。卷积神经网络模型[19-20]具有很强的特征提取能力,因此非常适合在跟踪任务中建立鲁棒的外观模型。其中最常用的一类方法是用卷积神经网络模型提取深度特征代替手工特征,如颜色特征、HOG特征等,然后利用相关滤波跟踪的框架进行精确跟踪。
1.2 孪生网络基于孪生网络(siamese network)的目标跟踪在跟踪速度和精度上都取得了良好的性能,已经成为目标跟踪的研究热点。由于不进行模板更新,因此能够达到较高的实时跟踪性能。孪生网络核心思想是,寻找一个映射函数,将输入图像转换到一个特征空间,每幅图像对应一个特征向量;通过简单的距离度量来表示向量之间的差异,如欧氏距离;最后利用这个距离来衡量输入图像之间的相似度差异。其模型公式如下:
| $ {{{E}}_W}({{{X}}_{\rm{1}}},{{{X}}_{\rm{2}}}) = \left\| {{{{G}}_W}({{{X}}_{\rm{1}}}) - {{{G}}_W}({{{X}}_{\rm{2}}})} \right\| $ | (1) |
式中:X1、X2为输入数据;W表示模型参数;GW的作用就是将输入数据转换为一组特征向量;EW用于衡量两个输入向量转换为特征向量之后,用欧氏距离来衡量两个特征向量之间的相似性。基于孪生网络的跟踪方法是把跟踪问题看成相似性度量的问题,用学习出来的度量去比较和匹配新的未知类别的样本来进行跟踪。后续出现了大量的基于孪生网络的改进方法,例如利用学习残差注意力机制网络,通过改进相似性度量的方式来提高匹配精度。最近,把其他领域如目标检测、图像识别、图像分割的网络引入到跟踪领域成了新的研究热点。这些方法在孪生网络中加入大量的优化技巧,实现了最高的跟踪精度。Li等[21]在孪生网络后加入线下训练好的区域检测网络,把跟踪问题看成一次局部检测任务,可以取得更好的性能。例如,Wang等[22]提出跟踪和分割统一的方法,通过生成与目标对象类别无关的二进制分割掩码,用来同时完成目标跟踪和图像分割任务。
2 区域损失函数的目标跟踪利用迁移学习的思想,通过像素级损失函数和区域损失函数反向传播的梯度进行特征选择。考虑了像素之间的空间结构关系,降低高层深度特征各个通道之间冗余性,增强了判别能力。尤其是对外观发生剧烈变化时,减少了高层信息的损失,能够更有效表示运动目标。
深度神经网络常见的损失函数包括均方误差、对数误差、hinge损失等,用来计算预测像素和真值高斯标签之间的误差值。采用线性模型岭回归对目标外观建模,这些单纯的像素级损失很容易丢失像素之间的空间位置结构信息,也不能精确表达与邻域像素之间的固有关系。因此在特征选择和尺度估计的损失函数中加入区域损失,提高在外观发生剧烈变化、低分辨率等场景下的跟踪鲁棒性。
2.1 目标感知特征选择在预训练的卷积神经网络中,每一个卷积核都提取了特定类型的特征信息,比如边缘、角点等。所有的卷积核提取的特征信息则构成了初始的特征空间。对于目标跟踪任务来说,理想的特征激活只针对需要跟踪的目标,对背景信息则不激活或激活值非常小。因此,对初始特征空间进行筛选,选择那些重要的卷积核激活,可以降低冗余和无相关信息,进一步增强特征表达能力,同时也能够降低过拟合和参数计算量。反向传播得到的梯度能够很好地反映分类的显著性,这些梯度能够决定卷积滤波核的重要性,从而筛选出不同通道的卷积激活。为提高计算效率,采用岭回归线性模型来进行特征选择。其次,为了不丢像素之间的空间结构位置关系,在岭回归模型中添加区域损失来增强特征选择能力。模型方程表示为
| $ \begin{array}{c} {\rm{Loss }}= \mathop {\min }\limits_{{W}} \displaystyle\sum \limits_{i,j} \left( {{{\left\| {{{{Y}}_{i,j}} - {{W}}*{{{X}}_{i,j}}} \right\|}^{{2}}}} \right. + {\lambda _1}\left\| {{{N}}\left( {{{{Y}}_{i,j}}} \right) - } \right.\\ \left. {{{\left. {{{W}}*{{N}}\left( {{{{X}}_{i,j}}} \right)} \right\|}^{{2}}}} \right) + {\lambda _2}{\left\| {{W}} \right\|^{{2}}} \end{array} $ | (2) |
式中:
| $ \begin{array}{c} \dfrac{{{\partial _{{\rm{Loss}}}}}}{{\partial {{{X}}_{{\rm{in}}}}}} = \displaystyle\sum\limits_{i,j} {2\left( {\left( {{{{Y}}_{i,j}} - {{W}}*{{{X}}_{i,j}}} \right) \times {{W}} + } \right.} \\ \left. {{\lambda _1}\left( {{{N}}\left( {{{{Y}}_{i,j}}} \right) - {{W}}*N\left( {{{{X}}_{i,j}}} \right)} \right) \times {{W}}} \right) \end{array} $ | (3) |
各个卷积核的重要性
| $ {\Delta _k} = G\left( {\frac{{{\partial _{{\rm{Loss}}}}}}{{{{{X}}_{{\rm{in}}}}}}} \right) $ | (4) |
根据计算出的卷积核重要性
| $ {{\chi }} = \psi \left( {{{X}};{\Delta _k}} \right) $ | (5) |
式(5)表示根据卷积核重要性
仅仅通过目标感知特征选择还不足以对运动目标的尺度进行估计,为了选择最有效的尺度估计,还需要筛选出那些对尺度变化敏感的特征。目标表示并不是连续的,可采用逼近的尺度估计方法,选择那些和采样对最接近的尺度。筛选方式和目标感知特征选择类似,根据损失函数反向传播的梯度,选择对尺度变化敏感,激活值大的卷积核。同样,在图像对损失函数中加入区域损失,方程可表示为
| $\begin{array}{c} {{{L}}_{{\rm{multiscale}}}} = {\rm{log}}\left( {1 + \displaystyle\sum\limits_{\{ ({x_i},{Y_i})\} _{i = 1}^K} {{\rm{exp}}\left( {f({x_i}) - f({x_j})} \right)} } \right) + \\ \displaystyle\sum\limits_c {\displaystyle\sum\limits_k {{\alpha _{ck}}} } {\ell _{{\rm{region}}}} \end{array}$ | (6) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\begin{array}{*{20}{c}} {} \end{array}\sum\limits_k {{\alpha _{ck}}} = 1,\quad{\alpha _{ck}} \geqslant 0 $ | (7) |
式(6)中,K个不同尺度的采样图像对构成训练样本空间,图像对
| $ {\ell _{{\rm{region}}}}{\rm{ = }}{\left\| {{{N}}\left( {{{{Y}}_{i,j}}} \right) - {{W*N}}\left( {{{{X}}_{i,j}}} \right)} \right\|^{{2}}} $ | (8) |
图像对之间比较的时间复杂度为
| $ \frac{{\partial {{{L}}_{{\rm{multiscale}}}}}}{{\partial {{f(x)}}}} = - \frac{1}{{{{{L}}_{{\rm{multiscale}}}}}}\sum\limits_{\{ ({x_i},{Y_i})\} _{i = 1}^K} {{{\varDelta }}{{{Y}}_{i,j}}} \exp ({{f(x)\varDelta }}{{{Y}}_{i,j}}) $ | (9) |
其中
| $\begin{array}{c} \dfrac{{\partial {{{L}}_{{\rm{multiscale}}}}}}{{\partial {{{X}}_{{\bf{in}}}}}} = \dfrac{{\partial {{{L}}_{{\rm{multiscale}}}}}}{{\partial {{f(x)}}}} \times \dfrac{{\partial {{f(x)}}}}{{\partial {{{X}}_{{\bf{in}}}}}}{\rm{ = }}\dfrac{{\partial {{{L}}_{{\rm{multiscale}}}}}}{{\partial {{f(x)}}}} \times {{W}} +\\ {{\alpha }}\displaystyle\sum\limits_{i,j} {2\left( {{{N}}\left( {{{{Y}}_{i,j}}} \right) - {{W*N}}\left( {{{{X}}_{i,j}}} \right)} \right) \times {{W}}} \end{array}$ | (10) |
计算梯度后,尺度特征的选择方法同目标感知特征选择,根据梯度的重要性来选择对尺度变化敏感的卷积核激活。跟踪检测方程可表示为
| $ {\rm{score}} = \mathop {{\rm{argmax}}}\limits_p \psi \left( {{{{X}}_1};{{{\varDelta }}_{}}} \right) * \psi \left( {{{{Z}}_t};{{{\varDelta }}_{}}} \right) $ | (11) |
score为匹配跟踪过程各个位置的置信度得分,
如图1所示,跟踪器的跟踪框架分为3个部分。首先是预训练深度特征提取,构成初始特征空间。然后是特征选择,根据不同损失函数计算的梯度重要性,选择对应的通道特征卷积核激活。最后对特征选择后进行特征拼接,融入到孪生网络中进行跟踪定位和尺度估计。

|
Download:
|
| 图 1 RLST跟踪流程图 Fig. 1 Framework of the proposed algorithm | |
具体过程为:根据式(3)和式(10)计算的梯度,用全局平均池化函数对梯度的大小进行排序。然后按重要性选择固定数量的卷积核对初始特征空间进行选择。最后计算特征之间的相似性得分,得到响应图。通常,响应图的大小为降采样后的尺寸,为得到精确跟踪位置,还需要利用线性插值的方式得到原图大小,响应值最大的点就是跟踪的目标位置。其次,为了对尺度变化更有效估计,模板图像采用固定的尺度大小,对当前帧搜索区域的特征图缩放到不同尺度大小。算法步骤表示如下。
算法
输入 视频序列
输出
1) 分别裁剪第1帧和待预测帧的图像块;
2) 用VGG-16预训练网络提取裁剪图像块的第4层卷积层和Relu层的特征;
3) 分别用式(3)和式(10)计算损失函数对所有输入的梯度,并保存结果用于下一帧计算;
4) 利用计算的梯度分别对原始特征空间进行筛选;
5) 利用式(11)计算响应,取max(score)为跟踪位置;
6) 重复上述过程,直到视频序列最后一帧。
返回跟踪结果。
3 实验结果与分析为验证所提跟踪算法RLST的有效性,在OTB-2013[23]、OTB-2015[24]、VOT2016[25]和TempleColor[26]公开基准数据集上进行实验。
3.1 实验设置实验过程的特征提取器采用的是预训练的VGG-16模型,为了减少池化降采样导致的空间分辨率低,从而导致高层信息丢失,只提取第4层卷积层和线性修正单元层的特征。其次,当感知特征提取和尺度特征选择网络的训练损失小于0.02时,停止对梯度更新,最大迭代次数设置为50。迭代完成后,分别选择卷积层和线性修正单元层前300和120个卷积核进行特征选择。
实验环境:CPU采用Intel Xeon Silver 4112 2.6 GHz,GPU采用NVIDIA GeForce RTX2080,内存为128 GB的工作站。
3.2 数据集和评价指标OTB-2013和OTB-2015分别包含50个和100个视频序列,每个视频序列都标记了真实矩形框和各种属性注释,比如光照变化、平面外旋转、尺度变化、快速运动、运动模糊、遮挡等。在VOT2016数据集中,包含60个不同挑战的视频序列,而TempleColor是一个公共基准测试数据集,由128个颜色视频序列组成。在各个数据集上评价指标不一样,后续实验采取的评价指标为:在OTB-2013和OTB-2015数据集实验中,采用一次通过(OPE)的精准度和成功率两个指标来定量描述各个跟踪器的性能。在VOT2016数据集中,主要采用平均重叠率(EAO)、精度(A)、鲁棒性(R)3个指标。而在TempleColor数据集中则选择AUC评分来衡量各个跟踪器的性能。
3.3 实验分析本节主要对卷积核实验、定量实验和定性实验进行讨论分析。
3.3.1 卷积核实验分析VGG-16结构中Conv4-1和Conv4-3层的卷积核个数都为512个。为了去除冗余信息,提高特征表达能力,首先对计算的梯度大小进行排序,然后各自筛选梯度信息重要的卷积核作为实验基准,分别为240、80,这些卷积核包含了大部分梯度信息。为了进一步观察卷积核数的影响,在TempleColor数据集上进行分组实验。首先,固定Conv4-1卷积核个数,逐步增加Conv4-3卷积核个数。然后,固定Conv4-3卷积核个数,逐步增加Conv4-1卷积核个数。实验结果如图2所示,增加卷积核数,AUC得分先增加后降低。在Conv4-1卷积核300个、Conv4-3卷积核120个时,AUC得分取得最好0.567。随着卷积核数进一步增加,AUC得分降低,这与卷积核之间的冗余信息有关。这也进一步验证了利用区域损失函数可以降低深度特征通道之间的冗余性,提高跟踪性能。

|
Download:
|
| 图 2 TempleColor数据集上卷积核个数对AUC得分的影响 Fig. 2 Influence of the number of convolution kernels on the score of AUC on TempleColor dataset | |
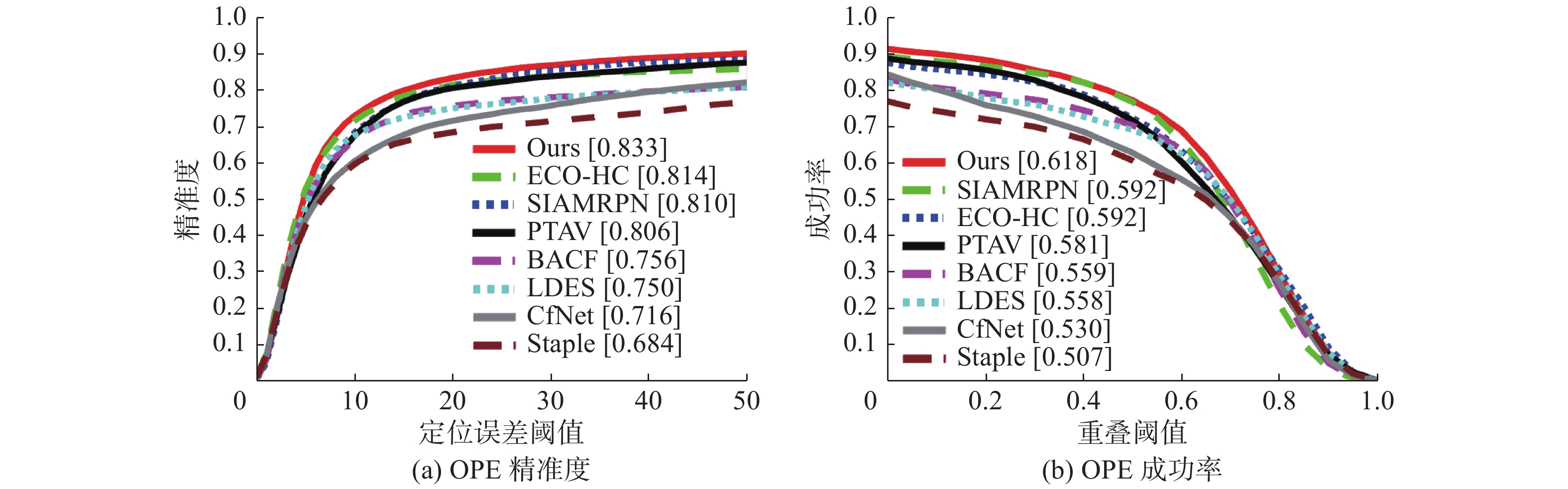
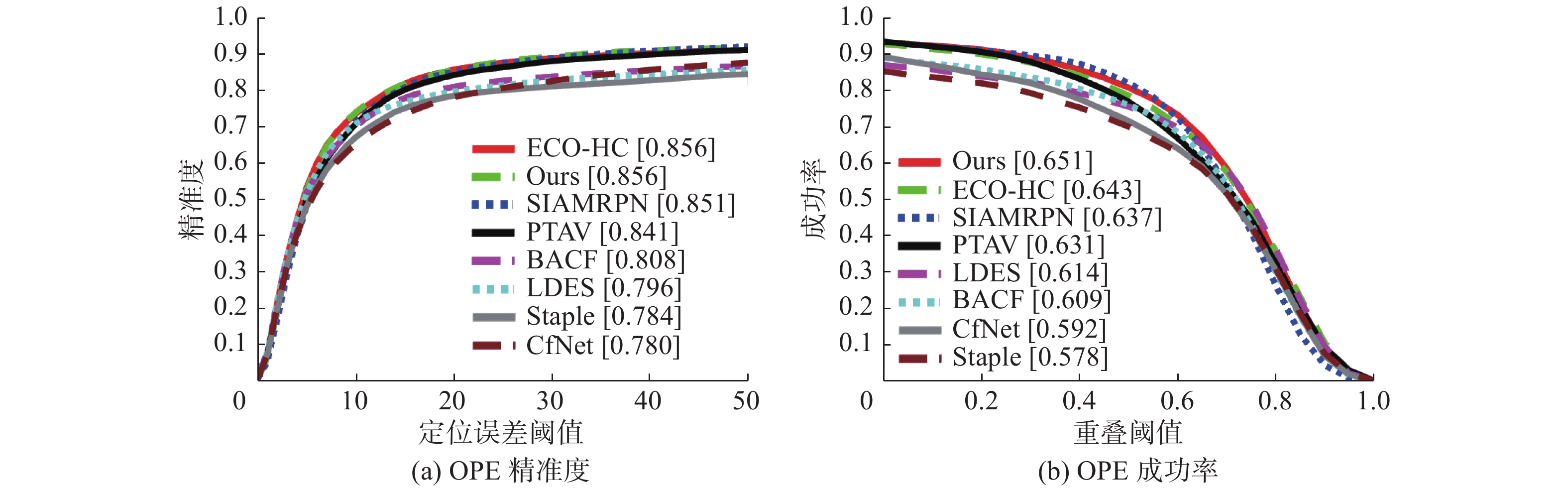
RLST在OTB-2013和OTB-2015数据集上与SIAMRPN[21]、ECO-HC[17]、PTAV[27]、BACF[28]、CF-Net[14]、Staple[29]、LDES[30]等7个先进视频跟踪算法进行比较。整体性能比较结果如图3和图4所示,跟踪器RLST在两个基准数据集上,一次通过的精准度和成功率都取得了很好的结果,在OTB-2013数据集上分别为83.3%和61.8%,在OTB-2015数据集上分别为85.6%和65.1%。所选的对比算法中,主要分为传统的相关滤波方法、结合深度特征的相关滤波方法以及基于孪生网络的跟踪方法。这些算法各自都具有代表性,与其进行比较更能验证RLST算法的有效性。RLST跟踪器利用了区域损失函数,比起单纯的像素级损失函数,建立的跟踪模型保留了更多的细节信息以及空间位置结构信息,更能精确表达与邻域像素之间的固有关系。因此能选择更加鲁棒的目标感知和尺度特征,实验结果也进一步表明了RLST能够取得比较高的性能表现。
|
Download:
|
| 图 3 在OTB-2013数据集上的精准度和成功率曲线 Fig. 3 Precision and success plots using one-pass evaluation on OTB-2013 Dataset | |
|
Download:
|
| 图 4 在OTB-2015数据集上的精准度和成功率曲线 Fig. 4 Precision and success plots using one-pass evaluation on OTB-2015 Dataset | |
为进一步分析RLST跟踪算法在各个属性上的表现,和7个先进视频跟踪算法在OTB-2015数据集各个属性上进行了比较。图5显示了RLST跟踪算法在光照变化、平面外旋转、尺度变化、低分辨率、快速运动和运动模糊等6个属性上都取得较高的性能。尤其是在低分辨率情况下,RLST取得了最好性能,这也验证了通过区域损失函数构建网络进行特征选择能够有效降低信息丢失。

|
Download:
|
| 图 5 在光照变化、平面外旋转、尺度变化、低分辨率、快速运动和运动模糊等6个属性上的精准度和成功率曲线 Fig. 5 Precision plots and success plots over six tracking challenges, including illumination variation, out-of-plane rotation, scale variation, low resolution, fast motion and motion blur | |
为了全面比较RLST在所有属性上的表现,表1列出了RLST跟踪算法在另外5个属性上的比较结果。在这些属性上,虽然RLST没有表现出最好性能,但在形变(DEF)、平面内旋转(IPR)和偏离视线(OV)属性上性能仅次于其他跟踪算法。在背景干扰(BC)和遮挡(OCC)属性上表现不佳,可能原因是特征选择网络对邻域采样。构建区域损失函数,将周围背景信息也考虑在内,增加了过拟合的风险。下一步,将着重研究如何降低背景信息干扰以及探索减少过拟合策略,应用到跟踪算法上以进一步提高性能。
| 表 1 在OTB-2015数据集上另外5个属性的AUC比较结果 Tab.1 AUC scores for another five attributes on the OTB-2015 Dataset |
为进一步验证所提跟踪算法在其他数据集上性能,选取了VOT2016和TempleColor两个比较常用的基准数据集进行实验。图6和表2显示了RLST跟踪算法与其他先进跟踪算法在VOT2016和TempleColor数据集上的对比实验结果。如图6和表2所示,RLST总体跟踪性能取得EAO评分0.327和AUC评分0.567的性能,分别仅次于C-COT的EAO评分0.3294、ECO的AUC评分0.600。尽管RLST没有取得最好的性能,但是C-COT[31]和ECO[17]都是非实时的跟踪算法。相比之下,所提跟踪算法能取得约28 f/s的实时跟踪性能。总体来说,RLST在这两个数据集上取得了比较好的跟踪效果,进一步验证了RLST跟踪算法的有效性。在OTB-2015数据集上定性比较结果如图7。

|
Download:
|
| 图 6 在VOT2016数据集上的对比实验结果 Fig. 6 Comparisons results on the VOT2016 dataset | |
| 表 2 在TempleColor数据集上的对比实验结果 Tab.2 Comparison experiment resultson TempleColor Dataset |

|
Download:
|
| 图 7 在OTB-2015数据集上的定性比较结果 Fig. 7 Qualitative evaluation of our proposed RLST and other trackers on OTB-2015 Dataset | |
为直观展示可视化跟踪结果,分别与C-COT[33]、Staple[29]、CFNet[14]、PTAV[27]、BACF[28]等5个先进跟踪算法进行了定性评估比较。如图7,从上到下依次为Bird1、Box、Skiing、Girl2和DragonBaby等5个视频序列。RLST跟踪算法在这5个视频序列上都表现出较好的性能,尤其在Box和Skiing视频序列,从初始帧到最后一帧,几乎没有出现跟踪失败的情况。在另外3个视频序列,虽然有些帧会发生微小的偏移,但基本上都能跟踪定位到运动目标。针对Skiing低分辨率视频序列,跟踪精度达到近98.7%。RLST通过区域损失函数构建特征选择网络,减少了预训练深度特征通道之间的信息冗余,通过损失函数反向传播的梯度能够有效地选择更鲁棒的目标和尺度特征,验证了所提算法的有效性和鲁棒性。
4 结束语本文提出了区域损失函数的孪生网络目标跟踪RLST。在像素级网络损失函数中,利用区域损失函数来降低深度特征通道之间的冗余性,有效地解决了预训练深度特征空间分辨率低,以及剧烈运动下运动目标空间细节信息丢失的问题,提高了跟踪精度和鲁棒性。在背景干扰和遮挡情况下,RLST性能表现并不是最好。因此,下一步将探索新的采样策略来减少背景信息干扰,以及寻求解决过拟合的方法来进一步提高跟踪精度和鲁棒性。
| [1] |
ZHANG Shengping, YAO Hongxun, SUN Xin, et al. Sparse coding based visual tracking: review and experimental comparison[J]. Pattern recognition, 2013, 46(7): 1772-1788. DOI:10.1016/j.patcog.2012.10.006 ( 0) 0)
|
| [2] |
FIAZ M, MAHMOOD A, JAVED S, et al. Handcrafted and deep trackers: recent visual object tracking approaches and trends[J]. ACM computing surveys, 2018, 52(2): 43. ( 0) 0)
|
| [3] |
TANG Siyu, ANDRILUKA M, ANDRES B, et al. Multiple people tracking by lifted Multicut and person re-identification[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 3701−3710.
( 0) 0)
|
| [4] |
LEE K H, HWANG J N. On-road pedestrian tracking across multiple driving recorders[J]. IEEE transactions on multimedia, 2015, 17(9): 1429-1438. DOI:10.1109/TMM.2015.2455418 ( 0) 0)
|
| [5] |
彭文亮, 梁祝, 李智峰. 基于机器视觉的无人机识别系统算法分析[J]. 电子设计工程, 2019, 27(11): 150-153. PENG Wenliang, LIANG Zhu, LI Zhifeng. Algorithm analysis of UAV recognition system based on machine vision[J]. Electronic design engineering, 2019, 27(11): 150-153. DOI:10.3969/j.issn.1674-6236.2019.11.034 (  0) 0)
|
| [6] |
王杰, 蒋明敏, 花晓慧, 等. 基于投影直方图匹配的双目视觉跟踪算法[J]. 智能系统学报, 2015, 10(5): 775-782. WANG Jie, JIANG Mingmin, HUA Xiaohui, et al. Binocular object tracking method using projection histogram matching[J]. CAAI transactions on intelligent systems, 2015, 10(5): 775-782. DOI:10.11992/tis.201410009 (  0) 0)
|
| [7] |
SONG Yibing, MA Chao, GONG Lijun, et al. CREST: convolutional residual learning for visual tracking[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 2574−2583.
( 0) 0)
|
| [8] |
TENG Zhu, XING Junliang, WANG Qiang, et al. Robust object tracking based on temporal and spatial deep networks[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 1153−1162.
( 0) 0)
|
| [9] |
SUN Chong, WANG Dong, LU Huchuan, et al. Correlation tracking via joint discrimination and reliability learning[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018: 489−497.
( 0) 0)
|
| [10] |
SUN Chong, WANG Dong, LU Huchuan, et al. Learning spatial-aware regressions for visual tracking[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018: 8962−8970.
( 0) 0)
|
| [11] |
宁欣, 李卫军, 田伟娟, 等. 一种自适应模板更新的判别式KCF跟踪方法[J]. 智能系统学报, 2019, 14(1): 121-126. NING Xin, LI Weijun, TIAN Weijuan, et al. Adaptive template update of discriminant KCF for visual tracking[J]. CAAI transactions on intelligent systems, 2019, 14(1): 121-126. DOI:10.11992/tis.201806038 (  0) 0)
|
| [12] |
BERTINETTO L, VALMADRE J, HENRIQUES J F, et al. Fully-convolutional Siamese networks for object tracking[C]//Proceedings of European Conference on Computer Vision. Amsterdam, the Netherlands, 2016: 850−865.
( 0) 0)
|
| [13] |
GUO Qing, FENG Wei, ZHOU Ce, et al. Learning dynamic Siamese network for visual object tracking[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 1781−1789.
( 0) 0)
|
| [14] |
VALMADRE J, BERTINETTO L, HENRIQUES J, et al. End-to-end representation learning for correlation filter based tracking[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 5000−5008.
( 0) 0)
|
| [15] |
NAM H, HAN B. Learning multi-domain convolutional neural networks for visual tracking[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 4293−4302.
( 0) 0)
|
| [16] |
DANELLJAN M, HÄGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 4310−4318.
( 0) 0)
|
| [17] |
DANELLJAN M, BHAT G, KHAN FS, et al. ECO: efficient convolution operators for tracking[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 6931−6939.
( 0) 0)
|
| [18] |
HUANG Chen, LUCEY S, RAMANAN D. Learning policies for adaptive tracking with deep feature cascades[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 105−114.
( 0) 0)
|
| [19] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. 2015: arXiv: 1409.1556v6.
( 0) 0)
|
| [20] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 770−778.
( 0) 0)
|
| [21] |
LI Bo, YAN Junjie, WU Wei, et al. High performance visual tracking with Siamese region proposal network[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake, USA, 2018: 8971−8980.
( 0) 0)
|
| [22] |
WANG Qiang, ZHANG Li, BERTINETTO L, et al. Fast online object tracking and segmentation: a unifying approach[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA, 2019: 1328−1338.
( 0) 0)
|
| [23] |
WU Yi, LIM J, YANG M H. Online object tracking: a benchmark[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA, 2013: 2411−2418.
( 0) 0)
|
| [24] |
WU Yi, LIM J, YANG M H. Object Tracking Benchmark[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 ( 0) 0)
|
| [25] |
KRISTAN M, LEONARDIS A, MATAS J, et al. The visual object tracking VOT2016 challenge results[C]//Proceedings of European Conference on Computer Vision. Amsterdam, The Netherlands, 2016: 777−823.
( 0) 0)
|
| [26] |
LIANG Pengpeng, BLASCH E, LING Haibin. Encoding color information for visual tracking: algorithms and benchmark[J]. IEEE transactions on image processing, 2015, 24(12): 5630-5644. DOI:10.1109/TIP.2015.2482905 ( 0) 0)
|
| [27] |
FAN Heng, LING Haibin. Parallel tracking and verifying: a framework for real-time and high accuracy visual tracking[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 5487−5495.
( 0) 0)
|
| [28] |
GALOOGAHI H K, FAGG A, LUCEY S. Learning background-aware correlation filters for visual tracking[C]//Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy, 2017: 1144−1152.
( 0) 0)
|
| [29] |
BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: complementary learners for real-time tracking[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 1401−1409.
( 0) 0)
|
| [30] |
LI Yang, ZHU Jianke, HOI S C H, et al. Robust estimation of similarity transformation for visual object tracking[C]//Proceedings of AAAI Conference on Artificial Intelligence. Hawaii, USA, 2019: 8666−8673.
( 0) 0)
|
| [31] |
DANELLJAN M, ROBINSON A, KHAN F S, et al. Beyond correlation filters: learning continuous convolution operators for visual tracking[C]//Proceedings of the 14th European Conference on Computer Vision. Amsterdam, The Netherlands, 2016: 472−488.
( 0) 0)
|
| [32] |
ZHANG Tianzhu, XU Changsheng, YANG M H. Multi-task correlation particle filter for robust object tracking[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 4819−4827.
( 0) 0)
|
| [33] |
MA Chao, HUANG Jiabin, YANG Xiaokang, et al. Hierarchical convolutional features for visual tracking[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 3074−3082.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


