随着生产全球化和制造规模化,大型制造企业为降低成本、提高生产柔性与生产效率以快速满足全球市场需求,生产方式正由集中性单车间生产向分布式车间生产转变。但是相关文献研究还主要集中在单个车间生产调度[1]。近年来,分布式车间调度问题(distributed job-shop scheduling problem,DJSP)在车间调度研究领域逐渐受到关注,如对关键路径的二车间综合调度问题[2]、分布式流程车间问题[3]、多工序同时结束的多车间逆序综合调度[4]和分布式工作车间问题[5-6]等。
经典的单车间调度问题[7](job-shop scheduling problem, JSP)中所有的工件都在同一车间内加工完成的,DJSP是将工件分配到更多的车间共同加工完成。DJSP是对JSP的扩展,结合了工件在分布式车间的分配和单个车间内调度两种问题,并且允许任何一个车间拥有加工完成任何一个工件的能力。
由于分布式车间调度需要考虑分配和排序两个阶段,因而DJSP更加复杂[8]:第一阶段将待加工的零件分配到f家车间中;第二阶段对已经分配到同一车间的工件进行排序(即单个车间调度问题)。第一阶段的工件分配很大程度上决定了多车间之间的工作量协同程度,对算法的结果具有至关重要的影响。为了更好地解决DJSP,Wagner[9]提出了DJSP模型,经过不断的改进能够准确地描述出分布式工作车间调度问题的特征,该模型的建立对求解DJSP具有重要意义。在该数学模型被提出之前,研究者一般使用标准遗传算法来解决分布式车间调度问题[10],之后的研究也是在标准遗传算法的基础上进行的局部改进,以解决中小规模的分布式车间调度问题[11]。该数学模型的提出促进了DJSP的研究进度,扩大了问题的可研究规模。Naderi等 [12]运用工件−车间分配原则将所有工件分配到每个车间后,再用贪婪式启发算法对每个车间内的工件进行排序,有效地解决了分布式车间调度问题;Chaouch等[13]在分配工件时结合运用了机器加工工件的工作量均衡原则和甘特图,再用改进的蚁群优化算法对每个车间的工件进行排序;Naderi等[14]在分配和排序的基础上又进行了优化,对当前解中不同车间中相同位置的工件进行随机挑选和互换形成新的解。杨敬松等[15]将遗传和模拟退火算法结合,相互补充弥补各自搜索能力的弱点形成混合遗传算法,用于寻找分布式车间调度问题的最短工艺路径。
遗传算法(genetic algorithm,GA)通过各种遗传算子(选择,交叉和突变)搜索解空间中的最优解,得出较优的解决方案[16]。GA已用于解决生产调度、设施布局、资源分配等生产制造中的问题,而GA没有机械学习能力,当迭代到一定代数后评价数值陷入局部最优,产生大量的无用计算降低了求解的精度和效率。为了跳出GA的局部最优,Chang等[17]提出了区块,并将区块与进化算法结合应用于解决组合优化问题,取得了不错的效果。近年来,通过挖掘区块保留优势解序列信息中的高频率基因链与启发式算法结合,优化原算法的搜索路径,减少无效迭代[18]。区块与猫群算法结合,统计猫群算法中的跟踪模式更新猫的速度和位置,从而更新优秀解序列产生子群体,增强了猫群算法的鲁棒性和全局搜索能力[19]。张敏等[20]运用区块的关联规则组合成大量的人造解注入到GA中,提高了解的多样性,并通过单点突变机制和两种不同的母体重组方式,保证算法的竞争优势。裴小兵等[21]提出一种将遗传算法与蚁群算法相结合的改进区块遗传算法,通过蚁群算法中的信息素浓度和区块两种方式分别统计搜索路径和搜索关联度,提炼精英染色体中的有效信息,比人造解与遗传算法结合的混合算法等更具有竞争性。区块能较大程度地平衡分布式车间之间和机器之间的工作量,使分配到同一车间的工件在每个机器上的加工时间相近,发挥加工车间之间的系统效应。在构建人工染色体的过程中,通过以工件为单位或以区块为单位插入到人工染色体的空白位置,提高了染色体的质量,加快了解的收敛速度[16]。
目前关于分布式车间调度问题的文献相对较少,现有研究将分配和排序两阶段分别考虑,在分配阶段仅考虑每个车间每台机器的工作量均衡,未涉及下一阶段的工件排序,其结果可能会增加分布式车间的最大完工时间。同时大部分针对分布式车间调度问题的优化算法没有清晰地说明如何通过变异、重组等操作使当前解集不断进化,部分文献仅对分配到不同车间的n个工件中的两个或少数几个工件进行连续调换来优化当前解,本文尝试同时调整解序列中车间的分配和工件的排序来增加解的多样性。本文基于区块构建高质量人工染色体改进传统遗传算法,应用区块保留并传递精英染色体中的高频率基因链,协调分布式车间调度问题中的分配和排序两阶段;改进区块遗传算法中的基因重组和人工染色体的构建,使之适应于分布式车间调度问题。本研究以改进后适应于分布式车间调度问题的遗传算法为构架,引入基于区块的人工染色体跳出遗传算法的局部最优。
1 数学模型的阐述为更好地解决调度问题,Wagner[9]提出了整数规划模型,将调度问题模型化,明确地描述了调度问题的特征。在Naderi等[12]首次尝试构建分布式车间调度问题数学模型之前,没有直接研究分布式车间调度问题的论文,用混合整数线性规划模型构建分布式车间调度问题为该问题的解决提供了基础。
分布式工作车间调度问题是将n件工件分配到f间车间中,每个车间以一定的顺序共同加工完成这批零件,确定这批工件分配和排序的方案。每个车间拥有m台机器,且具有独立加工完成每个工件的能力,与车间调度问题中的条件相同。假设分布在不同区域的f个车间的生产能力是相同的,具有相同的机器和车间布局;所需加工的工件可以在任意车间内加工完成,且加工所需的时间是相同的;不考虑工资水平、运输距离等因素。在工件加工过程中,已经分配到加工车间的工件禁止转移到其他车间加工,因为工件在车间之间的交叉加工将增加成本和技术难度。DJSP的约束条件为:1)每个工件只能分配到一个车间内,且每个工件都由特定的车间加工;2)每台机器只能同时加工一个零件,每个零件只能同时由一台机器加工;3)分配到同一车间内的工件都在该车间内顺序加工;4)n件工件的最大完工时间就是f个车间中完工时间最长的车间的最大完工时间。则DJSP整数线性规划模型为:
模型中用到的参数为:n表示工件数, j, k={1,2,…,n};m表示车间内机器数, i,u={1,2,…,m};f表示车间数, r={1,2,…, f};
决策变量为:
整体线性规划模型为:
式(1)是目标函数,寻找最小化的最大完工时间:
| ${\rm{Minimize}}\;{{{C}}_{{\rm{max}}}}$ | (1) |
Subject to:
式(2)表示将每个工件都安排到唯一的车间内进行加工:
| $\sum_{r = 1}^f {{Y_{j,r}}} = 1,{\rm{ }}{\forall _{{j}}}$ | (2) |
式(3)表示工件的完成时间大于该工件的加工时间:
| ${C_{j,i}} \geqslant {p_{j,i}} , {\forall _j}_{,i} $ | (3) |
式(4)表示在同一时间内,一个工件最多能在一台机器上加工。
| ${C_{j,i}} \geqslant {C_{j,l}} + {p_{j,i}}{\rm{ , }}{\forall _{j,i,l \ne i\left| {{a_{j,i,l}} = 1} \right.}}$ | (4) |
式(5)和(6)表示在同一工厂内,一台机器最多能同时加工一个工件;当且仅当
| $ {C_{j,i}} \geqslant {C_{k,i}} + {p_{j,i}} - M(3 - {X_{k,j,i}} - {Y_{j,r}} - {Y_{k,r}}),{\forall _{{{r,i,k}} < n,j > k}} $ | (5) |
| ${C_{k,i}} \geqslant {C_{j,i}} + {p_{k,i}} - M(2 + {X_{k,j,i}} - {Y_{j,r}} - {Y_{k,r}}),{\forall _{{{r,i,k}} < n,j > k}}$ | (6) |
式(7)表示最大完工时间:
| ${C_{\max }} \geqslant {C_{j,i}}{\rm{ }},{\forall _{{{j,i}}}}$ | (7) |
式(8)~(10)为决策变量。
| ${C_{j,i}} \geqslant 0 {\forall _{j,i}} $ | (8) |
| ${Y_{j,i}} \in \{ 0,1\} {\rm{ , }}{\forall _{{{j,i}}}}$ | (9) |
| ${X_{k,j,i}} \in \{ 0,1\} ,{\forall _{j < n,k > j,i}}$ | (10) |
在实际的分布式车间调度问题中,安排到每个车间的工件数n应该远远大于机器台数m,这样才能使得机器的生产能力得到有效的应用,缩短平均加工时间。
2 改进区块遗传算法为适应分布式车间调度问题的特征,对传统遗传算法进行了改进,将基因交叉过程中重叠的工件放入重组工件基因池中,再重新插入到解序列中进行重组。在遗传算法中注入基于区块的高质量的人工染色体增加解的多样性;从挑选的精英染色体中统计出工件−车间分配矩阵和工件−机器位置矩阵,然后根据概率矩阵挖掘区块,运用两种组合机制构建人工染色体,协调工作车间和车间内机器的工作量,优化搜索路径。算法步骤如下:
1)生成初始解。为保证初始解的质量和多样性,本文运用NEH和随机性两种方式,按照最早完工的原则初始化种群。
2)计算适应度并挑选精英染色体。计算每个染色体的适应值,并使适应度按从小到大的顺序进行排序,挑选出前30%的染色体作为精英染色体。
3)更新概率矩阵。分别建立工件−车间分配矩阵和工件−机器排序矩阵,并随着迭代过程不断地更新概率矩阵中的信息。
4)组合区块。根据概率矩阵中的信息,组合区块。
5)构建人工染色体。根据区块库和概率矩阵中的信息,运用轮盘赌的方式构建人工染色体。
6)对分布式车间调度问题的解序列进行重组。将父代的染色体以某一车间中工件加工的解序列片段为单位进行重组。
7)筛选优精英染色体。将从重组后的染色体与原父代的染色体进行融合,筛选出新的精英染色体作为下一次迭代的父代。
MBGA算法流程图(见图1)中,
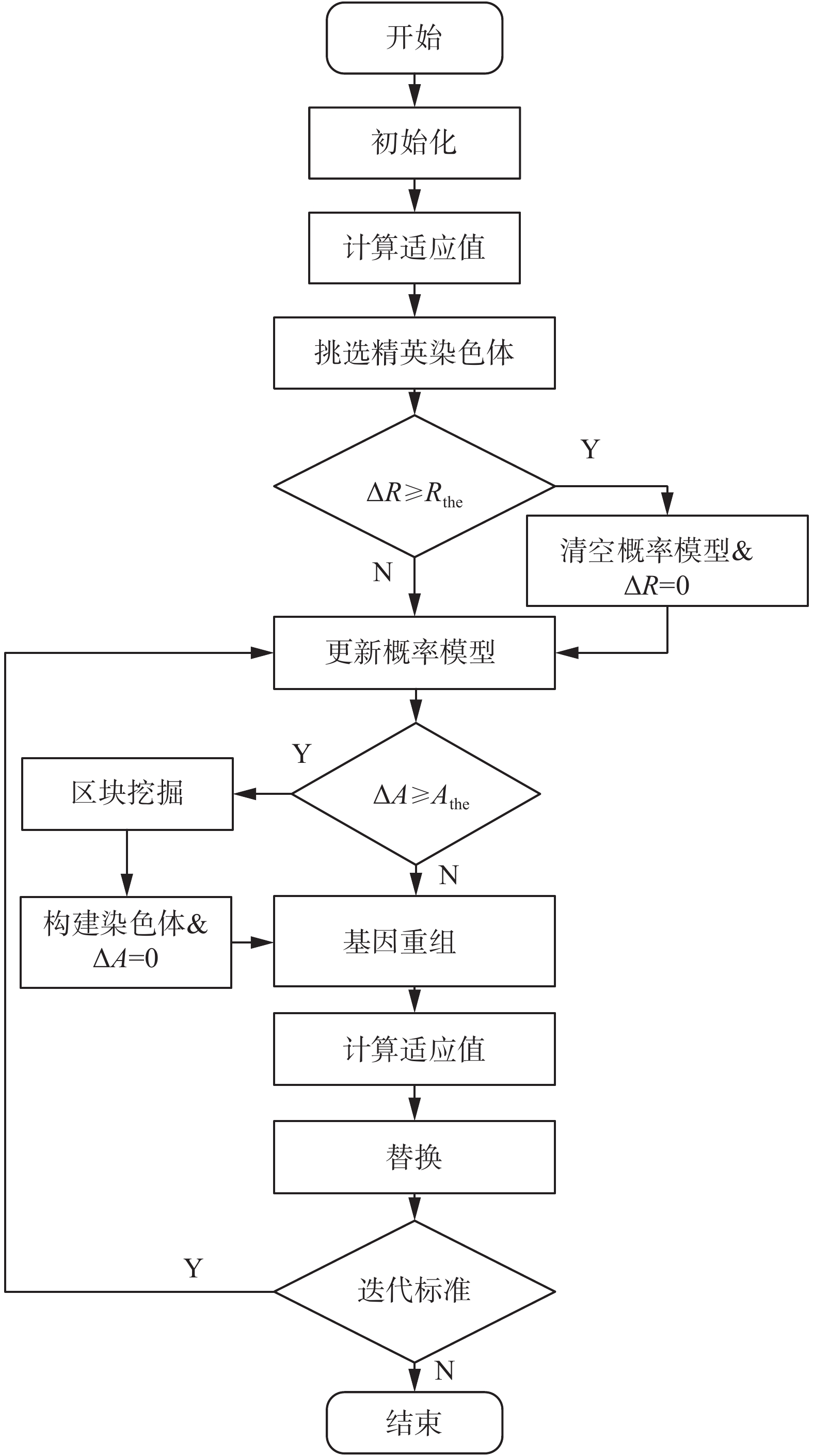
|
Download:
|
| 图 1 MBGA流程 Fig. 1 Flow chart of MBGA | |
传统GA随机生成初始解,生成的个体适应度较低,影响解的收敛速度和最终解的质量。本文混合应用NEH(Nawaz-Enscore–Ham)算法和完全随机两种方式构造初始解,既保证解的质量,又保持解的多样性。MBGA运用其中前n/2件工件用NEH算法排序,剩余的工件随机插入到f家车间的解序列片段中。分别计算n件工件中的每一个工件j在m台机器上的总加工时间,并对每个工件的总加工时间进行降序排序,将优先排序权赋予排序在前的工件。先将排序中的前f件工件分别分配到f家车间中,车间根据接受到工件的先后次序进行编号,第1个接受到工件的车间为f1,第2个接受到工件的车间为f2,依次生成车间编号。将前f件工件固化到f家车间中,剩余的n−f件工件可以跨车间分配。假设f家车间完全相同,将前f件工件固化到车间之后,能够有效地区分车间,避免在迭代过程中造成车间之间的混乱。其中前(n−f)/2的工件运用NEH进行排序,剩余的工件进行随机排序,生成不同的解序列。
每个工件在机器上的总加工时间为
| ${{\rm{workload}}_{(j,i)}} = \bigg(\sum\limits_{k \in {R_{j,i}}} {{p_{j,k}}} \bigg) + {p_{j,i}},{\rm{ }}{\forall _{i,j}}$ | (11) |
式中:
表1是分布式车间调度问题的案例,将8个需要加工的零件分配到两个车间进行加工,工件在车间上的加工路径和在每个机器上的加工时间已经确定。计算出每个工件的总加工时间并进行排序(如表2),确定工件分配的优先权。先将排序中的前两个工件分配到车间中确定车间的编码,再将排序在后的4件工件随机插入到车间1和车间2的加工序列中,根据获得的优先权和NEH原则对剩余的工件进行分配和排序,最终形成可行的分布式车间调度方案。
| 表 1 分布式工作车间中工件的加工时间和路径 Tab.1 Processing time and path in distributed job shop |
| 表 2 优先排序权 Tab.2 Job priority |
精英染色体是筛选出来的高适应度解序列。为了有效地挖掘区块,MBGA依据迭代过程中筛选的精英染色体构建了两个概率矩阵:一个是工件−车间分配矩阵,另一个是工件−机器排序矩阵。工件−车间排序矩阵强调的是工件和车间之间的关系,工件−机器排序矩阵强调的是工件在车间内机器上的加工顺序。
本文采用世代累加的方式建立概率模型,统计工件在机器上加工的频次,构建工件−机器排序矩阵。在构建和更新矩阵的过程中,工件j被分配到车间r,工件−车间分配矩阵中相应位置的频次就会增加1。工件k和工件j分配到同一车间,且在机器上先后加工,工件−机器排序矩阵中的相应位置增加1。然后,将相应的频次转化为概率矩阵,并随着迭代不断更新。
工件−车间分配矩阵的迭代公式为
| $\begin{array}{l} X_{ir}^k = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!1,\quad{{\text{如果工件}}i{\rm{ }}{\text{在工厂}}r} \end{array}\\ \begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!0,\quad{{\text{其他}}} \end{array} \end{array} \right.\\ i = 1,2, \cdots, n;\;{{ r}} = 1,2, \cdots, f;{\rm{ }}k = 1,2, \cdots, s \end{array}$ | (12) |
| $\begin{array}{l} {T_{ir}}(t) = {T_{ir}}(t - 1) + \displaystyle \sum\limits_{k = 1}^m {X_{ir}^k} ,{\rm{ }}i = 1,2, \cdots, n;\\ r = {\rm{1}},2, \cdots ,f;{\rm{ }}t = 1,2, \cdots, G;{\rm{ }}k = 1,2, \cdots, s \end{array}$ | (13) |
式(12)和(13)中,
工件-机器排序矩阵的迭代公式为
| $\begin{array}{l} X_{ir}^k = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!1,\quad{{\text{如果工件}}i{\rm{ }}{\text{在机器}}j} \end{array}\\ \begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!0,\quad{{\text{其他}}} \end{array} \end{array} \right.\\ i = 1,2, \cdots, n;{\rm{ }}j = 1,2,\cdots, n;{\rm{ }}k = 1,2, \cdots, m \end{array}$ | (14) |
| $\begin{array}{l} {T_{ij}}(t) = {T_{ij}}(t - 1) + \displaystyle \sum\limits_{k = 1}^m {X_{ij}^k} {\rm{ }},i = 1,2, \cdots, n;\\ j = 1 ,2,\cdots, n;{\rm{ }}t = 1,2, \cdots, G;{\rm{ }}k = 1,2, \cdots, s \end{array}$ | (15) |
式中:
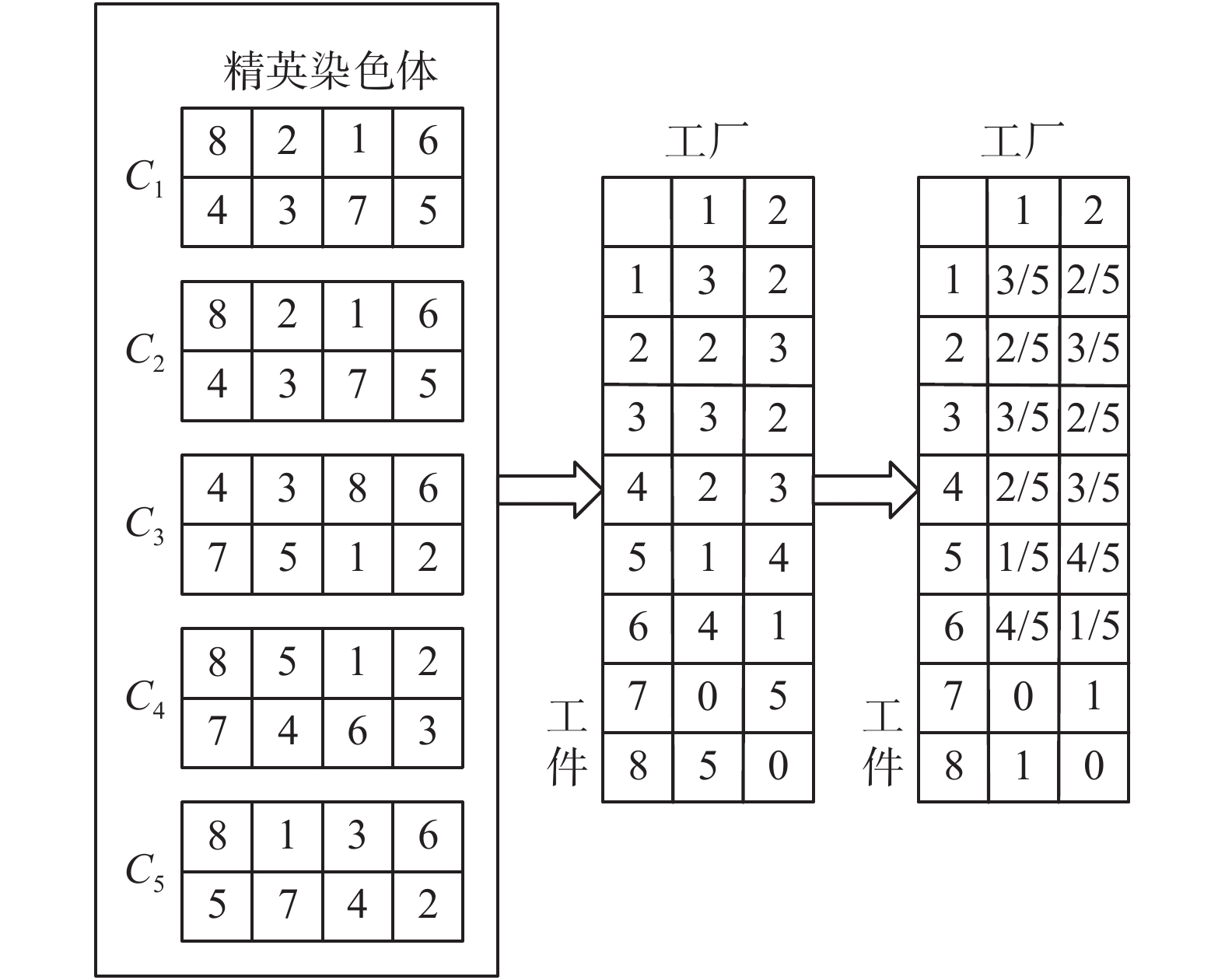
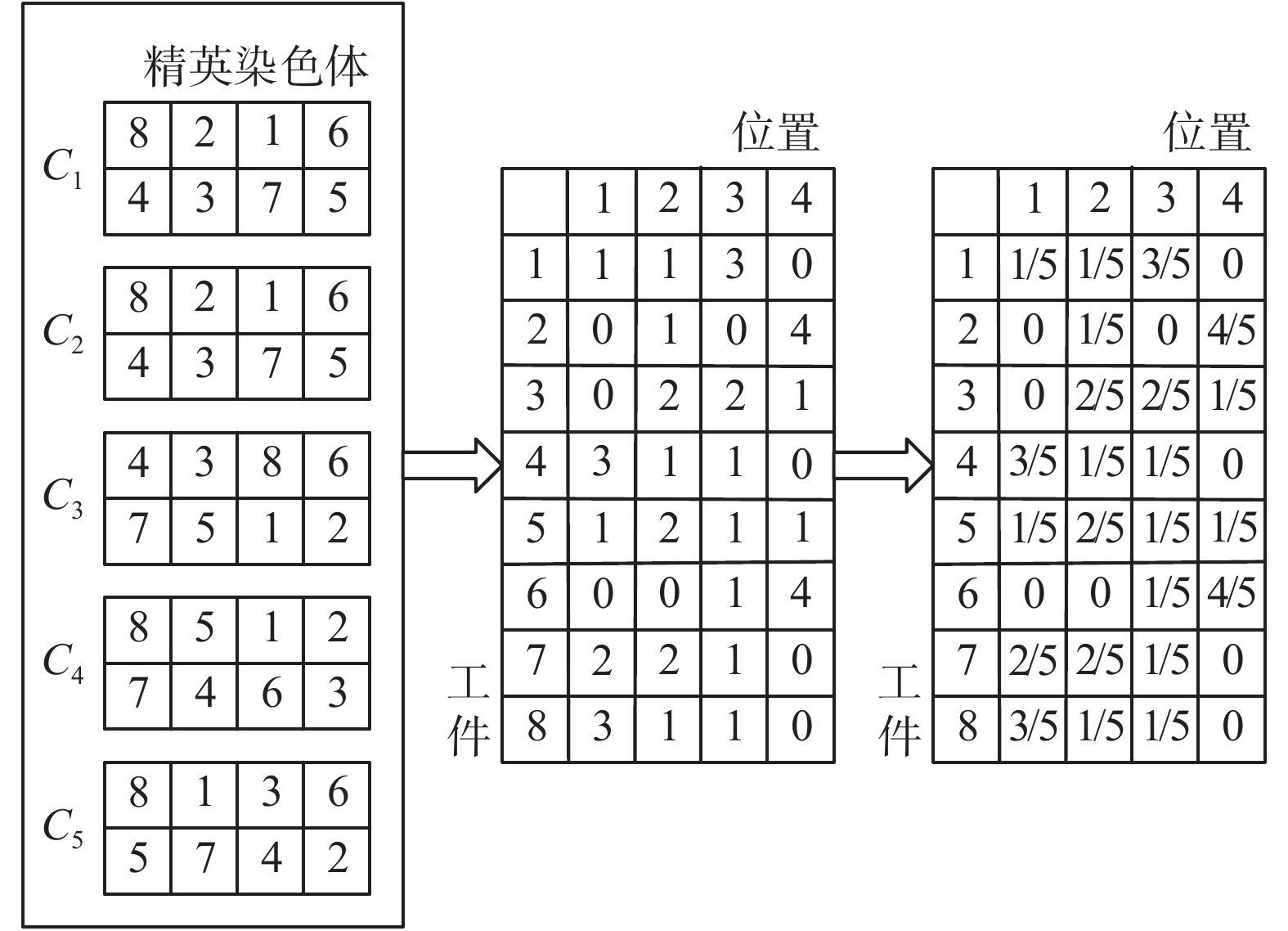
具体的工件−车间分配矩阵的更新过程如图2所示,假设C1,C2,…,C5为5个用于更新分配矩阵的精英染色体;以工件5为例,有1个精英染色体将工件5分配到车间1,有4个精英染色体将工件5分配到车间2,因此工件5分配到车间1的概率为1/5,分配到车间2的概率为4/5。工件−机器排序矩阵的更新原理同分配矩阵的更新原理相同(如图3)。
为确保工件j拥有分配到每个车间中每个位置的机会,将概率矩阵中每个位置的概率值增加0.01;在构建人工染色体的时,每个位置可以选到剩余工件的任意一个,增加了样本的多样性,避免缩小搜索空间。
|
Download:
|
| 图 2 工件−车间分配概率矩阵示意 Fig. 2 Schematic diagram of job-shop assignment probability matrix | |
|
Download:
|
| 图 3 工件−位置排序矩阵示意 Fig. 3 Schematic diagram of job-position sorting matrix | |
精英染色体的解序列中拥有相似的解序列片段,算法以区块的形式将这部分信息进行挖掘用于构建高质量的人工染色体。区块是高适应度解序列中的部分片段,由精英染色体中的高频率的基因链接组成。区块将不同机器上加工时间互补的工件组合起来,用于平衡工件在机器上的加工时间,优化同一车间内工件的排序过程,并确定工件的分配过程。高质量的区块保证了人工染色体的优势,又降低了排序的复杂程度。区块的规模越大,构建人工染色体的过程就越简单,但由于工件−车间分配矩阵和工件−机器排序矩阵中的概率都小于1(图4中的Pblock为挖掘该区块的频率),所以区块规模越大,挖掘该区块的概率就越低。本文运用了动态门槛值,适当地增加区块的规模;区块的长度为3~5,具体的长度根据门槛值来确定,并且门槛值随着迭代的进行从0.5~0.8不断增加。

|
Download:
|
| 图 4 工件−车间分配区块挖掘方式 Fig. 4 Job-shop assignment block mining method | |
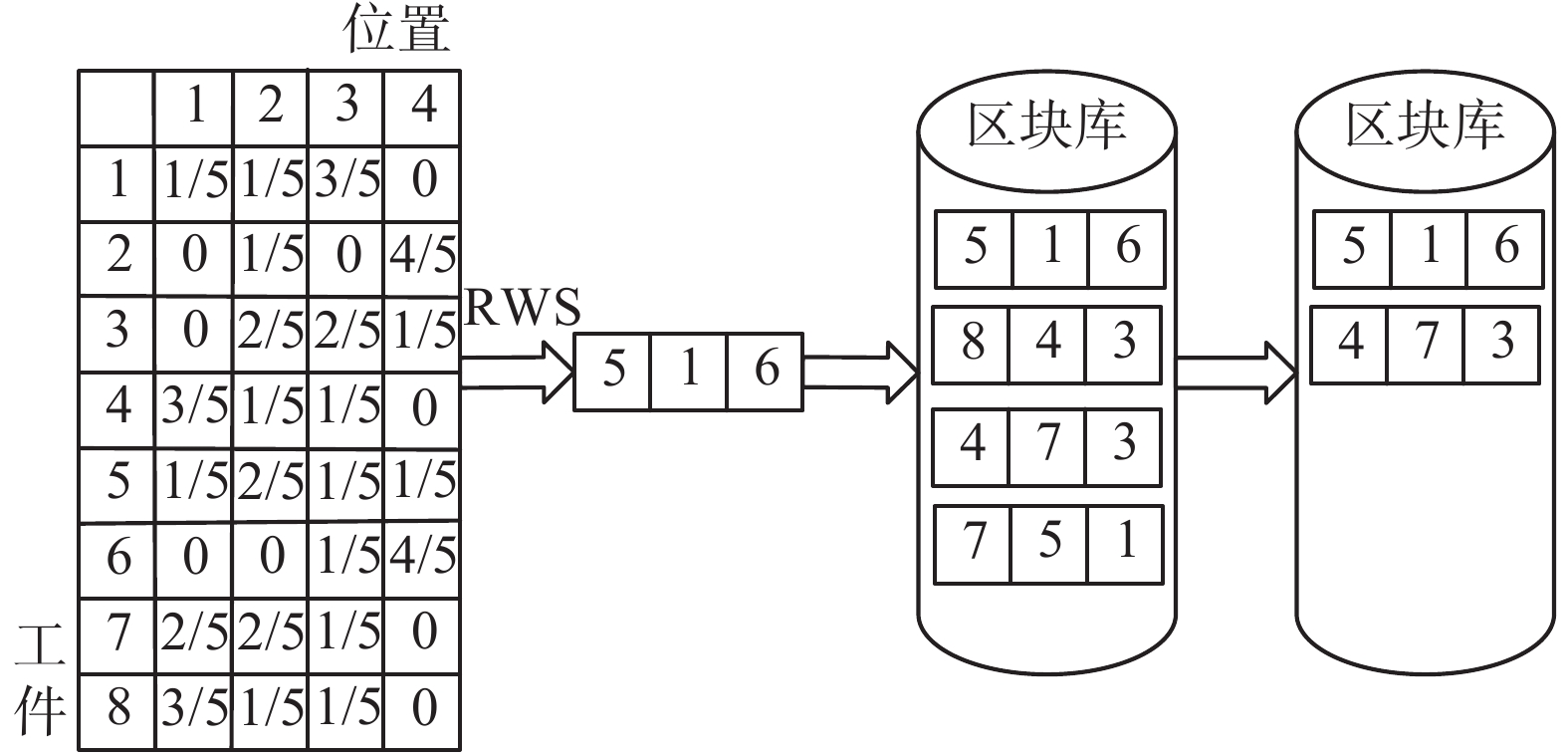
区块的组合过程如图5,根据工件−机器排序概率矩阵,通过累积计算区块生成的概率,再依据一定的筛选规则组合成区块库。
|
Download:
|
| 图 5 工件−位置排序区块挖掘方式 Fig. 5 Job-location sorting block Mining method | |
在区块库中存在部分重复的区块,通过区块竞争剔除质量较差并含有重叠部分的区块。区块重叠分为两种:区块中工件的重复和区块内机器重复次数超过所需要加工的工序数。在筛选高质量区块时,优化指标为组合区块的平均概率,平均概率越小,构建的区块质量就越差。平均概率为
| $P_{{B^{(n)}}}^{{\rm{avg}}} = {L^{ - 1}}\sum\limits_{i = 1}^L {P_{B_i^{(n)}}^{(p)}} $ |
式中:
构建人工染色体是算法的另一个重点,既要加快解的汇集速度,又要避免过早收敛,保证解的多样性和质量。MBGA运用了两种组合机制构造人工染色体,每种组合机制又分为两个阶段,第一阶段是将工件分配到车间中,第二阶段是为分配到同一车间的工件排序。组合机制1先根据分配概率和区块库将工件分配到车间中,再对分配到同一车间的工件进行排序,若挑选出的工件包含于区块中第一个位置,则将该区块插入到该染色体中,若没有找到相应的区块,则根据概率矩阵挑选下一个位置的工件;组合机制2先将区块库中的区块复制到染色体中的空白位置,减少工件排序的数量,再随机将没有分配的工件复制到人工染色体中剩余的空白位置。
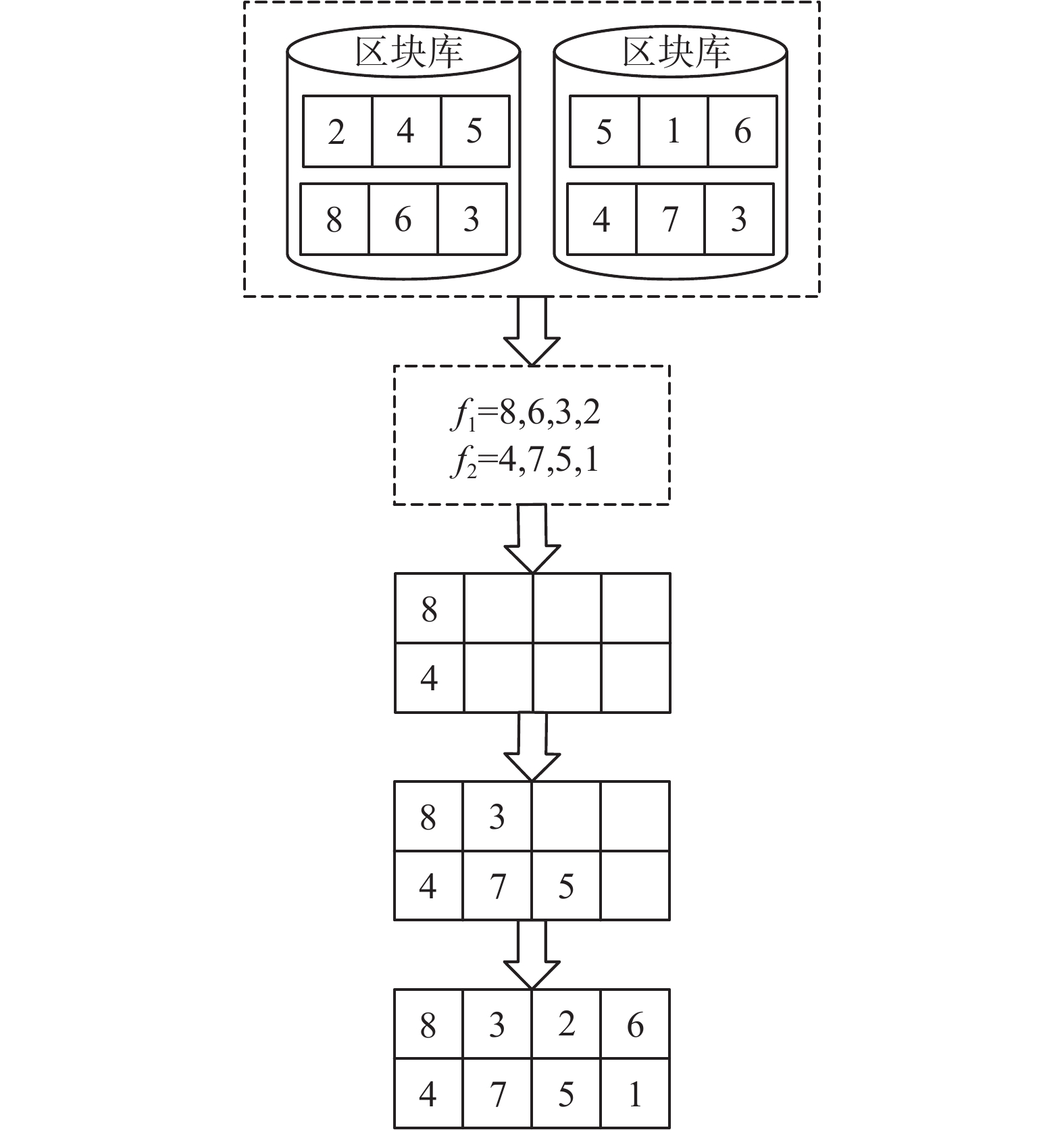
组合机制一的具体过程为:先根据工件−车间分配矩阵运用轮盘赌的方式分配工件,若所选的工件包含于工件−车间区块中,则将该区块中所包含的所有工件都分配到同一车间中;若没有包含于区块中,则继续为下一个车间筛选工件,依次将工件分配到总加工时间最少的车间。其次,依据工件−机器排序矩阵运用轮盘赌的方式为同一车间内的工件排序,如果挑选的工件位于工件−机器区块库中区块的第一个位置且包含的工件都在该车间加工,那么就将该区块插入到相应的位置;如果不是在区块的首位或者没有包含该工件的工件−机器排序区块,那么继续为下一个工件排序,直到所有确定所有工件的加工顺序。如图6,工件8分配到第一个车间即f1,工件6和工件3与工件8在同一个区块中,故工件8,6和3被分配到f1中,在剩余工件中随机的挑选出工件4,7,5和1分配到f2中,最后的工件2分配到f1中。在排序阶段,依据工件−机器排序矩阵运用轮盘赌的方式将工件8第排在第一个位置,将工件4排在f2中的第一个位置;工件4位于区块中的首位,将该区块复制到染色体的相应位置上;剩余的工件依据工件−机器排序矩阵运用轮盘赌进行排序,直到完成所有工件的排序。
|
Download:
|
| 图 6 第1种组合机制 Fig. 6 The first combination mechanism | |
组合机制2,先将工件−车间区块库中的区块随机地复制到人工染色体中的空白位置,具体位置由区块中首个工件分配到车间的概率和在机器上排序的概率决定;然后根据分配和排序矩阵,将未分配的工件插入到人工染色体的空白位置。首先,随机地将区块


|
Download:
|
| 图 7 第2种组合机制 Fig. 7 The second combination mechanism | |
通过基因重组发现改良的染色体,直到生成最优的染色体,MBGA改进了基因重组中的交叉产生新的子代。染色体中每行的解序列片段是某一车间内的工件加工顺序,所有工件恰好在f间车间内加工完成。在基因交叉的过程中,以每个车间内的工件加工序列(即每行的解序列片段)为交换单位,既能保留父代和每个车间的有效信息,又能搜索每个车间的所有可能解。
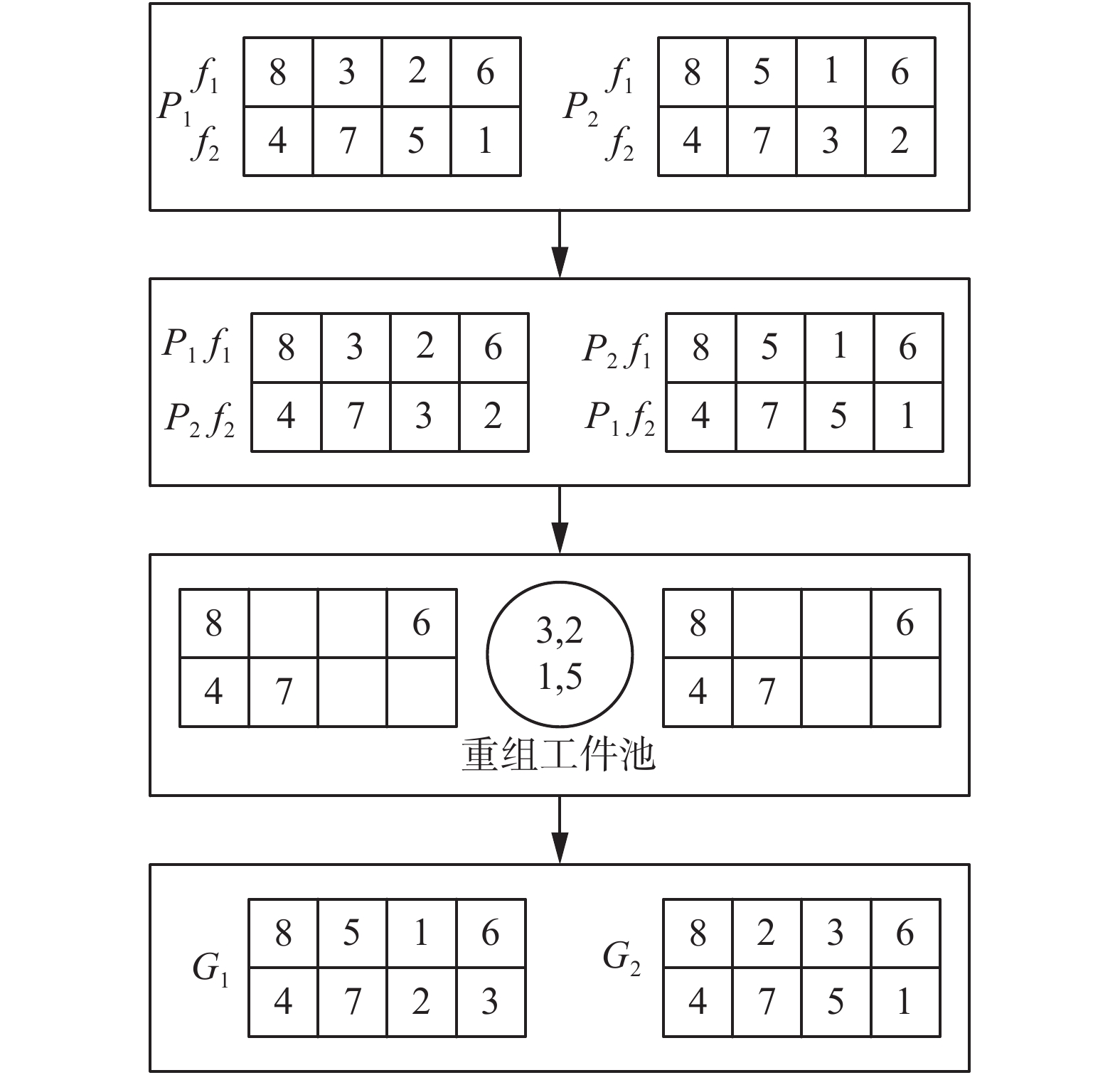
适应DJSP的MBGA中,基因交叉的例子如图8所示,挑选两个染色体为父代(P1,P2),从一个父代的解序列中随机选取f/2行解序列片段,剩余的f/2行解序列片段从另一个父代中选取,按照原行数重新构造解序列(G1),剩余的解序列片段恰好构成另一个子代(G2)。在两个新构造的解序列中,挖出解序列中重复加工的工件放进重组工件池,再将重组工件池中的工件分别、依次插入到总加工时间最短的行内,直到所有的工件都被插入到解序列中。重组工件池中的工件都是两个同时存在的,在选取工件时,应同时将两个工件分别插入到两个构造的解序列中。
|
Download:
|
| 图 8 基因交叉 Fig. 8 Gene crossing | |
为了测试和验证MBGA的求解能力,在Microsoft Visual Studio 2012中的C++上编写该算法程序,并在Window8、32位系统、主频3.40的酷睿CPU、4 GB内存的电脑上运行完成测试。本文测试所用的数据来自Taillard中的生产车间调度问题的基准实例,选取工件个数为15、20、30和机器台数为15、20共50个组合进行比较分析。比较标准是相对百分比偏差(relative percentage deviation, RPD),计算公式为
| ${\rm{RPD}} = \frac{{{\rm{A}}\lg - {\rm{Min}}}}{\rm{Min}} \times 100$ |
式中:Alg表示运用MBGA获得最优的最大完工时间;Min表示基准实例所给出的最小化的最大完工时间。
从Taillard中选择50种具有代表性的例题测试该算法的寻优性能[22]。表3中是在不同的n、m以及加工顺序下生成的50种实例组合下,每个组合的平均RPD是对不同车间数f=2, f=3, f=4, f=5的最优RPD平均值。有一半以上的平均RPD为0,证明一半以上的测算实例达到了目前已知的最大完工时间的下限值。
为进一步证明算法的准确性,将例题测算结果文献[14]提出的模拟退火算法(simulated annealing,SA)、启发式模拟退火算法(heuristic simulated annealing,HAS)和文献[22]总结的遗传算法得出的结果进行比较。表4给出了MBGA的平均PRD与其他算法的平均PRD的数值,MBGA的平均PRD数值最小为0.21。相较于GA、SA和HAS,MBGA得出的最大完工时间最小。
| 表 3 实例测试结果 Tab.3 Example test results |
| 表 4 不同算法的RPD Tab.4 RPD of different algorithms |
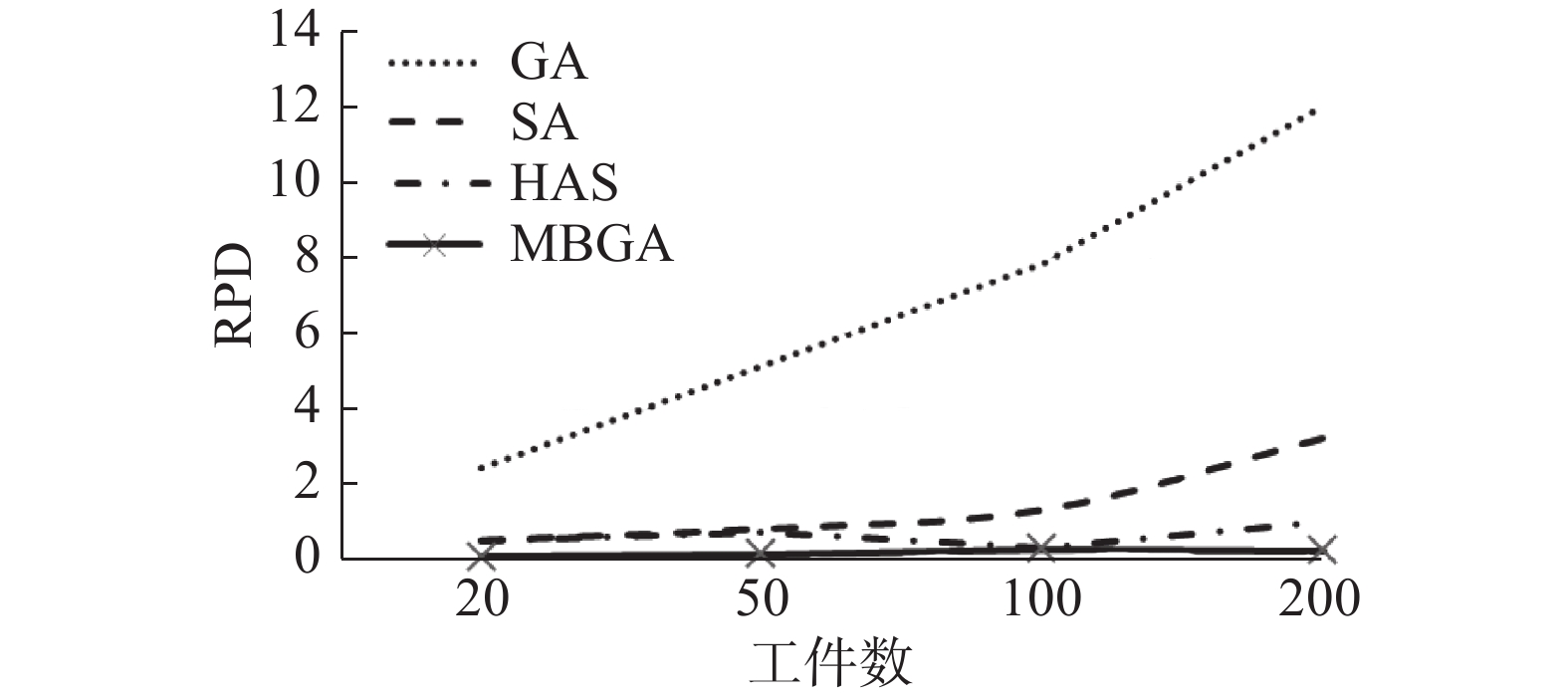
图9显示了每个算法的平均RPD与工件数的关系。从图中,能够清楚的看出,GA和SA的RPD值随着工件数的增加而增加,HAS的RPD值随着工件数的增加而波动,而MBGA的RPD比较稳定,且MBGA的RPD值均小于其他3个算法的RPD值,表明MBGA得到的解序列更加接近标准解序列。图10表示一批工件在不同数目工作车间加工,4种算法的RPD值变化趋势。GA的RPD随着车间数的增加而减小,SA、HAS和MBGA的RPD值都随着车间数的增加而减小,表明MBGA中基于区块的人工染色体对原有GA的改进更适合分布式车间调度问题。综上可得,MBGA具有较优的稳定性和准确性。
|
Download:
|
| 图 9 平均RPD与工件数的关系 Fig. 9 Relationship between average RPD and number of jobs | |

|
Download:
|
| 图 10 平均RPD与车间数的关系 Fig. 10 Relationship between average RPD and the number of jobs | |
本文针对分布式工作车间调度问题,提出了MBGA。算法构建了分配区块库和排序区块库,保留和传递了精英染色体中的高频率基因链,统一考虑了排序过程中每个车间机器工作量的平衡性和排序过程中工件加工的先后顺序。借助区块库中的区块,运用两种组合机制构建了高质量的人工染色体;一种组合机制应用区块通过先分配后排序的顺序构建了一类人工染色体,另一种组合机制先在人工染色体中填充区块,同步进行工件的分配和排序两个阶段,再将剩余的工件按照先分配后排序的顺序构建第二类人工染色体,增加了人工染色体的多样性。改进区块遗传算法中的基因重组大幅度地改良了当前代的人工染色体,保留了父代和每个车间的有效信息,又具有搜索每个车间的能力。算例测算表明,该算法具有较好的稳定性和准确性。
MBGA有效地解决了分布式生产车间调度问题,未来还可以尝试深入研究,如改变假设条件,当每个车间的工件的加工能力存在差异时,求解最优的调度方案。
| [1] |
JIA H Z, FUH J Y H, NEE A Y C, et al. Web-based multi-functional scheduling system for a distributed manufacturing environment[J]. Concurrent engineering, 2002, 10(1): 27-39. DOI:10.1177/1063293X02010001054 ( 0) 0)
|
| [2] |
谢志强, 周含笑, 桂忠艳, 等. 基于拟关键路径的二车间综合调度算法[J]. 计算机科学, 2013, 40(4): 193-198. XIE Zhiqiang, ZHOU Hanxiao, GUI Zhongyan, et al. Integrated scheduling algorithm of two workshops based on ACPM[J]. Computer science, 2013, 40(4): 193-198. DOI:10.3969/j.issn.1002-137X.2013.04.042 (  0) 0)
|
| [3] |
BARGAOUI H, DRISS O B, GHÉDIRA K. Minimizing makespan in multi-factory flow shop problem using a chemical reaction metaheuristic[C]//Proceedings of 2016 IEEE Congress on Evolutionary Computation. Vancouver, Canada, 2016.
( 0) 0)
|
| [4] |
谢志强, 郭禾, 苏文秀, 等. 存在多工序同时结束的多车间逆序综合调度算法[J]. 吉林大学学报(工学版), 2018, 48(2): 578-587. XIE Zhiqiang, GUO He, SU Wenxiu, et al. Reversal sequence integrated scheduling algorithm of multiple workshop with multi-procedures ended together[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(2): 578-587. (  0) 0)
|
| [5] |
王凌, 邓瑾, 王圣尧. 分布式车间调度优化算法研究综述[J]. 控制与决策, 2016, 31(1): 1-11. WANG Ling, DENG Jin, WANG Shengyao. Survey on optimization algorithms for distributed shop scheduling[J]. Control and decision, 2016, 31(1): 1-11. (  0) 0)
|
| [6] |
AZAB A, NADERI B. Greedy heuristics for distributed job shop problems[J]. Procedia CIRP, 2014, 20: 7-12. DOI:10.1016/j.procir.2014.05.025 ( 0) 0)
|
| [7] |
ZHANG Rui, SONG Shiji, WU Cheng. A dispatching rule-based hybrid genetic algorithm focusing on non-delay schedules for the job shop scheduling problem[J]. The international journal of advanced manufacturing technology, 2013, 67(1/2/3/4): 5-17. DOI:10.1007/s00170-013-4751-1 ( 0) 0)
|
| [8] |
GAREY M R, JOHNSON D S, SETHI R. The complexity of flowshop and jobshop scheduling[J]. Mathematics of operations research, 1976, 1(2): 117-129. DOI:10.1287/moor.1.2.117 ( 0) 0)
|
| [9] |
WAGNER H M. An integer linear-programming model for machine scheduling[J]. Naval research logistics quarterly, 1959, 6(2): 131-140. DOI:10.1002/nav.3800060205 ( 0) 0)
|
| [10] |
JIA H Z, NEE A Y C, FUH J Y H, et al. A modified genetic algorithm for distributed scheduling problems[J]. Journal of intelligent manufacturing, 2003, 14(3/4): 351-362. DOI:10.1023/A:1024653810491 ( 0) 0)
|
| [11] |
王和敏, 谷淼, 魏志谦, 等. 基于混合遗传算法的Job Shop问题研究与实现[J]. 新技术新工艺, 2017(8): 69-73. WANG Hemin, GU Miao, WEI Zhiqian, et al. The Research and implement of Job Shop problem based on hybrid genetic algorithm[J]. New technology & new process, 2017(8): 69-73. (  0) 0)
|
| [12] |
NADERI B, AZAB A. Modeling and heuristics for scheduling of distributed job shops[J]. Expert systems with applications, 2014, 41(17): 7754-7763. DOI:10.1016/j.eswa.2014.06.023 ( 0) 0)
|
| [13] |
CHAOUCH I, DRISS O B, GHEDIRA K. A modified ant colony optimization algorithm for the distributed job shop scheduling problem[J]. Procedia computer science, 2017, 112: 296-305. DOI:10.1016/j.procs.2017.08.267 ( 0) 0)
|
| [14] |
NADERI B, AZAB A. An improved model and novel simulated annealing for distributed job shop problems[J]. The international journal of advanced manufacturing technology, 2015, 81(1/2/3/4): 693-703. DOI:10.1007/s00170-015-7080-8 ( 0) 0)
|
| [15] |
杨敬松, 夏秀峰, 崔广才. 混合遗传算法在分布式车间作业调度中的应用[J]. 计算机工程与应用, 2005, 41(19): 213-215, 225. YANG Jingsong, XIA Xiufeng, CUI Guangcai. The Distribution method of planning and scheduling based on a hybrid genetic algorithm[J]. Computer engineering and applications, 2005, 41(19): 213-215, 225. DOI:10.3321/j.issn:1002-8331.2005.19.062 (  0) 0)
|
| [16] |
高雪瑶, 谭涛, 张春祥. 遗传退火算法的模型相似性计算方法[J]. 哈尔滨工程大学学报, 2020, 41(7): 1073-1079. GAO Xueyao, TAN Tao, ZHANG Chunxiang. Method of calculating model similarity based on genetic annealing algorithm[J]. Journal of Harbin Engineering University, 2020, 41(7): 1073-1079. (  0) 0)
|
| [17] |
CHANG P C, HUANG W H, WU J L, et al. A block mining and re-combination enhanced genetic algorithm for the permutation flowshop scheduling problem[J]. International journal of production economics, 2013, 141(1): 45-55. DOI:10.1016/j.ijpe.2012.06.007 ( 0) 0)
|
| [18] |
CHANG P C, CHEN Menghui. A block based estimation of distribution algorithm using bivariate model for scheduling problems[J]. Soft computing, 2014, 18(6): 1177-1188. DOI:10.1007/s00500-013-1136-1 ( 0) 0)
|
| [19] |
裴小兵, 于秀燕. 改进猫群算法求解置换流水车间调度问题[J]. 智能系统学报, 2019, 14(4): 769-778. PEI Xiaobing, YU Xiuyan. Improved cat swarm optimization for permutation flow shop scheduling problem[J]. CAAI transactions on intelligent systems, 2019, 14(4): 769-778. (  0) 0)
|
| [20] |
张敏, 汪洋, 方侃. 基于改进区块进化算法求解置换流水车间问题[J]. 计算机集成制造系统, 2018, 24(5): 1207-1216. ZHANG Min, WANG Yang, FANG Kan. Improved block-based evolutionary algorithm for solving permutation flowshop scheduling problem[J]. Computer integrated manufacturing system, 2018, 24(5): 1207-1216. (  0) 0)
|
| [21] |
裴小兵, 张春花. 应用改进区块遗传算法求解置换流水车间调度问题[J]. 智能系统学报, 2019, 14(3): 541-550. PEI Xiaobing, ZHANG Chunhua. An improved puzzle-based genetic algorithm for solving permutation flow-shop scheduling problems[J]. CAAI transactions on intelligent systems, 2019, 14(3): 541-550. (  0) 0)
|
| [22] |
CHAOUCH I, DRISS O B, GHEDIRA K. A survey of optimization techniques for distributed job shop scheduling problems in multi-factories[C]//Proceedings of the 6th Computer Science On-line Conference. Cham, Germany, 2017.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


