电力系统频率是电能质量的一个基本指标^[1]。电力系统的负荷是时刻变化的，任何一处负荷的变化，都会引起全系统功率的不平衡，导致频率的变化。为了减小频率的波动对用电设备和发电厂的运行产生的不利影响，以将系统频率维持在标称值并且尽可能使控制区域之间的未计划的联络线交换功率最小为目的的负荷频率控制(load frequency control，LFC)系统是必要的。

自Elgerd和Fosha于20世纪70年代年提出电力系统的负荷频率稳定控制问题以来，目前针对负荷频率控制这一问题己经有多种解决方法^[2]。传统的比例积分(PI)控制器是各种负载频率控制器中应用最广的控制器^[3]。在实现上简单易懂，具有较好的动态响应能力，但随着系统复杂度的增加，其性能较差^[4]，且PI控制存在使频率稳定的时间长、反调超调现象多、暂态频率偏差大等缺点^[5]。

为了提高LFC的动态性能，与先进控制算法结合的LFC得到广泛研究。文献[6]采用自适应控制、文献[7]采用变结构控制、文献[8]采用最优控制、文献[9]采用鲁棒控制、文献[10]采用预测控制，都有利于提高系统性能，但依赖系统模型参数，或需要有效的在线辨识以及控制器设计过于复杂，在实际中难以实现。

近年来，自抗扰控制(active disturbance rejection control，ADRC)器依靠其良好的控制性能，较高的控制精度和稳定性以及很强的鲁棒性，其设计不依赖于受控对象的数学模型，结构清晰，算法容易实现，有望在工业控制中取代仍占统治地位的PID控制^[11]。然而，非线性自抗扰控制需要调节多个参数，在实际应用中受到限制。

为了降低自抗扰控制器参数的整定难度，人工智能算法被用来对ADRC进行参数寻优。本文利用遗传算法，为了避免早熟，采取大变异概率的变异操作，即大变异遗传算法(big probability variation's genetic algorithm，bGA)，来优化自抗扰控制器的参数。研究表明，基于大变异遗传算法的负荷频率自抗扰控制能较好地抑制系统振荡，动态性能良好，能够应用于负荷频率控制系统。

1 自抗扰控制的基本原理

基于扩张状态观测器的自抗扰控制技术，把所有不确定因素都归结到系统的总扰动而给予估计和补偿^[12]。由非线性跟踪微分器(tracking differential, TD)、扩张状态观测器(extended state observer, ESO)和非线性误差反馈律(nonlinear state error feedback, NLSEF)构成自抗扰控制器。结构如图1所示^[13]。图1中， $y$ 和 $u$ 分别为系统的输出量和控制量， $d$ 为未知的外部扰动， ${b_0}$ 为模型参数，r为参考输入。

本文采用三阶自抗扰控制器数学模型如下：

TD模型：

$\left\{ \begin{array}{l} {v_1} = {v_1} + h{v_2} \\ {v_2} = {v_2} + h{v_3} \\ {v_3} = {v_3} + h{\rm{fh}} \\ {\rm{fh}} = {\rm{ - }}{r_0}{\rm{(}}{r_0}{\rm{(}}{r_0}{\rm{(}}{v_1}{\rm{) + 3}}{v_2}{\rm{) + 3}}{v_3}{\rm{)}} \\ \end{array} \right.$

ESO模型：

$\left\{ \begin{array}{l} e = {z_1} - y \\ {z_1} = {z_1} + h({z_2} - {\beta _{01}}e) \\ {z_2} = {z_2} + h({z_3} - {\beta _{02}}\;{\rm{fal}}\;(e,0.5,\delta )) \\ {z_3} = {z_3} + h({z_4} - {\beta _{03}}\;{\rm{fal}}\;(e,0.25,\delta ) + {b_0}u) \\ {z_4} = {z_4} + h( - {\beta _{04}}\;{\rm{fal}}\;(e,0.125,\delta )) \\ \end{array} \right.$

NLSEF模型：

$\left\{ \begin{array}{l} {e_1} = {v_1} - {z_1},{e_2} = {v_2} - {z_2},{e_3} = {v_3} - {z_3} \\ {u_0} = \displaystyle\sum\limits_{i = 1}^3 {{\beta _i}\;{\rm{fal}}\;({e_i},{\alpha _i},{\delta _0})} \\ u = \dfrac{{{u_0} - {z_4}}}{{{b_0}}} \\ \end{array} \right.$

其中， ${\rm{fal}}(e,\alpha ,\delta )$ 为非线性函数，表达式为

${\rm{fal}}(e,\alpha ,\delta ) = \left\{ \begin{array}{l} \dfrac{e}{{{\delta ^{\alpha - 1}}}},\;\;\;\;\;\;\;\;{\rm{ }}\left| e \right| \leqslant \delta \\ {\left| e \right|^\alpha }\;{\rm{sign}}\;(e),\;\;\;\;{\rm{ }}\left| e \right| > \delta \\ \end{array} \right.$

从自抗扰控制器的模型看，其结构简单，但包含了很多非线性元件，需要整定的参数有TD的 ${r_0}$ ，ESO的 ${\beta _{01}}{\text{、}} \; {\beta _{02}}{\text{、}} \; {\beta _{03}}{\text{、}} \; {\beta _{04}}{\text{、}} \; \delta $ , ELSEF的 $\; {\beta _1}{\text{、}} \; {\beta _2}{\text{、}}$ $\; {\beta _3}{\text{、}} \; {\delta _0}{\text{、}} \; {\alpha _1}{\text{、}} \; {\alpha _2}{\text{、}} \; {\alpha _3}{\text{、}} \; {b_0}$ ，多达14个，整定工作复杂艰巨，为避免手工调试的繁琐过程，本文利用遗传算法进行参数寻优，完成控制器的参数整定。

2 基于大变异遗传算法的自抗扰控制器

遗传算法 (genetic algorithm, GA) 是一类模仿生物界的进化规律演化而来的随机化搜索方法^[14]，它处理表示不同解的二进制种群，通过模拟自然选择和遗传中发生的选择、交叉和变异等现象，从初始种群出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中越来越好的区域。经过这样一代又一代地不断繁衍进化，最后收敛到一群最适合环境的个体，求得问题的最优解。因此，遗传算法具有隐式并行性，增强了搜索能力，当应用于复杂优化问题时，可以快速找到最优解^[15]。

然而，经典遗传算法存在“早熟”问题，也就是算法过早收敛于一个非全局最优点^[16]，从而降低了搜索性能，文献[17]提出大变异遗传算法来改善经典遗传算法的收敛速度和稳定性，即当某一代的最大适应度 ${F_{\max }}$ 与平均适应度 ${F_{{\rm{avr}}}}$ 满足 $\alpha {F_{\max }} < {F_{{\rm{avr}}}}$ ， $0 < \alpha < 1$ ，就将对该代设为最大适应度的个体的形式，除对一个个体不作操作外，种群其他个体均采取一个比原变异概率大的概率 ${P_{{\rm{mbig}}}}$ 进行变异操作。通过调整密集因子 $\alpha $ 和大变异概率 ${P_{{\rm{mbig}}}}$ 使种群快速脱离“早熟”的算法弊端。

基于大变异遗传算法的自抗扰控制算法操作描述如下：

1)初始种群选取。首先初始化种群规模和交叉及原始变异概率，确定自抗扰控制器需要整定的参数对应的二进制编码，选取初始染色体种群，解码得到控制器参数，运行系统仿真，并计算每个染色体的适应值。其中，ADRC参数编码描述如下：固定参数 ${r_0} = 4$ , $\delta = {\delta _0} = 0.05$ , ${\alpha _1} = 0.3$ , ${\alpha _2} = 0.8$ , ${\alpha _3} = 1.1$ 。然后剩余参数在如下范围内随机初始化取多组初值参与优化： $\;{\beta _{01}} \in [0,400],$ $\;{\beta _{02}} \in $ $[0,4\;000],$ $\;{\beta _{03}} \in [0,40\;000],$ $\;{\beta _{04}} \in [0,800\;000],$ $\;{\beta _1} \in [0,1\;000],$ $\;{\beta _2} \in$ $ [0,1\;500],$ $\;\;{\beta _3} \in [0,500],$ $\;{b_0} \in [1,500]$ 。

2)种群进化。根据适应值选择父母染色体，进行复制、交叉操作，判断是否满足大变异操作条件以确定变异概率，进行变异操作得到新的染色体种群，解码得到控制器参数，重新运行系统仿真，计算新种群中每个染色体的适应值。

3)种群优化。判断是否满足结束条件，不满足时重复操作2)直到满足为止。

算法流程图表示如图2所示。

3 负荷频率自抗扰控制 3.1 电力系统线性模型

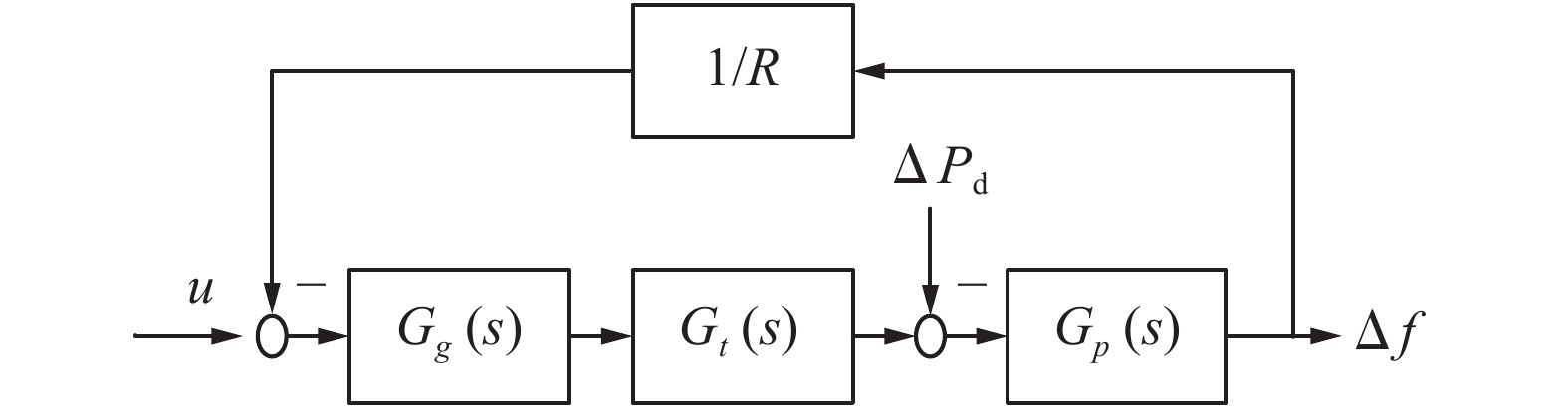
互联电力系统的控制对象包括调速器、汽轮机、发电机及负荷。互联电力系统中一个区域的线性模型如图3所示。

其常见的3个组成部分传递函数可表示^[18]为

调速器：

${G_g}(s) = \frac{1}{{{T_g}s + 1}}$

非再热汽轮机：

${G_t}(s) = \frac{1}{{{T_t}s + 1}}$

非发电机：

${G_p}(s) = \frac{{{K_p}}}{{{T_p}s + 1}}$

因此，系统开环传递函数为

$G(s) = \frac{{{K_p}}}{{({T_p}s + 1)({T_g}s + 1)({T_t}s + 1) + {K_p}/R}}$

相对阶次为3，故可采用三阶自抗扰控制器。

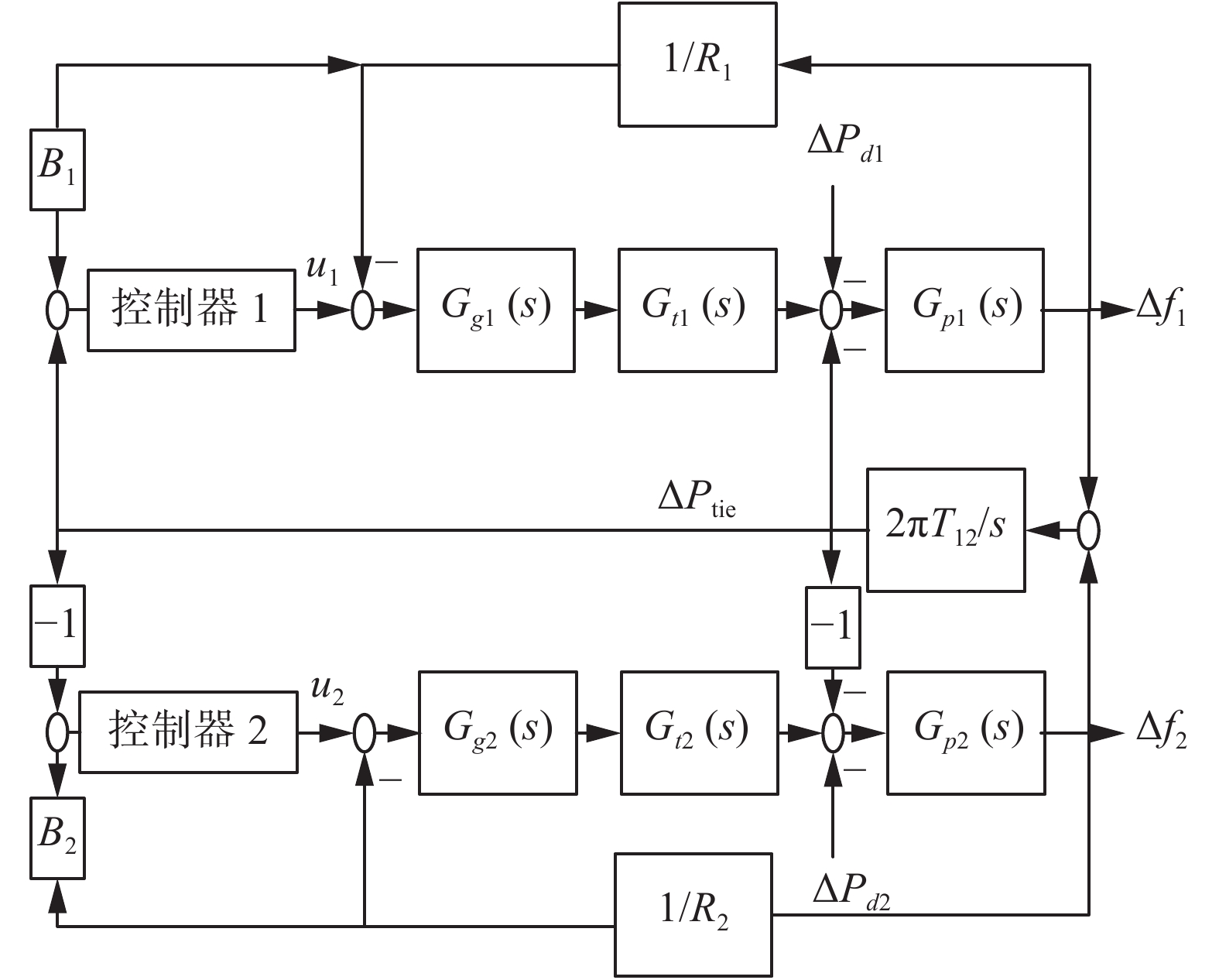
3.2 两区域频率控制系统

两个单区域电力系统通过联络线组合形成互联电力系统。互联电力系统的负荷频率控制除了要保持频率恒定(即使 $\Delta {f_i} = 0,i = 1,2$ )之外, 还要维持与联络线上的交换功率按计划运行(即使 $\Delta {P_{{\rm{tie}}}} = 0$ )。LFC 系统的控制模式有3种：定频率控制、定交换功率控制、联络线功率频率偏差控制。本文采用最常用的联络线功率频率偏差控制模式，即定义区域控制偏差 ${\rm{AC}}{{\rm{E}}_i} = \Delta {f_i} + \Delta {P_{{\rm{tie}}}}$ ，区域反馈控制量 ${u_i} = - {K_i}(s){\rm{AC}}{{\rm{E}}_i}$ 。当系统稳定时，有 $\Delta {f_i} = 0, \; \Delta {P_{{\rm{tie}}}} = 0, \; {\rm{AC}}{{\rm{E}}_i} = 0 \; (i = 1,2)$ 。考虑如图4所示的两区域负荷频率控制系统。

图4中两个区域为具有非再热汽轮机的相同电力系统，模型参数如下^[19]：

$\begin{array}{l} {K_{\rm{p}} } = 120,{T_p} = 20,{T_t} = 0.3,{T_{12}} = 0.3, \\ {a_{12}} = - 1,{T_g} = 0.08,R = 2.4,B = 0.425 \\ \end{array} $

对该系统设计三阶自抗扰控制器，并采用大变异遗传算法整定控制器参数，目标函数值取为^[20]

$J = {\rm{ITAE}} = \int_0^\infty {((\left| {\Delta {f_1}} \right| + \left| {\Delta {f_2}} \right| + \left| {\Delta {P_{{\rm{tie}}}}} \right|)} \cdot t){\rm{d}}t$

优化后的自抗扰控制器参数如表1所示。

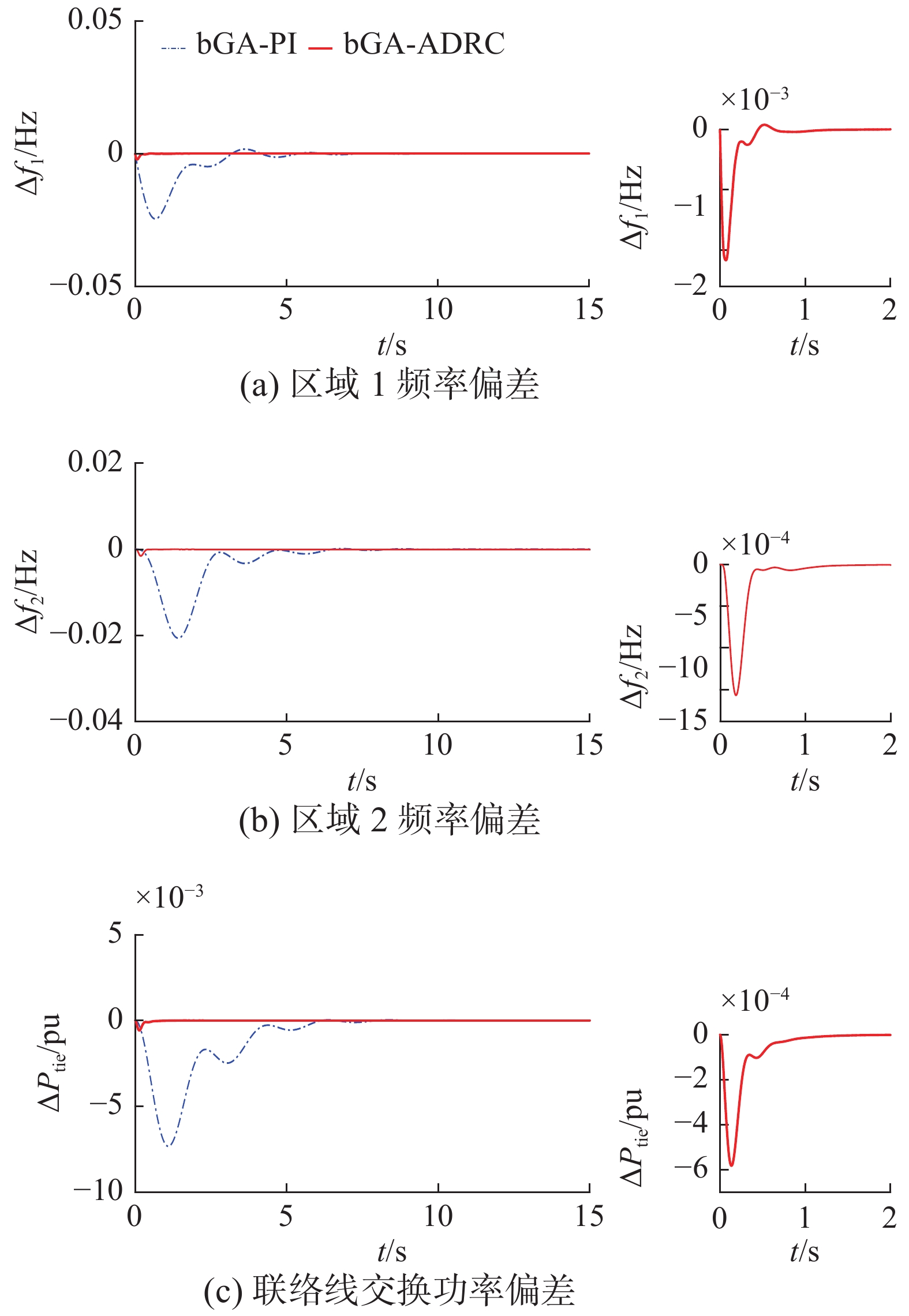
在区域1加入阶跃负荷扰动 $ \Delta {{P}_{d1}}=0.01$ ，自抗扰控制器的闭环系统响应如图5中实线所示。图5中点折线代表基于大变异遗传算法优化后的PI闭环响应( $K_{{\rm{P}}}=-0.295\;1, K_{{\rm{I}}}=0.375\;3$ )。表2显示了各区域频率偏差及联络线交换功率偏差调节时间、最大偏差以及ITAE性能指标的量化比较结果(本文调节时间定义为输出稳定在±0.005%以内的开始时间)。

从图5和表2可以看出，基于大变异遗传算法的负荷频率自抗扰控制闭环响应具有远小于参数优化后的PI控制器对应的响应调节时间和频率偏差，性能指标ITAE也缩小至1/6 000，且不同于PI控制出现明显的振荡，自抗扰控制器的响应几乎没有振荡，其效果远比优化参数后的PI控制的响应效果好，跟踪精度高。

为验证ADRC的鲁棒性，假设系统模型参数在标称值的基础上做±50%的摄动。在控制器参数不变的情况下，进行300次蒙特卡洛实验，检验控制器的性能鲁棒性。

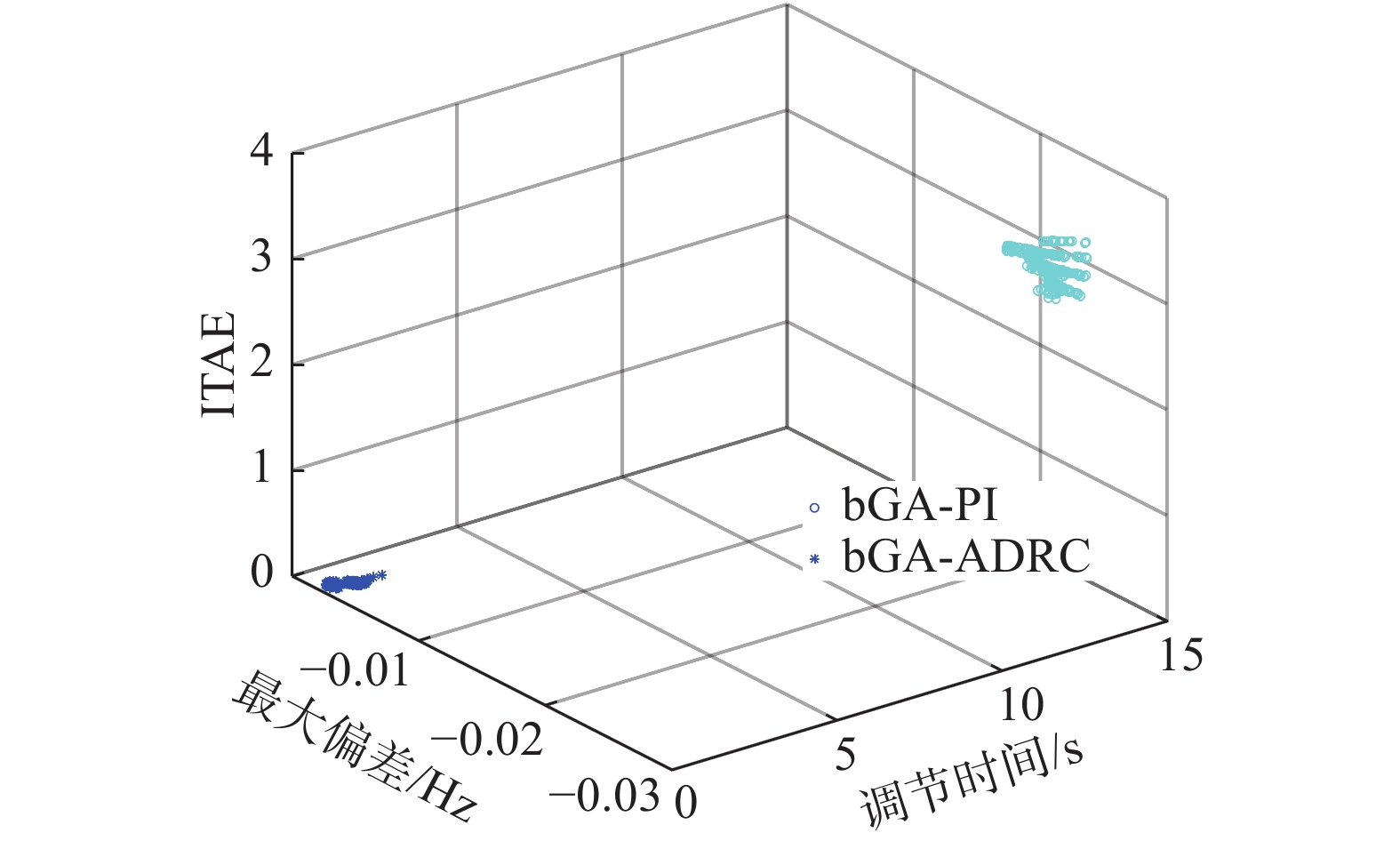
蒙特卡洛实验下基于3种算法的区域1输出频率偏差 $ \Delta {{f}_{1}}$ 的调节时间、最大偏差和ITAE的分布如图6所示。

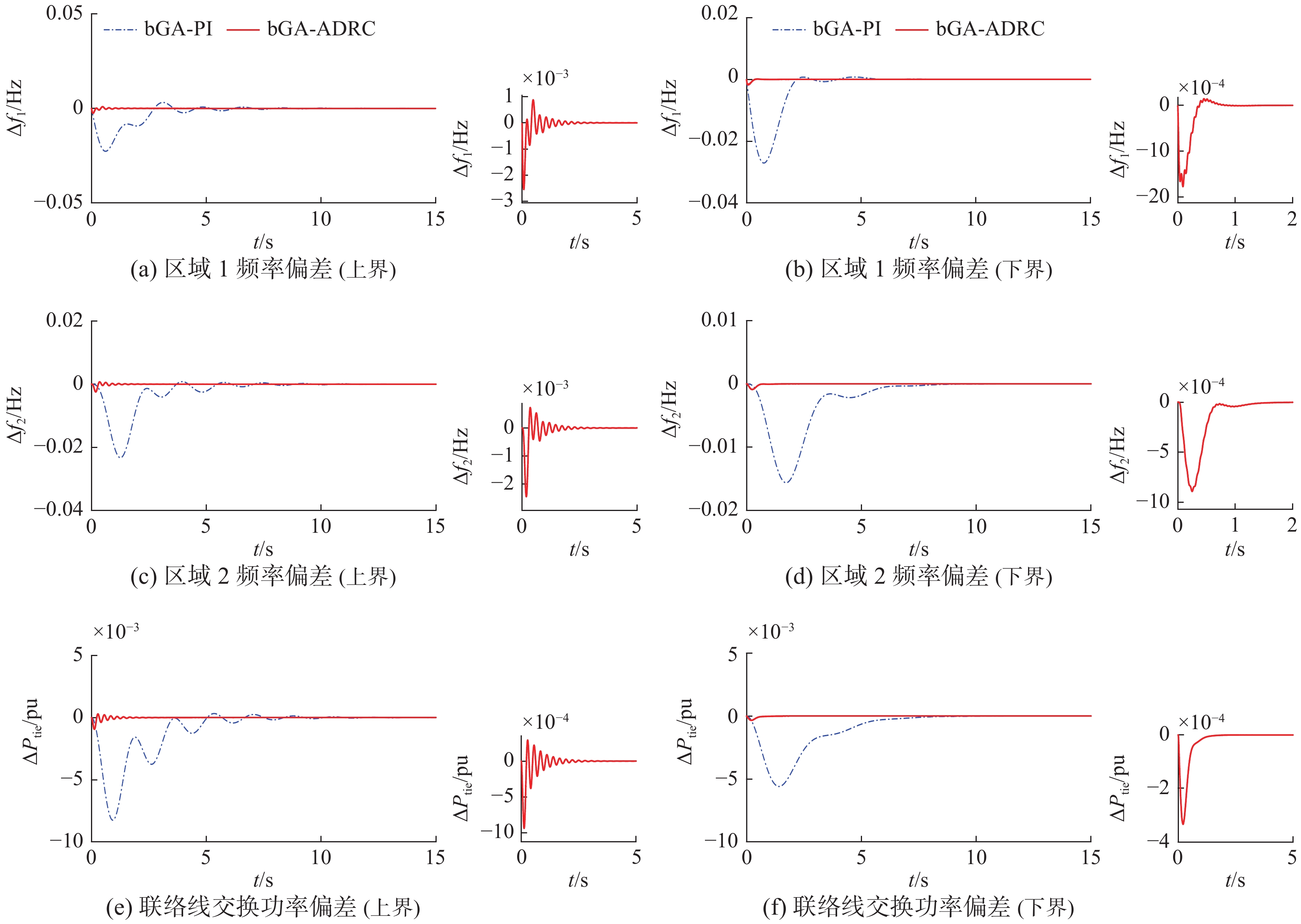
表3给出了图6的量化结果。各种算法在参数变化上、下界时的响应比较如图7所示。观察图6和表3所示蒙特卡洛实验结果，在模型参数摄动时，基于大变异遗传算法的ADRC控制下的系统ITAE值远基于大变异遗传算法的PI控制，且三维点集分布更集中。图6和表3表明基于大变异遗传算法的ADRC控制下的系统性能更优且鲁棒性较强。

图7所示临界参数摄动下的响应也体现了自抗扰控制器的快速性、稳定性和鲁棒性。

4 推广模型

在实际电力系统模型中，有时采用再热汽轮机或水轮机来替代非再热汽轮机，本章设计基于大变异遗传算法的ADRC对具有再热汽轮机或水轮机的两区域互联电力系统进行控制，并考虑发电速率约束(GRC)、调速器死区。

4.1 水轮机

水轮机动态为

$ \begin{array}{l} {G_t}(s) = \dfrac{{{a_{23}} + ({a_{23}}{a_{11}} - {a_{21}}{a_{12}}){T_w}s}}{{1 + {a_{11}}s}} \end{array} $

水体惯性的存在使得具有水轮机的负荷频率控制系统对象出现了非最小相位特性，在控制时会出现超调，增加了控制难度。

在图4所示的两区域互联电力系统模型中，假设区域1，2均为具有水轮机的相同电力系统，参数为^[22]

$ \begin{array}{l} {K_{\rm{p}}} = 120,{T_{p1}} = 20,{T_w} = 1.5,\\ {T_g} = 0.1,{R_1} = {R_2} = 2.4,{T_{12}} = 0.545,\\ {B_1} = {B_2} = 0.425,{a_{11}} = 0.491,\\ {a_{12}} = 0.789,{a_{21}} = 1.46,{a_{23}} = 0.74 \end{array} $

针对该互联电力系统，设计相应的自抗扰控制和PI控制器，使用大变异遗传算法优化控制器参数，整定结果如表4所示。

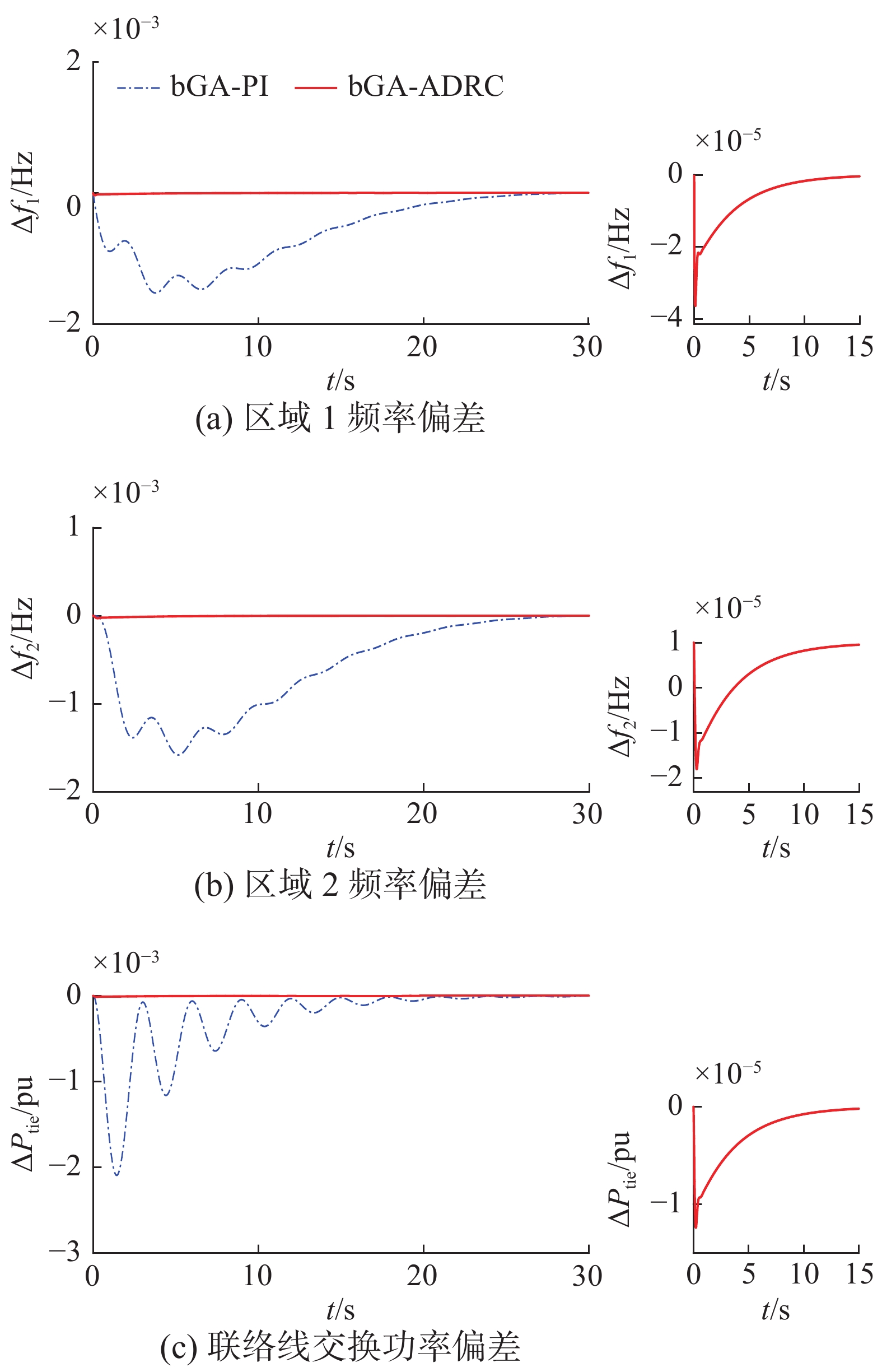
t=0时在区域1加入阶跃负荷扰动 $ \Delta {P_{d1}} = $ $0.01$ ，性能指标数值比较见表5。自抗扰控制器下的系统响应如图8实线所示。

结合表5和图8，与大变异遗传算法下的PI控制相比，加入阶跃负荷扰动后，ADRC下的闭环系统波动很小(10⁻⁵数量级)，频率偏差和调节时间远比PI下的系统响应小，这表明自抗扰负荷频率控制具有更好的抗干扰性能，对具有水轮机的两区域负荷频率控制系统控制效果极好。

4.2 再热汽轮机、发电速率约束与调速器死区

再热汽轮机的动态为

${G_t}(s) = \frac{{{K_r}{T_r}s + 1}}{{({T_t}s + 1)({T_r}s + 1)}}$

微分环节的引入会引起系统的震荡，而发电机组的发电速率约束(generation rate constraint, GRC)则是严重的非线性，调速器死区的存在更是加剧了这种非线性，发电速率约束和调速器死区的存在对系统的动态响应具有不可忽略的影响^[21]，严重时将直接导致电力系统的崩溃。图9表示考虑了发电速率约束和调速器死区的再热式两区域互联电力系统模型，参数在式(1)的基础上取 $ T_r =10, K_r=0.5$ ，并考虑3%的发电速率限制和调速器死区界限。

针对该非线性的引入，设计三阶自抗扰控制器，使用大变异遗传算法整定控制器参数，优化后的参数如表6。

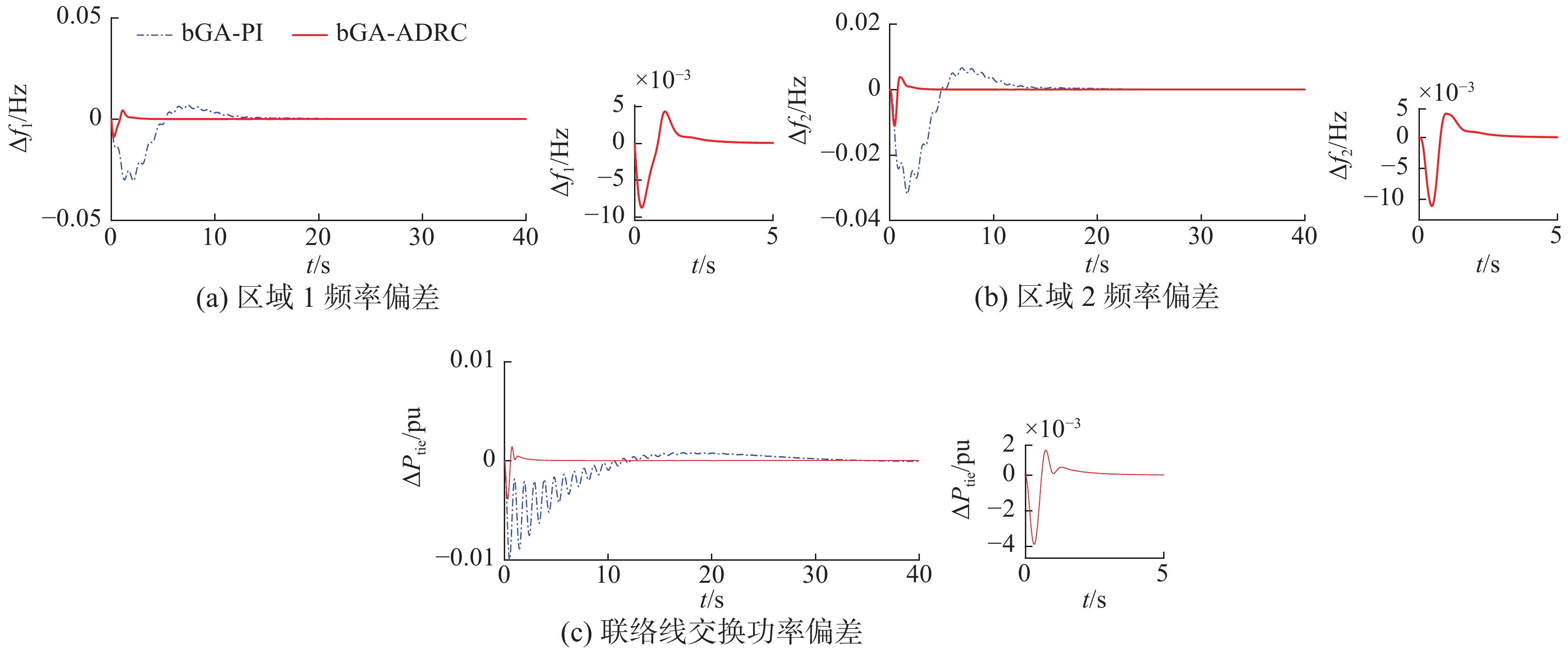
在区域1加入阶跃负荷扰动 $\Delta {P_{d1}} = 0.01$ ，考虑GRC和死区的闭环系统负荷频率和联络线交换功率动态响应曲线如图10所示，性能指标见表7 ( ${K_{\rm{P}}} = - 0.389\;6, \; {K_{\rm{I}}} =$ $0.218\;4$ )。

由图10中曲线和表7中量化数据，加入扰动负荷后，两种控制算法均实现了无静差的输出，在一致使用大变异遗传算法的前提下，与PI控制相比，电力系统在ADRC的负荷频率偏差及联络线功率偏差均更快稳定到零且最大偏差更小，震荡少，性能指标更不及千分之一，可见基于大变异遗传算法的自抗扰控制性能较优，控制效果极好。

5 结束语

本文研究了负荷频率控制系统的非线性自抗扰控制方法，并加入大变异遗传算法解决了自抗扰控制器参数繁多、不易整定的问题，针对三种两区域电力系统模型，通过与大变异遗传算法优化参数后的PI控制仿真比较，发现对线性系统、非线性系统以及非最小相位系统，自抗扰控制具有良好的控制性能，且响应快、偏差小、鲁棒性好、抗干扰能力强等优点，从而体现了基于大变异遗传算法的负荷频率自抗扰控制的有效性与优越性。