选址-路径(location-routing problem, LRP)问题是配送中心选址分配问题(location allocation problem, LAP)和车辆路径问题(vehicle routing problem, VRP)的组合问题。生鲜农产品配送对服务时效性有很高的要求，且同一客户经常具备送货和回收被取货的双向需求。因此，对传统的选址−路径问题进行扩展，同时解决生鲜农产品配送中心选址和基于同步取送方式下的路径优化问题有利于帮助企业全面协调配送系统中的各个环节，在最少成本下满足客户的取送需求。

近年来，国内外学者对生鲜农产品路径优化问题进行了大量研究。缪小红等^[1]采用遗传算法求解包含配送途中产生的货损成本、超出时间窗的惩罚成本等的生鲜农产品物流配送模型。吴瑶等^[2]设计混合遗传算法解决带时间窗的易腐食品集成生产−配送问题优化模型。Hsiao等^[3]应用混合遗传算法研究考虑食品类型和温度变化的路径优化问题。王淑云等^[4]设计集K-means聚类算法、蚁群算法和随机动态规划算法为一体的路径优化算法求解冷链商品多温共配路径优化模型。鲍春玲等^[5]考虑企业拥有多个配送中心、有限车辆数且各车辆可回到任一配送中心继续配送的情况，通过改进遗传算法解决冷链物流联合配送路径优化模型。在选址问题上，陈绍洵等^[6]建立双层规划选址模型来刻画企业选址决策及消费者偏好行为之间的相互关系。肖建华等^[7]研究非等覆盖半径思想下的生鲜农产品配送中心选址问题。狄卫民等^[8]考虑到农产品的易腐败特征和配送中心的配送能力限制建立了易腐农产品配送中心选址问题的0−1整数非线性规划模型。现有生鲜农产品选址−路径问题中以单一配送为主。其中包括带低碳^[9-10]、时间窗^[11-12]、容量约束^[13-14]、多目标^[15]等因素的选址−路径问题。对该问题的解决方法包括两阶段启发式算法^[16]、量子进化算法^[17]、量子进化算法与遗传算法协同的双智能算法^[18]、模拟退火算法^[19]等。

基本LRP以及衍生出不同类型的LRP中路径优化大多未考虑客户的取货双向需求。但是由于生鲜农产品易腐及易变质的特点，配送网点有退回商品的需求，因此企业需要同时满足客户的送货、取货需求。冀巨海等^[20]考虑配送过程带取送的双向作业模式，使用Gurobi对问题进行求解，但该模式为统一取完后再统一送的取送分离配送方式，求解后每条路径中车辆的配送性质相同，对车辆的利用率不能达到最高且行驶距离及行驶时间较长。

综上所述，本文提出考虑同步取送的选址-路径问题(ocation-routing problem with simultaneous pickup and delivery, LRPSPD)。设计一种融合中心评估指数及改进遗传算法的启发式算法(hybrid procedure combining central evaluation index and improved genetic algorithm，CEI&IGA)，以中心评估指数解决选址问题、以改进遗传算法解决路径优化问题。本文提出的选址−路径问题解决方法合理结合了企业按需求进行分区配送及取送同步路径优化两阶段问题，属于全局优化过程，可有效降低配送成本，为物流企业决策提供依据。

1 问题建模 1.1 问题描述

本文研究多车辆服务多个配送中心即“多对多”的生鲜农产品同步取送选址−路径优化问题。在该配送网络中，客户既有对生鲜农产品的送货需求，又有对腐烂变质农产品的取回需求。所有车辆从企业出发到各配送中心装货并前往客户点完成送货、取货后返回配送中心继续下一批任务，所有任务按批次进行处理。各配送批次中既可以有送货任务也可以有取货任务，即车辆同步取送。该选址−路径优化问题目标是首先选择配送中心、并为车辆指派配送区域，其次优化各车辆的配送路径以使车辆的总配送费用最小化。对比单一配送中心取送问题，本文提出多配送中心优化方案如图1所示。

1.2 LRPSPD问题假设

假定企业将生鲜产品储存于配送中心，根据顾客订单，在优化的配送路线下进行物流配送。为将现实的NP难题转换为数学模型进行量化求解，需要进行如下假设：1)企业拥有多辆车但车辆有限，车辆从配送中心出发完成配送任务后返回配送中心；2)车辆从企业到各配送中心过程中的成本忽略不计；3)有多个配送中心；4)客户位置及取送货需求已知；5)每个客户只能由一辆车服务；6)每辆车每批完成客户订单的量不能超过车辆的最大装载量，当承载量达到最大装载量时，车辆驶回配送中心；7)每辆车的规格相同。

1.3 模型建立 1.3.1 符号说明

1)符号

N表示客户集合，N={i |i= $ 0,1,2, \cdots $ , $\bar N$ }，其中i为客户编号， $\bar N$ 为客户总数，0表示企业车场。M表示配送中心集合，M={m | m= $0,1,2, \cdots $ , $\bar M$ }，其中m为配送中心编号， $\bar M$ 为配送中心总数。K表示企业拥有的车辆集合，K={k |k= $ 1,2, \cdots $ , $\bar K$ }，其中k为车辆编号， $\bar K$ 为车辆总数。Z表示配送性质集合，Z={z | z =1, 2}，其中z=1代表送货，z=2代表取货。d_ij表示由客户i到客户j的走行距离。t_ij表示客户i到客户j的走行时间，t表示单位货物作业时间。

2)参数

α(i)^z表示客户i的配送需求量；当z=1时，α(i)¹<0表示客户i的送货需求量，即车辆到客户i处进行卸货的作业数量为|α(i)²|；当z=2时，α(i)²>0表示客户i的取货需求量； ${\text{ET}}_j^1$ 表示客户j要求的最早送货时间， ${\text{LT}}_j^1$ 表示客户j要求的最晚送货时间； ${\text{ET}}_j^2$ 表示客户j要求的最早取货时间， ${\text{LT}}_j^2$ 表示客户j要求的最晚取货时间； $\left[ {{\text{ET}}_j^1{\text{,LT}}_j^1} \right]$ 和 $\left[ {{\text{ET}}_j^2{\text{,LT}}_j^2} \right]$ 分别表示客户j要求的送货、取货时间窗；C₁表示车辆单位运输成本；C₂表示早于时间窗配送的单位惩罚成本；C₃表示晚于时间窗配送的单位惩罚成本；Q表示车辆的最大承载量；e表示生鲜产品单位价格；m₁表示运输过程中的单位货损比例，m₂表示装卸过程中的货损比例。

3)变量

$T_{jk}^1$ 、 $T_{jk}^2$ 表示配送车辆k分别进行送货、取货到达客户中心j的时刻； $ f_{{\rm{wagon}}}^i$ 表示车辆到达客户i时的承载量；x_ijk表示如果车辆k由客户i驶向客户j，则决策变量x_ijk等于1，否则等于0；y_ik表示如果客户i由车辆k服务，则决策变量y_ik等于1，否则等于0。

1.3.2 数学模型

以总配送成本最小为优化目标构建物流配送优化模型如下：

$ \begin{array}{*{20}{l}} {\min Z = {C_1}\displaystyle\sum\limits_{i \in M \cup N} {\displaystyle\sum\limits_{j \in M \cup N} {\displaystyle\sum\limits_{k \in K} {{x_{ijk}}} } } {t_{ij}} + }\\ {{C_2}\displaystyle\sum\limits_{i \in M \cup N} {\displaystyle\sum\limits_{j \in M \cup N} {\displaystyle\sum\limits_{k \in K} {{x_{ijk}}} } } {{\left[ {\left( {{\rm{LT}}_j^1 - T_{jk}^1} \right) + \left( {{\rm{LT}}_j^2 - T_{jk}^2} \right)} \right]}^ + } + }\\ {{C_3}\displaystyle\sum\limits_{i \in M \cup N} {\displaystyle\sum\limits_{j \in M \cup N} {\displaystyle\sum\limits_{k \in K} {{x_{ijk}}} } } {{\left[ {\left( {T_{jk}^1 - {\rm{EL}}_j^1} \right) + \left( {T_{jk}^2 - {\rm{EL}}_j^2} \right)} \right]}^ + } + }\\ {e\displaystyle\sum\limits_{i \in M \cup N} {\displaystyle\sum\limits_{j \in M \cup N} {\displaystyle\sum\limits_{k \in K} {{x_{ijk}}} } } \left[ {{m_1}{d_{ij}} + {m_2}\Bigg(\left| {\alpha {{(i)}^1}} \right| + \alpha {{(i)}^2}\Bigg)} \right]} \end{array} $

(1)

$ \begin{array}{l} {\rm{s.t.}}\\ \displaystyle\sum\limits_{z \in Z} {\displaystyle\sum\limits_{i \in N} {f_{{\rm{wagon}}}^i} } + {x_{ijk}}\alpha {(j)^z} \leqslant {Q_k},k \in K,j \in N \end{array} $

(2)

$ \sum\limits_{i = 1}^{\bar N} {{x_{ijk}}} = {y_{jk}},\;\;\forall j \in N,\;k \in K $

(3)

$ \sum\limits_{j = 1}^{\bar N} {{x_{ijk}}} = {y_{ik}},\forall i \in N,k \in K $

(4)

$ T_{jk}^1{x_{ijk}} + \alpha {(i)^1}t \leqslant T_{jk}^2{x_{ijk}},\forall i,j \in N,k \in K $

(5)

$ T_{jk}^1 = T_{ik}^1 + {t_{ij}},\forall \;i,j \in N,k \in K $

(6)

$ T_{jk}^2 = T_{ik}^2 + {t_{ij}},\;\;\;\forall \;\;i,j \in N,k \in K $

(7)

$ {x_{ijk} = 0\;{\rm{or}}\;1},\forall \;i,j,k $

(8)

$ {y_{ik} = 0\;{\rm{or}}\;1},\;\;\forall i,k $

(9)

目标式(1)表示使总配送成本最小，总配送成本包括：运输成本、过早配送时间惩罚成本、过晚配送时间惩罚成本和货损成本。其中第2项和第3项中x⁺表示max(x，0)，意味着车辆送取过程中到达客户的时刻如果符合时间窗要求则惩罚成本为0，否则早到或者晚到都会产生成本。约束条件式(2)表示车辆k在每个客户点完成卸货或者装货任务后车辆承载的货物量不能超过该车辆最大装载量。约束条件式(3)、(4)表示对于任一客户点，仅能有一辆车访问并离开。约束条件式(5)表示车辆k到达点j进行取货的时刻必须晚于车辆k在点j完成卸货作业的时间；约束条件式(6)、(7)保证配送过程的连续性；约束条件式(8)、(9)表示变量约束。

2 CEI&IGA算法设计

本文所讨论的同步取送选址−路径问题首先要解决的问题就是确定配送中心，其次是为车辆指派配送区域并完成取送货过程中的路径优化。为解决此问题，第1步通过设计综合客户间距离、送取货的需求量、配送时间窗要求的中心评估指数确定配送中心，同时根据配送量均衡原则为各车指派配送区；第2步根据第1步车辆配送区域的信息使用改进遗传算法完成路径优化。在算法设计中，基于配送区域划分信息生成车辆的初始解，此外，通过引入自适应参数的交叉、变异操作以及选择操作完成所有车辆路径的迭代优化。

2.1 初始解的生成 2.1.1 基于CEI的配送中心确定

1)计算各客户时间窗要求相关度系数，记为

$ \begin{gathered} {\xi _{ij}} = \frac{1}{{\left| {{\text{ET}}_i^1 - {\text{ET}}_j^1} \right| + \left| {{\text{LT}}_i^1 - {\text{LT}}_j^1} \right|}} + \hfill \\ \frac{1}{{\left| {{\text{ET}}_i^2 - {\text{ET}}_j^2} \right| + \left| {{\text{LT}}_i^2 - {\text{LT}}_j^2} \right|}} \hfill \\ \end{gathered} $

2)计算任意两客户间的关联度 $ {r_{ij}} = \dfrac{{{\xi _{ij}}}}{{{d_{ij}}}} $ ，两客户间距离越近、时间窗要求相关度系数越大，关联度越大。

3)计算中心评估指数 $ {r_i} = \displaystyle\sum\limits_f {{r_{fi}}} ,i \in N $ ，即客户i评估指数r_i等于客户i与其他客户f的站间关联度r_fi之和。

4)初步确定聚类中心，根据中心评估指数分布，当客户i的r_i明显高于其他客户时，确定该客户i为一个配送中心m，m∈M，但配送中心的数量 $\bar M$ 应小于企业拥有的车辆总数 $\bar K$ 。

2.1.2 配送区域指派

确定配送中心后，根据距离最短原则为各车指派要服务的客户集合，指派过程中保持各车辆配送量均衡，步骤如下：

1) 记A_k为车辆k负责的客户集合，1≤k≤ $\bar M$ 。计算在配送区域数量确定的情况下各区域的平均需求量 $ \alpha \left( {\bar A} \right) $ ， $ \alpha \left( {\bar A} \right) = \left[ {\displaystyle\sum\limits_{i \in N} {\alpha {{\left( i \right)}^1} + \left| {\alpha {{\left( i \right)}^2}} \right|} } \right]/\bar M $ 。将 $\bar M$ 个配送中心随机依次放入客户集合A_k中。

2) 计算车辆k的配送量 $\alpha ({A_k})$ ， $ \alpha ({A_k}) = $ $\displaystyle\sum\limits_{i \in {A^k}} {\alpha {{\left( i \right)}^1}} + \left| {\alpha {{\left( i \right)}^2}} \right| $ 。

3) while i< $\bar N$ ， $\alpha ({A_k})$ ≤ $ \alpha \left( {\bar A} \right) $ 。

4) 计算客户i和 $\bar M$ 个配送中心的距离，记与i距离最近的配送中心为m_i。将客户i放入m_i所在的客户集合A_k中。

5) while i< $\bar N$ ， $\alpha ({A_k})$ > $ \alpha \left( {\bar A} \right) $ 。

6) 根据式(10)计算客户i将要放入的客户集合A_k中，保证各客户集内的需求量均衡：

$ \Delta {S_k} = \min {\left[ {\sum\limits_{k = 1}^{\bar M} {{{\left[ {\alpha \left( {{A_k}} \right) - \alpha (\bar A)} \right]}^2}} /\bar M} \right]^{1/2}} $

(10)

7) 令i = i+1，回到2)；

8) 得到各个车辆服务的客户集合A_k={ $ m, \cdots $ , $i, \cdots $ ,a_k, m ∈M, i∈N }，1≤ k ≤ $\bar M$ ，其中a_k表示车辆k负责的客户总个数。

2.1.3 生成初始解

首先编码，车辆k要访问同一客户点两次分别进行送货、取货，因此路径中某客户点会出现两次。一个解中包括2a_k个客户。采用特殊编码方式，记X_k ={δ(m), $ \cdots , $ δ(i), $ \cdots ,$ δ(a_k),Φ(m), $ \cdots, $ Φ(i), $ \cdots, $ Φ(a_k)}为车辆k的一个取送顺序解，解的长度记为2a_k；采用自然数进行编码，其中δ(i)表示车辆第1次访问客户i送货时的服务顺序，Φ(i)表示车辆第2次访问客户i取货时的服务顺序。针对车辆k随机生成R个长度为2a_k初始解集合，记为 $ {\bar H_k} = \left\{ {X_k^1, \cdots ,X_k^s, \cdots ,X_k^R} \right\} $ 。

2.2 选择操作

将适应度函数定义为总配送成本最小的倒数，即f(y)=1/Z(y)，其中y代表一个路径解X_k。根据式(11)计算路径解y的选择概率p(y)并根据轮盘赌规则从 $ {\bar H_k} $ 中选出数量为 $ \bar R $ 的顺序解集合H_k进入算法迭代中，集合 ${H_k} = \left\{ {X_k^1, \cdots ,X_k^s, \cdots ,X_k^{\bar R}} \right\} $ 。p(y)计算如下：

$ p(y) = \frac{{f(y)}}{{\displaystyle\sum\nolimits_{y = 1}^R f (y)}} $

(11)

2.3 交叉和变异操作

本文引入遗传参数的自适应调整策略以提高遗传算法的收敛精度和收敛速度。迭代初期安排较大的p_c，待迭代稳定后减小p_c；对适应度大的个体安排较小的p_c以保持其优良性，对适应度小的个体给予较大的p_c以加速求解。p_m同样也与迭代数及适应度有关。如下：

${p_{c\max }} = \left\{ \begin{array}{l} 0.8,\;\;\;\;{\rm{ }}g \leqslant \dfrac{G}{4}\\ 0.7,\;\;\;\;{\rm{ }}\dfrac{G}{4} < g \leqslant \dfrac{{3G}}{4}\\ 0.6,\;\;\;\;\dfrac{{3G}}{4} < g \leqslant G \end{array} \right.$

(12)

${p_{m\min }} = \left\{ \begin{array}{l} 0.002,\;\;\;\;{\rm{ }}g \leqslant \dfrac{G}{4}\\ 0.05,\;\;\;\;\dfrac{G}{4} < g \leqslant \dfrac{{3G}}{4}\\ 0.01,\;\;\;\;\dfrac{{3G}}{4} < g \leqslant G \end{array} \right.$

(13)

${p_{ci}} = \left\{ \begin{array}{l} {p_{c\max }} - ({p_{c\max }} - {p_{c\min }})\Bigg(\dfrac{g}{G} + \dfrac{{{f_i}}}{{{f_{\max }} - \overline f }}\Bigg),\;\;{f_i} \geqslant \overline f \\ {p_{c\max }},\;\;{f_i} < \overline f \end{array} \right.$

(14)

${p_{mi}} = \left\{ \begin{array}{l} {p_{m\min }} - ({p_{m\max }} - {p_{m\min }})\Bigg(\dfrac{g}{G} + \dfrac{{{f_i}}}{{{f_{\max }} - \overline f }}\Bigg),\;\;{f_i} \geqslant \overline f \\ {p_{m\min }},\;\;{f_i} < \overline f \end{array} \right.$

(15)

式中：p_cmax为最大交叉概率，p_mmin为最小变异概率，二者取值与当前迭代次数和最大迭代次数有关；p_ci为实际交叉概率；p_mi为实际变异概率；p_cmin为最小交叉概率，假定p_cmin=0.5；p_mmax为最大变异概率，假定p_mmax=0.05；f_i为个体适应度值，f_max为当前种群的最大适应值， $\overline f $ 为当前种群的平均适应度值；g为当前迭代次数，G为最大迭代次数。

结合交叉操作和变异操作求解问题，如下：

从H_k中选择两个顺序解 $X_k^\alpha $ 和 $ X_k^\beta $ (1≤α<β≤ $ \bar R $ )进行单点倒置交叉。

从H_k中选择一个顺序解 $ {\rm{X}}_k^\eta (1 \leqslant \eta \leqslant \bar R) $ 随机选取两点进行互换变异。

2.4 插入配送中心

车辆到达某客户j时的承载量计算如下：

$ f_{{\rm{wagon}}{\rm{ }}}^j = \left\{ {\begin{array}{*{20}{l}} {0,\;\;\;\;\;\;\;\;\;\;\displaystyle\sum\limits_{z \in Z} {\displaystyle\sum\limits_{i,j \in N} {f_{{\rm{wagon}}{\rm{ }}}^i} } + {x_{ijk}}\alpha {{(j)}^z} > Q}\\ {\displaystyle\sum\limits_{i \in N} {f_{{\rm{wagon}}}^i} ,\;\;\;\;\;{\text{否则}}} \end{array}} \right. $

(16)

式(16)表示车辆在前往下一客户时对当前装载量进行计算并判断是否能继续前进。当车辆剩余装载量空间不能满足下一客户的需求时，车辆需返回其配送中心使承载量归零。同时，车辆从配送中心出发、完成配送任务返回配送中心。记车辆k的配送中心为m_k，依次对H_k中每个解X_k进行修正，除在解的前后增加m_k外，车辆在运输途中超载也要在相应的位置加上m_k，可得到X_k={m_k $ , \cdots $ ,δ(i) $ ,\cdots $ ,m_k $ , \cdots $ ,δ(j) $ ,\cdots $ ,m_k}。

2.5 解码

根据客户和编码的对应关系对自然数编码解码可形成路径解，在m_k处对路径进行拆分得到车辆配送的各条子路径。计算适应度、根据轮盘赌选择后继续下一次迭代。

迭代完成后，输出某一车辆的最优路径，继续生成其他车辆的初始解并进行路径优化，直至所有车辆都得到最优路径。

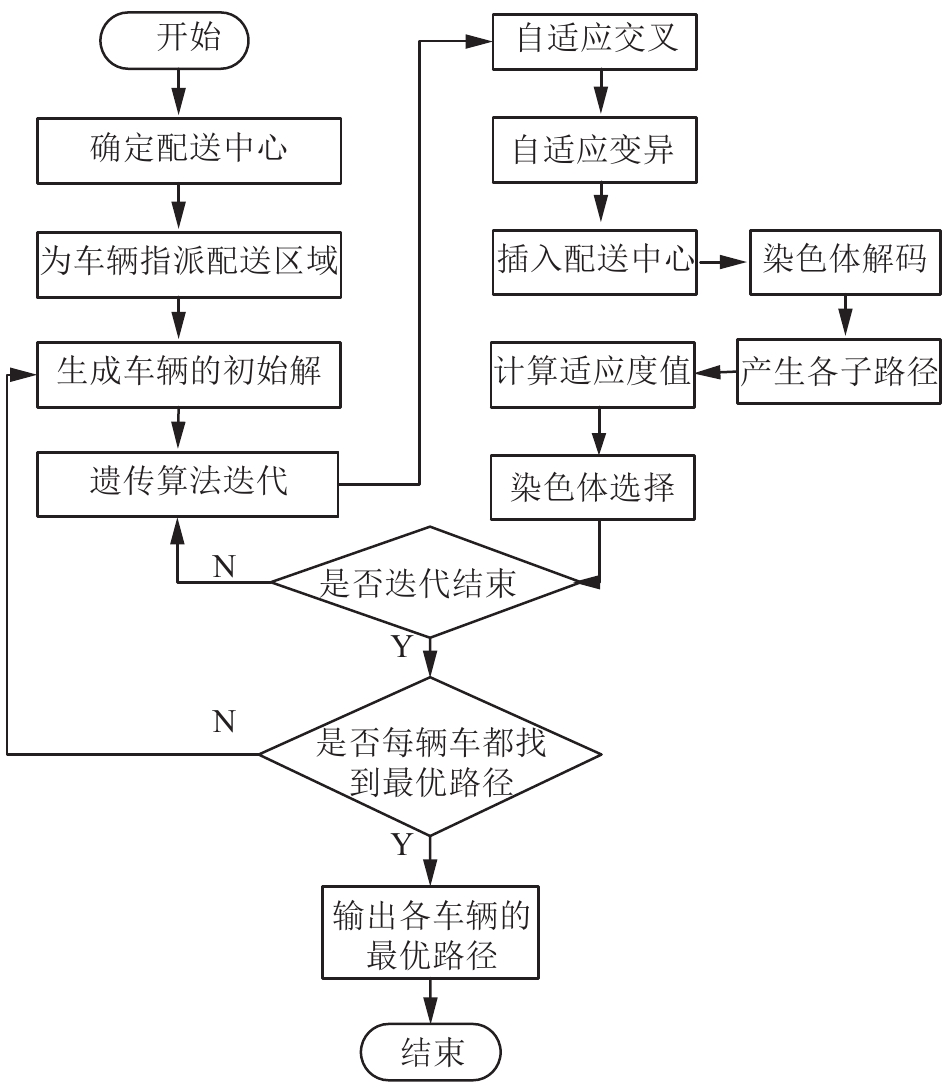
2.6 算法流程图

算法流程图如图2。

3 算例验证及分析

假设某物流企业有3辆车可供使用，配送车辆的单位运输费用为40元/km，早到的单位损失成本为C₂为10元/h，晚到的单位损失成本C₃为20元/h，车辆的最大承载量Q为50箱，生鲜产品价格为400元/箱，单位货物作业时间t为0.02 h/箱，运输过程的货损比例m₁为0.01%，装卸过程中的货损比例m₂为0.03%。如表1所示，设计有30个客户的实验场景，第3第4列表示客户的送货需求和取货需求，如表1所示。

使用本文提出的CEI&IGA算法设定种群个数为200、迭代次数为160次，使用MATLAB进行编程求解。

3.1 配送区划分

计算中心评估指数，以最大化原则利用企业内部的3辆车并确定3个配送中心：客户7、客户14、客户24。根据距离和配送均衡原则将其他客户匹配给各配送中心形成3个配送区，如下：

$ \begin{array}{l} {A_1} = \left\{ {7,4,8,10,16,20,25,26,27,29,30} \right\}\;\;\;\;\;\alpha \left( {{A_1}} \right) = 212\\ {A_2} = \left\{ {14,2,3,5,6,9,12,18,21,23} \right\}\;\;\;\;\;\alpha \left( {{A_2}} \right) = 213\\ {A_3} = \left\{ {24,1,11,13,15,17,19,22,28} \right\}\;\;\;\;\;\alpha \left( {{A_3}} \right) = 214 \end{array} $

3.2 路径优化

各车辆配送区域的路径优化结果如表2所示，可以看出，各子路径的开头或结束为配送中心。同时，同一批次中同一客户点会出现两次代表车辆前往该地分别进行送货、取货，这体现了本文提出的同步取送配送方式。

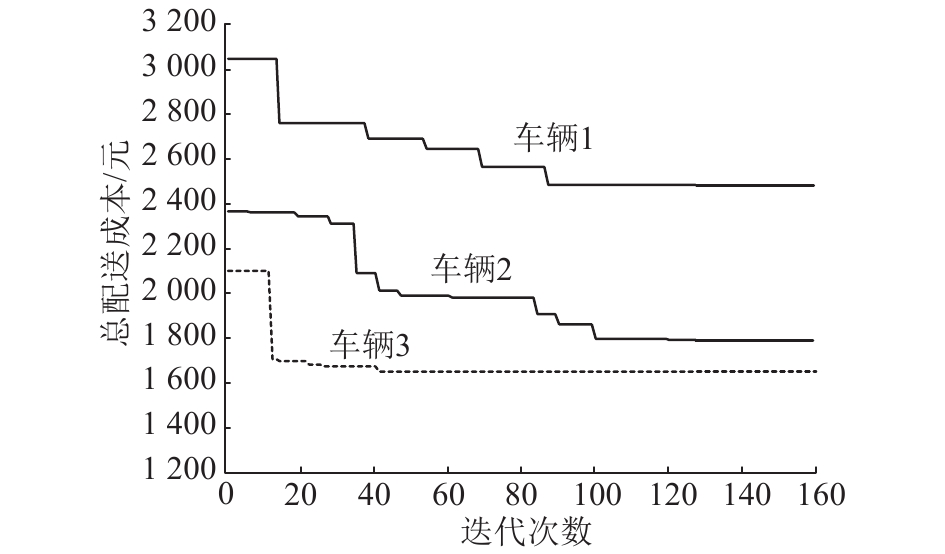
各配送区内配送费用计算结果见表3，各车辆的路径优化收敛结果见图3，因为a₁>a₂>a₃，所以车辆1负责的配送区域A₁产生的配送费用要大于其他两个配送区域。

3.3 取送分离与同步取送对比

取送分离方式下车辆统一送完货物后再进行取货，各批路线中配送性质相同，而本文提出的同步取送方式中各批配送性质不同。基于此，采用本文的实例及算法，针对3辆车在各自的配送区域以同步取送和取送分离的配送模式进行路径优化。取送分离优化后的路径结果如表4所示，优化后两种方式产生的路径数及各费用对比如表5所示。

从表4可看出，取送分离模式下路径数比较多且因为车辆容量约束的限制，部分路径总装载量很少，造成了车辆利用率低的问题。从表5可以看出，在同步取送模式下，路径数量大大减少，配送费用减少了13.71%。各费用降低验证了本文提出同步取送方式对车辆利用的有效性。

3.4 算法对比

在实验中保持控制参数不变，使用本文实例以及3.1中配送区域划分信息，使用传统遗传算法与本文提出的改进遗传算法进行3辆车在各自配送区域的路径优化。3组实验对比中，每组实验对应各个车辆在两个算法运行下的寻优迭代过程。

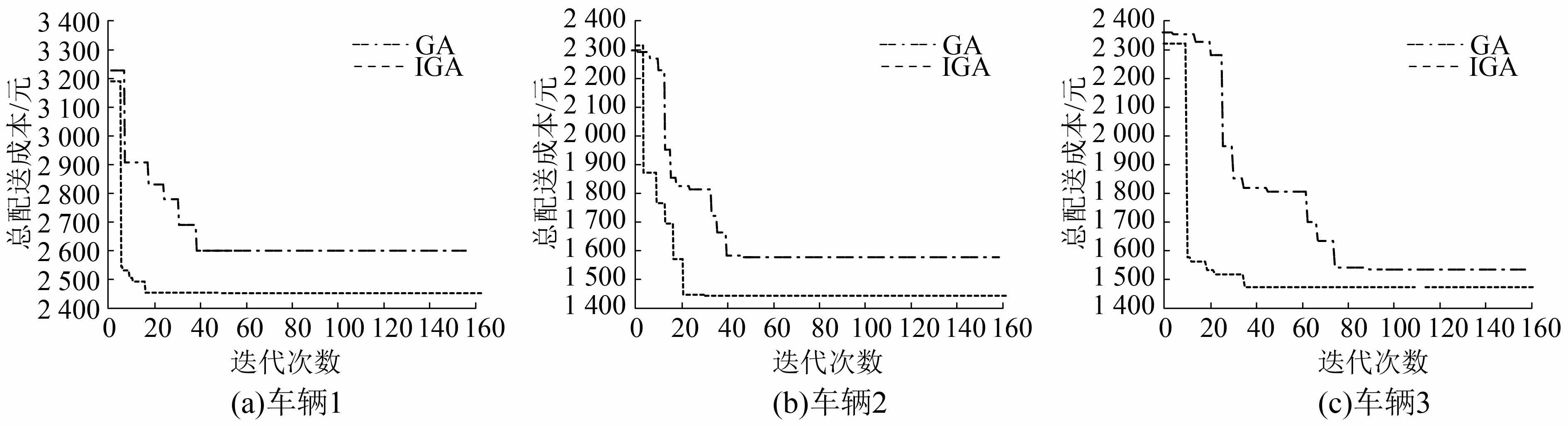
实验结果如图4所示，优化后的算法能够在更短的时间内得到全局最优解。两种算法在寻找3次最优路径的计算机总运行时间对比详见表6，改进后的遗传算法寻优效率更高，能够更快找到最优路径。

4 结束语

针对传统生鲜产品选址−路径优化未考虑客户的取送双向需求以及取送分离配送模式下对车辆利用不足、配送费用较高等问题，提出将多配送中心和取送同步结合的车辆同步取送机制。同步取送模式下，车辆在配送路径中可以既送货又取货。最后通过对比取送分离及同步取送两种配送模式的路径数、运输费用、时间惩罚费用及货损费用证明了本文提出的同步取送的合理性及有效性，同时也将本文提出的算法与传统遗传算进行对比，验证了算法改进的有效性。

本文对选址问题采取了为车辆分派区域的方式解决，在对车辆的利用上有一定局限，可在选址问题上采用联合配送的方式，使车辆可回到任意配送中心继续配送，同时目标函数可以考虑低碳成本来更好优化生鲜农产品的物流配送。