混合数据^[1]是非结构化的、互补的、超高维的，包含大量冗余信息，研究如何有效表示，特征选择和融合混合数据有重要的实际意义。尤其是在数字化时代，多通道传感器广泛化产生，混合数据的分类任务普遍存在于实际生活中，如文本情感分类，医学影像分析更多复杂的语义以混合属性值形式表示。数值型和符号型数据的相互作用，导致概念往往具有不一致性和模糊性。如何利用混合数据的上述性质降低此类数据的不确定性是一个值得研究的课题。

模糊粗糙集^[2]是一种处理不确定性问题的有效数学工具，然而现有的模糊粗糙集模型不能处理混合数据分类问题。因此，研究模糊粗糙集扩展模型，并应用于混合属性分类具有重要的理论创新价值。Mi等^[3]用对偶三角模构造逻辑算子，发展了粗糙近似算子的构造方法。Feng等^[4]用概率方法研究并构造了信任函数与似然函数。目前，模糊粗糙近似算子的构造大多使用一对三角模与蕴含算子作为逻辑算子，没有考虑对象或者属性之间的差异性。用多伴随对构造模糊Galois连接，模糊粗糙近似算子，可以体现数值型数据和符号型属性之间的偏好。近几年来，Medina等^[5]研究了多伴随理论，并探究其在多伴随概念格和多伴随粗糙集等概念上的应用，但混合数据的表示方面需进一步深入研究。不同类型属性获取所需的不同代价问题，是现实生活中数据处理时必不可少要考虑的因素。Tan^[6]提出代价敏感学习，并将其应用到许多方面，如遗传算法^[7]、粗糙集^[8-9]等。国内学者也研究进展颇丰，如Fan等^[8]针对测试代价敏感决策系统，构造数据模型。Ju等^[10]提出了带有多粒度指标的代价敏感粗糙集模型。一系列学者都将获取数据的代价作为数据处理时的重要因素。受上述工作的启发，本文引入代价敏感多伴随模糊粗糙集表示数值型属性和符号型属性之间的异构互补关系，使得伴随对与不同类型属性之间产生关联；在利用多伴随算子表达不同类型属性之间偏好的同时，兼顾了获取不同类型属性值的代价。

Yao^[11-12]提出的三支决策是处理数据分类任务时基于人类认知的高效决策模式，已有许多专家将其与其他模型结合，大大提高了数据分类能力。Liang等^[13-14]研究了处理多阶段信息和双犹豫模糊信息的基于直觉模糊粗糙集的三支决策模型。Qiao^[15]将三支决策引入到推荐系统时，考虑了代价和用户的偏好，极大改进了推荐质量。徐健锋^[16]以混淆矩阵为工具，多目标优化三支决策阈值求解模型，同时发现了三支决策的代价与决策的条件概率之间存在非单调现象^[17]。混合数据分类模型结合三支决策模型的研究已有成果，AL-Hmouz^[18]运用三支决策的思想做多模态生物识别系统的开发。赵天娜^[19]初步研究了多伴随直觉模糊粗糙集与三支决策模型的简单结合。鉴于模型与三支决策组合的优越性，本文将进一步深入地研究用三支决策模型处理混合数据分类问题更优化的方式，代价敏感多伴随模糊粗糙集模型赋予三支语义，并在决策代价最小化意义下优化混合数据三支分类结果，扩展三支决策理论的应用范围。

本文的贡献可从以下几个方面体现：混合数据的非结构化，互补以及大量冗余无关信息等特点造成数据的高度不确定性，因此数据分类不一致性和模糊性使得挖掘混合数据蕴含的内部信息有难度。找出数值型和符号型属性之间的各种关系，降低分类的不确定性是混合数据挖掘中亟待解决的问题。针对上述问题，本文用多个伴随对模拟不同类型属性之间的关系，多伴随算子可充分表达不同类型属性对对象之间的偏好，同时考虑了获取不同类型属性值的代价，提出代价敏感多伴随模糊粗糙集模型。给出充分体现此模型特点的概率公式，并优化了损失函数。改造三支决策模型，挖掘出不同类型属性的关系特点。针对混合数据的不确定性特点，提出此模型。此模型是数据特点驱动的，从数据本质出发，分析混合数据的特点，找出数值型属性和符号型属性之间的各种关系。

1 基本概念 1.1 多伴随模糊粗糙集理论

$\rm{Cornelis}$ 等^[20]提出的多伴随模糊粗糙集理论研究了多伴随对与模糊粗糙集理论结合的基本定义和简单性质。

定义1^[20] 　给定偏序集 $({P_1},{ \leqslant _1}){\text{、}\!\!}({P_2},{ \leqslant _2}){\text{、}}\!\!({P_3},{ \leqslant _3})$ 和映射 $\& :{P_1} \times {P_2} \to {P_3}$ ， $ \swarrow :{P_3} \times {P_2} \to {P_1}$ ， $ \nwarrow :{P_3} \times {P_1} \to $ ${P_2} $ ，称 $(\& , \swarrow , \nwarrow )$ 是一个伴随三元组，如果满足：

1 )对于 $x \in {P_1},y \in {P_2},z \in {P_3}$ ，都有 $x{ \leqslant _1}z \swarrow y \Leftrightarrow x\& y{ \leqslant _3} $ $z \Leftrightarrow y{ \leqslant _2}z \nwarrow x $ ；

2) $\& $ 在 ${P_1}{\text{、}}{P_2}{\text{、}}{P_3}$ 上是保序映射；

3) $ \swarrow , \nwarrow $ 在第1和第2论域上是保序映射。

定义2^[20] 　设 $({L_1},{L_2},P,{\rm{\& }}{}_1,\cdots,{{\rm{\& }}_n})$ 是多伴随框架，称 $(A,U,R,\tau )$ 为多伴随背景，其中 $A$ 是非空对象集， $U$ 是非空属性集， $R:A \times U \to P$ 是 $P$ -模糊关系，满足自反性和对称性。 $\tau :A \times A \to \{ 1,2,\cdots,n\} $ 是将 $A \times A$ 中元素对映射到多伴随框架上一个特定的伴随三元组。

定义3^[20] 　在模糊决策信息系统 $(U,A \cup \left\{ d \right\})$ 中，给定属性子集 $B \subseteq A$ ，和P-模糊关系 ${R_a}:X \times X \to $ $P, \forall a \in A, $ 对于 $x,y \in U$ ，模糊关系 ${R_B}:U \times U \to P$ 定义为：

${R_B}(x,y) = @(\phi _B^{x,y}({a_1}),\cdots,\phi _B^{x,y}({a_m}))$

(1)

其中 $@:{P^m} \!\to\! P$ 是一个聚合算子，对于 $a \in A$ ，有

$\phi _B^{x,y}(a) = \left\{ {\begin{array}{*{20}{c}} {{R_a}(x,y),\quad a \in B} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{T_P}{\rm{,}\quad}a \notin B} \end{array}} \right.$

其中 ${T_P}$ 是 $P$ 的最大值。

定义4^[20] 　在多伴随面向属性框架 ${(P,L,L, }$ ${{\rm{\&}}_1,\cdots,{{\rm{\& }}_n})}$ 下，考虑形式背景 $(U,U,{R_B},\tau )$ ，对于 $x,y \in U$ ，定义似然算子 ${ \uparrow _\pi }:{L^U} \to {L^U}$ 和必然算子 ${ \downarrow ^N}:{L^U} \to {L^U} $

$ {g^{{ \uparrow _\pi }}}(x) = {\rm{sup}}\{ {R_B}\left( {x,y} \right){{\rm{\& }}_{\tau (x,y)}}g(y)|y \in U\} $

(2)

$ {f^{{ \downarrow ^N}}}(y) = {\rm{inf}}\{ f(x){ \nwarrow _{\tau (x,y)}}{R_B}(x,y)|x \in U\} $

(3)

那么 ${g^{{ \uparrow _\pi }}}$ 是 $g$ 的上近似， ${f^{{ \downarrow ^N}}}$ 是 $f$ 的下近似。其中 $\!{L^U}\!$ 表示所有由 $\!U\!$ 映射到 $\!L\!$ 的函数的集合。

定义5^[20] 　对于模糊子集 $h \in {L^U}$ ， $({h^{{ \downarrow ^N}}},{h^{{ \uparrow _\pi }}})$ 称为多伴随模糊粗糙集。

1.2 基于决策粗糙集的三支决策

决策粗糙集模型用状态集和行动集来描述决策过程。状态集 $\varOmega = \{ C,\neg C\} $ 中的2个状态分别表示某事件属于 $C$ 和不属于 $C$ ，行动集 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 分别表示接受某事件、延迟决策和拒绝某事件3种行动，用 ${{\textit{λ}} _{{\rm{PP}}}}{\text{、}}{{\textit{λ}} _{{\rm{BP}}}}{\text{、}}{{\textit{λ}} _{{\rm{NP}}}}$ ； ${{\textit{λ}} _{{\rm{PN}}}}{\text{、}}{{\textit{λ}} _{{\rm{BN}}}}{\text{、}}{{\textit{λ}} _{{\rm{NN}}}}$ 表示采取不同的行动会产生不同的损失，分别表示当 $x$ 属于 $C$ 或 $x$ 不属于 $C$ 时采取行动 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 的损失。采取3种行动的期望损失函数由如下式子表示：

$R({a_P}|[x]) = {{\textit{λ}} _{PP}}P(C|[x]) + {{\textit{λ}} _{PN}}P(\neg C|[x])$

(4)

$R({a_B}|[x]) = {{\textit{λ}} _{BP}}P(C|[x]) + {{\textit{λ}} _{BN}}P(\neg C|[x])$

(5)

$R({a_N}|[x]) = {{\textit{λ}} _{NP}}P(C|[x]) + {{\textit{λ}} _{NN}}P(\neg C|[x])$

(6)

式中： $P(C|[x]) = \dfrac{{|C \cap [x]|}}{{|[x]|}}$ ； $| \cdot |$ 是基数； $\left[ x \right]$ 表示 $x$ 关于 $R$ 的等价类。

根据贝叶斯决策规则，以期望损失函数最小为原则选择最佳行动方案，决策规则如下：

(P) 若 $R({a_P}|[x]) \leqslant R({a_B}|[x])$ 且 $R({a_P}|[x]) \leqslant R({a_N}|[x])$ ，则 $x \in POS(C)$ ；

(B) 若 $R({a_B}|[x]) \leqslant R({a_P}|[x])$ 且 $R({a_B}|[x]) \leqslant R({a_N}|[x])$ ，则 $x \in {\rm{BND}}(C)$ ；

(N) 若 $R({a_N}|[x]) \leqslant R({a_P}|[x])$ 且 $R({a_N}|[x]) \leqslant R({a_B}|[x])$ ，则 $x \in {\rm{NEG}}(C)$ 。

2 代价敏感多伴随模糊粗糙集

混合数据的数值型和符号型属性是由多通道传感器产生的，获取途径差异很大，采集不同类型属性付出的代价均不相同。在现实生活中，考虑经济因素，研究人员希望用几个代价较小的属性，提取同样有价值的信息，因此不同类型的属性代价是必不可少要考虑的因素。本文希望用更少的代价获取更有价值的信息。

定义6　设 ${A^*} = \left( {U,A \cup D} \right)$ 是混合数据决策系统， $U$ 是非空论域， $A \cap D = \phi $ ， $A = {A_S} \cup {A_R}$ ，A_S = {a₁, $ {{a_2},\cdots,{a_i},\cdots,{a_m}}\} $ 和 ${A_R} = \left\{ {{a_{m + 1}},{a_{m + 2}},\cdots,{a_{m + i}},\cdots,{a_{m + n}}} \right\}$ 分别是符号和数值型条件属性的集合。获取对象 $x$ 分别关于不同模态属性 ${A_S}$ 和 ${A_R}$ 的信息付出的代价为 ${\rm{Cost}}{_r}$ 、 ${\rm{Cost}}{_R}$ 。考虑模态属性代价得到的权重 $w_i^C$ 定义如下：

1) 对于 ${a_i} \in {A_S},i \in \left\{ {1,2,\cdots ,m} \right\}$ ，每个属性的权重定义为:

$ w_S^C = \dfrac{1}{{\left| {{A_S}} \right|}}\dfrac{{{\rm{Cost}} { _S}}}{{{\rm{Cost}} { _S} + {\rm{Cost}} {_R}}} $

(7)

2) 对于 ${a_i} \in {A_R},i \in \left\{ {m + 1,m + 2,\cdots,m + n} \right\}$ ，每个属性的权重定义为：

$ w_R^C = \dfrac{1}{{\left| {{A_R}} \right|}}\dfrac{{{\rm{Cost}} {_R}}}{{{\rm{Cost}} {_S} + {\rm{Cost}} {_R}}} $

(8)

定义7　设 ${A^*} = \left( {U,A \cup D} \right)$ 是混合数据决策系统， $U$ 是非空论域， $A \cap D = \phi $ ，对于 $a \in A$ ， $a$ -模糊关系 $R_a^{}:U \times U \to [0,1]$ 定义如下：

${R_a}(x,y) = 1 - |\bar a(x) - \bar a(y)|$

$\forall B \subseteq A$ ， $B$ -模糊关系 $R_B^C$ 定义如下：

$\begin{array}{l} R_B^C(x,y) = w_S^C \phi _B^{x,y}({a_1}) + \cdots + w_S^C \phi _B^{x,y}({a_m}) + \\ \quad \quad \quad \quad w_R^C \phi _B^{x,y}({a_{m + 1}}) + \cdots + w_R^C \phi _B^{x,y}({a_{m + n}}) \end{array} $

(9)

其中 $\phi _B^{x,y}:A \to [0,1]$ 定义如下：

$\phi _B^{x,y} (a) = \left\{ {\begin{array}{*{20}{l}} {{R_a}(x,y), \quad a \in B{\rm{ }}} \\ {1{\rm{ }},\quad a \notin B} \end{array}} \right.$

性质1　 $R_B^C$ 满足自反性和对称性。

证明　1)由 $R_B^C$ 的定义可知， ${R_a}\left( {x,x} \right)$ =1，进而推出 $R_B^C\left( {x,x} \right)$ =1。因此， $R_B^C$ 满足自反性。

2)因为 ${R_a}\left( {x,y} \right) = 1 - \left| {\bar a\left( x \right) - \bar a\left( y \right)} \right|$ ，并且 ${R_a}\left( {y,x} \right) = $ $1 - \left| {\bar a\left( y \right) - \bar a\left( x \right)} \right|$ ，所以 ${R_a}\left( {x,y} \right) = {R_a}\left( {y,x} \right)$ 。由 $R_B^C$ 的定义可知， $R_B^C\left( {x,y} \right) = R_B^C\left( {y,x} \right)$ 。因此， $R_B^C$ 满足对称性。

性质2　 $R_B^C$ 满足单调性，即 ${B_1} \subseteq {B_2} \Rightarrow R_{{B_2}}^C \leqslant R_{{B_1}}^C$ 。

证明　1)若 ${B_1} = {B_2}$ ，则显然 $R_{{B_2}}^C = R_{{B_1}}^C$ 。

2)若 ${B_1} \subset {B_2}$ ，则必存在 ${a_i} \in {B_2}$ ，但是 ${a_i} \notin {B_1}$ 。由 $\varphi _{{B_1}}^{\left( {x,y} \right)}\left( {{a_i}} \right) \!=\! 1,\varphi _{{B_2}}^{\left( {x,y} \right)}\left( {{a_i}} \right) \!=\! {R_{{a_i}}}\left( {x,y} \right)$ ，则 $\phi _{{B_2}}^{\left( {x,y} \right)}\left( {{a_i}} \right) \leqslant \phi _{{B_1}}^{\left( {x,y} \right)}\left( {{a_i}} \right)$ 。对于其他属性 ${a_j} \in {B_1} \cap {B_2} = {B_1}$ ，有 $\phi _{{B_2}}^{\left( {x,y} \right)}\left( {{a_j}} \right) = \phi _{{B_1}}^{\left( {x,y} \right)}\left( {{a_j}} \right)$ 成立。由 $R_B^C$ 的定义可知， $R_{{B_2}}^C \leqslant R_{{B_1}}^C$ 。

定义8　在多伴随面向属性框架 $(P,L,L,{{\rm{\& }}_1},\cdots,$ ${{\rm{\& }}_n}) $ 下，考虑有代价的形式背景 $(U,U,R_B^C,\tau )$ ，对于 $m \in {L^U}$ ，定义似然算子 ${ \uparrow _\pi }:{L^U} \to {L^U}$ 和必然算子 ${ \downarrow _N}:{L^U} \to {L^U}$ ：对于 $x,y \in L$

$ m_C^{{ \uparrow _\pi }}(x) = {\rm{sup}}\{ R_B^C(x,y) {{\rm{\& }}_{\tau (x,y)}} m(y)|y \in U\} $

(10)

$ m_C^{{ \downarrow ^N}}(y) = {\rm{inf}}\{ m(x){ \nwarrow _{\tau (x,y)}}R_B^C(x,y)|x \in U\} $

(11)

其中， $m_C^{{ \uparrow _\pi }}$ 是 $m$ 的上近似， $m_C^{{ \downarrow ^N}}$ 是 $m$ 的下近似。

对于模糊子集 $m \in {L^X}$ ，称 $(m_C^{{ \downarrow ^N}},m_C^{{ \uparrow ^\pi }})$ 为代价敏感多伴随模糊粗糙集。

经过对代价敏感多伴随模糊粗糙集的研究，本文发现，添加一个简单条件后，它仍满足经典的粗糙集中上下近似的性质。由性质1和性质2可知，本文定义的关系 $R_B^C$ 满足文献[13]中关系 ${R_B}$ 的性质，因此，本文中代价敏感多伴随模糊粗糙集的上下近似需添加的条件和文献[7]中3.2中命题1的条件一致。

性质3　对于 $m \in {L^U}$ ，

1)若满足 $m(x){ \nwarrow _{\tau (x,x)}}{\rm{1}} \leqslant m(x)$ ，则 $m_C^{{ \downarrow ^N}}(y) \leqslant m(y)$ 。

2)若满足 $m(x) \leqslant {\rm{1}}{{\rm{\& }}_{\tau (x,x)}}m(x)$ ，则 $m(y) \leqslant m_C^{{ \uparrow ^\pi }}(y)$ 。

证明过程可参照文献[12]中3.2中命题1的证明。

3 基于代价敏感多伴随模糊粗糙集的新型三支决策模型

基于决策粗糙集的经典三支决策模型利用状态集 $\varOmega = \{ C,\neg C\} $ 和行动集 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 描述决策过程。采取不同的行动产生不同的损失函数矩阵如表1所示，这些损失函数满足 ${{\textit{λ}} _{{\rm{PP}}}} < {{\textit{λ}} _{{\rm{BP}}}} < {{\textit{λ}} _{{\rm{NP}}}}$ ； ${{\textit{λ}} _{{\rm{NN}}}} < {{\textit{λ}} _{{\rm{BN}}}} < {{\textit{λ}} _{{\rm{PN}}}}$ ，其中 ${{\textit{λ}} _{ \bullet \bullet}} \in (0,1)$ 。

由经验可知，对象属于状态集的概率直接影响决策过程。在三支决策模型中，体现为概率是定义决策目标函数(期望损失函数)的关键因素。因此，给出体现模型特点的概率定义对精确决策至关重要。

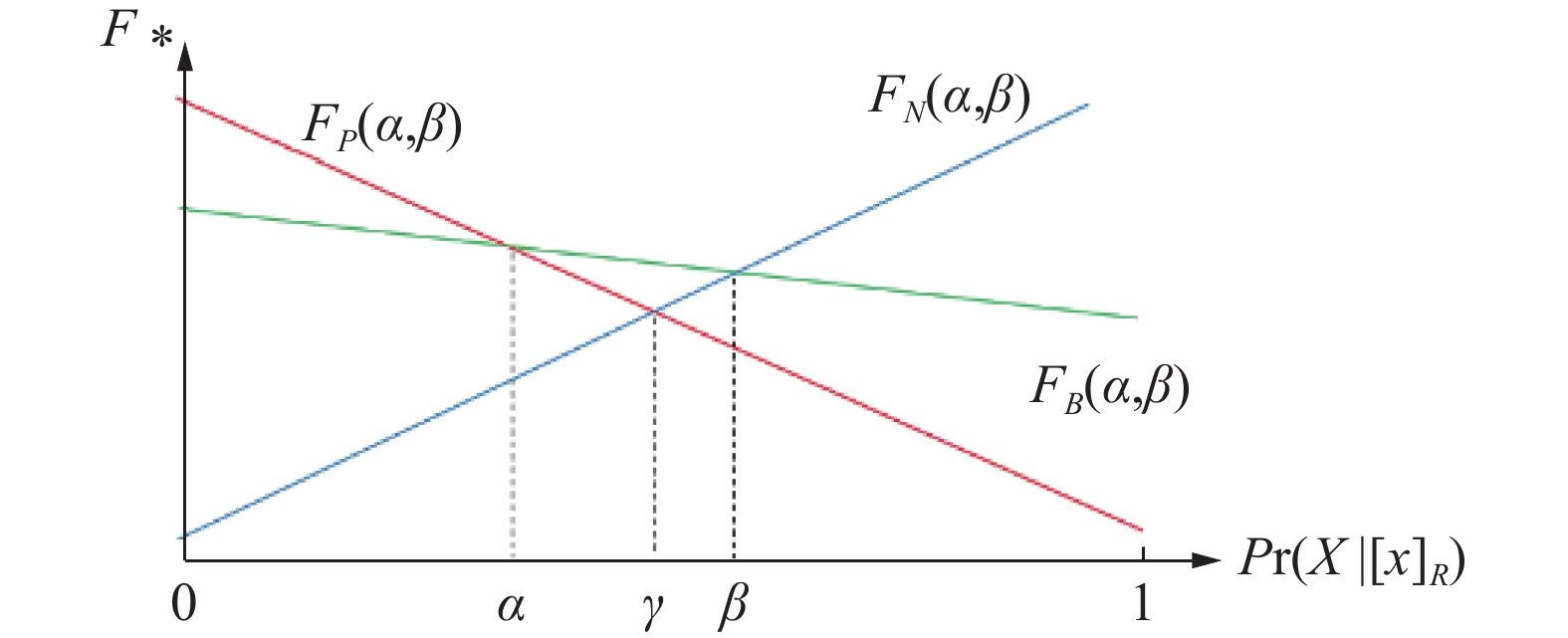
在经典的三支决策模型中，代价与决策的条件概率是单调的线性关系，如图1，但在实际生活中，三支决策的代价与决策的条件概率之间存在着非单调情况^[17]，如图2，针对这种现象，徐健锋等^[17]以延迟代价目标函数为研究对象，提出了一种双延迟代价目标函数的策略。本文借鉴这一思想，在代价敏感多伴随模糊粗糙集模型上，给出充分贴近此模型特点的概率定义，并优化做延迟决策 ${a_B}$ 时的非线性损失函数，期望得到更准确处理分类任务的三支决策模型。

3.1 改进的三支决策模型

改进的三支决策模型，与传统三支决策模型相比， ${{\textit{λ}} _{{\rm{PP}}}}{\text{、}}{{\textit{λ}} _{{\rm{PN}}}}{\text{、}}{{\textit{λ}} _{{\rm{NP}}}}{\text{、}}{{\textit{λ}} _{{\rm{NN}}}}$ 定义不变，只改进 ${\textit{λ}} {'_{{\rm{BP}}}}{\text{、}}{\textit{λ}} {'_{{\rm{BN}}}}$ 和 ${\textit{λ}} {''}{_{{\rm{BP}}}}{\text{、}}{\textit{λ}} {''}{_{{\rm{BN}}}}$ ，如表2，它们的含义为：分别从正域和负域视角出发，实际为正域元素和负域元素但决策时被划分为延迟域的2组代价函数。正域决策代价目标函数 ${F_P}$ 、负域决策代价目标函数 ${F_N}$ 不变，只改进双延迟决策代价目标函数，记为 $F{'_B}{\text{、}}F'{'_B}$ 。由于非线性函数 ${F_B}$ 有很多种定义方式，不同的定义方式导致不同的非线性函数 ${F_B}$ ，为了简化和一般性，本文选取最简单的非线性模型进行说明，由这2个线性函数组成一个非线性函数，并假设 ${{\textit{λ}} _{{\rm{NP}}}} - {{\textit{λ}} _{{\rm{NN}}}} > 0 > {{\textit{λ}} _{{\rm{PP}}}} - {{\textit{λ}} _{{\rm{PN}}}}$ 和 ${{\textit{λ}} _{{\rm{NP}}}} - {{\textit{λ}} _{{\rm{NN}}}} > {\textit{λ}} {'_{{\rm{BP}}}} - {\textit{λ}} {'_{{\rm{BN}}}} > {\textit{λ}}{{''}_{{\rm{BP}}}} - $ ${\textit{λ}} {{''}_{{\rm{BN}}}} > {{\textit{λ}} _{{\rm{PP}}}} - {{\textit{λ}} _{{\rm{PN}}}}$ ，本文只讨论图2这种非线性的情况。其他情况类似，在此不再赘述。

$\begin{gathered} {F_P} = {{\textit{λ}} _{{\rm{PP}}}} {\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) + {{\textit{λ}} _{{\rm{PN}}}}\left( {{\rm{1 - }}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right)} \right) \\ {F_N} = {{\textit{λ}} _{{\rm{NP}}}}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) + {{\textit{λ}} _{NN}}\left( {{\rm{1 - }}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right)} \right) \\ F{'_B} = {\textit{λ}} {'_{{\rm{BP}}}}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) + {\textit{λ}} {'_{{\rm{BN}}}}\left( {{\rm{1 - }}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right)} \right) \\ F'{'_B} = {\textit{λ}} {{''}_{{\rm{BP}}}}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) + {\textit{λ}} {{''}_{{\rm{BN}}}}\left( {{\rm{1 - }}{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right)} \right) \\ \\ \end{gathered} $

令 $F{'_B}{\rm{ = }}F'{'_B}$ ，解得 ${\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right){\rm{ = }}\mu $ 。

所以 ${F_B} = \left\{ {\begin{array}{*{20}{l}} {{{F''}_B},{\rm{ }}\quad{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) \geqslant \mu } \\ {{{F'}_B},{\rm{ }}\quad{\rm{Pr}} \left( {X\left| {{{\left[ x \right]}_R}} \right.} \right) < \mu } \end{array}} \right.$

多伴随模糊粗糙集充分考虑了数值型和符号型属性之间的互补性、关联性、大量无关冗余信息的特点，用此模型从混合数据中提取的蕴含信息高效体现对象属于状态集的可能性程度。本文用3种策略描述对象属于状态集的概率。

定义9　(平均概率)对象 $x$ 属于状态集 $C$ 的平均概率定义为：

$\bar P(C\left| x \right.) = \frac{1}{2}({m^{ \uparrow \pi }}(x) + {m^{{ \downarrow ^N}}}(x))$

(12)

定义10　对象 $x$ 分别采取 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 3种行动的平均模糊期望损失函数计算公式为：

$\overline {F({a_P}|x)} = {{\textit{λ}} _{{\rm{PP}}}}\bar P(C\left| x \right.) + {{\textit{λ}} _{{\rm{PN}}}}(1 - \bar P(C\left| x \right.))$

(13)

$\overline {F({a_B}|x)} = \left\{ {\begin{array}{*{20}{c}} {{\textit{λ}} {{''}_{{\rm{BP}}}}\bar P(C\left| x \right.) + {\textit{λ}} {{''}_{{\rm{BN}}}}\left( {{\rm{1 - }}\bar P(C\left| x \right.)} \right),{\rm{ }}\bar P(C\left| x \right.) \geqslant \mu } \\ {{\textit{λ}} {'_{{\rm{BP}}}}\bar P(C\left| x \right.) + {\textit{λ}} {'_{{\rm{BN}}}}\left( {{\rm{1 - }}\bar P(C\left| x \right.)} \right),{\rm{ }}\bar P(C\left| x \right.) < \mu } \end{array}} \right.$

(14)

$\overline {F({a_N}|x)} = {{\textit{λ}} _{{\rm{NP}}}}\bar P(C\left| x \right.) + {{\textit{λ}} _{{\rm{NN}}}}(1 - \bar P(C\left| x \right.))$

(15)

比较 $\overline {F({a_P}|x)} {\text{、}}\overline {F({a_B}|x)} {\text{、}}\overline {F({a_N}|x)} $ 的大小，确定行动 ${a_i}(i \in \{ P,B,N\} )$ 使平均模糊期望损失函数 $\bar F$ 最小。

定义11　(悲观概率)对象 $x$ 属于状态集 $C$ 的悲观概率定义为：

${P^P}(C\left| x \right.) = {m^{{ \downarrow ^N}}}(x)$

(16)

定义12　对象 $x$ 分别采取 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 3种行动的悲观模糊期望损失函数计算公式为：

$F{({a_P}|x)^P} = {{\textit{λ}} _{{\rm{PP}}}}{P^P}(C\left| x \right.) + {{\textit{λ}} _{{\rm{PN}}}}(1 - {P^P}(C\left| x \right.))$

(17)

$\!F{({a_B}|x)^P} \!=\! \left\{ {\begin{array}{*{20}{c}}\!\!\!\!\! {{\textit{λ}} {{''}_{{\rm{BP}}}}{P^P}(C\left| x \right.) + {\textit{λ}} {{''}_{{\rm{BN}}}}\left( {{\rm{1 - }}{P^P}(C\left| x \right.)} \right),{\rm{ }}{P^P}(C\left| x \right.) \geqslant \mu } \\ \!\!\!\!\!\!\!\!\! {{\textit{λ}} {'_{{\rm{BP}}}}{P^P}(C\left| x \right.) + {\textit{λ}} {'_{{\rm{BN}}}}\left( {{\rm{1 - }}{P^P}(C\left| x \right.)} \right),{\rm{ }}{P^P}(C\left| x \right.) < \mu } \end{array}} \right.\!\!\!\!\!\!\!\!$

(18)

$F{({a_N}|x)^P} = {{\textit{λ}} _{{\rm{NP}}}}{P^P}(C\left| x \right.) + {{\textit{λ}} _{{\rm{NN}}}}(1 - {P^P}(C\left| x \right.))$

(19)

比较 $F{({a_P}|x)^P}{\text{、}}F{({a_B}|x)^P}{\text{、}}F{({a_N}|x)^P}$ 的大小，确定行 动 ${a_i}(i \in \{ P,B,N\} )$ 使悲观模糊期望损失函数 ${F^P}$ 最小。

定义13　(乐观概率)

$ {P^O}(C\left| x \right.) = {m^{{ \uparrow _\pi }}}(x) $

(20)

定义14　对象 $x$ 采取 ${\cal{A}} = \{ {a_P},{a_B},{a_N}\} $ 3种行动的乐观模糊期望损失函数计算公式为：

$F{({a_P}|x)^O} = {{\textit{λ}} _{{\rm{PP}}}}{P^O}(C\left| x \right.) + {{\textit{λ}} _{{\rm{PN}}}}(1 - {P^O}(C\left| x \right.))$

(21)

$F{({a_B}|x)^O} \!=\! \left\{ {\begin{array}{*{20}{l}}\!\!\!\!\! {{\textit{λ}} {{''}_{{\rm{BP}}}}{P^O}(C\left| x \right.) + {\textit{λ}} {{''}_{{\rm{BN}}}}\left( {{\rm{1 - }}{P^O}(C\left| x \right.)} \right),{\rm{ }}{P^O}(C\left| x \right.) \geqslant \mu } \\ \!\!\! {{\textit{λ}} {'_{{\rm{BP}}}}{P^O}(C\left| x \right.) + {\textit{λ}} {'_{{\rm{BN}}}}\left( {{\rm{1 - }}{P^O}(C\left| x \right.)} \right),{\rm{ }}{P^O}(C\left| x \right.) < \mu } \end{array}} \right.\!\!\!\!\!\!\!\!$

(22)

$F{({a_N}|x)^O} = {{\textit{λ}} _{{\rm{NP}}}}{P^O}(C\left| x \right.) + {{\textit{λ}} _{{\rm{NN}}}}(1 - {P^O}(C\left| x \right.))$

(23)

4 基于代价敏感多伴随模糊粗糙集的三支决策算法

本文提出的基于代价敏感多伴随模糊粗糙集的三支决策算法，是处理具有偏好的模糊信息的不确定性决策理论，以最小期望损失为目标，得到损失最小的决策。

本文仅以乐观概率为例给出混合数据分类的基于代价敏感多伴随模糊粗糙集的三支决策算法。整个算法流程图，如图3所示。

比较 $F{({a_P}|x)^O}{\text{、}}F{({a_B}|x)^O}{\text{、}}F{({a_N}|x)^O}$ 的大小，确定行动 ${a_i}(i \in \{ P,B,N\} )$ 使乐观模糊期望损失函数 ${F^O}$ 最小。

算法1　基于代价敏感多伴随模糊粗糙集的乐观三支决策算法

输入　混合数据决策表 $\left( {U,A \cup D} \right)$ ，属性代价 ${\rm{Cost}}{_S}, $ 　 ${\rm{Cost}}{_R}$ ，模糊集 $m$ ，损失函数矩阵 ${{{\textit{λ}}} _{}}$ 。

输出　行动集 $\overrightarrow {{a_i}} $ ，分类精度 ${\rm{Acc}}$ 。

1) 根据定义7，计算模糊关系 $R_B^C$ ；

2) For 每个对象 $x \in U$

根据定义8，计算代价敏感多伴随模糊粗糙集 $(m_C^{ \downarrow N},m_C^{ \uparrow \pi })$ ；

根据定义13，计算乐观概率 ${P^O}(\left. C \right|x) = $ ${m^{{ \uparrow _\pi }}}(x) $ ；

根据定义14，计算采取3种行动 ${\cal{A}} = \{ {a_P},{a_B}, $ ${a_N}\} $ 的期望损失 ${F_{{a_P}}}{\text{、}}{F_{{a_B}}}{\text{、}}{F_{{a_N}}}$ ；

比较期望损失函数 ${F_{{a_i}}},i \in \{ P,B,N\} $ ，选择期望损失 ${F_{{a_i}}}$ 最小的行动集 ${a_i}$ 作为最佳行动方案；

　　计算分类精度 ${\rm{Acc}} = 1 - \dfrac{{{\rm{sum}}\left( {\left| {\bar a - \bar d} \right|} \right)}}{{\left| U \right|}}$ ；

　　End For

３) Return 行动集 $\overrightarrow {{a_i}} $ ，分类精度 ${\rm{Acc}}$ 。

5 实例验证

设混合数据的决策表 $\left( {U,A \cup D} \right)$ 如表3，获取符号型属性和数值型属性的代价比为 ${\rm{Cost}}{_S}:{\rm{Cost}}{_R} = $ 1，则由定义6得每个符号型属性和数值型属性的权重分别为 $w_S^C = \dfrac{1}{4}{\text{、}}w_R^C = \dfrac{1}{2}$ ，由定义7得到模糊关系 $R_B^C$ 。如表4所示。

设每个对象对应的m(x)的值分别为：0.76、0.17、0.15、0.76、0.53、1、0，由定义8，利用Godel t模和相应的蕴含算子构造的伴随对 $\left( {{\& _G},{ \swarrow _G},{ \nwarrow _G}} \right)$ ，Product t模和相应的蕴含算子构造的伴随对 $( {{\& _P},} $ ${ \swarrow _P},{ \nwarrow _P}) $ ，其中 $x{\& _G}y \!=\! \min \left\{ {x,y} \right\}$ ； $z{ \nwarrow _G}x \!=\! \left\{ {\begin{array}{*{20}{l}}{1,{\rm{ }}x \leqslant z}\\{z,{\rm{else}}}\end{array}} \right.$ ； ${ \swarrow _G} \!=\! $ $ { \nwarrow _G} $ ； $x{\& _L}y = x*y$ ； $z{ \nwarrow _P}x = \min \left\{ {1,z/x} \right\}$ ； ${ \swarrow _P} = { \nwarrow _P}$ 。

$\tau \left( {{x_i},{x_j}} \right) = \left\{ \begin{array}{l}G,\;\;j = 1,3,5,7,i \in \left| U \right|\\P,\;\;\;j = 2,4,6,\;\;i \in \left| U \right|\end{array} \right.$ ，得到代价敏感多伴随模糊粗糙集为：

$\begin{gathered} m_C^{{ \downarrow _N}}\left( {{x_1}} \right) = 0.50,m_C^{{ \downarrow _N}}\left( {{x_2}} \right) = 0.17,m_C^{{ \downarrow _N}}\left( {{x_3}} \right) = 0.15,m_C^{{ \downarrow _N}}\left( {{x_4}} \right) =\\ 0.50,m_C^{{ \downarrow _N}}\left( {{x_5}} \right) = 0.50,m_C^{{ \downarrow _N}}\left( {{x_6}} \right) \!=\! 0.50,m_C^{{ \downarrow _N}}\left( {{x_7}} \right) \!=\! 0;m_C^{{ \uparrow _\pi }}\left( {{x_1}} \right) \!=\!\\ 0.76,m_C^{{ \uparrow _\pi }}\left( {{x_2}} \right) = 0.17,m_C^{{ \uparrow _\pi }}\left( {{x_3}} \right) = 0.15,m_C^{{ \uparrow _\pi }}\left( {{x_4}} \right) = 0.76 \end{gathered}$

$m_C^{{ \uparrow _\pi }}\left( {{x_5}} \right) = 0.53,m_C^{_{{ \uparrow _\pi }}}\left( {{x_6}} \right) = 1,m_C^{{ \uparrow _\pi }}\left( {{x_7}} \right) = 0$

由对象属于状态集的概率的定义11，得 P (x₁) = 0.76、P (x₂) = 0.17、P (x₃) = 0.15、P (x₄) = 0.76、P (x₅) = 0.53、P (x₆) = 1、P (x₇) = 0。

参照徐健锋^[16]中双延迟代价双量化三支决策模型第4章模型1的参数：

$\begin{gathered} \;\\ {{\textit{λ}} _{{\rm{PP}}}} = 0.00,{{\textit{λ}} _{{\rm{PN}}}} = 2.00,{{{\textit{λ}} '}_{{\rm{BP}}}} = 0.25,{{{\textit{λ}} '}_{{\rm{BN}}}} = 1.00\\ {{{\textit{λ}} ''}_{{\rm{BP}}}} = 1.00,{{{\textit{λ}} ''}_{{\rm{BN}}}} = 0.25,{{\textit{λ}} _{{\rm{NP}}}} = 2.00,{{\textit{λ}} _{{\rm{NN}}}} = 0.00 \\ \end{gathered} $

以代价风险函数最小为原则，得到数据分类规则为：

${a} = \left\{ {\begin{array}{*{20}{l}} {{a_P},\;\;\;\;\;P\left( x \right) < 0.36} \\ {{a_B},\;\;\;\;\;0.36 \leqslant P\left( x \right) \leqslant 0.65} \\ {{a_N},\;\;\;\;\;P\left( x \right) < 0.65} \end{array}} \right.$

得到数据分类如表5所示，由此可知分类精度为85.7%。

表5是分别采用乐观概率，悲观概率，平均概率时，对每个对象的采取决策的结果，从结果可知，依据3种概率得到的期望损失函数的判断结果是一致的。

6 结束语

混合数据的分类问题是研究热点。本文从混合数据的模糊性和符号型、数据型属性的不一致性等特点出发，利用多伴随，模糊粗糙集给出不同类型属性之间的不同度量，考虑不同类型属性的代价，期望花费最小的代价得到最有价值的信息。在延迟代价双量化的基础上，研究了多种不同的模糊概率策略，构造了混合数据分类过程中的三支决策模型。该模型既能反应出数据本身的客观不确定性，也可以表达决策者主观上对不同类型属性的偏好及数值型和符号型属性数据获得难易程度的认识。未来可继续研究更多的模糊粗糙集的扩展模型，期望在超大规模数据集上刻画混合数据的精确表示，挖掘出更多数据内部蕴含的信息。