三支决策(Three-way decisions, 3WD)是由加拿大学者Yao ^[1]在2010年提出的一种朴素的“三分而治”和“化繁为简”的决策理论，其核心思想是通过粒计算将论域(整体)分为3个子集或3个部分，并对不同子集或部分采取不同的决策行为或分治策略，进而对相应的行为或策略进行评价和反馈。由于三支决策符合人类思维和认知特点，且能较好地处理实际决策过程中出现的不确定性问题，它一经提出便得到国内外学者的广泛关注，并已成为一种重要的粒计算和知识发现研究方法。

纵观三支决策发展脉络，它经历了孵化期(1980—2006)、羽化期(2007—2026)、成长期(2017—现在)3个阶段^[2]。对三支决策的思考最早可追溯到20世纪80年代波兰数学家Pawlak提出的粗糙集理论。众所周知，粗糙集理论是通过上下近似集对论域进行划分的，下近似集诱导的规则表示确定性规则；上近似集诱导的规则表示可能性规则。在这一时期，人们主要关注由下近似集诱导的确定性规则，而完全忽略由上近似集补集诱导的另一种确定性规则，究其原因是由于前者包含了有用(有趣)知识，对于决策者而言最有价值。三支决策的发展契机是20世纪90年代Yao ^[3]提出的决策粗糙集理论。决策粗糙集首次将决策风险的概念引入到粗糙集理论中，通过贝叶斯风险最小决策准则将论域划分为正域、负域和边界域3个区域。从正域里得到的正向确定性规则表示接受某概念(acceptance)；从负域里得到的负向确定性规则表示拒绝某概念(rejection)；从边界域里得到的不确定规则用于延迟决策(deferment)。这赋予了粗糙集理论一种新的语义解释，并开启了狭义三支决策研究时代。随着对粒计算和三支决策理论的不断深入研究，学者们纷纷意识到仅仅从粗糙集这一狭义视角来探讨三支决策已显得过于狭隘，对三支决策内涵和外延的理解应该更加广泛和深刻，系列广义三支决策研究如雨后春笋般在机器学习、数据挖掘、模式识别、推荐系统、认知模型、形式概念分析、数理逻辑、商空间等领域崛起并得到迅猛发展，对三支决策的狭义解释也延伸为三要素、三部分、三分量、三层次、三阶段、三步骤、三种类等广义认知^[4-6]。

经过近40年的发展，三支决策已在理论、方法和应用上取得了一系列研究成果。在理论层面上，现有文献主要集中在三支决策空间、三支认知模型、三支逻辑、三支形式概念分析等三支决策与数学理论的交叉研究上。胡宝清^[7]提出了三支决策空间的概念，并从数学上将模糊集、随机集、粗糙集等统一到三支决策空间研究框架中。李小南等^[8]提出了一种一般性的三支决策理论，它主要从子集评估的视角进行模型构造的。Yao ^[9]系统地研究了三支决策与认知计算的理论和方法，并认为认知计算是三支决策未来研究的一个重要方向。李金海等^[10]提出了一种基于多粒度的三支概念认知学习模型，并进一步研究了认知概念的增量学习方法。Davide等^[11]探讨了三支决策下的三值逻辑问题，并深入探讨了三支决策与三值逻辑之间的关系。祁建军等^[12]讨论了三支决策与概念格的理论模型，这赋予了形式概念分析和概念格新的语义解释。在方法层面上，不确定性三支决策、三支决策约简和规则获取、三支决策分类与聚类、代价敏感三支决策等是当前研究的热点。刘盾等^[13-16]考虑了不确定性决策环境下，当损失函数为几类典型的不确定性测度时，相应三支决策阈值的获取方法；进而将随机性、区间性和模糊性三种不确定度量引入到三支决策中，提出了一系列不确定性三支决策模型。李华雄^[17-19]等分别从保持正域最大、决策风险最小和代价敏感最小化等方面，对三支决策约简和规则获取作了大量工作。张贤勇等^[20]从粗糙集正域、边界域和负域3个层次对三支决策约简作了探讨。任睿思等^[21]将三支决策引入到概念格中，系统地研究了三支概念格的约简理论与方法。于洪等^[22]探讨了三支决策的聚类分析模型和聚类数的自动学习算法。周冰^[23]和刘盾^[24]分别讨论了基于贝叶斯决策和Logistic回归的多分类三支决策模型。闵帆等^[19]研究了基于代价敏感的三支决策方法。Li等^[25]在三支决策划分正、负域的基础上构建了两个边界向量，利用粗糙集方法和质心解来处理不确定边界的三支决策模型；Zhang等^[26]提出了一种三向增强卷积神经网络模型，提高了三支决策的分类性能。在应用层面上，张恒汝^[27]和汪敏^[28]等分别探讨了基于随机森林、回归分析和主动学习的三支推荐系统。Zhou等^[29]将三支决策思想用到垃圾邮件过滤上，所有待分类的邮件被分为正确邮件、垃圾邮件和可疑邮件。李华雄等^[30]将序贯三支决策算法应用到人脸识别中，取得了良好的效果。Li等^[31]在文本分类过程中将所有文本分为3种类型，即相关文本、可能相关文本和不相关文本。在产品检验上，Woodward和Naylor^[32]将生产产品划分为合格产品，不合格产品和需要进一步检测的产品三种类型。刘盾等^[33]将三支决策方法应用到石油开采和政策制定问题中，并从管理视角分析了延迟决策策略对决策过程的影响。上述研究从不同学科、不同视角和不同维度极大地促进了三支决策研究的发展。

此外，自2009年以来，国际粗糙集学会(IRSS)在每年的国际粗糙集联合学术会议上都举办了三支决策Workshop；中国粒计算与知识发现学会(CGCKD)也从2011年起组织了“三支决策、粒计算与粗糙集”相关的主题研讨会；国内外学者也相继出版了《三支决策理论与应用》^[34]、《三支决策与粒计算》^[35]、《三支决策：复杂问题求解方法与实践》^[36]、《粒计算、商空间及三支决策的回顾与发展》^[37]等多部专著来介绍三支决策的最新研究进展；国际重要信息科学SCI期刊《Information Sciences》、《International Journal of Approximate Reasoning》和《Knowledge-based Systems》等也分别出版多本专辑来介绍各个团队的最新研究成果。三支决策学习网站(http://www2.cs.uregina.ca/~twd/)和三支决策微信公众号也先后推出，来介绍三支决策的最新研究动态。

本文在充分整理和分析已有研究文献的基础上，介绍三支决策的基本模型和框架，并探讨三支决策与粗糙集理论之间的前世今生。从粒计算“多层次”和“多视角”两个方面来阐述三支决策的粒化思想和建模机理。提出了一个基于三支决策的粒计算研究框架模型。最后，对三支决策知识发现理论、方法和未来研究方向作出展望。

1 三支决策基本模型与框架

在认知科学时代，三支决策朴素的“分治”思想是一种全新的粒计算研究视角和方法，它可以帮助人们通过粒化策略去思考、求解和处理不确定性复杂问题。众所周知，儒家文化是中国传统文化的代表，其精髓在于中庸之道。正如《论语·庸也》中所说：“中庸之为德也，其至矣乎。”它说明：相对于两种极端的处世态度，中庸思想倡导不偏不倚，折中调和，强调中间点。可以看到，中庸之道与三支决策的“三”关系密切，其共同点为把一个问题“一分为三”。进一步地，《论语·先进》中的“过犹不及”和《孟子·尽心章句下》中的“尽信书，则不如无书”都恰当地反映了中庸之道中的三分治略，把做事和读书都理解为3种境界，即“过、及、不及”和“尽信、信、不信”，强调“三”的辩证思想，即“及”和“信”的重要性。此外，秦牧的《艺海拾贝·酷肖》中收录了近代书画大师齐白石说过的一段话：“作画妙在似与不似之间，太似为媚俗,不似为欺世。”它强调了绘画作品不能不逼真，画什么东西不像什么东西，这是对观者的欺骗。但又不能拘泥于物象外在的形象，而应该抓住物象特有的内在本质，发挥艺术想象，或突出或夸张，融入作者的情趣思考，体现出不同其他特象的独有特点。由此可见，三支决策思想突破了传统二值、二元或两极思维的束缚，将传统二支决策中的非黑即白、非对即错、非左即右、非上即下、非好即坏的绝对二类判定扩展到黑/灰/白、对/中/错、左/中/右、上/中/下、好/中/坏的三分法则。综上所述，三支决策的基本模型可由定义1给出。

定义1　假设 $S = (U,R)$ 为一信息系统，其中： $U = {\rm{\{ }}{x_1},{x_2}, \cdots ,{x_n}\} $ 表示论域，它是对象的非空有限集合； $R$ 是定义在论域 $U$ 上的一种二元关系。三支决策通过函数 $f$ 将论域 $U$ 划分为3个两两互不相交的区域： ${R_1}$ -域、 ${R_{\rm{2}}}$ -域和 ${R_{\rm{3}}}$ -域，即：

$f\;:\;U \to \{ {R_1},{R_2},{R_3}\} $

(1)

其中， ${R_1},{R_2},{R_3} \subseteq U$ ， $U = {R_1} \cup {R_2} \cup {R_3}$ ； ${R_1} \cap {R_2}=\text{Ø} $ ， ${R_{\rm{2}}} \cap $ $ {R_{\rm{3}}}=\text{Ø} $ ， ${R_1} \cap {R_{\rm{3}}}=\text{Ø} $ 。对于 ${R_i} \in U$ ，其补集的构造如下：

$ \begin{array}{l} R_1^c = {R_2} \cup {R_3}\\ R_{\rm{2}}^c = {R_{\rm{1}}} \cup {R_3}\\ R_{\rm{3}}^c = {R_{\rm{1}}} \cup {R_{\rm{2}}} \end{array} $

(2)

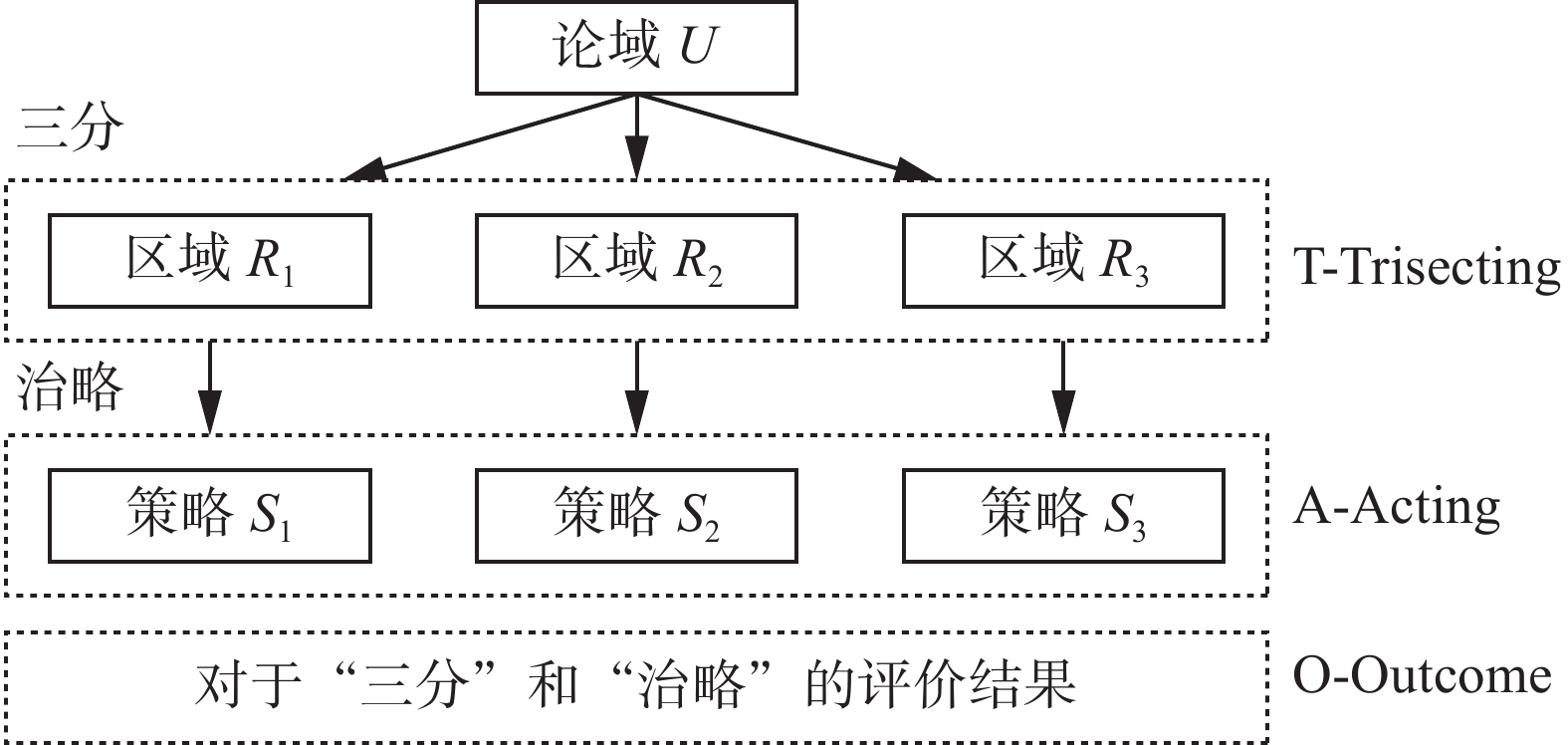
进一步地，Yao.Y.Y.深入探讨了三支决策与粒计算的相互关系并提出了一种新的三支决策的“分治效”(Ttrisecting-Acting-Outcome，TAO)^[2]模型，并进一步阐释了三支粒计算思想的作用和意义。图1为该模型的基本框架。

在图1中，第一阶段中的“三分”是指把一个整体 $U$ 划分成3个互不相交的区域，简记为 ${R_1}$ 、 ${R_{\rm{2}}}$ 和 ${R_{\rm{3}}}$ ；第二阶段中的“治略”是指在“三分”的基础上对不同的区域制定出相应的策略或采取相应的行动 ${S_1}$ 、 ${S_{\rm{2}}}$ 和 ${S_{\rm{3}}}$ ，使得整体目标收益/效用最大化或者成本/代价最小化；第三阶段“评价结果”是评估“三分”和“治略”的效果，以便定量评价和改进三支决策。上述3个阶段相互影响、相互制约：“三分”是“治略”的前提，“治略”是“三分”的目的，而“评价结果”是“三分”和“治略”的监督保障。如何构造一个整体的三分，如何设计策略去处理三分后的三个区域，如何评价三分和策略的效果，是三支TAO模型的核心任务。下面，我们引入几种不同的定量评价函数来刻画三支决策“三分”的数学表达。

定义2　假设U是一个有限非空的论域， $(L,\;\preceq )$ 是一个全序集合，其中偏序关系满足自反性、反对称性和传递性。给出一个评价函数 $v:U \to L$ ，对于 $\forall x \in U$ ， $v(x)$ 代表对象x的评价值。设置一对阈值 $\alpha $ 和 $\beta $ ( $\beta < \alpha $ )，可以将论域U划分为3个决策区域R₁、R₂和R₃：

$\begin{gathered} {R_1}(v(x)) = \{ x \in U|\,\,v(x)\,\geqslant \,\alpha \} \\ {R_2}(v(x)) = \{ x \in U|\beta < v(x) < \alpha \} \\ {R_3}(v(x)) = \{ x \in U|v(x)\,\,\leqslant \,\,\beta \} \end{gathered} $

(3)

我们用一个简单的例子来说明定义1。2018年四川省高考理科一本分数线是546分，二本分数线是458分。对于某一考生，高考成绩大于或等于546分可以报考一本大学；小于458分只能选择二本以下的专科或职业学院学习；考试分数在区间[458，546)进入二本高校学习。进一步地，下面定义3和定义4给出了三支多准则决策和三支多目标决策的基本数学模型。

定义3　假设U是一个有限非空的论域， $\left( {L,}\preceq \right)$ 是一个全序集合， $C = \{ {c_1},{c_2}, \cdots ,{c_m}\} $ 是m个决策准则构成的集合， ${v_{{c_i}}}:U \to L$ 定义了在准则 ${c_i}$ 下的评价函数值， $1 \leqslant i \leqslant m$ 。则对于 $\forall x \in U$ ，其总体评价结果可由一个线性加权组合来定义：

$\bar v(x) = {w_1}{v_{{c_1}}}(x) + {w_2}{v_{{c_2}}}(x) + \cdots + {w_n}{v_{{c_m}}}(x)$

(4)

其中 ${w_i}$ 为准则 ${c_i}$ 的权重，它满足 $\displaystyle\sum\limits_{i = 1}^m {{w_i}} = 1$ 。给定两个阈值 $M$ 和 $N$ ( $M > N$ )，其三支多准则决策结果可表示为

$\begin{gathered} {R_1}(\bar v(x)) = \{ x \in U|\,\,\bar v(x)\, \geqslant M\} \\ {R_2}(\bar v(x)) = \{ x \in U|N < \bar v(x) < M\} \\ {R_3}(\bar v(x)) = \{ x \in U|\bar v(x)\,\, \leqslant N\} \end{gathered} $

(5)

相对于定义2而言，定义3进一步考虑了各个准则的权重，这更符合实际决策问题中的需求。

定义4　假设U是一个有限非空的论域，U = ${R_1} \cup {R_2} \cup {R_3}$ ； ${\Re _1}(\alpha ,\beta )$ ， ${\Re _{\rm{2}}}(\alpha ,\beta )$ 和 ${\Re _{\rm{3}}}(\alpha ,\beta )$ 代表3个决策区域R₁、R₂和R₃所产生的决策风险，则总体决策风险可表示为

$\Re (\alpha ,\beta ) = a{\Re _1}(\alpha ,\beta ) + b{\Re _2}(\alpha ,\beta ) + c{\Re _3}(\alpha ,\beta )$

(6)

其中，a、b和c为 ${\Re _1}(\alpha ,\beta )$ 、 ${\Re _{\rm{2}}}(\alpha ,\beta )$ 和 ${\Re _{\rm{3}}}(\alpha ,\beta )$ 相对应的风险系数，三支多目标决策的任务是如何选取合适的 $\alpha $ 和 $\;\beta $ 值，使得下列式子中的总体决策风险最小：

$\arg \mathop {\min }\limits_{(\alpha ,\beta )} \Re (\alpha ,\beta )$

(7)

值得一提的是，不同于定义2和定义3，式(7)中 $\alpha $ 和 $\;\beta $ 的取值不是由决策者事先给定的，而是在实际决策问题中，通过目标函数和约束条件构建相应的优化数学模型求解得到。

2 三支决策、粗糙集与决策粗糙集

三支决策思想最早来源于粗糙集理论。众所周知，Pawlak粗糙集对信息系统不确定性的描述是通过上下近似集来实现的。两个近似集对论域的划分形成3个两两互不相交的决策区域：正域、负域和边界域，这自然形成了对三支决策的一种数学描述和解释。

定义5　假设论域 $U$ 是一个有限非空子集，记 ${\rm apr} = (U,R)$ 为粗糙近似空间。 $U$ 通过等价关系 $R$ 划分成互不相交的子集，形成论域 $U$ 上的一个划分 $U{\rm{/}}R = \{ [x]|x \in U\} $ 。对于 $X \subseteq U$ ，其上下近似可表示为

$\left\{\begin{gathered} \underline {\rm apr} (X) = \left\{ {x \in U|[x] \subseteq X} \right\}; \\ \overline {\rm apr} (X) = \left\{ {x \in U|[x] \cap X \ne \text{Ø} } \right\} = \\ \left\{ {x \in U|\neg ([x] \subseteq {X^c})} \right\} \\ \end{gathered} \right.$

(8)

上下近似将论域分为正域 ${\rm POS}(X)$ 、负域 ${\rm NEG}(X)$ 和边界域 ${\rm BND}(X)$ ，其定义分别为

$\left\{\begin{gathered} \rm{POS}(X) = \underline {\rm apr} (X) = \{ x \in U|[x] \subseteq X\} ; \\ { \rm BND}(X) = \overline {\rm apr} (X) - \underline {\rm apr} (X) \\ \{ x \in U|\neg ([x] \subseteq X\} \wedge \neg ([x] \subseteq {X^c})\} ; =\\ {\rm NEG}(X) = U - \overline {\rm apr} (X) = \\ \{ x \in U|[x] \subseteq {X^c}\} \\ \end{gathered} \right. $

(9)

由正域导出的正规则表示接受对象x属于X；由负域导出的负规则表示拒绝接受对象x属于X；而由边界域导出的不确定规则表示x可能属于X。可以看到，上述“三分而治”的思想赋予了粗糙集理论一种基于决策视角的语义解释。

进一步地，我们考虑概率粗糙集的情形，它通过引入两个阈值 $\alpha $ 和 $\;\beta $ 对Pawlak粗糙集上下近似集的定义进行扩展，使得获取的决策规则更为灵活。

定义6　假设论域U是一个有限非空子集，R是定义在U上的一种等价关系。记 ${\rm apr}{_{(\alpha ,\beta )}} = (U,R)$ 为概率粗糙近似空间，对于 $X \subseteq U$ ，令 $0 \leqslant \beta < \alpha \leqslant 1$ ，则概率粗糙集的 $(\alpha ,\beta )$ -上下近似集可定义为

$ \begin{array}{l} {\underline {\rm apr} _{(\alpha ,\;\beta )}}(X) = \{ x \in U|{\rm Pr}(X|[x]) \geqslant \alpha \}\\ {\overline {\rm apr} _{(\alpha ,\;\beta )}}(X) = \{ x \in U|{\rm Pr}(X|[x]) > \beta \} \end{array} $

(10)

其中， $Pr(X|[x]) = \;|[x] \cap X|/|[x]|$ 表示分类的条件概率， $ \left| \cdot \right| $ 表示集合中元素的基数。同样地，在概率粗糙集中， $(\alpha ,\beta )$ -上下近似集将论域分为3个部分： ${\rm POS}{_{(\alpha ,\;\beta )}}(X)$ ， ${\rm BND}{_{(\alpha ,\;\beta )}}(X)$ 和 ${\rm NEG}{_{(\alpha ,\;\beta )}}(X)$ ，其定义分别为

$ \begin{gathered} {\rm POS}{_{(\alpha ,\;\beta )}}(X) = \{ x \in U|{\rm Pr}(X|[x]) \geqslant \alpha \}\\ {\rm BND}{_{(\alpha ,\;\beta )}}(X) = \{ x \in U|\beta < {\rm Pr}(X|[x]) < \alpha \}\\ {\rm NEG}{_{(\alpha ,\;\beta )}}(X) = \{ x \in U|{\rm Pr}(X|[x]) \leqslant \beta \} \end{gathered} $

(11)

相对于式(9)，式(11)进一步考虑了决策规则的容错性，这更符合人类的决策认知。然而，在定义6中的阈值 $\alpha $ 和 $\;\beta $ 都是人为事先给定的，这在实际决策过程中往往过于主观和难以获取。为了回答和改进上述难题，决策粗糙集将贝叶斯理论引入到概率粗糙集中，利用损失函数来构造决策总体风险最小时的三支决策划分策略，极大地推进了粗糙集理论的发展。

决策粗糙集通过2个状态集 $\varOmega = \{ X,\neg X\} $ 和3个行动集 ${ A} = \{ {a_P},{a_B},{a_N}\} $ 来描述三支决策过程。其中，状态集 $\varOmega = \{ X,\neg X\} $ 表示事件的两种状态(属于概念X和不属于概念X)，行动集 ${ A} = \{ {a_P},{a_B},{a_N}\} $ 表示对于不同状态，采取相对应的接受、延迟和拒绝3种行动策略。考虑到采取不同行动会产生不同的损失，记 ${{\textit{λ}} _{PP}}$ 、 ${{\textit{λ}} _{BP}}$ 、 ${{\textit{λ}} _{NP}}$ 分别表示当 $x \in X$ 时，采取行动 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 下的损失；同样地，记 ${{\textit{λ}} _{PN}}$ 、 ${{\textit{λ}} _{BN}}$ 、 ${{\textit{λ}} _{NN}}$ 分别表示当 $x \notin X$ 时，采取行动 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 下的损失。因此，采取 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 3种行动下的期望损失可分别表示为

$\begin{gathered} R({a_P}|[x]) = {{\text{λ}} _{PP}}{\rm{Pr}}(X|[x]) + {{\text{λ}} _{PN}}{\rm{Pr}}(\neg X|[x]) \\ R({a_B}|[x]) = {{\text{λ}} _{BP}}{\rm{Pr}}(X|[x]) + {{\text{λ}} _{BN}}{\rm{Pr}}(\neg X|[x]) \\ R({a_N}|[x]) = {{\text{λ}} _{NP}}{\rm{Pr}}(X|[x]) + {{\text{λ}} _{NN}}{\rm{Pr}}(\neg X|[x]) \end{gathered} $

(12)

根据贝叶斯决策准则，选择期望损失最小的行动集作为最佳行动方案，可以得到如下三条决策规则：

(P) $R({a_P}|[x]) \leqslant R({a_B}|[x])$ 且 $R({a_P}|[x]) \leqslant R({a_N}|[x])$ 同时成立，则 $x \in {\rm POS}(X)$ ；

(B) $R({a_B}|[x]) \leqslant R({a_P}|[x])$ 且 $R({a_B}|[x]) \leqslant R({a_N}|[x])$ 同时成立，则 $x \in {\rm BND}(X)$ ；

(N) $R({a_N}|[x]) \leqslant R({a_P}|[x])$ 且 $R({a_N}|[x]) \leqslant R({a_B}|[x])$ 同时成立，则 $x \in {\rm NEG}(X)$ 。

由于 ${\rm{Pr}}(X|[x]) + {\rm{Pr}}(\neg X|[x]) = 1$ ，上述规则(P)、(B)、(N)只与分类条件概率 ${\rm{Pr}}(X|[x])$ 和损失函数 ${{\textit{λ}} _{ \bullet \bullet }} $ $( \bullet = P,B,N)$ 有关。此外，考虑到接受正确事物的损失不大于延迟接受正确事物的损失，且这两者都小于拒绝正确事物的损失；类似的，拒绝错误事物的损失不大于延迟拒绝错误事物的损失，且这两者都小于接受错误事物的损失。因此，损失函数之间的大小关系满足： $0 \leqslant {{\textit{λ}} _{PP}} \leqslant {{\textit{λ}} _{BP}} < {{\textit{λ}} _{NP}}$ 和 $0 \leqslant {{\textit{λ}} _{NN}} \leqslant {{\textit{λ}} _{BN}} < {{\textit{λ}} _{PN}}$ 。将条件概率关系和损失函数关系代入到式(11)中，决策规则(P)、(B)、(N)可改写为

(P1)：如果 ${\rm{Pr}}(X|[x]) \geqslant \alpha $ ，则： $x \in {\rm{POS}}(X)$ ；

(B1)：如果 $\beta < {\rm{Pr}}(X|[x]) < \alpha $ ，则： $x \in {\rm{BND}}(X)$ ；

(N1)：如果 ${\rm{Pr}}(X|[x]) \leqslant \beta $ ，则： $x \in {\rm{NEG}}(X)$ 。

其中：

$ \begin{gathered} \alpha \, = \,\dfrac{{({{\textit{λ}} _{PN}} - {{\textit{λ}} _{BN}})}}{{({{\textit{λ}} _{PN}} - {{\textit{λ}} _{BN}}) + ({{\textit{λ}} _{BP}} - {{\textit{λ}} _{PP}})}}\,\\ \beta \, = \,\dfrac{{({{\textit{λ}} _{BN}} - {{\textit{λ}} _{NN}})}}{{({{\textit{λ}} _{BN}} - {{\textit{λ}} _{NN}}) + ({{\textit{λ}} _{NP}} - {{\textit{λ}} _{PP}})}}\,\\ \gamma = \,\dfrac{{({{\textit{λ}} _{PN}} - {{\textit{λ}} _{NN}})}}{{({{\textit{λ}} _{PN}} - {{\textit{λ}} _{NN}}) + ({{\textit{λ}} _{NP}} - {{\textit{λ}} _{PP}})}}\, \end{gathered} $

(13)

可以看到， $\alpha $ 和 $\beta $ 的取值与损失函数 ${{\textit{λ}} _{ \bullet \bullet }}$ 有关，而三支决策的最终结果由条件概率和损失函数两者共同决定的。决策粗糙集从贝叶斯最小风险的角度对三支决策做出科学解释，并首次给出一种三支决策的精确数学定义。

综上所述，三支决策是粗糙集理论的扩展和外延，粗糙集理论是三支决策的特例和内涵。三支决策理论的提出是来源于粗糙集理论，但高于粗糙集理论；而决策粗糙集是三支决策在实际决策语义下的一个特殊数学模型。图2清晰地描绘了三支决策、粗糙集理论、概率粗糙集和决策粗糙集四者之间的蕴含关系，即决策粗糙集 $ \subseteq $ 概率粗糙集 $ \subseteq $ 粗糙集理论 $ \subseteq $ 三支决策。

3 三支决策的粒计算方法

三支决策的粒计算方法是利用“三分治略”思想来解决粒计算问题的。它通过在现实问题中对粒的抽象、在数学分析中对粒的描述、在模型构建中对粒间和粒层转换关系的刻画、在算法设计中对粒的合成与分解、在求解过程中对粒的使用，并将三支决策的“分治效”思想作为评估手段来分析和处理实际决策问题的。对于粒计算核心思想的诠释，近代著名诗人卞之琳在其现代诗《断章》有很好的解读：

你站在桥上看风景，

看风景的人在楼上看你。

明月装饰了你的窗子，

你装饰了别人的梦。

诗人通过对“风景”的刹那间感悟，把对粒计算中粒子、粒层与粒结构之间的“相对性”认知过程表现得淋漓尽致。此外，Yao. Y.Y.教授认为粒计算是一种粒化的思维方式及方法论，将粒计算和三支决策思想应用于不同学科中，能够对知识进行有效的整理、抽象和整合，并获取更高一层的、系统的粒计算原理^[2]。此外，他进一步总结了现有粒计算研究的3个主要观点，并提出了粒计算的三元论：一是基于结构化思维的哲学思想，二是基于结构化问题求解的方法论，三是基于结构化信息处理的计算模式。三支决策的粒计算方法就是将这3种观点紧密结合，并通过粒化原则、合成原则、分层原则等来构造粒结构，从而获得对问题在不同粒度下的理解。下面，主要从“多层次”和“多视角”两个维度来讨论三支决策的粒计算方法。

首先，考虑基于多层次粒计算下的三支决策方法。多层次三支决策的核心问题是如何选择合适的粒层和粒度。在粒计算中，粗层次的粒将与本层次不相关的细节忽略掉，为细层次的粒提供一种概要的描述；细层次的粒为粗层次的粒提供更详细的信息，但相较于粗层次会付出更多的成本和代价。图3给出了一个例子来说明上述思想。假设某位同学高考考入了西南交通大学学习，由于第一次来成都，不知道学校的准确地址。因此，该生借助百度地图来查找学校的具体方位。图3(a)是百度地图的粗粒度层次，在该地图里不能发现学校的位置；图3(b)是百度地图的中粒度层次，通过该地图可以初步发现学校位于成都市的北边，位于金牛区等粗略信息；图3(c)是百度地图的细粒度层次，根据该地图可以发现更为详细的信息，比如：交大位于二环路上，在金牛区政府和金牛区国土局附近。特别地，如果该生要到学校的某栋建筑报道注册，则在百度地图里无法搜寻目标，这需要在图3(d)中的交大的校区平面地图里去寻找。

通过图3(a)~(c)可以看到，对于不同的粒层对应了不同的解空间，每个解空间又决定了其对应解的精确程度。粒层越粗，花费的代价越小，得到的解越粗糙；反之，粒层越细，花费的代价越大，得到的解越精细。对于图3(d)可以得到，如果在低维空间里无法找到可行解，可以考虑通过数学映射变换到高维空间去处理问题。综上所述，选取一个合适粒层和满意解是多层次粒计算的关键任务。进一步地，结合三支决策思想，在不同的粒层都选取3种策略：接受和拒绝的对象在该粒层终止，延迟决策的对象进入下一粒层，通过“序贯三分而治”的策略来降低决策成本和学习代价，最终满足给定的终止条件(如：总体代价最小、边界域样本数最少等目标函数)作为最优粒层选择的依据。此外，国内外学者也给出了多层次三支决策的解决方案，具有代表性的研究方法有多粒度决策、多尺度决策和商空间方法等，上述相关研究从理论和方法上极大地丰富了多层次粒计算与三支决策的内涵和外延。

其次，考虑基于多视角粒计算下的三支决策方法。对于多视角下的粒计算经典案例来源于盲人摸象的故事。四位盲人张三、李四、王五和朱六同时摸一头大象，张三摸到了大象的鼻子，他认为大象像条弯弯的管子；李四摸到了大象的背部，他认为大象像一堵墙；王五摸到了大象的尾巴，他认为大象像一根粗粗的柱子；朱六摸到了大象的耳朵，他认为大象像一把大蒲扇。从局部来说，四位盲人都抓住了大象的部分特征；但从全局来说，四位盲人都是以偏概全、以部分代替整体。而造成上述结果的原因正是由于不同的人站在不同的角度上去思考和求解相同问题。

对同一事物的多视角还体现在中国的古现代诗词上。以庐山为例，诗仙李白笔下的《望庐山瀑布》是一首千古名篇的七言绝句：

日照香炉生紫烟，遥看瀑布挂前川。

飞流直下三千尺，疑是银河落九天。

全诗豪迈奔放、气势恢宏；夸张而又自然、新奇而又真切，突显出诗人万里一泻，未势犹壮的艺术风格。宋代大文豪，唐宋八大家之一苏轼在《题西林壁》一诗中写道：

横看成岭侧成峰，远近高低各不同。

不识庐山真面目，只缘身在此山中。

苏轼笔下的庐山有景有画，又富有哲理，揭示出从不同的方位看庐山，会有不同的印象，只有远离庐山，跳出庐山的遮蔽，才能全面把握庐山的真正仪态，这与粒计算的粒化思想不谋而合。此外，毛泽东对于庐山的描绘体现在《七律·登庐山》上：

一山飞峙大江边，跃上葱茏四百旋。

冷眼向洋看世界，热风吹雨洒江天。

云横九派浮黄鹤，浪下三吴起白烟。

陶令不知何处去，桃花源里可耕田？

诗中以庐山的雄伟突兀，长江的恢宏壮阔，透过诗人丰富的情思、雄健的笔力，显得气势磅礴，意气昂扬。

总而言之，以上三首诗词从不同角度对庐山进行了写实和写意，这赋予了粒计算一种新的语义感悟。下面，我们再用一个简单的数学例子来阐述多视角粒计算的重要性和有用性。

假设现在需要利用5、5、5、5、5这5个数字通过四则运算计算24，有哪些解题思路？

方案一　从宏观视角来看，可以从构造大的自然数方向去思考，因此有： $({\rm{5}} \times {\rm{5}} \times {\rm{5}} {\rm{ - }} {\rm{5}}) \div {\rm{5}} \,=\,{\rm{24}}$ 。

方案二　从微观视角来看，可以从构造分数和小数方向去思考，因此有： $({\rm{5}}\,{\rm{ - }}\,{\rm{5}} \div {\rm{5}} \div {\rm{5}}) \times {\rm{5}}\,=\,{\rm{24}}$ 。

方案一和方案二在数学上互为互补。此外，如果跳出四则运算的范畴，借鉴 $ 5 \times 5 - 1 = 24 $ 的一般思路去解决问题，则可以从中观视角得到问题的第3种求解方案：

$({\rm{5}} \times \sqrt {\rm{5}} \times \sqrt {\rm{5}} )\,{\rm{ - }}\,(\sqrt {\rm{5}} \div \sqrt {\rm{5}} \,)\,=\,\,{\rm{24}}$

根据上述例子，基于宏观、中观和微观3种不同视角下的思维方式也赋予了解决粒计算问题时一种新的思路。在实际决策过程中，可以通过不同视角将问题根据自身特性分解成若干子问题，在每个子问题中借鉴三支决策思想得到属于正域的有效解，最后通过对子问题有效解的集成来获取整个问题的解。正如张钹院士所说的那样：人类公认的一个特点，就是能从不同的粒度上观察和分析同一问题。人们不仅能在不同粒度的世界上进行问题求解，而且能够很快地从一个粒度世界跳到另一个粒度世界，往返自如，毫无困难。

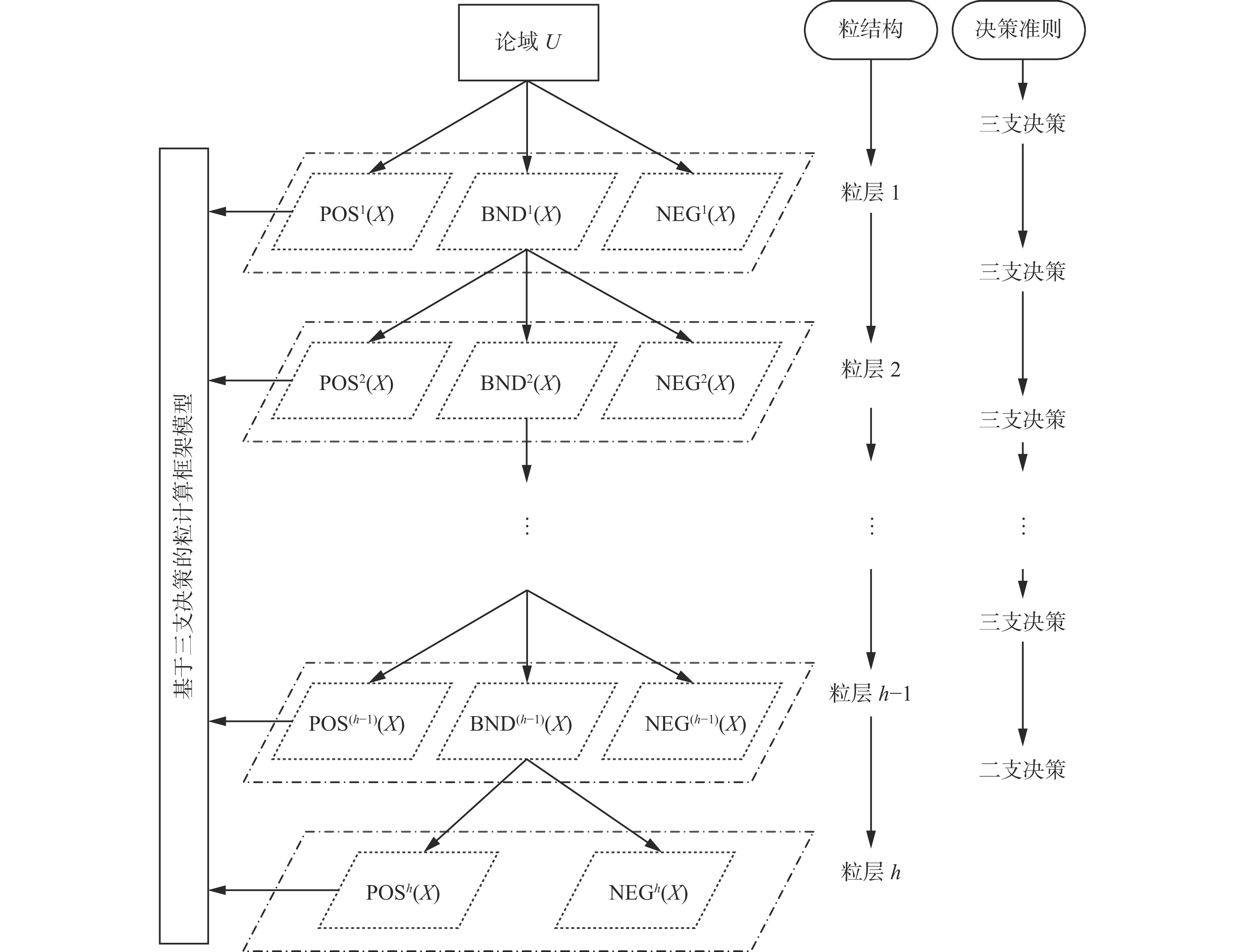
4 三支决策的粒计算框架模型

在很多实际决策问题中，粒计算的多层次和多视角两种属性往往是相生相伴、相互依存的。在划分多层次决策空间的过程中会采纳多视角的思想；通过多视角策略处理决策问题的过程中会自然形成多层次的粒结构。进一步地，将三支决策理论引入到粒计算中可以降低决策成本和学习代价。为了清晰地阐述三支决策的粒化思想，图4给出了一个基于三支决策的粒计算框架模型。

在图4中，U有限非空的论域，对 $X \subseteq U$ ，令 $0 \leqslant {\beta _{\rm{1}}} \leqslant \cdots \leqslant {\beta _{h{\rm{ - 1}}}} < {\gamma _h} < {\alpha _{h{\rm{ - 1}}}} \leqslant \cdots \leqslant {\alpha _1} \leqslant 1$ ，此时，随着粒层增加，正域和负域的规模单调递增、边界域的规模单调递减。令： ${\rm{POS}}{^k}(X)$ ， ${\rm{BND}}{^k}(X)$ 和 ${\rm{NEG}}{^k}(X)$ 分别表示第 $k$ 层( $k \in [1,\,\,h]$ )所对应的正域、边界域和负域。当 $k \in [1,\,\,h{\rm{ - 1}}]$ 时，我们有：

$ \begin{gathered} {\rm{BND}}{^k}(X)\,=\,\,{\rm{POS}}{^{k{\rm{ + 1}}}}(X) \cup {\rm{BND}}{^{k{\rm{ + 1}}}}(X) \cup {\rm{NEG}}{^{k{\rm{ + 1}}}}(X)\\ {\rm{POS}}{^k}(X) \subseteq {\rm{POS}}{^{k{\rm{ + 1}}}}(X)\\ |{\rm{POS}}{^k}(X)|\,\, \leqslant \,\,|{\rm{POS}}{^{k{\rm{ + 1}}}}(X)|\\ {\rm{NEG}}{^k}(X) \subseteq {\rm{NEG}}{^{k{\rm{ + 1}}}}(X)\\ |{\rm{NEG}}{^k}(X)|\; \leqslant \;|{\rm{NEG}}{^{k{\rm{ + 1}}}}(X)|\\ {\rm{BND}}{^{k{\rm{ + 1}}}}(X) \subseteq {\rm{BND}}{^k}(X)\\ |{\rm{BND}}{^{k{\rm{ + 1}}}}(X)|\; \leqslant \;|{\rm{BND}}{^k}(X)| \end{gathered} $

(13)

一方面，给定粒层 $k$ ，在前第 $k$ 层被划分到正域和负域的样本 $(\bigcup\limits_{i = 1}^{k{\rm{ - 1}}} {{\rm{POS}}{^i}(X)} ) \cup (\bigcup\limits_{i = 1}^{k{\rm{ - 1}}} {{\rm{NEG}}{^i}(X)} )$ 在第 $k$ 层不再考虑，这大大地降低了决策成本。另一方面，随着粒层 $k$ 的增大，边界域中的样本会越来越少，如果在某粒层 ${k^*}$ 达到决策目标，则可得到最优粒层的终止层数；如果在最细的粒层 $h$ 还未终止，则在第 $h$ 层采取二支决策策略，即将第 $h - 1$ 层中落在边界域中的样本 ${\rm{BND}}{^{h - 1}}(X)$ 在第 $h$ 层强行分到正域 ${\rm{POS}}{^h}(X)$ 和负域 ${\rm{NEG}}{^h}(X)$ 中。总而言之，上述基于粒计算的序贯三支决策策略也在一定程度上减少了系统的学习代价。

对于三支决策粒框架模型的实例验证和仿真分析，国内外学者从不同领域进行了富有成效的研究。李华雄等^[30]从人脸识别的视角构建了一种序贯三支图像识别方法，从代价敏感视角给出了图像粒层的构建过程，并利用总代价最小原则给出了最优粒度的选取准则。张恒汝等^[27]探讨了基于推荐系统的三支决策方法，利用回归分析的预测结果来构造推荐粒层，并以误分类代价和学习代价最小为目标来制定相应的推荐策略。叶晓庆等^[38]提出了一种基于协同过滤的三支粒推荐算法，根据项目特征粒化用户项目评分矩阵，形成用户对项目粒度的评分矩阵，并以此作为用户偏好的计算依据。进一步地，该研究考虑了推荐过程中产生的误分类成本和学习成本，通过引入三支决策来构建基于用户真实的评分偏好来构建三支推荐模型。上述文献从不同应用背景来论述三支决策的粒计算思想是如何应用到实际问题中去的，这也一定程度上验证了本文所提出框架模型的有效性。

5 结束语

本文系统地回顾、整理、分析和总结了近四十年来三支决策的发展踪迹，从孵化、羽化、成长三个时期详细介绍了三支决策的演化过程。首先，分析了三支决策与粗糙集理论的历史脉络、内在联系和相互关系；其次，从粒计算多层次和多视角两个维度来探讨三支决策的粒计算理论和方法，并利用丰富的例子来诠释基于多层次和多视角下的三支决策思想和原理；最后，通过构造序贯三支决策过程，给出一个三支决策的粒计算框架模型。虽然三支决策近年来在理论、方法、算法和应用上取得了不少研究进展，但其一般化理论还未完整构建，很多问题还有待深入研究。值得一提的是，近年来国内外学者已开始从不同学科来研究三支决策与粒计算问题，其中基础数学领域关注于三支决策的粒度描述和粒度表示；信息科学领域聚集于三支决策的粒度选择、粒度计算和粒度优化；管理决策领域集中于三支决策的粒度解释和粒度应用。如何从多学科视角去思考、从跨专业领域去融合、从理论到方法去协同，从模型到算法去应用，是今后三支决策与粒计算未来研究的重要方向。