2. 矿山数字化教育部工程研究中心,江苏 徐州 221116
2. Mine Digitization Engineering Research Center of Minstry of Education of the People's Republic of China, Xuzhou 221116, China
支持向量机(support vector machine, SVM) [1]是一种基于统计学习理论的VC维和结构风险最小化原理的机器学习方法,由Cortes和Vapik[2]于1995年提出。其在解决小样本、非线性和高维模式识别问题中有许多优势,目前已被应用到很多领域,例如文本分类、时间序列分析、模式识别和图像处理等[3-7]。为了提高支持向量机的性能,学者们提出了许多改进算法。例如最小二乘支持向量机[8]、近似支持向量机[9]和基于广义特征值的近似支持向量机[10]等。2007年,基于广义特征值近似支持向量机的思想,Jayadeva等[11]提出了孪生支持向量机。和SVM不同,TWSVM是生成两个非平行的分类超平面,使得其中一个超平面尽量接近一类样本,并且尽可能的远离另一类样本。TWSVM[12-13]将单个大型二次规划问题转化为两个较小的二次规划问题,明显缩短了运行时间。虽然孪生支持向量机的发展时间较短,但由于其坚实的理论基础和出色的性能表现,已经成为机器学习领域的一个研究热点。许多学者对TWSVM的研究做出了贡献,并取得了很多成果。例如光滑孪生支持向量机[14]、最小二乘孪生支持向量机[15-17]、模糊孪生支持向量机[18]和投影孪生支持向量机[19-20]等。
尽管近年来对TWSVM的研究在算法改进及其应用方面取得了很大的进展,但是仍有不足之处,其中之一就是TWSVM无法很好地处理参数选择问题。参数对分类结果有很大的影响,一个好的参数将直接提升TWSVM的性能。网格搜索[21]是最普遍的参数选择方法,但是这种方法很耗时。Ding等[22-23]采用粒子群算法和量子粒子群算法对TWSVM的参数进行优化。Zhai等[24]将粒子群算法与局部搜索算法结合,提出了一种混合粒子群算法来优化小波孪生支持向量机的参数。随后,Sartakhti等[25]将最小二乘孪生支持向量机与模拟退火算法结合来提高分类准确率。
人工鱼群算法(artificial fish swarm algorithm, AFSA)[26]是一种基于动物行为的群体智能优化算法。该算法具有收敛速度快、灵活性强、容错性强、准确率高等优点。本文将人工鱼群算法与孪生支持向量机进行结合,以分类准确率作为适应度值,来对惩罚参数和核参数进行优化,提高算法的有效性。
1 相关理论 1.1 孪生支持向量机假设在n维实空间Rn中有m个训练样本,其中属于+1类的有m1个,属于−1类的有m2个。令
| $K({{{x}}^{\rm{T}}},{{{C}}^{\rm{T}}}){{w}}{}_1 + {b_1} = 0,{\rm{ }}K({{{x}}^{\rm{T}}},{{{C}}^{\rm{T}}}){{w}}{}_2 + {b_2}{\rm{ = 0}}$ | (1) |
其中K为核函数, C=[A;B]代表所有的训练样本,
通过求解下面两个二次规划问题可以得到这两个超平面:
| $\begin{gathered} \mathop {\min }\limits_{{{w}_1},{{b}_1},{{\xi }_1}} \frac{1}{2}{\left\| {K({A},{{C}^{\rm{T}}}){{w}_1} + {{e}_1}{b_1}} \right\|^2} + {c_1}{e}_2^{\rm{T}}{{\xi }_2} \\ {\rm{s}}{\rm{.t}}{\rm{.\;- (}}K({B},{{C}^{\rm{T}}}){{w}_1} + {{e}_2}{b_1}) \geqslant {{e}_2} - {{\xi }_2},{{\xi }_2} \geqslant 0 \\ \end{gathered} $ | (2) |
| $\begin{gathered} \mathop {\min }\limits_{{{w}_2},{{b}_2},{{\xi }_2}} \frac{1}{2}{\left\| {K({B},{{C}^{\rm{T}}}){{w}_2} + {{e}_2}{b_2}} \right\|^2} + {c_2}{e}_1^{\rm{T}}{{\xi }_1} \\ {\rm{s}}{\rm{.t}}{\rm{. \;(}}K({A},{{C}^{\rm{T}}}){{w}_2} + {{e}_1}{b_2}) \geqslant {{e}_1} - {{\xi }_1},{{\xi }_1} \geqslant 0 \\ \end{gathered} $ | (3) |
其中c1和c2是惩罚参数,e1和e2是两个全1列向量,
测试样本离哪个超平面近,就属于哪一类别,若
| $K({{x}^{\rm{T}}},{{C}^{\rm{T}}}){w}{}_r + {b_r} = \mathop {\min }\limits_{i = 1,2} \left| {K({{x}^{\rm{T}}},{{C}^{\rm{T}}}){w}{}_i + {b_i}} \right|$ | (4) |
则x属于第r类,其中
人工鱼群算法是一种基于群体智能的优化算法,其灵感来自于鱼群行为。在AFSA中,每条人工鱼(artificial fish, AF)根据其当前状态和周围环境状态调整其行为。在每次迭代过程中,人工鱼通过觅食、聚群、追尾和随机这4种行为来更新自己。
假设
| ${{{X}}_j} = {{{X}}_i} + {\rm{Visual}} \cdot {\rm{Rand}}()$ | (5) |
| ${{X}}_i^{t + 1} = {{X}}_i^t + \frac{{{{{X}}_j} - {{X}}_i^t}}{{\left\| {{{{X}}_j} - {{X}}_i^t} \right.\left\| {} \right.}}{\rm{Step}} \cdot {\rm{Rand}}()$ | (6) |
人工鱼的4种行为描述如下:
1)觅食行为:AFi用式(5)在其视野范围内随机选择一个状态
2)聚群行为:假设
3)追尾行为:假设
4)随机行为:AFi在其视野范围内随机选择一个位置,然后向该方向移动一步,它是觅食行为的一个缺省行为。
以上4种行为在不同条件下会相互转换,人工鱼会选择合适的行为以找到更优解的位置。
2 AFSA-TWSVM算法AFSA-TWSVM的核心思想是通过AFSA找到TWSVM的最优参数。人工鱼AFi的位置
AFSA-TWSVM的算法步骤如下:
1) 初始化设置,包括人工鱼群规模
2) 以人工鱼的位置为参数计算孪生支持向量机的分类准确率,将分类准确率作为目标函数进行寻优。得到每个人工鱼的适应度值,并记录全局最优的人工鱼的位置。
3) 每个人工鱼都执行聚群行为和追尾行为,并判断个体是否得到改善。如果得到改善,则选择一个更优行为执行,否则执行觅食行为。
4) 执行人工鱼选择的行为,更新每条人工鱼的位置。
5) 更新全局最优人工鱼的状态。
6) 判断是否达到最大迭代次数,如果是则输出最优解和对应的参数组合,否则迭代次数加1,并跳转到2) 。
AFSA-TWSVM的流程图如图1所示,通过这个流程图可以直观地看出本文所提出算法的过程。
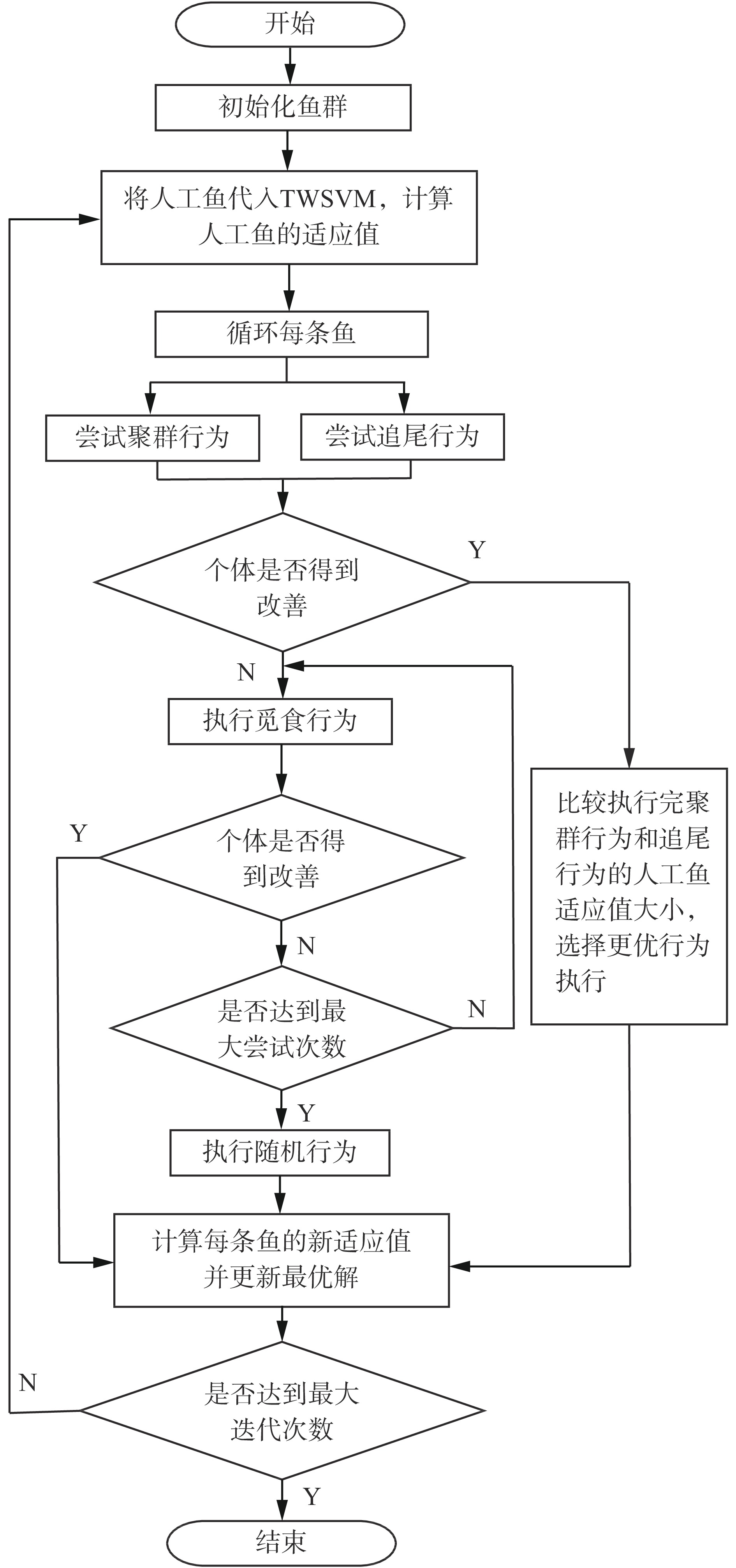
|
Download:
|
| 图 1 AFSA-TWSVM流程图 Fig. 1 The flowchart of AFSA-WTWSVM | |
为了验证基于人工鱼群算法的孪生支持向量机的有效性,选取UCI机器学习数据库中的8个常用数据集来进行测试,数据集的基本特征如表1所示。为了得到更可靠的测试结果,本文使用十折交叉验证方法。实验在Matlab环境下实现,硬件配置为Windows 10操作系统,4 GB内存,250 GB硬盘,i5-2400和3.1 GHz主频CPU的计算机。
| 表 1 实验数据集的特征 Tab.1 Data feature of the datasets |
在实验中,选取未优化参数的孪生支持向量、基于网格搜索的孪生支持向量机(Grid-TWSVM)和基于粒子群算法的孪生支持向量机(PSO-TWSVM)作为对比实验,与AFSA-TWSVM进行比较。由于Gauss径向基函数具有较好的适应性,故选取该函数作为核函数进行实验。
孪生支持向量机的惩罚参数
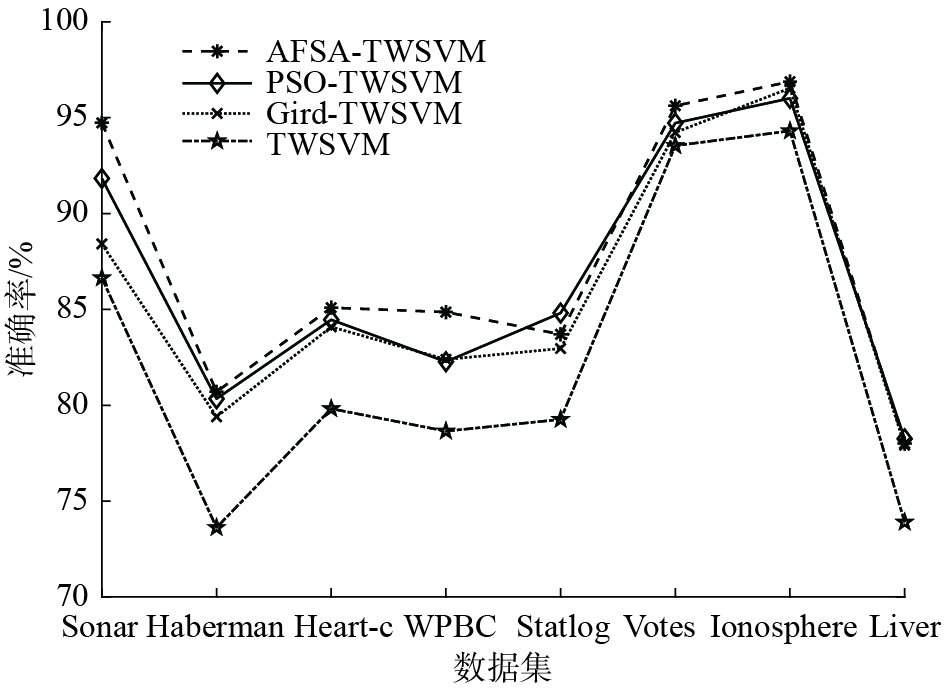
表2给出了4种算法的十折交叉验证的平均分类准确率和标准差,表3给出了在不同数据集上的运行时间,图2是分类准确率效果图。为了更好地体现算法的优越性,用加粗数字代表特定数据集下的最高分类准确率。同时,Mean acc 给出了所有算法的平均准确率,“W-T-L” (win-tie-loss)比较了AFSA-TWSVM与其他算法性能。从中可以看到,本文所提出的AFSA-TWSVM在大多数数据集中都获得了最佳分类准确率,并且平均分类准确率也是最好的。因此可以得出结论,与传统的分类算法相比,AFSA-TWSVM具有更好的分类性能。这是因为AFSA具有较好的全局搜索能力,能避免自己过早地陷入局部最优,从而能更精确地找到参数。由于有更好的参数选择,AFSA-TWSVM提高了TWSVM的分类准确率。
| 表 2 各算法在不同数据集上的分类准确率 Tab.2 Classification Accuracy of Different Algorithms on Different Datasets |
| 表 3 不同数据集上的运行时间 Tab.3 Running time on different data sets |
|
Download:
|
| 图 2 实验结果 Fig. 2 The effect diagram of experimental results | |
与传统的分类算法相比,TWSVM有许多特有的优势,但也存在着一些不足。本文针对TWSVM参数难以设置的问题,提出了一种基于人工鱼群算法的孪生支持向量机(AFSA-TWSVM),利用AFSA优化参数,避免了参数选择的盲目性。通过选取UCI数据集进行实验,与TWSVM、Grid-TWSVM和PSO-TWSVM相比,AFSA-TWSVM有更好的分类性能。但是不足之处在于,人工鱼群算法寻优速度较慢,如何进一步提高算法的寻优速度是下一步需要研究的问题。
| [1] |
丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 1-10. DING Shifei, QI Bingjuan, TAN Hongyan. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technol-ogy of China, 2011, 40(1): 1-10. DOI:10.3969/j.issn.1001-0548.2011.01.001 (  0) 0)
|
| [2] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [3] |
CHEN Zhensong, QI Zhiquan, WANG Bo, et al. Learning with label proportions based on nonparallel support vector machines[J]. Knowledge-based systems, 2017, 119: 126-141. DOI:10.1016/j.knosys.2016.12.007 ( 0) 0)
|
| [4] |
CHEN Zhenyu, FAN Zhiping. Distributed customer be-havior prediction using multiplex data: a collaborative MK-SVM approach[J]. Knowledge-based systems, 2012, 35: 111-119. DOI:10.1016/j.knosys.2012.04.023 ( 0) 0)
|
| [5] |
MORAES R, VALIATI J F, NETO W P G. Docu-ment-level sentiment classification: an empirical compar-ison between SVM and ANN[J]. Expert systems with ap-plications, 2013, 40(2): 621-633. DOI:10.1016/j.eswa.2012.07.059 ( 0) 0)
|
| [6] |
ZHANG Xiekai, DING Shifei, XUE Yu. An improved multiple birth support vector machine for pattern classi-fication[J]. Neurocomputing, 2017, 225: 119-128. DOI:10.1016/j.neucom.2016.11.006 ( 0) 0)
|
| [7] |
DING Shifei, ZHANG Xiekai, AN Yuexuan, et al. Weighted linear loss multiple birth support vector machine based on information granulation for multi-class classification[J]. Pattern recognition, 2017, 67: 32-46. DOI:10.1016/j.patcog.2017.02.011 ( 0) 0)
|
| [8] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural processing letters, 1999, 9(3): 293-300. DOI:10.1023/A:1018628609742 ( 0) 0)
|
| [9] |
FUNG G, MANGASARIAN O L. Proximal support vec-tor machine classifiers[C]//Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Dis-covery and Data Mining. San Francisco, California, 2001: 77–86.
( 0) 0)
|
| [10] |
MANGASARIAN O L, WILD E W. Multisurface proxi-mal support vector machine classification via generalized eigenvalues[J]. IEEE transactions on pattern analysis and machine intelligence, 2006, 28(1): 69-74. DOI:10.1109/TPAMI.2006.17 ( 0) 0)
|
| [11] |
JAYADEVA, KHEMCHANDANI R, CHANDRA S. Twin support vector machines for pattern classification[J]. IEEE transactions on pattern analysis and machine intel-ligence, 2007, 29(5): 905-910. DOI:10.1109/TPAMI.2007.1068 ( 0) 0)
|
| [12] |
HUANG Huajuan, WEI Xiuxi, ZHOU Yongquan. Twin support vector machines: a survey[J]. Neurocomputing, 2018, 300: 34-43. DOI:10.1016/j.neucom.2018.01.093 ( 0) 0)
|
| [13] |
丁世飞. 孪生支持向量机: 理论、算法与拓展[M]. 北京: 科学出版社, 2017: 16-31. DING Shifei. Twin support vector machine: theory, algo-rithm and extension[M]. Beijing: Science Press, 2017: 16–31. (  0) 0)
|
| [14] |
KUMAR M A, GOPAL M. Application of smoothing technique on twin support vector machines[J]. Pattern recognition letters, 2008, 29(13): 1842-1848. DOI:10.1016/j.patrec.2008.05.016 ( 0) 0)
|
| [15] |
KUMAR M A, GOPAL M. Least squares twin support vector machines for pattern classification[J]. Expert sys-tems with applications, 2009, 36(4): 7535-7543. DOI:10.1016/j.eswa.2008.09.066 ( 0) 0)
|
| [16] |
KUMAR M A, KHEMCHANDANI R, Gopal M, et al. Knowledge based Least Squares Twin support vector machines[J]. Information sciences, 2010, 180(23): 4606-4618. DOI:10.1016/j.ins.2010.07.034 ( 0) 0)
|
| [17] |
MIR A, NASIRI J A. KNN-based least squares twin sup-port vector machine for pattern classification[J]. Applied intelligence, 2018, 48(12): 4551-4564. DOI:10.1007/s10489-018-1225-z ( 0) 0)
|
| [18] |
CHEN Sugen, WU Xiaojun. A new fuzzy twin support vector machine for pattern classification[J]. International journal of machine learning and cybernetics, 2018, 9(9): 1553-1564. DOI:10.1007/s13042-017-0664-x ( 0) 0)
|
| [19] |
CHEN Xiaobo, YANG Jian, YE Qiaolin, et al. Recursive projection twin support vector machine via within-class variance minimization[J]. Pattern recognition, 2011, 44(10/11): 2643-2655. ( 0) 0)
|
| [20] |
XIE Xiaomin. Improvement on projection twin support vector machine[J]. Neural computing and applications, 2018, 30(2): 371-387. DOI:10.1007/s00521-017-3237-8 ( 0) 0)
|
| [21] |
XU Zongben, DAI Mingwei, MENG Deyu. Fast and effi-cient strategies for model selection of Gaussian support vector machine[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2009, 39(5): 1292-1307. DOI:10.1109/TSMCB.2009.2015672 ( 0) 0)
|
| [22] |
DING Shifei, YU Junzhao, HUANG Huajuan, et al. Twin support vector machines based on particle swarm optimi-zation[J]. Journal of computers, 2013, 8(9): 2296-2303. ( 0) 0)
|
| [23] |
DING Shifei, WU Fulin, NIE Ru, et al. Twin support vector machines based on quantum particle swarm opti-mization[J]. Journal of software, 2013, 8(7): 1743-1750. ( 0) 0)
|
| [24] |
ZHAI Shijun, PAN Juan, LUO Hongwei, et al. A new sense-through-foliage target recognition method based on hybrid particle swarm optimization-based wavelet twin support vector machine[J]. Measurement, 2016, 80: 58-70. DOI:10.1016/j.measurement.2015.11.027 ( 0) 0)
|
| [25] |
SARTAKHTI J S, AFRABANDPEY H, SARAEE M. Simulated annealing least squares twin support vector machine (SA-LSTSVM) for pattern classification[J]. Soft computing, 2017, 21(15): 4361-4373. DOI:10.1007/s00500-016-2067-4 ( 0) 0)
|
| [26] |
李晓磊, 邵之江, 钱积新. 一种基于动物自治体的寻优模式: 鱼群算法[J]. 系统工程理论与实践, 2002, 22(11): 32-38. LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animats: fish-swarm algo-rithm[J]. Systems engineering-theory & practice, 2002, 22(11): 32-38. DOI:10.3321/j.issn:1000-6788.2002.11.007 (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


