半监督回归是半监督学习领域一个重要的研究方向，其基本思想是利用无标签样本信息，以提高有标签样本的建模效果^[1-3]。现有的半监督回归方法依据其学习方法大致分为两类^[4-5]：基于流行学习的半监督回归算法和协同训练算法。其中，流行学习方面的研究大都着眼于样本结构信息，通过挖掘样本蕴含的结构信息，进而提高算法性能^[6-9]。协同训练的主要思路是对有标签样本建立两个学习器，在假设数据存在双视图的前提下，通过相互学习，逐步提高每个学习器的精度，从而实现对无标签样本信息的准确预测，进而达到提升模型精度的目的^[10-13]。此外，半监督思想能够与其他典型方法结合，充分发挥原有方法的优势和半监督思想的特点，在相关领域也获得了显著成果^[14-15]。

自训练(Self-Training)是半监督学习的一种重要的学习技术，一般结合其他算法来实现数据信息的充分挖掘^[16-19]。通常用于半监督分类，与SVM结合构成Self-Training SVM，通过充分利用无标签样本信息来提高分类器的泛化性能^[20]。但其最近也有一些新的发展，如仝小敏等^[21]将自训练思想应用于回归领域，充分挖掘并利用无标签样本信息，提高了回归准确率，为回归问题提供了一种新的思路。

上述方法有的考虑了有标签样本问题，有的考虑了无标签样本问题，有的考虑了置信度判断问题，有的考虑了利用的充分性等。但是，当有标签样本集很小时，上述方法的使用就会出现不足，如协同训练需要两个冗余的视图，流行学习大多利用有标签样本信息等。

本文针对有标签样本少的问题，综合考虑以上各个方面对建模的影响，为提升对无标签样本利用的准确性与充分性，提出一种自训练框架下的三优选半监督软测量算法。首先，对无标签样本与有标签样本进行优选，保证两类数据的相似性，以提高无标签样本预测的准确性；其次，利用高斯过程回归方法对所选有标签样本集建模，预测所选无标签样本集，得到伪标签样本集；接着，通过对伪标签样本集置信度进行判断，优选出置信度高的伪标签样本用于更新初始样本集；最后，为了进一步提高无标签样本利用的充分性，在自训练框架下，进行多次循环筛选以提高无标签样本的利用率。

1 相关知识 1.1 高斯过程回归

GPR是一种基于统计学习理论的非参数概率模型，适合处理高维度、小样本及非线性等数据的建模问题^[22]。高斯过程回归算法流程：给定训练样本集 $\left\{ {{{X}},{{y}}} \right\}$ ，其中 ${{X}} = \{ {{{x}}_{{i}}} \in {R^{{D}}}\}$ ， ${{y}} = \{ {{{y}}_{{i}}} \in {\bf{R}}\}$ ， $i = 1,2, \cdots ,n$ ，分别代表D维的输入和输出数据，通常观测值 ${{{y}}_{{i}}}$ 与输入 ${{{x}}_{\rm{i}}}$ 应满足 ${{{y}}_{{i}}} = f({{{x}}_{\rm{i}}}) + {{\varepsilon }}$ ，其中 $f$ 为未知函数形式，高斯噪声 ${{\varepsilon }}\sim N\left( {0,{\sigma ^2}} \right)$ 。对于一个新的输入 ${{{x}}^*}$ ，相应的预测值 ${y^*}$ 也满足高斯分布，其均值和方差如式(1)和(2)所示：

$\mu \left( {{{{y}}^*}} \right) = {{{k}}^{\rm{T}}}\left( {{{{x}}^*}} \right){{{K}}^{ - 1}}{{y}}$

(1)

${\sigma ^2}\left( {{{{y}}^*}} \right) = {{C}}\left( {{{{x}}^*},{{{x}}^*}} \right) - {{{k}}^{\rm{T}}}\left( {{{{x}}^*}} \right){{{K}}^{ - 1}}{{k}}\left( {{{{x}}^*}} \right)$

(2)

式中： ${{k}}\left( {{{{x}}^*}} \right)$ 为训练样本与测试样本之间的协方差矩阵； ${{K}}$ 为训练样本的自协方差矩阵； ${{C}}$ 为测试样本自协方差。

本文选择常用的高斯协方差函数，定义如下：

${{k}}\left( {{{{x}}_{\rm{i}}},{{{x}}_{\rm{j}}}} \right) = \nu \exp \left[ { - \dfrac{1}{2}\displaystyle \sum\limits_{d = 1}^D {{{{\omega }}_{{d}}}\left( {{{x}}_{{i}}^{{d}} - {{x}}_{{j}}^{{d}}} \right)} } \right]$

(3)

式中： $v$ 为先验知识的总体度量； ${{{\omega }}_{{d}}}$ 表示每个成分 ${{{x}}^{{d}}}$ 的重要性程度。

根据式(1)~(3)确定模型的均值与方差，对任意输入 ${{{x}}^*}$ ，即可预测其输出 ${{{y}}^*}$ 。详细的GPR建模过程可参考文献[23]。

1.2 半监督回归置信度判断

置信度判断是半监督回归中一个至关重要的问题，其决定了能否选出可信的伪标签样本更新有标签样本集，直接影响算法预测性能。

现有的算法一般借鉴COREG算法中的假设：若利用了置信度最高的无标签样本，则对更新后的有标签样本集建模能获得最好的预测效果。换言之，置信度最高的样本是指样本加入有标签样本集后使标签样本的预测值与实际值最一致的样本^[24]。该类算法已取得不错的效果。如文献[14]中，通过将式(4)最大化取出置信度最高的无标签样本：

$ {\Delta _u} = \sqrt {\displaystyle \sum\limits_{{{{x}}_{{i}}} \in {{{\varOmega }}_{{u}}}} {{{\left( {{{y}_{{i}}} - h\left( {{{{x}}_{{i}}}} \right)} \right)}^2}/k} } - \sqrt { \displaystyle \sum\limits_{{{{x}}_{{i}}} \in {{{\varOmega }}_{{u}}}} {{{\left( {{{y}_{{i}}} - h'\left( {{{{x}}_{{i}}}} \right)} \right)}^2}/k} } $

(4)

式中： ${\Delta _u}$ 为预测误差的差值； ${{{\varOmega }}_{{u}}}$ 为无标签样本 ${{{x}}_{{u}}}$ 的 $k$ 个近邻有标签样本组成的集合； ${{y}_{{i}}}$ 为验证集的真值； $h$ 为 ${{{\varOmega }}_{{u}}}$ 训练所得初始学习器； $h'$ 为 ${{{\varOmega }}_{{u}}}$ 加上 ${{{x}}_{{u}}}$ 及其标签 $h\left( {{{{x}}_{{u}}}} \right)$ 后的集合训练所得新学习器。

1.3 自训练算法

自训练是半监督学习中一种重要的学习技术，一般结合其他算法用于半监督分类上，其作用是提高无标签样本的利用率，以提高模型的泛化性能^[25]。其工作流程：首先，根据已有的少量有标签样本训练出一个初始的分类器；然后，利用分类器预测无标签样本的标签，选出置信度高的一部分伪标签样本加入有标签样本集；最后，重复执行以上步骤，若达到预期性能或循环次数限制，则跳出循环。

将自训练框架融入本文算法，能实现对无标签样本充分准确地利用，算法思想如图1所示。

2 本文算法 2.1 算法分析

半监督学习的基本思想是假设数据分布服从三大假设，建立学习器以预测无标签样本标签值^[1]。半监督学习的基本设置：给定一个未知分布的有标签样本集 ${{S}} = \left\{ {\left( {{{{x}}_1},{y_1}} \right),\left( {{{{x}}_2},{y_2}} \right), \cdots ,\left( {{{{x}}_{|{{S}}|}},{y_{|{{S}}|}}} \right)} \right\}$ 以及一个无标签样本集 ${{M}} = \left\{ {{{{{x'}}}_1},{{{{x'}}}_2}, \cdots, {{{{x'}}}_{|{{M}}|}}} \right\}$ ，期望得到模型 $f:{{X}} \to {{y}}$ ，能准确预测无标签样本 ${{x'}}$ 的标签。此处， ${{{x}}_{{i}}},{{{x'}}_{{i}}} \in {{X}}$ ， ${y_{{i}}} \in {{y}}$ 为样本 ${{{x}}_{{i}}}$ 的标签，针对回归问题，一般假设 ${{y}}$ 服从流行假设，即局部邻域输出具有相似性； $|{{S}}|$ 与 $|{{M}}|$ 分别为 ${{S}}$ 与 ${{M}}$ 集的势，即其所包含的样本数。

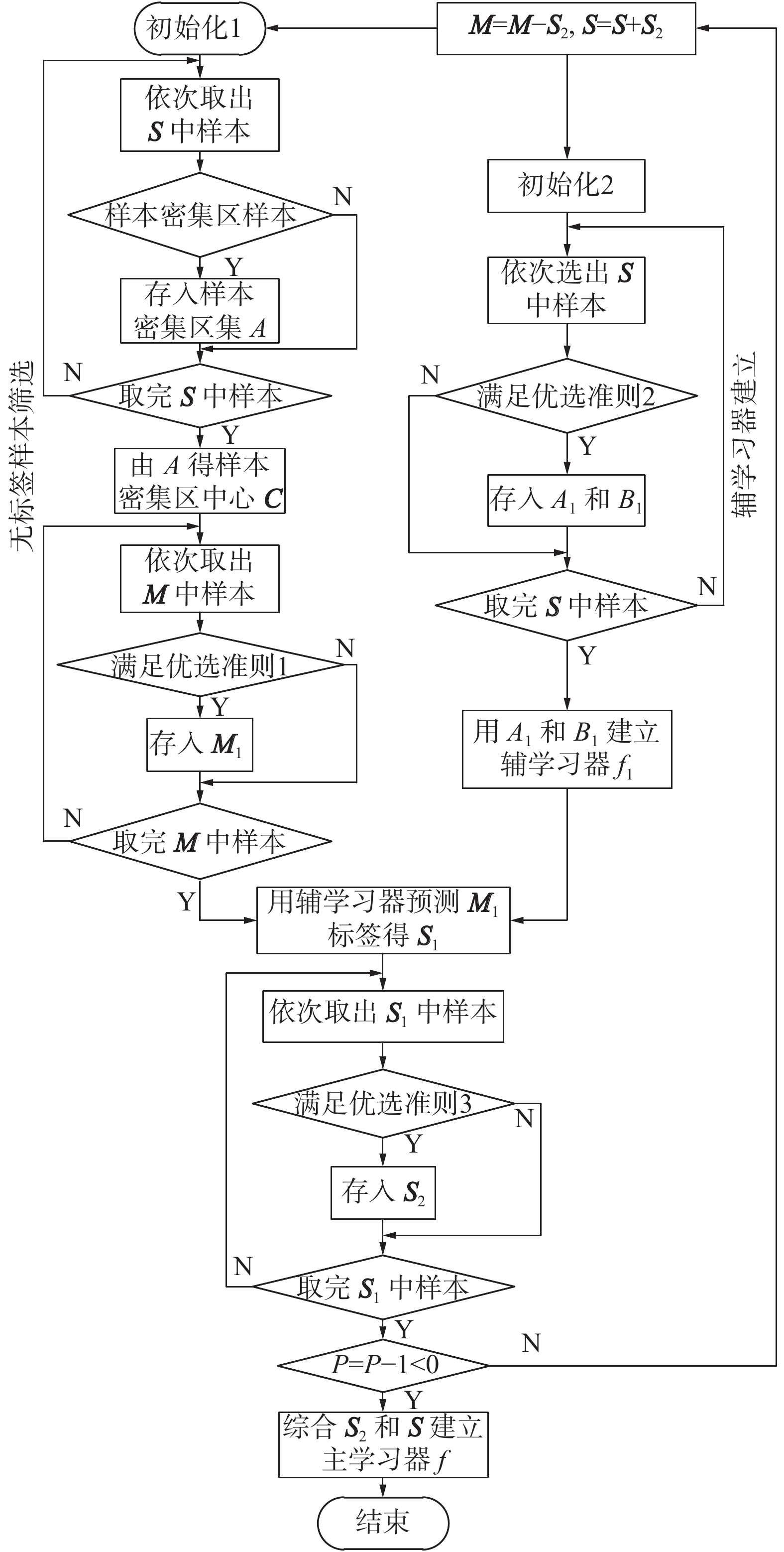
图2为自训练框架下的三优选半监督回归算法的流程图，主要包含自训练框架，无标签样本筛选，有标签样本筛选和置信度判断4个部分。由于初始有标签样本数量少，仅通过现存有标签样本无法对大多数无标签样本进行准确预测，为了实现无标签样本的准确预测，依据有标签样本的分布特点，先对无标签样本进行筛选，选出能够被准确预测的无标签样本。同时，由于有标签样本少，可能存在的有标签样本的离群点会对辅学习器的性能产生较大影响，故根据有标签样本的分布特点，剔除离群点，然后建立辅学习器，实现对无标签样本更准确地预测。

通过以上两步筛选过程，准确预测了部分无标签样本，但是也导致无标签样本利用率不高，故引入了自训练的框架，通过多次循环提高无标签样本利用率。由于自训练对预测准确度要求很高，一旦达不到精度要求，易造成误差的累积，大幅度降低模型预测精度，故通过置信度判断，对预测的无标签样本进一步筛选，进一步提高无标签样本预测的准确性。

在本文算法学习过程中，首先根据无标签样本筛选过程，对无标签样本集 ${{M}}$ 筛选得到 ${{{M}}_1}$ ；同时根据辅学习器建立过程，通过筛选有标签样本集 ${{S}}$ 得到 ${{{A}}_1}$ 和 ${{{B}}_1}$ ，建立辅学习器 ${f_1}$ ；然后利用 ${f_1}$ 预测 ${{{M}}_1}$ 得到伪标签样本集 ${{{S}}_1}$ ；最后利用置信度判断筛选 ${{{S}}_1}$ 得到 ${{{S}}_2}$ 。重复上述过程 $P$ 次，将 ${{{S}}_2}$ 结合 ${{S}}$ 建立主学习器，所得主学习器将拥有良好的预测精度和泛化能力。

2.2 三优选策略

本文提出的三优选策略，综合考虑无标签样本筛选、有标签样本筛选以建立学习器，以及基于置信度判断的伪标签样本筛选等三方面问题，进而达到准确预测无标签样本的目的，以防止自训练过程误差累积情况的发生。优选策略中对无标签样本和有标签样本进行的优选，不仅保证初期仅预测有标签样本分布范围内的无标签样本，而且排除了有标签样本中可能的离群点的影响，因此初始预测误差不会过大，避免了在有标签样本少的情况下自训练算法初期可能产生过大震荡。

2.2.1 三优选准则

优选准则1：给定一个阈值 ${\theta _1}$ ，利用马氏距离^[26]度量无标签样本 ${{{x'}}_{{i}}}$ 与有标签样本密集区中心 ${{C}}$ 的相似度，若 ${{{x'}}_{{i}}}$ 与 ${{C}}$ 的距离小于 ${\theta _1}$ ，则 ${{{x'}}_{{i}}}$ 满足优选条件。

优选准则2：给定一个阈值 ${\theta _2}$ ，利用马氏距离度量有标签样本间的相似度，统计有标签样本 ${{{x}}_{{i}}}$ 与其余有标签样本的马氏距离小于 ${\theta _2}$ 的有标签样本数量 $m$ ，若 $m$ 不小于2，则 ${{{x}}_{{i}}}$ 满足优选条件。

优选准则3：给定一个阈值 ${\theta _3}$ ，判断每一个伪标签样本加入建模过程后对模型预测效果的影响，若模型对测试样本预测方差 $\operatorname{var} $ 小于阈值 ${\theta _3}$ ，则该伪标签样本可信，能够用于更新有标签样本集。

上述3个优选准则，优选准则1通过马氏距离选出以有标签样本密集区中心为球心 ${\theta _1}$ 为半径的超球体内全部的无标签样本点，该准则有利于选出能被准确利用的无标签样本。优选准则2采用了Knorr等^[27]提出的离群点的定义，利用马氏距离度量相似度，剔除了阈值 ${\theta _2}$ 限定下的离群点，从而提升辅学习器的预测精度。准则1和准则2的阈值一般由工程经验设定，也可通过枚举法获取，即先固定阈值 ${\theta _2}$ ，更改阈值 ${\theta _1}$ ，由其对模型预测结果的影响确定 ${\theta _1}$ 最优质阈值范围，同理可得阈值 ${\theta _2}$ 范围，然后利用枚举法，在范围内枚举 ${\theta _1}$ 与 ${\theta _2}$ ，根据模型预测结果得 ${\theta _1}$ 与 ${\theta _2}$ 。优选准则3通过对伪标签样本的筛选，选出其中可信的伪标签样本用于更新有标签样本集与无标签样本集，其基本思想是假设当前样本集为最优样本集，根据当前有标签样本数据集计算阈值，利用该阈值通过优选准则3判断某伪标签样本的加入对算法预测效果的影响，若算法的预测误差变小，则该伪标签样本可信，用于更新样本集；另外，不可信的伪标签样本不采用其标签，等待更新后的样本集对其重新预测，根据该准则能够显著提高无标签样本集预测的准确性。有标签样本 ${{{x}}_{{i}}}$ 与 ${{{x}}_{{j}}}$ 之间马氏距离 $d\left( {{{{x}}_{{i}}},{{{x}}_{{j}}}} \right)$ 计算公式为

$d\left( {{{{x}}_{{i}}},{{{x}}_{{j}}}} \right) = {\rm{sqrt}}\left[ {{{\left( {{{{x}}_{{i}}} - {{{x}}_{{j}}}} \right)}^{\rm{T}}}{{{S}}^{ - 1}}\left( {{{{x}}_{{i}}} - {{{x}}_{{j}}}} \right)} \right]\\$

(5)

${{S}} = \dfrac{1}{{n - 1}}\displaystyle \sum\limits_{i = 1}^n {\left( {{{{x}}_{{i}}} - {{\bar x}}} \right){{\left( {{{{x}}_{{i}}} - {{\bar x}}} \right)}^{\rm{T}}}}\\ $

(6)

${{\bar x}} = \dfrac{1}{n} \displaystyle \sum\limits_{i = 1}^n {{{{x}}_{{i}}}}\\ $

(7)

式中： ${{S}}$ 是有标签样本的协方差矩阵； $n$ 为变量个数； ${{\bar x}}$ 为有标签样本均值。

另外，优选准则1中 ${{{x'}}_{{i}}}$ 与 ${{C}}$ 的距离 ${d_{{i}}}$ 同样可用式(5)~(7)获得。优选准则3中的阈值 ${\theta _3}$ 与预测方差 $\operatorname{var} $ 计算为

${f_{{\rm{gpr}}}} = {\rm{gprtrain}}({{{B}}_1},{{{A}}_1})\\$

(8)

${{{y}}_{{\rm{predict}}}} = {f_{{\rm{gpr}}}}\left( {{{{x}}_{{\rm{test}}}}} \right)\\$

(9)

${\theta _3} = {\displaystyle \sum\limits_{i = 1}^N {\left( {{{{y}}_{{\rm{predict}}}}\left( i \right) - {{{y}}_{{\rm{test}}}}\left( i \right)} \right)} ^2}\\$

(10)

从 ${{{S}}_1}$ 中依次选择样本加入 ${{{B}}_1}$ 和 ${{{A}}_1}$ 中，组成 ${{{{{B}}_1'}}}$ 和 ${{{{{A}}_1'}}}$ ，再用其建模。

${f'_{{\rm{gpr}}}} = {\rm{gprtrain}}({{{{{B}}_1'}}},{{{{{A}}_1'}}})\\$

(11)

${{{\hat y}}_{{\rm{predict}}}} = {f'_{{\rm{gpr}}}}\left( {{{{x}}_{{\rm{test}}}}} \right)\\$

(12)

$\operatorname{var} = {\displaystyle \sum\limits_{i = 1}^N {\left( {{{{{\hat y}}}_{{\rm{predict}}}}\left( i \right) - {{{y}}_{{\rm{test}}}}\left( i \right)} \right)} ^2}\\$

(13)

式中： ${f'_{{\rm{gpr}}}}$ 和 ${f_{{\rm{gpr}}}}$ 表示所建立模型； ${\rm{gprtrain}}({{{B}}_1},{{{A}}_1})$ 表示根据 ${{{B}}_1}$ 和 ${{{A}}_1}$ 建立GPR模型； ${{{B}}_1}$ 和 ${{{A}}_1}$ 分别为有标签样本集的辅助变量和标签值； ${{{x}}_{{\rm{test}}}}$ 和 ${{{y}}_{{\rm{test}}}}$ 分别为测试样本集的辅助变量和标签值； ${{{y}}_{{\rm{predict}}}}$ 为模型对 ${{{x}}_{{\rm{test}}}}$ 的预测值； ${{{{{B}}_1'}}}$ 和 ${{{{{A}}_1'}}}$ 分别为加入伪标签样本后有标签样本集的辅助变量和标签值； ${{{\hat y}}_{{\rm{predict}}}}$ 为更新后的有标签样本集对 ${{{x}}_{{\rm{test}}}}$ 的预测值。

2.2.2 无标签样本筛选

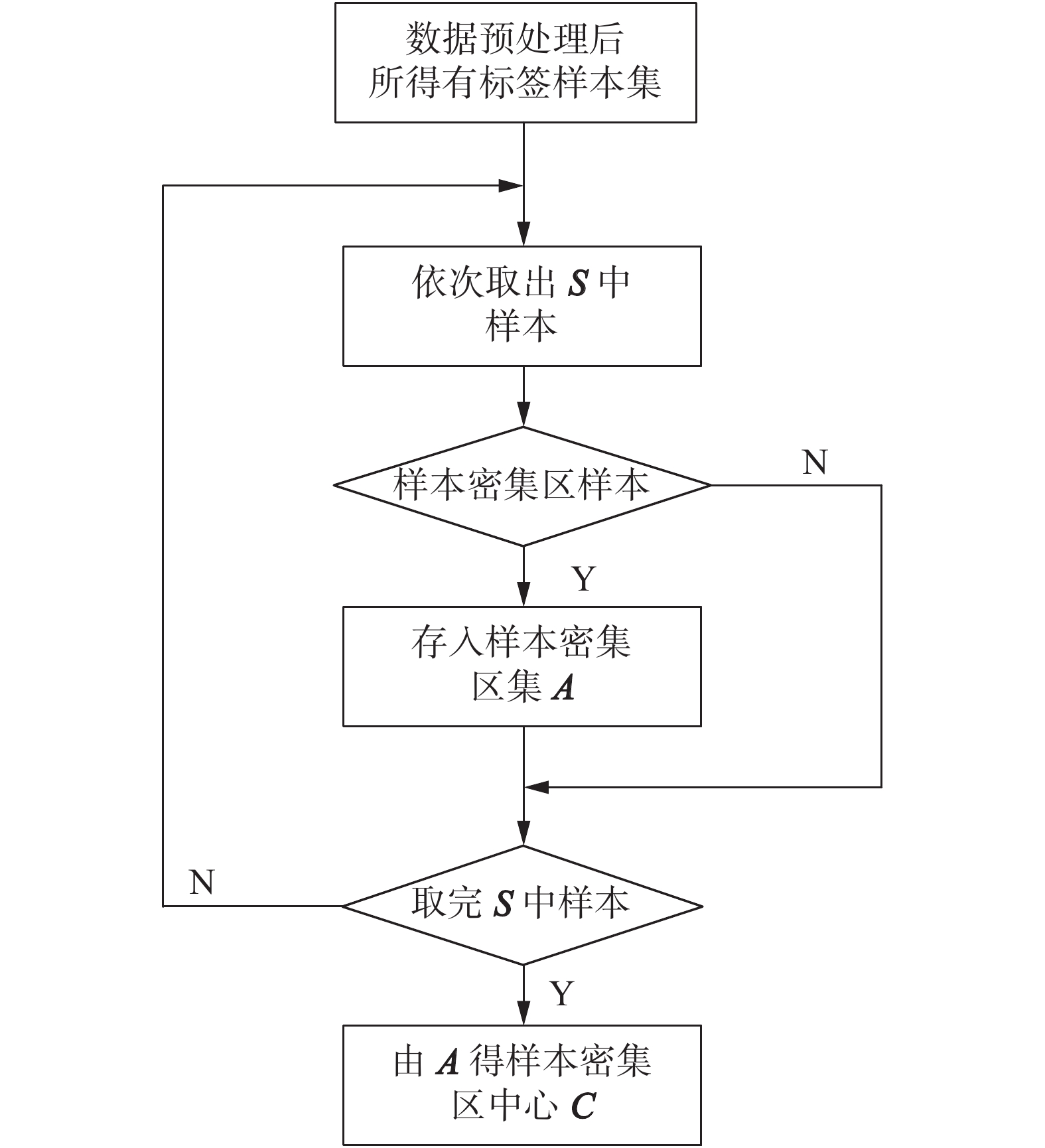
为了选出能够被准确预测的无标签样本，利用优选准则1对无标签样本进行筛选，选出满足条件的无标签样本，保证所选出的无标签样本分布于有标签样本所分布的范围内，以降低无标签样本预测错误的可能性，同时避免自训练算法初期可能存在过大误差导致算法初期过大的震荡。而准则1能否做出有效筛选，取决于能否获得准确的有标签样本分布范围，尤其是有标签样本数目比较少的情况，此时有标签样本分布范围对离群点更敏感。针对此类情况，提出一种寻找有标签样本密集区中心的方法。算法流程如图3所示。

获得样本密集区中心后，准则1的筛选效果得以保证，再利用其筛选无标签样本。算法流程如图4所示。

以上算法流程图中，图3为获取样本密集区中心的流程，图4为无标签样本优选，按照流程，首先进行样本密集区中心的计算，然后根据所得密集区中心优选无标签样本，具体算法步骤：

1)初始化参数。 ${{A}}$ 、 ${{{M}}_1}$ 初始赋空集，初始化阈值 ${\theta _1}$ 和 ${\theta _4}$ 及有标签样本集 ${{S}}$ 和无标签样本集 ${{M}}$ ；

2)依次取出 ${{S}}$ 中样本 ${{{x}}_i}$ ；

3)由式(5)~(7)计算得 ${{{x}}_{\rm{i}}}$ 与其余有标签样本间的马氏距离 $d\left( {{{{x}}_{{i}}},{{{x}}_{{j}}}} \right)$ ；

4)统计满足条件 $d\left( {{{{x}}_{{i}}},{{{x}}_{{j}}}} \right) < {\theta _4}$ 的次数，若次数不小于2，则 ${{{x}}_{{i}}}$ 为样本密集区样本，将其存入 ${{A}}$ ；

5)判断是否取完 ${{{S}}_1}$ 中样本，若取完，根据 ${{A}}$ 计算样本密集区中心 ${{C}}$ ，跳转至6)，开始优选无标签样本，否则，跳转至2)，继续寻找样本密集区样本；

6)依次取出 ${{M}}$ 中样本 ${{{x_j'}}}$ ；

7)由式(5)~(7)计算得 ${{{x_j'}}}$ 与样本密集区中心 ${{C}}$ 的马氏距离 ${d_{{j}}}$ ；

8)判断是否满足优选准则1，若满足，将 ${{{x_j'}}}$ 存入 ${{{M}}_1}$ ，跳转至9)，否则，直接跳转至9)；

9)判断是否取完 ${{M}}$ 中样本，若取完，跳出循环，否则，跳转至6)，继续优选无标签样本。

2.2.3 辅学习器建立

为获得富有针对性的辅学习器，已知 ${{{M}}_1}$ 分布于 ${{C}}$ 周围的前提下，利用优选准则2筛选出与 ${{{M}}_1}$ 特性更相符的有标签样本，即可根据所选有标签样本建立辅学习器，实现对 ${{{M}}_1}$ 更准确的预测。辅学习器建立流程图如图5所示。

如图5所示，利用马氏距离度量样本间的相似度，判断每一个有标签样本是否满足优选准则2，选出其中满足条件的样本，分别存入 ${{{A}}_1}$ 和 ${{{B}}_1}$ ， ${{{A}}_1}$ 中存辅助变量， ${{{B}}_1}$ 中存对应的标签值，然后利用GPR建立辅学习器 ${f_1}$ 。

2.2.4 置信度判断

在自训练框架下，若加入不准确的伪标签样本，容易造成主学习器误差累积，从而导致预测效果差，故必须对伪标签样本进行置信度判断。现有的置信度判断方法大都利用文献[19]所提的方法，其每次选出置信度列表上最高的伪标签样本加入有标签样本集，随着过程的进行，部分置信度不高的伪标签样本升到置信度列表的最高位置，现有的置信度算法无法避免这部分置信度不高的伪标签样本加入有标签样本集。其次，在有标签样本很少的情况下，某些无标签样本集很可能拥有相同的 $k$ 个近邻有标签样本组成的集 ${\varOmega _{{u}}}$ ，从而导致部分伪标签样本具有相同的置信度而无法选出最高置信度的伪标签样本；最后，由于无标签样本少， $k$ 个近邻有标签样本组成的集 ${\varOmega _{{u}}}$ 较小，导致所有的无标签样本本身无法得到准确的预测，即使每次选出置信度列表上最高的伪标签样本，也无法显著提高主学习器预测效果。

综上，为了对有标签样本少的情况进行置信度判断，结合所提优选准则3，提出了一种新的半监督回归置信度判断方法，具体算法步骤如下：

1)初始化，伪标签样本集 ${{{S}}_1}$ ，阈值 ${\theta _3}$ ；

2)根据式(8)~(10)计算得阈值 ${\theta _3}$ ；

3)依次取出 ${{{S}}_1}$ 中样本 ${{{x}}_i}$ ；

4)根据式(12)~(14)计算得 $\operatorname{var} $ ；

5)判断是否满足优选准则3，若满足，将 ${{{x}}_i}$ 存入 ${{{S}}_2}$ ，跳转至6)，否则，直接跳转至6)；

6)判断是否取完 ${{{S}}_1}$ 中样本，若取完，跳出循环，否则，跳转至2)，继续优选。

2.3 算法总体步骤

自训练框架下的三优选半监督回归算法步骤如下：

1)初始化参数，包括有标签样本集 ${{S}}$ ，无标签样本集 ${{M}}$ ，循环次数 $P$ ；

2)筛选无标签样本，得到无标签样本集 ${{{M}}_1}$ ；

3)筛选有标签样本，得到 ${{{B}}_1}$ 和 ${{{A}}_1}$ ，并利用其建立辅学习器 ${f_1}$ ；

4)利用 ${f_1}$ 预测 ${{{M}}_1}$ 的标签值，得到伪标签样本集 ${{{S}}_1}$ ；

5)对伪标签样本集 ${{{S}}_1}$ 进行置信度判断，筛选出其中可信的伪标签样本组成 ${{{S}}_2}$ ；

6)根据 ${{{S}}_2}$ 更新有标签样本集 ${{S}}$ 与无标签样本集 ${{M}}$ ；

7)重复进行2)~6)，循环 $P$ 次；

8)根据更新后的有标签样本集 ${{S}}$ 建立主学习器 $f$ 。

本文算法使用了自训练算法的框架，本文算法的收敛性能分析如下：假设第一次循环初始样本建模预测误差为h， ${\rm{rmse}}_0^{{k}}$ 为第k次循环学习器初始误差， $\theta _3^{{k}}$ 为第k次循环优选准则3置信度评判指标， ${\rm{rmse}}_1^{{k}}$ 为第k次循环结束时学习器预测误差。每次循环初始误差为上次循环结束时的误差，即 ${\rm{rmse}}_{\rm{0}}^{{k}} = {\rm{rmse}}_{\rm{1}}^{{{k - 1}}}$ ，根据优选准则3的定义，每次寻找使初始预测误差更小的伪标签样本，用于更新样本集，每一轮的最终预测误差均会不大于初始预测误差，即 ${\rm{rmse}}_{\rm{1}}^{{k}} \leqslant {\rm{rmse}}_{\rm{0}}^{{k}}$ ，且由式(8)~(10)计算 $\theta _3^{{k}}$ ，有 ${\rm{\theta }}_{\rm{3}}^{{k}} = {\rm{rmse}}_{\rm{0}}^{{k}}$ ，若算法共循环了p次，则有 ${\rm{rmse}}_{\rm{1}}^{{p}} \!\leqslant\! {\rm{rmse}}_{\rm{0}}^{{p}} \!=\! {\rm{rmse}}_{\rm{1}}^{{{p - 1}}} \!\leqslant \!{\rm{rmse}}_{\rm{0}}^{{{p - 1}}} \! = \!\cdots\! =\! {\rm{rmse}}_{\rm{1}}^{\rm{1}}\! \leqslant \!{\rm{rmse}}_{\rm{0}}^{\rm{1}} \!=\! h $ ，所以，本文算法是不发散的。

3 脱丁烷塔仿真研究

为了验证本文所提方法的实际效果，以脱丁烷塔过程^[28]作为对象。脱丁烷塔装置的产品丁烷的浓度对石油产量和质量影响很大，但丁烷浓度难以直接测量，如何建立准确模型预测丁烷浓度是石油炼制领域一直以来的一个重要研究课题。脱丁烷塔过程样本数据有7个辅助变量：塔顶温度 ${x_1}$ 、塔顶压力 ${x_2}$ 、塔顶回流量 ${x_3}$ 、塔顶产品流出 ${x_4}$ 、第6层塔板温度为 ${x_5}$ 、 ${x_6}$ 为塔底温度1、 ${x_7}$ 为塔底温度2。主导变量是塔底丁烷浓度。详细的工艺过程描述见文献[29]。

该实验过程数据共2394组样本。为模拟有标签样本少而无标签样本多的情况，对数据进行截选，有标签样本和无标签样本分别为150组与500组。

为了详细展现本文算法性能，纵向比较了几点创新对模型跟踪效果的影响，具体比较如下：

1)GPR方法^[30]。仅利用已有的有标签样本建立GPR模型。

2)无优选半监督GPR(none-optimal semi-supervised GPR, NS-GPR)方法^[30]。直接利用有标签样本建模，获取辅学习器，然后预测无标签样本的标签，进而利用伪标签样本更新初始有标签样本集，进而建模。

3)双优选半监督GPR(double-optimal semi-supervised GPR, DS-GPR)方法^[30]。利用优选准则1筛选无标签样本，同时利用优选准则2筛选有标签样本，接着对其建模得到辅学习器，后续同方法2。

4)自训练双优选半监督GPR(double-optimal semi-supervised GPR from self-training framework, SFDS-GPR)方法。在双优选的基础上，引入自训练框架，循环执行双优选建模过程。

5)三优选半监督GPR(three-optimal semi-Supervised GPR, TS-GPR)方法。在双优选的基础上，利用优选准则3，对预测的无标签样本进行置信度的判断，筛选出其中可信的伪标签样本。

6)本文方法。

图6为几种方法对丁烷浓度真实值的跟踪效果，其中，基准线上的点表示预测值与真实值一致，故样本点离基准线越近，表示预测效果越好。

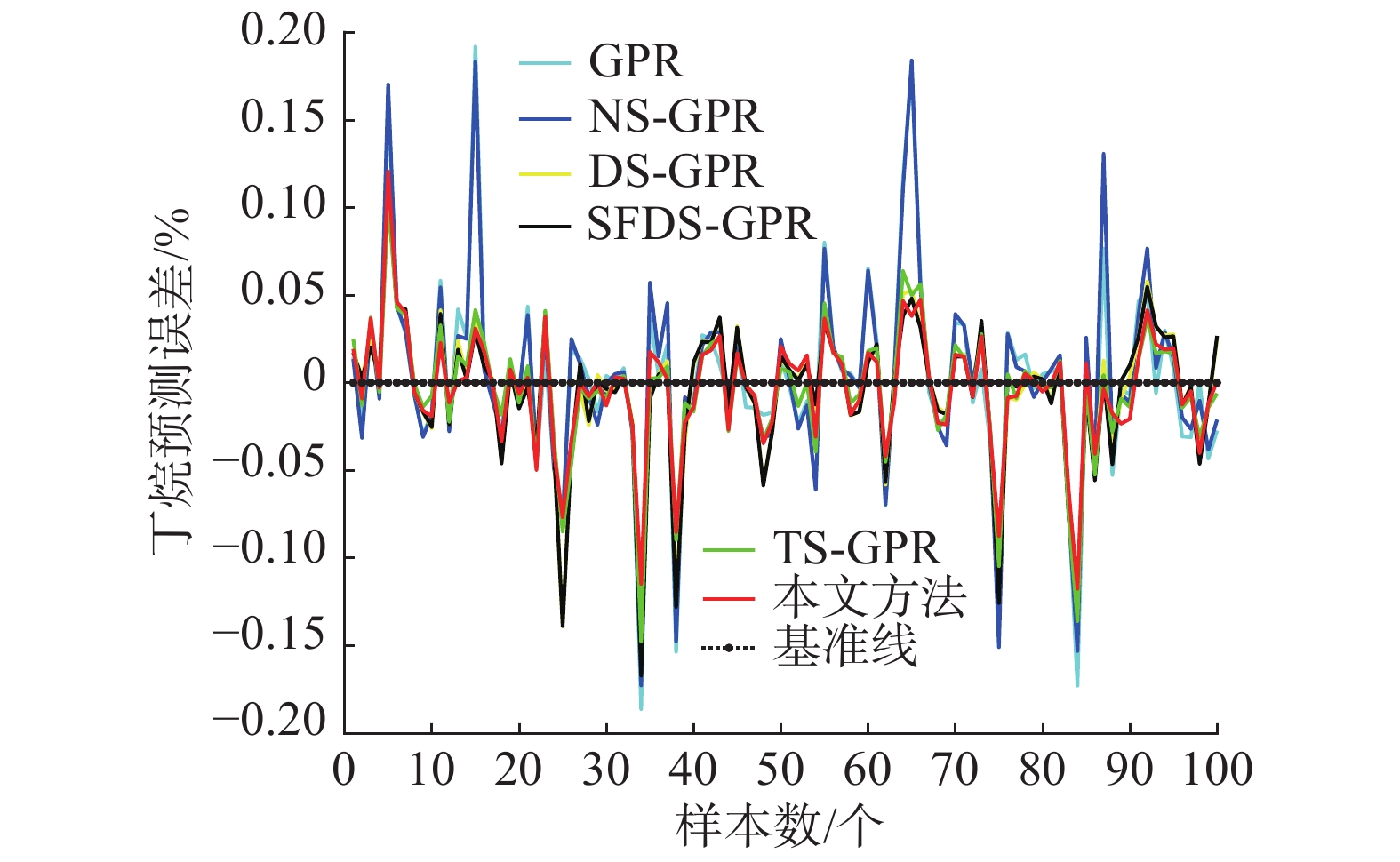
由图6可知，本文方法的效果更好，尤其在丁烷浓度高的区域。为了更直观地对比各方法的预测效果，图7展现了对真实值的跟踪误差。

综合图6和图7可知，NS-GPR虽然考虑了无标签样本信息，但其无差别的利用将会带来大量噪声，而DS-GPR由于经过了双优选过程，提升了对初始无标签样本预测的准确性，主学习器对丁烷浓度预测效果有了明显的提高。SFDS-GPR在DS-GPR的基础上加入了自训练框架，期望达到提高无标签样本利用率的目的，但是，由于自训练框架对初始无标签样本预测准确性要求较高，DS-GPR达不到精度要求，故引入自训练框架无法提高主学习器预测效果，反而会由于误差累积带来大量噪声，降低主学习器预测效果。TS-GPR在DS-GPR的基础上加入了置信度判断，对预测所得伪标签样本进行置信度判断，选出其中可信的伪标签样本更新有标签样本集，对主学习器预测效果有了更明显的提升。

本文方法在考虑无标签样本利用准确性的同时，引入了置信度判断，进一步提升伪标签样本的准确性，引入了自训练框架提高无标签样本的利用率，综合考虑了无标签样本利用的准确性和充分性，充分利用了无标签样本所包含的信息，获得了良好的效果。

为了展现方法在每个区间的预测效果，统计真实值与各方法预测值的分布情况如图8所示。

分析图8各方法在不同区域的预测效果，发现在0.1%~0.15%内GPR和NS-GPR对丁烷浓度真实值的预测效果较差，在0.4%~0.5%内，DS-GPR、SFDS-GPR和TS-GPR都有一定的预测误差，而本文方法在上述区域中的预测误差都相对较小。

以上对比证明了本文方法的优越性，为了更加直观地体现优选过程，选取了样本中塔顶压力、塔顶产品流出及塔底温度1等3个维度的量，利用三维图表现出了这些量在三优选过程中分布的变化。

由图9的过程发现，第1次优选过程中无标签样本集与有标签样本集有明显差异，可知初始无标签样本集无法准确预测所有的无标签样本，仅能够准确预测少量无标签样本，经过三优选过程后，发现筛选后的无标签样本集主要集中在筛选后的有标签样本集附近，样本集的相似度显著提升，故筛选后的无标签样本被准确预测的概率更高；在第2次优选过程中，经过样本集更新，有标签样本集对无标签样本的预测能力加强，在一次三优选过程后，筛选后的无标签样本集与筛选后的有标签样本集相似度进一步提升，筛选所得无标签样本被进行更准确地预测；一直到第4次优选过程，有标签样本集经过更新，所蕴含信息已经能够对这一过程进行准确解释，本着充分挖掘无标签样本所有信息的目的，再一次进行三优选过程，发现此次筛选前后无标签样本集基本没有差异，即已经完成对无标签样本信息的充分利用，其余少数未被选到的无标签样本是无法进行准确预测的，强行预测并利用其信息只会带来明显的误差，对建模有害无益。最终充分准确地利用了无标签样本所包含的有用信息，使得建模更准确可靠。

上述分析对比验证了本文方法的实际效果。发现在对无标签样本进行准确充分地利用后，即使初始有标签样本较少，依然能够取得很好的预测效果。各方法具体跟踪效果如表1所示。

4 结束语

本文所提算法，通过所定义的3个优选准则和自训练框架，从无标签样本、有标签样本、置信度判断与样本利用率等角度，实现了对样本信息充分准确地利用。充分利用有标签样本已有信息，准确估计无标签样本缺失信息，进而利用所估计的无标签样本信息，扩充有标签样本已有信息，从而大幅度提升了主学习器的预测效果。用脱丁烷塔过程数据验证本文算法实际效果，实验结果表明，所提方法在有标签样本较少时，具有良好的预测效果，为半监督回归提供了一种新思路。