聚类是数据挖掘、模式识别等许多研究领域中的基本问题之一，聚类分析的目的是将给定的数据集划分为紧凑的聚类，使聚类内的数据对象比不同的聚类中的数据对象更加相似。其中谱聚类可以适应更广泛的几何形状，并检测非凸模式和线性不可分离的簇，而不存在局部最优问题，被广泛用于数据挖掘和图像分割。

谱聚类算法虽然性能良好，但由于其计算复杂度高，很难适用于大规模的数据集。近些年来，研究人员为了加快谱聚类算法的计算速度和降低谱聚类算法对于大规模数据集的计算复杂度问题，探索研究了一系列的方法来提高谱聚类算法对于大规模数据集的可拓展性。Li等^[1]提出了一种精确的、可扩展的Nystrom算法，使用最近的随机低秩矩阵逼近算法对内部子矩阵进行近似的SVD，降低随机采样引起的不稳定性和采样误差。赵晓晓等^[2]结合稀疏表示和约束传递，提出一种结合稀疏表示和约束传递的半监督谱聚类算法，进一步提高了聚类准确率。Ding等^[3]提出一种基于hmrf模型的半监督近似谱聚类算法，利用hmrf半监督聚类与近似加权核k均值之间的数学联系，利用近似加权核k-均值计算hmrf谱聚类的最优聚类结果。He等^[4]提出了一种有效的大规模数据谱聚类方法，谱聚类的复杂度比现有的Nystrom近似在大规模数据上的复杂度要低。显著加快谱聚类中的特征向量逼近和效益预测速度。林大华等^[5]针对现有子空间聚类算法没有利用样本自表达和稀疏相似度矩阵，提出了一种新的稀疏样本自表达子空间聚类方法，所获得的相似度矩阵具有良好的子空间结构和鲁棒性。Yang等^[6]提出了一种新的基于层次二部图的谱聚类方法，采用无参数而有效的邻域分配策略构造相似矩阵，避免了调整相似性矩阵的需要，大大降低了算法的计算复杂度。虽然众多改进的谱聚类算法在一定程度上减小了谱聚类的时间复杂度，但仍然要对拉普拉斯矩阵进行特征分解，对于大规模的数据集来说内存消耗过大，具有巨大的空间复杂度。最近，深度学习^[7]在计算机视觉、语音识别和自然语言处理中得到了广泛的研究。一些深度学习的方法已经被提出来用于数据聚类^[8]。Tian等^[9]利用叠加稀疏自编码器得到原始图的非线性嵌入，然后对嵌入表示进行k-均值聚类，得到聚类结果，用叠加的自动编码器代替特征分解，有效地降低了计算复杂度。Shao等^[10]提出了一种新的快速图谱聚类深度线性编码方案，该方法同时学习了线性变换和编码，并利用深层结构进一步细化了识别特征。Song等^[11]提出了一种新的基于自编码网络的聚类方法，通过设计数据与聚类中心之间距离的约束，得到了一种更适合于聚类的稳定而紧凑的表示形式。这种深层次的结构可以学习到强大的非线性映射，数据可以很好地在变换后的空间中进行分割。上述基于深度自编码的聚类算法可以提高大规模应用的效率，但它们都需要使用整个数据集的相似度矩阵作为自动编码器的输入，保存了所有数据点的相似性，由于内存消耗大，不适用于大规模数据集。

本文采用加权PageRank算法，选取数据亲和图中最具代表的点作为地标点。以选定的地标点与其他数据点之间的相似关系来逼近相似度矩阵作为叠加自动编码器的输入，通过采样几个数据点来代替所有数据点。用叠加式自动编码器代替拉普拉斯矩阵的特征分解，然后进行k-means聚类。同时进一步改进聚类和嵌入表示，通过迭代优化基于Kullback Leibler(KL)散度的聚类损失，将聚类和表示联合更新，从而能够获得更强大的表示和更精确的聚类结果。

1 相关算法理论 1.1 基于加权PageRank算法的地标选择

PageRank算法^[12]是使用最广泛的页面排序算法之一。但是原始PageRank算法也存在一些问题，假设两个节点 $u$ 和c彼此指向但没有指向其他节点，并且存在第3个节点 $w$ 指向其中一个节点。这个循环将累积秩，但不会将任何秩分配到前两个节点，因为没有输出链路。为了处理这个问题，通过一个迭代过程来近似节点 $u$ 的PageRank值PR $\left( u \right)$ 。则有式（1）：

$ {\rm PR}\left( u \right) = \left( {1 - d} \right) + d\sum\limits_{v \in B\left( u \right)} {\frac{{{\rm PR}\left( v \right)}}{{{N_v}}}} $

(1)

其中， $d$ 是一个阻尼因子，通常设置为0.85^[12]。

加权PageRank算法在文献[13]中提出，加权PageRank算法根据节点的重要性为节点分配排序值。这种重要性是根据传入链路和传出链路的权重来分配的，其中，链路表示各自的基于内容的关系，分别以 $w_{\left( {a,b} \right)}^{\rm in}$ 和 $w_{\left( a,b \right)}^{\rm{out}}$ 表示。 $w_{\left( {a,b} \right)}^{\rm in}$ 是 $\left( {a,b} \right)$ 的传入链路权重，它是根据到节点 $b$ 的传入链路数和到节点 $a$ 的所有参考节点的传入链路数来计算的，其公式为

$ w_{\left( {a,b} \right)}^{\rm in} = \frac{{{i_b}}}{{\displaystyle\sum\limits_{c \in {R_a}} {{i_c}} }} $

(2)

其中， ${i_b}$ 是节点 $b$ 的传入链路数； ${i_c}$ 是节点 $c$ 的传入链路数； ${R_a}$ 是节点 $a$ 的参考节点集(基于内容的最近邻域)。 $w_{\left( {a,b} \right)}^{\rm out}$ 是 $\left( {a,b} \right)$ 的传出链路权重，它是根据节点 $a$ 的所有参考节点的传出链路数计算的，其公式为

$ w_{\left( {a,b} \right)}^{\rm out} = \frac{{{o_b}}}{{\displaystyle\sum\limits_{c \;\in {R_a}} {{o_c}} }} $

(3)

其中， ${o_b}$ 是节点 $b$ 的传出链路数； ${o_c}$ 是节点 $c$ 的传出链路数。

${\rm wpr}\left( b \right)$ 的计算需要迭代过程来调整近似到理论真值， ${\rm wpr}$ 表示节点的加权PageRank权重，所有节点的 ${\rm wpr}$ 初始值初始化为 ${1 / n}$ ， $n$ 为节点数。在每个迭代中，每个节点 $b$ 的 ${\rm wpr}\left( b \right)$ 计算如下：

$ {\rm wpr}\left( b \right) = \left( {1 - d} \right){\rm wpr}\left( a \right) + d\sum\limits_{a \in R\left( b \right)} {{\rm wpr}\left( a \right)} w_{\left( {a,b} \right)}^{\rm in}w_{\left( {a,b} \right)}^{\rm out} $

(4)

在每次迭代中，所有节点的 $\rm wpr$ 值都是基于式(4)减小的^[13]。对于所有节点当满足以下的停止准则时，迭代过程停止：

$ \frac{{{\rm wpr}{{\left( b \right)}_{{\rm iter} - 1}} - {\rm wpr}{{\left( b \right)}_{{\rm iter}}}}}{{{\rm wpr}{{\left( b \right)}_{{\rm iter}}}}} \leqslant \beta $

(5)

其中，分数是前一次迭代与当前迭代之间的归一化差值， $\;\beta $ 是一个预定义的停止阈值，这里设置 $\;\beta = {10^{ - 3}}$ 。最后当式(5)成立时，选择 $\rm wpr$ 最高的 $p$ 节点作为地标点。

2 改进地标表示的自编码谱聚类算法 2.1 构造新的拉普拉斯矩阵

在文献[14-15]中，提出了基于地标点的谱聚类算法来加速谱聚类，在给定 $n$ 个数据点的数据集的情况下，选择 $p \ll n$ 个具有代表性的数据点作为地标的特征点，将原始数据点表示为这些地标的线性稀疏组合，然后利用基于地标的表示来高效地计算数据的谱嵌入，并通过理论分析证明其性能优于Nystrüom和快速谱聚类方法，有效地利用稀疏表示矩阵逼近了整个图的相似度矩阵。它表示选定的 $p$ 个地标点与 $n$ 个数据点之间的成对相似性。

给定数据矩阵 ${{X}} = \left\{ {{{{x}}_1},{{{{x}}}_2} \cdot \cdot \cdot {{{{x}}}_{{ n}}}} \right\} \in {{\bf{R}}^{{{ n}} \times {{ d}}}}$ ，它可以近似为 ${{X}} \approx {{UZ}}$ 。 $ U$ 每一列都可以看作捕捉数据中较高层次特征的基向量。选定的地标点可以看作是基向量。假设对于任何数据，已经有了地标矩阵 ${{U}}$ 。对于任意点 ${{{{x}}}_{{i}}}$ ，它的近似 ${{ {\hat{x}}}_i}$ 计算为

${{\hat{ x}}_{i}} = \sum\limits_{{{j = 1}}}^{{p}} {{{{z}}_{{{ji}}}}} {{{u}}_{{j}}}$

(6)

根据稀疏编码策略，假设当 ${{{x}}_{{i}}}$ 更接近 ${{{u}}_{{j}}}$ 时，矩阵 ${{Z}}$ 的第 ${{j}}$ 个元素应该更大。为了强调这一假设,创建 ${{Z}}$ 亲和稀疏矩阵的稀疏表示,通过选择 $r < p$ 个最近的地标点,代替 $p$ 个地标点( ${{U}} \in {\bf{R}}^{d \times p}$ )，例如，如果 ${{{u}}_{{j}}}$ 不是 $r$ 的最近的地标之一，则 ${{{z}}_{{{ji}}}}$ 的值为0，生成稀疏表示矩阵 ${{Z}}$ 。设 ${{{U}}_{\left\langle i \right\rangle }} \in {\bf{R}}^{d \times r}$ 表示 ${{U}}$ 的子矩阵，由 ${{{x}}_{{i}}}$ 最近的 $r$ 个地标点组成，然后计算出每个 ${{{z}}_{{{ji}}}}$ 元素如下：

${{{z}}_{ji}} = \frac{{\varPhi \left( {{{{x}}_{{i}}}, {{\rm{u}}_{{j}}}} \right)}}{{\displaystyle\sum\limits_{j' \in {U_{\left\langle i \right\rangle }}} {\varPhi \left( {{{{x}}_{{i}}}, {{\rm{u}}_{{j}}}} \right)} }}\begin{array}{*{20}{c}} ,&{i \in 1,2, \cdot \cdot \cdot } \end{array},n,{\rm and},j \in {U_{\left\langle i \right\rangle }}$

(7)

其中， $\varPhi \left( \cdot \right)$ 是一个具有尺度参数 $\sigma $ 的高斯核函数， $\varPhi \left( {{{{x}}_{\rm{i}}}, {{{u}}_{\rm{j}}}} \right) = \exp \left( {{{ - \left\| {{{{x}}_{\rm{i}}}{{ - }}{{{u}}_{\rm{j}}}} \right\|} / {2{\sigma ^2}}}} \right)$ 是最常用的高斯核函数之一，其中， $\sigma $ 控制着每个数据点的局部邻域。根据核尺度参数 $\sigma $ 的自调整策略，在本文所提算法中，设置 ${\sigma ^2} = {\sigma _i} {\sigma _j},\forall \varPhi \left( {{{{x}}_{{i}}}, {{{u}}_{{j}}}} \right)$ ，其中 ${\sigma _i}$ 是 $i$ 的邻居点的平均距离，也是 ${{Z}} \in {\bf{R}}^{p \times n}$ 的稀疏表示中的非零元素。对于 $ W$ 亲和矩阵，认为 ${{W = }} $ ${{\hat{ Z}}^{\rm{T}}}{\hat{ Z}}$ ，其中 ${\hat{ Z }} ={{{D}}^{{{{{ - 1}}} / {{2}}}}}{{Z}}$ 是 ${{D} = }\displaystyle\sum\nolimits_{{j}} {{{{Z}}_{{{ji}}}}} $ 度矩阵的归一化 ${{Z}}$ 。

如果计算所有数据点的相似性矩阵并将其作为堆叠式自动编码器的输入，对于大型数据集来说空间消耗非常高。代替计算给定数据与所有其他数据点的相似性，本文算法只考虑选择的地标点与其他数据点之间的相似性。在这里重写了如下拉普拉斯矩阵的形式：

${{{L}}_{{\rm{new}}}} ={{ S}}{{{S}}^{\rm{T}}}$

(8)

在这里使用 ${{S}}$ 作为叠加自编码器的输入，从前文可以知道归一化相似矩阵可以用稀疏表示矩阵 ${{Z}}$ ，为了进一步降低计算复杂度，在这里使用一种简单的方法计算度矩阵 ${{{D}}_{\rm{2}}}$ ，矩阵的主要对角线元素一般计算如下:

${{{d}}_{{{2ii}}}} = \sum\nolimits_{{i}} {{{{w}}_{{{ij}}}}} = \sum\nolimits_{\rm{i}} {{\hat{ z}}_{{i}}^{\rm{T}}} {{\hat{ z}}_{{j}}}$

(9)

对式(11)进行运算演化可以得到：

$ {{{d}}_{{{2ii}}}} = \sum\limits_{{{j = 1}}}^{{n}} {{{{w}}_{{{ij}}}}} = \sum\limits_{{{j = 1}}}^{{n}} {{\hat{ z}}_{{i}}^{\rm{T}}} {{\hat{ z}}_{{j}}}= {{ \hat z}}_{{i}}^{\rm{T}}\sum\limits_{{{j = 1}}}^{{n}} {{{{\hat{ z}}}_{{j}}}} {{ = \hat z}}_{{i}}^{\rm{T}}{{\hat{ Z}}^{{s}}} $

(10)

其中， ${{\hat{ Z}}^{{s}}}$ 是一个 $p \times 1$ 的向量，第 $k$ 个元素是 ${\hat{ Z}}$ 中第 $k$ 行元素的和。

${{{D}}_{\rm{2}}}{\rm{ = diag}}\left( {{{{\hat{ Z}}}^{\rm{T}}}{{{\hat{ Z}}}^{{s}}}} \right)$

(11)

在这里新的拉普拉斯矩阵的构造如下:

$ {{{L}}_{{\rm{new}}}}={{ D}}_{{2}}^{{{{{ - 1}}} / {{2}}}}{{WD}}_{{2}}^{{{{\rm{ - 1}}} / {\rm{2}}}}={{ D}}_{{2}}^{{{{{ - 1}}} / {{2}}}}{{\hat{ Z}}^{\rm{T}}}{\hat{ ZD}}_{{2}}^{{{{{ - 1}}} / {{2}}}} $

(12)

$ {{S} ={ D}}_{\rm{2}}^{{{{\rm{ - 1}}} / {\rm{2}}}}{{\hat{ Z}}^{\rm{T}}} $

(13)

最后，将相似度矩阵 $ S$ 输入到自动编码器中，最后运行k-means聚类，从而得到聚类结果。

2.2 自编码器与聚类优化

自动编码器是一种用于有效编码和降维的无监督学习的人工神经网络。自动编码器的目的是使原始输入 ${x_i}$ 和新的嵌入表示 ${y_i}$ 的重构输出 ${m_i}$ 之间的重构损失最小化^[16-19]。重构损失定义如下:

$ {L_r} = \sum\limits_{i = 1}^N {l\left( {{x_i},g\left( {f\left( {{x_i};{\theta _1}} \right);{\theta _2}} \right)} \right)} $

(14)

其中， $\left\{ {{\theta _1},{\theta _2}} \right\} = \left\{ {{h_1},{b_1},{h_2},{b_2}} \right\}$ 是自动编码器的参数。

虽然用自编码器配合得到聚类结果，有效地降低了计算复杂度，减小了空间复杂度。但是，由于需要计算和保存所有数据点的相似关系，因此内存消耗进一步增加。学习表示与聚类分离，嵌入表示是不可靠的，对聚类有负面影响。为了将聚类和学习表示联合更新，并且能够获得更强大的表示和更精确的聚类结果，将这两个过程集成到一个具有基于KL散度的聚类损失函数的单一框架中，并迭代地优化了自动编码器和聚类中心的参数。聚类损失被定义为分布在 $P$ 和 $Q$ 之间的KL散度，其中 $Q$ 是由t-SNE测量的软标签的分布， $P$ 是由 $Q$ 导出的目标分布。聚类损失可以用来同时更新堆叠式自动编码器和聚类中心的参数，如式（15）所示：

$ {L_c} = KL\left( {P\left\| Q \right.} \right) = \sum\limits_i {\sum\limits_j {{p_{ij}}} } \log \frac{{{p_{ij}}}}{{{q_{ij}}}} $

(15)

其中， $q{}_{ij}$ 是由t-SNE测量的嵌入表示 ${y_i}$ 和聚类中心 ${c_j}$ 的相似性。

$ {q_{ij}} = \frac{{{{\left( {1 + {{\left\| {{y_i} - {c_j}} \right\|}^2}} \right)}^{ - 1}}}}{{\displaystyle\sum\limits_j {{{\left( {1 + {{\left\| {{y_i} - {c_j}} \right\|}^2}} \right)}^{ - 1}}} }} $

(16)

${p_{ij}}$ 是由 $q{}_{ij}$ 确定的目标分布：

${p_{ij}} = \frac{{{{q_{ij}^2} / {\displaystyle\sum\limits_i {{q_{ij}}} }}}}{{\displaystyle\sum\limits_j {\left( {{{q_{ij}^2} / {\displaystyle\sum\limits_i {{q_{ij}}} }}} \right)} }}$

(17)

因为， ${p_{ij}}$ 是由 $q{}_{ij}$ 确定的目标分布，所以 ${L_c}$ 的最小化可以看作是自我训练的一种形式。重构损失保证了嵌入空间能够保持数据的局部结构，因此将重构损失和聚类损失作为优化参数的目标函数。

$L = {L_c} + \lambda {L_r}$

(18)

其中， ${\textit{λ}} \left( {{\textit{λ}} \geqslant 0} \right)$ 是一个控制嵌入空间失真程度的因子。

利用最小批量随机梯度下降可以得到自动编码器的聚类中心和参数的优化，计算出 ${L_c}$ 关于嵌入表示 ${y_i}$ 和聚类中心 ${c_j}$ 的梯度。

$\frac{{\partial {L_c}}}{{\partial {y_i}}} = 2{\sum\limits_{j = 1}^k {\left( {1 + {{\left\| {{y_i} - {c_j}} \right\|}^2}} \right)} ^{ - 1}}\left( {{p_{ij}} - {q_{ij}}} \right)\left( {{y_i} - {c_j}} \right)$

(19)

$\frac{{\partial {L_c}}}{{\partial {c_j}}} = 2{\sum\limits_{i = 1}^k {\left( {1 + {{\left\| {{y_i} - {c_j}} \right\|}^2}} \right)} ^{ - 1}}\left( {{q_{ij}} - {p_{ij}}} \right)\left( {{y_i} - {c_j}} \right)$

(20)

${{\partial {L_c}} / {\partial {y_i}}}$ 可以传递到叠加的自动编码器，并用于反向传播以计算参数 ${{\partial {L_c}} / {\partial {M_1}}}$ 、 ${{\partial {L_c}} / {\partial {M_2}}}$ 的梯度。编码器权重的更新公式如下：

${M_1} = {M_1} - \frac{\eta }{m}\displaystyle\sum\limits_{i = 1}^m {\left( {\frac{{\partial {L_c}}}{{\partial {M_1}}} + \lambda \frac{{\partial {L_r}}}{{\partial {M_1}}}} \right)} $

(21)

译码器的权重公式更新如下：

${M_2} = {M_2} - \frac{\eta }{m}\sum\limits_{i = 1}^m {\left( {\frac{{\partial {L_r}}}{{\partial {M_2}}}} \right)} $

(22)

聚类中心 ${c_j}$ 的更新公式如下：

${c_j} = {c_j} - \frac{\eta }{m}\sum\limits_{i = 1}^m {\frac{{\partial {L_c}}}{{\partial {c_j}}}} $

(23)

式中： $m$ 是小批量的样本数； $\eta $ 是学习速率。

2.3 所提算法流程

加权PageRank改进地标表示的自编码谱聚类算法步骤：

输入　数据集 $X$ ，目标聚类数 $k$ ，地标数目 $p$ ，最近邻地标数目 $r$ ，停止阈值 $\beta $ ，迭代数目 $t$ ，停止阈值 $h$ 。

输出　实际聚类数目 $y$ ，聚类损失 ${L_c}$ ，重构损失 ${L_r}$ 。

1) 根据式(2)~(4)计算 ${\rm wpr}\left( b \right)$ 的值，迭代计算 ${\rm wpr}$ 直到满足式(5)，根据最高的 ${\rm wpr}$ 值选择 $p$ 个地标点。

2) 通过式(7)计算稀疏表示矩阵 ${{Z}}$ ，所选地标点 $p$ 和具有 $r$ 个最近邻地标点的矩阵 ${{U}}$ 。

3) 通过式(12)计算新的拉普拉斯矩阵 ${{{L}}_{{{new}}}}$ 。

4) 使用 ${{D}}_{{2}}^{{{{{ - 1}}} / {{2}}}}{{\hat{ Z}}^{{T}}}$ 作为自动编码器的输入。接着对叠加式自动编码器进行训练，得到嵌入表示 ${h_i}$ 。

5) 在最后一个隐藏层的嵌入表示 ${h_i}$ 上进行k-means聚类，以初始化聚类中心 ${c_j}$ 。根据式(22)、(23)更新自动编码器的参数和聚类中心 ${c_j}$ 。

2.4 算法复杂度分析

假设从 $n$ 个数据点中选择 $p$ 个地标，则所提算法采用加权PageRank选择地标点，该步骤的时间复杂度为 $O\left( {tpn} \right)$ ，其中 $t$ 为迭代次数。为了构造新的相似矩阵，只需根据方程计算稀疏表示矩阵 ${{Z}}$ ,这一步的时间复杂度为 $O\left( {pn} \right)$ 。堆叠式自动编码器和优化算法的时间复杂度为 $O\left( {n{D^2} + ndk} \right)$ ， $k$ 是簇数， $D$ 是隐藏层的最大单元数， $d$ 是嵌入层的维数。通常 $k \leqslant d \leqslant D$ ，所以时间复杂度可写为 $O\left( {tpn + pn + n{D^2}} \right)$ 。基于地标点的谱聚类算法^[15]的时间复杂度为 $O\left( {tpn + pn + {p^2}n + {p^3}} \right)$ ，又 $p \ll n$ ，则 ${p^3} \ll $ $ {p^2}n$ ，故 ${p^2}n + {p^3} \approx {p^2}n$ ，所以基于地标点谱聚类算法的时间复杂度可写为 $O\left( {tpn + pn + {p^2}n} \right)$ ，其中 $p$ 与 $D$ 的取值相近且远小于 $n$ ，因此，可推断本文方法与基于地标点谱聚类算法时间复杂度相当，但由于算法改进中通过采样少数几个数据点来推断数据集的全局特征，空间复杂度有所降低。

3 实验与结果分析 3.1 实验环境及性能指标

在本文算法实验中，选取了几个数据量较大的数据集进行实验，它们分别为手写数字数据集USPS、Pendigits、MNIST、英文字母表数据集LetterRec和UCI数据库中的数据集CoverType，表1给出了数据集的详细特征。本文算法实验是在Python 3.6，计算机的硬件配置为Intel Core i7-7700 CPU 3.60 GHz、16 GB内存的平台下进行。

总体而言，提出的方法在ACC和NMI上均优于其他所列的对比方法。

本文算法与文献[1]中基于nystrom的方法，文献[9]中基于叠加稀疏自动编码器聚类方法GraEn，文献[10]中基于深度学习编码的快速图聚类方法DLC，文献[14-15]基于地标点采样的快速谱聚类方法LSC-R和LSC-K，文献[17]中深层嵌入聚类方法DEC和文献[19]基于改进可拓展的nystrom方法RSNy这些算法进行实验对比。

本文实验的具体的实验参数设置如下：基于地标点采样的快速谱聚类方法LSC有两个参数需要设置，分别为地标点 $p$ 的数目，最近邻地标点 $r$ 的数目，在这里，我们统一设置 $p = 1\;000$ 和 $r = 5$ 。在加权PageRank算法中，我们设置收敛阈值 $\;\beta = {10^{ - 3}}$ 。编码器被设置为维数为 $p - 500 - 500 - $ $2\;000 - 10$ 的多完全连接层，适用于所有的数据集。解码器是维数为 $10 - 2\;000 - 500 - 500 - p$ 的编码器的镜像。并且，将最小批量设置为256个，初始学习速率 $\eta $ 设为0.1。停止阈值设为 $h = {10^{ - 3}}$ ，同时将控制嵌入表示空间失真程度的 $\lambda $ 值设为0.1。

3.2 实验结果分析

为了验证本文算法的性能，采用文献[20]中聚类准确率ACC和归一化互信息NMI两种聚类度量指标来对聚类结果进行评估和分析比较。ACC和NMI的取值范围都在 $0 \sim 1$ 之间，较高的值表示较好的聚类结果。

根据表2可以看出，基于聚类准确率(ACC)的实验结果表明，提出的加权PageRank改进地标表示的自编码谱聚类算法在USPS、Pendigits、MNIST、LetterRec、Covtype数据集上相较于基于nystrom的方法、基于地标点采样的快速谱聚类方法、基于深度学习自编码的快速图聚类方法都取得了最好的结果，所提方法在聚类准确率方面都优于以上所提其他方法。特别是在MNIST数据集上，GraEn、DLC、DEC和提出的方法这些基于深度学习自编码的谱聚类方法的聚类结果均明显高于传统nystrom的方法、RSNy方法和基于地标点的方法(LSC-R，LSC-K)，其中相较于传统nystrom的方法，本文所提的方法在MNIST数据集上聚类准确率方面提高了35.91%。相较于基于地标点的快速谱聚类方法LSC-R，提高了30.71%。可以看出，所提方法相较于这些方法聚类精度的提高是巨大的。相较于其他几种快速谱聚类方法，所提方法在MNIST数据集上分别提高了18.73%和16.91%，总体而言也是相当可观。同时，从表中可以看出基于地标点的方法在USPS、Pendigits、LetterRec和Covtype数据集上的聚类准确率比基于自编码的方法在一定程度上还要好。但是所提的方法相较于这些方法而言，实验得到的聚类准确率方面均是最优的。

同时，根据表3可以看出所提的方法与其他几种方法相比在NMI上均得到了提高，并且相较于其他几种方法是最优的。同样在MNIST数据集上，所提的方法相较于传统nystrom方法和基于地标的快速谱聚类方法都取得了大幅的提高。相对于传统nystrom方法和基于地标点的谱聚类方法LSC-R，所提的方法在NMI上分别提高了40.31%和29.22%，在其他数据集上，所提的方法相较于其他方法而言也均有不同幅度的提高。从表2和表3中均可以看出，对于最原始的基于自编码的方法GraEn。在MNIST数据集上，它的ACC和NMI相较于传统nystrom方法和基于地标点的谱聚类方法而言均有所提高。与DEC方法相比，DEC方法的ACC和NMI分别提高了4.69%和8.96%，结果表明，联合更新聚类中心和学习嵌入表示可以提高聚类结果，这也适用于其他4个数据集。尽管在USPS数据集上，基于自编码的方法的聚类精度没有基于地标点方法的聚类精度好，但是在其他几个高维大规模数据集上基于自编码的方法在聚类精度方面要更好，说明基于自编码的方法和所提的方法更加适用于高维的大规模数据。

总体而言，提出的方法在ACC和NMI上均优于其他所列的对比方法。

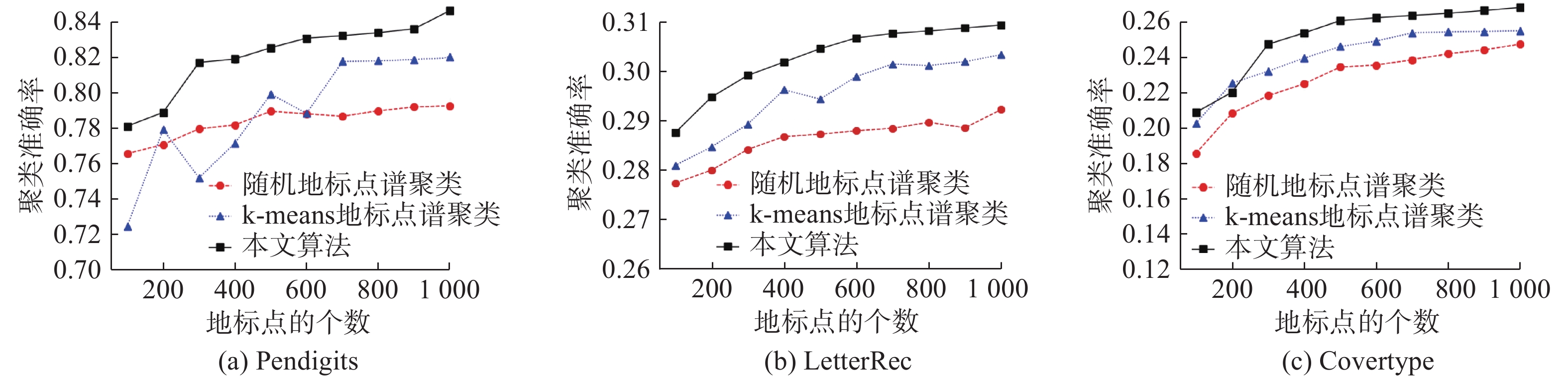
图1和图2显示了选取的3个不同的数据集中，随着地标点数量 $p$ 从100~1 000变化，基于地标点的谱聚类算法LSC-R和LSC-K与所提方法的聚类指标ACC和NMI的对比实验。从图1中可以看出，随着地标点个数的增加，3种方法的ACC也随之增加，总体均呈现增幅形式，最后均趋于稳定，并且所提算法在3个数据集上的ACC均高于其他两种对比算法的ACC。

由图2可知，所提的方法在LetterRec和Covtype数据集上在初始阶段，随着地标点的增加NMI存在低于其他方法的情况，这是因为所选LetterRec数据集的字符图像基于26种不同的字体，26种字体中的每一个字母都被随机扭曲。Covertype数据集是一个从地图变量预测森林覆盖类型的数据集，它们都主要是在荒野地区发现的，所以覆盖类型在实际地理上是非常接近的，相对于其他手写数字数据集而言，这两个数据集数据特性更加复杂。并且在选取较少地标点时，采用加权PageRank算法选择地标点与随机选择地标点和基于k-menas算法选择地标点相比并不能展现出较大的优势，所以在选取较少地标点时聚类性能存在低于其他方法的情况，但在总体情况下，随着选取地标点的增多，所提算法展现出较快的增长优势和较好的聚类性能，在地标点达到1 000左右时趋于稳定，展现出均优于对比算法的聚类性能。

4 结束语

本文提出了一种加权PageRank改进地标表示的自编码谱聚类算法，该算法利用加权PageRank算法选取数据亲和图中最具代表性的点作为地标点，然后以选定的地标点与其他数据点之间的相似度矩阵作为叠加自动编码器的输入，以减少内存消耗，用叠加式自动编码器代替拉普拉斯矩阵的特征分解，降低了时间复杂度。通过迭代优化基于KL散度的聚类损失对聚类进行了进一步细化，结合重构损失和聚类损失考虑了数据的局部结构，同时更新了自动编码器和聚类中心的参数。证明了该方法对不同类型数据集的有效性，实验结果表明，与传统谱聚类算法、基于地标点的谱聚类算法和其他基于深度学习自编码的方法相比，在几个大规模的数据集上，提出的方法具有更好的聚类性能。在未来，致力于研究更加有效的地标点采样方法，结合优化的自动编码器从而更好的提高谱聚类的聚类性能。