模板匹配是基于已知的模板在待匹配图中找到最佳匹配位置的过程，是数字图像处理中一个重要内容，已广泛应用于工业对位^[1]、目标检测识别^[2-3]、跟踪^[4]等。近年来模板匹配研究已经有一些有效的算法^[5]。但现有的模板匹配过程大多将模板与场景图像进行卷积，计算模板与场景图像之间的相似度以确定位置^[6]。由于相关性的计算量很大，因此需要低成本的相关性算法进行实时处理。文献[7]提出了大量相关类型的算法。这些方法大多分为两类：1)对模板和场景图像都使用图像金字塔，并通过自顶向下搜索来执行匹配^[8]；2)采用两次搜索算法，在第1次搜索过程中使用亚模板在粗网格中搜索，第2次在先前发现的候选点附近搜索更好的匹配^[9]。但是，当检测目标发生旋转时，以上算法将不再有效。

近年来国内外学者相继提出了一些可以任意旋转的方法。Lowe^[10]提出了一种尺度不变特征变换(SIFT)，它利用检测区域的梯度分布，具有缩放和旋转不变性，但是当图像特征点过少或出现重复结构时，基于SIFT的匹配容易失败，且运算量大。文献[11]提出一种将SIFT和旋转不变LBP结合的图像匹配方法，提高了运算速度，但是当图像细节纹理过多时，该算法匹配性能将显著降低。基于圆投影的旋转不变性，Tang等^[12]提出了用圆的各向同性和投影特征进行任何角度匹配，但原始的圆投影匹配计算量较大。后续不断有学者对圆投影算法进行改进。Tsai等^[13]使用环形投影技术表示多通道图像中的模板，通过计算彩色环形投影信息之间的NCC来快速选择候选模板，然后通过旋转模板来估计旋转。为了减少计算复杂度，文献[14]使用了一种快速检测到相似候选项的消除策略。文献[15]将原始圆投影向量进行改进，使得改进后的圆投影匹配算法对光照、噪声、对比度变化有更好的鲁棒性。文献[16]提出了两阶段匹配方法，利用第1阶段环形投影的矢量和选择候选点，然后对第1阶段存留的候选点使用旋转不变属性进行Zernike矩模板匹配。文献[17]将圆投影和序贯相似性检测结合起来，通过跳跃大量匹配点，减少非匹配点的计算量。文献[18]提出了一种扩展的圆投影算法(extended RPT，E-RPT)，通过添加辅助点约束的方法来有效提高匹配精度。但是上述算法忽略了圆投影向量本身对于同质区域无法识别的问题，同时具有计算复杂度较高、识别率较低等缺点。

针对上述应用中的问题，本文设计了一种新的改进的圆投影匹配算法，主要贡献为：1)提出了混合圆投影向量，提供稳定和独特的特征；2)使用图像金字塔，结合顶层局部聚类和逐层金字塔筛选，提升运算速度；3)构建角度直方图，估计精确的旋转角度。实验结果表明，本算法对任意旋转的物体能精确地定位并估计角度，计算速度也有了明显提升。

1 标准圆投影匹配算法

圆投影匹配以模板中心为圆心，模板图片最大内切圆的半径R为半径创建圆型模板。如图1所示，采用极坐标系表示图像T，以图像中心“O”为圆心建立极坐标系，定义半径为r上的圆投影向量P(r)为

$P(r) = \sum\limits_{\theta = 0}^{2\pi } {T(r,\theta )} ,\;0 \leqslant r \leqslant R$

(1)

式中R为图像最大的内切圆半径。

当图像旋转时，图像上的像素会随着图像的旋转而旋转，P(r)为固定量，因此圆投影算法抗旋转。当半径r不同时，所对应图像圆投影向量为

${ P} = (p(0),p(1), \cdots ,p(R))$

(2)

为了方便计算，有时也定义圆投影向量P(r)为

$P(r) = \frac{1}{{n(r)}}\sum\limits_{\theta = 0}^{2\pi } {T(r,\theta )} ,\;0 \leqslant r \leqslant R$

(3)

式中n(r)为半径为r的圆周上的像素个数。

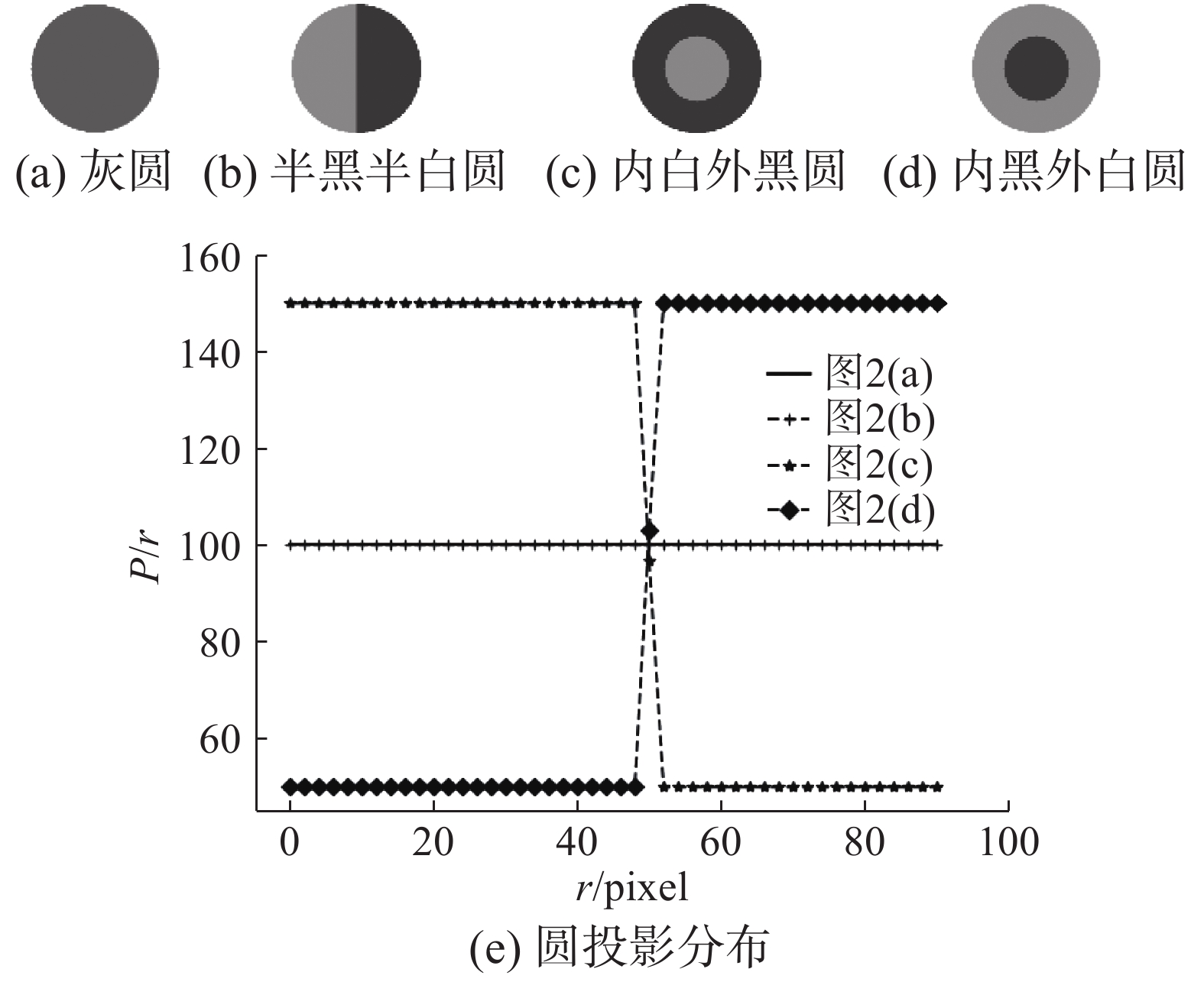
然而，标准圆投影向量对于相近灰度值(同质)的区域是无法识别的。如图2所示，图2(a)为半径为r的圆，圆上所有像素点灰度值都为100，图2(b)为等半径圆上，一半像素点值为50，另一半为150，计算圆投影向量如图2(e)所示，可以看到原始圆投影向量对于图2(a)、(b)这种同质区域是无法区别的。

2 改进的圆投影算法 2.1 圆投影向量的改进

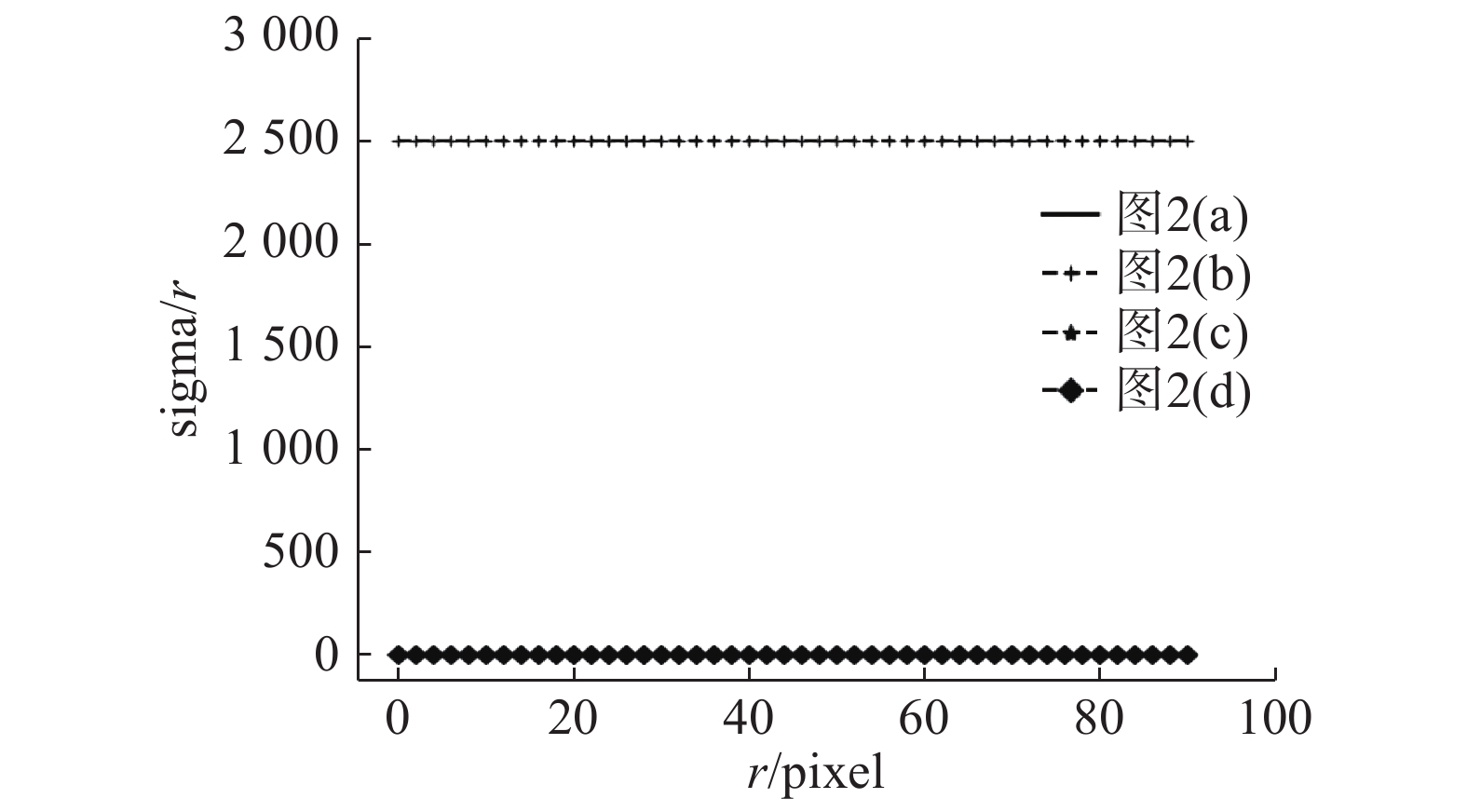
圆投影变换得到图像特征，是为了降低计算复杂度，而且这些特征必须是稳定而且独特的。而原始圆投影向量对于图2(a)、(b)这种相近灰度值(同质)的区域无法区分，因此必须找到这些图片的独特之处来加以区分。为解决这个问题，引入了对应半径r上的方差投影 $\sigma (r)$ ，定义为：

$\sigma (r) = \sqrt {\frac{1}{{n(r)}}\sum\limits_{\theta = 0}^{2\pi } {{{[T(r,\theta ) - C(r)]}^2}} } $

(4)

式中： $T(r,\theta )$ 为模板图上对应点的灰度值； $C(r) = $ $\dfrac{{P(r)}}{{n(r)}} = \dfrac{1}{{n(r)}}\displaystyle\sum\limits_{\theta = 0}^{2\pi } {T(r,\theta )} $ 为半径为r的圆上灰度平均值；n(r)为半径为r的圆周上的像素个数。

如图3所示，方差投影向量表明图2(b)和图2(a)、(c)、(d)有显著区别。图2(a)、(c)、(d)这3类图片无法用方差投影区分，但是可以用式(3)中的圆投影向量区分出来，如图2(e)所示。

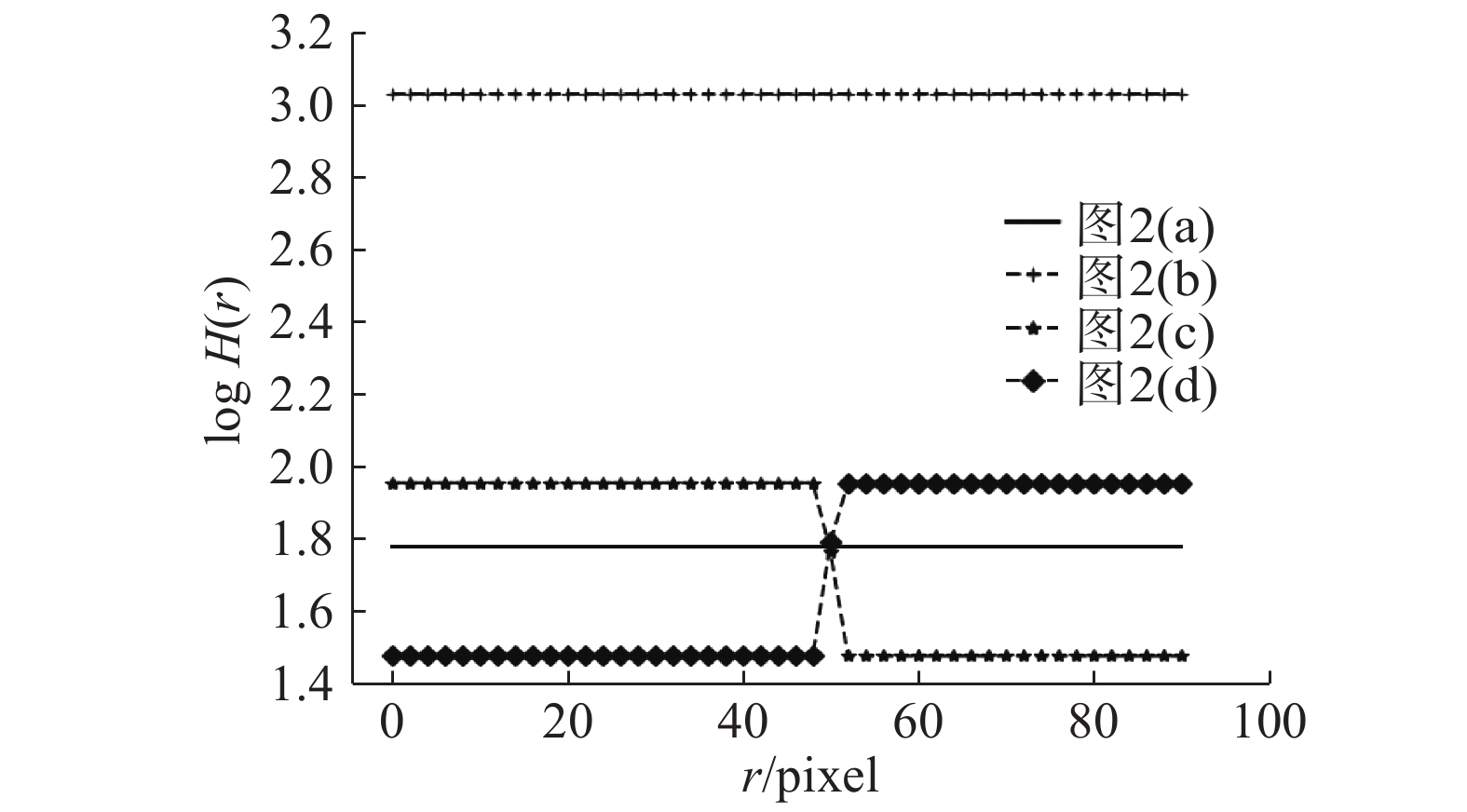
为了兼顾稳定性和独特性，结合式(3)和式(4)，得到了混合投影，用于模板图和待搜索子图的混合投影H_p(r)、H_s(r)分别定义如下：

${H_p}(r) = {\omega _m} \times {P_p}(r) + {\omega _\sigma } \times {\sigma _p}(r)$

(5)

${H_s}(r) = {\omega _m} \times {P_s}(r) + {\omega _\sigma } \times {\sigma _s}(r)$

(6)

式中： ${\omega _m}$ 、 ${\omega _\sigma }$ 分别为均值投影和方差投影的权重因子。

如图4所示，为图2(a)~(d)对应的混合投影向量分布图。此处使用 ${\omega _m} = 0.6,{\omega _\sigma } = 0.4$ . 可以看到，通过混合圆投影变换，4幅图片有较好的区分度。

2.2 相似度函数

使用归一化互相关(normalized cross correlation, NCC)计算匹配的相似度，具体计算如下：

$f = \dfrac{{\displaystyle\sum\limits_{r = {R_{\min }}}^{{R_{\max }}} {[{H_p}(r) - \overline {{H_p}} ] \times [{H_s}(r) - \overline {{H_s}} ]} }}{{\displaystyle\sum\limits_{r = {R_{\min }}}^{{R_{\max }}} {{{[{H_p}(r) - \overline {{H_p}} ]}^2}} \times \displaystyle\sum\limits_{r = {R_{\min }}}^{{R_{\max }}} {{{[{H_s}(r) - \overline {{H_s}} ]}^2}} }}$

(7)

得到的相似度f在−1~1。待搜索子图和模板完全匹配时，f=1。

2.3 图像金字塔加速

为了提高匹配效率，这里使用了图像金字塔进行加速。这里分2个步骤：1)将图像降采样到给定层，使用缩小后的图像和模板进行粗搜索，得到若干候选点；2)逐层对候选点过滤，直到选出最匹配的点。假设取样层数为n−1层，设置每一层的相似性阈值thresh[n]={T₀,T₁,···,T_n-1}，只有大于阈值的匹配点才能够被保留下来。

2.3.1 顶层局部聚类

在最顶层使用对应层数模板和待匹配子图的圆投影向量匹配。为了提高效率，这里引入了局部聚类算法，基本思想是将候选点按照位置分成若干个团簇，每个团簇内的点拥有同一个簇编号，不同簇彼此不相邻。

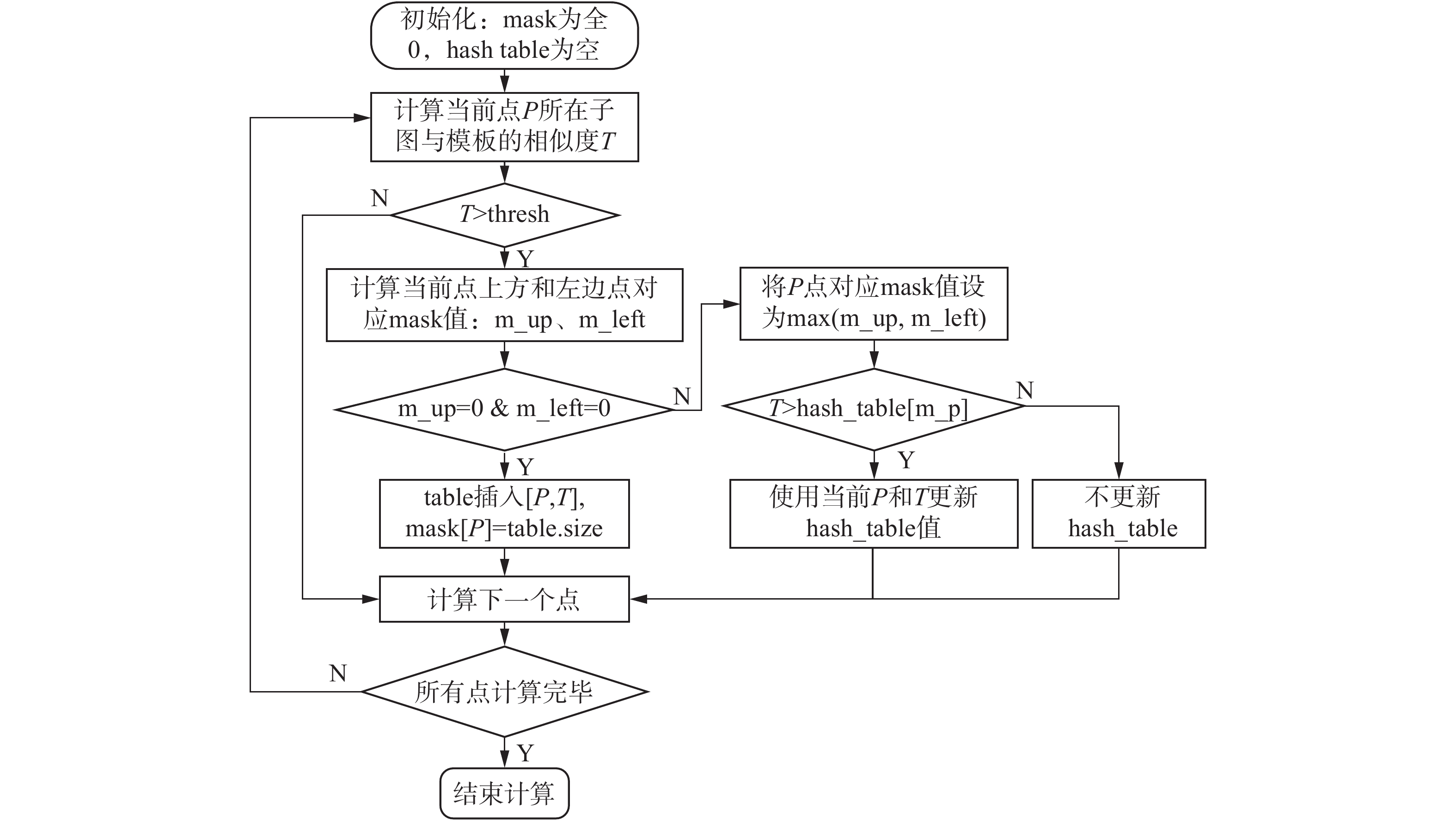
如图5所示的流程图，算法流程表述如下：

1) 构建一个和待匹配图相同大小的掩码图mask(里面存储候选点所在团簇编号)，以及团簇相关信息的hash_table(里面存储簇内最相似点位置和相应的相似度)。

2) 计算某点P所在子图与模板的相似度T，如果T大于相似度阈值T_n-1，则计算该点上方和左边点对应的mask值m_up和m_left。

① 如果m_up和m_left不都为零，说明这是已经存在的某个簇的一部分，将P点加入到该簇中，即将该点对应mask值设置为m_up和m_left的较大值，如果P点对应相似度大于簇中最相似点的相似度，则更新簇中最相似点的位置和相似度，否则不更新hash_table；

② 反之，如果m_up和m_left都为零，说明P是新的点，将P对应位置和相似度放入hash_table中，将对应mask点的值设置为hash_table，以此建立新的簇种子点。

3) 计算下一个点，重复步骤2)，直到所有的点遍历完，计算结束。

4) 最终将hash_table中的点位置保存下来。

以LENA图像为例，使用局部聚类之后的mask图像如图6所示。

可以看到，使用局部聚类，可以在线性时间内快速滤除干扰点，将相邻候选点聚集成簇，减少后续候选点数，减少了计算量。

2.3.2 逐层金字塔筛选

上一层得到若干候选点之后，传入本层，对候选点相应位置进行扩大区域方法搜索，如果计算相似度大于阈值，将其传入到本层候选点集合中。但是在本层候选集合中有很多候选点，全都传入下一层进行扩散搜索是非常耗时的。为了减少运算量，这里引入非极大值抑制(non-maximum suppression, NMS)，选取本层最终候选点。

NMS的基本思想是保留局部最大值、抑制非极大值，计算流程如下：对于候选点列表B及其对应的相似度S，结果候选点集合为D，采用下面的计算方式：

1) 将候选点集合B根据相似度得分进行降序排列。

2) 选择具有最大得分的点P，将其从B集合中移除并加入到最终的候选点集合D中。

3) 计算B中剩余候选点中与P距离dis，将dis小于阈值d(此处阈值一般选择为模板的内切圆半径) 的点从B中移除。

4) 重复这个过程，直到B为空或D中候选点数已超过一定数量。此时D中保留的候选点，作为本层最终的候选点集。

NMS流程示意图如图7所示。刚开始O₁~O₄计算得到的分值分别为0.9、0.7、0.6、0.8；通过选择最大得分O₁加入候选集D并在B中删除，删除B中与O₁距离在r以内的点(O₂、O₃)，在B中选择最大得分的点(仅有O₄)，加入到D中，并将其从B中删除，得到D{O₁、O₄}。

使用NMS减少了相邻候选点的出现，避免结果的重叠，同时可以根据输入目标点数的要求，得到最终指定数量的匹配目标。

2.4 角度估计

由于保存了所在圆环上像素的灰度，就可以比较容易地计算出旋转角度。图8为环上像素值分布图(r=100)。

可以看到，旋转之后，环上所有像素的灰度值发生了环形移位(简称环移)。由此，在半径为r的环上，旋转角度 ${\theta _r}$ 可以定义为

${\theta _r} = {k_r} \times {\varphi _r}$

(8)

式中： ${k_r}$ 为偏移量； ${\varphi _r}$ 为步进角度， ${\varphi _r} = {360^ \circ }/{N_r}$ ，其中 ${N_r}$ 为半径为r的环上像素数量。

偏移量 ${k_r}$ 定义为

${k_r} = \arg \max ({\delta _r}(k)),k \in [0,{N_r}]$

(9)

${N_r}$ 为半径为r的环上像素数量。 ${\delta _r}(k)$ 为偏移k像素之后和模板中环的归一化互相关系数，定义为

${\delta _r}(k) = \frac{{\displaystyle\sum\limits_{n = 0}^{{N_r}} {[{{{p}}_r}(n) - \overline {{{{p}}_r}(n)} ] \times [{{{p}}_r}'(n) - \overline {{{{p}}_r}'(n)} ]} }}{{\displaystyle\sum\limits_{n = 0}^{{N_r}} {{{[{{{p}}_r}(n) - \overline {{{{p}}_r}(n)} ]}^2}} \times\sum\limits_{n = 0}^{{N_r}} {{{[{{{p}}_r}'(n) - \overline {{{{p}}_r}'(n)} ]}^2}} }}$

(10)

式中： ${{{p}}_r}(n)$ 和 ${{{p}}_r}'(n)$ 分别为模板图和待搜索子图对应半径圆上像素灰度值。

采用式(8)~(10)，就可以计算出半径为r处候选点的旋转角度。为了提升角度估计的准确性，提出了一种用角度直方图(angle histogram estimation, AHE)估计角度的方法。详细表述为

1)构建一个维数为360的数组a[360]，存放旋转角度对应的环的数量。

2)计算半径为r处的旋转角度 ${\theta _r}$ ，四舍五入后angle放入直方图，即a[angle]加1。

3)对所有半径进行步骤2)，最终构建角度分布的直方图。

4)检查步骤3)得到的角度直方图中的众数，即为最终角度。

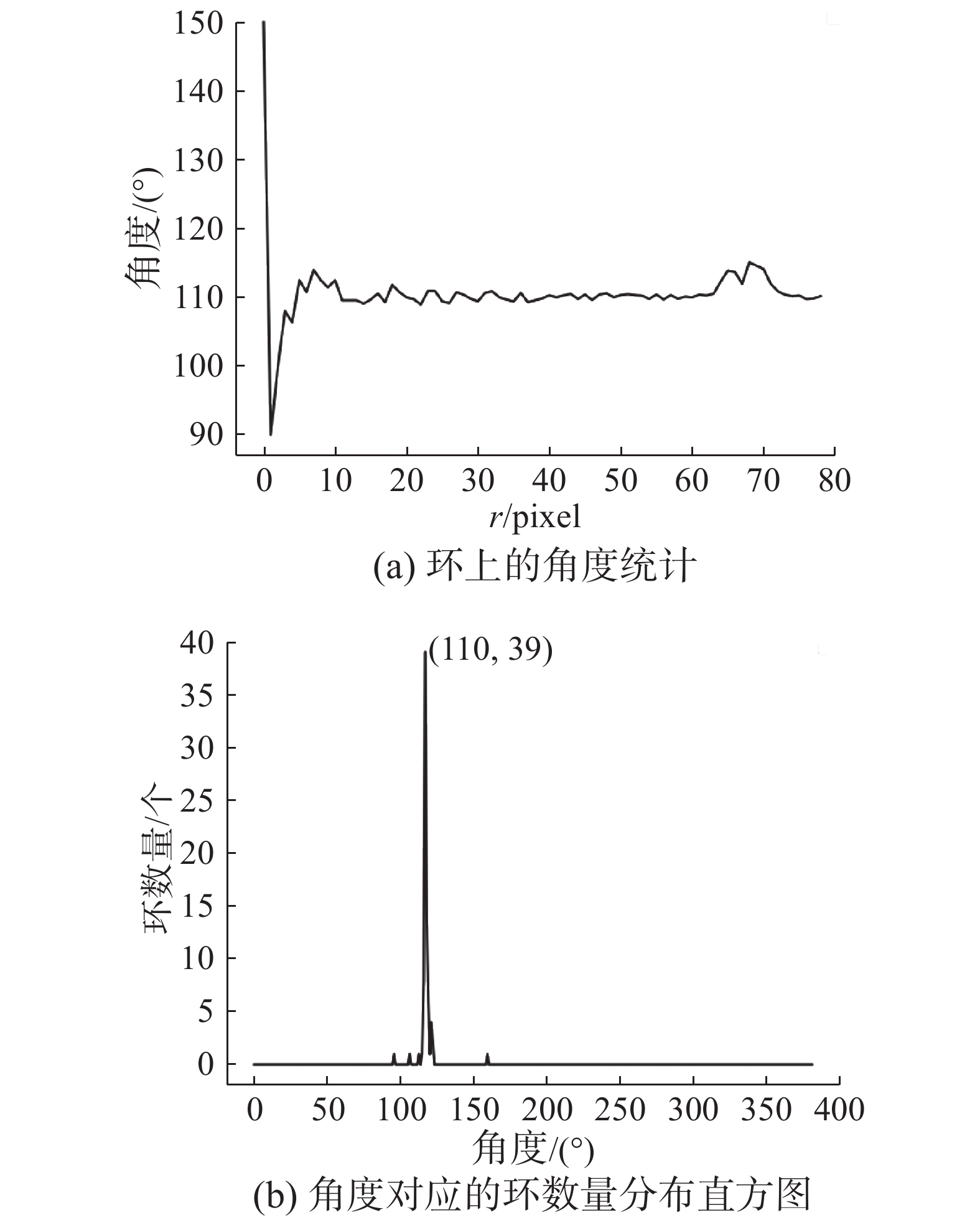
图8(b)以图8(a)为模板，计算旋转角度之后的角度统计图如图9。

可以看到，通过AHE，计算得到最终角度，为直方图中的众数(即尖峰即110°)，和理论旋转角度相符合。使用AHE可以对角度有较好的估计，避免r过小时计算角度误差较大，另外，对于环上存在同质区域(灰度值分布一致)时角度计算不正确的情况，也具有一定的抗干扰能力，提高了角度估计的鲁棒性。

2.5 计算复杂度分析

假设模板图像T大小为 $m \times m$ (半径为 $\dfrac{m}{2}$ )，搜索图像S大小为 $M \times M$ 。

原始圆投影匹配中，预先计算模板中的圆投影向量，然后进行匹配。在匹配过程中，先计算搜索图中每一个子图的圆投影向量，然后计算和模板圆投影的相似度，最后取其相似度最大值为最佳匹配位置。其中子图数量为 $\left( {M - m} \right) \times \left( {M - m} \right)$ ，每一个子图计算圆投影时间为 $O\left( {m \times m} \right)$ ，计算相似度时间为 $O\left( {m \times m} \right)$ ，整个匹配过程的时间复杂度为 $O\left[ {{{\left( {M - m} \right)}^2} \times {m^2}} \right]$ 。随着模板和搜索图尺寸的增加，搜索时间将成倍増长。

本文算法使用金字塔策略，采用局部聚类和逐层筛选策略优化搜索速度。假设降采样到L层，计算缩小后的模板混合圆投影向量，则缩小的模板大小为 $\dfrac{m}{{{2^L}}} \times \dfrac{m}{{{2^L}}}$ ，搜索子图数量为 ${(M - m)^2}/$ ${2^{L + 1}} $ ，顶部聚类时间为 $O\left[ {{{\left( {M - m} \right)}^2} \times {m^2}/{2^{(L + 1)}}} \right]$ 。只有少数候选点进入后续筛选过程，假设只保留n个点进入最后匹配，则后续匹配耗时为 $O(n \times {m^2})$ ，整体匹配过程时间复杂度为 $O\Bigg\{ {m^2} \times \Bigg[\dfrac{{{{(M - m)}^2}}}{{{2^{L + 1}}}} + n\Bigg]\Bigg\} $ 。保守估计，当M=400，m=100，L=2，n=3时，本文算法相对原始圆投影算法提升了约8倍。

3 实验结果

使用上述方法，本文试验了多组同一目标在发生不同变化下的匹配效果。为了验证本方法的有效性，将结果与文献[17]和文献[19]中的方法进行了比较。所有实验均在一台使用VS2013、OpenCV3.0.0、Intel Core i5 1.6 Hz CPU和8 GB内存的电脑上进行。

3.1 光照变化

图10是不同光照下使用工业相机拍摄的槟榔干图片，图10(a)为模板图片，图10(b)~(f)为光照变化时匹配图片，圆圈内为匹配结果。可以看到，本算法针对过曝、欠曝图片都可以很好地识别出来，具有很强的光照不变性。

3.2 角度估计结果

图11是旋转测试图片，用于估计所提出算法的角度精度，图11(a)为旋转基准图( $1\;296 \times 972$ )，图11(b)为模板( $180 \times 180$ )。将原始图像在0~360°范围内每间隔 10°做一次旋转，一共得到36张图片，然后使用本文的算法，对旋转后的 36幅图片和原始基准图进行匹配。角度误差为匹配出来的角度和真实旋转角度之差的绝对值。为了提供一个全面的精度评价，使用误差Er的3个性能指标来定量地展示性能：误差的均值Er_m、误差的标准差Er_std和最大误差Er_max。匹配结果如表1所示。

从表1可以看出，本算法误差均值、标准差、最大值分别为0.098 8、0.183 6、1.107。文献[17]中使用序贯相似性检测对匹配进行加速，但只用圆投影向量进行目标的定位，并没有计算旋转角度，这里不便进行比较。在文献[19]中，角度精度严重依赖于预先建立的旋转模板和使用归一化互相关系数(NCC)估计出来的位置。如果没有精确定位将无法准确估算出角度，文献[19]使用9个预先建立的旋转模板。可以看到，本文算法能进行较好的角度估计，且适用于任意旋转的物体。

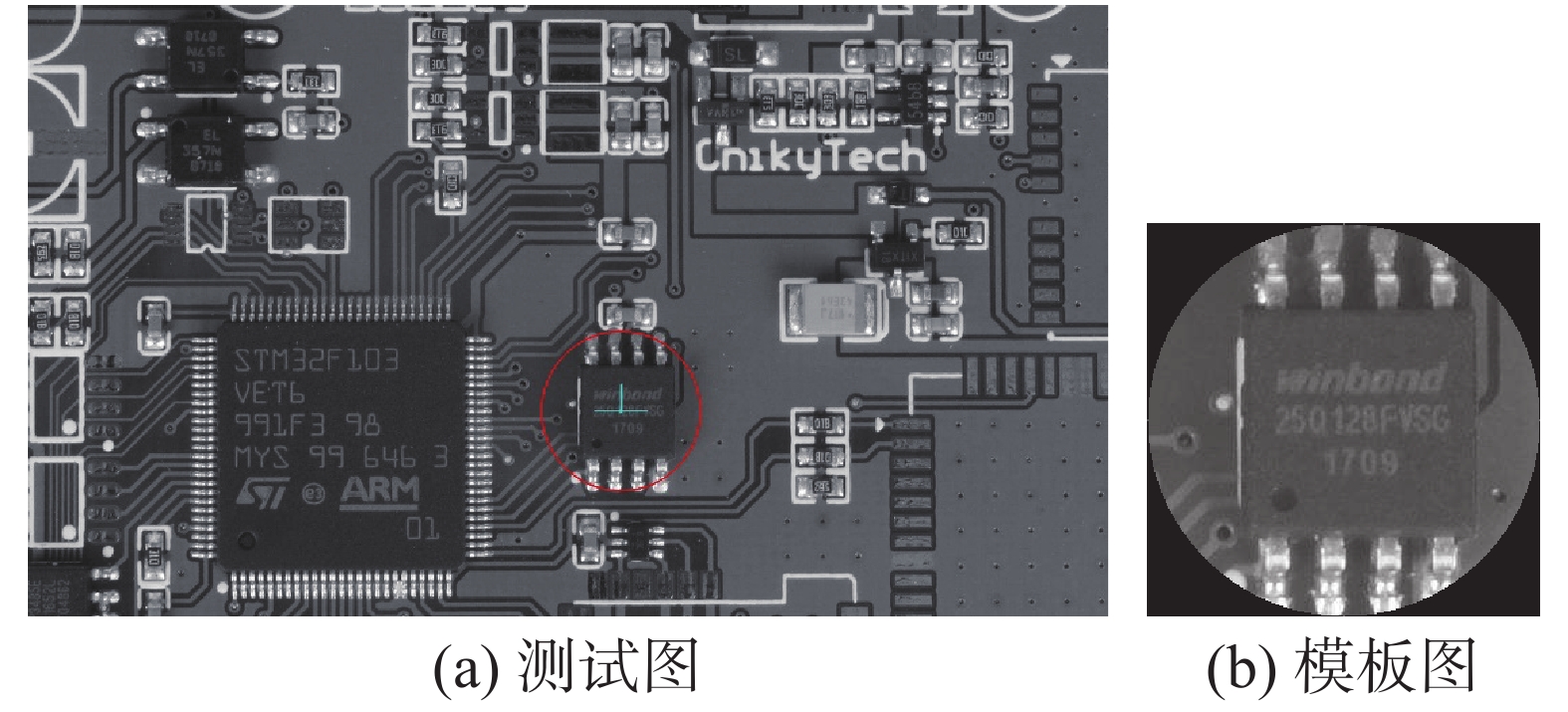
3.3 运行速度测试

使用工业相机捕获的PCB图像进行了运行速度的测试。所用测试和相应的模板图像如图12所示。测试图像的大小为 $1\;920 \times 1\;080$ ，模板图像为 $283 \times 283$ 。本实验根据匹配结果对计算性能进行了评估。此外，为了保证比较的公平性，本文还利用图像金字塔搜索框架对比较方法进行了优化。效率和金字塔层数的统计结果如表2所示。

由表2可以看出，本方法相对其他方法在运行效率上有明显的优势，另外金字塔搜索策略可以显著提高匹配效率。

4 结束语

本文提出了一种快速的基于旋转不变圆投影向量的模板匹配方法。结合混合圆投影向量和图像金字塔搜索策略，可以减少计算量，提升匹配效率。另外结合环移和角度直方图统计，可以精确地估计出旋转角度。结果表明，该方法的旋转估计优于其他同类方法。此外，该算法可以在旋转、偏移、光照变化场景图像中获得准确、鲁棒的结果。各种实验结果表明，该方法适用于工业场景中的图像匹配。