可能性匹配知识迁移原型聚类算法

引用本文

聂飞, 高艳丽, 邓赵红, 等. 可能性匹配知识迁移原型聚类算法[J]. 智能系统学报, 2020, 15(5): 978-989. DOI: 10.11992/tis.201810028.

NIE Fei, GAO Yanli, DENG Zhaohong, et al. Possibility-matching based knowledge transfer prototype clustering algorithm[J]. CAAI Transactions on Intelligent Systems, 2020, 15(5): 978-989. DOI: 10.11992/tis.201810028.

基金项目

国家自然科学基金面上项目（61170122）

通信作者

邓赵红. E-mail：dengzhaohong@jiangnan.edu.cn

作者简介

聂飞，硕士研究生，主要研究方向为智能计算与模式识别;
高艳丽，主要研究方向为不确定性人工智能和计算技术;
邓赵红，教授，主要研究方向为不确定性人工智能及其应用。主持国家和省部级项目多项，获得教育部科技进步一等奖。Neuro computing等6个国际期刊编委。发表学术论文100余篇

文章历史

收稿日期：2018-10-24
网络出版日期：2019-05-22

Contents Abstract Full text Figures/Tables PDF

可能性匹配知识迁移原型聚类算法

聂飞 ¹, 高艳丽 ², 邓赵红 ¹, 王士同 ¹

1. 江南大学数字媒体学院，江苏无锡 214122;
2. 江南计算机技术研究所，江苏无锡 214083

收稿日期：2018-10-24；网络出版日期：2019-05-22

基金项目：国家自然科学基金面上项目（61170122）

作者简介：聂飞，硕士研究生，主要研究方向为智能计算与模式识别;
高艳丽，主要研究方向为不确定性人工智能和计算技术;
邓赵红，教授，主要研究方向为不确定性人工智能及其应用。主持国家和省部级项目多项，获得教育部科技进步一等奖。Neuro computing等6个国际期刊编委。发表学术论文100余篇.

通信作者：邓赵红. E-mail：dengzhaohong@jiangnan.edu.cn.

摘要：针对迁移原型聚类的优化问题，本文以模糊知识匹配迁移原型聚类为基础，介绍了聚类场景中从源域到目标域的迁移学习机制，明确了源域聚类中心辅助目标域得到更好的聚类效果。但目前此类迁移机制依然面临如下的挑战：1）如何克服已有迁移原型聚类方法中不同类别间的知识强制性匹配带来的负作用。2）当源域与目标域相似度较低时，如何避免模糊强制性匹配的不合理性以及过于依赖源域知识的缺陷被放大。为此，研究了一种新的迁移原型聚类机制，即可能性匹配知识迁移原型机制，并基于此实现了2个具体的迁移聚类算法。借鉴可能性匹配的思想，该算法可以自动选择和偏重有用的源域知识，克服了源域和目标域之间的强制性匹配限制，具有较好的可调节性。研究结果表明：在不同迁移场景下模拟数据集和真实NG20groups数据集上的实验研究表明，提出的算法较已有的相关算法展现了更好的性能。

关键词：迁移原型聚类迁移学习机制强制性匹配可能性匹配原型聚类可调节性

Possibility-matching based knowledge transfer prototype clustering algorithm

NIE Fei ¹, GAO Yanli ², DENG Zhaohong ¹, WANG Shitong ¹

1. School of Digital Media, Jiangnan University, Wuxi 214122, China;
2. Jiangnan Institute of Computing Technology, Wuxi 214083, China

Abstract: Aiming at the optimization problem of migration prototype clustering, this paper introduces a migration learning mechanism from the source domain to the target domain in the clustering scene, considering fuzzy knowledge matching migration prototype clustering, and clarifies that the source domain clustering center assists the target domain to obtain better clustering effect. However, this method still faces the following challenges: 1) how to overcome the negative effect brought by knowledge matching among different classes in existing transfer prototype clustering methods. 2) when the similarity between the source domain and target domain is low, how to avoid the irrationality of fuzzy mandatory matching and the magnification of the defect of overdependence on knowledge from the source domain. Therefore, a new transfer prototype clustering mechanism called possibility matching-based knowledge transfer prototype clustering algorithm is proposed, and two transfer prototype clustering algorithms are further presented. Referring to the idea of possibility matching, the proposed algorithm can automatically select and focus on useful source domain knowledge, overcome the constraint of mandatory matching between the source domain and target domain, and has better adjustability. Experimental results on synthetic datasets and real NG20 text datasets in different transfer scenarios show that the proposed algorithms outperform the existing related algorithms.

Key words: transfer prototype clustering transfer learning mechanism mandatory matching possibility matching prototype clustering adjustability

近年来，迁移学习^[1]已经引起了广泛的关注和研究。迁移学习在学习过程中利用来自源域的有用信息来辅助获得目标域的有效模型。其主要假设或特点可以总结如下：1) 目标域中的数据不足以生成良好的模型。2)源域与目标域不同但在一定程度上相似，这使得源域上的训练模型不能直接适用于目标域，但源域知识对于目标域模型的学习是有用的。3)迁移学习的关注点在于增强目标域的建模效果，源域仅用于辅助学习的功能。

在过去的十年，迁移学习已被广泛地研究并用于各种场景，如文本分类^[2]和室内WiFi位置估计^[3]。在已有研究中，从应用场景的角度迁移学习一般可以分为如下4类：1)分类^[4-8]; 2)特征提取^[9-10]; 3)回归^[11-15]和4)聚类^[16-17]。尽管现实世界中的聚类应用范围很广，较之于分类、回归和特征抽取，聚类方面迁移学习技术的研究还非常有限。

作为一个重要的研究方向，聚类技术得到了广泛的关注和研究。聚类算法大致可以划分以下几类：1)划分式聚类算法(partitioning method)^[18]；2)层次化聚类算法(hirearchical method)^[19-20]；3)基于网格和密度的聚类算法(gird-based and density-based method)^[21-22]；4)其他聚类算法,如ACODF(ant colony optimization with different favor，具有不同偏好的蚁群算法)^[23]。在这些传统聚类学习中，必须有足够可利用的训练样本才能够充分发挥算法应有的性能。对此，迁移学习技术可以有效地解决数据不充分给聚类带来的挑战。

为了使传统聚类算法适应样本不足的场景，已有一些迁移聚类算法被提出，并展现了一定的有效性，如Dai 等^[16]提出的Self-taught clustering (STC)自学习聚类，以及Hang等^[24]提出的transfer affinity propagation clustering algorithm 迁移近邻传播聚类算法等聚类算法。特别地，文献[25]提出了一个面向原型聚类的迁移聚类框架，并实现了几个具体的迁移原型聚类算法。提出的多个迁移聚类算法较好地解决了在数据集不充分情景下，如何利用相关场景知识辅助提高当前场景聚类性能的问题。

虽然文献[25]中的几种迁移原型聚类展现出了较好的迁移学习能力，但是其模糊知识匹配迁移学习机制，也还有一定的局限性，主要表现在：1)源域和目标域间不同类别间的知识强制性匹配可能带来负作用。2)当源域与目标域相似度较低时，模糊强制性匹配的不合理性以及过于依赖源域知识的缺陷被放大。

针对已有迁移原型聚类算法存在的上述不足，本文提出一种新的迁移聚类知识匹配策略，即可能性匹配知识，并基于此提出了2种具体的算法。通过借鉴可能性度量的思想，提出的算法可以自动选择和偏重有用的源域知识，克服了源域和目标域之间的强制性匹配限制，具有较好的可调节性。在不同迁移场景下模拟数据集和真实NG20groups数据集上的实验研究表明，提出的算法较之已有的相关算法展现了更好的性能。

1 基于模糊知识匹配迁移的原型聚类算法 1.1 模糊C均值聚类和迁移FCM聚类E-TFCM

在众多原型聚类算法中，FCM是一个被广泛应用的算法。它的目标函数定义如下：

${\rm FCM}:\mathop {\min }\limits_{{ U},{ V}} {J_{\rm FCM}} = \sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {u_{ij}^m{{\left\| {{{{x}}_j} - {{{v}}_i}} \right\|}^2}} } $

${\rm s.t}.\;\;\;\;{u_{ij}} \in \left[ {0,1} \right],{\rm{ }}\sum\limits_{i = 1}^C {{u_{ij}}} = 1$

$0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N$

(1)

式中： $C$ 是聚类个数 $\left( {i = 1,2, \cdots ,C} \right)$ ； $N$ 是数据样本个数； ${{{x}}_j} \in {{\bf R}^d}$ 是第 $j$ 个样本点； ${u_{ij}}$ 表示第 $i$ 个数据 ${{{x}}_j}$ 属于第 $j$ 类的模糊隶属度； ${{ v}_i}$ 表示第 $i$ 类的聚类中心。

为了让FCM具有迁移学习的能力，文献[25]提出了迁移FCM聚类算法E-TFCM(extended transfer FCM)。该算法的优化目标函数如下：

$\begin{gathered} \mathop {\min }\limits_{{ U},{ V},{ R}} \mathop J\nolimits_{\rm E - TFCM} \!=\! \sum\limits_{i = 1}^{\mathop C\nolimits_t } {\sum\limits_{j = 1}^N {\mathop u\nolimits_{ij}^{\mathop m\nolimits_1 } \mathop {\left\| {{{{x}}_j} - {{{v}}_i}} \right\|}\nolimits^2 \!+\! \mathop {\textit{λ}} \nolimits_1 \sum\limits_{i = 1}^{\mathop C\nolimits_t } {\sum\limits_{l = 1}^N {\mathop r\nolimits_{il}^{\mathop m\nolimits_2 } \mathop {\left\| {{{{\tilde{ v}}}_l} - {{{v}}_i}} \right\|}\nolimits^2 } } } } \\ {\rm s.t.} \;\;\;\;\;\; {u_{ij}} \in \left[ {0,1} \right],{\rm{ }}\sum\limits_{i = 1}^{\mathop C\nolimits_t } {{u_{ij}}} = 1,{\rm{ }}0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N \end{gathered}$

${r_{il}} = \left[ {0,1} \right],\sum\limits_{l = 1}^{{C_s}} {{r_{il}}} = 1,0 < \sum\limits_{l = 1}^{{C_s}} {{r_{il}}} < {C_s}$

(2)

式(2)中的各项作用如下：

1)第1项继承于经典的FCM，主要用于从目标域的可用数据中学习；

2)第2项用于从源域知识中学习。在该项中， ${r_{il}}$ 表示目标域中的第 $i$ 类和源域中的第 $l$ 个类之间的匹配度。这一项意味着，如果目标域中的第 $i$ 类和源域中的第 $l$ 类更相似，则目标域中的第 $i$ 类将从源域中的第 $l$ 类学习更多的知识。

E-TFCM算法的参数更新规则如下：

${v_i} = \dfrac{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}{x_{ij}}} + \displaystyle\sum\limits_{l = 1}^{{C_s}} {{{\textit{λ}} _1}r_{il}^{{m_2}}{{{\tilde{ v}}}_l}} }}{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}} + \displaystyle\sum\limits_{l = 1}^{{C_s}} {{{\textit{λ}} _1}r_{il}^{{m_2}}} }}$

(3)

${u_{ij}} = {\left. {\mathop {\left( {\dfrac{1}{{\mathop {\left\| {{{{x}}_j} - {{{v}}_i}} \right\|}\nolimits^2 }}} \right)}\nolimits^{\dfrac{1}{{{m_1} - 1}}} } \right/ {\sum\limits_{k = 1}^{\mathop C\nolimits_t } {\mathop {\left( {\dfrac{1}{{\mathop {\left\| {{{{x}}_j} - {{{v}}_k}} \right\|}\nolimits^2 }}} \right)}\nolimits^{\dfrac{1}{{{m_1} - 1}}} } }}$

(4)

${r_{il}} = \dfrac{1}{{\displaystyle\sum\limits_{k = 1}^{{C_s}} {\mathop {\left( {{{\mathop {\left\| {{{{\tilde{ v}}}_l} - {{{v}}_i}} \right\|}\nolimits^2 } / {\mathop {\left\| {{{{\tilde{ v}}}_k} - {{{v}}_i}} \right\|}\nolimits^2 }}} \right)}\nolimits^{\dfrac{{\rm{1}}}{{{m_2} - 1}}} } }}$

(5)

基于式(3)~(5)，可以容易地实现E-TFCM算法。

1.2 模糊子空间聚类FSC和迁移模糊子空间聚类E-TFSC

近年来，基于原型的软子空间聚类得到越来越多的关注^[26]。与传统的基于中心的原型聚类相比，此类算法在高维数据上表现出更好的性能，其聚类的原型不仅包含聚类中心还包含代表每类的软子空间权向量。一个代表性的软子空间聚类算法是FSC^[27]，其目标函数定义为

$\mathop {\min }\limits_{{ U},{ V},{ W}} \mathop J\nolimits_{\rm FSC} = \sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {{u_{ij}}} } \sum\limits_{k = 1}^d {w_{ik}^\tau {{\left( {{x_{jk}} - {v_{ik}}} \right)}^2}} + \sigma \sum\limits_{i = 1}^C {\sum\limits_{k = 1}^d {w_{ik}^\tau } } $

${\rm s.t.} \;\;\;\;\;\;\;{u_{ij}} \in \left\{ {0,1} \right\},\sum\limits_{i = 1}^C {{u_{ij}}} = 1,0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N$

${w_{ik}} \in \left[ {0,1} \right],\sum\limits_{k = 1}^d {{w_{ik}}} = 1.0 < \sum\limits_{i = 1}^C {{w_{ik}}} < C$

式中： ${ W} = {[{w_1, {{w_2},\cdots ,}}{w_c}]^{\rm{T}}}$ 是加权向量矩阵： $\tau $ 是模糊加权指数； ${ U} = {[{u_{ij}}]_{C \times N}}$ 是硬划分矩阵，其他参数可以参考式(1)。

基于FSC，文献[26]提出了其迁移学习版本E-TFSC(extended transfer FSC)，其目标函数如下：

$\begin{gathered} \mathop {\min }\limits_{{ U},{ V},{ W}} \mathop J\nolimits_{\rm E - TFSC} = \sum\limits_{i = 1}^{\mathop c\nolimits_t } {\sum\limits_{j = 1}^N {{u_{ij}}} \sum\limits_{k = 1}^d {w_{ik}^\alpha {{\left( {{x_{jk}} - {v_{ik}}} \right)}^2}} } + \\ \varepsilon \sum\limits_{i = 1}^{\mathop c\nolimits_t } {\sum\limits_{k = 1}^d {w_{ik}^\alpha } } + \mathop \lambda \nolimits_1 \sum\limits_{i = 1}^{\mathop c\nolimits_t } {\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_1}}} \sum\limits_{k = 1}^d {\tilde w_{ik}^\alpha \mathop {\left( {{{\tilde v}_{lk}} - {v_{ik}}} \right)}\nolimits^2 } } \\ \end{gathered} $

${\rm s.t.}{\rm{ }}\;\;\;{u_{ij}} \in \left[ {0,1} \right],\sum\limits_{i = 1}^{{C_t}} {{u_{ij}}} = 1,0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N$

${r_{il}} \in \left[ {0,1} \right],0 < \sum\limits_{i = 1}^{{C_s}} {{r_{il}}} < {C_t},\sum\limits_{l = 1}^{{C_s}} {{r_{il}}} = 1$

${w_{ik}} \in \left[ {0,1} \right],\sum\limits_{k = 1}^d {{w_{ik}}} = 1$

(6)

式中： ${\tilde{ w}} = \left( {\tilde w_{i1}^\alpha , {\tilde w_{i2}^\alpha }, \cdots ,\tilde w_{ik}^\alpha } \right)$ 是源域的加权向量矩阵， ${\tilde{ {v}}} = \left( {{{\tilde v}_{l1}}, {{\tilde v}_{l2}}, \cdots ,{{\tilde v}_{lk}}} \right)$ 是源域的聚类心矩阵; ${C_t}$ 是目标域的聚类个数; ${C_s}$ 是源域的聚类个数。基于式(6)，可以利用E-TFCM类似的优化技术得到其参数学习规则和相应算法。

1.3 迁移原型聚类存在的不足

虽然基于模糊知识匹配的迁移聚类算法^[25]提高了传统算法在面对不充分数据的聚类性能，但是，在处理源域和目标域之间的迁移关系上有两点亟需进一步改进。1)源域和目标域大都只是局部相似，意味着有些源域知识是无用的，显然，算法^[25]归一化源域和目标域相似度矩阵做法是有一定缺陷的。这种强制性匹配的知识迁移，会让不相关的源域知识对目标域产生较大的影响，甚至导致源域负相关知识在这情况下变得对目标域的聚类影响会放大，进而由这些算法建立的模型性能往往会达不到预期效果。2)该算法未充分考虑如何加强有用知识的迁移，削弱无用或有害知识的迁移。从实际角度出发，应当是有选择的充分利用源域知识，不应该强制性利用。从全局来看，迁移学习应当具有一定的自适应性，自动选择和偏重有用的源域知识，而不是简单的加强源域和目标域之间的联系。

2 基于可能性知识匹配的迁移聚类 2.1 模糊匹配和可能性匹配

针对已有迁移原型聚类方法存在的不足，本文提出了基于可能性知识匹配的迁移聚类新方法。我们借鉴经典的可能性聚类C均值聚类算法(possibilistic c-means clustering algorithm，PCM)^[28]中的可能性度量机制，来搭建源域到目标域之间的知识迁移桥梁，实现源域和目标域的可能性知识匹配。

提出的新方法针对上述挑战所采用的解决方案如下：

对于问题1)，引入可能性理论。该理论建立在模糊理论的基础之上^[29]。此时，模糊性表现为数据点对聚类中心的典型性隶属度，但该隶属度之间并不一定满足概率约束关系，即放松相似度的矩阵归一化约束。理论证明，典型性隶属度比归一化隶属度在噪声环境下性能要好，它能够自动降低噪声点和孤立点的影响。因此，不管源域知识是“好的”、“一般的”、“较差的”，提出的新算法都更具有较好的适应性和稳定性。

对于问题2)，在可能性理论基础之上，引入奖惩因子，则是很好的辅助该问题的解决。显然，对于有用的知识我们给予奖励，对于无用的知识给予惩罚，继而更加精确的选择和偏重有用的源域知识，最小化负相关的源域知识，从而更加合理利用源域知识，辅助目标域获得更好的聚类效果。图1示出了强制性模糊知识匹配和可能性知识匹配2种迁移策略的的思想及它们之间的区别。

	Download: JPG larger image
图 1 聚类任务需要迁移学习的情况 Fig. 1 Clustering tasks need to transfer learning

图1中显示了2类源域(左上)对3类目标域(左下)的迁移学习。右边红色点代表源域聚类中心，蓝色点代表目标域聚类中心。右边白色的五角星为真实的目标域聚类中心点。从右上图可以看出，基于强制性模糊知识匹配，导致2个源域知识对目标域五角星聚类中心分别以0.4、0.6比例产生负拉拽影响，使其偏离原来的位置更加严重。右下图的可能性知识匹配则将以0.2、0.1可能性分配给源域，显然对目标域的负影响进一步降低。

2.2 基于可能性知识匹配的迁移FCM

本节通过引入可能性知识匹配，提出相应的迁移FCM(possibility matching based transfer FCM, PM-TFCM)聚类算法。其优化目标函数如下：

$\begin{gathered} \mathop {\min }\limits_{{ U},{ V},{ R}} \mathop J\nolimits_{\rm PM - TFCM} = \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}} } \mathop {\left\| {{{{x}}_j} - {{{v}}_i}} \right\|}\nolimits^2 + \\[-4pt] \mathop {\textit{λ}} \nolimits_1 \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}} } \mathop {\left\| {{{{\tilde{ v}}}_l} - {{{v}}_i}} \right\|}\nolimits^2 + \mathop {\textit{λ}} \nolimits_1 \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{l = 1}^{{C_s}} {{{\bf{\eta }}_i}{{\left( {1 - {r_{il}}} \right)}^{{m_2}}}} } \\ \end{gathered} $

${\rm s.t.}{\rm{ }}\;\;\;{u_{ij}} \in \left[ {0,1} \right],\sum\limits_{i = 1}^{{C_t}} {{u_{ij}}} = 1,0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N,{r_{ij}} \in \left[ {0,1} \right]$

(7)

对于式(7)，其各项描述如下：

1)第1项直接继承于经典的FCM，主要用于从目标域数据中学习；

2)第2项用于从源域知识中学习。这里使用了可能性匹配机制，放开了目标域知识到源域知识匹配的归一化强制约束；

3)第3项用于加强对源域有用知识的学习和削弱无用知识的学习。 $\eta $ 为惩罚因子，辅助学习源域知识。

基于和PM-TFCM类似的优化策略，易得到提出的PM-TFCM的更新规则如下：

${v_i} = \frac{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}} {{{x}}_j} + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}{{{\tilde{ v}}}_l}} }}{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}} + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}} }}$

(8)

${u_{ij}} = {\left. {\mathop {\left( {\dfrac{1}{{{{\left\| {{{{x}}_j} - {{{v}}_i}} \right\|}^2}}}} \right)}\nolimits^{{1 / {\left( {{m_1} - 1} \right)}}} } \right/ {\sum\limits_{k = 1}^{{C_t}} {\mathop {\left( {\dfrac{1}{{\mathop {\left\| {{{{x}}_j} - {{{v}}_k}} \right\|}\nolimits^2 }}} \right)}\nolimits^{{1 / {\left( {{m_1} - 1} \right)}}} } }}$

(9)

${r_{il}} = {1 \left/ {\left( {{{\left( {\dfrac{{\mathop \lambda \nolimits_1 }}{{{{\bf{\eta }}_i}}}{{\left\| {{{{\tilde{ v}}}_l} - {{{v}}_i}} \right\|}^2}} \right)}^{{1 / {{m_2} - 1}}}} + 1} \right)}\right. }$

(10)

${\eta _i} = K\tfrac{{\displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^m} \mathop {\left\| {{{{\tilde{ v}}}_l} - {{{v}}_i}} \right\|}\nolimits^2 }}{{\displaystyle\sum\limits_{s = 1}^{{C_s}} {r_{is}^m} }},K > 0$

(11)

基于式(9)~(11)，PM-TFCM算法描述如下：

PM-TFCM 算法：

输入　聚类个数 ${C_t}$ ，最大迭代次数为 ${t_{\max }}$ 。随机初始化目标域聚类中心矩阵 ${{ v}_t}$ 。以及利用fcm获得源域聚类中心 ${\tilde { v}_l}$ ，由此计算 $\eta $ ,并在当前获得最好聚类效果时，才会更新。设定平衡参数 ${{\textit{λ}}_1}$ 取值范围，迭代次数初始化为 $t = 0$ 、 ${\rm error }= 1$ 、 $\mathop {{\rm Obj} = J}\nolimits_{\rm PM - TFCM} $ 。

重复：

$t = t + 1$ ；

根据式(10)更新隶属度矩阵U；

根据式(11)更新相似矩阵R；

根据式(9)更新目标域聚类中心V；

直到 $\rm error \!=\!$ $\left| {\rm NewObj \!-\! Obj} \right|$ <10e ⁻⁵或者 $t \!=\! {t_{\max }}$

输出　 U、R、V。

2.3 基于可能性知识匹配的迁移FSC

本节通过引入可能性知识匹配，提出相应的迁移FSC(possibility matching based transfer FSC，PM-TFSC)聚类算法。其优化目标函数如下：

$\begin{gathered} \mathop {\min }\limits_{{ U},{ V},{ W}} \mathop J\nolimits_{\rm PM - TFSC} = \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{j = 1}^N {{u_{ij}}} \sum\limits_{k = 1}^d {w_{ik}^\alpha {{\left( {{x_{jk}} - {v_{ik}}} \right)}^2}} } + \\[-3pt] \varepsilon \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{k = 1}^d {w_{ik}^\alpha } } + \mathop {\textit{λ}} \nolimits_1 \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_1}}} } \sum\limits_{k = 1}^d {\tilde w_{ik}^\alpha {{\left( {{{\tilde v}_{lk}} - {v_{ik}}} \right)}^2}} + \\[-3pt] \mathop {\textit{λ}} \nolimits_1 \sum\limits_{i = 1}^{{C_t}} {\sum\limits_{l = 1}^{{C_s}} {{{\bf{\eta }}_i}{{\left( {1 - {r_{il}}} \right)}^{{m_1}}}} } \\ \end{gathered} $

$\begin{gathered} {\rm s.t.}{\rm{ }}\;\;\;{u_{ij}} \in \left[ {0,1} \right],\sum\limits_{i = 1}^{{C_t}} {{u_{ij}}} = 1,0 < \sum\limits_{j = 1}^N {{u_{ij}}} < N \\[-6pt] {r_{il}} \in \left[ {0,1} \right],0 < \sum\limits_{l = 1}^{{C_s}} {{r_{il}}} < {C_s},{w_{ik}} \in \left[ {0,1} \right],\sum\limits_{k = 1}^d {{w_{ik}}} = 1 \\ \end{gathered} $

(12)

类似于式(6)，式(11)借鉴了可能性度量来实现源域和目标域的可能性匹配。这里表示匹配的可能性，对其不存在归一化强制匹配。利用类似于PM-TFCM中的优化方法，可得PM-TFSC的参数更新规则如下：

${v_{ik}} = \dfrac{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}w_{ik}^\tau {x_{jk}}} + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}w_{ik}^\tau {{\tilde v}_{lk}}} }}{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}w_{ik}^\tau } + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}w_{ik}^\tau } }}$

(13)

${r_{il}} = {1 \left/ {\left( {1 + \mathop {\left( {\dfrac{{\displaystyle\sum\limits_{k = 1}^d {{{\tilde w}_{lk}}{{\left( {{{\tilde v}_{lk}} - {v_{ik}}} \right)}^2}} }}{{{{\bf{\eta }}_i}}}} \right)}\nolimits^{{1 / {{m_2} - 1}}} } \right)}\right. }$

(14)

$ \begin{array}{l} {u_{ij}} = \dfrac{{1/{{\left( {\displaystyle\sum\limits_{k = 1}^d {w_{ik}^\tau } } \right)}^{1/{m_1} - 1}}}}{{\displaystyle\sum\limits_{s = 1}^{{C_t}} {{{\left( {\dfrac{1}{{\displaystyle\sum\limits_{s = 1}^{{C_t}} {w_{sk}^\tau } {{\left( {{x_{jk}} - {v_{sk}}} \right)}^2}}}} \right)}^{1/{\rm{ }}{m_1} - 1}}} }} \\ \overrightarrow {{d_{ij}} = \displaystyle\sum\limits_{k = 1}^d {w_{ik}^\tau {{\left( {{x_{jk}} - {v_{ik}}} \right)}^2}} } = \\{\left[ {1/{d_{ij}}} \right]^{1/{m_1} - 1}}/\displaystyle\sum\limits_{s = 1}^{{C_t}} {{{\left[ {1/{d_{sj}}} \right]}^{1/{m_1} - 1}}} \end{array} $

(15)

${v_{ik}} = \dfrac{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}w_{ik}^\tau {x_{jk}}} + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}\tilde w_{ik}^\tau {{\tilde v}_{lk}}} }}{{\displaystyle\sum\limits_{j = 1}^N {u_{ij}^{{m_1}}w_{ik}^\tau } + \mathop {\textit{λ}} \nolimits_1 \displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_2}}\tilde w_{ik}^\tau } }}$

(16)

${w_{ik}} = \dfrac{{{{{1 \left/ {\left( {\displaystyle\sum\limits_{j = 1}^{N} {{u_{ij}}{{\left( {{x_{jk}} - {v_{ik}}} \right)}^2} + \varepsilon } } \right)}\right. }}^{{1 / {\alpha - 1}}}}}}{{\displaystyle\sum\limits_{s=1}^d {{{\left( {{1 \left/ {\displaystyle\sum\limits_{j=1}^N {{u_{ij}}{{\left( {{x_{js}} - {v_{is}}} \right)}^2} + \varepsilon } }\right. }} \right)}^{{1 / {\alpha - 1}}}}} }}$

(17)

${\eta _i} = \dfrac{{\displaystyle\sum\limits_{l = 1}^{{C_s}} {r_{il}^{{m_1}}} \displaystyle\sum\limits_{k = 1}^d {\tilde w_{lk}^\alpha \mathop {\left( {{{\tilde v}_{lk}} - {v_{ik}}} \right)}\nolimits^2 } }}{{\displaystyle\sum\limits_{s = 1}^{{C_s}} {r_{is}^{{m_1}}} }}$

(18)

基于式(14)~(18)，可以容易地获得PM-TFSC算法。

PM-TFSC 算法：

输入　聚类个数 ${C_t}$ ，最大迭代次数为 ${t_{\max }}$ 。随机选择 ${C_t}$ 个点初始化目标域聚类中心矩阵Vt。fcm获得源域聚类中心 ${\tilde { v}_l}$ 。随机初始化权值 $\tilde { w}$ ，由此计算惩罚因子 $\eta $ ，同样也是在当前聚类效果最好时，才更新。设定平衡参数 ${{\textit{λ}} _1}$ 取值范围，初始化迭代次数 $t = 0$ 、 $\rm error = 1$ 、 $\mathop {{\rm Obj} = J}\nolimits_{\rm PM - TFSC} $ 。

重复：

$t = t + 1$ ；

根据式(14)更新隶属度矩阵U；

根据式(13)更新相似矩阵R；

根据式(15)更新目标域聚类中心V；

根据式(16)更新权值W；

直到 $\rm error \!=\!$ $\left| {\rm NewObj \!-\! Obj} \right|$ <10e ⁻⁵或者 $t \!=\! {t_{\max }}$

输出　 U、R、V、W。

3 实验结果

在本节中，将在合成数据集和真实世界数据集上进行实验评估所提出的算法的聚类性能。首先描述了用于性能评价的指标和实验装置。然后，对所提出的算法在合成和真实世界文本数据集上的性能进行了报道和讨论，并与其他相关算法进行了综合比较。所有算法都在MATLAB上实现，实验在3.6 GHz CPU 64-GB RAM的计算机上运行。

3.1 性能指标和实验设置

本文采用2个评价指标，即兰德指数(RI)和归一化互信息(NMI)，用于评估聚类算法的性能。

RI通常被定义为

${\rm RI} = \frac{{{f_{00}} + {f_{11}}}}{{{{N(N - 1)} / 2}}}$

式中： ${f_{00}}$ 是具有不同类标签且属于不同簇的数据点对的数目；N是整个数据集的大小。

NMI根据以下公式进行定义和计算：

${\rm NMI}{\rm{ = }}\dfrac{{{{\displaystyle\sum\limits_{i = 1}^C {\displaystyle\sum\limits_{j = 1}^C {{N_{i,j}}\log N \times {N_{i,j}}} } } / {{N_i} \times {N_j}}}}}{{\sqrt {{{\displaystyle\sum\limits_{i = 1}^C {{N_i}} \times \log {N_i}} / {{{N \times \displaystyle\sum\limits_{j = 1}^C {{N_j}} \times \log {N_j}} / N}}}} }}$

式中： ${N_{ij}}$ 是簇 $i$ 和类 $j$ 之间的相同样本的数目； ${N_i}$ 是簇 $i$ 中数据点的数量； ${N_j}$ 是 $j$ 类中数据点的数量； $N$ 是整个数据集的大小。RI和NMI都在区间[0, 1]内取值。值越高，聚类性能越好。

3.2 合成数据集

在这项研究中，生成了几个合成数据集来评估所提出的算法的性能。

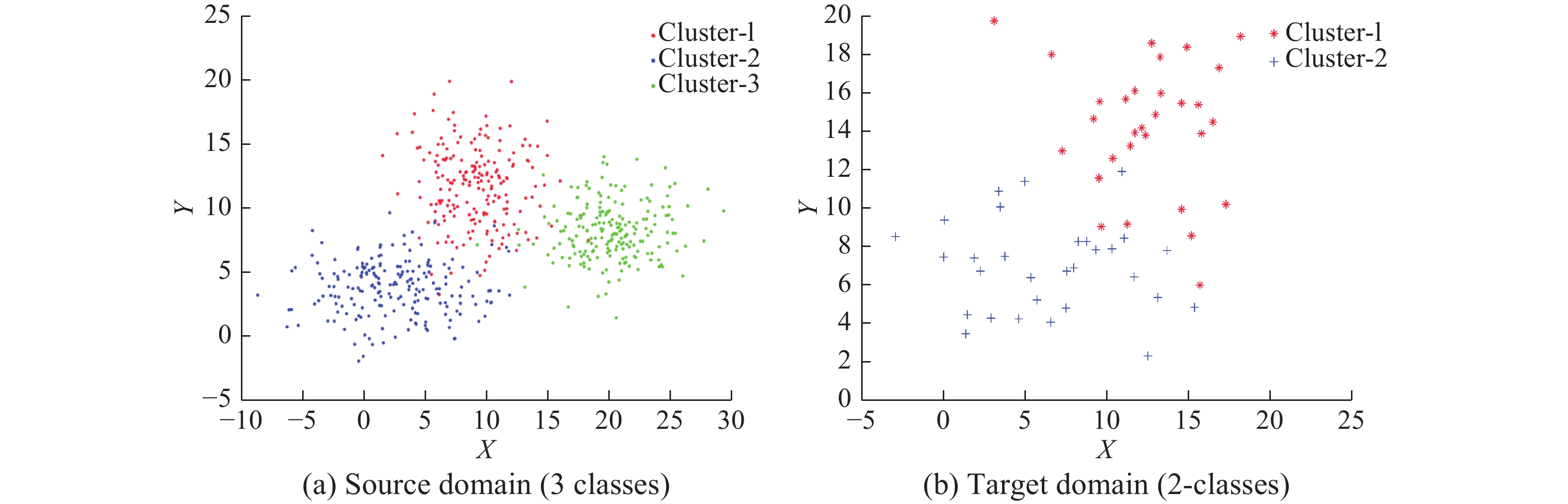
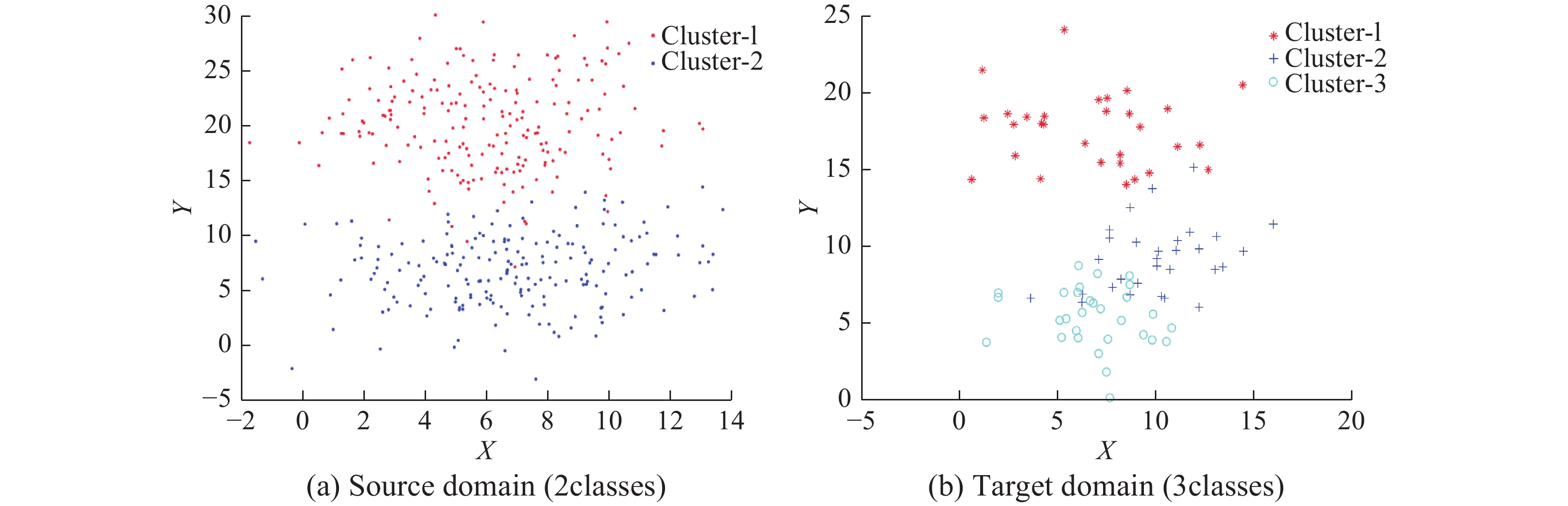
本部分分别生成了2组数据集来评估提出的PM-TFCM和PM-TFSC算法。所有数据集都是由高斯分布函数生成。通过源域和目标域对应的类别相似来构造源域和目标域，即均值相似以及方差相似。用于评估PM-TFCM的数据生成参数如表1所示，生成的数据集如图2、3所示。用于评估PM-TFSC的数据生成参数如表2所示，生成的数据集如图4、5所示。

表 1 用于评估PM-TFCM的合成数据集 Tab. 1 Synthetic datasets for evaluating PM-TFCM

Source domain with three clusters				Source domain with two clusters
Cluster	Cluster-1	Cluster-2	Cluster-3	Cluster	Cluster-1		Cluster-2
$ u$	$ \left[ {9{\rm{\;\;12}}} \right]$	$ \left[ {{\rm{3\;\;4}}} \right]$	$ \left[ {{\rm{20\;\;8}}} \right]$	$ u$	$ \left[ {{\rm{6\;\;15}}} \right]$		$ \left[ {{\rm{7\;\;7}}} \right]$
$ \displaystyle\sum {} $	$ \left[ {\begin{array}{*{20}{c}} 6&0 \\ 0&9 \end{array}} \right]$	$ \left[ {\begin{array}{*{20}{c}} {15}&0 \\ 0&4 \end{array}} \right]$	$ \left[ {\begin{array}{*{20}{c}} 9&0 \\ 0&5 \end{array}} \right]$	$ \displaystyle\sum {} $	$ \left[ {\begin{array}{*{20}{c}} 7&0 \\ 0&{18} \end{array}} \right]$		$ \left[ {\begin{array}{*{20}{c}} {10}&0 \\ 0&9 \end{array}} \right]$
Size	600			Size	400
Target domain with two clusters				Target domain with three clusters
Cluster	Cluster-1		Cluster-2	Cluster	Cluster-1	Cluster-2	Cluster-3
$ u$	$ \left[ {{\rm{13\;\;14}}} \right]$		$ \left[ {{\rm{5\;\;6}}} \right]$	$ u$	$ \left[ {{\rm{ 7\;\;{18}}}} \right]$	$ \left[ {{\rm{ 10\;\; 9}}} \right]$	$ \left[ {{\rm{7\;\; 6}}} \right]$
$ \displaystyle\sum {} $	$ \left[ {\begin{array}{*{20}{c}} 7& 0 \\ 0& {11} \end{array}} \right]$		$ \left[ {\begin{array}{*{20}{c}} {19}& 0 \\ 0& 8 \end{array}} \right]$	$ \displaystyle\sum {} $	$\left[ {\begin{array}{*{20}{c}} {16}&0 \\ 0&6 \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} 9& 0 \\ 0& 5 \end{array}} \right]$	$ \left[ {\begin{array}{*{20}{c}} 4& 0 \\ 0& 6 \end{array}} \right]$
Size	60			Size	90

表 1 用于评估PM-TFCM的合成数据集 Tab.1 Synthetic datasets for evaluating PM-TFCM

	Download: JPG larger image
图 2 2种基于原型的迁移模型简单对比示意 Fig. 2 A brief comparison of two prototype based transfer models

	Download: JPG larger image
图 3 表1左列参数生成的合成数据集1 Fig. 3 Synthetic dataset 1 corresponding to the parameters in the left column of Table 1

表 2 用于评估PM-TFSC的合成数据集 Tab. 2 Synthetic datasets for evaluating PM-TFSC

Source domain with three clusters				Source domain with two clusters
Cluster	Cluster-1	Cluster-2	Cluster-3	Cluster	Cluster-1		Cluster-2
$u$	$\left[ {{\rm{8\;\;14\;\;18}}} \right]$	$\left[ {{\rm{4\;\;2\;\;7}}} \right]$	$\left[ {{\rm{15\;\;15\;\;20}}} \right]$	$u$	$\left[ {{\rm{10\;\;12\;\;15}}} \right]$		$\left[ {{\rm{15\;\;7\;\;2}}} \right]$
$\displaystyle\sum{} $	$\left[ {\begin{array}{*{20}{c}} {15}&0&0 \\ 0&7&0 \\ 0&0&{14} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&8&0 \\ 0&0&3 \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} 7&0&0 \\ 0&{15}&0 \\ 0&0&8 \end{array}} \right]$	$\displaystyle\sum{} $	$\left[ {\begin{array}{*{20}{c}} 3&0&0 \\ 0&{10}&0 \\ 0&0&8 \end{array}} \right]$		$\left[ {\begin{array}{*{20}{c}} 3&0&0 \\ 0&9&0 \\ 0&0&8 \end{array}} \right]$
Size	600				Size	400
Target domain with two clusters				Target domain with three clusters
Cluster	Cluster-1		Cluster-2	Cluster	Cluster-1	Cluster-2	Cluster-3
$u$	$\left[ {{\rm{11\;\;18\;\;9}}} \right]$		$\left[ {{\rm{8\;\;4\;\;11}}} \right]$	$u$	$\left[ {{\rm{12\;\;14\;\;18}}} \right]$	$\left[ {{\rm{16\;\;10\;\;5}}} \right]$	$\left[ {{\rm{7\;\;8\;\;7}}} \right]$
$\displaystyle\sum{} $	$\left[ {\begin{array}{*{20}{c}} {16}&0&0 \\ 0&{12}&0 \\ 0&0&{17} \end{array}} \right]$		$\left[ {\begin{array}{*{20}{c}} 3&0&0 \\ 0&9&0 \\ 0&0&8 \end{array}} \right]$	$\displaystyle\sum{} $	$\left[ {\begin{array}{*{20}{c}} 6&0&0 \\ 0&{12}&0 \\ 0&0&9 \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} {10}&0&0 \\ 0&6&0 \\ 0&0&{10} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} {15}&0&0 \\ 0&8&0 \\ 0&0&6 \end{array}} \right]$
Size	60				Size	90

表 2 用于评估PM-TFSC的合成数据集 Tab.2 Synthetic datasets for evaluating PM-TFSC

	Download: JPG larger image
图 4 表1右列参数生成的合成数据集2 Fig. 4 Synthetic dataset 2 corresponding to the parameters in the right column of Table 1

	Download: JPG larger image
图 5 表2左列参数生成的合成数据集3 Fig. 5 Synthetic dataset 3 corresponding to the parameters in the left column of Table 2

在合成数据集的实验结果如表3、4所示。从实验结果可以看出，在几种不同的情况下，所提新迁移聚类算法较之于传统原型聚类算法和已有的迁移原型聚类算法，性能都得到了一定程度的改进。这也说明本文引入的可能性匹配迁移学习机制具有更好的适应性。

表 3 3种FCM算法在合成数据集上的性能比较 Tab.3 Performance comparison of three FCM algorithms on synthetic datasets

表 4 3种FSC算法在合成数据集上的性能比较 Tab.4 Performance comparison of three FSC algorithms on synthetic datasets

3.3 20 NG20 文本数据集

在本节，将提出的算法应用到真实的20新闻组(20 Newsgroups (or NG20))文本数据集^[30]。NG20数据集是高维数据集。采用卡方检验结合词频进行了降维，最终NG20降到了800维用于聚类分析。

为了模拟本文所研究的场景，构造了源域以及目标域的各个类的数据集。表5详细给出了本文所采用的4组文本数据。然后基于这4组数据构造了5对适宜于迁移学习场景的数据对。5组数据对详情见表6。该5组数据可分为3类，分别为：

表 5 20篇新闻组的文本数据在本研究中使用 Tab.5 Clustters of 20 newsgroups text data used in this study

表 6 对20个新闻组文本数据集用于性能评估 Tab. 6 for 20 newsgroup text datasets for performance evaluation

Data Pair	Source domain			Target domain
Data Pair	Dataset	Number of clusters	Clusters and subcluser	Dataset	Number of clusters	Clusters and subcluster
1	NG20-S1	2	comp(comp.sys.ibm.pc.hardware	NG20-T1	3	comp(comp.os.ms-windows.misc)
			comp.sys.mac.hardware			rec(rec.sport.hockey)
			comp.windows.x)			sci(sci.crypt)
			rec(rec.autos
			rec.motorcycles
			rec.sport.baseball)
		size	2931+2978		size	979+995+993
2	NG20-S1	2	comp(comp.sys.ibm.pc.hardware	NG20-T2	4	comp(comp.os.ms-windows.misc)
			comp.sys.mac.hardware			rec(rec.sport.hockey)
			comp.windows.x)			sci(sci.crypt)
			rec(rec.autos			talk(talk.politics.guns)
			rec.motorcycles
			rec.sport.baseball)
		size	2931+2978		size	979+995+993+912
3	NG20-S2	3	rec(rec.motorcycles	NG20-T3	3	rec(rec.autos)
			rec.sport.baseball			sci(sci.crypt)
			rec.sport.hockey)			talk(talk.politics.guns)
			sci(sci.electronics
			sci.med
			sci.space)
			talk(talk.politics.mideast
			talk.politics.misc
			talk.religion.misc)
		size	2978+2979+2804		size	992+993+912
4	NG20-S3	3	comp(comp.os.ms-windows.misc	NG20-T4	2	comp(comp.windows.x)
			comp.sys.ibm.pc.hardware			sci(sci.space)
			comp.sys.mac.hardware)
			rec(rec.autos
			rec.motorcycles
			rec.sport.baseball)
			sci(sci.crypt
			sci.electronics
			sci.med)
			2935+ 2978+ 2979
		size			size	975+ 986
5	NG20-S4	4	comp(comp.os.ms-windows.misc	NG20-T4	2	comp(comp.windows.x)
			comp.sys.ibm.pc.hardware			sci(sci.space)
			comp.sys.mac.hardware)
			rec(rec.autos
			rec.motorcycles
			rec.sport.baseball)
			sci(sci.crypt
			sci.electronics
			sci.med)
			talk(talk.politics.guns
			talk.politics.mideast
			talk.politics.misc)
		size	2935+ 2978+ 2979+2718		size	975+ 986

表 6 对20个新闻组文本数据集用于性能评估 Tab.6 for 20 newsgroup text datasets for performance evaluation

1) 源域类别数少于目标域类别数，该类数据包括表6中的数据对1和2。

2) 源域类别数等于目标域类别数，该类数据包括表6中的数据对3。

3) 源域类别数多于目标域类别数，该类数据包括表6中的数据对4和5。

为了保证各个算法的公平性，对每个参数赋予10个值进行网格搜索，详情见表7。

表 7 各个算法参数取值情况 Tab. 7 Performance index of several algorithms

算法	算法说明	相关参数	相关参数寻优范围设置
FCM	模糊C均值聚类算法	模糊指数m
E-TFCM	模糊C均值聚类和迁移模糊FCM聚类	模糊指数 ${m_1}{\rm{ }}{m_2}$ ，平衡参数 ${\lambda _1}$	${m_1}{\rm{ }}{m_2} = [{2^ \wedge}4,{2^ \wedge}3,\cdots,{2^ \wedge}5]$
E-TFCM	模糊C均值聚类和迁移模糊FCM聚类	模糊指数 ${m_1}{\rm{ }}{m_2}$ ，平衡参数 ${\lambda _1}$	${\lambda _1} = [0,{2^ \wedge}4,{2^ \wedge}3,\cdots,2^ \wedge5]$
PM-TFCM	基于可能性知识匹配的迁移FCM	模糊指数 ${m_1}{\rm{ }}{m_2}$ ，平衡参数 ${\lambda _1}$	${m_1}{\rm{ }}{m_2} = [{2^ \wedge}4,{2^ \wedge}3,\cdots,{2^ \wedge}5]$
PM-TFCM	基于可能性知识匹配的迁移FCM	模糊指数 ${m_1}{\rm{ }}{m_2}$ ，平衡参数 ${\lambda _1}$	${\lambda _1} = [0,{2^ \wedge}4,{2^ \wedge}3,\cdots,2^ \wedge5]$
FSC	子空间聚类算法	加权指数 $\tau $ ，平衡参数 $\sigma $	$\tau = [{2^ \wedge}1,{2^ \wedge}2,\cdots,{2^ \wedge}10]$
FSC	子空间聚类算法	加权指数 $\tau $ ，平衡参数 $\sigma $	$\sigma = [{5^ \wedge}{\rm{ - }}9,{5^ \wedge}{\rm{ - }}8,\cdots,{5^ \wedge}0]$
E-TFSC	模糊子空间聚类FSC和迁移模糊子空间聚类	模糊指数 ${m_1}$ ,加权指数 $\alpha $ ，平衡参数 ${\lambda _1}$	${m_1} = [{2^ \wedge}{\rm{ - 2}},{2^ \wedge}{\rm{ - 1}},\cdots,{2^ \wedge}{\rm{8}}]$
			$\alpha {\rm{ = [2^ \wedge1,2^ \wedge2,}}\cdots{\rm{,2^ \wedge10]}}$
			${\lambda _1} = [0,{2^ \wedge}4,{2^ \wedge}3,\cdots,2^ \wedge5]$
PM-TFSC	基于可能性知识匹配的迁移FSC	模糊指数 ${m_1}$ ,加权指数 $\alpha $ ，平衡参数 ${\lambda _1}$	${m_1} = [{2^ \wedge}{\rm{ - 2}},{2^ \wedge}{\rm{ - 1}},\cdots,{2^ \wedge}{\rm{8}}]$
			$\alpha {\rm{ = [2^ \wedge1,2^ \wedge2,}}\cdots{\rm{,2^ \wedge10]}}$
			${\lambda _1} = [0,{2^ \wedge}4,{2^ \wedge}3,\cdots,2^ \wedge5]$

表 7 各个算法参数取值情况 Tab.7 Performance index of several algorithms

通过表8的Part A部分，不难发现，我们的算法(PM-TFCM、PM-TFSC)均优于对比算法(E-TFCM、E-TFSC)。在基于传统FCM聚类的迁移聚类方法上，PM-TFCM 比E-TFCM的性能指标平均提高了0.02以上。特别地，在FSC的2个迁移版本聚类方法上，基于可能性知识匹配子空间迁移聚类算法PM-TFSC的性能指标明显优于基于强制性模糊知识匹配子空间迁移聚类算法E-TFSC的指标，其平均性能指标高出0.04左右。

表 8 各算法的运行结果 Tab. 8 Results of several algorithms

数据集	Part A: 源域类别数少于目标域类别数
数据集	性能指标	FCM	E-TFCM	PM-TFCM	FSC	E-TFSC	PM-TFSC
NG20-T1 (NG20-S1 ⇒ NG20-T1)	RI_mean	0.482 45	0.698 79	0.714 68	0.706 87	0.749 44	0.770 94
	RI_std	0.000 397	0.041 032	0.034 525	0.078 714	0.103 24	0.062 257
	NMI_mean	0.023 969	0.438 96	0.464 88	0.383	0.478 49	0.527 5
	NMI_std	0.001 195	0.067 252	0.070 364	0.153 15	0.134 88	0.138 37
NG20-T2 (NG20-S1 ⇒ NG20-T2)	RI_mean	0.478 39	0.679 582	0.685 415	0.732 87	0.753 92	0.781 01
	RI_std	0.001 039	0.059 877	0.056 451	0.060 879	0.047 396	0.044 765
	NMI_mean	0.032 985	0.281 6	0.300 037	0.378 569	0.400 18	0.449 14
	NMI_std	0.001 68	0.084 91	0.065 879	0.052 514	0.057 617	0.033 958
数据集	Part B: 源域类别数等于目标域类别数
数据集	性能指标	FCM	E-TFCM	PM-TFCM	FSC	E-TFSC	PM-TFSC
NG20-T3 (NG20-S2 ⇒ NG20-T3)	RI_mean	0.502 37	0.627 22	0.630 35	0.634 33	0.676 2	0.684 17
	RI_std	7.19E-08	0.053 115	0.048 987	0.058 425	0.050 099	0.059 193
	NMI_mean	0.079 306	0.281 84	0.295 19	0.222 29	0.280 81	0.318 16
	NMI_std	3.58E-05	0.083 169	0.059 944	0.113 36	0.078 226	0.092 16
数据集	Part C: 源域类别数多于目标域类别数
数据集	性能指标	FCM	E-TFCM	PM-TFCM	FSC	E-TFSC	PM-TFSC
NG20-T4 (NG20-S3 ⇒ NG20-T4)	RI_mean	0.500 52	0.542 22	0.571 17	0.633 87	0.670 51	0.743 63
	RI_std	1.16E-16	0.076 941	0.111 71	0.100 88	0.083 816	0.016 126
	NMI_mean	0.002 46	0.108 59	0.138 14	0.230 2	0.294 14	0.401 7
	NMI_std	4.55E-19	0.070 741	0.188 1	0.159 05	0.180 34	0.022 894
NG20-T4 (NG20-S4 ⇒ NG20-T4)	RI_mean	0.501 18	0.541 12	0.551 65	0.640 05	0.686 45	0.720 09
	RI_std	0.00E+00	0.067 762	0.100 43	0.085 854	0.103 03	0.081 048
	NMI_mean	0.004 194	0.106 63	0.136 17	0.247 97	0.320 43	0.401 19
	NMI_std	9.10E-19	0.095 343	0.118 03	0.134	0.156 31	0.103 02

表 8 各算法的运行结果 Tab.8 Results of several algorithms

从表8的Part B部分可以看出，较之于传统迁移原型聚类，此时我们的算法提升度虽然不大。这是因为，此实验模拟场景偏适合于强制性模糊知识匹配算法，因而不能充分发挥可能性知识匹配算法的优势。但提出的算法依然得到了高度可竞争的结果，这也较好地佐证提出的算法的高度适应性。表8给出了各算法的运行结果。

通过表8的Part C部分可知：在源域存在较多负面知识的情况下，在基于传统FCM聚类的迁移聚类方法上，PM-TFCM比E-TFCM在性能指标上平均提高了0.03。在FSC的2个迁移版本聚类方法上，基于可能性知识匹配子空间迁移聚类算法(PM-TFSC)的性能指标明显优于基于强制性模糊知识匹配子空间迁移聚类算法的性能，其平均性能指标高出0.07以上。从实验结果分析可知，我们的算法对克服源域不好知识负面影响的能力相对较好，能较好地抑制源域无用知识对目标域的负面影响。

4 结束语

针对已有的典型迁移原型聚类存在的源域和目标域类别之间的强制性匹配存在的缺陷，本文引入可能性匹配机制来进行改进。可能性匹配降低了强制性匹配的约束，便于减弱负面知识的影响，具有更好的适应性。但是本文提出的基于可能性知识匹配的迁移原型聚类算法，仍然具有一定的不足。例如，对于算法中的超参数如何来快速地找到合适的值，依然是一个挑战性的问题。我们拟在将来的工作中做更深入地探讨。

参考文献

[1]	PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE transactions on knowledge and data engineering, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 (0)
[2]	TAO Jianwen, CHUNG F L, WANG Shitong. On minimum distribution discrepancy support vector machine for domain adaptation[J]. Pattern recognition, 2012, 45(11): 3962-3984. DOI:10.1016/j.patcog.2012.04.014 (0)
[3]	SUN Zhuo, CHEN Yiqiang, QI Juan, et al. Adaptive localization through transfer learning in indoor Wi-Fi environment[C]//Proceedings of the 7th International Conference on Machine Learning and Applications. San Diego, CA, USA: IEEE, 2008: 331–336. (0)
[4]	BICKEL S, BRÜCKNER M, SCHEFFER T. Discriminative learning for differing training and test distributions[C]//Proceedings of the 24th International Conference on Machine Learning. Corvalis, Oregon, USA: ACM, 2007: 81−88. (0)
[5]	LAWRENCE N D, PLATT J C. Learning to learn with the informative vector machine[C]//Proceedings of the 21st International Conference on Machine Learning. Banff, Alberta, Canada: ACM, 2004: 65. (0)
[6]	GAO Jing, FAN Wei, JIANG Jing, et al. Knowledge transfer via multiple model local structure mapping[C]//Proceedings of the 14th ACMKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas, NV, United States: ACM, 2008: 283–291. (0)
[7]	MIHALKOVA L, MOONEY R J. Transfer learning by mapping with minimal target data[C]//Proceedings Association for the Advancement of Artificial Intelligence AAAI’08) Workshop Transfer Learning for Complex Tasks. Chicago: AAAI, 2008. (0)
[8]	DAVIS J, DOMINGOS P. Deep transfer via second-order Markov logic[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Quebec, Canada: ACM, 2009: 217–224. (0)
[9]	PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE transactions on neural networks, 2011, 22(2): 199-210. DOI:10.1109/TNN.2010.2091281 (0)
[10]	WANG Zheng, SONG Yangqiu, ZHANG Changshui. Transferred dimensionality reduction[C]//European Conference on Machine Learning and Knowledge Discovery in Databases. Antwerp, Belgium: Springer, 2008: 550–565. (0)
[11]	YANG Pei, TAN Qi, DING Yehua. Bayesian task-level transfer learning for non-linear regression[C]//Proceedings of 2008 International Conference on Computer Science and Software Engineering. Hubei, China: IEEE, 2008: 62–65. (0)
[12]	BORZEMSKI L, STARCZEWSKI G. Application of transfer regression to TCP throughput prediction[C]//Proceedings of the 1st Asian Conference on Intelligent Information and Database Systems. Dong Hoi, Vietnam: IEEE, 2009: 28–33. (0)
[13]	LIU Junfa, CHEN Yiqiang, ZHANG Yadong. Transfer regression model for indoor 3D location estimation[C]//Proceedings of the 16th International Multimedia Modeling Conference on Advances in Multimedia Modeling. Chongqing, China: Springer, 2010: 603–613. (0)
[14]	DENG Zhaohong, JIANG Yizhang, CHOI K S, et al. Knowledge-leverage-based TSK Fuzzy System modeling[J]. IEEE transactions on neural networks and learning systems, 2013, 24(8): 1200-1212. DOI:10.1109/TNNLS.2013.2253617 (0)
[15]	DENG Zhaohong, JIANG Yizhang, CHUNG F L, et al. Knowledge-leverage-based fuzzy system and its modeling[J]. IEEE transactions on fuzzy systems, 2013, 21(4): 597-609. DOI:10.1109/TFUZZ.2012.2212444 (0)
[16]	DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Self-taught clustering[C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland: ACM, 2008: 200–207. (0)
[17]	JIANG Wenhao, CHUNG F L. Transfer spectral clustering[C]//European Conference on Machine Learning and Knowledge Discovery in Databases. Bristol, UK: Springer, 2012: 789–803. (0)
[18]	HARTIGAN J A, WONG M A. Algorithm AS 136: a K-means clustering algorithm[J]. Journal of the royal statistical society. series C, 1979, 28(1): 100-108. (0)
[19]	陈黎飞, 姜青山, 王声瑞. 基于层次划分的最佳聚类数确定方法[J]. 软件学报, 2008, 19(1): 62-72. CHEN Lifei, JIANG Qingshan, WANG Shengrui. A hierarchical method for determining the number of clusters[J]. Journal of software, 2008, 19(1): 62-72. (0)
[20]	VURAL V, DY J G. A hierarchical method for multi-class support vector machines[C]//Proceedings of the 21st International Conference on Machine Learning. Banff, Alberta, Canada: ACM, 2004: 105. (0)
[21]	ZHAO Yanchang, SONG Junde. GDILC: a grid-based density-isoline clustering algorithm[C]//Proceedings of 2001 International Conferences on Info-Tech and Info-Net. Beijing, China: IEEE, 2001: 140–145. (0)
[22]	MA W M, CHOW T W S. A new shifting grid clustering algorithm[J]. Pattern recognition, 2004, 37(3): 503-514. DOI:10.1016/j.patcog.2003.08.014 (0)
[23]	TSAI C F, TSAI C W, WU Hanchang, et al. ACODF: a novel data clustering approach for data mining in large databases[J]. Journal of systems and software, 2004, 73(1): 133-145. DOI:10.1016/S0164-1212(03)00216-4 (0)
[24]	杭文龙, 蒋亦樟, 刘解放, 等. 迁移近邻传播聚类算法[J]. 软件学报, 2016, 27(11): 2796-2813. HANG Wenlong, JIANG Yizhang, LIU Jiefang, et al. Transfer affinity propagation clustering algorithm[J]. Journal of software, 2016, 27(11): 2796-2813. (0)
[25]	DENG Zhaohong, JIANG Yizhang, CHUNG F L, et al. Transfer prototype-based fuzzy clustering[J]. IEEE transactions on fuzzy systems, 2016, 24(5): 1210-1232. DOI:10.1109/TFUZZ.2015.2505330 (0)
[26]	HUANG J Z, NG M K, RONG Hongqiang, et al. Automated variable weighting in k-means type clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(5): 657-668. DOI:10.1109/TPAMI.2005.95 (0)
[27]	GAN G, WU J. A convergence theorem for the fuzzy subspace clustering (FSC) algorithm[J]. Pattern recognition, 2008, 41(6): 1939-1947. DOI:10.1016/j.patcog.2007.11.011 (0)
[28]	KRISHNAPURAM R, KELLER J M. The possibilistic C-means algorithm: insights and recommendations[J]. IEEE transactions on fuzzy systems, 1996, 4(3): 385-393. DOI:10.1109/91.531779 (0)
[29]	BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press, 1981. (0)
[30]	DAI Wenyuan, XUE Guirong, YANG Qiang, et al. Co-clustering based classification for out-of-domain documents[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose, California, USA: ACM, 2007: 210–219. (0)