织物检测是纺织品制造中质量控制的关键组成部分。目前，人工检测是纺织品瑕疵检测的主要方式，但由于人为错误和眼睛疲劳使得检测效率降低。织物的自动视觉检测(AVI)应用计算机视觉技术后，不仅可以采用高效、低成本和准确的方法代替劳动力，而且还能扩展检测能力，以涵盖从最简单到最复杂的更广泛的不同的织物图案。现阶段纺织品种类大致能够分为2种：1)无图案的纺织品，结构简单，不包含复杂的图案，一般包含平纹与斜纹；2)有图案的纺织品，结构复杂，包含复杂的图案，同时图案信息具有周期变化的结构。

针对无图案的纺织品,研究者提出了较为成熟的方法，可以分为：统计学方法，例如，规律性测量^[1]、分形特征测量^[2]、形态学滤波器^[3-4]等；光谱的方法，例如，傅里叶变换^[5]、Gabor ^[6]、小波^[7]等；模型的方法，例如，高斯马尔可夫随机场^[8]、稀疏字典重建^[9]等；学习的方法，例如，神经网络^[10]、支持向量机^[11]和结构的方法^[12]。

相比之下只有少数方法能够针对有图案的纺织品，例如：小波预处理黄金图像减法(WGIS)^[13]、布林线波段法(BB)^[14]、正则带法(RB)^[15]和图像分解(ID)^[16]，还有基于模板校正(TC)^[17]。

本研究的重点是复杂图案的织物。图案化织物由基本单元组成，其基本组成单元称为图案。图案化织物检测方法可以进一步分为3类：分区匹配的方法、统计的方法和基于模态的方法。

分区匹配方法包括WGIS和ER方法^[18]。在Haar小波分解之后，WGIS方法使用无缺陷分区对图像执行移动减法操作以获得决策边界。ER方法通过随机竞赛获得决策边界。然而，由于训练阶段无缺陷分区选择的随机性，这2种方法的检测结果都不稳定。统计方法包括BB和RB方法，通过移动平均值和标准差的不同组合获得决策边界。尽管这些通过阈值分割实现的方法是有效的，但是它们包含过多的模型参数导致过度依赖人为经验。基于模态的方法包括ID方法。ID方法将图像分解为卡通部分和纹理部分，将卡通图像转换为二值图像进而实现检测。但这种方法在检测时要获取与待测图像最相似的无瑕图，将无暇图的分解系数作为参数，对待测图像进行分解。上述提出的方法利用有限参数描述图像不同像素间的统计相关性。此外，这些方法直接检测像素级的图像缺陷，会导致某些像素的误检。

马慧等^[19]针对静脉图像采样过程中出现旋转、平移等因素造成静脉图像定位不准确的问题，提出了采用旋转校正的指静脉图像感兴趣区域提取方法。Wang等^[20]根据人眼视觉系统提出了基于结构相似度的图像质量评价方法(SSIM)。根据图像信号是高度结构化的，特别是若像素点间相互接近时，具有较强结构相关性，以此来区分图像间的差异。Wang提出结构相似性评价标准，并且提供了评价感知质量指标的条件，包括与人类视觉神经生物学和感知的联系，以及针对人类受试者评级的指数的直接验证。由于SSIM不能准确地评价局部畸变类型的图像，很难准确地找到织物中瑕疵的精确部分。

针对上述出现的问题，本文利用图像中的晶格间结构信息变化，有效描述了图像纹理的结构特性，提出一种基于结构相似性与模板校正的织物瑕疵检测方法。将具有周期性结构的图像自动分割成网格,每个晶格包含大致相同的图案特征，为特征提取、实验的分析和比较提供了非常有利条件。为了减少纺织品图案局部拉伸的影响而引入一种循环移位的算法改变晶格的排列组合，减少晶格间不匹配的影响。在校正的基础上建立一个无瑕模板，区分无瑕晶格和模板之间的不同，以减少晶格间错位的变化，提高了检测的准确性。通过计算所有校正后晶格间的结构相似性，并将相似关系通过传递闭包的方式得到等价关系，进行格子间的聚类，识别疵点晶格的区域。通过阈值分割方法将获取的瑕疵晶格进行有效的检测，得到像素级的疵点。

1 相关工作

SSIM是基于感知的方法，其将图像失真转为结构信息中的感知变动，并且结合亮度与对比度等重要的感知方式。若像素位置相互靠近,具有显著的结构相关性。此类特征包含目标结构的关键信息。亮度掩蔽是一种图像畸变现象，主要表现为在明亮区域中不可见。对比度掩蔽是指图像纹理间形变较小。该方法根据亮度、对比度、结构度对待测图像与模板图像完成对比，加权相乘求得子图的结构相似度，最后计算所有子图像的结构相似度的平均值得到SSIM值。

假设待检测图像为X，参考图像为Y，SSIM如式(1)：

${\rm{SSIM}}(x,y) = {[l(x,y)]^\alpha } {[c(x,y)]^\beta } {[s(x,y)]^\gamma }$

(1)

其亮度计算为

$l(x,y) = \frac{{2{\mu _{\rm{x}}}{\mu _y} + {C_1}}}{{\mu _x^2 + \mu _y^2 + {C_1}}}$

对比度计算为

$c(x,y) = \frac{{2{\sigma _{\rm{x}}}{\sigma _y} + {C_2}}}{{\sigma _x^2 + \sigma _y^2 + {C_2}}}$

结构相似度计算为

$s(x,y) = \frac{{{\sigma _{xy}} + {C_3}}}{{{\sigma _x}{\sigma _y} + {C_3}}}$

式中： ${\mu _x}$ 、 ${\mu _y}$ 分别为图像X和Y的灰度平均值； ${\sigma _x}$ 、 ${\sigma _y}$ 分别为图像X和Y的标准偏差； ${\sigma _{xy}}$ 为图像X和Y的协方差； ${C_1}$ 、 ${C_2}$ 、 ${C_3}$ 为正数，为了避免出现分母是0或接近0的不稳定情况； $\alpha $ 、 $\beta $ 、 $\gamma $ 分别代表调整亮度、对比度、结构相似度的权重值。当 $\alpha {\rm{ = }}\beta {\rm{ = }}\gamma {\rm{ = }}1$ ， ${C_3}{\rm{ = }}{C_2}/2$ ，式(1)简化为

${\rm{SSIM}}\left( {x,y} \right) = \frac{{(2{\mu _x}{\mu _y} + {C_1}) + (2{\sigma _{xy}} + {C_2})}}{{(\mu _x^2 + \mu _y^2 + {C_1})(\sigma _x^2 + \sigma _y^2 + {C_2})}}$

2 基于结构相似性与模板校正的算法 2.1 算法描述

本文算法分为训练和测试2个部分。

训练部分：

1)对无瑕图像采用自动分割，获得N个晶格集合 ${B_i}$ ( $i = 1, 2,\cdots ,N$ )。

2)针对上述完成分割的晶格采用循环移位的算法改变格子的排列组合，实现晶格的校正。

3)在校正的基础上建立一个统一的无瑕模板，根据结构相似性量化校正后无瑕晶格和模板之间的差异，获得用于瑕疵晶格定位的决策边界t。

测试部分：

1)对瑕疵图像采用自动分割，获得N个晶格集合 ${A_i}$ ( $i = 1,2, \cdots ,N$ )。

2)针对上述分割后的格子采用循环移位的算法改变晶格的排列组合，实现晶格的校正。

3)计算集合 ${A_i}$ 内部元素间的结构相似系数，得到N个结构相似系数矩阵R_ei。

4)使用训练阶段求得的决策边界t，对结构相似系数矩阵R_ei进行阈值分割，得到疵点晶格的区域。

5)通过阈值分割方法对疵点晶格完成像素级的精确检测。

2.2 自适应分割

对于具有周期结构的图案化织物图像，应用损失函数 $f$ 得到单位图案大小：

$(r*,c*) = {\rm{Arg}} {\rm{min}} f(r,c) $

式中：(r*,c*)是单位图案大小，对图像I截取r×c大小的晶格，当r、c为单位图案周期大小时， $(r,c)$ 即为单位晶格大小。 $f(r,c)$ 函数为

$f(r,c) = \frac{1}{{r \times c}}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{S^2}(i,j)} } $

式中 ${S^2}(i,j)$ 表示晶格间方差，定义为

${S^2}(i,j) = \frac{1}{{m \times n}}\sum\limits_{k = 0}^{m{\rm{ - }}1} {\sum\limits_{l = 0}^{n{\rm{ - }}1} {(I} } (i + k \times r,j + l \times c) - \overline {I(i,j)} {)^2} $

式中： $m = \left\lfloor {\dfrac{R}{r}} \right\rfloor {\text{；}}n = \left\lfloor {\dfrac{C}{c}} \right\rfloor$ 。将大小为R×C的图像B分割成m×n幅晶格子图。I(i,j)为图像I中第i行第j列上的灰度值。定义为

$\overline {I(i,j)} = \frac{1}{{m \times n}}\sum\limits_{k = 0}^{m{\rm{ - }}1} {\sum\limits_{l = 0}^{n{\rm{ - }}1} I } (i + k \times r,j + l \times c)$

当格子间标准差和为最小值，获取单位格子尺寸，图1为单元图案大小的确定及分割图。

2.3 图像校正方法 2.3.1 校正的定义

对图像进行自动分割后，分割后的晶格出现不匹配的结果。针对这种现象造成的影响,提出了图像校正的方法。因为晶格拉伸产生的形变的现象是局部的，所以分割后的每个晶格具有周期图案的完整特征。由于每个晶格都是数字矩阵，因此采用循环移位的算法，避免因为拉伸产生形变的影响。提出了以下模型：

${\rm{(}}p{\rm{,}}q{\rm{)}} = {\rm{Argmin}} \left\| {B - {{({{{T}}_v})}^{p{\rm{*}}}} \cdot A \cdot {{({{{T}}_h})}^{q{\rm{*}}}}} \right\|_{\rm{2}}^2$

(2)

式中：A为待校正的晶格；B为一个无瑕格； $p_{}^ * $ 表示行移动的量， $p_{}^ * $ ∈[0,r−1]； $q_{}^ * $ 表示列移动的量， $q_{}^ * $ ∈[0,c−1]；T_v和T_h分别表示 r×r 和 c×c尺寸的矩阵，如下：

$ {{{T}}_v} = {\left[ {\begin{array}{*{20}{c}} 0& \cdots &0&1 \\ 1& \cdots &0&0 \\ \vdots &{}& \vdots & \vdots \\ 0& \cdots &1&0 \end{array}} \right]_{r \times r}},\begin{array}{*{20}{c}} {}&{{{{T}}_h} = {{\left[ {\begin{array}{*{20}{c}} 0& \cdots &0&1 \\ 1& \cdots &0&0 \\ \vdots &{}& \vdots & \vdots \\ 0& \cdots &1&0 \end{array}} \right]}_{c \times c}}} \end{array} $

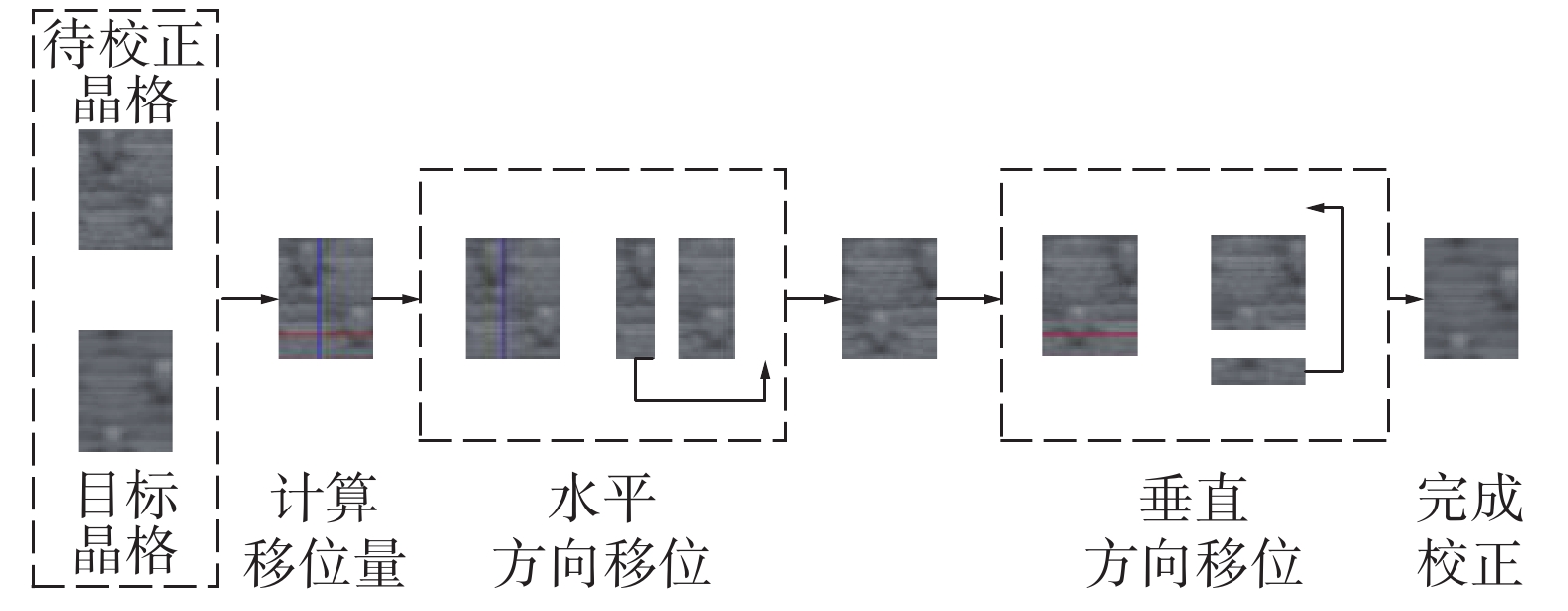
图2为图像校正结果，根据式(2)得出的p和q，将A在水平方向上分割成尺寸q×r以及(c−q)×r的两个区域。若要消除水平方向的拉伸,则将第一个区域转移到后一区域的右方；同理，在垂直方向上采取同样的处理，最后获得校正后的格子。

2.3.2 模板的建立

对N张无瑕图采用自动分割，并计算每张无瑕图中所有晶格的均值矩阵，定义为 ${{{P}}_i}$ ， $i = 1, 2,\cdots , N$ 。将无瑕图的矩阵 ${{{P}}_1}$ 当作无瑕参考标准,其他无瑕图的矩阵按照 ${{{P}}_1}$ 进行校正，校正完成的格子为 ${{{O}}_i}$ 。模板计算如式(3)：

${\rm{TM}}(x,y){\rm{ = }}\frac{1}{N}({{{O}}_1}(x,y) + {{{O}}_2}(x,y)+ \cdots + {{{O}}_n}(x,y))$

(3)

式中：x∈[1,r]；y∈[1,c]。为了减少光照不均和晶格间错位的影响，选取的样本为无瑕图像的所有晶格的灰度均值矩阵。

2.4 晶格间结构相似性

使用结构相似性对比格子之间的相似程度是模糊的。可以建立等价关系矩阵，完成等价类的划分。要获取格子之间的等价联系，首先要得到相似性矩阵,然后再求相似性矩阵的传递闭包可以得出近似的等价联系，最终可以对无瑕格子进行聚类操作。

首先建立一个表示晶格间相似关系的矩阵，采用结构相似性来衡量晶格的相似性，将图像自动分割，获得一个格子集合A={ ${A_1}, {A_2},\cdots ,{A_n}$ }。设 ${S_{ij}}$ 表示晶格 ${A_i}$ 与晶格 ${A_j}$ 的SSIM值，定义如下：

${S_{ij}}\left( {x,y} \right) = \frac{{(2{\mu _x}{\mu _y} + {C_1}) + (2{\sigma _{xy}} + {C_2})}}{{(\mu _x^2 + \mu _y^2 + {C_1})(\sigma _x^2 + \sigma _y^2 + {C_2})}}$

结构相似性具有以下性质:1)有界性， ${S_{ij}}$ ∈[0,1]，当值越临近1，晶格间相似性越强；2)极值唯一性，当晶格间相似性是1时,两幅图相同。

通过11×11大小的窗口在晶格 ${A_i}$ 和晶格 ${A_j}$ 上移动，计算窗口相应子图的结构相似度，并求得所有子图结构相似度的均值，得到晶格间的结构相似性为

${\rm{MSSIM}}\left( {X,Y} \right){\rm{ = }}\frac{1}{M}\sum\limits_{i = 1}^M {{\rm{SSIM}}({x_i},{y_i})} $

式中M为子图像的总数。MSSIM的值越大,晶格 ${A_i}$ 与晶格 ${A_j}$ 间的相似性就越高。记R_e = ${({r_{ij}})_{N \times N}}$ 为SSIM特征矩阵， ${r_{ij}}$ ∈[0, 1]。要完成无暇格子的聚类,相似关系矩阵应经过关系矩阵求传递闭包矩阵。传递闭包矩阵可以作为等价关系矩阵。设A、B为两个n阶矩阵,若存在元素间关系 ${a_{ij}}$ ≤ ${b_{ij}}$ ，i，j=1,2,…，n，则A≤B。

求取传递闭包的方法如下。设S为有限集O上的二元关系,则S是传递的充分必要条件是: S的关系矩阵MS满足MS²≤MS,MS²=MS·MS，若MS²≤MS，t(MS)=MS,否则比较MS和MS²的元素，将MS中的数值为0的元素而在MS²中相同位置数值为1的全部元素变为1，得到一个新矩阵 ${{\bf{MS}}_1}$ ，当 ${{\bf{MS}}_1}$ ≤ ${\bf{MS}}_1^2$ 时，t(MS)= ${{\bf{MS}}_1}$ ；如不满足此条件，重复上述步骤，当 ${{\bf{MS}}_k}$ ≤ ${\bf{MS}}_k^2$ 时，t(MS)= ${{\bf{MS}}_k}$ 。

2.5 瑕疵晶格的定位

根据关系矩阵获取传递闭包矩阵，对传递闭包矩阵进行阈值分割后,能够实现无瑕晶格间的聚类，获得疵点晶格的定位。设t是阈值,对传递闭包矩阵进行阈值分割,当 ${S_{ij}}$ ≥t时，晶格 ${A_i}$ 与晶格 ${A_j}$ 间为等价关系,当 ${S_{ij}}$ <t时，晶格 ${A_i}$ 与晶格 ${A_j}$ 间不存在关系。无瑕晶格间的结构相似度大于无瑕晶格与瑕疵晶格之间的结构相似度。阈值t在区间[0, 1]动态变换可以获得动态变换的聚类效果。

在训练过程中,以步长值d在区间[0, 1]对P幅无瑕图像进行遍历，得到无瑕图像发生分类时的数值 ${t_i}$ 。阈值为

$t = \min ({t_i})$

2.6 瑕疵晶格阈值化

为了对瑕疵晶格进行像素级的检测,提出了一种阈值分割方法。对每个检测到的瑕疵晶格进行如下计算：

$\left\{ \begin{array}{l} \begin{array}{*{20}{l}} \!\!\!\!{{\rm{LD}}(x,y) = 0},\quad{{\rm{TM}}(x,y) - \lambda \times \sigma (x,y) \leqslant {\rm{LD}}(x,y)} \end{array} \leqslant \\ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {}&{}&{} \end{array}}&{}&{} \end{array}}&{}&{} \end{array}}&{ {\rm{TM}}(x,y) + \lambda \times \sigma (x,y)} \end{array} \\ {{\rm{LD}}(x,y) = 1},\quad{\text{其他}} \\ \end{array} \right.$

式中：TM为式(3)求得的模板； $\sigma (x,y)$ 表示晶格 ${{{O}}_i}$ 的标准差； $\lambda $ 代表常数；LD(x,y)为瑕疵晶格x行y列上的灰度值。 $\lambda =$ 2时会有一些像素点被误检，使得查准率降低，查全率较高。 $\lambda =$ 3时会有一些像素点被漏检。本文方法 $\lambda =$ 2。

$\sigma (x,y){\rm{ = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({{{O}}_i}(x,y) - {\rm{TM}}(x,y))}^2}} } $

由于平均值和标准偏差是指示一组数据变化的良好度量。因此，由平均值和标准偏差组成的阈值对正常变化存在良好的鲁棒性。

由于在检测时晶格经过校正,所以在瑕疵晶格阈值化之前采用以下操作进行还原。

$L = {({{{T}}_v})^{(r - p)}} \cdot {{LD}} \cdot {({{{T}}_h})^{(c - q)}}$

式中：r、c为晶格的大小；p、q为位移值。

3 实验结果及分析

本实验使用的数据库为香港大学电气与电子工程系工业自动化实验室织物样本库。样本库共含有102幅256×256大小的纺织品图像，共有3种图案的织物图像，即星形图、盒形图、点形图。瑕疵种类有断经(broke end)、破洞(hole)、网纹(netting multiple)、粗条纹(thick bar)、细条纹(thin bar)。用于对比的方法有WGIS、BB、ER、RB、TC。定义TPR(true positive rate)为查全率,该评价指标确定瑕疵基准图(ground-truth image)中瑕疵所在的像素被正确标记的比例；FPR(false positive rate)为误检率,确定瑕疵基准图中背景像素被算法错误标记为瑕疵所占的比例；PPV(positive predictive value)为查准率,确定算法标记的瑕疵在瑕疵基准图中的瑕疵所占比例；NPV(negative predictive value)为阴性预测值,确定算法标记的背景在瑕疵基准图中背景所占的比例。定义f值作为检测情况分析的参考，f值的计算方法如下：

$f = \frac{{({\alpha ^2} + 1) \times {\rm{TPR}} \times {\rm{PPV}}}}{{{\alpha ^2} \times ({\rm{TPR + PPV)}}}} $

式中：f表示查全率与查准率的几何加权平均值； $\alpha $ 为权重。文献[21]将 $\alpha $ 置为1，表示当手工标记为无瑕却被误检的部分和手工标记为瑕疵却被漏检的部分增加时，其检测结果与手工标记的结果不同时，f值会减少。当 $\alpha > 1$ 时表示查准率比较重要，当 $\alpha < 1$ 时表示查全率比较重要。本文中将 $\alpha $ 置为1，f值越接近1代表检测效果越好。这种评价方法结合了查全率和查准率，避免了非同量级数值相加时代数与数值较大的数接近的影响。

3.1 基于相似关系的瑕疵晶格定位算法结果

对检测完成的瑕疵结果图进行二值化操作，完成瑕疵晶格的定位。对检测为瑕疵的晶格标记为1，无暇疵晶格标记为0。实验结果如表1～3所示。

3.2 基于模板的瑕疵精确检测结果

为了确定瑕疵形状的大小，对3种类型的纺织品应用基于模板的方法进行检测。部分检测结果如图3。

3.3 对比实验

本文与WGIS、RB、BB、ER、TC 5种算法对星形图、盒形图、点形图的瑕疵了进行了对比实验。表4～6是瑕疵检测算法的结果。

3.3.1 星形图

由图4～6可知,本文方法在3种类型瑕疵图中检测结果优于其他5种方法。表4列出了星形图的检测结果,在破洞型、粗条纹型瑕疵的PPV值检测结果中本文算法优于其他5种算法，在断端型、破洞型瑕疵中f值为最优值。

3.3.2 盒形图

分析图7～9的检测结果，本文方法在断端、破洞瑕疵类型图中的检测效果近乎接近瑕疵基准图，在粗条纹型瑕疵检测结果图中，存在少量像素点的误检，BB方法对3种类型图检测效果较差，RB方法对断端和粗条纹类型图检测效果较好。WGIS方法查全率较高。

表5列出了盒形图的检测结果，WGIS方法在粗条纹型瑕疵检测中的TPR值为最优值，TC方法在断端型、破洞型瑕疵检测中的PPV值达到最优。本文方法在破洞型瑕疵检测中的TPR值为最优值，且在破洞型、粗条纹型瑕疵中f值均达到最优。总体来看，本文方法的查全率和查准率整体优于其他5种算法。

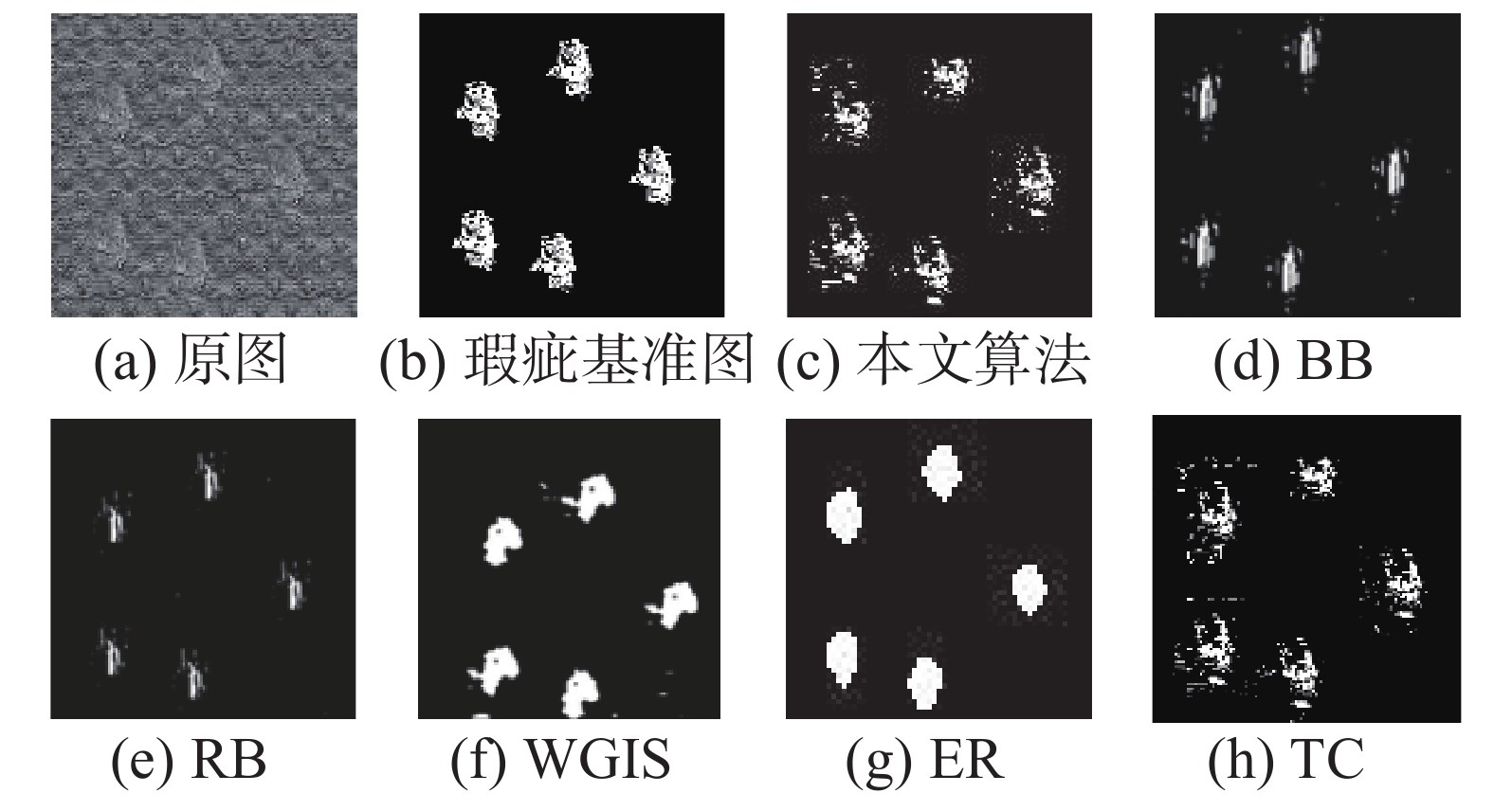
3.3.3 点形图

分析图10～12的检测结果，本文方法在细条纹、粗条纹瑕疵类型图中的检测效果优于其他5种算法，在绳结型瑕疵检测结果图中，存在部分误检的情况。表6列出了点状图的检测结果，本文方法在细条纹、粗条纹型2种类型瑕疵检测结果中的PPV值均为最优值。在绳结型瑕疵检测结果图中ER方法f值、TPR值、PPV值均达到最优。TC方法在细条纹、粗条纹瑕疵检测中f值达到最优。总体来看，本文方法的查全率优于其他5种算法。

4 结束语

本文提出了一种基于结构相似性与模板校正的织物瑕疵检测方法。针对包含复杂周期的图案织物的疵点检测问题，将图像按周期自动分割，为了减小由图像局部形变造成的晶格间不匹配的局限性的影响。通过基于模板的方法进行校正，再利用晶格间的SSIM，将瑕疵点检测问题转为图像晶格的二分类问题，对瑕疵晶格进行标记，完成瑕疵晶格的定位，根据提出的阈值准则对晶格进行像素级的检测。本文算法对星形图和盒形图在PPV、TPR、f值对比传统算法有很大的提高。点形图两种瑕疵图检测结果TPR比传统算法要好,但会出现少部分像素点的误检，因为点形图类型纺织品的图案较为复杂,图像具有较多的纹理信息。在实际应用中还需进一步探讨基于图像特征的晶格分割的方法。