2. 东北大学 信息科学与工程学院,辽宁 沈阳 110819;
3. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
2. College of Information Science and Engineering, Northeastern University, Shenyang 110819, China;
3. School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China
德州扑克属于一种典型且复杂的非完全信息动态博弈问题[1-2],它是近年来计算机博弈领域的学者们重点研究的热点问题。2006年,加拿大阿尔伯特大学(University of Alberta)作为主办方举办了首届国际计算机扑克大赛[3];2007年,德州扑克博弈系统Polaris首次战胜了职业扑克选手[4]。2015年1月,加拿大阿尔伯特大学在Science期刊上发表了一篇关于德州扑克博弈问题最新研究成果的文章[5],该研究小组开发了两人参与的有赌注上限的德州扑克博弈系统,并得到了该博弈问题的理论解。但是二人赌注无上限的德州扑克问题,由于具有更高的复杂度(文献[6]证明了此类问题属于NP-hard问题),一直没有实现求解。2017年1月30日,美国卡耐基梅隆大学开发的德州扑克博弈系统Libratus与4名人类顶尖德州扑克选手之间的“人机大战”在美国匹兹堡结束,最终人工智能取得胜利[7]。这是人工智能在各种棋牌博弈中对人类取得的又一个胜利。本文提出一种二人赌注无上限的德州扑克博弈系统架构,构建了一个专家经验库;利用海量历史牌局训练得到基于CNN的深度学习网络模型;在系统的搜索模块中,构建了一种分阶段的德州扑克博弈树,利用专家经验和历史经验引导德州扑克博弈树的展开;对于系统的估值核心模块,构建了一种基于哈希技术的牌型对照表,以提高系统判定胜负的效率。
1 二人赌注无上限德州扑克 1.1 二人赌注无上限德州扑克规则二人赌注无上限德州扑克是一种双人的扑克游戏。一共有52张牌,没有大、小王。每个玩家分两张扑克牌作为底牌(只有本方可见,其他玩家不可见),另有5张是所有玩家可见的公共扑克牌被陆续发出。其具体规则[8]如下。
首先,每个玩家分别得到两张底牌(称为Preflop阶段),随着第一轮两个玩家交替下注后,开始陆续发公共牌:
1)第1次发牌将同时发3张公共牌(称为flop阶段),然后由小盲注开始表态,玩家可以选择下注、加注或者盖牌放弃,若有一个玩家弃牌,则此次牌局结束;
2)第2次发牌只发1张公共牌(即第4张公共牌,Turn阶段),由小盲注开始轮流表态;
3)第3次发牌是发第5张公共牌(River阶段),由小盲注开始轮流表态。
最后,亮底牌并开始比牌(Showdown阶段),由手中的2个底牌、5张公共牌中的任意3张,组成5张最大的牌型进行互相比较,牌型最大的玩家赢得赌注池中的筹码。牌型大小依次为:同花顺、四条(如4张2)、葫芦(3带2)、同花、顺子、三条、两对、一对、高牌。若两个玩家拥有的5张牌牌型大小相同,则赌池中的筹码被两个玩家平分。小盲注双方轮换担任,每一局有4轮下注的机会,每一轮加注次数不限。
1.2 德州扑克博弈系统架构中的模块组成德州扑克问题是一种典型的非完全信息动态博弈问题,其博弈系统架构与完全信息动态博弈问题(如围棋、中国象棋等)相似,具体的模块组成如图1所示。

|
Download:
|
| 图 1 德州扑克博弈系统架构中的模块组成 Fig. 1 Modules of the system architecture of Texas Hold’em | |
德州扑克博弈系统主要由5个模块组成,其中数据表示,主要指德州扑克博弈问题中的扑克牌和走法(即下注行为)如何在计算机系统中表示,根据德州扑克的规则,共有52张牌,没有大、小王。本系统采用二维数组来表示52张扑克牌,即poker[4][13],第一维表示扑克牌的花色,下标0、1、2、3分别表示黑桃、红心、方块、梅花;对于走法,在德州扑克中就是两个玩家的下注行为,根据规则,玩家的下注行为包括下注、加注、看牌、跟注和弃牌,在系统中用5个整型常量(1~5)来表示。
走法生成模块是指对于某个德州扑克局面,用此模块产生具体的走法,德州扑克的牌局局面分为玩家下注时对应的局面和发公共牌的局面。对于下注时对应的局面,其走法就是玩家的下注行为,根据规则,每个发牌阶段先表态的玩家允许的下注行为包括下注、看牌和跟注,后表态的玩家允许的下注行为包括加注、跟注和弃牌;对于发公共牌的局面,其走法就是生成某个发牌阶段所有可能被发放的公共牌组合。搜索引擎、估值核心和知识库这3个模块的设计将在后面的章节详细阐述。
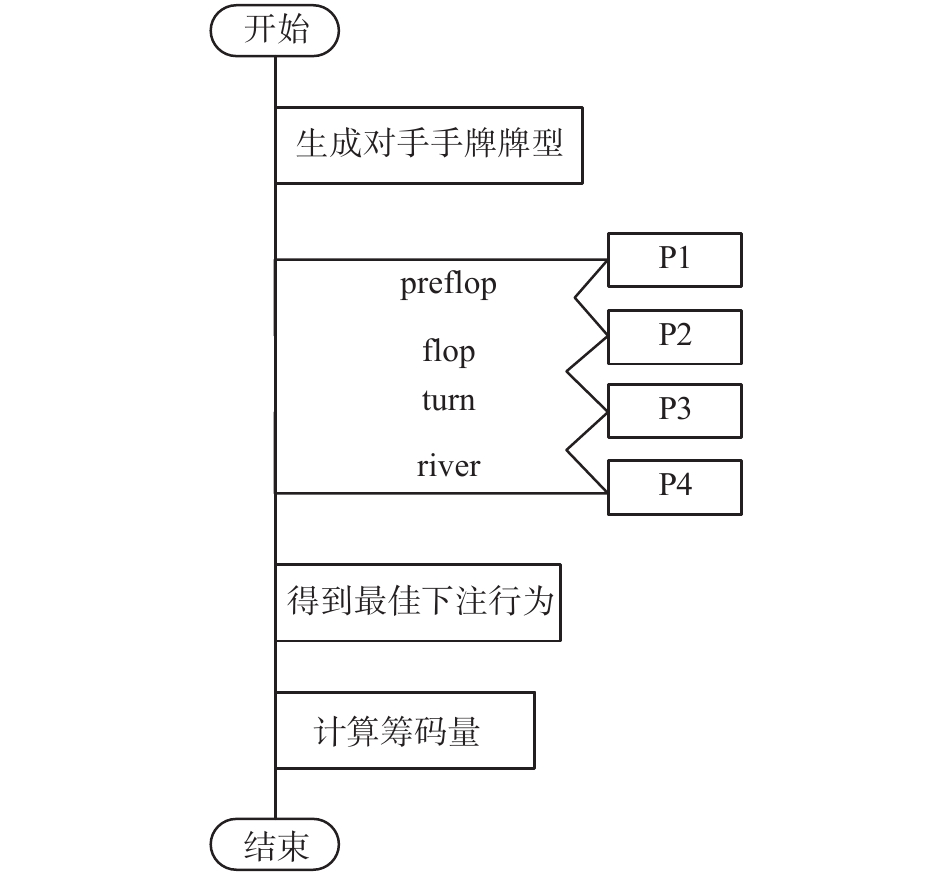
2 分阶段的德州扑克博弈树 2.1 德州扑克博弈树总体设计对于德州扑克问题,下注阶段包括Preflop、Flop、Turn、River共4个阶段。随着手牌及公共牌的发放,随机性和不确定性的逐渐降低,各个阶段的搜索策略并不相同。对于系统的搜索引擎模块,本文设计了一种分阶段的二人赌注无上限德州扑克博弈树(总体流程图见图2),由于对方手牌不可见,博弈树搜索模块首先要生成所有可能的对方手牌牌型,然后根据每两张具体牌型以及目前牌局所处的下注阶段展开一轮下注过程,以此类推,进而描述在该下注阶段之后,牌局的完整对弈过程。当博弈树展开到叶子节点(Showdown node),调用估值函数,判定胜负关系并计算输赢筹码量。
|
Download:
|
| 图 2 德州扑克博弈树搜索总体PAD图 Fig. 2 Overall problem analysis diagram of the game tree | |
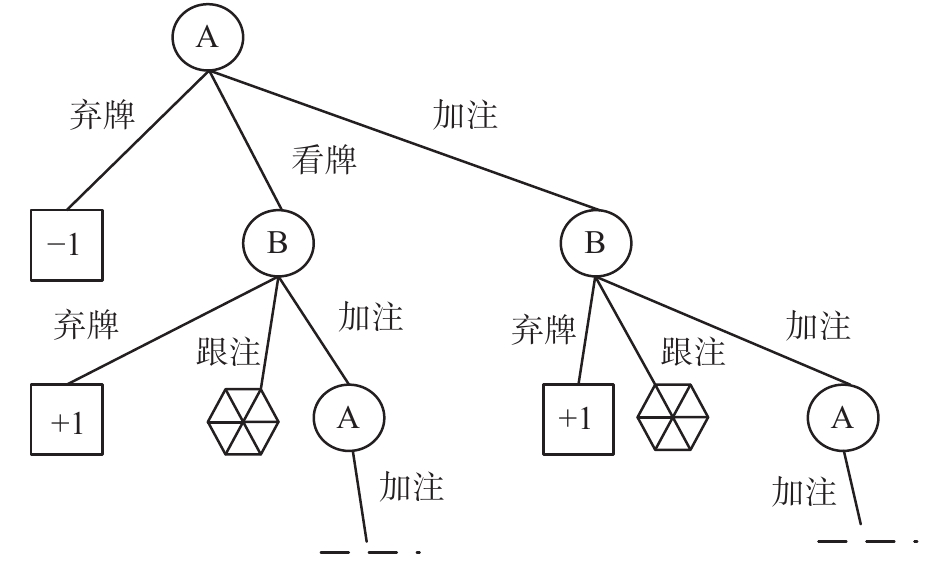
根据德州扑克的规则,每个发牌阶段发完公共牌之后,两个玩家需要交替下注,图3显示了德州扑克一轮下注过程的博弈树[9],博弈树包括:
1)玩家节点(如图3中的圆形节点)。对于二人的德州扑克问题,该节点表示本方玩家或对方玩家,这两种节点在博弈树中交替出现。
2)机会节点(如图3中的六边形节点)。该节点表示当前牌局进入下一轮发牌阶段。
3)每个玩家节点包含3种下注行为(如图3中的分支)。根据规则,每个玩家只有3种下注行为,即弃牌、下注/加注、看牌/跟注。
|
Download:
|
| 图 3 德州扑克一轮下注过程的博弈树示意图 Fig. 3 A part of the betting round | |
在博弈树展开到叶子节点(亮底牌)时,需要调用估值函数来评价每个叶子节点的优劣。根据德州扑克对弈规则,Showdown阶段需要比较双方5张扑克牌的牌型大小,牌型大小依次为:同花顺、四条、葫芦、同花、顺子、三条、两对、一对、高牌。通过程序进行牌型在线判断的方式,过于繁琐且影响系统的搜索效率。
本文提出一种基于哈希技术[10]的牌型大小对照预置表。哈希技术在棋类博弈问题(比如中国象棋[11])启发式搜索及开局、残局库中经常用到,基于哈希技术的置换表是启发式搜索中最为重要的算法,在计算机博弈系统中起着十分重要的作用。作为混合博弈树搜索引擎中的一种启发式搜索算法,在搜索中如果有和置换表中相同的节点,不用再向下搜索,可以直接调用表中的记录,这样省去了很多时间,从而提高了搜索引擎的效率[12-14]。本文将哈希技术用于建立德州扑克牌型大小对照表,在程序启动时,将牌型大小对照表加载到内存中,采用查表的形式代替繁琐的牌型判断,缩短判断牌型大小所需的时间,以提高引擎的搜索效率。
3.1 牌型对照表的设计牌型对照表由牌型种类、同类牌型中的排名、是否已有数据标志位及牌型识别码4个字段组成。表的每一行占16个字节,表的尺寸为2.6M×16B≈42MB(其中2.6 M为
struct HashItem
{
short type;//牌型类型标示位
short flag;//该位置是否已存放数据的标志位
int ranking;//同类牌型中的排名
unsigned _int64 checksum;//5张扑克牌的64位识别码
}
3.2 牌型对照表的构建在系统启动时,生成基于哈希技术的牌型对照表,利用查表代替繁琐的程序判断,实现快速比较双方在Showdown阶段的牌型大小。具体构建的流程如下:
1)牌型对照表由基本表和溢出表组成(这种设计主要用于解决哈希冲突问题,在3.4节有具体阐述);
2)随机生成扑克牌的32位随机整数和64位随机整数;
3)分别生成同花、四条、葫芦、顺子等5张扑克牌牌型种类中的所有牌型,并存放到哈希表中。以同花顺为例,根据4种花色和每个花色将“A”到“5”的牌型作为循环嵌套:
①分别取5张连续的扑克牌,取出相应扑克牌32位、64位随机整数,做异或运算;
② 根据异或得到的32位整数,计算26位地址;
③ 计算并写入排名字段,标志位flag置1;
④ 写入类型字段;
⑤ 写入64位哈希值,作为牌型识别码。
3.3 查询牌型对照表德州扑克博弈树在展开到叶子节点(Showdown节点)时,需要查询牌型对照表来确定双方的胜负关系。查询牌型对照表的步骤如下:
1)分别从双方的7张扑克牌中,找到牌型最大的5张扑克牌牌型,即
①首先从7张扑克牌中,生成所有的5张扑克牌组合;
② 遍历这个集合,排除高牌的牌型;
③ 查询牌型对照表,得到具体牌型类型和在该类型中的排名;
④ 相互比较,得到最大的牌型;
⑤ 若所有牌型都为高牌,则对这些牌型按照数值降序排列,再相互比较得到最大的牌型;
2)与对方的最大牌型进行比较,判定胜负关系。
3.4 哈希冲突的解决方法基于哈希技术的牌型对照表虽然可以提高查询效率,但是哈希技术存在一个缺陷,即哈希冲突。哈希冲突是指:关键字key1≠key2,但是H(key1)=H(key2),这里H表示哈希函数。无论哈希函数多么地散列,哈希表存在的冲突都无法避免[15]。对于博弈树搜索中的基于哈希技术的置换表来说,即使存在冲突,可以通过搜索代替查表,影响的只是搜索效率;而本文提出的牌型对照表,用于Showdown阶段比较双方牌型大小,包含了所有的5张扑克牌牌型,不允许存在冲突。
本文采取建立公共溢出区与开放定址法[16]相结合的方式来解决哈希表存在的冲突,具体设计思路如下:
1) 将哈希表尺寸扩大到64 MB,提高表的散列度;
2) 将数据存放到基本哈希表;
3) 若哈希值冲突,则存放到公共溢出表中;
4) 若公共溢出表中也存在相同哈希值的数据,则采用开放定址法解决此冲突,即采用线性探测再散列的方法[16],将哈希值做加1、加2等处理,找到接近冲突地址且空的位置,存放数据。
3.5 得到两个表的最佳内存分配方案以一种德州扑克牌局局面为例,根据分配给基本哈希对照表和溢出表不同的存储空间,比较冲突数和搜索时间的差别;这里设定了一个Flop阶段的牌局状态,通过完成一次搜索来比较表占用内存的大小、发生的冲突数对搜索效率的影响,进而得到一个最佳的内存空间分配方案。
以一个局面状态为例,根据分配给基本哈希对照表和溢出表不同的存储空间,比较冲突数和搜索时间的差别;这里设定了一个Flop阶段的牌局状态,通过完成一次搜索来比较表占用内存的大小、发生的冲突数对搜索效率的影响,进而得到一个最佳的内存空间分配方案。测试例子:AI手牌为“AsKh”,Flop阶段的公共牌为“9d8s7d”,其中,s表示黑桃,h表示红桃,d表示方块。
根据表1和表2的测试结果,最终得到基本表和溢出表的最佳分配方案为:基本表占用128 MB、溢出表占用128 MB。
| 表 1 占用内存空间、发生的冲突数及查询时间对照表(溢出表大小为128 MB) Tab.1 Comparison of memory space, hash collisions and time consumed (size of the overflow table: 128 MB) |
| 表 2 占用内存空间、发生的冲突数及查询时间对照表(溢出表大小为256 MB) Tab.2 Comparison of memory space, hash collisions and time consumed (size of the overflow table: 256 MB) |
德州扑克属于非完全信息动态博弈问题,对弈过程中对手的底牌不公开,导致博弈树中对手节点的决策行为难以判断,这就加大了博弈树的复杂度。本文在德州扑克博弈系统中构建了知识库:通过对历史牌局的学习,提高系统的对弈经验,根据经验展开对手神经网络建议的决策行为;构建了专家经验库,根据当前牌局局面给出本方玩家节点的决策行为建议。这在一定程度上降低了博弈树的复杂度,提高了搜索效率。
4.1 适用于德州扑克问题的深度学习神经网络本文采用一种深度学习方法[17-18]——卷积神经网络[19] (convolutional neural networks,CNN),以海量历史牌局作为学习样本,利用已有知识预测对手的决策习惯[20]。通过国际计算机扑克博弈大赛网站提供的历届若干位高水平德州扑克博弈系统的历史牌局(约2千万个牌局)作为学习样本,将历史牌局视为完全信息动态博弈,对每一场德州扑克牌局采用卷积神经网络学习这些历史数据,从而掌握对手的决策行为建议。
4.1.1 总体设计为了使卷积神经网络可以识别历史对弈数据,需要对牌局文件(txt文件)做处理,就是要一行一行地读取文件中的牌局数据,并转换成卷积神经网络可以识别的csv文件。图4描述了深度学习模块的总体设计。

|
Download:
|
| 图 4 深度学习模块功能示意图 Fig. 4 Overall design of the deep learning module | |
依据德州扑克对弈规则[5],共有52张扑克牌,系统可以采用二维数组表示对弈过程中的牌型,即poker[4,13],每个数组元素用1表示已发放,0表示未发放。对于卷积神经网络的设计,本文采用20×20的张量表示一张扑克牌,就是将4×13矩阵扩展到20×20矩阵,空位用0填补。牌局中出现的玩家决策行为及产生的筹码量也放在这个矩阵中。
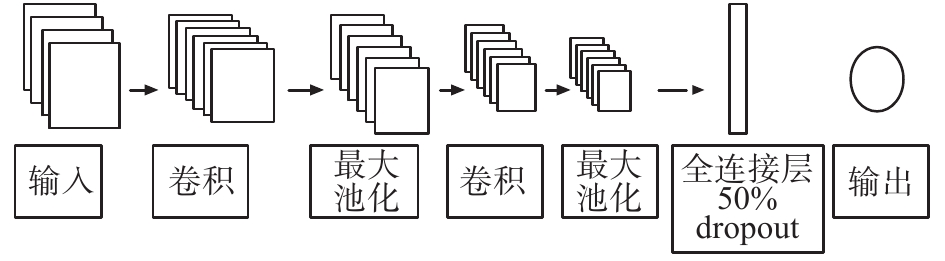
本文设计的卷积神经网络 (图5),需要2个卷积层,即一个最大池化层(尺寸为2×2)和一个dropout层;每个卷积层都采用同一尺寸的卷积核(尺寸为5×5)。
|
Download:
|
| 图 5 卷积神经网络结构设计示意图 Fig. 5 Design of the convolutional neural network | |
为了得到精度较高的深度学习神经网络,本文做了如下实验:
1) 从2 000万个牌局中,随机抽取10万个;
2) 设定训练参数,并输出神经网络模型;
3) 从剩余的海量牌局中,随机抽取6万个;
4) 设定测试参数,输出显示测试精度。
通过实验,得到如表3所示的实验结果,当训练次数达到5 000次,每次抽取1 024个样本,测试精度可以达到99.74%。
| 表 3 训练参数设置及测试精度对照表 Tab.3 Comparison of the training parameters’ setting and test accuracy |
博弈树展开过程中,对于玩家节点,一般有3种下注行为(即着法,博弈树中玩家节点的分支)。为了提高德州扑克博弈树展开的效率,本文依据专家经验,为本方玩家节点选择最佳决策行为。
德州扑克在Preflop阶段,没有发放公共牌,不确定性过大,如果展开博弈树,由于博弈树中包含太多随机因素,搜索效率很低且不够准确。因此,本文在Preflop阶段,不展开博弈树,而是根据本方手牌牌型和对方的下注行为,来查询专家库,直接决定本方下注行为。本文分别建立了Preflop阶段手牌分析专家库及Flop、Turn、River阶段专家库。
4.3 实验将专家库+深度学习(以下简称为EXP + CNN)德州扑克博弈系统与专家库+专家库(以下简称为EXP+EXP)版本的博弈系统进行对弈1 000局(对弈规则:每局双方分别拥有20 000个筹码,筹码量一局一复位;大小盲注身份一局一交换;以最终赢得筹码量的多少判定胜负关系),根据胜负关系来比较两个系统的优劣。
根据表4显示的对弈结果可知,EXP + CNN版本的系统对弈EXP+EXP版本时,赢得了比较多的筹码,说明利用深度学习模型预测对手行为更加准确;实验中的人类玩家就是专家库的开发者,从表4可看到,人类玩家与EXP+EXP版本的系统对弈水平十分接近。另外,EXP + CNN版本的德州扑克博弈系统在2018中国大学生计算机博弈大赛上获得季军。没有取得更好成绩的主要原因:作为深度学习神经网络的输入数据,历史牌局没有经过仔细的筛选,如果选择那些更高水平德州扑克博弈系统比赛的历史牌局作为输入数据,训练得到的深度学习网络模型一定能够给出更优的决策行为。
| 表 4 两个版本博弈系统对弈1 000局的胜负关系 Tab.4 Results of two versions of the game system playing 1 000 games |
本文提出一种二人赌注无上限的德州扑克博弈系统架构,在系统的搜索模块中,构建了一种分阶段的德州扑克博弈树;在知识库模块中,构建了专家经验库,引导博弈树中本方玩家节点的决策分支展开;并通过学习海量历史牌局数据得到一个深度学习神经网络,利用历史经验引导德州扑克博弈树中对方玩家节点的决策分支展开;对于系统的估值核心模块,构建了一种基于哈希技术的牌型对照表,以提高系统判定胜负的效率。实验表明,该博弈系统具有较高的博弈水平。对于未来的研究工作,应该参考冷扑大师的算法架构,在博弈系统中加入虚拟遗憾最小化算法(counterfactual regret minimization,CFR),进一步提高德州扑克博弈系统的对弈水平。
| [1] |
OSBORNE M J, RUBINSTEIN A. A course in game theory[M]. Cambridge: MIT Press, 1994.
( 0) 0)
|
| [2] |
胡裕靖, 高阳. 扑克游戏中的不完美信息博弈[J]. 中国计算机学会通讯, 2014, 10(9): 37-42. HU Yujing, GAO Yang. Games with incomplete information in Pokers[J]. China computer society newsletter, 2014, 10(9): 37-42. (  0) 0)
|
| [3] |
LITTMAN M, ZINKEVICH M. The 2006 AAAI computer-poker competition[J]. ICGA journal, 2006, 29(3): 166-167. DOI:10.3233/ICG-2006-29314 ( 0) 0)
|
| [4] |
HARRIS M. The first “Man-Machine Poker Championship” begins tomorrow[N]. Poker News, 2007-07-22.
( 0) 0)
|
| [5] |
BOWLING M, BURCH N, JOHANSON M, et al. Heads-up limit hold’em poker is solved[J]. Science, 2015, 347(6218): 145-149. DOI:10.1126/science.1259433 ( 0) 0)
|
| [6] |
BLAIR J R S, MUTCHLER D, LIU C. Games with imperfect information[R]. AAAI Technical Report FS-93-02. American: AAAI, 1993.
( 0) 0)
|
| [7] |
HINTZE H. Libratus scores convincing sweep in man v. machine poker match[N]. Misc, News, 2017-01-31.
( 0) 0)
|
| [8] |
BILLINGS D, DAVIDSON A, SCHAEFFER J, et al. The challenge of poker[J]. Artificial intelligence, 2002, 134(1/2): 201-240. ( 0) 0)
|
| [9] |
BILLINGS D. Algorithms and assessment in computer poker[D]. Alberta: University of Alberta, 2006.
( 0) 0)
|
| [10] |
ZOBRIST A L. A new hashing method with application for game playing[R]. Madison, USA: University of Wisconsin, 1970.
( 0) 0)
|
| [11] |
WANG Jiao, LI Sizhong, XU Xinhe. A minors hash table in Chinese-chess programs2[J]. ICGA journal, 2010, 33(1): 18-33. DOI:10.3233/ICG-2010-33103 ( 0) 0)
|
| [12] |
BREUKER D M, UITERWIJK J W H M, VAN DEN HERIK H J. Replacement schemes for transposition tables[J]. ICGA journal, 1994, 17(4): 183-193. DOI:10.3233/ICG-1994-17402 ( 0) 0)
|
| [13] |
BREUKER D M, UITERWIJK J W H M, HERIK H J. Information in transposition tables[J]. Advances in computer chess, 1997, 27: 199-211. ( 0) 0)
|
| [14] |
NELSON B L. Hash tables in Cray blitz[J]. ICGA journal, 1985, 8(1): 3-13. DOI:10.3233/ICG-1985-8102 ( 0) 0)
|
| [15] |
HYATT R M, COZZIE A. The effect of hash signature collisions in a chess program[J]. ICGA journal, 2005, 28(3): 131-139. DOI:10.3233/ICG-2005-28302 ( 0) 0)
|
| [16] |
TENENBAUM A M, LANGSAM Y, AUGENSTEIN M J. Data structures using C[M]. Englewood Cliffs: Prentice Hall, 1990: 456–461, 472.
( 0) 0)
|
| [17] |
DENG Li, YU Dong. Deep learning: methods and applications[J]. Foundations and trends in signal processing, 2014, 7(3): 197-387. ( 0) 0)
|
| [18] |
BENGIO Y. Learning deep architectures for AI[M]. Hanover: Now Publishers Inc., 2009.
( 0) 0)
|
| [19] |
FUKUSHIMA K. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position[J]. Biological cybernetics, 1980, 36(4): 193-202. DOI:10.1007/BF00344251 ( 0) 0)
|
| [20] |
YAKOVENKO N, CAO Liangliang, RAFFEL C, et al. Poker-CNN: a pattern learning strategy for making draws and bets in poker games[C]. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. Phoenix, USA, 2016: 360–367.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


