随着当前数据量的增多，在数据处理和数据分析过程中，应用有效的数据挖掘技术能够大大提升数据处理和分析的速度，同时也能够提升数据处理的准确性。其中，数据挖掘就是从大量的、不完全的、有噪声的、模糊的及随机的数据集中提取隐含在其中的、事先不知道的但又潜在的有用的信息和知识的过程^[1]。异常检测是数据挖掘中的重要任务之一，目的是从给定的数据集中发现异常的数据对象^[2]。异常检测又称为离群点检测、偏差检测、孤立点检测等，用于反作弊、故障诊断、金融诈骗等领域。随着移动通信、云计算等技术的快速发展，数据量的日渐增多^[3]，传统基于单机内存设计的异常检测算法面临着很大的挑战。因此研究适用于大规模数据的异常检测算法具有重要的应用价值。

近年来，已经出现许多异常检测算法，主要包括两类^[4]：有监督性的^[5-6]和无监督性的^[7-13]。有监督性的异常检测算法在监测异常数据前需要大量的样本进行模型检测，但实际应用中往往无法事先获取大量的训练样本。因此无监督的异常检测算法具有更高的实用价值。

在无监督异常检测算法中，Breunig等^[10]提出的Local Outlier Factor(LOF)算法，通过计算每个点的局部异常因子(LOF值)从而判断一个数据对象的异常程度。该算法与其他算法相比，理论简单、适应性较高，并且能有效地检测全局异常和局部异常。然而LOF算法是基于局部密度设计的，算法复杂度较高且假设不存在大于或等于 $k$ 个重复点。在这个算法的基础上，Bhatt等^[11]提出了一种改进的LOF算法，将k-distance修改为 m-distance以提高算法性能。其中，k-distance是数据点与其最近的第 $k$ 个数据点之间的距离，而m-distance是数据点与其 $k$ 邻域内点距离的平均值。Miao等^[12]提出了一种基于核密度的局部离群因子算法(KLOF)来计算每个数据点离群程度。Tang等^[13]引入了相对密度的离群值用来度量数据对象的局部异常，其中数据对象的密度分布是根据数据对象的最近邻来估计的。此外，进一步考虑了反向最近邻和共享最近邻估计对象的密度分布。虽然以上算法一定程度上提高了LOF算法的有效性，但其处理数据规模受限于内存容量和数据的复杂性。因此，设计一种既能保证LOF算法优点又能高效和有效地处理大量数据的异常检测算法是件有意义的工作。

本文主要针对算法的计算量和算法中重复点对局部异常因子的影响这两个方面对LOF异常检测算法进行了深入分析，并根据Hadoop作业调度机制和MapReduce计算框架，设计了一种基于MapReduce和LOF思想的并行异常检测算法(MR-DLOF)。在MR-DLOF算法中，为了避免数据集中存在大于或等于 $k$ 个重复点而导致数据点局部密度为无穷大的情况，重新定义了k-邻近距离。同时为了减少计算量，将整个数据集逻辑地划分为多个数据块，利用MapReduce原理并行处理各个数据块中的数据，使得每个数据点的k-邻近距离和LOF值的计算仅在单个块中执行；然后，将每个数据块中LOF值较高的数据点合并后进一步计算，得到最终异常数据点，从而提高算法的准确性和灵敏性。

1 Hadoop技术

Hadoop是Apache软件基金会开发的分布式系统基础架构。其理论基础是Google在国际上发表的关于MapReduce^[14]、GFS^[15]和BigTable^[16]的三篇论文。Hadoop由HDFS、MapReduce、HBase、Hive和Zookeeper等成员组成，其中HDFS和MapReduce是两个最重要的成员。HDFS可以实现不同节点、不同类型计算机的数据整合，MapReduce通过Map函数和Reduce函数建模来实现可靠的分布式计算。实践证明，大量基于MapReduce的并行算法的实现有效地提高了算法的计算能力^[17-20]。

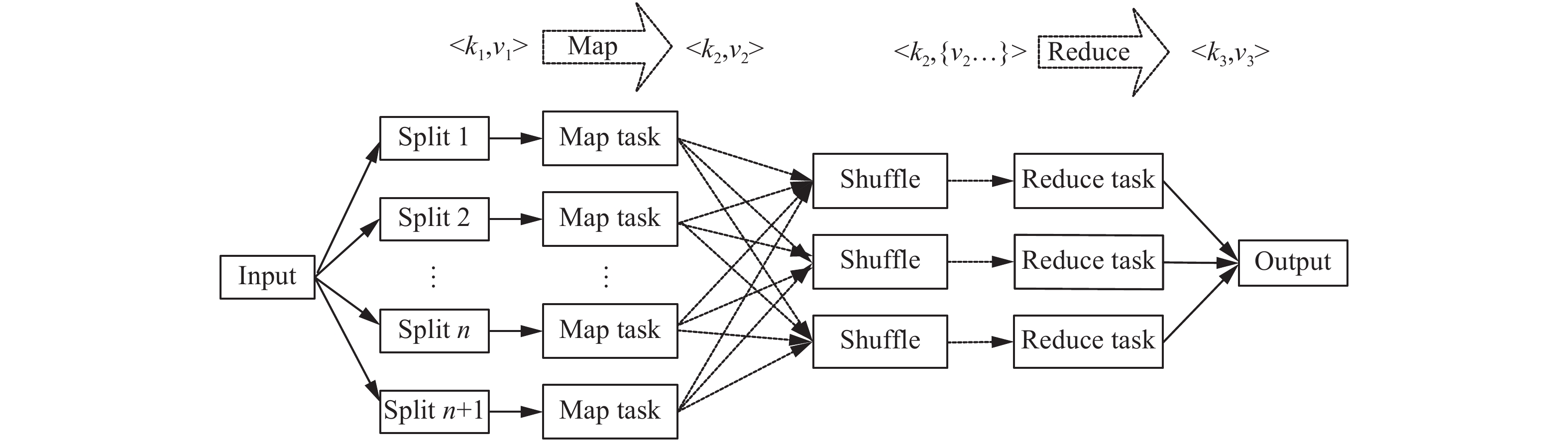
1.1 Hadoop MapReduce

Hadoop MapReduce 的实现采用了Master/Slave 结构。MapReduce分布式计算框架主要包含两个处理过程：Map阶段和Reduce阶段。Map阶段的Map函数和Reduce阶段的Reduce函数都由用户根据需求进行自定义。Map函数主要处理输入数据集并产生中间输出，然后通过某种方式将这些中间输出通过Reduce函数组合在一起导出最终结果。此过程均以键值对(key/value)形式成对地输入和输出数据，保证了数据的安全性和可靠性。当Reducer函数输出最后一个键值对时，MapReduce任务完成。图1为MapReduce详细流程。HDFS首先根据数据大小和块大小对数据进行物理分割，用户可根据需求对数据进行逻辑分割，经过Map阶段，对每一块数据执行Map任务后，对数据进行排序后进入Reduce阶段合并结果，最后将结果写入HDFS中。

1.2 Hadoop HDFS

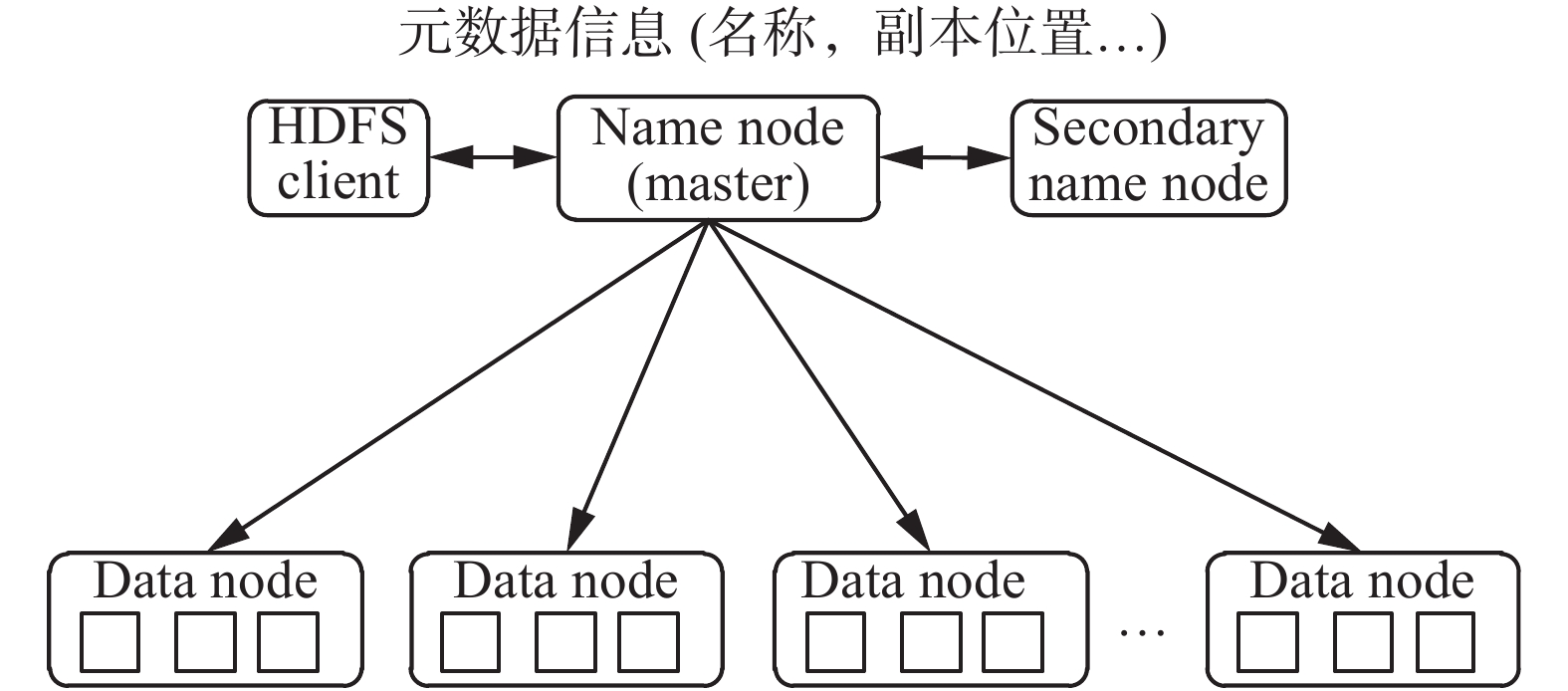
Hadoop Distributed File System (HDFS) 采用Master/Slave结构，其作为一个高度容错且易扩展的分布式文件系统，主要包含NameNode、Secondary NameNode和DataNode三类节点^[21]。图2详细地描述了HDFS结构。

NameNode为主节点且只有一个，负责接收用户的操作请求，记录每个文件数据块在各个DataNode上的位置和副本信息。Secondary NameNode为可选节点，与NameNode进行通信，定期保存HDFS元数据快照。DataNode为从节点且可以有多个，主要负责存储数据。同时为了保证数据安全，文件会有多个副本(默认为3个)。DataNode定期向NameNode上报心跳，NameNode通过心跳响应来控制DataNode。

2 算法设计 2.1 LOF算法

LOF是基于密度的经典算法，其核心部分是关于数据点密度的刻画。由数据点的k-邻近距离，计算各个数据点的局部可达密度和局部异常因子，根据局部异常因子大小判断数据点的异常程度从而得到异常点。算法的基本概念如下：

1) k-邻近距离 (k-distance): 对于任意正整数 $k$ ，点 $p$ 的k-邻近距离定义为 $k{\rm{ - }}{\rm distance}{\rm{ }}(p) = d(p,o)$ ，如果满足以下条件：

① 在样本空间中，至少存在 $k$ 个点 $q$ ，使得 $d(p,q) \leqslant d(p,o)$ 。

② 在样本空间中，至多存在 $k - 1$ 个点 $q$ ，使得 $d(p,q) < d(p,o)$ 。

其中， $d(p,o)$ 为点 $p$ 与点 $o$ 之间的距离。

2) k-距离邻域(k-neighbor): 点 $p$ 的k-距离邻域 ${N_k}(p)$ 即与点 $p$ 的之间距离小于 $k{\rm{ - }}{\rm distance}{\rm{ }}(p)$ 的对象的集合。

3) 可达距离 (reachability distance): 给定参数 $k$ 时，数据点 $p$ 到数据点 $o$ 的可达距离 ${\rm reach}{\rm{ - }}{\rm dis}(p,o)$ 为数据点 $o$ 的 $k{\rm{ - }}{\rm distance}{\rm{ }}(o)$ 和数据点 $p$ 与点 $o$ 之间距离的最大值，即

${\rm reach}{\rm{ - }}{{\rm dis}_k}(p,o) = \max \{ k{\rm{ - }}{\rm distance}(o),d(p,o)\} $

4) 局部可达密度 (local reachability density): 数据点 $p$ 的局部可达密度为它与k-距离邻域内数据点的平均可达距离的倒数，即

$lr{d_k}(p) = \frac{{|{N_k}(p)|}}{{\sum\nolimits_{o \in {N_k}(p)} {{\rm reach}{\rm{ - }}{{\rm dis}_k}(p,o)} }}$

(1)

5) 局部异常因子 (local outlier factor): 数据 $p$ 的局部相对密度(局部异常因子)为点 $p$ 的邻域内点的局部可达密度和数据点 $p$ 的局部可达密度的比值的平均值，即

${\rm{LOF}}{_k}(p) = \frac{{\sum\nolimits_{o \in {N_k}(p)} {\displaystyle\frac{{{\rm lrd}(o)}}{{{\rm lrd}(p)}}} }}{{|{N_k}(P)|}}$

(2)

根据局部异常因子的定义，如果数据点 $p$ 的LOF值在1附近，表明数据点 $p$ 的局部密度跟它的邻居们差不多；如果数据 $p$ 的LOF值小于1，表明数据点 $p$ 处在一个相对密集的区域，不是一个异常点；如果数据点 $p$ 的LOF得分远大于1，表明数据点 $p$ 跟其他点比较疏远，很可能是一个异常点。

2.2 MR-DLOF算法

LOF算法是基于密度的异常检测算法，计算量大，且在LOF算法中关于局部可达密度的定义存在假设：不存在大于或等于 $k$ 个重复点。当这样的重复点存在的时候，这些点的平均可达距离为零，局部可达密度就变得无穷，从而影响了算法的有效性。

算法1　MR-DLOF algorith

输入　 $X = {x_1},{x_2}, \cdots ,{x_N}$ : data set

$k$ : number of nearest neighbor

$N$ : data block number

$\theta $ : threshold for LOF

输出　Abnormal data and LOF values

Get data set which $lo{f_i} > \theta $ from 算法 2 add in $XX$

Calculate $lo{f_i} > \theta $ of ${x_j} \in XX$

return Abnormal data and LOF

由于LOF算法不足，本文重新定义了k-邻近距离的概念，并结合MapReduce框架提出并行异常检测算法。重新定义的k-邻近距离概念如下。

k-邻近距离(k-distinct-distance): 对于任意正整数 $k$ ，点 $p$ 的k-邻近距离定义为 $k{\rm{ - }}{\rm distance}{\rm{ }}(p) = $ $ d(p,o)$ ，如果满足以下条件：

1) 在样本空间中，至少存在 $k$ 个点 $q$ ，使得 $d(p,q) \leqslant d(p,o)$ 。

2) 在样本空间中，至多存在 $k - 1$ 个点 $q$ ，使得 $0 < d(p,q) < d(p,o)$ 。

其中， $d(p,o)$ 为点 $p$ 与点 $o$ 之间的距离。

算法2　Compute $lo{f_i} > \theta $

输入　data set $X = {x_1},{x_2}, \cdots ,{x_N}$

$k$ : number of nearest neighbor

$\theta $ : threshold for LOF

$N$ : data block number

输出　data set which ${\rm lo{f}_i} > \theta $

Initialize a Hadoop Job

　　Set TaskMapReduce class

Logically divide X into multiple data blocks: ${D_1},{D_2}, \cdots ,{D_N}$ .

In the j-th TaskMapReduce

FirstMapper

　　输入　 $D = {d_1},{d_2}, \cdots ,{d_m}$

　　输出　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left[ {\left( {{\rm{ }}{o_k},{\rm dis}({d_i},{o_k})} \right),{\rm{ }}k{\rm{ - }}{\rm dis}({d_i})} \right] > $

for each data ${d_i},i = 1,2, \cdots ,m$ do

　Calculate ${\rm di{s}_{ij}} = {\rm distance}({d_i},{d_j}),j = 1, \cdots ,m$

　　Sort ${\rm di{s}_{ij}}$ of ${d_i}$

　　for each ${\rm di{s}_{ij}}$ of ${d_i}$ do

　　　if ${\rm di{s}_{ij}} \ne 0{\kern 1pt} \& {\kern 1pt} |k{\rm{ - }}{\rm neighbour}| < k$

　　　　add ${d_i}$ and ${\rm di{s}_{ij}}$ in k-distinct-neighbor record $\left( {{\rm{ }}{o_k},{\rm dis}({d_i},{o_k})} \right)$

　　end

　　Calculate k-distinct-distance record $k{\rm{ - }}{\rm dis}({d_i})$

end

FirstReducer

　　输入　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left[ {\left( {{\rm{ }}{o_k},{\rm dis}({d_i},{o_k})} \right),{\rm{ }}k{\rm{ - }}{\rm dis}({d_i})} \right] > $

　　输出　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left[ {\left( {{\rm{ }}{o_k},{\rm dis}({d_i},{o_k})} \right),{\rm{ }}k{\rm{ - }}{\rm dis}({d_i})} \right] > $

SecondMapper

　　输入　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left[ {\left( {{\rm{ }}{o_k},{\rm dis}({d_i},{o_k})} \right),{\rm{ }}k{\rm{ - }}{\rm dis}({d_i})} \right] > $

　　输出　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left( {{\rm{ }}{o_k},{\rm reach}{\rm{ - }}{\rm dis}({d_i},{o_k})} \right) > $

for ${o_k} \in k{\rm{ - }}{\rm distinct}{\rm{ - }}{\rm neighbour}$ do

　　if $k{\rm{ - }}{\rm dis}({o_k}) < {\rm dis}({d_i},{o_k})$

　　　　 ${\rm reach}{\rm{ - }}{\rm dis}({d_i},{o_k}) = {\rm dis}({d_i},{o_k})$

　　else ${\rm reach}{\rm{ - }}{\rm dis}({d_i},{o_k}) = k{\rm{ - }}{\rm dis}({d_i},{o_k})$

end

SecondReducer

　　输入　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i},\left( {{\rm{ }}{o_k},{\rm reach}{\rm{ - }}{\rm dis}({d_i},{o_k})} \right) > $

　　输出　 $ < {\rm key,value} > {\rm{ = }} $ 　　　　 $ < {d_i},{\rm lrd}({d_i}) > $

for value do

　　 ${\rm lrd}({d_i}) = k/\sum {{\rm reach}{\rm{ - }}{\rm disk}({d_i},{o_k})} $ , 　　　　　 ${o_k} \in k{\rm{ - }}{\rm distinct}{\rm{ - }}$ neighbour

end

ThirdMapper

　　输入　 $ < {\rm key,value} > = < {d_i},{\rm lrd}({d_i}) > $

　　输出　 $ < {\rm key,value} > = $ 　　　　 $ < {d_i}({\rm lof}({d_i}) > \theta ),{\rm lof}({d_i}) > $

for ${o_k} \in k{\rm{ - }}{\rm distinct}{\rm{ - }}{\rm neighbour}$ do

　　 ${\rm lof}({d_i}) = (\sum {{\rm lrd}({o_k})/k} )/{\rm lrd}({d_i})$ , 　　　　　 ${o_k} \in k{\rm{ - }}{\rm distinct}{\rm{ - }}$ neighbour

end

if ${\rm lof}({d_i}) > \theta $

　　output

ThirdReduce

输入　 $ < {\rm key,value} > = < {d_i}({\rm lof}({d_i}) > \theta ),{\rm lof}({d_i}) > $

　　输出　 $ < {\rm key,value} > = < {d_i}*,{\rm lof}({d_i}*) > $

for value do

　　Sort ${\rm lof}({d_i})$ for ${d_i}$ and record ${d_i}*$

end

本部分主要介绍了MR-DLOF算法基本思想和步骤。首先，将数据集存放在HDFS上并将原始数据集逻辑地切分为多个数据块；然后，根据MapReduce原理并行处理各个数据块中的数据，使得每个数据点的k-邻近距离和LOF值的计算仅在单个块中执行；最后将每个数据块中局部异常因子小于设定阈值的点剔除，并将大于设定阈值的数据点合并成一个新的数据集，更新其k-邻近距离和LOF值，从而提高算法的准确度和灵敏度。Algorihm1和Algorihm2为算法伪代码。

3 实验与分析

实验平台配置：3台PC机(通过局域网连接)，节点配置为VMware Workstation Pro 12.0.0 for Windows下的CentOS-7，JDK为1.8版本，Hadoop为2.7.4版本。本文所有算法均采用JAVA语言实现，eclipse编译环境。实验环境为基于云平台的Hadoop集群，共有3个节点：1个控制节点和2个计算节点，控制节点内存为32 GB，计算节点内存为8 GB。节点信息如下表1。

实验数据集：为了验证MR-DLOF算法的有效性和高效性，本文选用网络入侵数据集KDD-CUP1999^[22]，KDD-CUP1999数据集中每个连接用41个特征和1个标签来表述：其中3个特征以CSV格式写成。这41个特征包含7个离散变量，34个连续变量，并且第20个变量数据全为0。

LOF和MR-DLOF算法中采取距离的方法进行计算，由于每个特征属性的度量方法不同，为了避免出现“大数吃小数”的现象，消除属性度量差异对计算结果的影响，需要对数据集进行预处理。本文对除去全为0变量和CSV格式变量后的37个变量进行标准化处理。

3.1 算法的有效性验证

性能衡量标准：异常检测算法对正常数据与异常数据的检测结果如表2所示。

准确度：

${\rm{Accuracy = }}\frac{{{\rm{TP + TN}}}}{{{\rm{TP + TN + FP + FN}}}}$

(3)

灵敏度：即真正辨识率，是正确检测出异常数据的个数与实际异常数据个数之比。

${\rm{Sensitivit = }}\frac{{{\rm{TN}}}}{{{\rm{TN + FN}}}}$

(4)

本文主要对比LOF算法和MR-DLOF算法处理相同规模数据集的准确度和灵敏度，来验证MR-DLOF算法的有效性。针对每种规模的数据集，分别从KDD-CUP1999标准化处理后的数据库中随机选取10组不同的数据集，并使所选取的每种规模数据集中攻击数据(即异常点)在该数据集中占比为1%~2%。使用LOF算法和MR-DLOF算法分别计算其准确度和灵敏度，并取其平均值作为评价指标，其中设定阈值 $\theta = 1.2$ 。

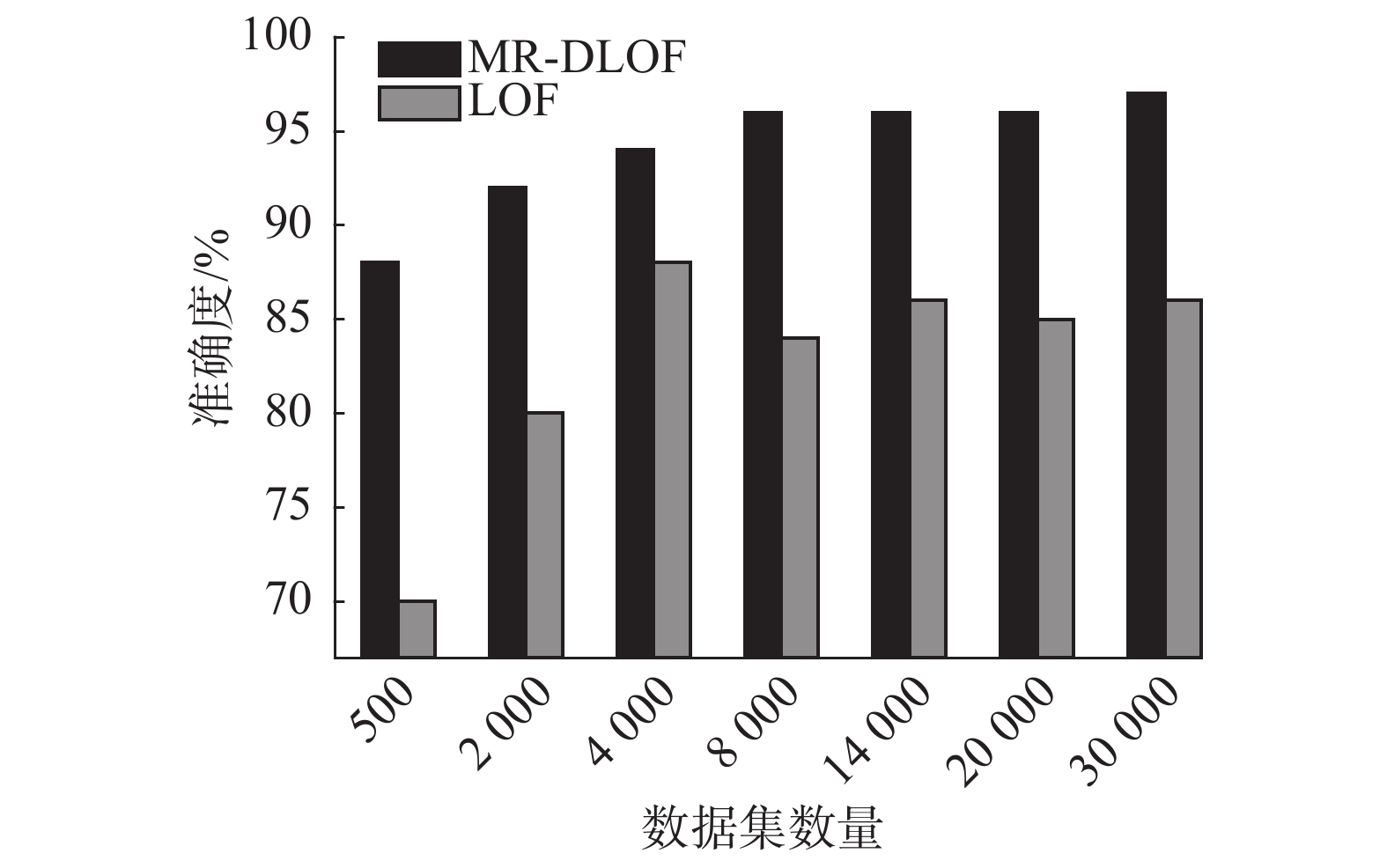
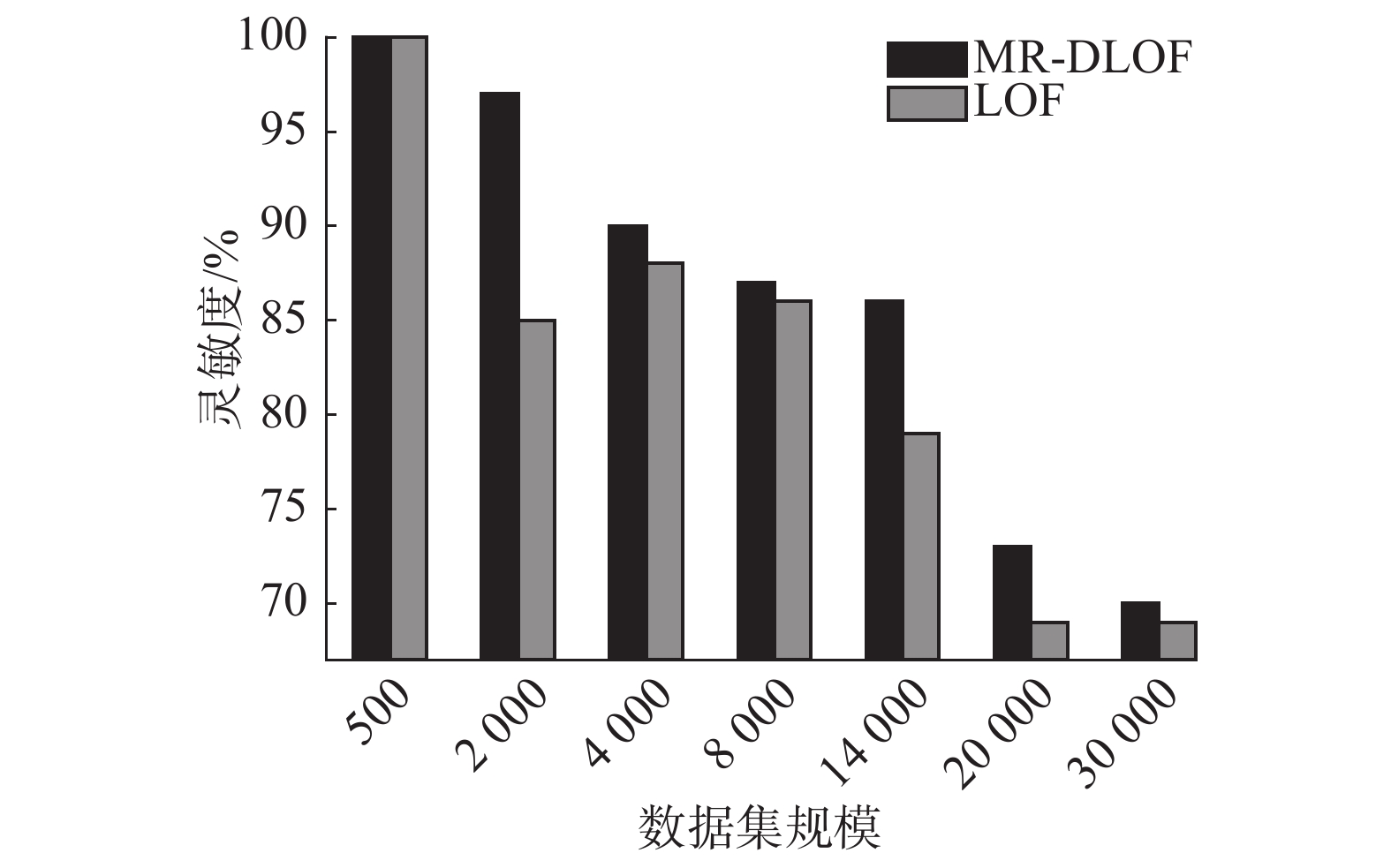
由图3～4可知，LOF和MR-DLOF在处理相同数据集时，MR-DLOF算法在保证其灵敏性的基础上，大大提高了其准确率。

3.2 算法的高效性验证

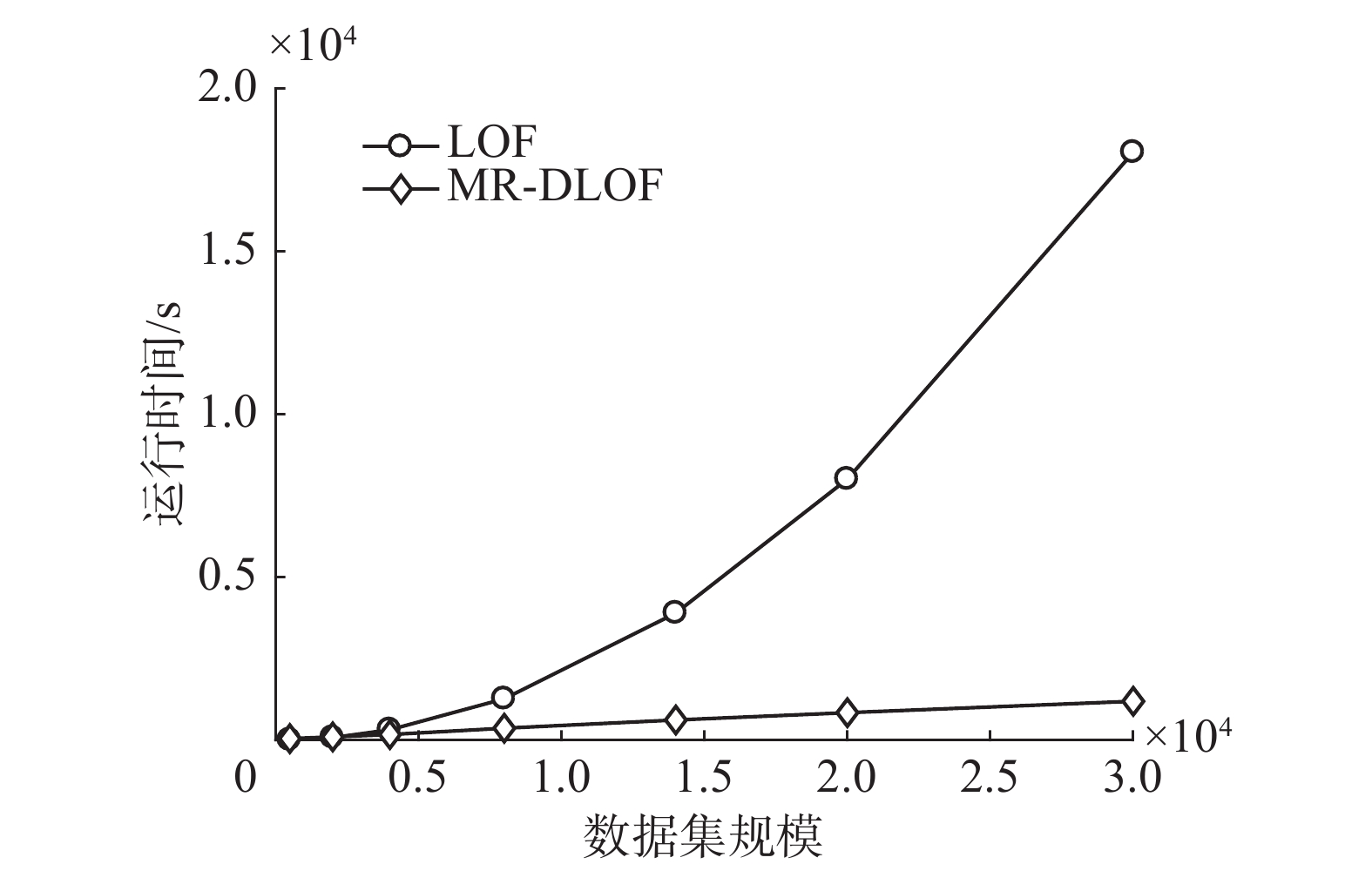
本文主要对比LOF算法和MR-DLOF算法处理相同规模数据集的执行时间，来验证MR-DLOF 算法的执行效率。如图5所示，可以看出当数据量比较大时，MR-DLOF的执行效率明显优于LOF算法。数据量少时LOF算法执行效率优于MR-LOF算法的原因是Hadoop调度Map任务和Reduce任务时需要一定的时间；但当数据量比较大时，将数据分块后，Hadoop会调度多个MapReduce并行执行任务，效率明显增加。

3.3 算法的可扩展性验证

为了验证MR-DLOF算法的可扩展性，本文通过扩大数据规模来比较MR-DLOF在不同计算节点下的执行效率，由图6可以看出，在相同数据集规模下，当集群计算节点增加时，算法的执行效率提高。因此当数据集增大时，MR-DLOF算法具有可扩展性，可通过扩充Hadoop集群中计算节点的方法来提高算法的执行效率。

4 结束语

本文通过分析LOF算法的不足，设计了一种基于MapReduce和LOF算法的并行异常检测算法。该算法修正了k-邻近距离的概念，从而避免某些点的可达距离为零、局部可达密度为无穷大的情况，以提高算法的有效性，同时，为了减少计算量，将分块、利用MapReduce框架思想并行化处理各个数据块中的数据点，大大提高了算法的执行效率。最后，通过真实数据集验证算法的有效性、高效性和可扩展性。