随着Internet的普遍应用，对于兴趣点(point of interests, POIs，如餐厅、电影院、旅馆、旅游景点等)的空间关键字查询已成为当前空间数据库的研究热点^[1]。空间关键字查询条件的形式为：

q: {位置，＜关键字1，关键字 $2, \cdots $ ，关键字m＞}

其中“位置”代表空间位置查询条件，可以是一个空间点(通常用经纬度表示)，也可以是一个空间范围；“关键字”代表文本信息查询条件，通常用若干关键字表示。空间数据库中的每个空间对象(也称为兴趣点)都包含2类信息：空间信息(spatial information，如经纬度)和文本信息(text information，如POI的名称、设施、评论等文本描述信息)。

由于空间数据库通常蕴含海量数据，因此一个普通空间关键字查询很可能会导致多查询结果问题。例如，在Yelp网站上搜索“San Francisco”地理范围内的“Chinese Restaurants”，会返回1 108条查询结果。这种情况下，绝大多数用户期望空间数据库查询系统能够快速返回前k个与当前查询在位置和文本上最为相关且具有代表性、典型性的结果。

近年来，有关空间关键字查询的研究工作在一些主流期刊和会议上涌现出来^[2-10]。根据文献[2-3]，这些查询方法可分为3类：1)布尔k近邻查询^[4-6]：该类方法用于检索文本描述信息中包含所有查询关键字且距离查询位置最近的前k个空间对象，查询结果按其对查询的位置相近性进行排序。2)top-k范围查询^[7-8]：用于检索位于查询区域内且与查询关键字具有较高文本相似度的前k个空间对象，查询结果按其对查询关键字的文本相似度进行排序。3)top-k k近邻查询^[3，9-11]：该类方法根据空间对象的文本相似性和位置相近性进行top-k检索和排序，查询结果按其对查询的位置相近性和文本相似度进行综合排序。上述3类方法中，第3类是当前空间关键字查询最为常用的方法。为了获取top-k查询结果，上述3类方法都需要先从目标数据集中获取与查询位置相近且文本与查询关键字全部或部分匹配的候选结果，然后再根据评分函数从候选结果中选取top-k个结果。为了快速获取候选结果集合，上述方法通常采用空间索引与文本索引相结合的混合索引结构。空间搜索的索引技术主要有R-tree^[12]、R*-tree^[13]和Quad-tree(四分树)^[14]等，其中R-tree是最基本的空间索引结构。文本搜索的索引技术主要有倒排文件(inverted file)、签名文件(signature file)和位图索引(bitmap)等。空间与文本索引相结合的空间-文本数据混合索引结构可归为以下几类：1)两阶段索引^[15]: 该类索引先利用R-tree或Quad-tree获取与查询位置相近的候选结果，然后再用倒排文件(inverted file)从候选结果中获取包含查询关键字的最终查询结果。该类方法的缺点是无法确定第1阶段产生的候选结果个数，当候选结果个数过少时，很可能会导致最终结果不能满足查询关键字的匹配需求，而候选结果过多时，又可能会导致计算资源的浪费。2)IR-tree索引^{[9-10, 16]}：该类索引将倒排文件集成到R-tree节点中，当查询到来时，判断IR-tree节点与查询的位置距离以及该节点对应的倒排文件是否包含查询关键字。该类方法同时判断节点与查询的位置关系和文本匹配度，在很大程度上提升了查询效率。该类方法的缺点是，对于满足查询位置要求和(全部或部分)包含查询关键字的树节点都要进行遍历，从而得到候选结果集合，然后再按评分函数从中选取前k个综合分数最高的结果。3)Quad-tree索引^{[14, 17]}：该类索引将倒排文件与Quad-tree相结合，与IR-tree类似，在查询过程中同时判断节点与查询的位置范围重叠程度以及节点对应的倒排文件是否包含查询关键字。Quadtree索引的优点是区域搜索效率高，缺点是存储代价高，树结构不平衡，top-k结果选取的耗时较长。综上可见，给定一个空间关键字查询，现有方法利用混合索引结构从空间对象集合中获取候选结果，由于产生的候选结果数量通常多于最终的top-k结果数量，并且在top-k结果选取中需要根据评分函数计算所有候选结果对象与当前查询的位置与文本综合相关度才能确定最终结果，因此top-k选取效率仍有提升空间。此外，现有方法按空间对象与查询的综合相关度获取top-k结果，结果之间往往比较相似，实际上用户希望看到既与查询相关且彼此之间又具有一定差异的代表性查询结果。

针对现有空间关键字查询研究工作存在的问题，本文提出一种基于位置-文本关系的空间对象top-k查询与排序方法，该方法可分为2个处理阶段：在离线阶段，计算空间对象集合中任意一对空间对象之间的位置相近度和文本相似度，二者结合构成空间对象的关系紧密度，然后根据空间对象之间的关系紧密度从空间对象集合中获取少数代表性对象，并为每个代表性对象创建一个序列，序列中的元素是数据集中除该空间对象之外的所有空间对象，序列中的对象按其对代表性对象的关系紧密度降序排列。在线查询处理阶段，对于一个给定的空间关键字查询，首先计算该查询与每个代表性空间对象之间的关系紧密度，然后使用阈值算法(threshold algorithm，TA)在预创建的序列上快速选出前k个与当前查询最为接近的空间对象，其中查询条件与代表性空间对象之间的关系紧密度作为评分函数的权重，即当前查询条件与某个代表性空间对象在位置和文本上越接近，那么该代表性空间对象对应的序列对结果影响越大。该算法的优势在于：1)在线查询处理阶段不需要检查所有与查询匹配的对象就能够快速识别出top-k结果。2)选取的top-k结果对象在全局中具有代表性，也就是典型化程度高。

1 空间对象的位置-文本关系度量

本节分别讨论空间对象的位置相近度和文本相似度的度量方法，二者的线性叠加构成了空间对象之间的位置-文本关系紧密度。

表1给出了一个空间数据库实例，每行代表一个空间对象。下文将以表1为例，阐述空间对象的位置相近度和本文相似度计算方法。

1.1 空间对象的位置相近度

空间对象的位置信息通常由经纬度表示，现有方法大多采用两个空间对象之间的欧氏距离来计算二者之间的位置相近度。给定一对空间对象o_i和o_j，它们之间的欧氏距离定义如下：

$D({{ o}_i},{{ o}_j}) = \sum\limits_{k = 1}^n {d({ o}_i^{(k)},{ o}_j^{(k)})} $

(1)

其中n代表空间对象的空间维度。基于式(1)，空间对象o_i和o_j在位置上的相近度定义为：

${\rm Si}{{\rm m}_{{\rm{Loc}}}}({{ o}_i},{{ o}_j}) = 1 - D({{ o}_i},{{ o}_j})/{\rm Max}D$

(2)

其中MaxD代表所有空间对象之间的最大距离。式(2)得到的是一个归一化结果，即Sim_Loc()的值介于0和1之间。表2给出了表1中所有空间对象之间的位置相近度。

1.2 空间对象的文本相似度

给定一个空间对象o，其文本信息o.doc可由对象o的名字、设施描述、用户评论所构成，本文利用jieba、wikipedia等工具先对空间对象的文本信息进行关键字提取，进而o.doc将由一组关键字集合表示，其中每个关键字都有一个权重w(t|o.doc)，权重的计算方法采用传统的TF-IDF计算方法：

$w(t|{ o}.{\rm doc}) = {\rm tf}(t|{ o}.{\rm doc}) * {\rm idf}(t,{ O})$

(3)

式中：词频为 ${\rm tf}(t{ o}.{\rm doc}){\rm{ = }}\dfrac{{f(t,{ o}.{\rm doc})}}{\rm{MaxFrequency}}$ ； $f(t|{ o}.{\rm doc})$ 表示t在o. doc中出现的次数；MaxFrequency表示在o. doc中关键字的最多出现次数； ${\rm idf}(t,{ O}) = $ ${\rm{log}}$ $ \dfrac{{|{ O}|}}{{f(t|{ O}) + 1}}$ ，其中 $f(t|{ O})$ 表示空间对象集合O中包含关键字t的对象数量；|O|表示空间对象集合中的对象总数。

在此基础上，给定一对空间对象(o₁，o₂)，其中每个对象的文本信息可转换成相应的向量表示，向量的维度是空间数据库中所有空间对象文本信息中包含的所有不同关键字个数。然后，利用Cosine相似度评估方法得到一对空间对象的文本相似度，计算方法如下：

${\rm Si}{{\rm m}_{{\rm{Doc}}}}({{ o}_{\rm{1}}},{{ o}_{\rm{2}}}){\rm{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^{n} {{{ { o}}_1}[i] {{ { o}}_2}[i]} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^{n} {{{ { o}}_1}{{[i]}^2}} } *\sqrt {\displaystyle\sum\limits_{i = 1}^{n} {{{ { o}}_2}{{[i]}^2}} } }}$

(4)

式中： ${{\mathop { o}\limits^ \rightharpoonup} _1}$ 、 ${{\mathop { o}\limits^ \rightharpoonup} _2}$ 分别是对象o₁、o₂中关键字的向量表示。根据式(4)，数据集中任意一对空间对象之间的文本相似度都可以在离线阶段计算得到。表3给出了表1中所有对象的文本相似度。

1.3 空间对象的位置-文本关系紧密度

空间对象o_i、o_j在位置上的相近度和在文本上的相似度通过线性叠加构成了它们之间的关系紧密度，用Sim(o_i, o_j)表示：

${\rm Sim}({{ o}_i},{{ o}_j}) = \alpha {\rm Si}{{\rm m}_{{\rm{Loc}}}}({{ o}_i},{{ o}_j}) + (1 - \alpha ) {\rm Si}{{\rm m}_{{\rm{Doc}}}}({{ o}_i},{{ o}_j})$

(5)

其中α是一个调节参数(α∈[0,1])，α值越大，空间对象的位置相近度对总体紧密度的影响就越大；反之，空间对象在文本上的相似度对总体紧密度的影响越大。需要指出的是，利用式(5)得到的空间对象之间的位置−文本关系紧密度在[0, 1]范围内。表4给出了表1中所有空间对象的位置-文本关系紧密度(其中α=0.5)。

所有空间对象之间的位置−文本关系紧密度可用一个n阶矩阵R表示(假设共有n个空间对象)，其中元素r_ij代表了空间对象o_i和o_j之间的位置−文本关系紧密度。由于矩阵R是一个对称矩阵，因此仅存储上半矩阵即可。

2 top-k结果选取与排序方法

令q代表一个空间关键字查询，O是空间对象集合，查询结果的top-k选取与排序问题定义如下：

${\Gamma _k} = \arg {\max _\Gamma }\sum\limits_{i = 1}^{k(k \ll n)} {{\rm Sim}(q,{{ o}_i})} $

(6)

式中： ${\Gamma _{\rm{k}}}$ 是包含k个结果对象的有序列表；n表示数据集中空间对象的总数。top-k结果选取的目的是从数据集中快速获取与给定查询在位置和文本上相关且具有代表性的前k个空间对象。

本文方法分为3个步骤：1)从数据集中选取少量代表性空间对象。2)为代表性空间对象创建序列，该序列是由数据集中其他对象与代表性对象之间的位置−文本关系紧密度的降序排列。3)在线计算当前查询条件与所有代表性对象之间的紧密度，然后在预先创建的对象序列上使用TA算法快速获取top-k个结果对象。

2.1 选取代表性空间对象

选取代表性对象的基本思想：根据第2节的空间对象之间的位置−文本关系评估方法，使用代表性对象选取算法获取l(l $ \ll $ n)个代表性空间对象，代表性空间对象集合用W_l表示，代表性对象用 ${\bar { o}_i}$ 表示，即 $ {W_l} = \{ {\bar { o}_i}|i \in l\} $ 。

本文提出了一种基于概率密度优先选取代表性对象的方法。该方法的基本思想是利用高斯核函数评估某个空间对象在整个对象集合中的概率密度，某个对象的概率密度越大，表明与其关系紧密的对象越多，则该对象也就越有代表性，即典型程度越高^[18]。本文采用概率密度估计算法从空间对象集合中选取代表性对象。

对于一个空间对象集合 $ { O} = \left\{ {{{ o}_1},{{ o}_2}, \cdots ,{{ o}_n}} \right\}$ ，对象o的概率密度f(o_i)可以表示为：

$f({{ o}_i}) = \frac{1}{n}\sum\limits_{j = 1}^n {{G_h}({{ o}_i},{{ o}_j})} = \frac{1}{{n\sqrt {2{\text{π}} } }}\sum\limits_{j = 1}^n {{{\rm{e}}^{ - \frac{{{\rm{d}}{{({{ o}_i},{{ o}_j})}^2}}}{{2{h^2}}}}}} $

(7)

式中：d(o_i, o_j)²是o_i和o_j的位置−文本距离(用1减去空间对象之间的位置−文本关系紧密度)； ${G_h} $ $({{ o}_i},{{ o}_j}) = \dfrac{1}{{n\sqrt {2{\text{π}} } }}\displaystyle\sum\limits_{j = 1}^n {{{\rm{e}}^{ - \frac{{{\rm{d}}{{({{ o}_i},{{ o}_j})}^2}}}{{2{h^2}}}}}} $ 是高斯核函数。

根据空间对象的位置-文本距离矩阵M(可从对象之间的位置-文本关系紧密度矩阵R转化而来)和概率密度估计方法，下面采用淘汰思想选取代表性空间对象。该方法的基本过程如下：

1)将空间对象集合O随机划分成若干小组，每个小组都包含u个空间对象，即将集合O划分成了n/u个小组，接着在每个小组中利用式(7)计算所有空间对象的概率密度，选取每个小组中概率密度最高的对象构成一个集合，然后从O中将其他对象去除。

2)对于新得到的集合，重复上述过程，直到空间对象集合O中只剩下一个对象为止，并将该对象放入代表性对象候选集合中(上述过程记为一次选取过程)。

3)为了保证选取对象的准确性，需要将上述选取过程重复执行m次(记为一轮)，这样代表性对象候选集合中最多会包含m个空间对象，接着在最初的空间对象集合O上计算这m个对象的概率密度，最后将具有最高概率密度的对象作为当前轮次的选取结果，并从O中将该空间对象去除。上述整个过程重复l轮，这样就能得到l个近似于准确解的代表性空间对象。

该算法的时间复杂度为O(lmun)。在本文实验部分，将重点比较在所提2种算法得到的代表性对象序列上进行top-k结果选取的效果和性能。

2.2 创建空间对象序列

对于每个代表性空间对象 ${\bar { o}_i}$ ，为其构建一个序列 ${{ \tau }_{\rm{i}}}$ ，该序列中的元素是数据集中除该空间对象外的所有空间对象，这些对象按其对代表性空间对象的紧密度降序排列。如图1是一个包含n个空间对象和3个代表性对象的空间对象序列示意图。权重是通过计算查询条件与代表性对象之间的紧密度获取的，每个序列左侧表示数据集中除代表性对象之外的空间对象ID，右侧表示空间对象在该序列中对应的分数，该分数由对象在序列中的位置决定，计算方法为

$s({{ o}_i}|\tau ) = n - p({{ o}_i}) + 1$

(8)

其中p(o_i)表示对象o_i在序列中的位置。

由于选取了l个代表性对象，因此将生成l个代表性对象序列，这些序列用于使用TA算法的查询结果top-k选取。

2.3 top-k结果选取与排序

在代表性对象序列上，TA算法通过顺序访问方式发现每个序列中的某个空间对象的排序分数，然后利用随机访问方式从其他序列中发现该对象的排序分数，这些分数之和作为该对象在所有序列中的总分数^[19](注意，总分数是以查询条件与该对象对应的代表性对象之间的位置−文本关系紧密度作为权重系数，进行加权求和得到)，定义如下：

${\rm{score(}}{ q},{{ o}_j}{\rm{)}} = \sum\limits_{i = 1}^l {{\rm Sim}({ q},{{\bar { o}}_i}) s({{ o}_j}|{{\tau} _i})} $

(9)

式中： ${\tau _{{i}}}$ 是对应代表性对象 ${\bar { o}_i}$ 的序列； ${\rm Sim}({ q},{\bar { o}_i})$ 表示代表性对象 ${\bar { o}_i}$ 与查询q之间的位置-文本关系紧密度。需要注意的是，在计算 ${\bar { o}_i}$ 与q之间的文本相似度时，转换成的向量的维度为查询q和所有代表性对象中包含的不同关键字总数。

基于上述思想，top-k结果选取与排序算法处理步骤如下：

算法1　top-k结果选取与排序算法

输入　代表性序列集合L，空间关键字查询q，top-k中的k值

输出　top-k结果对象

1) 令B={ }是一个缓存

2) 令L是一个大小为l的数组，存储每个序列中最近一次检索得到的分数(score)

3) repeat

4) for each $ i \in \left\{ {1,{\rm{ }}2, \cdots ,l} \right\}$ do

5) 从序列 ${{ \tau} _i}$ 中检索下一个对象o_j，计算o_j在 ${{\tau} _i}$ 中的分数： $s({{ o}_j},q) = {\rm Sim}({ q},{\bar { o}_i}) s({{ q}_j}|{{\tau} _i})$

6) 用对象o_j在 ${\tau _i}$ 中的分数更新L中对应于对象o_j的分数

7) 利用随机访问方式获取o_j在其他序列中的分数，将所有检索到的分数加权求和，得到score(o_j,q)

8) 按照降序方式，将<o_j, score(o_j,q)>插入到B中的正确位置

9) end for

10) until $ B\left[ k \right]{\rm score} \geqslant \sum\limits_{i = 1}^l {L[i]}$

11) return B

算法1的处理过程由以下3步组成：

1)循环访问每个代表性序列。在每次循环过程中，当一个空间对象o_j在某个序列 ${{\tau} _{{i}}}$ 中被发现时，计算它在该代表性序列中的分数，计算公式为

$s({{ o}_j},{ q}) = {\rm Sim}({ q},{\bar { o}_i}) s({{ o}_j}|{{\tau} _i})$

(10)

该分数由2部分构成：一部分是 ${\rm Sim}({ q},{\bar { o}_i})$ ，表示查询条件q与序列 ${{\tau} _{{i}}}$ 对应的代表性空间对象 ${\bar { o}_i}$ 之间的位置−文本关系紧密度；另一部分是 $s({{ o}_j}|{{\tau} _i})$ ，表示对象o_j在序列 ${{\tau} _{{i}}}$ 中的排序分值。之后，通过随机访问方式获取o_j在其他序列中的分数，由式(9)可计算出对象o_j对于查询q的综合分数。

2)令 $s({{ o}_m}|{{\tau} _i})$ 为第m次循环结束后，在每个序列 ${{\tau} _{{i}}}$ 中最后被访问对象的分数。TA算法阈值threshold为第j次循环结束后数组L中的分数之和。

${\rm threshold} = \sum\limits_{i = 1}^l {{\rm Sim}({ q},{{\bar { o}}_i})} s({{ o}_m}|{{ \tau} _i})$

(11)

阈值threshold根据式(11)由算法自动计算得到，每当进行新一轮循环(算法1中的3)~10))时，算法1会重新自动计算一次阈值，当缓存B中存在k个总体排序分数都不小于当前阈值的对象时，算法终止。通过使用阈值threshold，使得第1步无需遍历每个代表性序列中的所有对象就能够提前结束算法执行，因此提高了执行效率。

3)在所有被发现的空间对象中，输出前k个具有最高总体排序分数的对象。

注意，当第2)步完成后，对于任意一个没有在循环访问中被发现的对象o_n，它的总体排序分数都将小于设定的阈值，即s(o_n, q)<threshold。

3 性能实验分析 3.1 实验环境

所有实验在Windows 10操作系统、Intel i7 3.1-GHz CPU和12 GB内存的电脑上运行，使用下列真实数据来评估所提算法的性能和效果。

数据集：测试数据使用Yelp数据集（该数据集来自Yelp数据集官网：http://www.yelp.com/dataset），Yelp是美国最大的点评网站，包含了用户签到信息、POI地点信息、用户评论信息等数据。实验截取经度在−115.0到−110.9之间，纬度在32.3至35.6之间的53 516个兴趣点作为分析数据。每个兴趣点都包含位置信息和文本信息，位置信息通过经度和纬度表示，文本信息由POI的name、city、categories、postal_code、stars等属性对应的信息构成。数据存放在文本文件中。测试数据集的特点如表5所示。

3.2 top-k结果的准确性和典型性测试

从数据集中获取前k个与给定查询最为相关的空间对象，准确方法是计算给定查询与数据集中所有空间对象之间的位置-文本关系紧密度，然后再按紧密度大小选取出top-k个空间对象。因此，本实验需要验证准确获取top-k个空间对象与利用TA算法在代表性对象序列上选出的top-k个空间对象之间的重叠程度，即本文top-k查询方法的准确性。这里用R(Rep, k)表示在代表性对象序列上选取的top-k个对象；R(All, k)表示通过计算数据集中所有对象与给定查询之间的紧密度选取的top-k个对象。这两个集合的重叠度可用Jaccard系数进行评估：

${\rm{J}}(R({\rm Rep},k),R({\rm All},k)){\rm{ = }}\frac{{\left| {R({\rm Rep},k) \cap R({\rm All},k)} \right|}}{{\left| {R({\rm Rep},k) \cup R({\rm All},k)} \right|}}$

(12)

Jaccard系数的值在[0,1]之间，值越高表明2个集合的重叠度越高，即top-k结果的准确性也就越高。

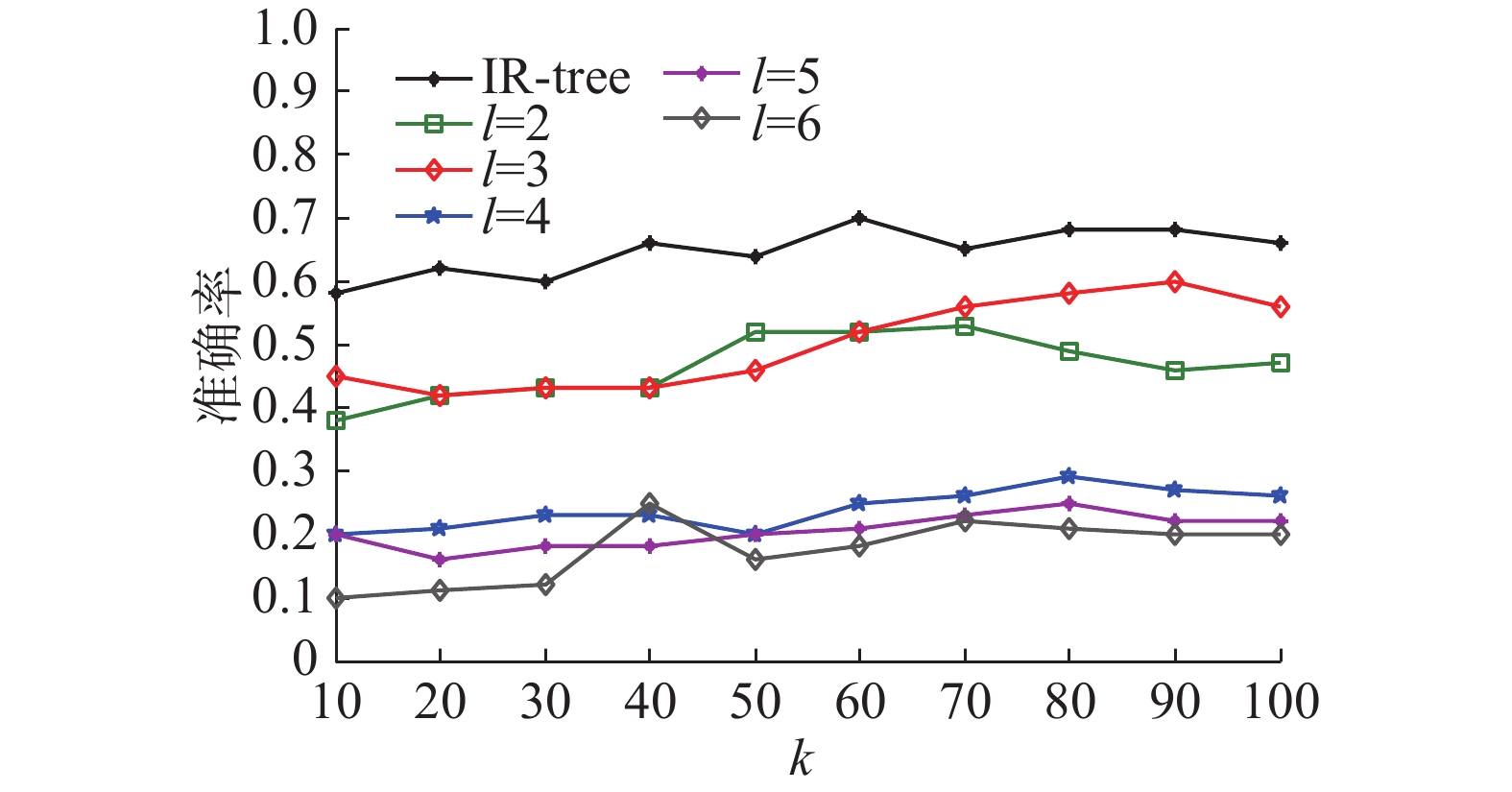
从数据集中随机抽取10个空间对象，再从每个空间对象的文本描述信息中随机抽取2−4个关键字，最后将每个空间对象的经纬度信息和抽取的关键字组合在一起形成空间关键字查询。此外，用参数l表示代表性对象序列的个数(选取与当前查询紧密度最高的前l个代表性对象对应的序列)，k表示返回的结果个数。在空间对象之间以及代表性对象与当前查询的位置-文本关系紧密度计算中，式(5)的调节参数α设为0.5。图2给出了在Yelp数据集上分别使用本文方法(当l={2, 3, 4, 5, 6}时)和IR-tree索引结构在不同k值下得到的top-k结果的准确性对比。

从图2可以看出：1)IR-tree方法得到的top-k结果的准确性一直优于本文方法，top-10，20，···，100的平均准确性达到66%。2)当l={2，3}时，使用本文方法得到的top-k结果的准确性较高，当l=3时准确性最高，top-10，20，···，100的平均准确性为51%。但当代表性序列超过3个时，准确性就会降低，原因是参与top-k结果选取的序列数越多，序列对应的代表性对象与当前查询的紧密度越低，因此参与序列与真实结果序列的相关度就越低，进而导致top-k结果准确性就越低。

需要指出的是，虽然IR-tree方法的准确性一直优于本文方法，但本文目的是在确保top-k结果具有一定准确性的前提下，同时具有更高的多样性和典型性。因此，还需测试本文方法得到的top-k结果与利用IR-tree索引得到的top-k结果，二者在典型程度上的差别。查询结果典型程度的评价标准为：

${\rm Typicality}(T) = \frac{{\displaystyle\sum\limits_{i = 1}^k {f({o_i})} }}{k}$

(13)

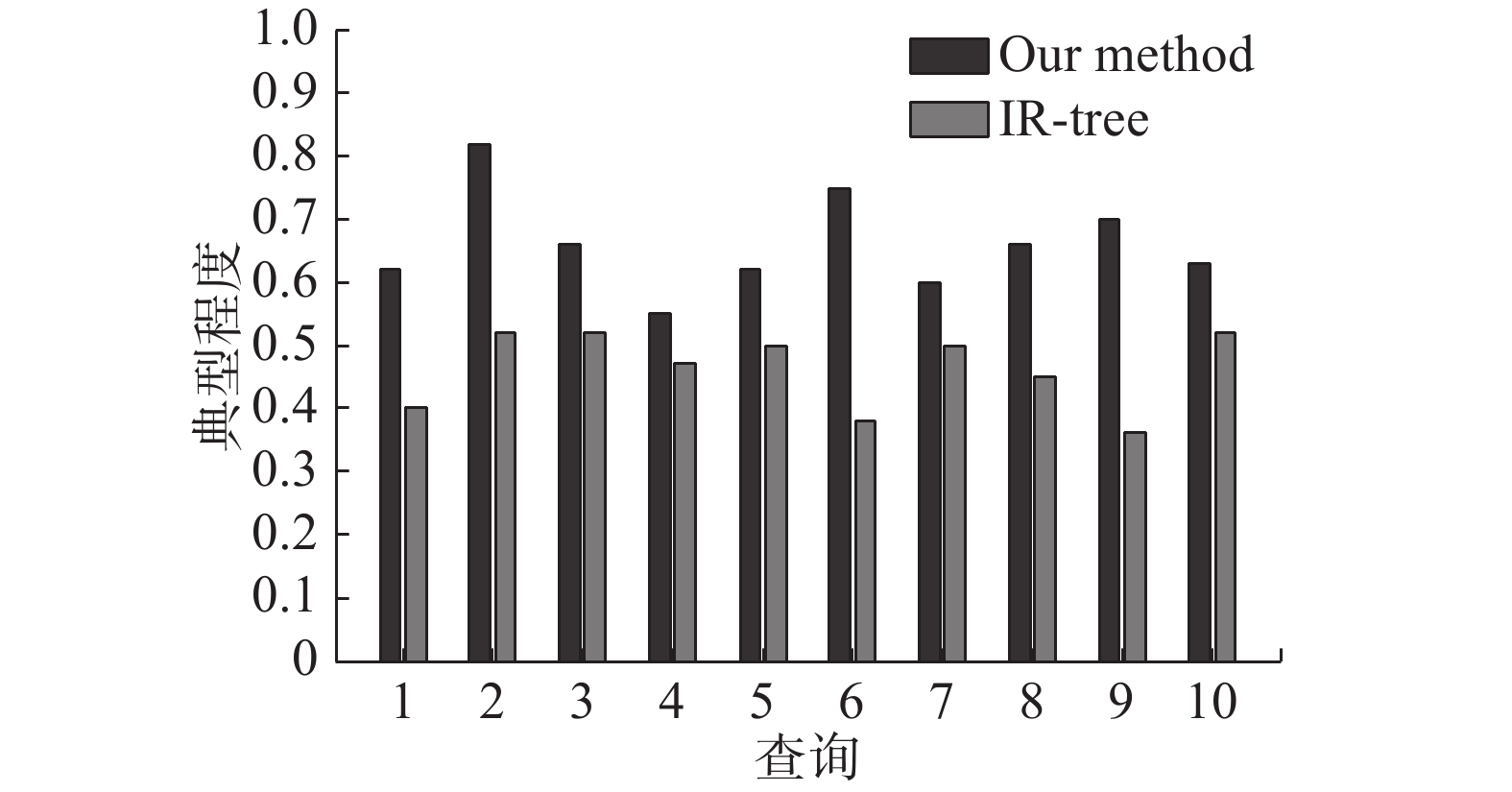
式中：T代表top-k结果集合；k表示结果对象个数；f(o_i)根据式(7)计算。该实验中令k=10。top-k结果典型程度的计算范围按如下方法确定：取本文方法和IR-tree方法得到的top-k结果中与给定查询紧密度最低的对象作为阈值，高于该阈值的对象构成的集合就是计算top-k结果典型程度的对象范围。top-k结果的典型程度越高，说明结果对象越能体现整个相关结果集合的总体特征，因此也就越能开阔用户视野和有助于用户对查询相关结果集合的总体认知。典型程度比较的基准是在对应计算范围内，利用式(7)计算得到的典型程度最高的前10个对象的平均典型程度。图3给出了不同测试查询下本文方法和IR-tree索引得到的top-k结果典型程度在基准下的对比。

图3显示了本文方法得到的top-k结果的典型程度一直明显高于IR-tree，原因是本文方法是从代表性对象对应的序列中获取结果，这些结果对象与代表性对象的紧密度较高，相应地典型程度也就较高，而IR-tree方法得到的top-k结果之间通常比较相似，多样性和典型程度相对较低。综合图2和图3还可以得出，本文方法在准确性较高的前提下，在很大程度上提高了查询结果的典型程度，即结果对象更具代表性，能够更好地满足用户对查询结果的相关性和典型性查询需求。

3.3 top-k查询算法的性能测试

该实验的目的是测试本文提出的top-k查询算法的响应时间。在该实验中，设置代表性序列个数l分别为2、3、4和5，然后测试在不同k值下，分别使用本文方法和IR-tree索引获取top-k结果的响应时间(如图4所示)。

从图4可以看出，当l={2, 3}时本文方法与IR-tree索引的响应时间相近，并且当k≤40时，响应时间要低于IR-tree，这也说明了TA算法在k值较小时具有优越的性能。此外，本文方法的响应时间随着k和l值的增加而逐渐增长，其原因是当k和l增加后，算法需要处理的对象个数也会增多，因此导致响应时间增加。

4 结束语

本文提出了一种基于位置-文本关系的空间对象top-k查询与排序方法，目的是从空间数据库中快速获取与查询位置和文本相关且具有代表性的top-k空间对象。实验结果表明，提出的top-k查询与排序方法同时具有较高的准确性、典型性和执行效率，特别适用于大规模空间数据库的空间关键字top-k检索。

本文方法与现存方法有2个方面不同：1)提出了基于概率密度的代表性对象选取算法来获取代表性空间对象，进而构建代表性空间对象序列，为快速选取top-k结果提供基础。2)将阈值算法threshold algorithm(TA)算法应用到了对空间对象的top-k查询与排序中，在确保较高查询准确性的前提下兼顾了查询结果的典型性，并且具有较快的响应时间。下一步工作将研究如何将公路网络(road network)应用于空间对象之间的距离计算，以及如何进行查询结果的局部典型化和多样典型化选取。