传统的算法多是面向均衡数据集,有较好的分类性能,而实际应用中的数据集多是不均衡、异构的。面向不均衡数据分类的研究是数据挖掘、机器学习等领域当前的研究热点之一[1-16],主要集中在数据层面[1-8]和算法层面[9-16]。
数据层面的方法[1-5],又称为重采样法,多采用减少多数类样本或增加少数类样本,使得数据集均衡化,过采样[1-3]是依据少数类样本的空间特征,通过一定的方法增加少数类样本数量,该方法容易导致过拟合,为此许多研究者提出了解决方法,例如合成少数类样本过采样技术(synthetic minority oversampling technique,SMOTE)及对SMOTE的改进算法;欠采样[5-6]则是通过一定的方法删除多数类样本中信息重复或者包含信息量较少的样本,但由于计算方法的不同,会删除包含丰富信息的样本,导致欠学习,为此研究者结合集成学习和重采样思想,不删除样本,而是对多数类样本按照一定策略进行抽取,然后与少数类样本一起构成训练子集[7]。
算法层面的方法则是提出新方法或者改进已有算法,减少数据不均衡对分类性能的影响,主要包括代价敏感学习[8-9]、单类学习、集成学习[10-14]等。其中集成学习方法是通过迭代逐步把弱分类器提升为强分类器,能够较好的提高分类器的性能,也是解决不均衡分类问题的常用方法,在一些领域得到应用[15-16]。文献[11]首先将数据集划分为多个均衡的子集,训练各个子集获得多个分类器,然后把多个分类器按照一定的规则(文中给出5种集成规则)进行集成,从而提高分类性能,该方法中对数据集的划分方法对最终的分类器性能有较大的影响,为此,文献[5]中通过聚类对多数类样本进行欠取样,获得与少数类样本数量相同的样本,然后采用Adaboost算法获得最终分类器,该方法保证所选样本的空间分布,但不能对分类错误样本和正确样本进行区别对待,而文献[6]利用抽样概率进行抽样,通过迭代不断修正抽样概率,对于分类错误的样本加大抽样概率,而分类正确的样本减小抽样概率,目的是争取下轮迭代中能选中进行学习。因此,本文方法既要充分考虑样本的空间分布,又要考虑到正确分类和错误分类样本之间的区别,采用聚类和抽样概率的方式进行数据集的划分,获得多个均衡的数据子集。
KNN算法是一种简单而有效的分类算法,通过计算与样本最近的K个样本的类别来判断样本的类别,计算样本的K近邻经常采用欧氏距离、相关距离等,而对于异构数据集下,这些距离不能准确的表达样本的相似程度,针对此问题,Wilson等[18]提出了异构距离,可以更准确的度量异构数据下2个样本之间的相似度,因此,本文采用基于异构距离的KNN算法作为弱分类器。
基于以上分析,本文提出一种面向不均衡异构数据的集成学习算法(imbalanced heterogeneous data ensemble classification based on HVDM-KNN, HK-Adaboost算法),提高异构不均衡数据下的分类性能。该算法首先用聚类算法把数据集划分为多个均衡的数据子集,对于每个子集采用基于异构距离的KNN算法,然后用Adaboost算法对弱分类器进行训练,然后依据一定的评价指标进行调整,获得最终的强分类器。
1 相关概念 1.1 异构距离定义1 异构不均衡数据(heterogeneous data):设数据集X上的每条记录共有m个属性,k(0<k<m)个属性取值为连续值,其余m-k个属性取值为离散值,则称该数据集为异构数据集,若该数据集中类样本数量有较大差异,则称数据集为异构不均衡数据集。
根据样本到类中心的距离判断样本的类别,其实质就是计算样本与类的相似度,然而欧氏距离以及其它距离都不能准确度量异构数据集中记录的相似度。为了有效度量异构数据之间的相似度,实现数据分类,Wilson等[18]提出HVDM(heterogeneous value difference metric)距离函数,能够反映出不同属性对相似度的影响,有效度量数据之间的差异,其定义如下:
定义2 异构距离:设
| ${{H}}(x,y) = \sqrt {\sum\limits_{i = 1}^m {{{d}}_j^2} ({x_j},{y_j})} $ | (1) |
式中:
| $ {{{d}}_j}({x_j},{y_j}) = \left\{ \begin{array}{l} 1,\quad{x_j}\;or\;{y_j}\\ {d_{{\rm{vdm}}}}({x_j},{y_j}), \quad{x_j},{y_j}{\text{为离散属性}}\\ {d_{{\rm{diff}}}}({x_j},{y_j}), \quad{x_j},{y_j}{\text{为连续属性}} \end{array} \right. $ | (2) |
| ${d_{{\rm{diff}}}}({x_j},{y_j}) = \frac{{|{x_j} - {y_j}|}}{{4{\sigma _j}}}$ | (3) |
| ${d_{{\rm{vdm}}}}({x_j},{y_j}) = \sum\limits_{i = 1}^k {|\frac{{{N_{a,x,i}}}}{{{N_{a,x}}}}} - \frac{{{N_{a,y,i}}}}{{{N_{a,y}}}}|$ | (4) |
式中:
K-近邻算法通过取测试样本的K个近邻,然后依据K个近邻的类别进行投票,确定测试样本的类别,由于算法简单、易于实现等特点,被广泛应用。KNN是依据K个近邻的类别决定测试样本的类别,因此K个近邻的选取将影响算法的性能,与测试样本越相近实质就是与测试样本越相似,而计算相似度可以采用距离、夹角余弦等方法,基于距离相似度中常采用欧氏距离,尤其是对连续属性的向量之间,能较好的度量2个向量间的相似程度。而对于既有数值属性又有字符属性的异构数据,采用欧氏距离不能准确描述2个向量间的相似程度,而实际应用中的数据有相当部分属于这样的异构数据集,进行训练、分类时多是采用简单的数字替换,把数据集转换为数值型的向量,例如red、blue、yellow 3种颜色,若用1、2、3进行代替,原来red与blue之间的差别与red与yellow之间的差别是相同的,但是用数字替换后的距离计算中,(1−2)2与(1−3)2间的差别是不相同的,因此本文的KNN算法中采用文献[18]给出的异构距离作为度量选择K个近邻样本。
1.3 数据均衡化在集成学习中,对多个训练集进行训练获得分类器,然后把分类器进行集成,Adaboost算法是通过修改每个样本的权重,改变原有的数据分布从而得到新的训练集,但是该方法无法改变2类样本数量不成比例的问题,为此,文献[11]提出一种新的面向不均衡数据的集成方法,把多数类样本划分为多个与少数类样本规模相当的子集,然后与少数类样本一起构成多个均衡的子集,该方法的关键是如何对多数类样本进行划分;文献[5]采用K均值聚类,产生与少数类样本数量相同的簇数,用簇代表原来的多数类样本,从而对数据进行均衡化,该方法会导致丢掉较多的样本,进而导致出现欠学习现象;文献[6]中依据抽样概率从多数类样本中随机抽取与少数类样本数量相等的样本,与少数类一起构成训练集,这样同样会导致丢掉较多的样本,为此,文中采用迭代的方式多次抽取,每次抽取都会修改样本的抽样概率,一方面该方法仍然会有部分样本不被选中,另一方面,抽取的样本无法保持原有数据的空间分布,为此本文采用先聚类再抽取的方式对多数类样本进行划分,划分方法如算法1。
该方法抽取的样本包含有对应簇的空间信息,使得针对每个子集获得的分类器有较好的分类性能,另外选取合理的m值,几乎不会有样本不被抽取,并且抽取的样本与多数类样本有相似的空间分布。
算法1 数据划分
输入 数据集
| ${\rm{train}}\_{\rm{data}} = \{ ({x_i},{y_i})\} ,{x_i} \in {{\bf R}^n},{y_i} \in { Y} = \{ - 1,1\} $ |
1)把数据集分为
2)若
3)分别从
输出 获得m个均衡的子集
算法需要依据每个子分类器的分类性能计算每个子分类器的权重,这里采用子分类器的分类错误率描述子分类器的权重,子分类器的权重表示为
| $w_i^t = \frac{1}{2}\ln ((1 - e_i^t)/e_i^t)$ | (5) |
式中:
在第t轮迭代中需要更新样本的权重,改变子分类器的分类性能,新样本的权重依据式(6)进行更新:
| ${{ D}_{(t + 1)i}}(j) = {{ D}_{ti}}\exp ( - w_i^t{y_j}h_i^t({x_j}))/{z_{ti}}$ | (6) |
每轮迭代结束,对分类器进行集成时,要考虑上轮所获得的分类器和本轮分类器进行集成,集成方法如下:
| ${{H}}_i^t(x) = {{{H}}_{t - 1}}(x) + \sum\limits_{t = 1}^{\rm{T}} {} {w_i^th_i^t(x)} $ | (7) |
计算每轮迭代结束所获得分类器的分类性能提升情况,并获得该轮迭代后的分类器:
| ${{{H}}_t}(x) = {{H}}_i^t(x),t = \arg \max ({\sigma _{ti}})$ | (8) |
对
| ${a_t} =1- \frac{1}{{2l}}\sum\limits_{i = 1}^l {} {|{{{H}}_t}({x_i}) - {y_i}} |$ | (9) |
迭代结束后获得最终分类器为
| ${{H}}(x) = \frac{1}{Z}\sum\limits_{i = 1}^t {} {{a_i}{{{H}}_i}(x)} $ | (10) |
算法2的详细过程如下:
算法2 HK-Adaboost算法
输入 数据集
输出 最终分类器为
1)用K均值聚类算法对数据集进行划分,获得m个均衡的子集
2)初始化样本权重:
for t=1:T
3) for i=1:M
调用分类器
利用式(5)计算每个分类器权重;
利用式(6)对各子集中样本进行权重更新;
利用式(7)获得本轮结束时分类器
end for i
4)计算所得各子分类器
若分类效果没有提升,则结束该子集上的迭代,若有提升,则依据公式(8)选择提升效果最好的分类器作为第t次迭代后的分类器;
利用公式(9)计算分类器的分类性能
end for t
5)利用式(10)获得最终分类器
1)中,利用K均值聚类算法对多数类样本进行聚类,K值为少数类样本数,得到K个簇,然后采用有放回抽样,从每个簇中随机取出一个样本,与少数量样本一起构成一个均衡的训练子集,然后重复该步骤,产生m个均衡的训练子集。
2)是对每个训练子集中的每个样本赋予权值,初始权值都相等。
3)是第t次迭代时,每个训练子集上的训练过程,依据Adaboost算法思想,对每个子集上的每个样本的权重进行更新,当第t次迭代结束后获得的分类器为第t-1次迭代获得分类器与第i个子集上前t-1次迭代获得的分类器的加权和。每个分类器的分类性能评价指标可以是F1值、G-mean、AUC等,本文算法中采用与Adaboost一致的评价方式-分类错误率。
式(5)是依据分类器对样本的分类错误样本的权重之和计算分类器的权重,然后依据Adaboost算法中更新样本权重的思想,应用式(6)更新每个样本的权重,第t轮迭代结束。
4)是计算第t次迭代结束后获得的分类器,如果分类效果比上次迭代好,则进行后面步骤,否则丢弃该次迭代产生分类器。这里从m个子分类器中选择提升效果最好的分类器作为第t次迭代后的分类器,提升效果的评价仍然可以采用F1值、G-mean、AUC等评价指标进行评价,本文为简化算法,仍采用准确率作为评价指标,获得本轮迭代的分类器。然后计算本轮所得分类器的分类性能,并计算本轮迭代所得分类器在最终分类器中的权重。
5)获得最终分类器,是每轮迭代所得分类器的加权和,其中
本文选择8组不同的数据集进行实验,8组数据集来自UCI数据库,Car Evaluation、TIC-TAC-Toe Endgame、Liver Disorders、Breast Cancer、Haberman’s Survival、Blood transfusion、Contraceptive Method Choice和Teaching Assistant Evaluation,所选实验数据集的详细信息如表1所示,可以看到数据集在一定程度上都是不均衡的,并且数据集的各个属性是不连续的,另外本文算法是针对2类分类的,因此把数据集都转化为2类的数据集[17,19]。
| 表 1 实验数据集 Tab.1 dataset |
针对均衡数据的分类多采用分类精度作为评价指标,而对于不均衡数据,更多关注的是少数类样本的分类情况,这种基于相同错分代价的评价指标不能很好描述分类性能。针对不均衡数据分类的评价指标多采用Recall、Precision、F-mean、G-mean、ROC曲线和AUC等,这些性能指标是基于混淆矩阵来计算的,对于二分类问题的混淆矩阵如表2所示。
| 表 2 混淆矩阵 Tab.2 Obfuscation matrix |
依据混淆矩阵可以计算上面评价指标的计算公式:
| ${\rm{Re call}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}$ | (11) |
| ${\rm{\Pr ecision}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}$ | (12) |
| ${\rm{F_1}} = \frac{{2 \times {\rm{\Pr ecision}} \times {\rm{Re call}}}}{{{\rm{\Pr ecision}} + {\rm{Re call}}}}$ | (13) |
| ${\rm{G - mean}} = \sqrt {\frac{{{\rm{TN}}}}{{{\rm{TN}} + {\rm{FP}}}} \times \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}} $ | (14) |
Recall表示正类的查全率;Precision表示正类的查准率;F-mean同时考虑查全率和查准率,只有当两个都大时F-mean的值才较大,可以较好的描述不均衡数据集下的分类性能;G-mean综合考虑2类的准确率,任何一类准确率较低时,G-mean的值都会较小,因此能够较好评价不均衡数据集下的分类性能。
ROC曲线则是以正负类的召回率为坐标轴,通过调整分类器的阈值而获得一系列值对应的曲线,由于ROC曲线不能定量评价分类器的分类性能,因此常采用ROC曲线下的面积AUC来评价分类器的分类性能,AUC值越大代表分类器的分类性能越好,本文实验主要从上面所列评价指标来对比算法的性能。
3.2 异构距离有效性验证表3中HDVM_KNN是指采用HDVM距离的K近邻算法,KNN指采用欧氏距离的K近邻算法,其中K取值为5的实验结果,SVM是依据动态错分代价的支持向量机算法,SVM和KNN是对数据进行归一化操作后采用matlab中自带的支持向量机算法进行实验的结果,Car数据集的实验是从数据集中隔一条记录取一条的方式选取训练集,用全部样本作为测试集的结果,其他数据集均是全部数据既是训练集又是测试集的结果。实验结果主要依据常见的性能指标样本准确率ACC、Recall、Precision、F-mean、G-mean和AUC验证算法的性能,实验更加关注少数类样本的分类性能。
| 表 3 实验结果 Tab.3 Experimental result |
由表3的实验结果可以看出,基于异构距离的KNN实验结果除了Breast数据集的准确率和Contraceptive数据集的AUC、F1值外,其他指标都优于采用欧氏距离的KNN算法的实验结果,说明对于异构数据集,异构距离比欧氏距离能更准确的描述2个样本之间的相似度。
3.3 与其他算法的性能对比用每个数据集的全部数据作为训练集,同时用该数据作为测试集的实验结果,详细实验数据如表4所示,其中KNN是K近邻算法、Adaboost用的是matlab中自带的算法、OK-Adaboost是本文所提算法(K近邻算法采用欧氏距离进行计算)、HK-Adaboost是本文所提算法(K近邻算法采用异构距离进行计算),实验中中K近邻算法的K取值为5,划分子集数m取值为5,Adaboost算法迭代100次、OK-Adaboost和HK-Adaboost算法迭代20次。
| 表 4 算法性能对比1 Tab.4 Algorithm performance comparison 1 |
由于训练集和测试集相同,各个算法的各项指标都比较好,但是每项指标本文算法的性能都优于其他算法,KNN算法和Adaboost算法没有考虑数据集不均衡的问题,算法OK-Adaboost中若分离器采用的是欧氏距离,不能准确描述样本间的相似程度。
表5给出的是各个数据集,取一半作为训练集、一半作为测试集。从第一条开始隔一条去一条作为训练集,剩余为测试集,实验中取m=5,K=5,T=20,详细的实验结果如表5所示。由于采用一半作为训练集,一半作为测试集,实验所得各项性能指标明显比表4要差,尤其是在Car和Contraceptive数据集上的分类性能,可以看到基于欧氏距离的算法要比基于异构距离的算法效果要好,查看样本之间的异构距离,发现他们之间的差异远远小于欧氏距离之间的差异。分析数据发现计算样本
| 表 5 算法性能对比 2 Tab.5 Algorithm performance comparison 2 |
|
Download:
|
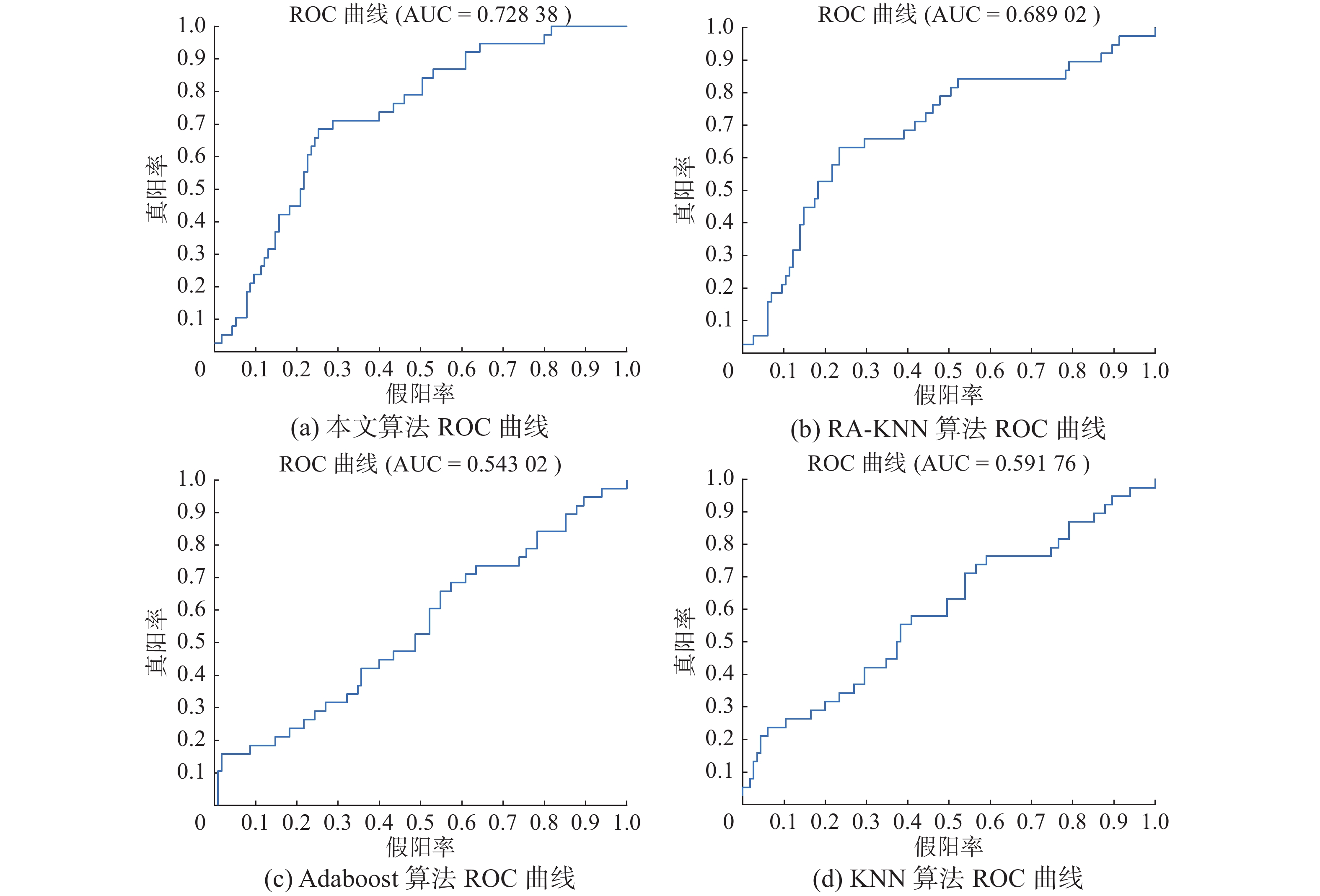
| 图 1 Haberman数据集的ROC曲线对比 Fig. 1 RCO figure of Haberman dataset | |
|
Download:
|
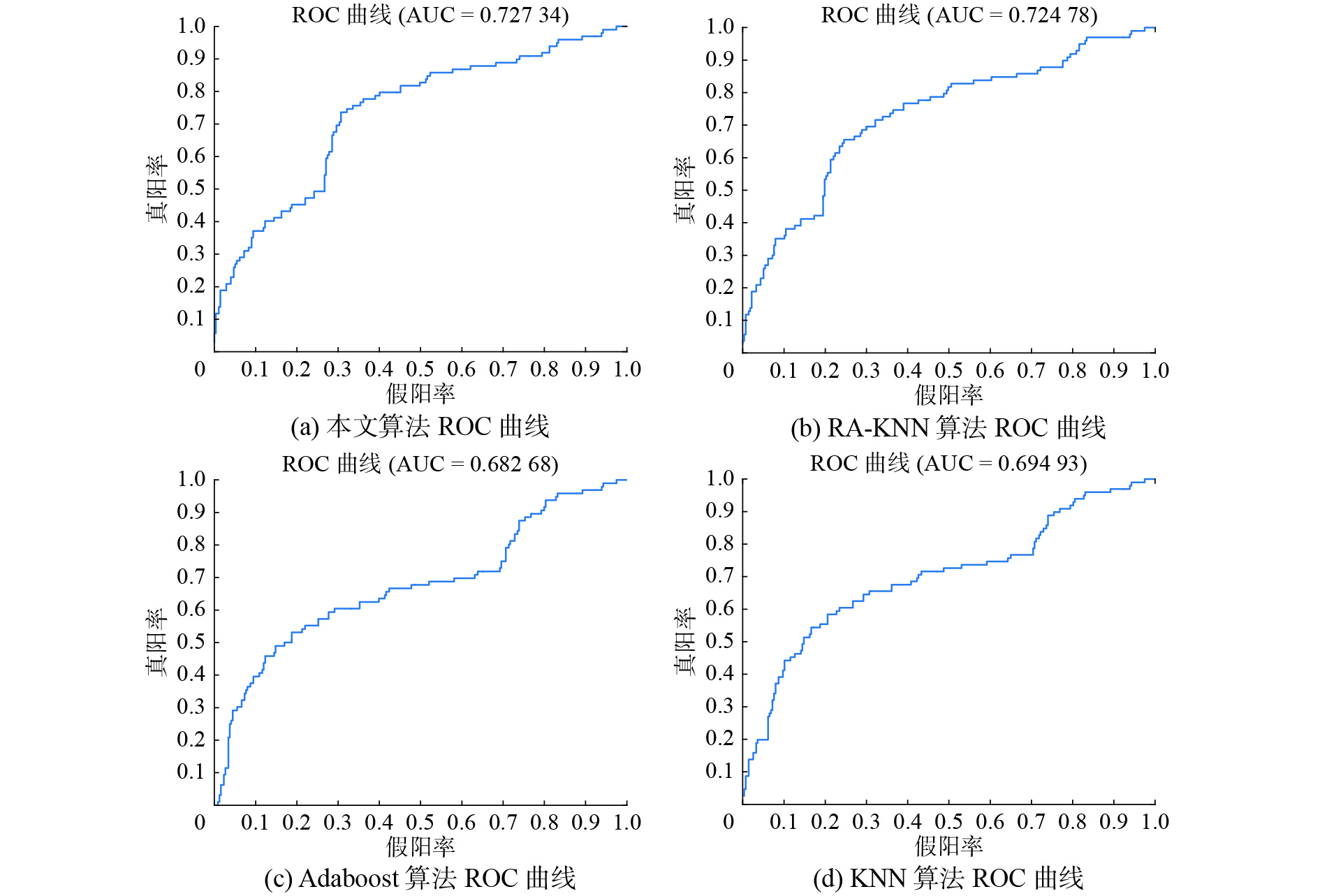
| 图 2 Blood数据集ROC曲线对比 Fig. 2 RCO figure of Blood dataset | |
针对异构不均衡数据集下的分类问题,本文提出一种面向不均衡异构数据的集成学习算法-HK-Adaboost算法,该算法从数据划分、基于异构距离的KNN及多个分类器的迭代集成等方面进行改进,可以提高分类器在异构不均衡数据集下的分类性能,通过在8组UCI异构数据集上进行实验,验证了算法在异构不均衡数据上的分类性能。但实验中遇到一些问题,如Adaboost算法对数据进行归一化后的分类性能会更差、异构距离计算时间复杂度高、数据划分子集的个数如何最优、如何扩展到多类问题等问题将是下阶段的主要工作。
| [1] |
胡峰, 王蕾, 周耀. 基于三支决策的不平衡数据过采样方法[J]. 电子学报, 2018, 46(1): 136-144. HU Feng, WANG Lei, ZHOU Yao. An oversampling method for imbalance data based on three-way decision model[J]. Acta electronica sinica, 2018, 46(1): 136-144. (  0) 0)
|
| [2] |
SÁEZ J A, LUENGO J, STEFANOWSKI J, et al. SMOTE–IPF: addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering[J]. Information sciences, 2015, 291: 184-203. DOI:10.1016/j.ins.2014.08.051 ( 0) 0)
|
| [3] |
PRUSTY M R, JAYANTHI T, VELUSAMY K. Weighted-SMOTE: a modification to SMOTE for event classification in sodium cooled fast reactors[J]. Progress in nuclear energy, 2017, 100: 355-364. DOI:10.1016/j.pnucene.2017.07.015 ( 0) 0)
|
| [4] |
MATHEW J, LUO Ming, PANG C K, et al. Kernel-based SMOTE for SVM classification of imbalanced datasets[C]//Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society. Yokohama, Japan, 2015: 1127-1132.
( 0) 0)
|
| [5] |
武森, 刘露, 卢丹. 基于聚类欠采样的集成不均衡数据分类算法[J]. 工程科学学报, 2017, 39(8): 1244-1253. WU Sen, LIU Lu, LU Dan. Imbalanced data ensemble classification based on cluster-based under-sampling algorithm[J]. Chinese journal of engineering, 2017, 39(8): 1244-1253. (  0) 0)
|
| [6] |
陈旭, 刘鹏鹤, 孙毓忠, 等. 面向不均衡医学数据集的疾病预测模型研究[J]. 计算机学报, 2019, 42(3): 596-609. CHEN Xu, LIU Penghe, SUN Yuzhong, et al. Research on disease prediction models based on imbalanced medical data sets[J]. Chinese journal of computers, 2019, 42(3): 596-609. (  0) 0)
|
| [7] |
JIAN Chuanxia, GAO Jian, AO Yinhui. A new sampling method for classifying imbalanced data based on support vector machine ensemble[J]. Neurocomputing, 2016, 193: 115-122. DOI:10.1016/j.neucom.2016.02.006 ( 0) 0)
|
| [8] |
DU Hongle, TENG Shaohua, ZHANG Lin, et al. Support vector machine based on dynamic density equalization[C]//Proceedings of the Second International Conference on Human Centered Computing. Colombo, Sri Lanka, 2016: 58-69.
( 0) 0)
|
| [9] |
ZHOU Yuhang, ZHOU Zhihua. Large margin distribution learning with cost interval and unlabeled data[J]. IEEE transactions on knowledge and data engineering, 2016, 28(7): 1749-1763. DOI:10.1109/TKDE.2016.2535283 ( 0) 0)
|
| [10] |
WANG Shuo, MINKU L L, YAO Xin. Resampling-based ensemble methods for online class imbalance learning[J]. IEEE transactions on knowledge and data engineering, 2015, 27(5): 1356-1368. DOI:10.1109/TKDE.2014.2345380 ( 0) 0)
|
| [11] |
SUN Zhongbin, SONG Qinbao, ZHU Xiaoyan, et al. A novel ensemble method for classifying imbalanced data[J]. Pattern recognition, 2015, 48(5): 1623-1637. DOI:10.1016/j.patcog.2014.11.014 ( 0) 0)
|
| [12] |
GUO Haixiang, LI Yijing, LI Yanan, et al. BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification[J]. Engineering applications of artificial intelligence, 2016, 49: 176-193. DOI:10.1016/j.engappai.2015.09.011 ( 0) 0)
|
| [13] |
WANG Qi, LUO Zhihao, HUANG Jincai, et al. A novel ensemble method for imbalanced data learning: bagging of extrapolation-SMOTE SVM[J]. Computational intelligence and neuroscience, 2017, 2017: 1827016. ( 0) 0)
|
| [14] |
POTHARAJU S P, SREEDEVI M. Ensembled rule based classification algorithms for predicting imbalanced kidney disease data[J]. Journal of engineering science and technology review, 2016, 9(5): 201-207. DOI:10.25103/jestr ( 0) 0)
|
| [15] |
ZHAI Junhai, ZHANG Sufang, WANG Chenxi. The classification of imbalanced large data sets based on MapReduce and ensemble of ELM classifiers[J]. International journal of machine learning and cybernetics, 2017, 8(3): 1009-1017. DOI:10.1007/s13042-015-0478-7 ( 0) 0)
|
| [16] |
YU Hualong, NI Jun. An improved ensemble learning method for classifying high-dimensional and imbalanced biomedicine data[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2014, 11(4): 657-666. DOI:10.1109/TCBB.2014.2306838 ( 0) 0)
|
| [17] |
HAQUE M N, NOMAN N, BERRETTA R, et al. Heterogeneous ensemble combination search using genetic algorithm for class imbalanced data classification[J]. PLoS one, 2016, 11(1): e0146116. DOI:10.1371/journal.pone.0146116 ( 0) 0)
|
| [18] |
WILSON D R, MARTINEZ T R. Improved heterogeneous distance functions[J]. Journal of artificial intelligence research, 1997, 6(1): 1-34. ( 0) 0)
|
| [19] |
ZHANG Yishi, YANG Anrong, XIONG Chan, et al. Feature selection using data envelopment analysis[J]. Knowledge-based systems, 2014, 64: 70-80. DOI:10.1016/j.knosys.2014.03.022 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


