近年来随着互联网科技的发展，大数据在促进社会进步的同时，也带来了“信息过载”问题。如何快速从海量数据中获取有价值的信息成为当前大数据发展的关键性问题^[1]。为满足人们在大数据中快速获取有价值信息的需求，推荐系统应运而生。推荐系统的目标是根据用户的个性化需求将最符合用户喜好的信息挑选出来并推荐给用户，以减轻用户的选择负担。协同过滤推荐算法是一种目前应用最广泛的推荐算法^[2]，可以在用户没有明确提出自己需求的情况下，根据用户的行为对用户进行推荐。但由于大数据环境下用户和项目的数量不断增长，协同过滤推荐算法面临着严重的数据稀疏性和可扩展性问题^[3]。

针对稀疏性问题，许多学者从不同角度进行了相关研究。SUN等^[4]采用聚类和时间影响因子矩阵来监测用户兴趣漂移程度，更准确的预测项目的评分。彭宏伟等^[5]提出一种基于矩阵分解的上下文感知POI推荐模型，有效地缓解稀疏性问题。WU等^[6]将异构信息网络建模为张量，并提出两种随机梯度下降方法同时进行分解。MA等^[7]提出了一种局部概率矩阵分解的方法，降低稀疏性的同时有效地缓解了每个局部模型的过拟合问题。以上的方法均通过缓解数据稀疏性问题来提高推荐的准确度。

针对协同过滤推荐算法在处理大规模数据所遇到的可扩展性问题，许多学者在并行方法上进行了相关研究。杨志文^[8]、LU F^[9]、KUPISZ^[10]等将协同过滤推荐算法部署在Hadoop和Spark并行平台上，取得了良好的执行效率。

本文针对协同过滤推荐算法的数据稀疏性问题和可扩展性问题进行研究。针对稀疏性问题，在皮尔逊相关相似度的基础上引入交占比系数来计算用户的直接相似度，提出了一种基于图游走的协同过滤推荐算法(GW_CF)，使用图游走的方法计算用户的间接相似度，然后根据直接相似度和间接相似度重建用户的相似度矩阵，最后进行推荐。在Movielens-100k数据集和IPTV数据集上实验，验证GW_CF在提高推荐准确度上的有效性。针对可扩展性问题，在Spark平台上实现GW_CF算法，并使用Movielens-1M和Movielens-100k数据集进行实验，验证GW_CF算法的可扩展性。

1 相关工作 1.1 问题定义

基于近邻的协同过滤问题可以描述为^[11]：已知用户集合表示为 $U = \left\{ {{u_1},{u_2}, \cdots ,{u_a}, \cdots {u_b}, \cdots ,{u_n}} \right\}$ ，项目集合表示为 $S = \left\{ {{s_1},{s_2}, \cdots ,{s_i}, \cdots ,{s_j}, \cdots {s_m}} \right\}$ ，用户-项目评分矩阵 ${{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}} \\ \vdots & \vdots & & \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array}} \right]$ ， ${r_{ai}}$ 表示用户 ${u_a}$ 对项目 ${s_i}$ 的评分。基于近邻的协同过滤推荐算法的流程：1)根据评分矩阵R计算用户的相似度；2)计算目标用户的近邻用户集合；3)根据近邻用户的评分预测目标用户对未评分项目的评分，从而生成推荐列表。

1.2 用户相似度

用户相似度指用户与用户之间行为中表现出的相似程度，皮尔逊相关相似度是一种常用的计算相似度的方法，反映了两个用户的偏好信息的线性相关程度。用户 ${u_a}$ 和用户 ${u_b}$ 的皮尔逊相关相似度计算公式^[12-13]如下：

${\rm{sim}}(a,b) = \frac{{\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{ai}} - {{\bar{r}_a}} } \right)\left( {{r_{bi}} - {{\bar{r}_b}} } \right)} }}{{\sqrt {\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{ai}} - {{\bar{r}_a}} } \right)} } \sqrt {\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{bi}} - {{\bar{r}_b}} } \right)} } }}$

(1)

式中： ${s_{ab}}$ 为用户 ${u_a}$ 和用户 ${u_b}$ 共同评分项目的集合； ${r_{ai}}$ 为用户 ${u_a}$ 对项目 ${s_i}$ 的评分； ${{\bar{r}_a}} $ 为用户 ${u_a}$ 对集合 ${s_{ab}}$ 中项目评分的平均值。 ${\rm{sim}}(a,b)$ 的值域为 $\left[ { - 1,1} \right]$ ， ${\rm{sim}}(a,b)$ 越大，表示两个用户的相似度越高。

1.3 近邻用户

近邻用户表示与目标用户偏好信息最相似的一组用户，可以通过式(1)计算用户的相似度，然后计算目标用户的近邻用户。目标用户的多个近邻用户组成目标用户的近邻用户集合，常用的计算近邻用户集合的方法分为两类：基于数量的近邻用户集合和基于阈值的近邻用户集合。

基于阈值的近邻用户集合包含以目标用户为中心，与目标用户的相似度大于Value的用户。基于数量的近邻用户集合包含与目标相似度最大的Top-K个近邻用户。

1.4 个性化推荐

首先计算目标用户的近邻用户集合，然后对目标用户进行推荐。目标用户 ${u_a}$ 对未评分项目 ${s_i}$ 预测评分的计算公式^[14]如式（2），最后将预测评分最大的K个项目推荐给目标用户。

${r_{ai}} = {{\bar{r}_a}} + \frac{{\sum\limits_{{u_b} \in {N_{{u_a}}}} {{\rm{sim}}\left( {a,b} \right) \times \left( {{r_{bi}} - {{\bar{r}_b}} } \right)} }}{{\sum\limits_{{u_b} \in {N_{{u_a}}}} {{\rm{sim}}\left( {a,b} \right)} }}$

(2)

式中： $\bar {{r_a}} $ 表示用户 ${u_a}$ 已评项目的平均评分； $\bar {{r_b}} $ 表示用户 ${u_b}$ 已评项目的平均评分； ${N_{{u_a}}}$ 表示用户 ${u_a}$ 的近邻用户集合； ${\rm{sim}}\left( {a,b} \right)$ 表示目标用户 ${u_a}$ 与近邻用户 ${u_b}$ 的相似度。

2 改进的皮尔逊相关相似度

皮尔逊相关相似度计算方法如式(1)，仅仅考虑了用户的共同评分项，而忽视了共同评分项目与每个用户所有评分项的比例关系。这会导致如果两个用户仅有极少数共同评分项目，并且两个用户对共同评分项目的评分极度相似，使用皮尔逊相关相似度计算得到的用户的相似度，远远大于用户的真实相似度，降低了推荐的准确度。例如，用户 ${u_a}$ 曾对200个项目进行了评分，用户 ${u_b}$ 对300个项目进行了评分，两个用户仅拥有10个共同评分项目，且两个用户对每个共同评分项目的评分均相同。使用传统皮尔逊相关相似度计算两者的相似度为1(两个用户完全相似)。但实际上，除了10个共同评分项目以外，用户 ${u_a}$ 和用户 ${u_b}$ 还各自拥有大量的非共同评分项目，两个用户的喜好并不完全相同，利用皮尔逊相关相似度得到的结果远远大于两个用户的真实相似度。针对这个问题，本文在皮尔逊相关相似度基础上，引入交占比系数来缓解共同评分项占比的问题，交占比反映了两个用户的共同评分项在两个用户评分中的占比，加入交占比系数的皮尔逊相关相似度计算公式如下：

${\rm{sim}}(a,b) = \frac{{2 \times \left| {{s_{ab}}} \right|}}{{\left| {{s_a}} \right| + \left| {{s_b}} \right|}} \times \frac{{\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{ai}} - {{\bar{r}_a}} } \right)\left( {{r_{bi}} - {{\bar{r}_b}} } \right)} }}{{\sqrt {\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{ai}} - {{\bar{r}_a}} } \right)} } \sqrt {\sum\limits_{{s_i} \in {s_{ab}}} {\left( {{r_{bi}} - {{\bar{r}_b}} } \right)} } }}$

(3)

式中： $\left| {{s_{ab}}} \right|$ 表示用户 ${u_a}$ 和用户 ${u_b}$ 共同评分项目的个数； $\left| {{s_a}} \right|$ 表示用户 ${u_a}$ 的评分项目个数； $\left| {{s_b}} \right|$ 表示用户 ${u_b}$ 的评分项个数；其他变量的含义和式(1)相同。

表1为用户评分示例， ${u_1}$ 、 ${u_2}$ 和 ${u_3}$ 表示3个用户， ${s_1}, {s_2} \cdots, {s_8}$ 表示8个项目，表中的值表示用户对项目的评分，表中的空值(—)表示该用户未曾对该项目评分。根据式(1)计算用户 ${u_1}$ 和用户 ${u_2}$ 的相似度， ${u_1}$ 和 ${u_2}$ 的共同评分项集合 ${s_{12}} = \left\{ {{s_3},{s_4},{s_5}} \right\}$ ， ${u_1}$ 和 ${u_2}$ 对 ${s_{12}}$ 的评分均为 $\left[ {2,3,5} \right]$ ，得到 ${\rm{sim}}(1,2) = 1$ ，显然这并不能准确的反映用户 ${u_1}$ 和用户 ${u_2}$ 的相似程度。使用加入交占比的式(3)计算用户 ${u_1}$ 和用户 ${u_2}$ 的相似度， $\left| {{s_{12}}} \right| = 3$ ， $\left| {{s_1}} \right| = 6$ ， $\left| {{s_2}} \right| = 5$ ，得到 ${\rm{sim}}(1,2) \approx $ $0.545$ ，显然 $0.545$ 更符合用户 ${u_1}$ 和用户 ${u_2}$ 的真实相似度。

3 基于图游走的协同过滤推荐算法(GW_CF)

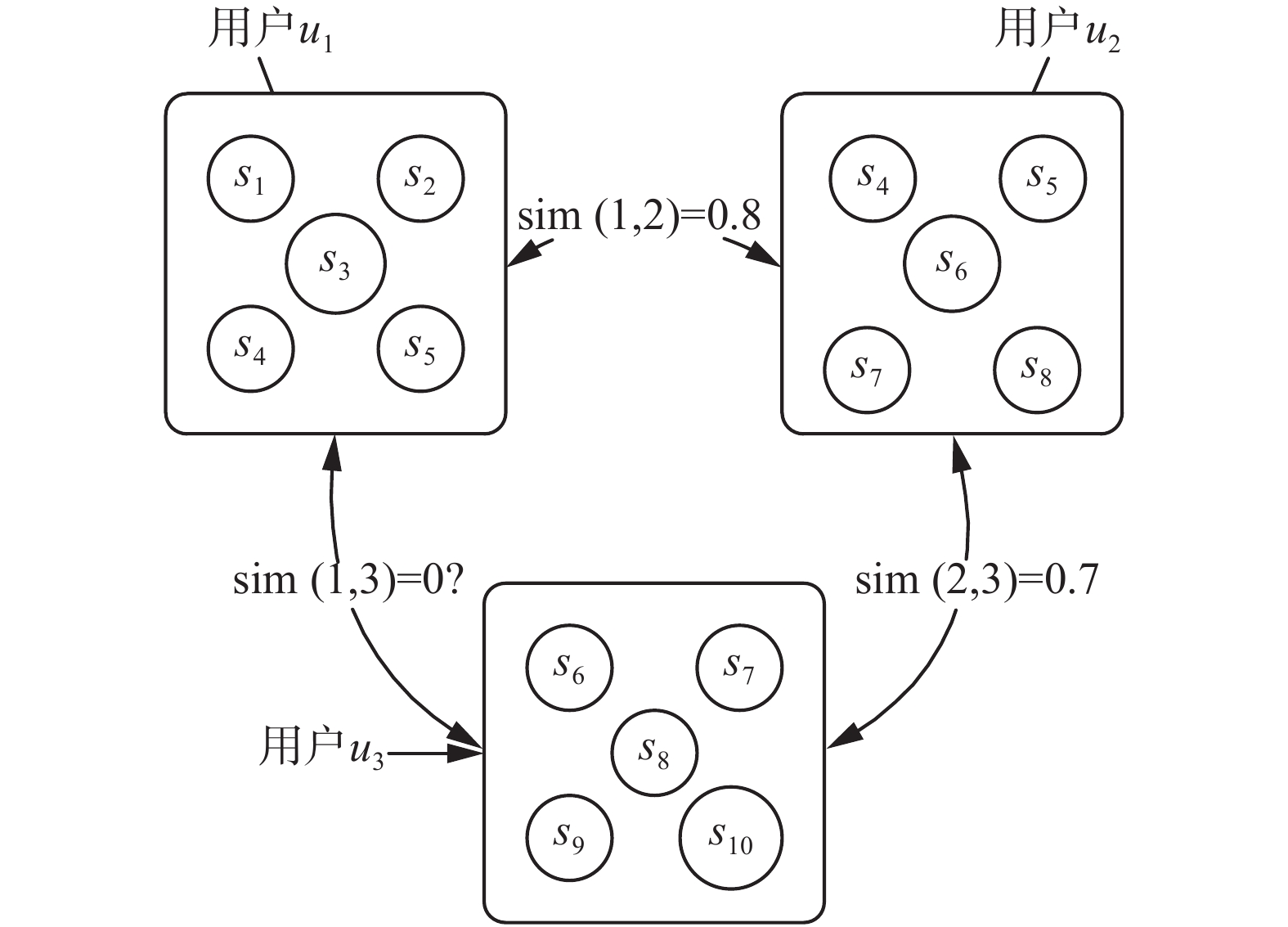
相似度计算是协同过滤推荐算法的关键部分，得到用户相似度之后可以确定用户的近邻用户集合。但以往计算用户的相似度时只考虑用户的直接相似相似度，这样将会遗失目标用户的间接近邻用户^[15-16]。例如图1所示， ${u_1}$ 、 ${u_2}$ 和 ${u_3}$ 表示3个用户， ${s_1},{s_2}, \cdots, {s_5}$ 表示用户 ${u_1}$ 的评分项目， ${s_4},{s_5}, \cdots {s_8}$ 表示用户 ${u_2}$ 的评分项目， ${s_6},{s_7}, \cdots, {s_{10}}$ 表示用户 ${u_3}$ 的评分项目。 ${\rm{sim}}\left( {1,2} \right)$ 、 ${\rm{sim}}\left( {2,3} \right)$ 、 ${\rm{sim}}\left( {1,3} \right)$ 表示用户 ${u_1}$ 、 ${u_2}$ 和 ${u_3}$ 的相似度。依据式(3)计算用户 ${u_1}$ 和用户 ${u_3}$ 的相似度，由于用户 ${u_1}$ 和用户 ${u_3}$ 没有共同评分项，所以 ${\rm{sim}}\left( {1,3} \right)=0$ 。但是用户 ${u_1}$ 和 ${u_2}$ 拥有共同评分项目 ${s_4}$ 和 ${s_5}$ ，那么 ${\rm{sim}}(1,2) > 0$ ，同理 ${\rm{sim}}(2,3) > 0$ 。由于相似性具有传递性，因此用户 ${u_1}$ 和 ${u_3}$ 可以通过共同的相似用户 ${u_2}$ 建立间接相似度，使得 ${\rm{sim}}\left( {1,3} \right) > 0$ 。如果两个用户没有共同评分项目，但间接相似度大于0，称这两个用户为间接近邻用户。在数据稀疏时，为用户寻找间接近邻用户能够有效地提高推荐的准确度。本文提出了基于图游走的方法，首先根据用户的直接相似度矩阵建立用户网络图，其次在用户网络图上进行游走计算间接相似度，然后根据间接相似度和直接相似度重建用户的相似度矩阵，最后进行推荐。

3.1 构建用户网络图

使用用户网络图来说明用户间的相似关系,从目标用户开始游走后停留在某个用户的概率越高意味着它与目标用户更相似。为了建立用户网络图，首先使用式(3)计算用户间的直接相似度，然后根据直接相似度建立用户近邻矩阵。为每个用户选择T个直接近邻用户，其他非T用户的相似度置0，得到的近邻矩阵如式(4)所示：

${\bf{SU}} = \left[ {\begin{array}{*{20}{c}} {{\rm{s{u}}_{11}}}&{{\rm{s{u}}_{12}}}& \cdots &{{\rm{s{u}}}_{1n}} \\ {{\rm{s{u}}_{21}}}&{{\rm{s{u}}_{22}}}& \cdots &{{\rm{s{u}}}_{2n}} \\ \vdots & \vdots & & \vdots \\ {{\rm{s{u}}}_{n1}}&{{\rm{s{u}}}_{n2}}& \cdots &{{\rm{s{u}}}_{nn}} \end{array}} \right]$

(4)

式中：对每个用户 ${u_a}$ 建立T近邻集合 ${N_{{u_a}}}$ ；如果用户 ${u_b}$ 不是用户 ${u_a}$ 的T近邻用户，则 ${\rm{s{u}}}_{ab} = 0$ ；若用户 ${u_b}$ 是用户 ${u_a}$ 的T近邻用户，则 ${\rm{s{u}}}_{ab} = {\rm{sim}}\left( {a,b} \right)$ 。在游走过程中不考虑用户和自身的相似度，所以令 ${\rm{s{u}}}_{aa} = 0$ 。

然后对矩阵 ${\bf{SU}}$ 按列进行归一化，得到矩阵 ${\bf{S{U}}^*}$ ，以矩阵 ${\bf{S{U}}^*}$ 作为邻接矩阵建立用户网络图。矩阵 ${\bf{S{U}}^*}$ 中的 ${\rm{SU}}_{ab}^*$ 表示从当前用户节点 ${u_b}$ 下一步游走到用户节点 ${u_a}$ 的概率。

3.2 基于用户网络图游走

用向量 ${{{r}}^k} = \left[ {r_1^k \;r_2^k \ldots r_b^k \ldots r_n^k} \right]$ 中 $r_b^k$ 表示第k次游走之后停留在节点 ${u_b}$ 的概率，向量 ${\bf{s{u}}}_a = \left[ {{\bf{s{u}}}_{a1}}\; \cdots \right.$ $\left.{\bf{s{u}}}_{ab}\;\cdots \;{\bf{s{u}}}_{an} \right] $ 中 ${\bf{s{u}}}_{ab} = {\rm{SU}}_{ab}^*$ ，则向量 ${{r}}_a^{k + 1}{\rm{ = }}{\bf{s{u}}}_a \times {\left( {{{{r}}^k}} \right)^{\rm{T}}}$ 为k+1次游走后停留在节点 ${u_a}$ 的概率。整个用户网络图的游走过程公式如下：

${\left( {{{{r}}^{k + 1}}} \right)^{\rm{T}}}={\bf{S{U}}^*} \times {\left( {{{{r}}^k}} \right)^{\rm{T}}}$

(5)

式中： ${\bf{S{U }}^*}$ 为用户网络图的邻接矩阵； ${{{r}}^k}$ 为第 $k$ 次游走后停留在各个节点的概率向量； $r_b^0 = $ $ \left\{ \begin{array}{l} 1,b = a\\ 0,b \ne a \end{array} \right.$ ，其中 $b = a$ 表示从用户节点 ${u_a}$ 开始游走。

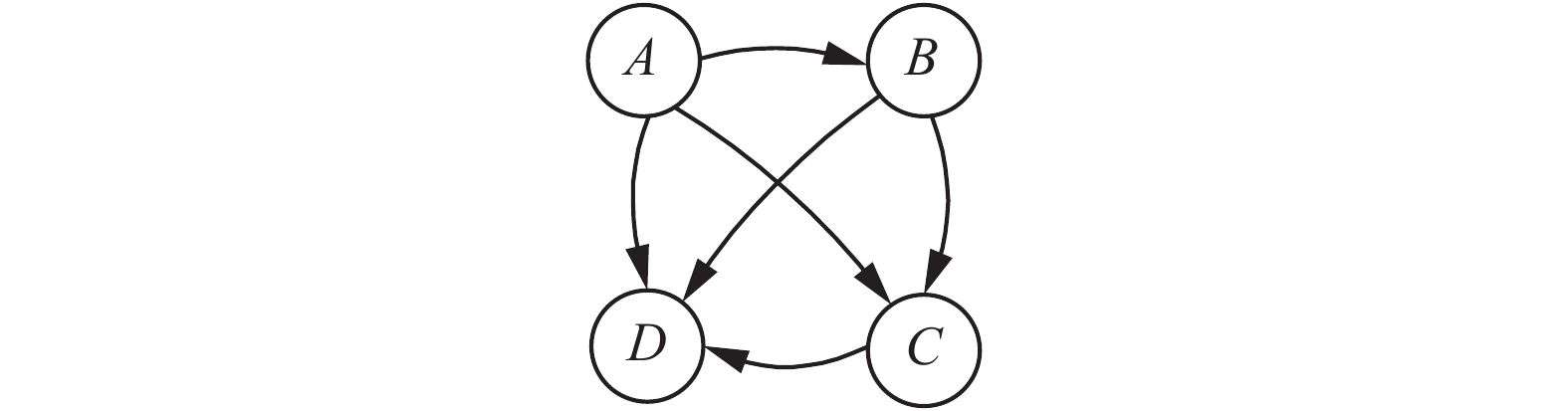
在用户网络图中存在着与其他用户的相似度都很低甚至可以忽略不计的特殊用户节点。在用户网络图中此类节点只有入度，没有出度，如图2中节点D，此时由于图中D节点只有入度，没有出度，用户网络图演变为非强连通图，以式(5)的方法游走到图中节点D时将无法跳转到其他节点。整个用户网络图的游走最终停留在类似节点D的死节点，无法求得用户的间接相似度，因此对式(5)进行变形如下：

${\left( {{{{r}}^{k + 1}}} \right)^{\rm{T}}} = p \times {\bf{S{U}}^*} \times {\left( {{{{r}}^k}} \right)^{\rm{T}}} + \left( {1 - p} \right) \times {{{t}}^{\rm{T}}}$

(6)

式中： $p$ 表示 $n$ 次游走后在当前节点继续游走的概率； $\left( {1 - p} \right)$ 表示随机远程跳转到目标节点的概率。 $p$ 的大小与式(6)的收敛速度成反比， $p$ 太大会导致收敛速度太慢从而影响算法的性能， $p$ 如果太小则无法反映游走的效果，因此令 $p = 0.85$ 。向量 ${{t}} = \left[ {{t_1}\;{t_2}\; \cdots {t_n}} \right]$ 表示远程跳转的目标节点， ${t_b} = \left\{ \begin{array}{l} 1,b = a\\ 0,b \ne a \end{array} \right.$ 。

当式(6)经过有限次迭代后，向量 ${{{r}}^k}$ 收敛^[17-18]。在理想情况下，当 $k$ 趋于无穷大时， ${{{r}}^{{{k}} + 1}}={{{r}}^k} = r$ ，那么式(6)可以表示为 ${{{r}}^{\rm{T}}} = p \times {\bf{S{U}}^*} \times {{{r}}^{\rm{T}}} + (1 - p$ $) \times {{{t}}^{\rm{T}}}$ 。对式(6)进一步变形得到式(7)，在从不同用户顶点开始游走查找它的间接相似用户时， $(1 - p) \times $ $ {({{I}} - p \times {\bf{S{U}}^*})^{ - 1}}$ 只需要计算一次。相对于式(6)的多次迭代，式(7)大大降低了计算的复杂度。

${{{r}}^{\rm{T}}} = (1 - p) \times {({{I}} - p \times {{{S}}^*})^{ - 1}} \times {{{t}}^{\rm{T}}}$

(7)

式中：向量 ${{r}} = \left[ {{r_1}\; \cdots \;{r_b} \cdots \;{r_n}} \right]$ 中 ${r_b}$ 表示从用户 ${u_a}$ 开始游走最终停留在用户 ${u_b}$ 的概率； ${r_b}$ 被视作用户 ${u_a}$ 和用户 ${u_b}$ 的相对相似程度。不考虑用户和它本身的相似度，因此令 ${r_{b = a}}{\rm{ = 0}}$ 。 ${r_b}$ 越大，表示用户 ${u_a}$ 和目标用户 ${u_b}$ 的间接相似度越高。

3.3 重建相似度矩阵

向量 ${{r}}$ 反映了各个用户与目标用户的相似程度相对大小，游走过程中的多次累加导致 ${r_b}$ 过大，进行推荐之前需要将向量r映射到直接相似度同一个数量级上，因此需要重建相似度矩阵。

集合 ${N'_{{u_a}}} = \left\{ {{u_b}|{u_b} \in {N_{{u_a}}}且{\rm{s{u}}_{ab}} \ne 0} \right\}$ 表示直接近邻集合 ${N_{{u_a}}}$ 中和目标用户相似度大于0的用户集合。利用该集合中用户与目标用户的直接相似度和向量 $r$ 对应元素的映射关系，将向量 ${{r}}$ 转化为目标用户和其他用户的间接相似度向量，重建的相似度计算公式为：

${\rm{sim}}(a,b) = \left\{ \begin{gathered} \frac{{\sum\limits_{{u_{_b}} \in {{N'\!}_{{u_a}}}} {\displaystyle\frac{{{\rm{s{u}}_{ak}}}}{{{r_k}}}} }}{{\left| {{{N'\!}_{{u_a}}}} \right|}} \times {r_a} \hfill \\ {\rm{s{u}}}_{ab}\;\; {{u_b} \in {{N'}_{{u_a}}}} \hfill \\ \end{gathered}, \right.\;\; {{u_b} \notin {{N'\!}_{{u_a}}}} $

(8)

式中： ${\rm{sim}}(a,b)$ 表示目标用户 ${u_a}$ 和用户 ${u_b}$ 的重建相似度； ${\rm{s{u}}}_{ab}$ 表示目标用户 ${u_a}$ 和用户 ${u_b}$ 的直接相似度； $\left| {{{N'}_{{u_a}}}} \right|$ 表示集合 ${N'\!_{{u_a}}}$ 中用户个数。

3.4 生成推荐结果

以每个用户顶点为起点进行游走查找其间接相似用户，得到重建的用户相似度矩阵，进一步得到目标用户的近邻用户集合。然后利用式(2)对目标用户的未评分项目进行评分预测，并将评分最高的Top-K个项目推荐给目标用户。

4 基于图游走的并行协同过滤推荐算法 4.1 Spark介绍

Spark是基于内存的分布式并行计算平台^[19]，它拥有Hadoop平台和MapReduce框架的全部优点，并且Spark运算的中间结果能存储在内存中，提高了并行计算的速度，因此Spark更适合进行数据挖掘与机器学习等需要迭代处理算法的实现^[19-21]。Spark集群启动时包括一个Master节点和若干个Worker节点，其中Master节点主要负责集群资源的管理，Worker节点主要负责数据的计算。当在Master节点使用spark-submit命令提交作业时，首先在本地客户端启动一个Driver进程；Driver进程会根据设置的参数向Master节点申请相应的集群资源，主要有Worker节点个数、每个Worker节点上Executor的内存和CPU数量；Master节点与Worker节点进行通信，通知Worker节点启动Executor并向Driver进程注册；Driver进程与Worker节点连接起来，将需要执行的任务分配给集群中的各个Worker节点，Worker节点按照任务分配从HDFS上读取数据并缓存到内存中，Driver进程对各个Worker节点处理完的结果进行收集和汇总。在Spark平台实现基于图游走的协同过滤算法能够有效地提高算法的时间效率。

4.2 相似性计算的并行化

由于皮尔逊相关相似度计算公式较为复杂，全局搜索较多，因此在实现本文方法并行化时引入中间变量 $Q$ ， ${Q_{ai}}$ 反映了用户 ${u_a}$ 在项目 ${s_i}$ 上的相似度权重，计算公式如下：

${Q_{ai}} = \frac{{\left( {{r_{ai}} - {{\bar r_{a}}} } \right)}}{{\sqrt {\sum\limits_a {({r_{ai}} - {{\bar r_{a}}} )} } }}$

(9)

式中： ${r_{ai}}$ 表示用户 ${u_a}$ 对项目 ${s_i}$ 的评分； ${{\bar r_a}} $ 表示用户 ${u_a}$ 的评分均值。皮尔逊相关相似度公式可以变形为

${\rm{sim}}\left( {a,b} \right) = \frac{{2 \times \left| {{s_{ab}}} \right|}}{{\left| {{s_a}} \right|{\rm{ + }}\left| {{s_b}} \right|}} \times \sum\limits_{{s_i} \in {s_{ab}}} {{Q_{ai}} \times {Q_{bi}}} $

(10)

因此，求用户 ${u_a}$ 和用户 ${u_b}$ 的相似度 ${\rm{sim}}(a,b)$ 的过程转化为5步：1）对于用户 ${u_a}$ 和用户 ${u_b}$ 的共同评分项 ${s_i} \in {s_{ab}}$ ，计算中间变量 ${Q_{ai}}$ 和 ${Q_{bi}}$ ；2）求用户 ${u_a}$ 和用户 ${u_b}$ 的 $Q$ 乘积 ${Q_{ai}} \times {Q_{bi}}$ ；3）计算 $\sum\limits_{{s_i} \in {s_{ab}}} $ ${Q_{ai}} \times $ $ {Q_{bi}} $ 得到皮尔逊相关相似度；4）交占比系数得到用户的直接相似度；5）使用游走的方法求得用户的间接相似度并重建相似度。

4.3 基于图游走的协同过滤算法并行化流程

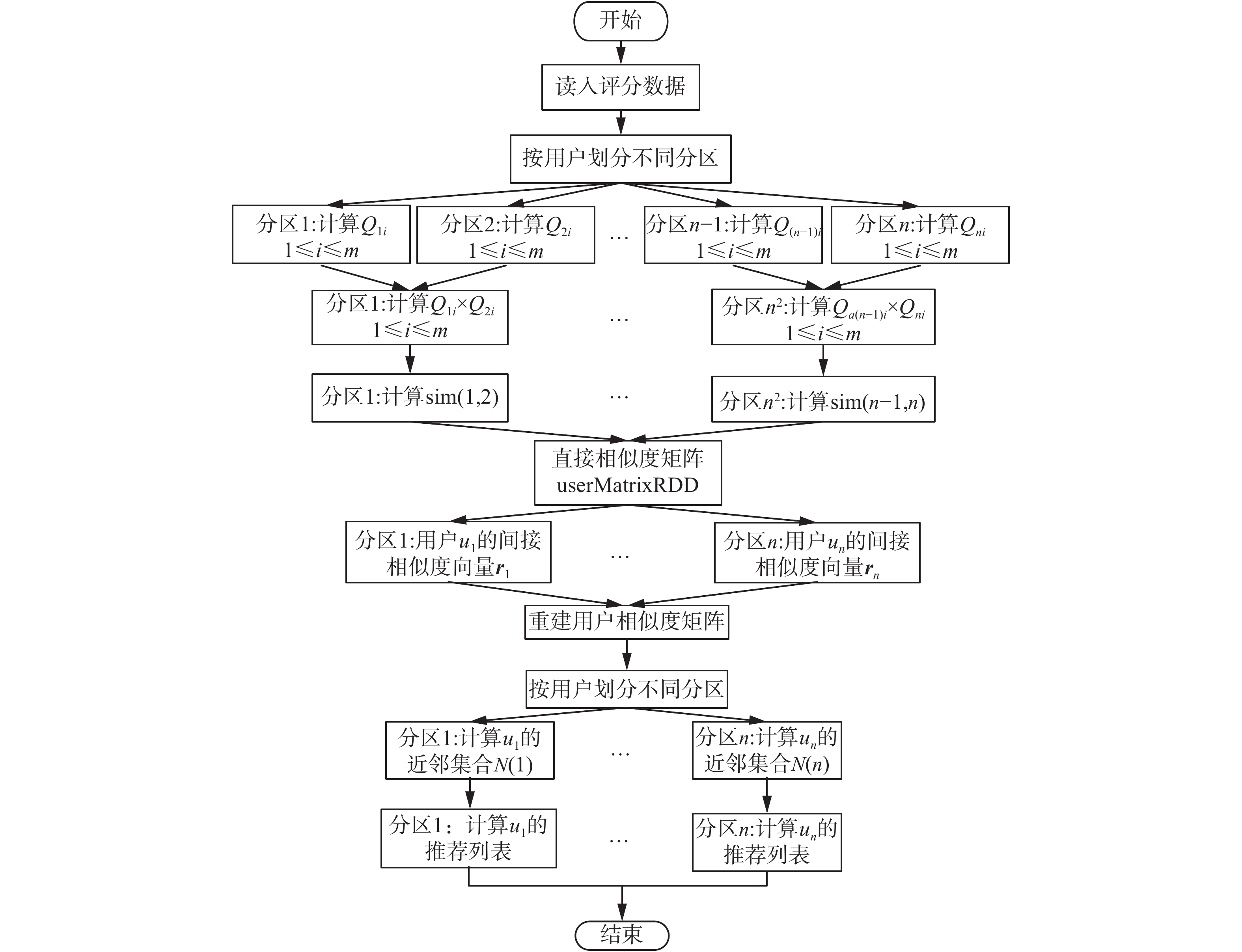
基于图游走的协同过滤推荐算法在Spark平台上的并行化包括3部分，分别是读入数据创建RDD、计算用户的相似度以及生成推荐列表，该算法的并行化主要体现在计算用户相似度和生成推荐列表。基于图游走的并行协同过滤推荐算法示意图如图3所示。

具体过程如下：

1) 读入用户行为数据，构建RDD₁；

2) 将RDD₁转换成 $({u_a},({s_i},{r_{ai}}))$ 形式的RDD₂， $(1 \leqslant a \leqslant n,1 \leqslant i \leqslant m)$ 按照用户ID进行聚集得到RDD₃ $({u_a},{\rm{Iterable}}[({s_i},{r_{ai}})])$ ，使用flatMap算子计算每个用户的中间变量 $Q$ ，并按照项目ID进行聚集得到RDD₄；

3) 根据RDD₄计算用户 ${u_a}$ 和用户 ${u_b}$ 的 ${Q_{ai}} \times {Q_{bi}}$ ，得到形如 $(({u_a},{u_b}),({Q_{ab}},1,{\rm{toNum}}))$ 的RDD₅, 其中的1和toNum是为了便于计算交占比系数而设置的；

4) 将3)的RDD₅使用ReduceByKey算子统计其共同评分项，计算结合交占比系数的相似度，得到形如 $(({u_a},{u_b}),{\rm{si{m}}}_{ab})$ 的RDD₆；

5) 利用4)的相似度RDD₆，构造用户相似度矩阵userMatrixRDD，使用Spark中的线性代数库Breeze，调用其库函数inv()计算userMatrixRDD的逆矩阵invMatrixRDD，进一步通过式(7)和(8)求得得间接相似度，重建相似度矩阵得到RDD₇；

6) 根据RDD₇按用户划分得到RDD₈，并进一步得到目标用户的近邻用户集合RDD₉，最后进行推荐。

5 实验与评价

实验使用Movielens数据集和IPTV数据集^[20]进行实验。Movielens是一个基于Web的研究型推荐系统，用于接收用户对电影的评分并提供电影的推荐列表，Movielens数据集在协同过滤研究领域得到了广泛研究，也是使用最多的数据集之一。IPTV数据集来源于天津市IPTV电视用户的收视日志数据，经过对日志数据进行预处理和隐式评分处理，形成IPTV数据集。相比于Movielens数据集，IPTV数据集应用性更高。Movielens-100k数据集包含943用户，1 682项目，共10万条评分记录；Movielens-1M数据集包含6 040个用户和3 952个项目，共计100万条评分记录。IPTV数据集选取193用户，8 200项目，共计43 175条评分记录。

使用平均绝对误差 ${\rm{MAE}}$ 和准确率 ${\rm{precision}}$ 作为衡量推荐准确度的指标。 ${\rm{MAE}}$ 反映了评分预测误差的大小，误差越小表明推荐准确度越高，计算公式(11)如下：

${\rm{MAE}} = \frac{{\sum\limits_{i = 1}^N {\left| {{r_i} - r_i^{'}} \right|} }}{N}$

(11)

式中： $N$ 表示预测评分记录数量， ${r_i}$ 表示该条记录的预测评分， ${r_i}^\prime $ 表示该条记录的实际评分。

准确率 ${\rm{precision}}$ 反映了推荐的准确度，准确率越高，表明推荐的准确度越高。准确率的计算公式为

${\rm{precision}} = \frac{{\sum\limits_{u \in U} {\left| {R\left( u \right) \cap T\left( u \right)} \right|} }}{{\left| {R\left( u \right)} \right|}}$

(12)

式中： $\left| {R(u)} \right|$ 表示推荐给用户的所有项目个数； $\left| {R(u) \cap T(u)} \right|$ 表示推荐给用户的项目中推荐正确的项目个数。

以加速比作为可扩展性的实验指标，加速比为

$S_{\!\!p} = \frac{{{T_1}}}{{{T_p}}}$

(13)

式中： ${T_1}$ 表示使用1个节点时任务执行时间； ${T_p}$ 表示使用 $p$ 个节点时任务执行时间； ${S_p}$ 表示加速比，反映了并行后运行效率的提升情况。 ${S_p} = p$ 时为线性加速比，加速比越接近线性加速比时，算法的可扩展性越好。

5.1 相似度交占比系数的有效性验证实验

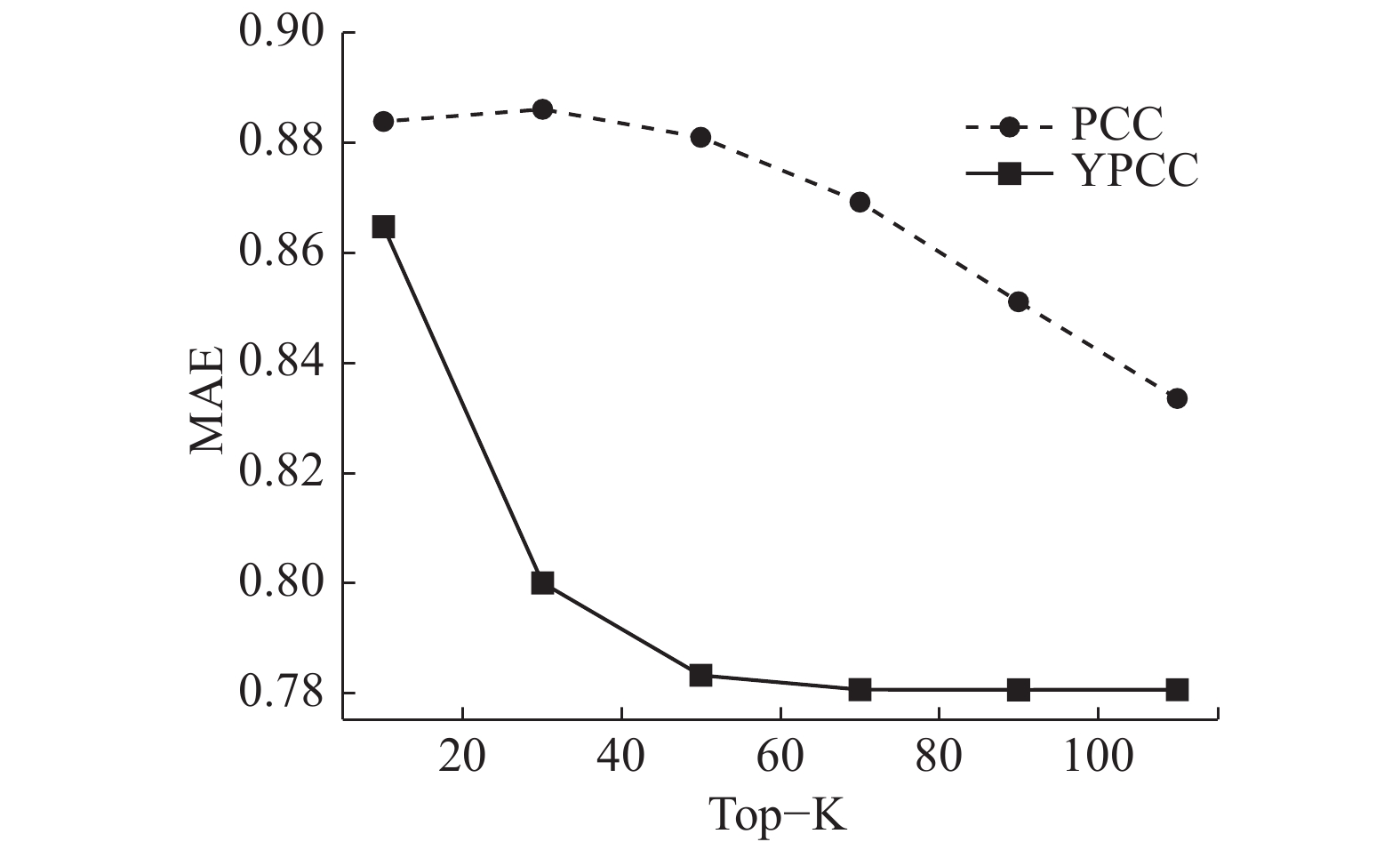
在原始的皮尔逊相关相似度的基础上，为了比较加入交占比(YPCC)和未加入交占比(PCC)对预测评分误差的影响进行本次实验。此次实验使用Movielens-100k数据集，共943用户，1 682个项目，共10万条评分记录，稀疏度为94.12%，训练集和测试集按8:2分割。实验结果如图4。

图4中，Top-K表示近邻用户选取的个数， ${\rm{MAE}}$ 表示评分预测的平均绝对误差，PCC表示未加入交占比系数计算用户相似度进行评分预测的误差曲线，YPCC表示加入交占比系数计算用户相似度进行推荐的误差曲线。

从图4中可以看出，协同过滤推荐算法的预测评分误差受到近邻用户个数Top-K的影响。随着近邻用户个数Top-K的增加，PCC和YPCC曲线均呈现下降趋势并最终趋于稳定，但是YPCC曲线明显低于PCC曲线，尤其Top-K在[40, 60]时差距最明显。实验结果表明，无论近邻用户个数如何选取，在皮尔逊相关相似度上加入交占比系数均可以有效地减小评分预测误差。

5.2 基于图游走方法的有效性验证实验 5.2.1 Movielens数据集实验

为了验证基于图游走方法在降低评分预测误差和提高推荐准确率上的有效性，本次实验使用Movielens-100k数据集，训练集和测试集按8:2分割。先通过实验确定用户直接近邻个数T的最优取值，然后比较在不同的推荐近邻个数Top-K下，本文方法和基于用户的协同过滤推荐算法(BSCF)与基于聚类的协同过滤推荐算法(k-means_CF)的 ${\rm{MAE}}$ 和 ${\rm{precision}}$ 。

图5为选取不同直接近邻个数时的评分预测误差曲线，T表示直接近邻用户选取的个数。图5表明，当T＞60时， ${\rm{MAE}}$ 趋于稳定。

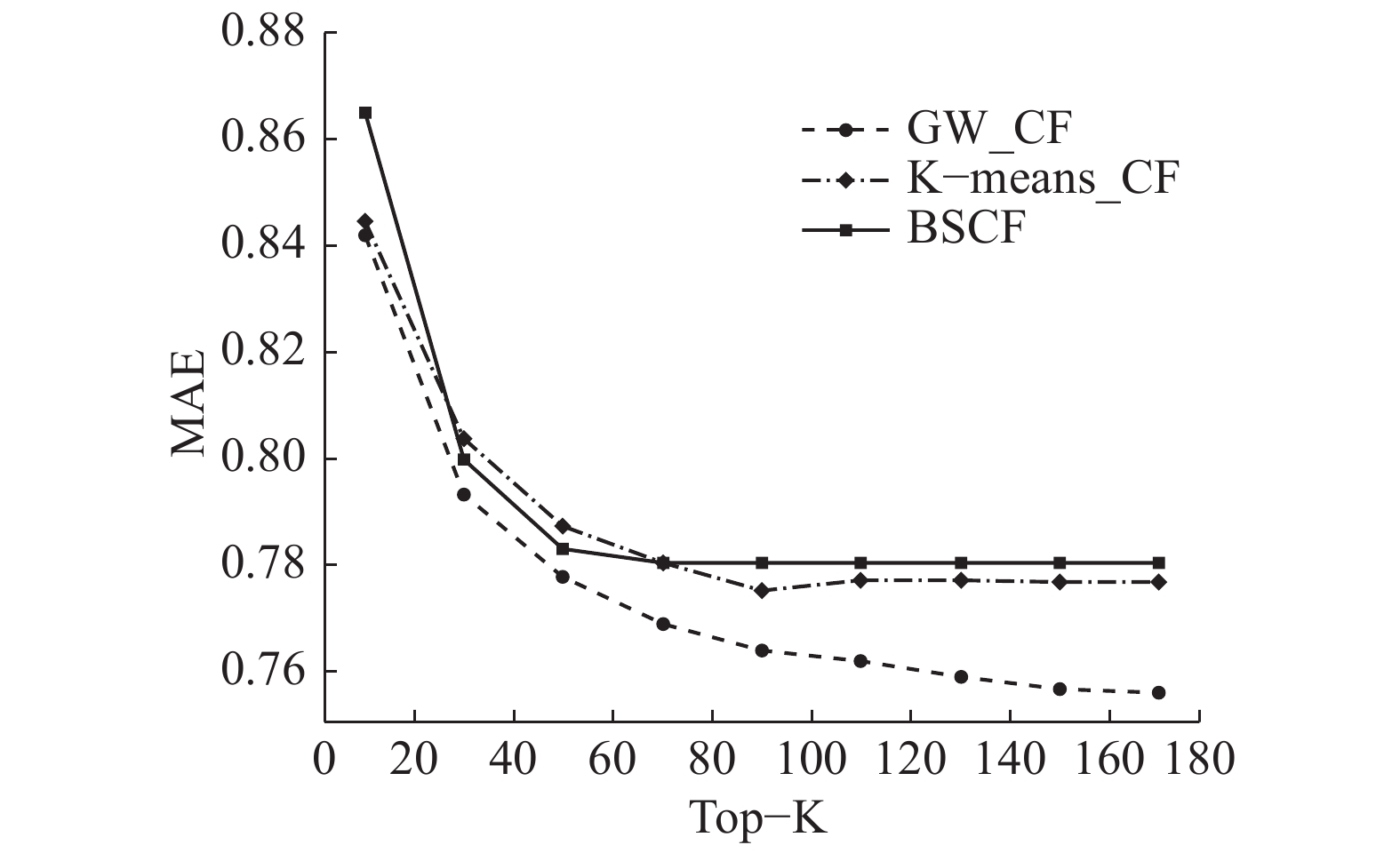
图6的实验中T=60。推荐时近邻用户个数Top-K作为单一变量，对基于图游走的协同过滤推荐算法(GW_CF)、基于用户的协同过滤推荐算法(BSCF)、基于聚类的协同过滤推荐算法(k-means_CF)进行对比实验。图6Top-K表示推荐时近邻用户选取的个数， ${\rm{MAE}}$ 表示评分预测的平均绝对误差。从图中可以看出，随着近邻用户个数Top-K的增加，3条曲线均呈下降趋势，BSCF曲线和k-means_CF曲线比较接近，GW_CF曲线明显低于另两条曲线，当Top-K大于80时更加明显。实验结果表明：GW_CF算法在降低评分预测误差方面是有效的。

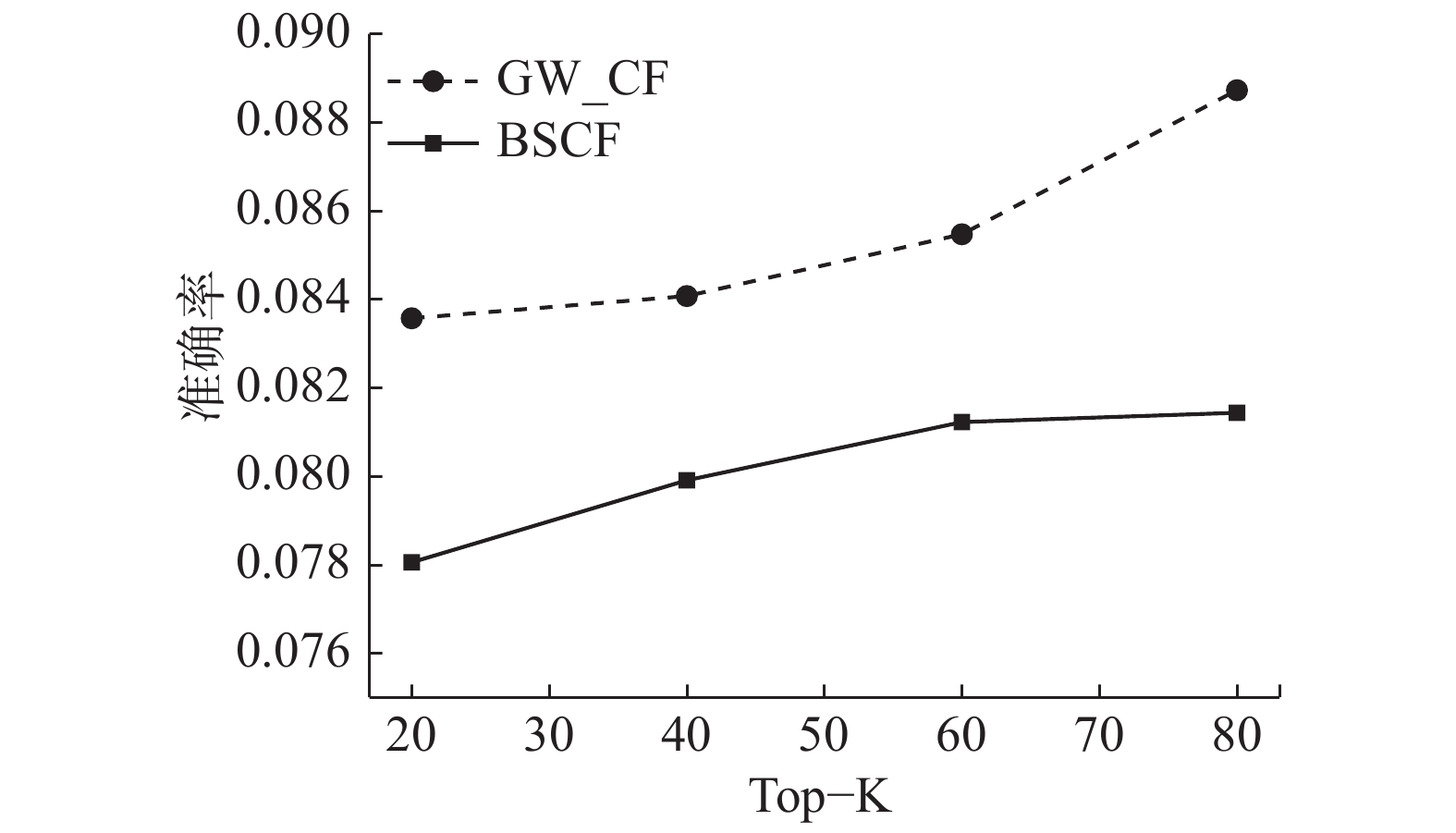
图7中虚线反映了使用GW_CF推荐的准确度，实线反映了使用BSCF推荐的准确度。生成推荐列表时推荐项目数为10，从图中可以看出，随着近邻用户个数Top-K的增加，两条曲线呈上升趋势，GW_CF准确率曲线高于BSCF曲线。实验结果表明，基于图游走的协同过滤推荐算法GW_CF可以有效地提高推荐准确率。

5.2.2 IPTV隐式评分数据集实验

为了验证基于图游走方法在降低评分预测误差和提高推荐准确率上的有效性，本次实验使用IPTV数据集，训练集和测试集按8:2分割。先通过实验确定用户直接近邻个数T的最优取值，然后比较在不同的推荐近邻个数Top-K下，基于图游走的协同过滤推荐算法(GW_CF)和基于用户的协同过滤推荐算法(BSCF)的 ${\rm{MAE}}$ 和 ${\rm{precision}}$ 。

图8为选取不同直接近邻个数时的评分预测误差曲线。图8表明，当T＞20时， ${\rm{MAE}}$ 趋于稳定。

图9的实验中T=20，推荐近邻用户Top-K作为单一变量，对基于图游走的协同过滤推荐算法(GW_CF)和基于用户的协同过滤推荐算法(BSCF)进行对比实验。从图9 中可以看出，随着近邻用户个数Top-K的增加，两条曲线均呈下降趋势，GW_CF曲线明显低于BSCF曲线。实验结果表明：GW_CF算法在降低评分预测误差方面是有效的。

图10中生成推荐列表时推荐项目数为10，随着近邻用户个数Top-K的增加，两条曲线呈上升趋势，GW_CF准确率曲线趋势更明显并且高于BSCF曲线。实验结果表明，在一般情况下，GW_CF比BSCF拥有更高的推荐准确率。

5.3 基于图游走的并行协同过滤推荐算法可扩展性实验

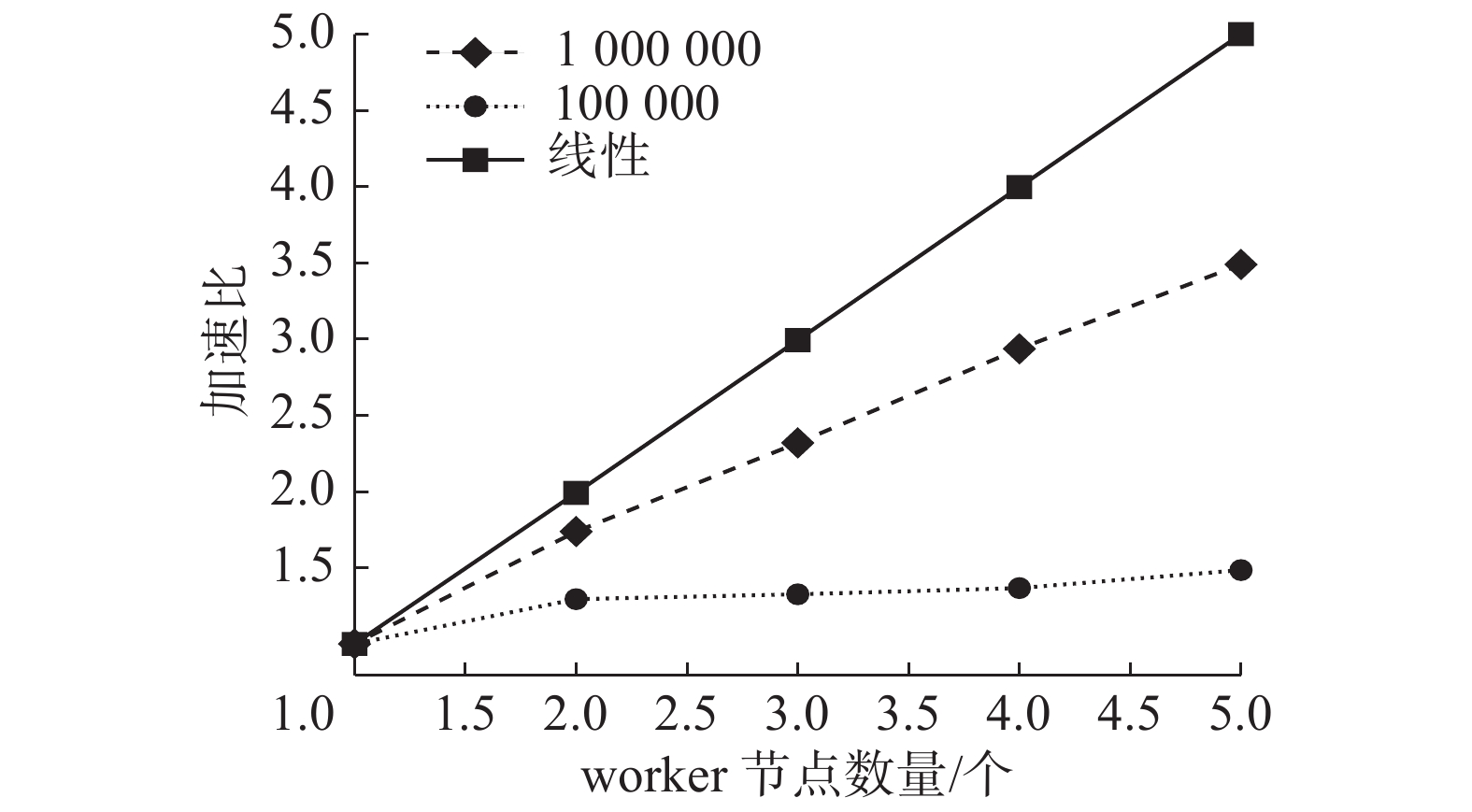
为了验证基于图游走的并行协同过滤推荐算法的可扩展性，使用Movielens-1M和Movielens-100k数据集在Spark平台进行实验。其中1M数据集包含6 040个用户和3 952个项目，共计100万条评分记录；100k数据集包含943用户，1 682项目，共10万条评分记录。实验在Spark集群上实现，集群环境包括6个节点，一个Master节点，5个worker节点，每个节点的配置相同，且处在同一个局域网内，操作系统为CentOs6.5，CPU为E5-2620 v4，核心频率2.10 GHz，节点内存32 GB。加速比结果如图11。

从图11中可以看出，随着节点个数的增加，加速比呈现上升趋势，100万数据集更逼近线性加速比。实验结果表明，并行协同过滤推荐算法在大规模数据集的情况下有较好的可扩展性。

6 结束语

本文针对协同过滤推荐算法中的数据稀疏性问题和可扩展性问题进行研究。针对稀疏性问题，在基于用户的协同过滤推荐算法的基础上，首先为传统的皮尔逊相关相似度引入交占比系数来计算用户的直接相似度，其次提出一种基于图游走方法来计算用户间接相似度，并重建相似度矩阵和进行推荐。针对可扩展性问题，在Spark平台上实现本文方法的并行化。通过在Movielens数据集和IPTV数据集上进行实验，先后验证了加入交占比系数和基于图游走的方法在提高推荐准确度上的有效性，以及本文方法的可扩展性。实验结果表明，本文的方法在提高推荐准确度上是有效的，并且在大规模数据上拥有较好的可扩展性。