目前，在机器人技术的研究中，如何使机器人具备类似于人类的智能行为已成为一大研究热点^[1]。而从人类学习中发展而来的模仿学习，作为机器人直接获取知识和技能的一种方式，在机器人的智能性的提升方面越来越发挥出巨大的作用，越来越多地受到学术界的关注和研究^[2-6]。一方面，相对于传统的机器人编程控制，模仿学习将使机器人编程更加容易，提高了机器人的作业效率；另一方面，模仿学习赋予机器人获取知识、学习知识的能力，使其更加具备智能性^[7]。

机器人模仿学习一般分为3个步骤完成：示教过程、学习过程、再现过程。当前，模仿学习的研究，主要集中在对学习过程的研究，已经出现了多种模仿学习的算法用来实现机器人的学习过程^[8-11]。其中基于轨迹匹配的机器人模仿学习算法主要有高斯混合模型(GMM)^[12]和高斯混合回归GMR(gaussian maxture regression)^[12-13]、局部加权回归LWR(locally weighted regression)^[14-15]、人工神经网络ANN(artificial neural networks)^[16-17]等，这些算法的特点是将示教运动轨迹数据建模为回归过程，以期获得控制策略指导机器人对示教运动进行再现。虽然基于轨迹匹配的回归算法具有较强的数据表征能力和抗噪能力，但是也存在泛化能力差、稳定性差等缺点^[18]。Ijspeert等^[19]提出的一种基于动态运动基元DMP(dynamic morement primitives)的机器人模仿学习方法。该方法将运动行为轨迹建模为一组微分方程，并通过线性动态系统保证了目标的全局稳定性，可以从一个简单的示教中学习较复杂的运动行为，已有广泛的使用^[19-22]。然而，DMP对时间具有依赖性，使其对时间扰动较为敏感，稳定性受到一定影响；而且泛化能力有限，其背后的物理意义也比较难于理解。

动态系统(DS)法^{[13, 23]}是近些年出现的一种对运动数据建模的机器学习方法。DS可以表征更丰富的行为，可以在状态空间的不同部分学习不同的运动。然而，由于DS存在稳定性的问题，常规的基于GMR、GPR(gaussian process regression)^[24]以及LWR的回归方法与DS结合也没有实现在目标点上的稳定收敛^[25]。其往往是找到关于系统的一个局部最优模型，此局部最优模型的约束条件无法保证系统收敛到稳定的目标点，仍然存在稳定性差和泛化能力不足的问题。

针对以上问题，本文通过GMM将示教运动建模为非线性DS，附加约束条件以确保DS的全局渐近收敛，将动态系统模型的参数学习问题转化为求解一个约束优化问题，通过优化问题的求解得到DS的参数，获得关于示教运动的非线性DS模型，并将其作为控制策略应用于机器人以实现对示教运动的模仿。通过将动态系统方法引入模仿学习，并考虑其在目标点处全局渐近收敛的约束条件，相对于基于轨迹匹配的机器人模仿学习方法，其除了具有较强的数据编码能力和抗噪能力，而且可以保证生成的轨迹收敛到目标点，避免了先前方法稳定性差的问题。同时，从未示教区域开始的再现运动轨迹也可以保证收敛到目标点，泛化能力将大大提高。以7bot机械臂为实验对象，进行仿真实验和机器人实验研究，实验结果表明：基于DS的模仿学习方法再现生成的模仿轨迹具有全局渐近收敛的特点，从不同起始位置开始的生成轨迹最终都可以到达目标点，学习得到的运动模型在稳定性和泛化能力两方面表现较好。

1 基于动态系统的示教运动建模 1.1 示教运动的表示及动态系统模型

在机器人模仿示教者示教运动的过程中，示教者通过直接或者间接的方式指导机器人手臂完成一次或多次的运动，机器人通过其内部的关节传感器或者位置传感器，或者是外部传感器，如：Kinect视觉传感，来捕获关于示教运动的相关信息。其中示教运动的轨迹信息可以表示为如下的集合形式

$\left\{ {{\zeta _{t, n}}, {{\dot \zeta }_{t, n}}} \right\}_{t = 0, n = 1}^{{T_n}, N}$

(1)

式中：状态变量 $\zeta $ 表示机器人手臂末端执行器在笛卡尔坐标系下的位置；对于不同的示教任务， $N$ 表示在某个模仿任务下的示教次数。而对于每一次的示教轨迹数据集可以表示为 ${{{X}}_{{n}}} = [{\zeta _0}, {\zeta _1}, {\zeta _2}, \cdots , {\zeta _{{T_n}}}]$ 。一阶动态系统被用来建模所记录的示教轨迹数据，动态系统的一阶自治常微分方程表示为：

$\dot \zeta = f\left( \zeta \right) + \varepsilon $

(2)

式中： $f:{{\bf{R}}^{\rm{d}}} \to {{\bf{R}}^{\rm{d}}}$ 是非线性连续可微函数； $\zeta $ 表示机器人末端的位置； $\dot \zeta $ 对应于速度； ${{\varepsilon}} $ 表示均值为0的高斯噪声项，代表了传感器测量的不准确性以及示教过程的不稳定所带来的示教数据的误差。且函数 $f$ 可以由一组参数 ${{\theta}} $ 来描述。具体地，采用相应的方法，建模式(2)为具体表达形式，进而可以求解 ${{\theta}} $ 的值。

1.2 基于统计方法的高斯混合模型建模动态系统

为了得到动态系统具体的表达形式，考虑使用基于统计方法的GMM来建立对于DS的概率描述/估计。高斯混合模型是一种有限混合模型，其通过有限的高斯函数的混合来建立对示教运动数据的粗略的表示，同时消除数据的噪声。给定一组 $N$ 次示教轨迹数据 $\left\{ {{\zeta _{t, n}}, {{\dot \zeta }_{t, n}}} \right\}_{t = 0, n = 1}^{{T_n}, N}$ ，GMM由以下概率密度函数表示

$p\left( {{\zeta _n}} \right) = \sum\limits_{k = 1}^K {{\omega _k}{\rm{GP}}\left( {{\zeta _n}|{{{\mu}} _k}, {{{\varSigma}} _k}} \right)} $

(3)

$\begin{gathered} {\rm{GP}}\left( {{\zeta _n}|{{{\mu}} _k}, {{{\varSigma}} _k}} \right) = \\ \displaystyle\frac{1}{{\sqrt {{{\left( {2\pi } \right)}^{2d}}\left| {{{{\varSigma}} _k}} \right|} }}\exp\left\{ { - \displaystyle\frac{1}{2}{{\left( {{\zeta _n} - {{{\mu}} _k}} \right)}^{\rm{T}}}\Sigma _k^{ - 1}\left( {{\zeta _n} - {{{\mu}} _k}} \right)} \right\} \\ \end{gathered} $

(4)

式(3)、(4)中： ${\rm{GP}}( \cdot )$ 为高斯过程概率密度函数，或可简化表示为 $N( \cdot )$ ； $K$ 为GMM中高斯分布的个数/混合模型的个数； ${\omega _k}$ 为第 $k$ 个高斯分布的权重，且 $\displaystyle\sum\limits_{k = 1}^K {{\omega _k} = 1} $ ； ${{{\mu}} _k}$ 为该密度函数的均值向量； ${{{\varSigma}} _k}$ 为协方差矩阵；相应的GMM的待确定参数可以表示为 ${\theta _k} = \left\{ {{\omega _k}, {{{\mu}}_k}, {{{\varSigma}} _k}} \right\}, k = 1, 2, \cdots , K$ ；且全部参数表示为 ${{\theta}} = \left\{ {{\theta _1}, {\theta _2}, \cdots , {\theta _K}} \right\}$ 。

给定 $\zeta $ 、 $\dot \zeta $ 的条件概率分布为

$p\left( {\dot \zeta |\zeta , k} \right) = N\left( {\dot \zeta |{{\tilde {\dot \zeta }}_k}, {{\tilde {{\varSigma}} }_{\dot \zeta \dot \zeta k}}} \right)$

(5)

其中：

${\tilde {\dot \zeta} _k} = {{{\mu}} _{\dot \zeta k}} + {{ {\varSigma}} _{\dot \zeta \zeta k}}{{{\varSigma}}^{ - 1} _{\zeta \zeta k}}\left( {\zeta - {{{\mu}} _{\zeta k}}} \right)$

(6)

${\tilde { {\varSigma}} _{\dot \zeta \dot \zeta k}} = {{ {\varSigma}} _{\dot \zeta \dot \zeta k}} - {{ {\Sigma}} _{\dot \zeta \zeta k}}{{ {\varSigma}}^{ - 1} _{\zeta \zeta k}}{{{\varSigma}} _{\zeta \dot \zeta k}}$

(7)

由此， $\dot \zeta $ 对应于 $\zeta $ 的条件概率可以定义为

$p\left( {\dot \zeta |\zeta } \right) = \sum\limits_{k = 1}^K {{\beta _k}} N\left( {\dot \zeta |{{\tilde {\dot \zeta} }_k}, {{\tilde {{\varSigma}} }_{\dot \zeta \dot \zeta k}}} \right)$

(8)

${\beta _k} = \displaystyle\frac{{{\omega _k}p\left( {\zeta |k} \right)}}{{\displaystyle\sum\limits_{k = 1}^K {{\omega _k}p\left( {\zeta |k} \right)} }} = \displaystyle\frac{{{\omega _k}N\left( {\zeta |{{{\mu}} _{\zeta k}}, {{{\varSigma}} _{\zeta {\zeta _k}}}} \right)}}{{\displaystyle\sum\limits_{i = 1}^K {{\omega _i}N\left( {\zeta |{{{\mu}} _{\zeta i}}, {{{\varSigma}} _{\zeta \zeta i}}} \right)} }}$

(9)

由条件期望可求得整个高斯混合模型中 $\dot \zeta $ 的总的期望为

$\dot \zeta = \tilde f\left( \zeta \right) = \sum\limits_{k = 1}^K {{{{H}}_k}} \left( \zeta \right)\left( {{{{A}}_k}\zeta + {{{B}}_k}} \right)$

(10)

其中：

$\left\{ {\begin{array}{*{20}{l}} {{{{A}}_k} = {{{\varSigma}} _{\dot \zeta \zeta k}}{{{\varSigma}}^{ - 1} _{\zeta \zeta k}}} \\ {{{{H}}_k}\left( \zeta \right) = \displaystyle\frac{{{\omega _k}p\left( {\zeta |k} \right)}}{{\displaystyle\sum\limits_{i = 1}^K {{\omega _i}p\left( {\zeta |i} \right)} }}} \\ {{{{B}}_k} = {{{\mu}} _{\dot \zeta k}} - {{{A}}_k}{{{\mu}} _{\zeta k}}} \end{array}{\rm{ }}\forall k = 1, 2, \cdots , K} \right.$

(11)

式(10)、(11)得到的动态系统表示为一组线性动态系统的非线性加权的形式，也即得到了关于示教运动的动态系统模型的具体表达形式。

2 动态系统全局稳定的充分条件

由以上得到的动态系统模型，为了保证动态系统模型在示教的目标点具有全局收敛的特性以及提高其泛化能力，也即将在不同的初始点开始最终到达同一目标点的模仿学习任务转化为具有全局收敛的学习任务，则需要考虑其稳定性问题。对于由 $\dot \zeta = f\left( \zeta \right)$ 定义的动态系统，根据Lyapunov稳定性理论：其在点 ${\zeta ^ * }$ 处全局渐近稳定的充分条件是存在一个连续可微的Lyapunov函数 $V\left( \zeta \right):{{\bf{R}}^d} \to {\bf{R}}$ 满足：

$\left\{ \begin{aligned} & V\left( \zeta \right) > 0, \forall \zeta \in {{\bf{R}}^d}, \zeta \ne {\zeta ^ * } \\ & \dot V\left( \zeta \right) < 0, \forall \zeta \in {{\bf{R}}^d}, \zeta \ne {\zeta ^ * } \\ & V\left( {{\zeta ^ * }} \right) = 0, {\rm{ }}\dot V\left( {{\zeta ^ * }} \right) = 0{\rm{ }} \end{aligned} \right.$

(12)

为了得到式(10)中DS的稳定条件，可以构造如下的Lyapunov函数：

$V\left( \zeta \right) = \frac{1}{2}{\left( {\zeta - {\zeta ^ * }} \right)^{\rm{T}}}\left( {\zeta - {\zeta ^ * }} \right), \forall \zeta \in {{\bf{R}}^d}$

(13)

由式(12)、(13)可以求得保证DS全局稳定的充分条件

$\left\{ \begin{gathered} \left( {{{{A}}_k}{\zeta ^ * } + {{{B}}_k}} \right) = 0 \\ {{{A}}_k} + {\left( {{{{A}}_k}} \right)^{\rm{T}}} < 0 \\ \end{gathered} \right.{\rm{ }}\forall k = 1, 2, \cdots , K$

(14)

将式(14)作为DS的约束条件，则DS满足全局收敛的特性。同时，考虑高斯混合模型的性质和式(14)的条件，其共同组成了具有全局渐进稳定的动态系统的完整的约束条件。此后，需要求解动态系统模型的相应参数，得到对于动态系统完整的描述。

3 动态系统参数学习

为了学习得到具有全局渐近稳定的DS，需要对其参数进行求解。由以上可知DS的未知参数为 ${{\theta}} =\left\{ {{\omega _1},{\omega _2}, \cdots , {\omega _k};{{{\mu}} _1},{{{\mu}} _2}, \cdots , {{{\mu}} _k};{{{\varSigma}} _1},{{{\varSigma}} _2}, \cdots , {{{\varSigma}} _k}} \right\}$ 。本文通过将动态系统参数学习的过程转化为求解一个非线性优化问题，在保证模型全局渐近稳定的约束条件下求解优化问题来计算 ${{\theta}} $ 的最优值。使用对数似然函数作为优化的目标函数

${\rm{arg}}\mathop {{\rm{min}}}\limits_{{\theta}} J\left( {{\theta}} \right) = - \frac{1}{{\cal{T}}}\sum\limits_{n = 1}^N {\sum\limits_{t = 0}^{{T_n}} {\log } } p\left( {{\zeta _{t, n}}|{{\theta}} } \right)$

(15)

对应的约束条件为

$\left\{ \begin{aligned} & {\rm{ }}\left( {{{{A}}_k}{\zeta ^ * } + {{{B}}_k}} \right) = 0 \\ & {\rm{ }}{{{A}}_k} + {\left( {{{{A}}_k}} \right)^{\rm{T}}} < 0 \;\;\\ & {\rm{ }}{{{\varSigma}} _k} > 0 \qquad\quad\;\;\\ & {\rm{ }}0 < {\omega _k} \leqslant 1 \quad\;\\ & {\rm{ }}\sum\limits_{k = 1}^K {{\omega _k} = 1} \end{aligned} \right.{\rm{ }}\forall k = 1, 2, \cdots , K \;\;\;$

(16)

式中 ${\cal{T}} = \displaystyle\sum\limits_{n = 1}^N {{T_n}} $ 是训练数据点总的数量，也即示教数据的数量。

对于以上优化问题，可以将其化为非线性规划问题，借助于标准的优化约束技术可以很好地解决，最终得到具有全局渐近稳定的动态系统的最优参数 ${{\theta}} $ ，实现对于动态系统的完整描述。

4 机器人模仿学习系统的设计

在以上内容的基础上，设计了基于DS的机器人模仿学习系统。所设计的机器人模仿学习系统工作流程如图1所示。在机器人模仿学习系统中，本文主要集中在对示教过程和学习过程的研究。

对应于模仿学习的3个基本的步骤，模仿学习系统工作流程，首先，对于某个固定的模仿任务(如：绘画或书写、拿放物品、篮球投篮等任务)，通过手把手地抓取机器人手臂末端执行器进行多次目标点相对固定的轨迹示教，获得示教轨迹数据；然后，将获得的示教轨迹数据预处理后送入学习算法学习关于动态系统模型的参数，得到动态系统模型。最后，将动态系统模型作为机器人的控制策略，设置机器人手臂初始的运动位置，结合机器人的控制系统完成对示教任务的模仿。

5 机器人模仿学习实验研究

为了验证基于动态系统的机器人模仿学习方法的有效性，在已设计的模仿学习系统的框架下进行仿真实验和机器人实验研究。

5.1 机器人平台和示教数据的获取

实验中的机器人平台是7bot机械臂，如图2所示。7bot机械臂是一款桌面应用级的机械臂，也是一款6轴的全金属智能机械臂。借助于Processing和Arduino Due实现开发和控制，使用USB线与计算机之间完成数据通信，能够实现在三维空间的多种运动，使用方便灵活。

实际中，对于示教数据的获取，是在机械臂的运动空间内通过抓取7bot机械臂末端进行 $N$ 次运动轨迹示教。由机器臂自身携带的关节角度传感器记录运动轨迹信息。另外，也可以通过在仿真环境中拖动虚拟机械臂，进行示教并获取示教数据。

具体地，实际中的示教数据是由上位机程序处理示教轨迹信息，得到关于机械臂末端执行器在笛卡尔坐标系中的位置 ${{x}}\left( {{{x}} \in {{\bf{R}}^d}, d = 2{\rm{/}}d = 3} \right)$ ，即为示教数据。对应于算法中的表述，经过计算，对于示教数据有 $\zeta = {{x}}$ 、 $\dot \zeta = \dot {{x}}$ 。

而对于具体的运动轨迹的示教，模仿学习示教过程如图3所示。示教者通过抓取机械臂末端进行运动示教，此运动可以是一个拿放物品的运动。图中的几个关键子过程可以说明整个示教过程是如何完成的，黑色的圆点代表示教运动的起始点，黑色的星形点代表示教运动的终点或目标点，实线代表已完成的示教运动过程，虚线代表未完成的示教运动过程。

5.2 实验步骤

本文在MATLAB环境中进行相关仿真实验，为了简化实验操作的复杂性，主要在MATLAB环境中进行二维平面的模仿学习仿真实验，具体步骤如下：

1)将实际采集的或在仿真环境中生成的多次示教运动轨迹信息在MATLAB中进行预处理并可视化，完成模仿学习的示教过程。

2)设置算法的相关初始值，将示教运动数据由GMM模型编码为一动态系统模型。

3)通过求解带有全局渐近稳定性约束条件的动态系统相关参数集合 ${{{\theta}} _k}=\left\{ {{\omega _k}, {{{\mu}} _k}, {{{\varSigma}} _k}} \right\}$ ，学习得到动态系统模型，完成模仿学习的学习过程。

4)由学习得到的动态系统模型生成新的模仿运动轨迹，并分析生成的运动轨迹的相关结果。

5)最后将学习得到的动态系统模型作为控制策略，结合机器人控制系统，完成对模仿学习过程中示教运动的模仿。

5.3 仿真实验

本部分主要针对简单示教运动和较复杂示教运动进行实验仿真。通过将示教运动轨迹与提出的方法生成的轨迹相比较来验证方法的有效性；并结合仿真环境中的两连杆机械臂系统，展示最终的学习效果。其中，规定简单示教运动是具有一定弯曲度的类直线运动。而较复杂示教运动相比于简单示教运动其示教运动体现出更多的示教变化，如二次及以上的曲线形状的运动、自相交运动或者它们的组合等。

模仿学习性能的量化指标可采用机械臂末端位置与目标点的距离 $d$ 、示教与再现运动的路径积分长度之差 ${\rm{diff}} = \left| {\int_\zeta {{\rm d}s} - \int_{\tilde \zeta } {{\rm d}s} } \right|$ 以及机器人完成模仿任务的时间与示教时间的差 $\left| {\Delta t} \right|$ ，以此来衡量。

5.3.1 简单示教运动实验

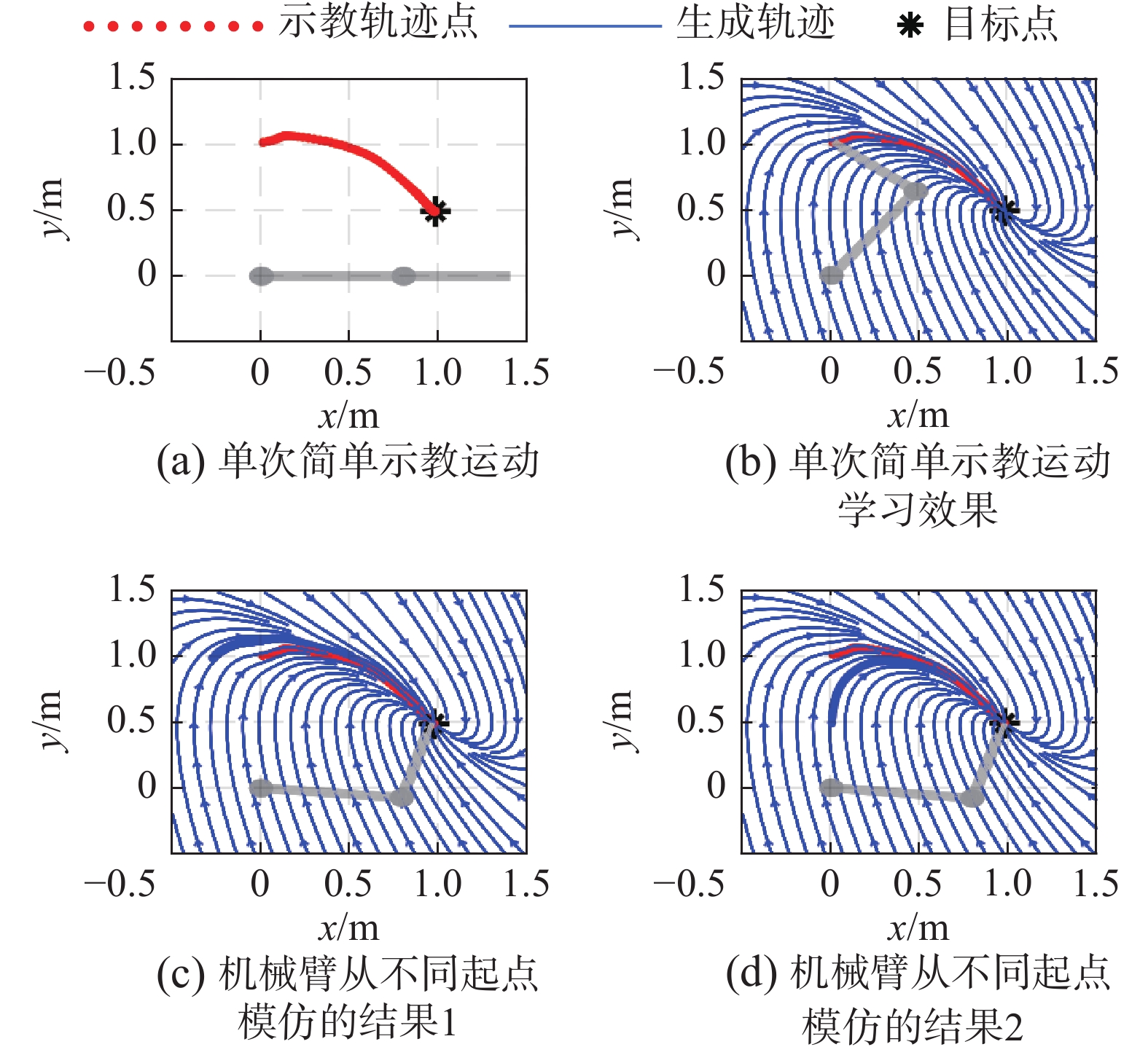
图4给出了单次简单示教的仿真结果。示教运动代表的任务类型可以是绘画任务中的一笔或者是拿和放物品的运动等。图4中，(a)为在MATLAB环境中简单示教运动轨迹，起点是 ${[0\;\;1]^{\rm{T}}}$ ，目标点 ${[1\;\;0.5]^{\rm{T}}}$ ；(b)为使用文中的学习方法，模型生成的使机器人到达目标点的平滑轨迹流图，可见所有生成轨迹均收敛到目标点；(c)、(d)中蓝色虚线为在MATLAB中模拟的一个两连杆机械臂系统，将学习得到的运动模型作为控制策略，从不同起点执行模仿的结果，起点分别为 ${[ - 0.25\;\;1]^{\rm{T}}}$ 、 ${[0\;\;0.5]^{\rm{T}}}$ 。最终，机械臂末端与目标点的距离分别为 $d = {\rm{0}}{\rm{.011\;3\;m}}$ 、 $d = {\rm{0}}{\rm{.009\;1\;m}}$ 。

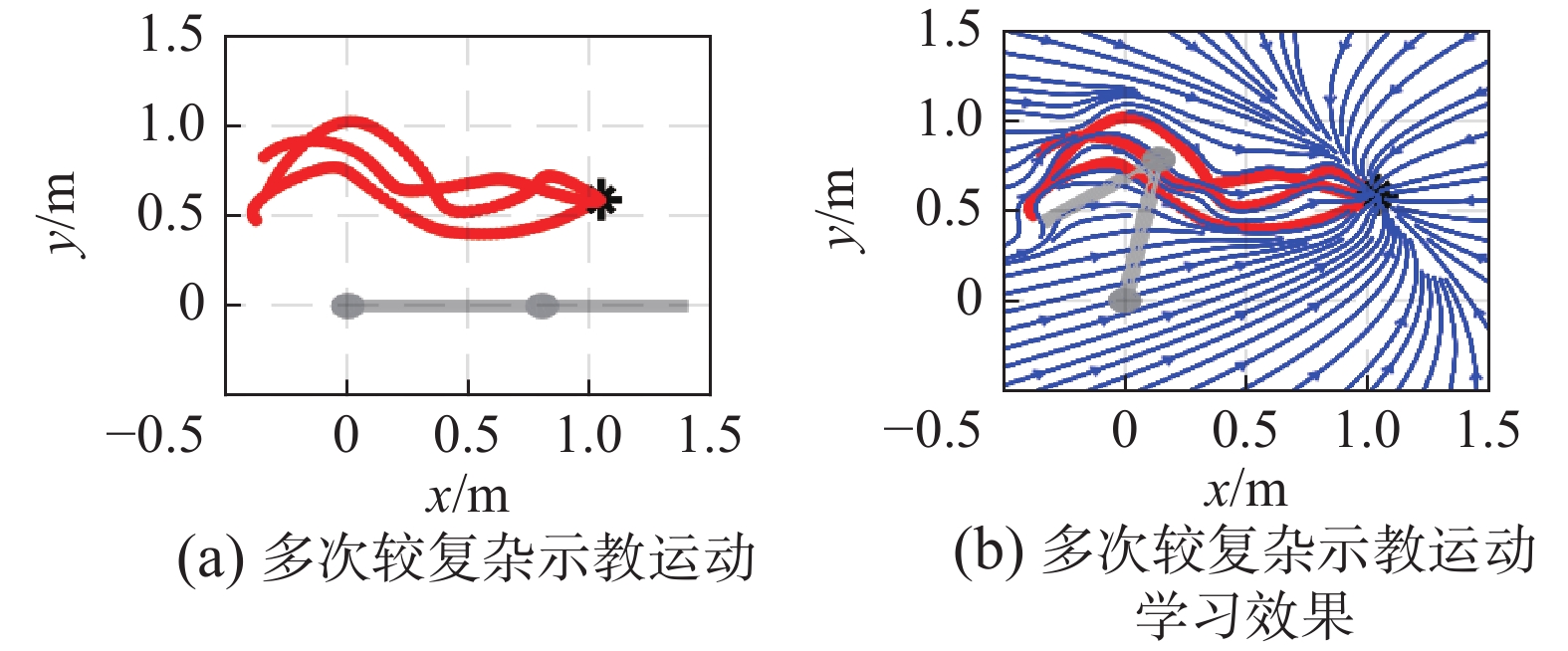
在实际示教过程中，机器人可能需要多次示教。图5分别为多次示教运动轨迹和经算法学习后生成的平滑的轨迹流图，可见生成的轨迹均收敛到示教运动的目标点。

由以上可知，学习得到的运动模型一方面具有很强的稳定性，轨迹均收敛到同一个目标点。另一方面，由未示教区域开始的再现运动也可以在具有一定模仿相似性的前提下到达目标点附近，误差较小，体现出模型具有较好的泛化能力。

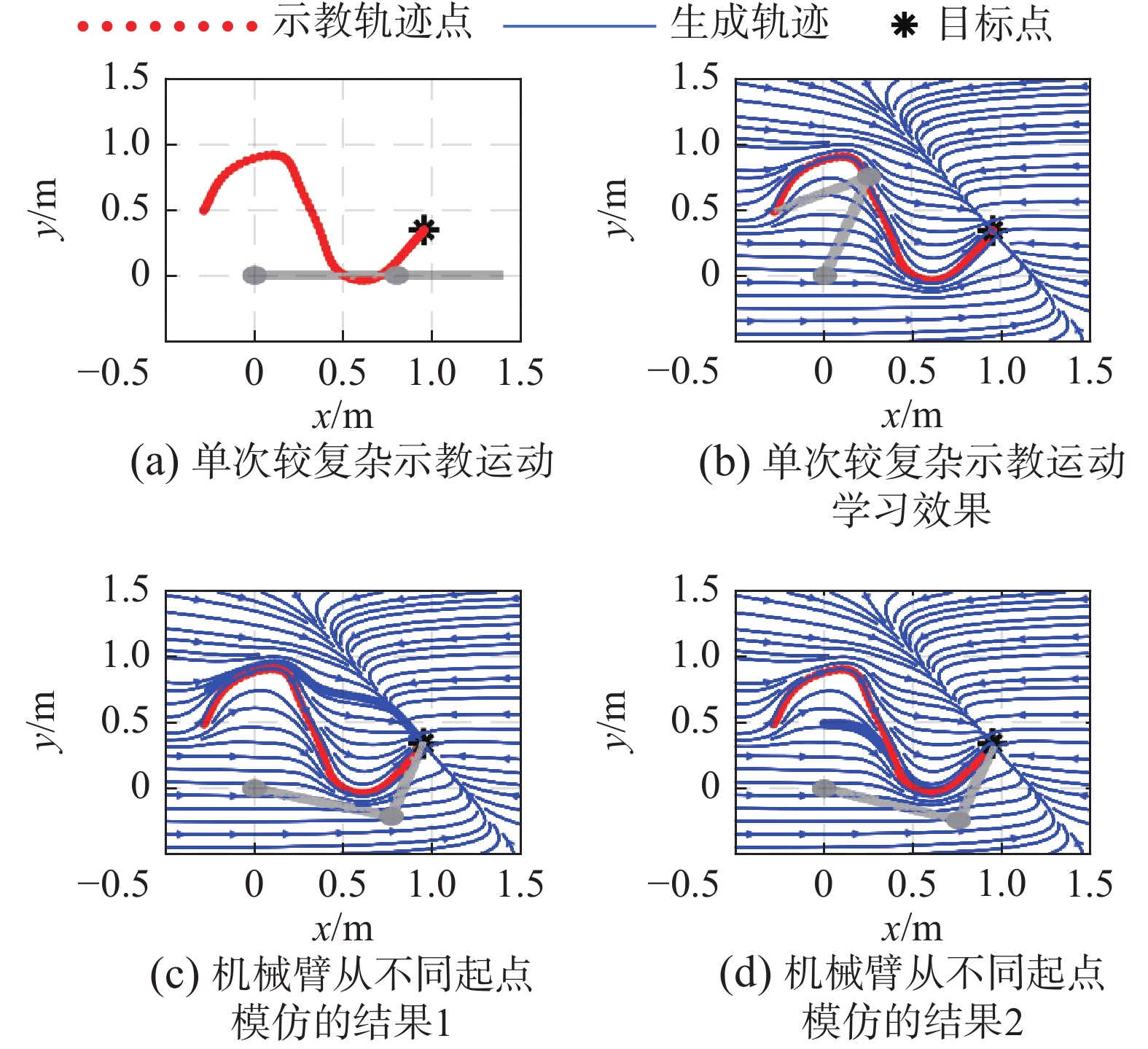
5.3.2 较复杂示教运动实验

对于较复杂的示教运动，相应的仿真结果如图6、7所示。其中图6是对机器人进行单次示教后的实验结果。单次示教的起点为 ${[ - 0.25\;\;0.5]^{\rm{T}}}$ ，目标点为 ${[0.9\;\; 0.4]^{\rm{T}}}$ 。通过算法学习后，模型生成的轨迹均收敛到目标点 ${[0.9\;\;0.4]^{\rm{T}}}$ 。类似地，分别从不同的起点 ${[ - 0.25\;\; 0.75]^{\rm{T}}}$ 和 ${[0\;\;0.5]^{\rm{T}}}$ 开始再现模仿，实验结果如图6(c)、(d)所示。机械臂末端与目标点的距离分别为 $d = {\rm{0}}{\rm{.016\;2\;m}}$ 、 $d = {\rm{0}}{\rm{.014\;6\;m}}$ ，误差较小。

同样地，在实际的机器人示教过程中，需要多次示教时，实验结果如图7所示。其中，经过算法学习后，学习得到的运动模型生成的轨迹收敛到同一个目标点。

由此可知，学习得到的运动模型对于此类较复杂的示教运动也有不错的学习效果，模型的稳定性较好，未示教空间的泛化能力也较好。

5.4 机器人实验

此部分结合实际的7bot机器人系统来验证学习方法的有效性。

图8、9分别展示了二维平面中单次示教时，机器人真实示教运动轨迹和经算法学习后的学习效果。红色虚线为示教轨迹，蓝色实线为生成轨迹。由图可知，所有生成轨迹最终都收敛到目标点，体现了运动模型具有全局渐进稳定性的特点；但对于有交叉点的自相交运动，其在交叉点的学习效果并不明显，忽略了部分的学习，学习效果有待提高。

图10、11展示了通过7bot机械臂系统对示教运动进行模仿的结果。将学习得到的运动模型作为控制策略，设定机器人的初始位置，由机器人系统进行模仿实现。实验结果显示其成功实现了对运动的模仿，到达目标点附近。

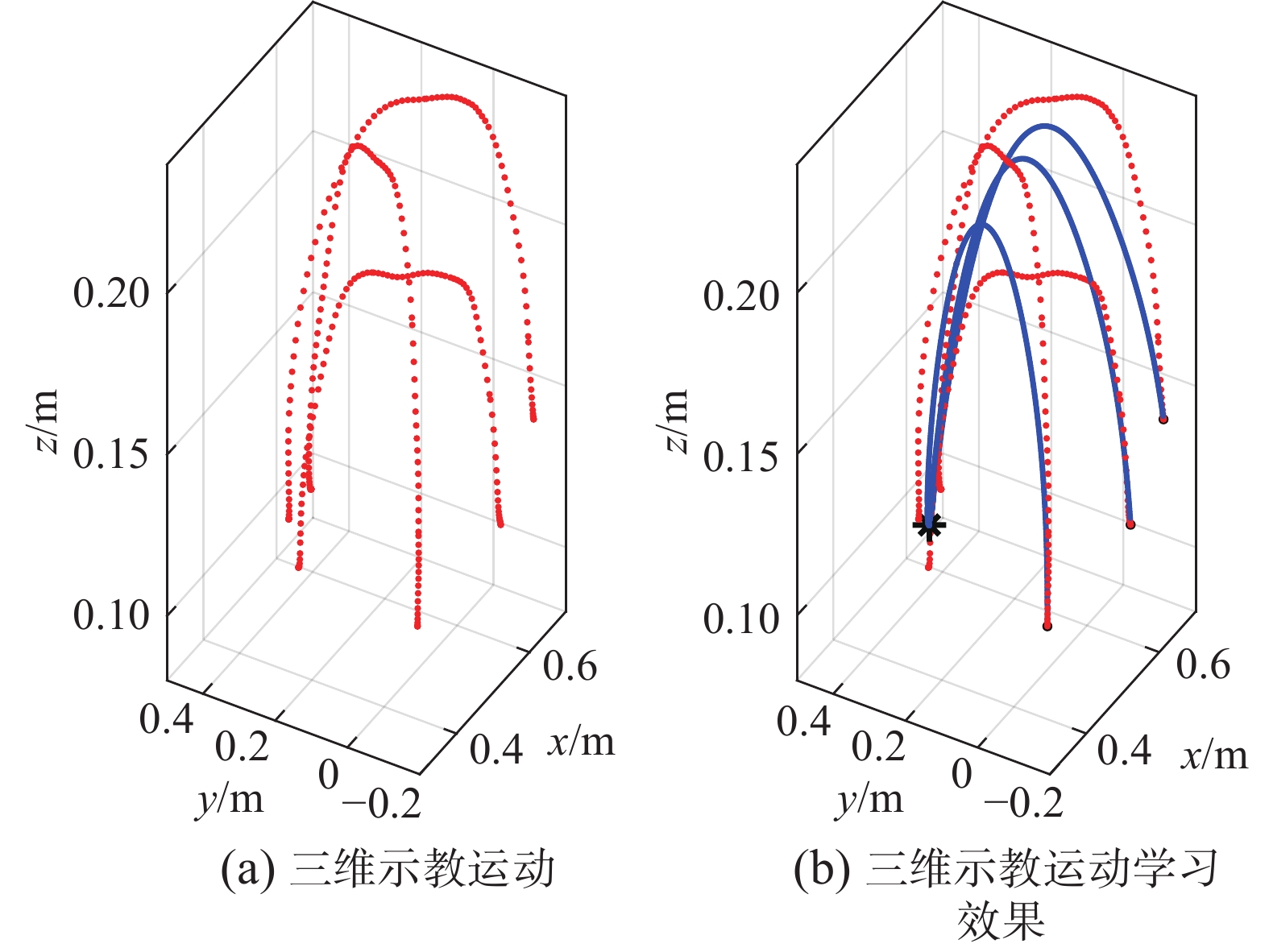
同样，图12中分别为在三维空间中的示教及学习效果。可以看出从起始点开始的三条生成轨迹均收敛到目标点，表明运动模型的稳定性很好。图13是7bot机械臂对示教运动进行模仿的结果，可见其也很好地完成了对示教运动的模仿，到达目标点附近。

表1给出了机器人实验中机器人模仿性能的量化结果。可以看出运动模仿结束后，机械臂末端距离目标点较近，误差较小；示教时间和模仿时间相差不大；但是在自相交运动上轨迹长度之差比较大。

综上实验结果，基于DS的模仿学习方法在简单示教运动、较复杂示教运动以及真实示教运动的学习上，通过附加稳定性约束条件的方法，再现的生成轨迹均收敛到目标点，一方面使运动模型的稳定性更强；另一方面，使运动模型具有较好的泛化能力。

6 结束语

本文针对当前机器人模仿学习过程中，运动模仿稳定性差，泛化能力不足，引入了一种基于动态系统的模仿学习方法来解决以上问题。首先，通过使用高斯混合模型将示教运动建模为一动态系统；然后，考虑稳定性问题，基于Lyapunov稳定性理论，给出动态系统全局渐近稳定的充分条件；最后，建立一个包含多约束的非线性优化问题，迭代求解以得到最优参数，进而得到动态系统模型，并作为机器人的控制策略实现对示教运动的模仿。从实验中可以得到以下结论：

1)文中提出的模仿学习方法在简单示教运动和较复杂的示教运动的仿真实验中，学习得到的运动模型从示教起始点生成的轨迹均能够到目标点，轨迹平滑，稳定性好。

2)将示教运动建模为动态系统，通过附加稳定性约束条件，保证了学习得到的运动模型生成的轨迹都收敛到目标点。

3)文中的方法可以实现从单一到多次示教运动的学习，对于未被示教的状态空间其模型也可以生成平滑的轨迹收敛到目标点，具有较强的泛化能力。

4)存在的问题是对于复杂的自相交的示教运动，模型忽略了运动的关键信息，运动再现相似度将会稍差。同时，在其他机器人系统上的应用还有待进一步验证。对于非精密要求场合、目的为导向的机器人工作场合，此方法的通用性和稳定性具有较大优势。

在未来，可以结合具有高精度控制的机器人来实现实时调整再现轨迹提高模仿的相似性；同时，可以通过提高系统的阶次来学习复杂的自相交运动；另外，结合快速控制技术可以将其扩展到快速捕获运动目标的领域。