置换流水车间调度问题(permutation flow shop scheduling problem,PFSP)是智能制造的核心问题之一,具有很重要的工程应用价值。研究表明,该问题属于NP难题[1](non-deterministic polynomial-time hard,NP)。常见的PFSP求解方法可分为:精确算法、启发式算法[2]等。启发式算法能够快速求得问题的可行解,但这些算法结构比较复杂,求解最优解比较困难。
在有限的资源条件下,对PFSP的优化可有效增加企业收益,相关人士一直致力于研究和开发高效的优化技术,希望能够快速找到PFSP的最优解。受猫日常行为启发,Chu[3]在2006年提出了猫群算法(cat swarm optimization,CSO)。猫群算法将猫的行为分为搜寻模式和跟踪模式,这两种模式通过结合律MR(mixture ratio)进行交互转换。搜寻模式下,通过对个体进行扰动从而使得每个个体向局部最优个体靠近;跟踪模式下,猫通过一定速度来跟踪目标,从而使得个体向全局最优靠近。近年来,猫群算法被应用于很多领域,并取得较好效果。在识别领域,Ganapati[4]将该算法运用到无线脉冲响应(IIR)系统识别;Pradhan[5]将猫群算法应用于图像识别;Guo等[6]基于以上研究基础,运用猫群算法对光伏系统进行优化。在数学研究领域,Pappula等[7]将猫群算法用于函数优化问题,但收敛速度较慢;为提高猫群算法的全局搜索速度,Tsai等[8]提出了猫群算法并行结构,同时验证了在种群规模较小及总迭代次数较少的情况下,该并行结构能有效提高收敛速度。在多目标生产调度方面,Pradhan[5]运用猫群算法求解多目标优化问题;刘琼等[9]将该算法运用到混流装配线排序问题。
尽管猫群算法在以上领域取得了一些研究成果,但在单目标置换流水车间调度领域的研究较少。Bouzidi等[10]针对置换流水车间调度问题利用标准的猫群算法来求解;此外,Bouzidi等[11]还将猫群算法与遗传算法中的相关解码操作结合起来对置换流水车间进行求解;马邦雄等[12]运用猫群算法对置换流水车间调度问题进行求解并与其他算法进行比较。针对置换流水车间调度问题,尽管上述研究都取得较好效果,但求解过程中该算法收敛速度较慢,同时,当问题规模变大时容易出现“维数灾难”。为加快寻优速度,同时避免“维数灾难”,本研究提出一种基于分布估计算法的改进猫群算法(EDA-CSO)用于解决PFSP。
目前,分布估计算法(estimation of distribution algorithms,EDA)已应用于智能学习、函数优化、图像识别、多目标规划[13]等多个领域。EDA算法利用概率矩阵模型描述解序列在空间的分布,利用统计学知识分析概率模型,同时,利用概率矩阵产生子群体。为得到更好的解,TZENG等[14]将蚁群算法与EDA算法相结合,用于求解PFSP;Chang等[15]将EDA算法与遗传算法相结合来解决旅行商问题(traveling salesman problem,TSP);同时,Chang等[16]将区块模型与分布估计算法(block-based estimation distribution algorithm,BBEDA)相结合来求解PFSP问题;鉴于EDA良好的收敛速度,本研究将CSO算法与EDA相结合,得到高适应度的人工解,同时利用3种变异算子对解序列重组以提高解序列的质量和多样性,并通过仿真实例验证EDA-CSO算法的有效性及良好的鲁棒性。
1 置换流水车间调度问题数学模型PFSP是许多生产调度问题的简化模型,该问题主要研究了n个工件
若PFSP以最大完工时间为目标,则该问题可以用n、m、prmu、
上述问题的数学描述如下:令t(
| $C({{\pi} _1},1) = {{t}}\left({{{\pi} _1},1} \right)$ |
| $ C({{\pi} _i},1) = C({\pi} {}_{i - 1},1) + t({{\pi} _i},1)\;\;\;i = 2,3,\cdots,n $ |
| $ C\left({{{\pi} _1},j} \right) = C\left({{{\pi}_1},j{\rm{ - }}1} \right) + \left({{{\pi} _1},j} \right)\;\;\;j = 2,3,\cdots,n $ |
| $ \begin{align} C\left({{\pi}_i},{j} \right)=&\max \left\{ C\left({{\pi}_{{i}-1}},{j} \right),C\left({{\pi}_{{i}}},{j}-1 \right) \right\}+{t}\left({{\pi}_{{i}}},{j} \right) \\ & i=2,3,\cdots ,n;j=2,3,\cdots ,m \end{align} $ |
| ${C_{{\rm{max}}}} = C\left({{{\pi} _n},m} \right)$ |
该问题的目标是得到最优的工件加工顺序
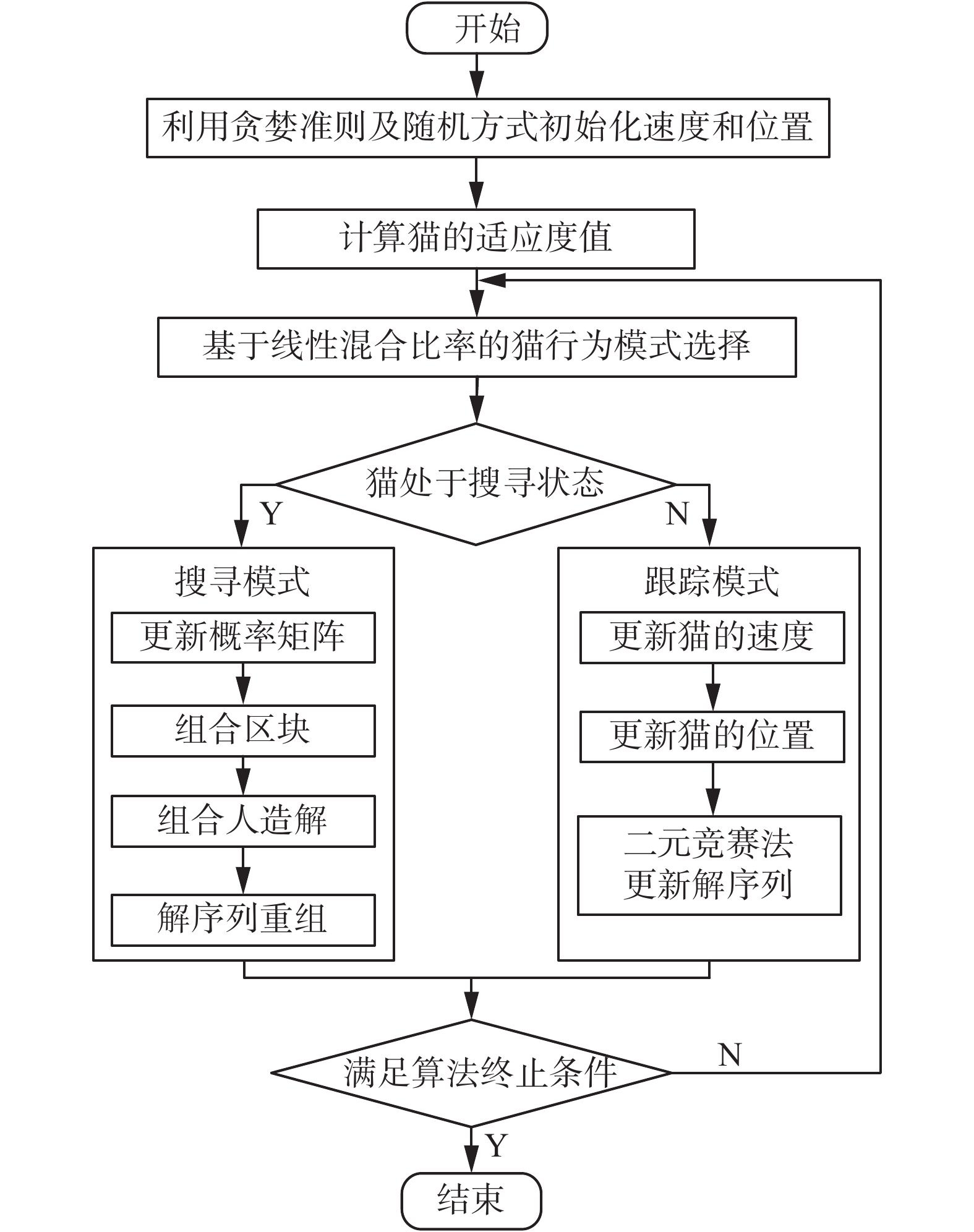
基于以上优化目标及约束条件,改进的猫群算法求解PFSP的流程如下:
1) 初始化种群;
2) 计算猫的适应度值;
3) 改进的猫群算法通过利用混合比率将猫群分为搜寻模式和跟踪模式的2个子群,对不同子群采取不同的方法处理;
4) 在搜寻模式下,利用概率模型更新记录可行解信息并更新可行解;
5) 先后运用区块挖掘及区块竞争来得到适应度较高的人工解;
6) 为提高人工解的质量和多样性,运用搜寻算子对人工解进行重组;
7) 在跟踪模式中利用基于二元竞赛法的速度−位移模型对猫的速度、位置更新,直至达到全局最优;
8) 算法终止条件判断。
基于区块的猫群算法求解PFSP的具体流程如图1所示。
|
Download:
|
| 图 1 EDA-CSO流程图 Fig. 1 The flow chart of EDA-CSO | |
一般而言,时间复杂度能够度量算法的运行时间及算法的优劣。假设种群规模为N,猫处于搜寻模式下的概率为MR,迭代次数为T,根据改进猫群算法的步骤进行时间复杂度分析。
步骤1) 中种群初始化需要N次操作,所以步骤1)的时间复杂度为O(N);
步骤2) 中用以计算适应度的时间复杂度为O(N);
步骤3) 中用以选择猫行为方式的时间复杂度为O(N);
步骤4)~6) 中执行搜寻模式的猫,每次迭代更新概率矩阵1次,挖掘区块n次,区块竞争1次,组合人造解1次,解序列重组1次,故搜寻模式下的时间复杂度为O(MRN +MR2N2+MRN +MRN +MRN );
步骤7) 中执行跟踪模式的猫,每次迭代速度更新1次,位置更新1次,解序列更新1次,故跟踪模式下的时间复杂度为O((1-MR)(N+N+N));
步骤8) 中终止条件判断需要1次操作,故此步骤的时间复杂度为O(1)。
由以上可知,该算法的时间复杂度为O(T(MR+5)N+TMRN 2),故时间复杂度主要与与初始种群规模、混合比率及迭代次数有关。
2.2 初始化种群传统的猫群算法通过轮盘赌的方式生成初始种群,由于初始种群个体适应度较低,在一定程度上制约了算法的收敛速度。本研究利用贪婪准则[16]寻及轮盘赌相结合的方式优化初始化种群,以达到加快收敛速度的同时,增加初始解的多样性。在利用贪婪准则初始化种群时,随机选取第一个工件
| $\begin{aligned} {{x}_{{i,j}}}={{x}_{\min ,j}}+\frac{{{x}_{\max ,j}}-{{x}_{\min ,j}}}{n}\cdot ({{s}_{i,j}}-1+{{r}_{3}}), \\ j=1,2,\cdots ,m \qquad\quad\qquad\\ \end{aligned}$ | (1) |
式中:
初始位置及速度产生方式为
| ${X_i} = {X_{\min }} + ({X_{\max }} - {X_{\min }}){r_1}$ | (2) |
| ${V_i} = {V_{\min }} + ({V_{\max }} - {V_{\min }}){r_2}$ | (3) |
式中:
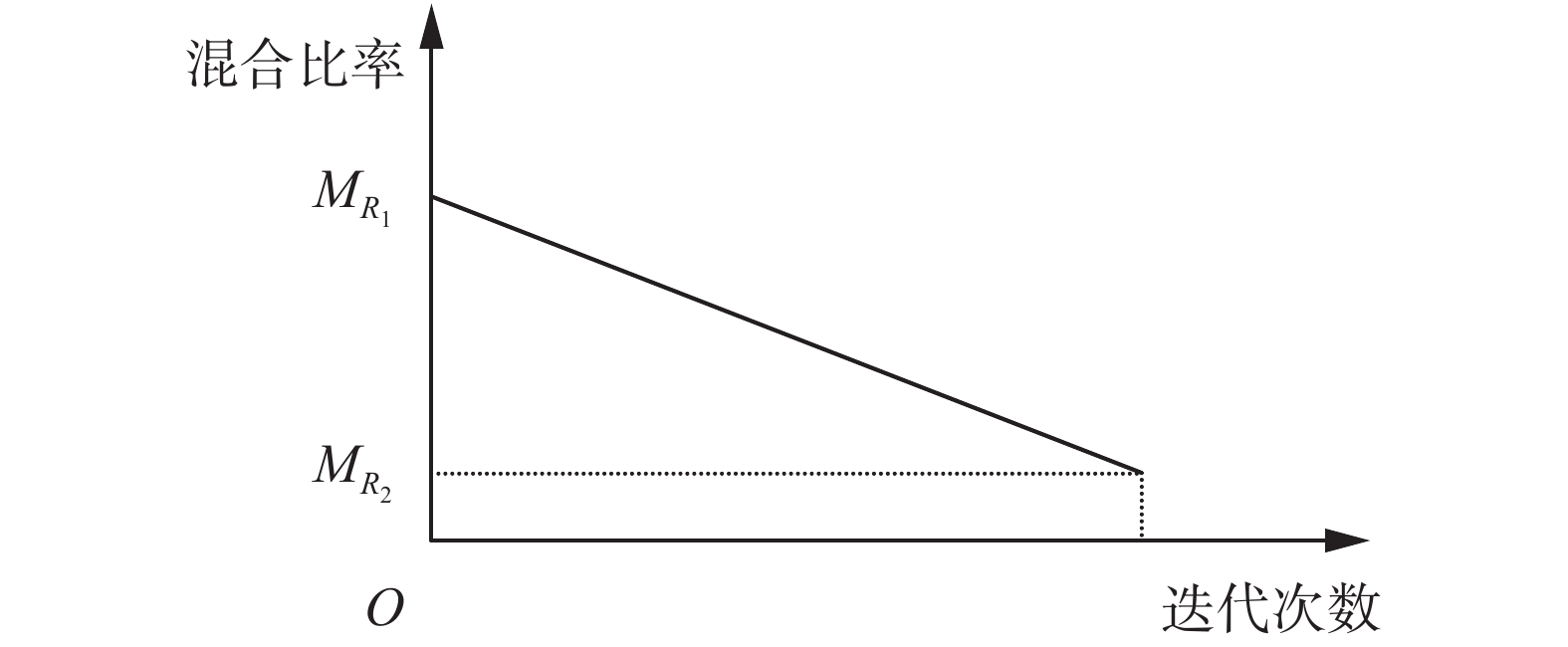
传统的猫群算法不能根据算法的迭代次数合理分配局部搜索和全局搜索的比重,若在算法迭代前期采用较大的混合比率的跟踪猫,可以增加算法的全局搜索能力,但在算法迭代后期搜寻猫所占比率较大,可以提高解精度和收敛性。因此,本研究采用文献[9]中的一种猫行为混合比率选择法,具体如图2所示。
|
Download:
|
| 图 2 混合比率分配 Fig. 2 The allocation of mixed ratio | |
该线性混合比率的计算公式为
| $M_R = {{M_{R_1}}} + \frac{{\left({{{M_{R_2}}} -{ {M_{R_1}}}} \right) \times T}}{{{T_0}}}$ | (4) |
式中:
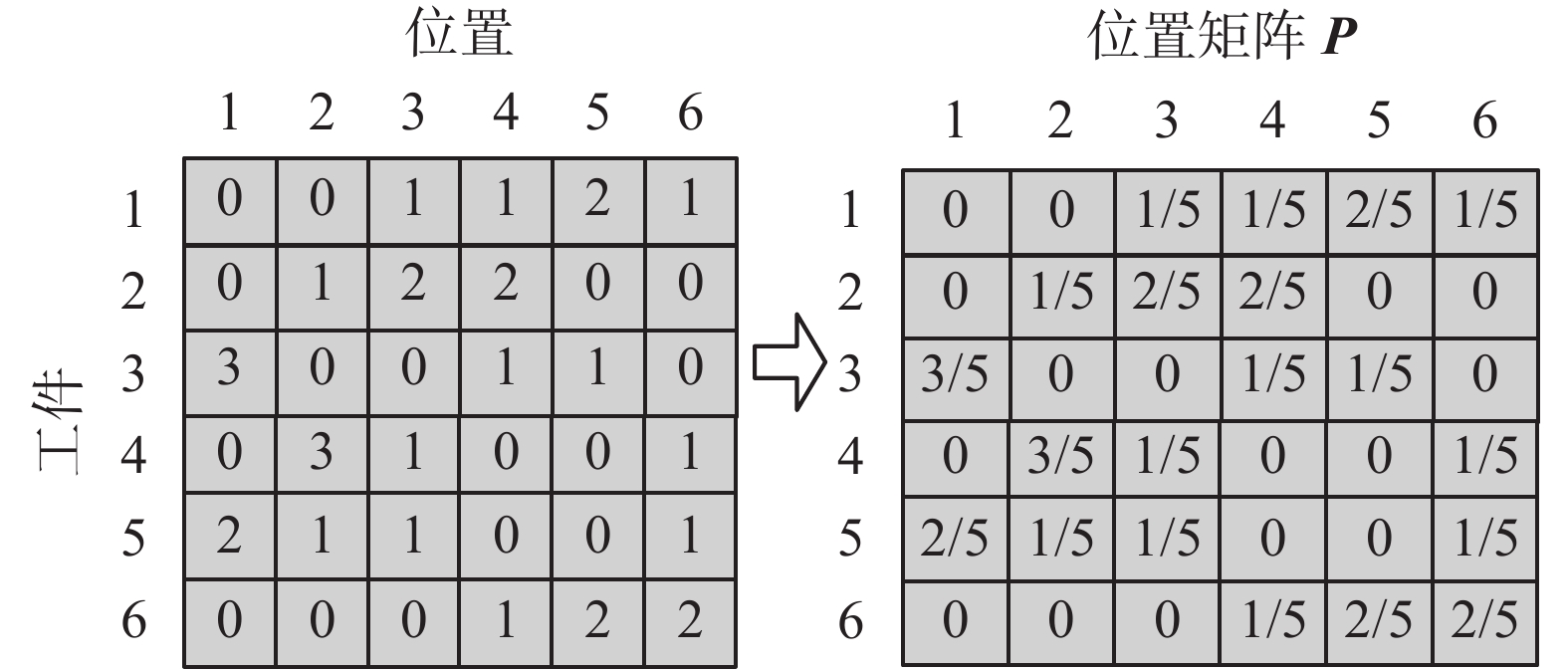
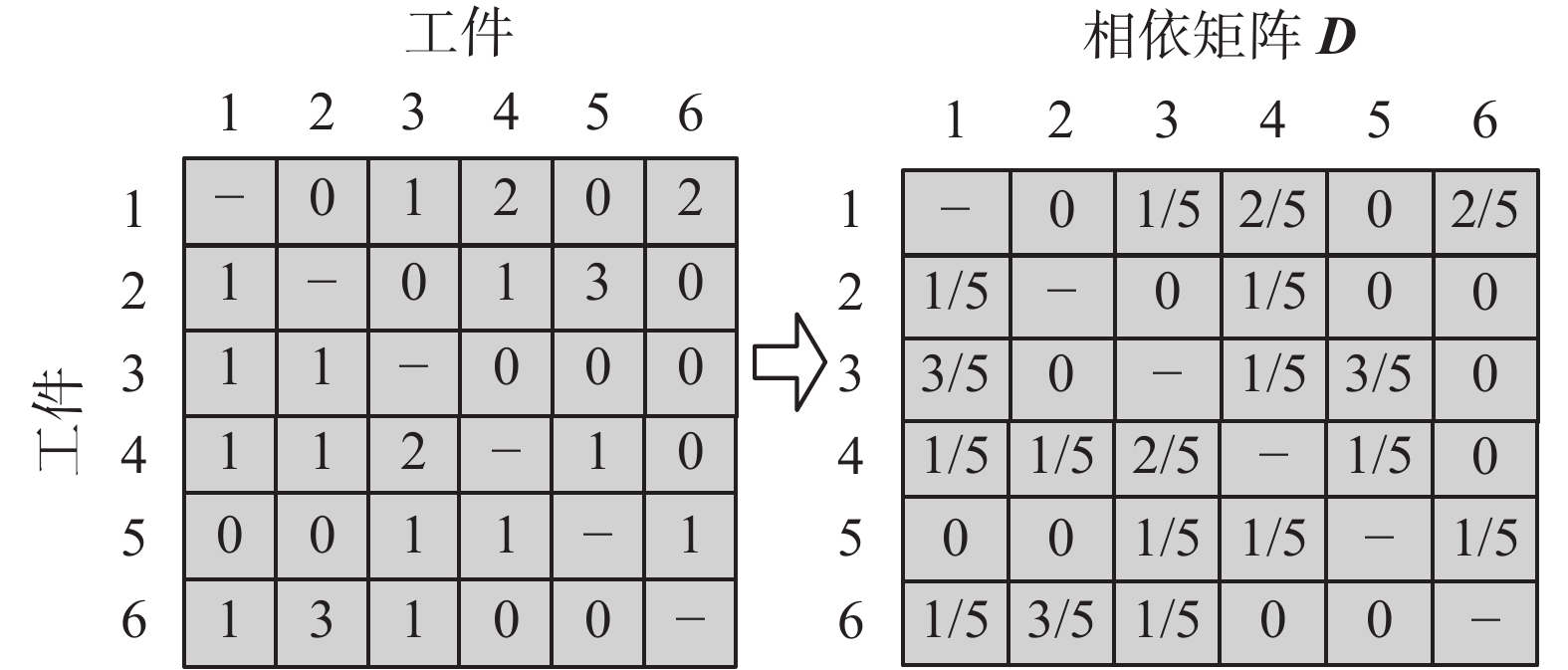
本研究采用位置矩阵和相依矩阵来记载不同的加工信息,位置矩阵用来表示工件和所处加工位置之间的关系,相依矩阵用来表示任意两个工件之间的加工前后顺序。
对初始解的适应度函数值从小到大排序,选择前
| $ \begin{aligned} & B_{ij}^{k}=\left\{ {\begin{aligned} & 1,\ \ \text{如果工件}i\text{位于}j\text{位置上} \\ & 0,\ \ \text{否则} \end{aligned}}\right.\\ & i=1,2,\cdots, n; \,\, j=1,2,\cdots, m;\,\, k=1,2,\cdots, s \\ \end{aligned}$ | (5) |
| $\begin{aligned} & {{T}_{{ij}}}\left({t} \right)={{T}_{{ij}}}\left({t}-1 \right)+\sum\limits_{{k}=1}^{{s}}{B_{{ij}}^{{k}}}, \\ & i=1,2,\cdots, n; \,\, j=1,2,\cdots, m; \,\, k=1,2,\cdots ,s \\ \end{aligned}$ | (6) |
| $\begin{array}{l} Y_{il}^{k}=\left\{ \begin{array}{l} \!\!\!\! 1,\ \ \text{如果工件}i\text{紧邻}l \\ \!\!\!\! 0,\ \ \text{否则} \\ \end{array} \right. \\ i=1,2,\cdots, n;\,\, l=1,2,\cdots, n;\,\, k=1,2,\cdots ,s \\ \end{array}$ | (7) |
| $\begin{aligned} & {{T}_{{ij}}}\left({t} \right)={{T}_{{ij}}}\left({t}-1 \right)+\sum\limits_{{k}=1}^{{s}}{Y_{{ij}}^{{k}}}, \\ & i,l=1,2,\cdots ,n; \,\, j=1,2,\cdots ,m; \,\, k=1,2,\cdots ,s \\ \end{aligned}$ | (8) |
|
Download:
|
| 图 3 位置矩阵更新方式 Fig. 3 Updating method of position matrix | |
|
Download:
|
| 图 4 相依矩阵更新方式 Fig. 4 Updating method of dependency matrix | |
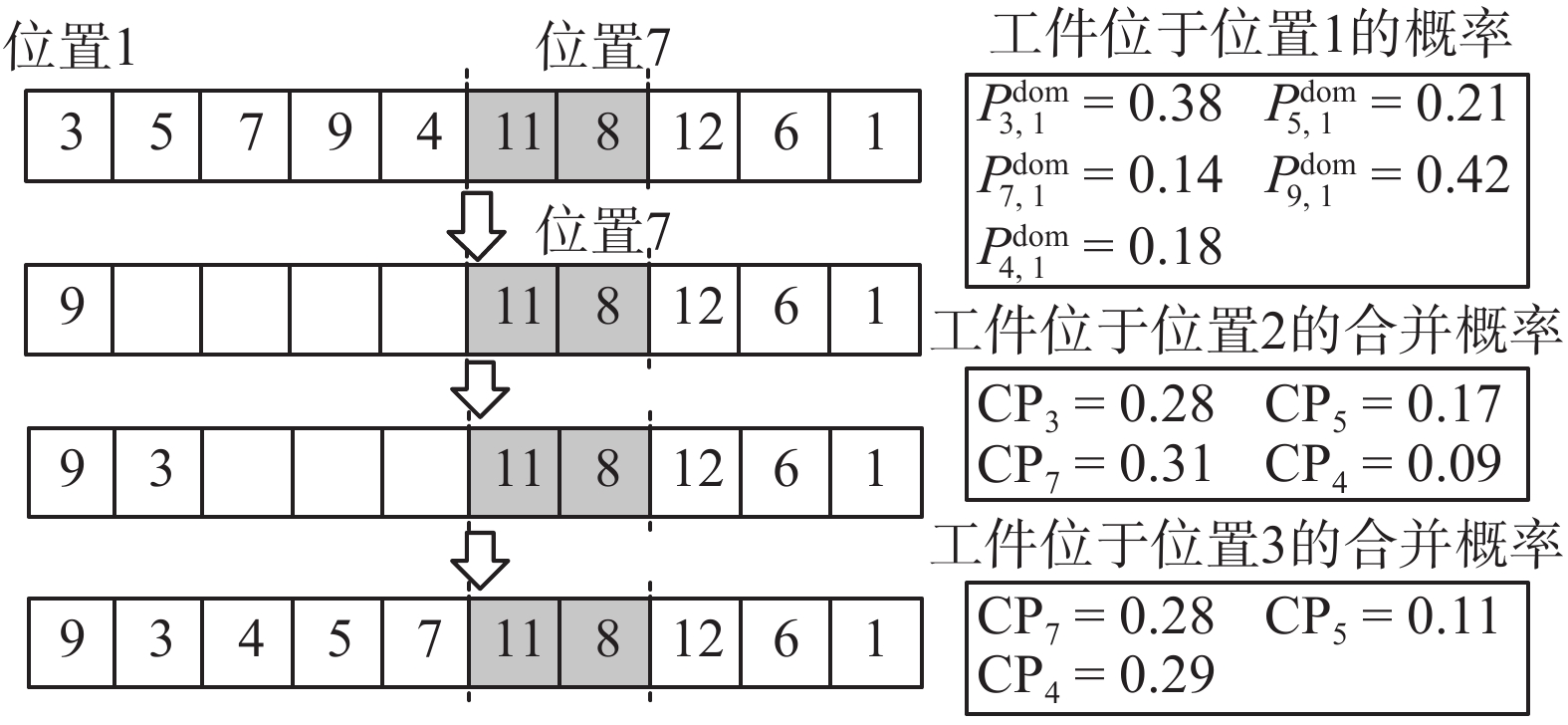
组合区块能够降低种群迭代复杂度,降低解的维度,加快收敛速度。以单个机器10个工件的排序为例,如图5所示,未组合区块之前母体中的工件{工件1,工件2,

|
Download:
|
| 图 5 种群迭代复杂度比较 Fig. 5 The comparison of iterative complexity of population | |
1) 区块挖掘
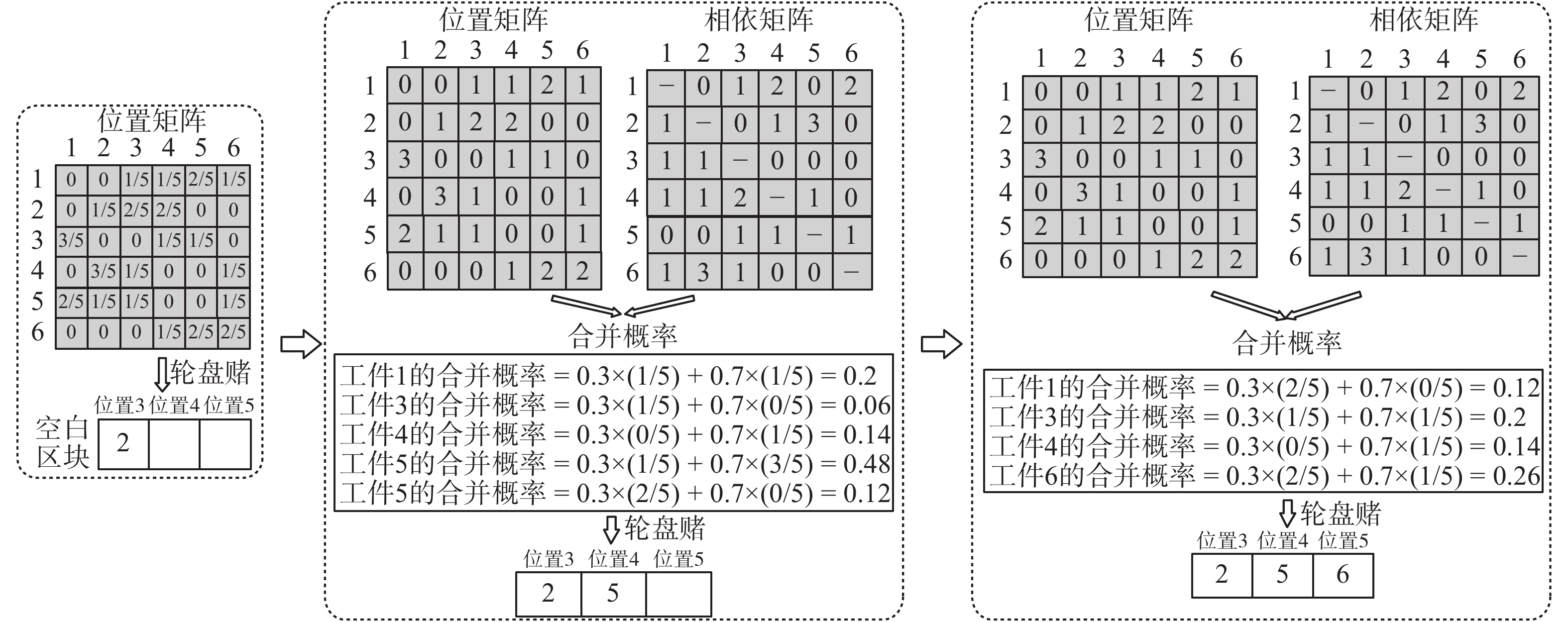
根据位置矩阵和相依矩阵模型提供的相关信息,进行相应的区块挖掘。以随机的方式选择区块的起始位置,产生一个符合最小长度的空白区块,设区块的最小长度为3。
在空白区块中放入最适合的工件,为计算方便,将各工件在位置矩阵与相依矩阵中的累计结果转化为概率,同时,将两矩阵的概率整合成一个合并概率(combination probability,CP),利用轮盘赌对合并概率进行挑选,其中,起始位置按照依据位置矩阵的概率,以轮盘赌进行选择。选出第1个工件后,以合并概率对第2个、第3个工件等进行选择。经一系列研究发现,在进化前期前后关系相比位置关系更能影响解序列的适应度高低[17],相反,在进化中后期位置关系比工件前后关系更重要,因而在进化的不同阶段,令位置矩阵的权重随着世代数由0.3增加到0.7,反之,相依矩阵由0.7递减到0.3。合并概率的计算如式(9)所示,其中,
| $ \begin{aligned} & {\rm C{{P}}}_{i}=({{W}_{\rm dom}}\times P_{i,j}^{\rm dom})+({{W}_{\rm \rm dep}}\times P_{i,\gamma }^{\rm dep}) \\ & i,\gamma =1,2,\cdots, n;\,\,j=1,2,\cdots ,m \end{aligned} $ | (9) |
计算出所有工件的合并概率,并运用轮盘赌选择出区块的第2个工件及第3个工件等,具体如图6所示。
|
Download:
|
| 图 6 以合并概率挖掘区块 Fig. 6 Mining blocks by combining probability | |
随着区块长度的增长,总概率逐渐降低,即错误的概率越大。例如,一个由5个工件{工件1,工件2,工件3,工件4,工件5}组成的区块,其概率分别为0.5、0.8、0.6、0.4、0.3,此区块的总概率0.5×0.8×0.6×0.4×0.3=0.028 8,若该区块由3个工件{工件1,工件2,工件3}组成,则总概率为0.5×0.8×0.6=0.24,由此可见,错误概率随着区块长度的增长而变大。为保证区块的质量不会随着区块长度的增加而降低,设计一个阈值用以筛选上述挖掘的区块,阈值随着迭代次数的增加由0.24增到0.8。将符合阈值的区块暂存在区块库中,区块库中保留着本次迭代中全部符合阈值的区块。
2) 区块竞争
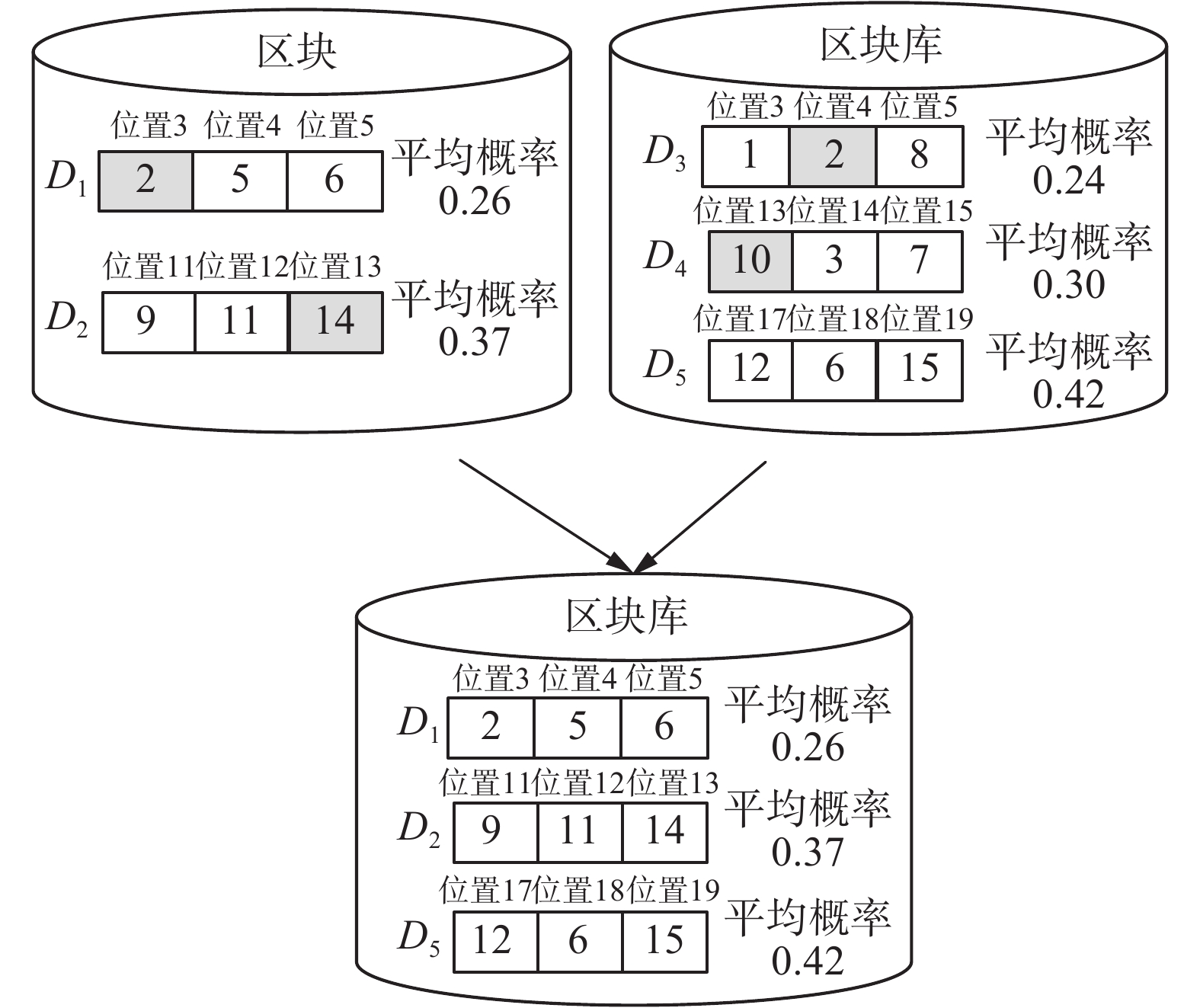
区块挖掘完成后,利用区块竞争选择竞争力较大的区块,每迭代一次,其产生的区块与区块库中的区块进行比较,最终选择其中竞争优势较大的区块,更新区块库。区块进行竞争时,如果几个区块之间工件重复或者区块之间包含的位置出现重复,利用平均概率对这几个区块比较,淘汰概率较小的区块。
平均概率的计算方法:区块的第一个工件位置矩阵概率加上其余工件的合并概率之和除以区块总长度,即可求出该区块的平均概率。平均概率的计算如式(10)所示:
| $P_{{B^{{i}}}}^{\rm AVG} = \frac{{P_{B_l^h}^{{\rm{dom}}} + \sum\limits_{l = {\rm{2}}}^{{n_1}} {C{P_{B_l^h}}} }}{{{n_1}}}$ | (10) |
式中:h为区块编号;
具体的区块竞争如图7所示,新产生的2个区块{D1,D2},区块库包含3个区块{D3,D4,D5},新产生的区块D1与区块库中的D3重复出现工件6,此时对D1与D3的平均概率进行比较,D1的平均概率为0.26,大于D3的平均概率0.23,故D1取代D3进入区块库中,D3被淘汰删除。D2与D4在位置11重叠,比较与D4的平均D2概率由图可知D2高于D4,故淘汰D4。D5未与任何区块发生工件或位置重复,因此继续保存于区块库中。
|
Download:
|
| 图 7 区块竞争 Fig. 7 The competition of blocks | |
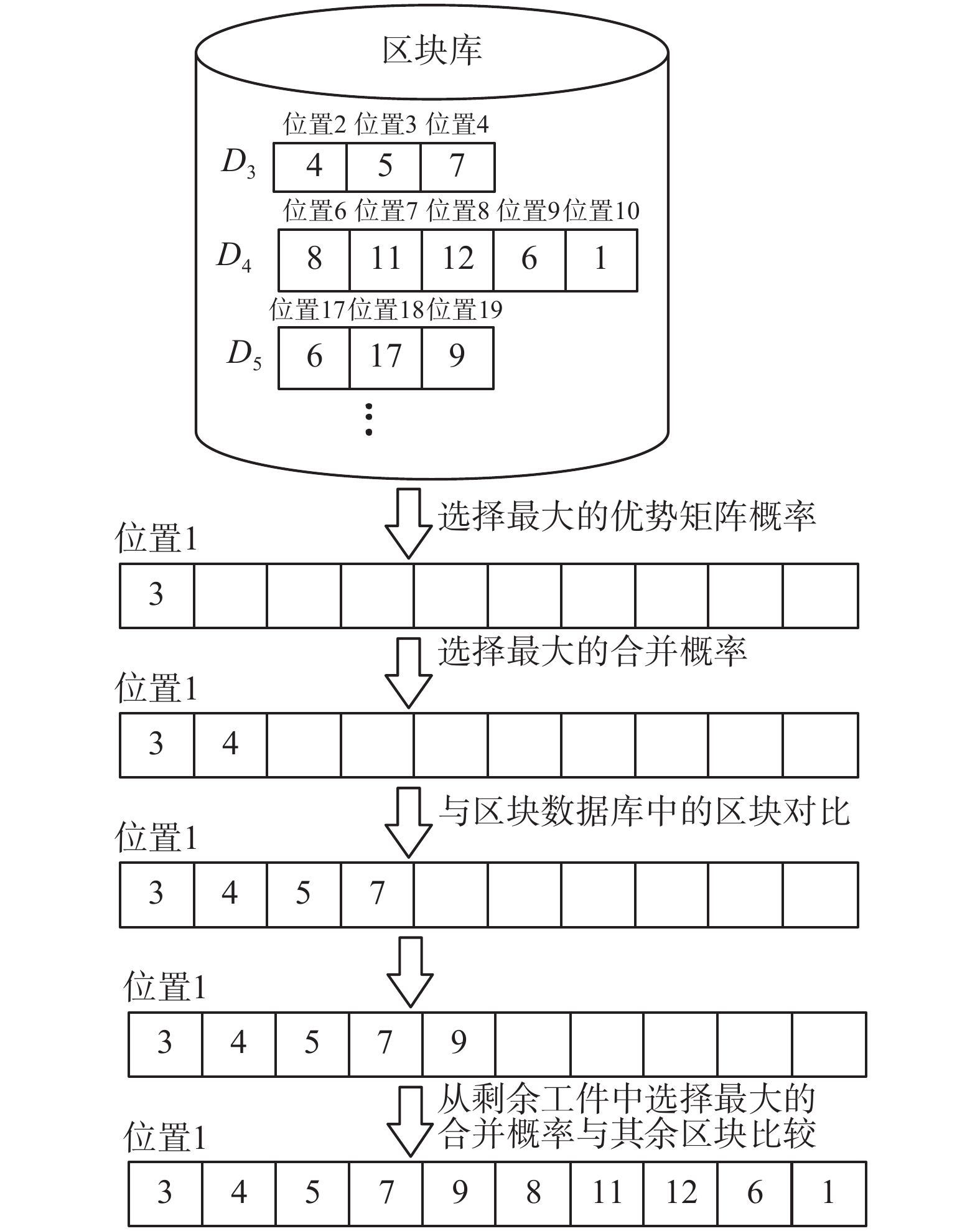
为提高解序列的质量,在完成区块挖掘后,利用区块库中保留的区块组合人工解,具体步骤如下:
1) 从人工解的第一个位置开始挖掘,挖掘方法与上述区块挖掘相同,第一个位置利用位置矩阵中概率以轮盘赌的方式选择工件;
2) 其余N−1个位置以轮盘赌的形式对合并概率进行选择;
3) 每选出一个工件,将该工件与所有其他区块的起始位置进行比较,若与其他区块的位置及工件都相同,则将此区块直接复制到人工解中,然后从下个位置继续进行选择和比较,直至人工解组合完成。
具体的操作方式如图8所示。
|
Download:
|
| 图 8 人工解组合过程 Fig. 8 The combination process of artificial solution | |
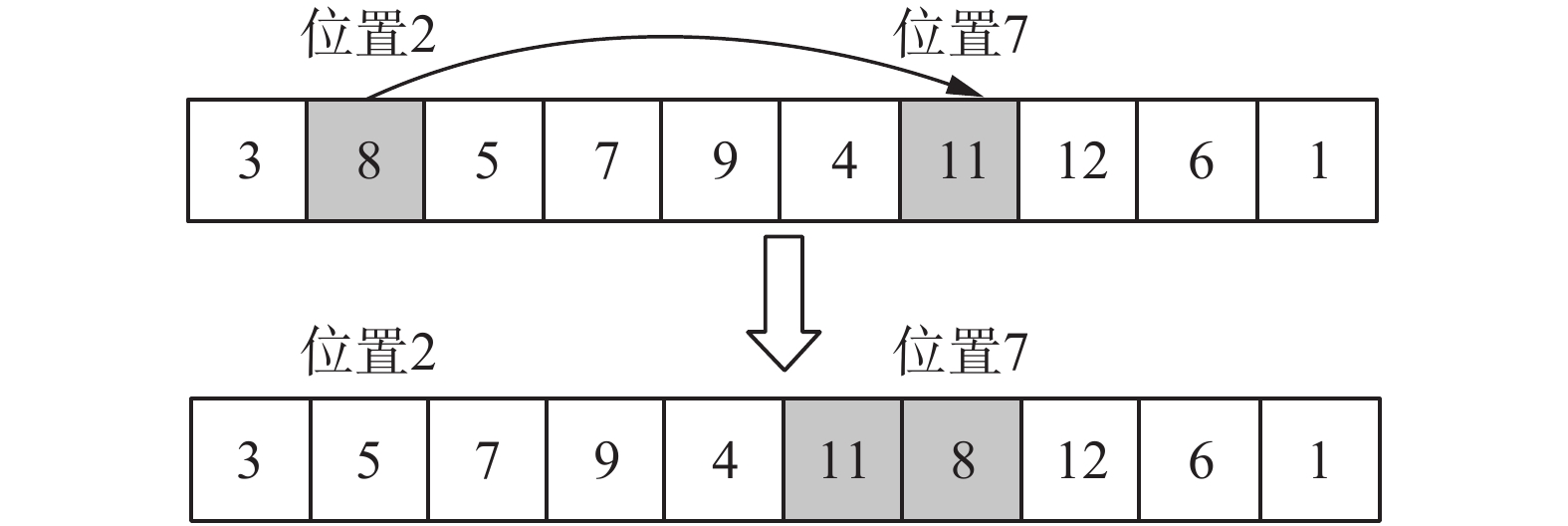
为了增加该算法寻找最优解的概率,本研究对每只猫即解序列进行相应的重组操作。首先每只猫在记忆池中将自身位置复制H份,对记忆池中的猫即解序列进行相应的重组操作,使得所有猫能够到达新位置,计算记忆池中所有猫的适应度,然后将适应度最高的猫代替当前猫,以完成猫的位置更新。在记忆池进行变异操作时,为避免局部最优及增加解序列的多样性,本研究将解序列随机切成N个片段,选取最短的两个片段,利用遗传算法中的插入搜寻算子操作,对解序列重组,使得两个最短片段形成一个基因片段。若重组之后的片段不再是最短片段,则对解序列中的最长片段及该片段按照合并概率重组,若区块库含有以被选择的工件开头的区块,则直接插入,具体如图9和图10所示。
|
Download:
|
| 图 9 插入搜寻算子 Fig. 9 Insert search operator | |
|
Download:
|
| 图 10 利用概率重组解序列 Fig. 10 Using probability recombination solution sequence | |
猫的跟踪模式是为了使个体靠近全局最优解,在该模式下,猫与群体最优位置进行比较来更新个体速度与位置[18]。跟踪模式可以根据以下两步进行。
1) 速度的更新。
任意时刻,每个猫都有一个速度,第i只猫的当前速度可表示为
| $V_i(n + 1) = {V_i}(n) \times w + c \times {\rm rand} \times [{X_{\rm best}}(n) - V(n)]$ | (11) |
| $w = {w_{\max }} - ({w_{\max }} - {w_{\min }}) \times (t/{t_{\max }})$ | (12) |
式中:Vi(n+1)表示更新后第i只猫的速度;w为惯性权重,w的大小由式(12)决定;t表示迭代信息;tmax表示最大迭代次数;c代表加速度常数;rand服从[0,1]均匀分布。
2) 位置更新。
每只猫的位置更新由式(13)决定:
| ${X_i}(n + 1) = {X_i}(n) + {V_i}(n + 1)$ | (13) |
式中
3) 如果第i只猫分的新位置超出搜索空间,则将速度乘以−1,从反方向继续搜索。
4) 利用二元竞赛法更新解序列,即将母体种群与子群的适应度两两对比并将适应度最高的子群代替母体种群,进行下一次搜索。
3 仿真测试 3.1 参数设置为了验证基于区块的猫群算法的性能,本研究测试数据采用Carlier[19]中的Car类基准例题集进行测试,应用该算法求解这些案例,并与其他文献中的算法进行比较。本研究程序利用Visual Studio2015中的C++,在操作系统为Windows8,处理器的主频为2.71 G的Intel(R)Core(TM)i5-6400处理器8 G内存的电脑上进行仿真测试。参数设计:仿真测试次数为20,初始种群的数量为100,最大的迭代次数为100。本研究将各个算法的最优相对误差(BRE)、平均相对误差(ARE)及最差相对误差(WRE)进行比较。其中,C*表示已知算例的最优解,
| ${\rm BRE} = \frac{({C_{\min }}{\rm{ - }}{C^ * })}{C^ * } \times 100\text{%} $ | (14) |
| ${\rm{ARE}} = {\rm{ }}\frac{{(\bar C{\rm{ - }}{C^*})}}{{{C^*}}} \times 100\text{%} $ | (15) |
| ${\rm WRE} = \frac{({C_{{\rm{max}}}}{\rm{ - }}{C^ * })}{C^ * } \times 100\text{%} $ | (16) |
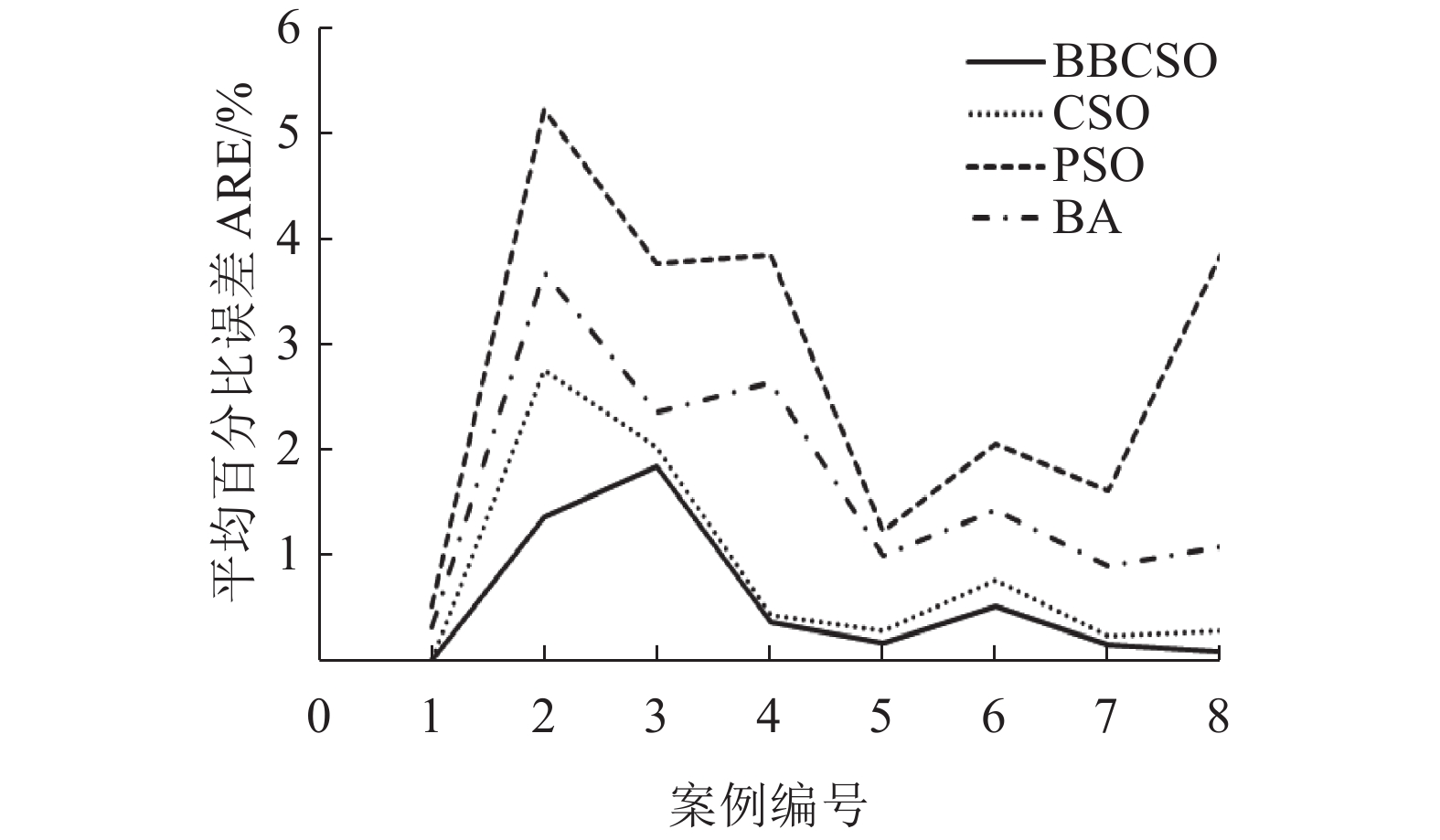
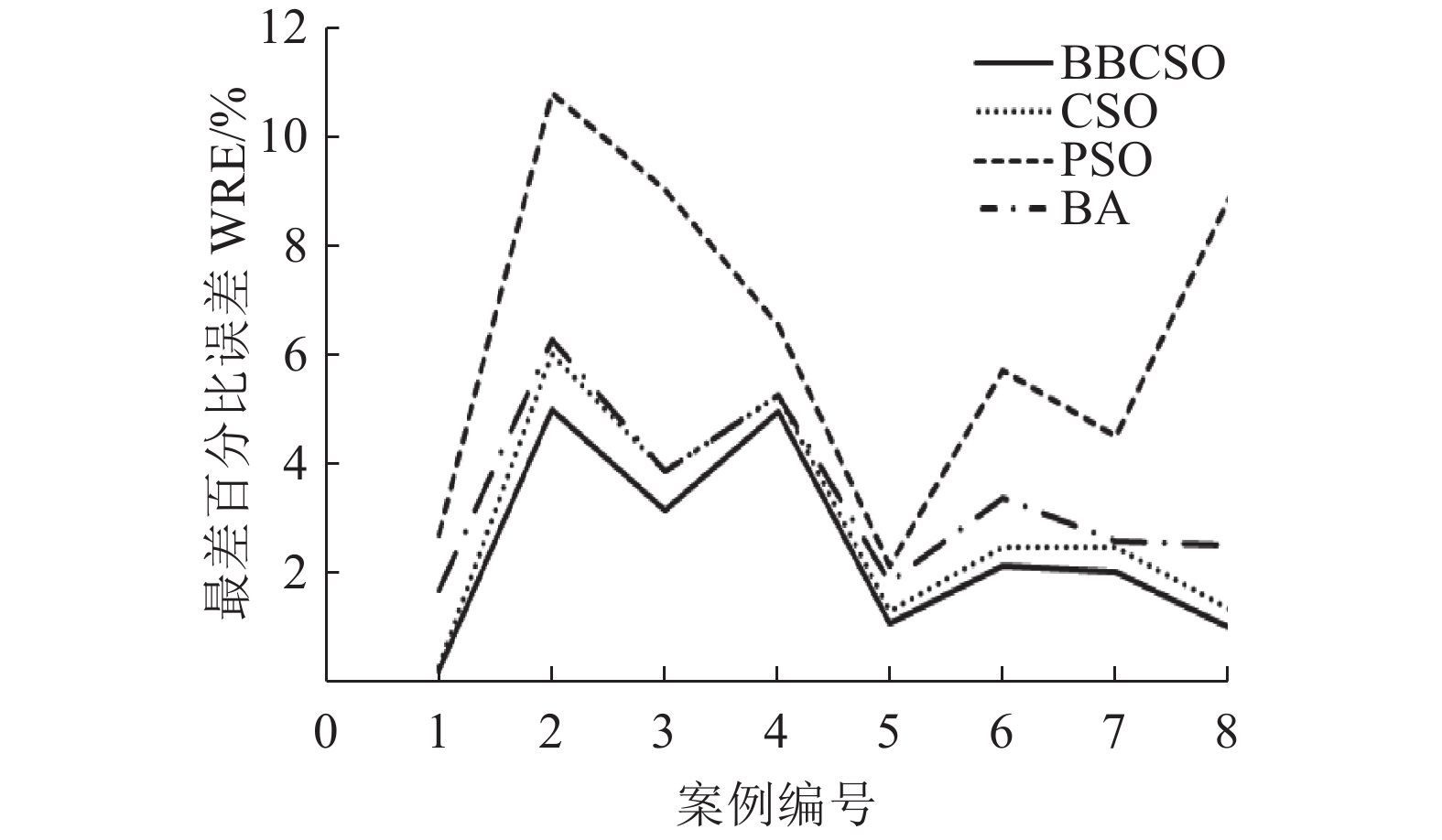
针对Carlier例题,本研究将基于分布估计算法的改进猫群算法(EDA-CSO)与猫群算法(CSO)[12]、标准粒子群算法(PSO)[12]、蝙蝠算法(BA)[12]进行比较。具体比较结果如表1所示。
| 表 1 EDA-CSO、CSO、PSO和BA的测试结果对比 Tab.1 Comparison of test results for EDA-CSO、CSO、PSO and BA |
由表1和图11、图12可知,尽管这4种算法在Carlier案例中均能求出问题的最优解(BRE为0),然而EDA-CSO的ARE均优于其他算法。表明了本算法的整体求解性能优于其他算法。此外,EDA-CSO显然比CSO、PSO、BA的ARE和WRE更小,这是因为通过调整猫的混合比率,迭代前期采用较大的混合比率的跟踪猫,增加了算法的全局搜索能力,在算法迭代后期增加搜寻猫所占比率较大,增加了局部搜索能力,减少了求解误差,提高了精度和收敛性,因此EDA-CSO算法明显优于文中其他算法。
|
Download:
|
| 图 11 平均相对误差比较 Fig. 11 Comparison of average relative error | |
|
Download:
|
| 图 12 最差相对误差比较 Fig. 12 Comparison of the worst relative error | |
为进一步验证算法的有效性,针对Reeves[20]例题,将基于猫群算法的改进估计分布算法(EDA-CSO)与猫群算法(CSO)[10]、基于区块的分布估计算法(BBEDA)[17]、基于粒子群算法的分布估计算法(PSO-EDA)[21]各迭代20 000次并进行比较。具体结果如表2所示。其中,Cmin表示所求解的最优值,s;G表示算法的运行时间,s。
| 表 2 Reeves案例测试结果比较 Tab.2 Performance comparison on Reeves’s instances |
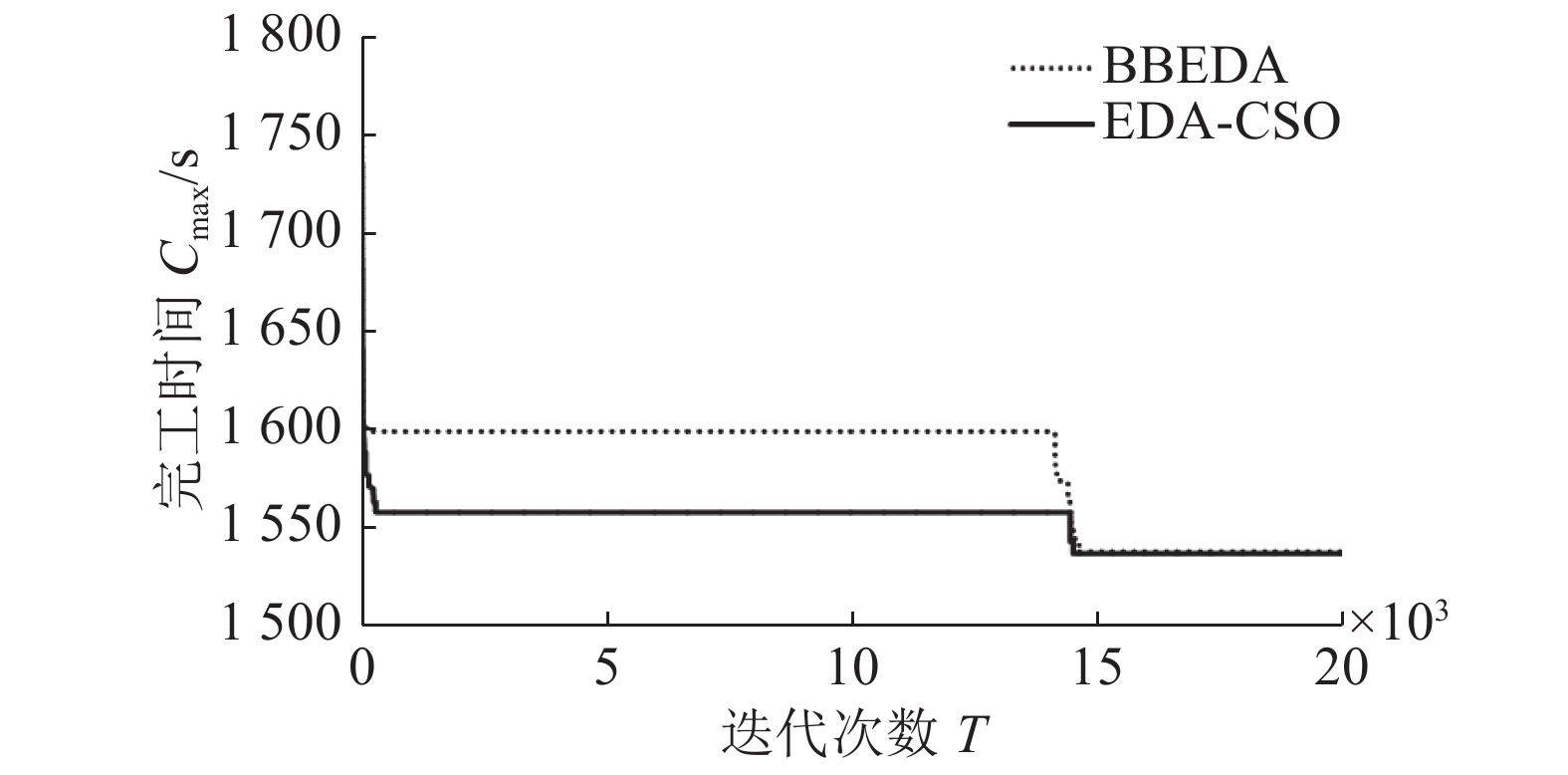
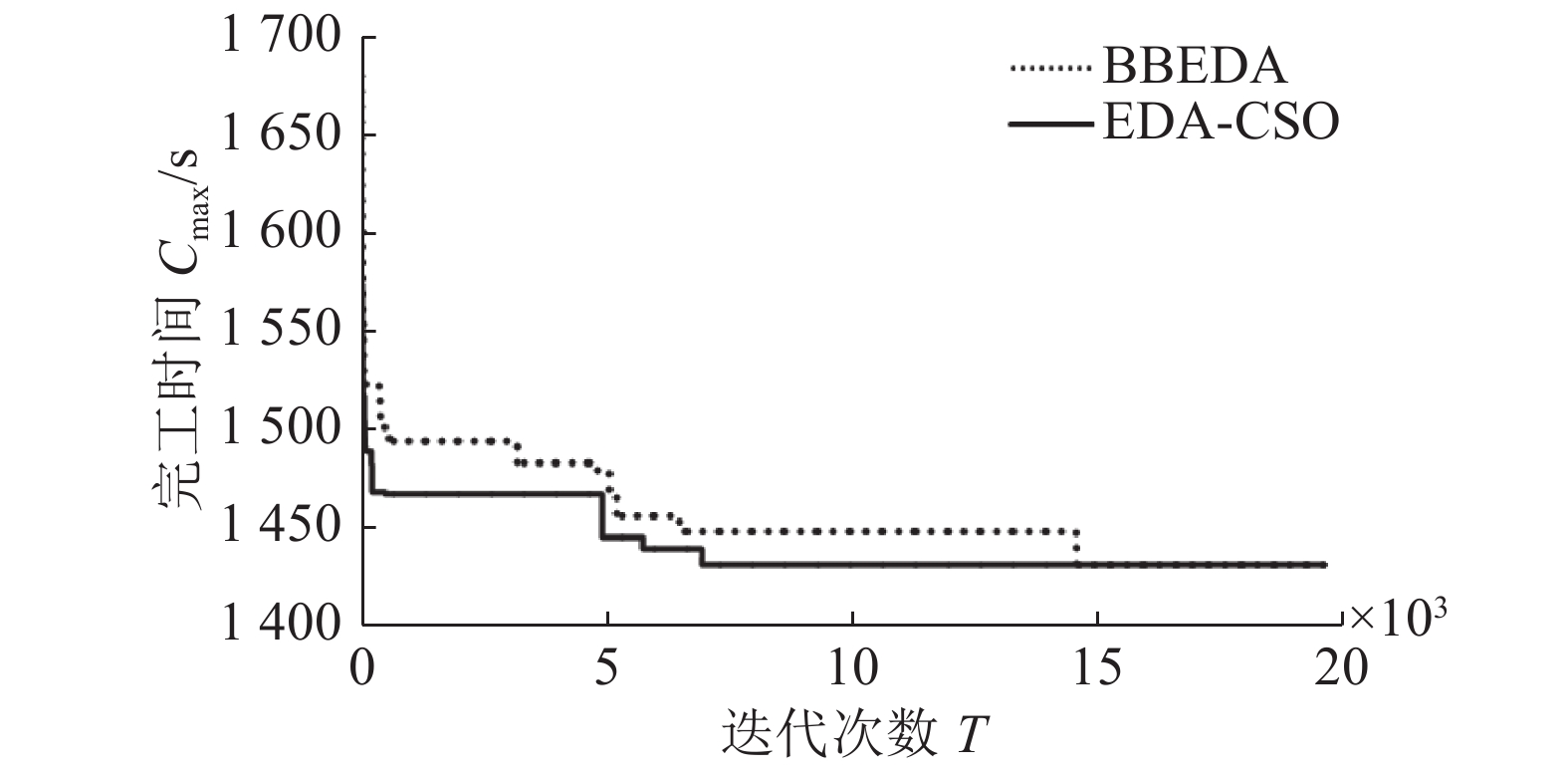
由表2可知,由于增加算子,尽管本算法在求解Rec01、Rec05、Rec07时,处理时间上慢于CSO算法,但BRE均优于CSO、BBEDA及PSO-EDA算法。这是因为虽然迭代过程中增加了算子,但由于区块具有降维的作用,且随着问题复杂度的增加,效果越明显,因而在一定程度上降低了运算时间。为直观体现本算法降低复杂度,加快收敛速度的性能,以EDA-CSO、BBEDA求解Rec09、Rec11、Rec13、Rec15为例,具体如图13~16所示。
|
Download:
|
| 图 13 Rec09收敛图 Fig. 13 Rec09 convergence graph | |
|
Download:
|
| 图 14 Rec11收敛图 Fig. 14 Rec11 convergence graph | |

|
Download:
|
| 图 15 Rec13收敛图 Fig. 15 Rec13 convergence graph | |
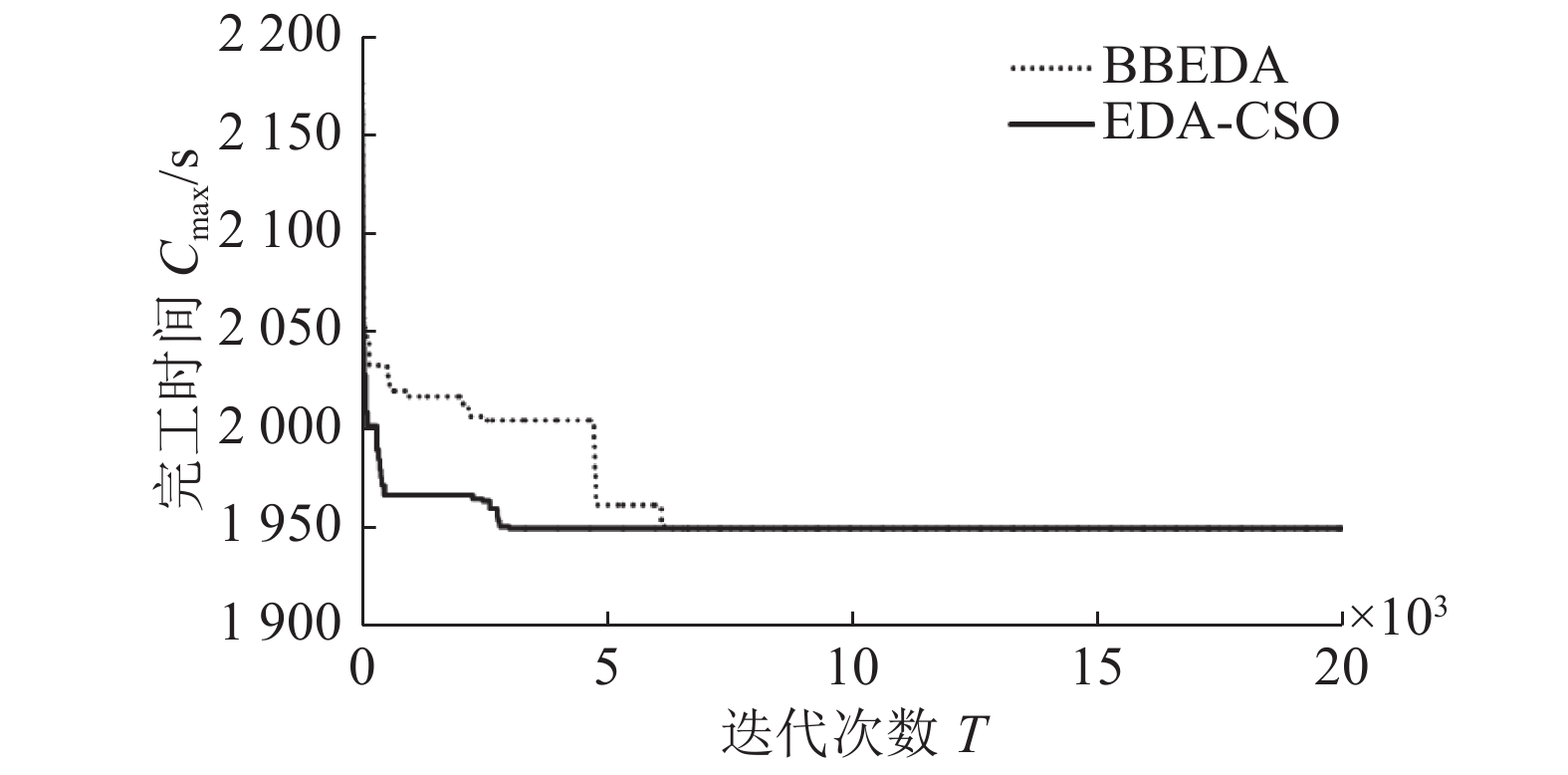
|
Download:
|
| 图 16 Rec15收敛图 Fig. 16 Rec15 convergence graph | |
从图13~16可以看出,在相同的迭代次数下,EDA-CSO与BBED算法相比,尽管两者最优误差均为0,但EDA-CSO的收敛速度均优于BBEDA算法的收敛速度。
4 结束语本研究在猫群算法的基础上进行改进,提出了基于分布估计算法的改进猫群算法,用以解决置换流水车间调度问题。在猫搜寻阶段,运用贪婪准则于轮盘赌相结合的方式初始化种群,加快收敛速度;采用位置矩阵与相依矩阵结合的方式挖掘区块;利用区块竞争产生人工解;在不同的进化阶段采用不同的变异方式以提高人工解的质量和多样性;同时,为了使个体靠近全体最优解,通过与群体最优位置进行比较来更新个体速度与位置。针对Carlier和Reeves标准案例运用该算法进行求解,最后,将各个算法的实验结果进行比较,验证了该算法的有效性和鲁棒性。
本研究仅将该算法应用于置换流水车间调度问题,未将该算法应用于混流生产线、TSP等其他组合优化问题,今后可以进一步从这几个方面展开研究。
| [1] |
GAREY M R, JOHNSON D S, SETHI R. The complexity of flowshop and jobshop scheduling[J]. Mathematics of operations research, 1976, 1(2): 117-129. ( 0) 0)
|
| [2] |
李小缤, 白焰, 耿林霄. 求解置换流水车间调度问题的改进遗传算法[J]. 计算机应用, 2013, 33(12): 3576-3579. LI Xiaobin, BAI Yan, GENG Linxiao, et al. Improved genetic algorithm for solving permutation flow shop scheduling problem[J]. Journal of computer applications, 2013, 33(12): 3576-3579. DOI:10.3969/j.issn.1001-3695.2013.12.014 (  0) 0)
|
| [3] |
CHU Shuchuan, TSAI P W, PAN J S. Cat swarm optimization[C]//Proceedings of the 9th Pacific Rim International Conference on Artificial Intelligence. Guilin, China, 2006, 4099: 854–858.
( 0) 0)
|
| [4] |
GANAPATI P, PRADHAN P M, MAJHI B. ⅡR system identification using cat swarm optimization[J]. Expert systems with applications, 2011, 38(10): 12671-12683. DOI:10.1016/j.eswa.2011.04.054 ( 0) 0)
|
| [5] |
PRADHAN P M, PANDA G. Solving multiobjective problems using cat swarm optimization[J]. Expert systems with applications, 2012, 39(3): 2956-2964. ( 0) 0)
|
| [6] |
GUO Lei, MENG Zhuo, SUN Yize, et al. A modified cat swarm optimization based maximum power point tracking method for photovoltaic system under partially shaded condition[J]. Energy, 2018, 144: 501-514. DOI:10.1016/j.energy.2017.12.059 ( 0) 0)
|
| [7] |
PAPPULA L, GHOSH D. Cat swarm optimization with normal mutation for fast convergence of multimodal functions[J]. Applied soft computing, 2018, 66: 473-491. DOI:10.1016/j.asoc.2018.02.012 ( 0) 0)
|
| [8] |
TSAI P W, PAN J S, CHEN S M, et al. Parallel cat swarm optimization[C]//Proceedings of 2008 International Conference on Machine Learning and Cybernetics. Kunming, China, 2008: 3328–3333.
( 0) 0)
|
| [9] |
刘琼, 范正伟, 张超勇, 等. 基于多目标猫群算法的混流装配线排序问题[J]. 计算机集成制造系统, 2014, 20(2): 333-342. LIU Qiong, FAN Zhengwei, ZHANG Chaoyong, et al. Mixed model assembly line sequencing problem based on multi-objective cat swarm optimization[J]. Computer integrated manufacturing system, 2014, 20(2): 333-342. (  0) 0)
|
| [10] |
BOUZIDI A, RIFFI M E. Cat swarm optimization to solve flow shop scheduling problem[J]. Journal of theoretical and applied information technology, 2015, 72(2): 239-243. ( 0) 0)
|
| [11] |
BOUZIDI A, RIFFI M E. Cat swarm optimization to solve job shop scheduling problem[C]//Proceedings of the Third IEEE International Colloquium in Information Science and Technology. Tetouan, Morocco, 2015: 202–205.
( 0) 0)
|
| [12] |
马邦雄, 叶春明. 利用猫群算法求解流水车间调度问题[J]. 现代制造工程, 2014(6): 12-15, 71. MA Bangxiong, YE Chunming. The research of flow-shop scheduling problem based on cat swarm optimization[J]. Modern manufacturing engineering, 2014(6): 12-15, 71. DOI:10.3969/j.issn.1671-3133.2014.06.003 (  0) 0)
|
| [13] |
陶新民, 徐鹏, 刘福荣, 等. 组合分布估计和差分进化的多目标优化算法[J]. 智能系统学报, 2013, 8(1): 39-45. TAO Xinmin, XU Peng, LIU Furong, et al. Multi-objective optimization algorithm composed of estimation of distribution and differential evolution[J]. CAAI transactions on intelligent systems, 2013, 8(1): 39-45. (  0) 0)
|
| [14] |
TZENG Y R, CHEN C L, CHEN C L. A hybrid EDA with ACS for solving permutation flow shop scheduling[J]. The international journal of advanced manufacturing technology, 2012, 60(9/10/11/12): 1139-1147. ( 0) 0)
|
| [15] |
CHANG P C, HUANG W H, TING C J. Dynamic diversity control in genetic algorithm for mining unsearched solution space in TSP problems[J]. Expert systems with applications, 2010, 37(3): 1863-1878. ( 0) 0)
|
| [16] |
KIM D, HALDAR J P. Greedy algorithms for nonnegativity-constrained simultaneous sparse recovery[J]. Signal processing, 2016, 125: 274-289. DOI:10.1016/j.sigpro.2016.01.021 ( 0) 0)
|
| [17] |
CHANG P C, CHEN Menghui. A block based estimation of distribution algorithm using bivariate model for scheduling problems[J]. Soft computing, 2014, 18(6): 1177-1188. DOI:10.1007/s00500-013-1136-1 ( 0) 0)
|
| [18] |
RAUTRAY R, BALABANTARAY R C. Cat swarm optimization based evolutionary framework for multi document summarization[J]. Physica a: statistical mechanics and its applications, 2017, 477: 174-186. DOI:10.1016/j.physa.2017.02.056 ( 0) 0)
|
| [19] |
CARLIER J. Ordonnancements à contraintes disjonctives[J]. RAIRO-operations research, 1978, 12(4): 333-350. ( 0) 0)
|
| [20] |
REEVES C R. A genetic algorithm for flowshop sequencing[J]. Computers and operations research, 1995, 22(1): 5-13. ( 0) 0)
|
| [21] |
LIU Hongcheng, GAO Liang, PAN Quanke. A hybrid particle swarm optimization with estimation of distribution algorithm for solving permutation flowshop scheduling problem[J]. Expert systems with applications, 2011, 38(4): 4348-4360. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


