基于位置的社交网络LBSN^[1](location based social network)实现了用户对其访问地理位置的签到功能，并能够发布相应的评论、图片、视频信息与好友分享。通过LBSN可以提供好友推荐^[2-3]、兴趣点推荐^[4-5]等多种个性化服务。兴趣点推荐的目标是向特定用户推荐满足其需求的、具有一定长度的未知兴趣点列表，来增强用户体验。一般来说，推荐的兴趣点包括地点(如饭馆、商场、公园和影院等)和活动(如演唱会、公益活动等)两类。与传统电子商务网站的推荐系统不同，兴趣点推荐有如下的特性：

1) 数据的弱语义性：传统的推荐系统中，用户对商品的评分是显现的，可以表达其偏好程度，如五级评分制中5代表很喜欢，而1代表不喜欢。在兴趣点推荐系统中，只能获取用户对兴趣点的访问次数，而签到次数的多少并不能反映用户的偏好程度。换句话说传统的推荐数据中同时包含正例和负例，而兴趣点推荐数据仅包含正例，这就使得很多成熟的推荐方法如协同过滤算法等并不直接适用于兴趣点推荐。

2) 数据的稀疏性：用户对兴趣点的签到矩阵相比于传统的用户−商品评分矩阵更加稀疏，如国外著名的LBSN网络——Gowalla的数据稀疏度为2.08×10⁻⁴。传统的推荐算法难以直接适用于兴趣点推荐。此外用户的历史活动记录具有聚集性，通常只集中在居住地或工作地等少数几个区域。当用户外出时，由于缺少该区域的历史签到记录无法做出准确的推荐。

3) 社交影响不大：传统在线社交网络上的“朋友”往往具有相似的兴趣爱好，因此很多推荐算法通过引入社交关系来处理数据的稀疏性问题，提高效率。但是在LBSN中的“朋友”不一定具有相同的兴趣爱好，引入社交关系对兴趣点推荐影响不大。

鉴于此，本文提出了一种新的推荐模型——用户−内容−区域主题模型(user-content-region topic model, UCRTM)。该模型同时分析了用户兴趣、地点特定主题以及所属地理区域主题等多个特征，以隐含主题为基础，用统一的框架将各种特征进行融合，在一定程度上克服了用户签到数据的稀疏性和弱语义性等问题，实验证明能获得较好的用户体验。

1 相关工作

目前基于位置社交网络的兴趣点推荐算法可归纳为3类：

1) 传统推荐算法的直接运用：这类方法认为用户对兴趣点的签到次数能够代表其偏好程度，构造用户−兴趣点签到矩阵并利用传统的推荐算法进行推荐。如：文献[6]提出的基于用户和兴趣点的混合协同过滤算法；文献[7]提出的基于正则化矩阵分解(RMF)算法和文献[8]提出的概率矩阵分解(PMF)算法等。这类方法的本质是尽量完善推荐模型，但由于数据集本身过度稀疏，以及数据的弱语义性导致推荐质量并不高。

2) 引入地理因素的推荐算法：在LBSN中，用户与兴趣点的地理距离也是推荐的重要因素，这也是有别于商品推荐的重要特征，这类算法将地理信息融入到模型中，如文献[6]认为用户签到的兴趣点在地理位置上是符合幂律分布，文献[8]则认为用户的活动区域是围绕多个中心点展开的，进而引入了多中心高斯分布模型。事实证明对地理信息建模有助于推荐效果的提升。

3) 引入社交影响的推荐算法：这类方法认为社交网络上的“朋友”拥有相同的兴趣爱好，结合朋友的签到访问历史记录进行推荐，如文献[9]利用相似用户进行推荐时，直接利用好友进行推荐，而忽略LBSN中其他用户。文献[8]将社交关系直接融入到矩阵分解(PMF)算法中，但是实验证明社交关系对推荐准确率的影响不大。

还有一些方法同时考虑了地理因素、用户的偏好以及社交关系。如文献[10]设计了一种UPS(user, proximity and social-based)算法，将社交影响因子融合到基于用户偏好的协同过滤算法中，以此来提高用户相似度计算的准确性。实验证明该算法在稀疏数据环境下的推荐效果并不是很好，而且该算法没有考虑用户在不同的地理位置的影响。文献[11]提出了USG (user, social and geographical influence based recommendation)推荐算法，综合考虑了用户偏好、社交影响和地理影响，采用线性融合技术集成这3种因素,以此来提高算法的准确率。该方法虽然考虑了地理因素，但是只考虑了用户常驻地特征，推荐的地点都是常驻地附近区域，而且算法的参数不能自适应地调节。此外还有很多学者利用概率产生式模型对位置社交网络的推荐系统进行研究，将影响用户签到决策的各种因素进行综合考虑和集成，比如文献[12]提出的LCARS系统从用户兴趣、地理位置、兴趣点当地特色3个方面分析，来对用户的签到行为进行建模，文献[13]提出的JUMAI系统更是从用户兴趣、兴趣点所在区域与用户所在区域的距离、签到时间，以及兴趣点类别4个角度来指导签到决策。文献[14]在此基础上还考虑了用户在新的地点会产生兴趣漂移情况。但是这些模型均没有考虑兴趣点本身的内容，其次上述模型在对各因素进行建模时，没有体现自适应的特性，即针对不同的兴趣点，何种因素对决策起支配作用。本文提出了用户−区域−内容主题模型，真实地模拟了用户对兴趣点签到的决策过程，实验证明在稀疏的数据集下有较理想的推荐效果。

2 用户−区域−内容主题模型 2.1 模型介绍

用户是否会对特定的兴趣点签到，会受到以下3种因素的影响：

1) 用户自身偏好的影响：一般来说，只有兴趣点满足用户的喜好，用户才会欣然前往并产生签到行为。比如球迷可能去看CBA联赛，而音乐爱好者可能去听演唱会。

2) 兴趣点自身内容的影响：LBSN中基本包含了对兴趣点的介绍信息，图1是豆瓣活动网站的页面信息，该页面显示了活动的时间、地点以及主题。当用户浏览该页面时，可能被活动的主题信息中某个特征所吸引，才促使了用户的签到行为。

3) 兴趣点所属区域的影响。用户根据自身爱好或是事先知晓兴趣点的内容而产生的签到行为可认为是有目的，有主观倾向性的。但并不是所有的访问签到行为都是如此。用户的某次签到行为可能开始是漫无目的的，只是随机选择某一地理区域的某一兴趣点。但是此处的随机也受以下两点约束：1)兴趣点所属区域离用户的距离。当该区域离用户较近时，被用户访问的概率较大，否则访问概率较小。2)区域的主题。当用户外出到新的区域时，对该区域一无所知，也无法从其“相似用户”获得信息，在做决策是否访问某一兴趣点时，往往会受到该区域主题的影响。比如该区域的风俗习惯、当地人的兴趣喜好，或是当地比较著名的人文景点等。

用户对兴趣点签到，必定是受到以上3种因素其中之一的影响。因此本文提出了一种基于用户−区域−内容的联合推荐模型，利用隐主题因子表示上述3种因素，将用户对3种因素的选择过程进行建模。

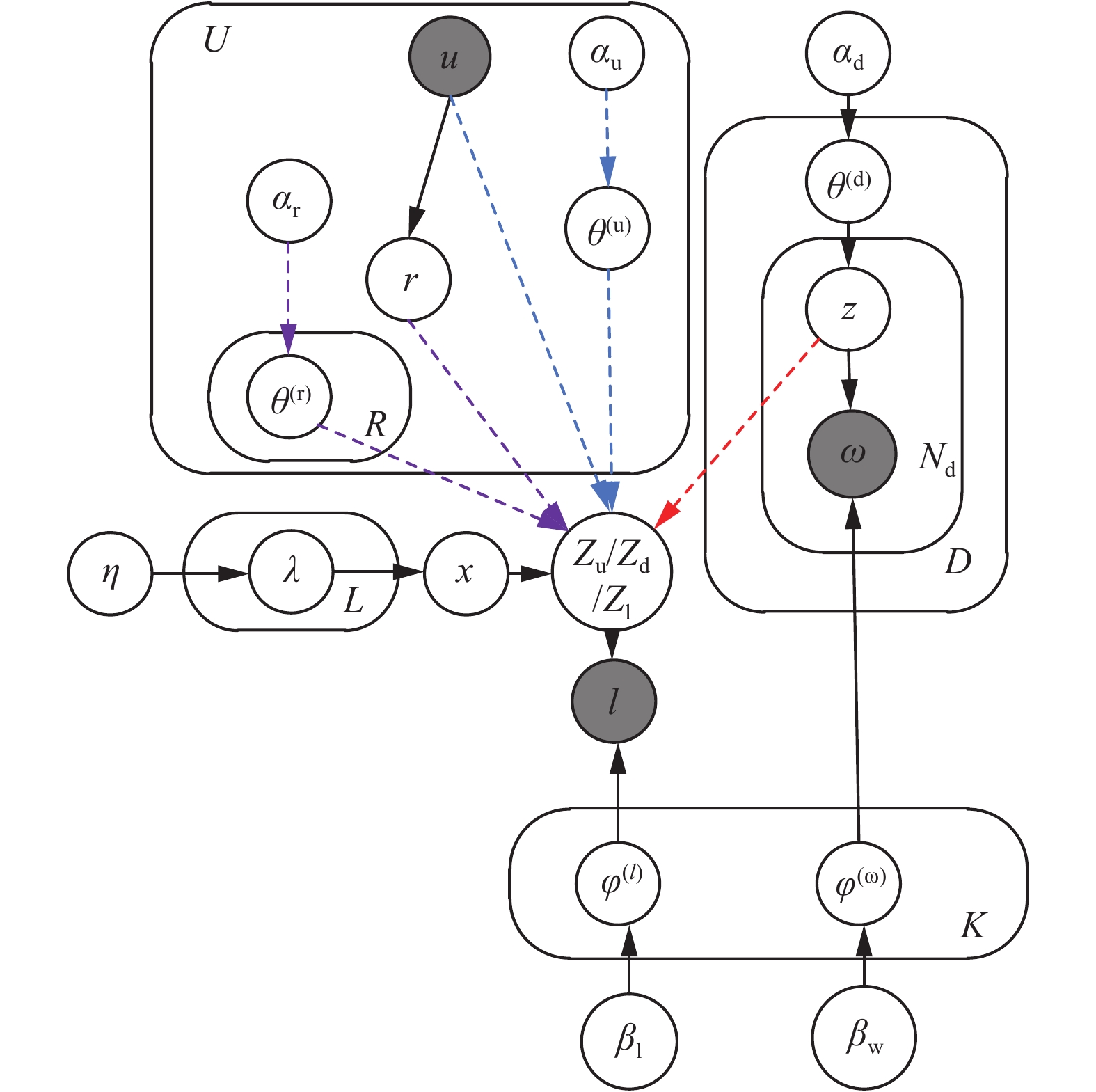
2.2 模型的形式化

图2为用户−区域−内容联合推荐模型对应的概率图。该图右边的部分是一个简单的LDA模型，构造了兴趣点描述文档的生成过程。当用户 $u$ 对兴趣点 ${l_u}$ 签到时 ${l_u}$ 的介绍文档 $d$ 已经存在,文档和单词的主题分布可分别独立计算。当用户对兴趣点 ${l_u}$ 签到时，首先要确定 ${l_u}$ 的主题 $z$ ， $z$ 有3种来源，分别为兴趣点介绍文档 $d$ 中出现过的主题、用户的兴趣以及兴趣点所属地理区域的主题。采用选择变量 $X$ 来控制兴趣点的主题 $z$ 的来源， $X$ 满足多项式分布，其值分别为user、region和content。

假设模型中用户集合为 $U$ ，兴趣点集合为 $L$ ，介绍文档集合为 $D$ ，单词集合为 $W$ ,区域集合为 $R$ ，以及主题集合为 $K$ ，具体生成过程如下：

1) 对于任意文档 $d$ ( $d \in D$ )，根据 ${\rm{Dirichlet}}({\alpha _d})$ 分布得到文档 $d$ 在主题上的多项式分布 ${\theta ^{(d)}}_K$ 。

2) 对于任意主题 $k$ ( $k \in K$ )，根据 ${\rm{Dirichlet}}({\beta _w})$ 分布可得到词 $w$ 在主题 $k$ 上的概率分布 ${\varphi ^{(w)}}_k$ ；根据 ${\rm{Dirichlet}}({\beta _l})$ 分布可得到兴趣点 $l$ 在主题 $k$ 上的分布 ${\varphi ^{(l)}}_k$ 。

3) 对于任意用户 $u$ ( $u \in U$ ),根据 ${\rm{Dirichlet}}({\alpha _u})$ 得到用户 $u$ 的主题分布 ${\theta ^{(u)}}_K$ ,根据 ${\rm{Dirichlet}}({\alpha _{\rm{r}}})$ 得到区域 $r$ 的主题分布 ${\theta ^{(r)}}_K$ ,根据 ${\rm{Dirichlet}}({\alpha _{ur}})$ 得到用户 $u$ 在区域 $r$ 上分布 ${\theta ^{(u{\rm{r}})}}_r$ 。

4) 长度为 ${N_d}$ 的文档 $d$ 中，词 ${w_i}$ 的生成过程为：

①根据文档d的主题分布 ${\theta ^{(d)}}_K$ 抽样获得主题 ${{\textit{z}}_i}$ ；

②利用单词在 ${{\textit{z}}_i}$ 上的概率分布 ${\varphi ^{(w)}}_{{{\textit{z}}_i}}$ 抽样产生单词 ${w_i}$ 。

5) 用户 $u$ 对兴趣点 $l$ 的签到过程如下：

①根据 ${\rm{Dirichlet}}(\eta)$ 抽样得到 ${\lambda _{\rm{l}}}$ ,根据 ${\rm{Mu}}{\rm{ltinomial}}({\lambda _{\rm{l}}})$ 分布得到控制值 $x$ ；

②如果 $x = {\rm{document}}$ ,说明兴趣点的主题由文档 $d$ 生成。此前已抽样得到文档 $d$ 中所有单词的主题集合 $\{ {{\textit{z}}_{{w_1},}}{{\textit{z}}_{{w_2},}} \cdots, {{\textit{z}}_{{w_{Nd}}}}\} $ ,根据 ${\rm{Uniform}}({{\textit{z}}_{{w_1},}}{{\textit{z}}_{{w_2},}} \cdots, {{\textit{z}}_{{w_{Nd}}}})$ 分布抽样生成兴趣点的主题 ${{\textit{z}}_l}$ ；

③如果 $x = {\rm{user}}$ ，说明兴趣点的主题来自于的用户的偏好：根据兴趣主题分布 ${\theta ^{(u)}}_K$ 抽样获得兴趣点的主题 ${{\textit{z}}_l}$ ；

④如果 $x = {\rm{region}}$ ，兴趣点的主题由兴趣点所属区域的主题生成，首先利用用户 $u$ 在区域 $r$ 上分布 ${\theta ^{(u{\rm{r}})}}_r$ 得到区域 $r$ , 根据区域 $r$ 在主题 $k$ 上的概率分布 ${\theta ^{({\rm{r}})}}_k$ 获得主题 ${{\textit{z}}_l}$ 。

6) 最后利用兴趣点在主题 ${{\textit{z}}_l}$ 上的概率分布 ${\varphi ^{({\rm{l}})}}_{{{\textit{z}}_l}}$ 得到 $l$ 。

2.3 确定参数值

模型中变量的联合概率分布为

$\begin{gathered} p(u,r,l,{\textit{z}},x,w) = \\ p(w)p(l{\rm{|}}{\textit{z}},x,r,u)p({\textit{z}},r,u{\rm{|}}x)p(x) = \\ p(w)(p(l{\rm{|}}{\textit{z}},x)p({\textit{z}}{\rm{|}}x,{\theta ^u})p(x = {\rm{user}}) + \\ p(l{\rm{|}}{\textit{z}},x)p({\textit{z}}{\rm{|}}x,{\theta ^d})p(x = {\rm{document}}) + \\ p(l|{\textit{z}},x)p(r{\rm{|}}u)p({\textit{z}}{\rm{|}}x,{\theta ^r})p(x = {\rm{region}})) \\ \end{gathered} $

(1)

由式(1)可知该模型需要估计以下6个参数：1)文档的主题分布 ${\theta ^{(d)}}_{}$ ；2)主题−词分布 ${\varphi ^{(w)}}$ (参数1)、2)为基本LDA模型对应的参数，用于求 $p(w)$ )；3)兴趣点的主题分布 ${\varphi ^{(l)}}$ (即 $p\left( {l{\rm{|}}{\textit{z}},x} \right)$ )；4)用户兴趣分布 ${\theta ^{(u)}}$ ；5)用户活动区域分布 ${\theta ^{(ur)}}_{}$ ；6)选择概率 ${\textit{λ}} $ 的多项式分布(即 $p(x)$ )。

文中采用Gibbs抽样方法，过程如下，具体的参数说明见表1。

1) 利用式(2)计算单词在主题上的后验概率，进而对单词的主题进行抽样，

$ P({{\textit{z}}_i} = k|{w_i},{{\textit{z}}_{ - i}},w{}_{ - i},{\alpha _d},{\beta _w}) \propto \frac{{C_{kd, - i}^{KD} + {\alpha _d}}}{{\sum\limits_{{k'}} {C_{kd, - i}^{KD} + K{\alpha _d}} }} \cdot \frac{{C_{wk, - i}^{WK} + {\beta _w}}}{{\sum\limits_{{w'}} {C_{wk, - i}^{WK} + V{\beta _w}} }} $

(2)

2) 计算兴趣点主题的后验概率，分3种情况:

①当选择变量x=user时，抽样方程为

$\begin{gathered} P({{\textit{z}}_{\rm{j}}} = k,x = {\rm{user}}|{l_j},{{\textit{z}}_{ - j}},{\alpha _u},{\beta _l},\eta) \propto \\ \frac{{C_{ku, - j}^{KU} + {\alpha _u}}}{{\sum\limits_{{k'}} {C_{{k'}u, - j}^{KU} + K{\alpha _u}} }} \cdot \frac{{C_{lk, - j}^{LK} + {\beta _l}}}{{\sum\limits_{{l'}} {C_{{l'}k, - j}^{LK} + L{\beta _l}} }} \cdot \\ \frac{{{\eta _{{\rm{user}}}} + {n_{{l_j},{\rm{user}}, - j}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }} \\ \end{gathered} $

(3)

②当选择变量x=document时，抽样方程为

$\begin{gathered} P({{\textit{z}}_j} = k,x = {\rm{document}}|{l_j},{{\textit{z}}_{ - j}},{\beta _l},\eta) \propto \\ \frac{{C_{kd}^{KD}}}{{{N_{\rm{d}}}}} \cdot \frac{{C_{lk}^{LK} + {\beta _l}}}{{\sum\limits_{{l'}} {C_{{l'}k}^{LK} + L{\beta _l}} }} \cdot \frac{{{\eta _{{\rm{document}}}} + {n_{{l_j},{\rm{document}}, - j}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }} \\ \end{gathered} $

(4)

③当选择变量x=region时，抽样方程为

$\begin{gathered} P({{\textit{z}}_j} = k,{r_j} = r,x = {\rm{region}}|{l_j},{{\textit{z}}_{ - j}},{\alpha _u},{\alpha _{u{\rm{r}}}},{\beta _l},\eta) \propto \\ \frac{{C_{ru, - j}^{RU} + {\alpha _{u{\rm{r}}}}}}{{\sum\limits_{{r'}} {C_{{r'}u, - j}^{RU} + R{\alpha _{ur}}} }} \cdot \frac{{C_{k{\rm{r}}, - j}^{KR} + {\alpha _r}}}{{\sum\limits_{{k'}} {C_{{k'}r, - j}^{KR} + K{\alpha _r}} }} \cdot \\ \frac{{C_{lk, - j}^{LK} + {\beta _l}}}{{\sum\limits_{{l'}} {C_{{l'}k, - j}^{LK} + L{\beta _l}} }} \cdot \frac{{{\eta _{{\rm{region}}}} + {n_{{l_j}{\rm{,region}}, - j}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }} \end{gathered} $

(5)

当式(2)~(5)迭代一定次数后状态稳，可用式(6)~(14)近似计算模型的参数值。

$\theta _{}^{\left( d \right)} = \frac{{C_{kd}^{KD} + {\alpha _d}}}{{\sum\limits_{{k'}} {C_{{k'}d}^{KD} + K{\alpha _d}} }}$

(6)

$\varphi _{}^{\left( w \right)} = \frac{{C_{wk}^{WK} + {\beta _w}}}{{\sum\limits_{{w'}} {C_{{w'}k}^{WK} + W{\beta _w}} }}$

(7)

$\theta _{}^{\left( u \right)} = \frac{{C_{ku}^{KU} + {\alpha _u}}}{{\sum\limits_{{k'}} {C_{{k'}u}^{KU} + K{\alpha _u}} }}$

(8)

$\varphi _{}^{\left( l \right)} = \frac{{C_{lk}^{LK} + {\beta _l}}}{{\sum\limits_{{l'}} {C_{{l'}k}^{LK} + L{\beta _l}} }}$

(9)

$\theta _{}^{\left( {ur} \right)} = \frac{{C_{ru}^{RU} + {\alpha _{ur}}}}{{\sum\limits_{{r'}} {C_{{r'}u}^{RU} + R{\alpha _{ur}}} }}$

(10)

$\theta _{}^{\left( r \right)} = \frac{{C_{k{\rm{r}}}^{KR} + {\alpha _r}}}{{\sum\limits_{{k'}} {C_{{k'}r}^{KR} + K{\alpha _r}} }}$

(11)

${{\textit{λ}} _{l,{\rm{user}}}} = \frac{{{\eta _{{\rm{user}}}} + {n_{l,{\rm{user}}}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }}$

(12)

${{\textit{λ}} _{l,{\rm{document}}}} = \frac{{{\eta _{{\rm{document}}}} + {n_{l,{\rm{document}}}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }}$

(13)

${{\textit{λ}} _{l,{\rm{region}}}} = \frac{{{\eta _{{\rm{region}}}} + {n_{l,{\rm{region}}}}}}{{L + \sum\limits_{x \in \{ {\rm{user,region,document}}\} } {{\eta _x}} }}$

(14)

2.4 模型的推荐

估计模型参数后便可用于在线推荐阶段。对于特定的用户 $u$ 、兴趣点l以及其对应的介绍文档 $d$ ，根据式(15)可得 $u$ 对l签到概率：

$\begin{split} & p(l|d,u) = p(x = d)\sum\limits_{k = 1}^K {p(l|{{\textit{z}}_k})} {p_{{\rm{test}}}}({{\textit{z}}_k}|d) + \\ p(x = u)& \sum\limits_{k = 1}^K {p(l|{{\textit{z}}_k})} p({{\textit{z}}_k}|u)+ p(x = r)\sum\limits_{r = 1}^R {\sum\limits_{k = 1}^K {p(r|u)p({{\textit{z}}_k}|r} } ) \end{split}$

(15)

式中 $p(l|{{\textit{z}}_k})$ 、 $p(x)$ 、 $p({{\textit{z}}_k}|u)$ 、 $p(r|u)$ 、 $p\left( {{{\textit{z}}_k}|r} \right)$ 、 ${p_{{\rm{test}}}}({{\textit{z}}_k}|d)$ 可以通过模型训练获得。如果是新的兴趣点l，可以先将其对应文档d的主题分布 ${p_{{\rm{test}}}}({z_k}|d)$ 在线计算，即将文档d加入到测试集D中，重新用Gibbs抽样的方法获得。如果是新的用户，可以直接根据式(16)来计算：

$p(l|d,u) = \sum\limits_{k = 1}^K {p(l|{{\textit{z}}_k})} {p_{test}}({{\textit{z}}_k}|d)$

(16)

这也在一定程度上解决了用户或资源的冷启动问题。

3 实验结果与分析 3.1 数据集

豆瓣活动是我国最大的社交网络，用户可以在该平台上发布和参与各类活动并签到。该数据集包含了100 000多个用户，300 000个事件，以及3 500 000条签到记录。本文经过预处理后选择了其中20 000个用户、15 000个活动的150 000条签到记录作为实验数据集。

Foursquare是一个大型的公开数据集，该数据集包含11 326个用户，182 968个兴趣点，实验中通过筛选选择其中10 000个用户、25 000个兴趣点进行分析。

3.2 实验结果

为了验证算法的准确性，本文采用了文献[15]提出的评估方法,具体如下：

1)对于任意用户u，随机选择其签到数据中的90%作为训练集S，剩余的10%作为测试数据集T。由于本文要分别计算算法对本地兴趣点和外地兴趣点推荐的准确率，T根据不同的情况划分为本地数据和外地数据(以兴趣点所属城市来区分)。

2)在测试过程中，随机选择用户u尚未签到的200个活动构成集合E，假设这些活动是用户不感兴趣的。

3)将包含用户u的测试集中任意活动e加入到E中构成201个新的活动集合，根据推荐算法选择评分最高的前200个活动作为top-200推荐列表，如果活动e出现在推荐列表中，将hits增1，否则hits保持不变(hits为评分常量)。

4) 评估标准查全率为

${\rm{Recall}} = \frac{{{\rm{\# }}{\rm{hits}}}}{{|T|}}$

(17)

本文选择以下4种算法进行比较：

1) 文献[17]提出的IKNN算法(item-based k-nearest neighbors algorithm)，该算法利用 “近邻用户”来推荐感兴趣的活动，然后根据活动地点离用户的远近进行过滤，优先选择离用户较近的感兴趣的活动。

2)文献[16]提出了CKNN算法(category-based k-nearest neighbors algorithm)，该方法实质上也是协同过滤，将用户的兴趣映射到具体的主题，进而进行推荐。

3) 文献[11]提出的 USG推荐算法，该算法的核心思想还是协同过滤，线性框融合用户偏好、社交影响和地理影响这3种因子。

4) User-Content Topic Model(UCTM) 模型和User-Region Topic Model (URTM)模型，这两种模型可看作UCRTM模型的子模型。当 ${{\textit{λ}} _{l,{\rm{document}}}}$ =0时，此时模型忽略兴趣点介绍文档的内容信息，UCRTM模型退化为URTM模型。当 ${{\textit{λ}} _{l,{\rm{region}}}}$ =0时，此时模型忽略兴趣点所处区域的主题信息，UCRTM模型退化为UCTM模型。

3.3 实验结果

该模型有9个超参数需要设置，对于主题模型来说，超参数的值对最后的输出结果影响不大，但是会影响模型的收敛速度，这里设置 ${\alpha _u}$ 、 ${\alpha _d}$ 、 ${\alpha _{ur}}$ 、 ${\alpha _r}$ 为0.1， ${\beta _w}$ 、 ${\beta _{\rm{l}}}$ 为0.05，所有 $\eta $ 的值为0.01。

1) UCRTM模型为概率产生式模型，本文使用困惑度(Perplexity)作为评价标准，对本模型的预测能力进行评估，判断测试集Dtest中兴趣点生成的不确定性，Perplexity的值越小，表示模型生成兴趣点的性能越好。Perplexity的计算式为

${\rm{Perplexity}}\left( {{D_{{\rm{test}}}}} \right) = \exp \left\{ { - \frac{{\mathop \sum \limits_{d = 1}^{{D_{{\rm{test}}}}} \log \left( {p\left( {{l_d}} \right)} \right)}}{{\left| {{D_{{\rm{test}}}}} \right|}}} \right\}$

(18)

式中p(l_d)由式(15)或(16)得出。由于本模型中包含了两个隐含变量(主题数 $K$ 和区域数 $R$ )，为了分析这两个变量对模型生成能力的影响，首先固定隐含区域数，来观察Perplexity随不同主题数的变化情况。

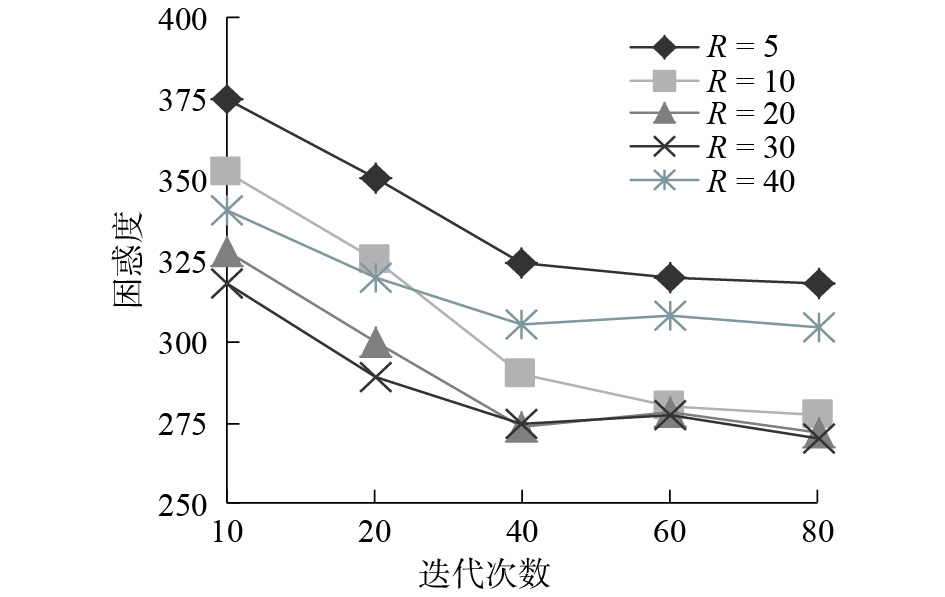
从图3可以看出，当区域个数固定为R=30时，对于不同的主题数，Perplexity 均随着迭代次数的增加不断减小，当迭代次数达到40次后，Perplexity趋于收敛。而且Perplexity还随着主题数K的增大不断减小，当主题数增加到一定程度后，Perplexity不会持续下降，反而会有一些回升。如当K=160时，Perplexity的值相比于K=80时反而增大了，这也在一定程度上说明，合适的主题数K可以提高模型的推荐效果。同理固定主题数K=80，来观察隐含区域数R对Perplexity的影响。如图4所示，区域数与主题数的变化情况类似，当R=30时，可以得到最小的Perplexity值。因此本实验中主题数K设置为80，而区域数R为30。

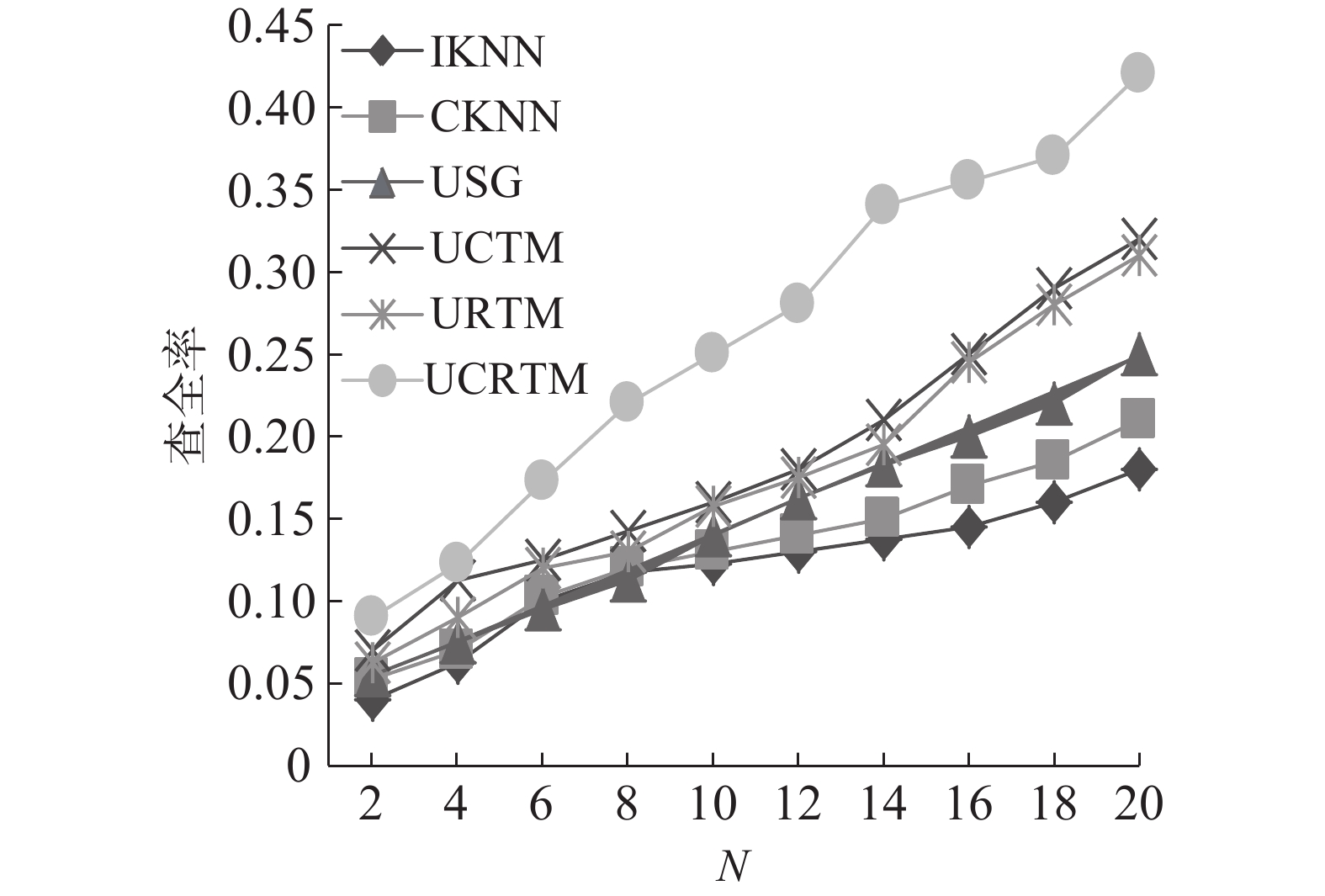
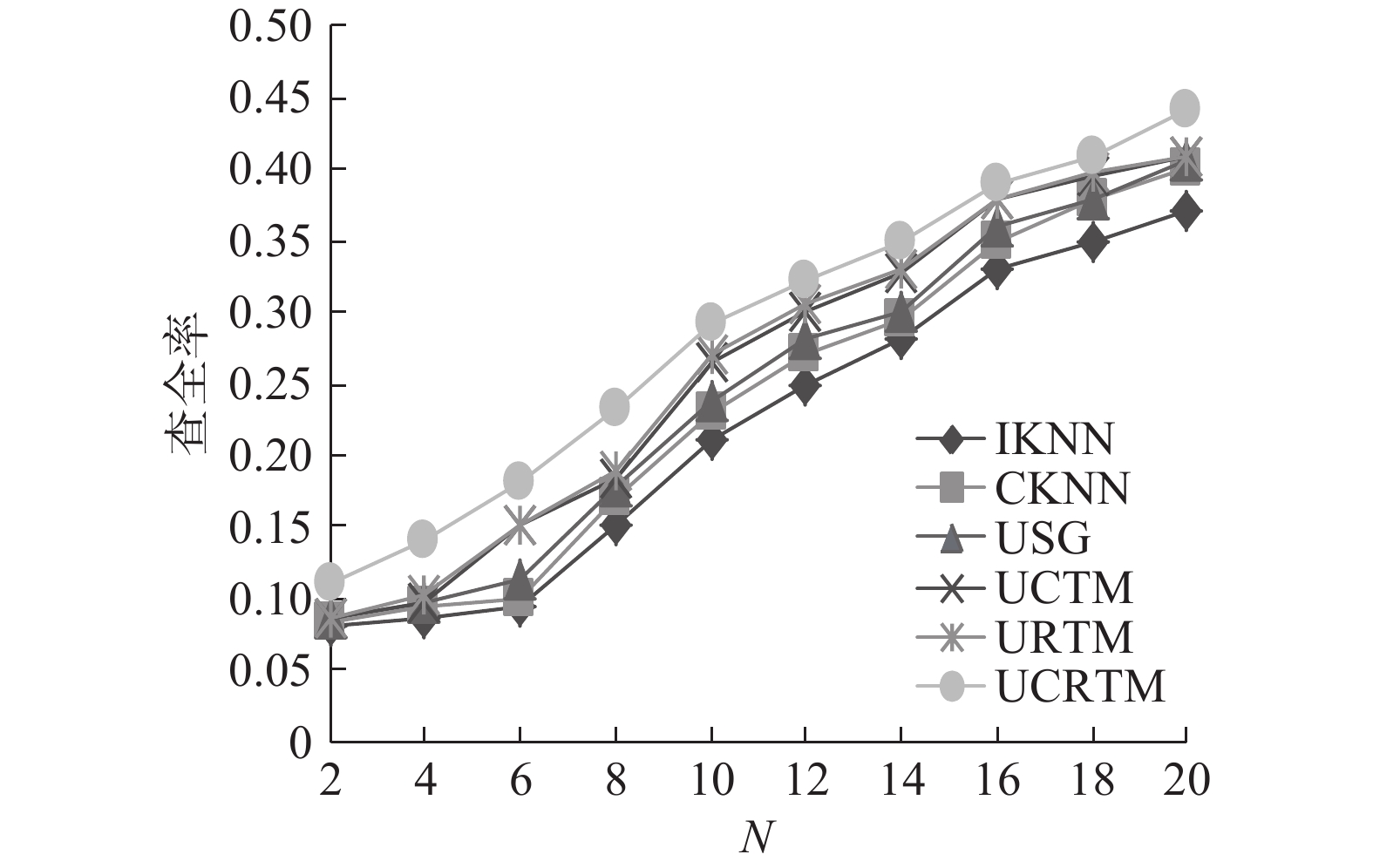
2) 其次比较了各种算法的推荐准确率，因为用户的签到具有地域聚集性，本文将测试集分为两类：用户的本地活动测试集、用户的外地活动测试集。对豆瓣数据集和Foursquare数据集进行了分析。图5~8分别给出了6种算法在两种数据集下的top-N推荐准确率，推荐列表的长度N在2~20变化。

由图5和图6可以看出，随着N的不断增加，各种算法的准确率都是不断提高的。对于外地活动的推荐,UCRTM、UCTM、URTM优于USG、CKNN、IKNN算法，因为后3种方法为协同过滤算法，数据的稀疏性对其影响较大，用户或地点相似性在稀疏的环境下计算不准确，导致推荐准确率不高。由于USG算法考虑了社交好友的影响，推荐效果略好于CKNN和IKNN算法。而隐含主题模型受数据稀疏性的影响较小，在模型中兴趣点的隐含主题同时由用户兴趣分布、兴趣点介绍文档主题分布以及兴趣点所属区域的主题分布的影响，这些信息是对用户签到数据的有益补充。UCTM和URTM均只考虑了其中两方面的影响，所以其推荐的准确程度不如UCRTM模型。

由图7和图8可以看出，在本地活动推荐中，UCRTM模型同样优于其他各种方法，但考虑到用户本地签到的数据较多，采用协同过滤类的算法本身能够准确计算用户的相似性，不需要其他补充信息也能获得较高的准确率，因此最终各种方法的性能差距不大。但是本模型能够扩展更多的上下文信息，可靠性更高。

4 结束语

本文提出的用户−区域−内容联合推荐模型能够克服数据稀疏性以及弱语义性的影响，与其他方法相比有较高的推荐的准确率。以后还将进一步改善模型，增加环境、时间等上下文因素。其次该模型除了应用于兴趣点推荐外，还能将学习出的重要参数(如用户的兴趣爱好、用户的活动特性、地理区域的主题等)用于其他的web服务中。