随着计算机信息技术的发展，每天都会产生大量电信服务、电子商务、金融市场、交通流量、网络监控、超市零售等方面的数据，这些数据是持续增加且不断变化的。由于数据特征会随着时间逐渐变化，针对这些非静态数据的分类、回归、聚类模型也在随着时间而缓慢漂移，称为概念漂移^[1-2]。对概念漂移的研究已在理论上^[1-4]及交通流量预测^[5]、超市客户行为分析^[6]、气体传感器阵列漂移^[7]、垃圾邮件过滤^[8]等应用场合取得了良好的效果。概念漂移建模过程中每个时刻的数据量都很少，因而需要借助相邻时刻的一些数据来构建合适的当前时刻模型。以往针对概念漂移分类所作的工作大多是基于滑动窗算法^[9-11]的思路，即采用一定时间窗口(区间)内的数据进行建模。2011年，Grinblat等^[12]借鉴Crammer等在多任务学习中兼顾局部优化与全局优化的策略，提出了时间自适应支持向量机^[13]方法来求解渐变的子分类器。Shi等^[14]提出了增强型时间自适应支持向量机方法，在提高分类性能的同时，从理论上保证了其对偶为凸二次规划问题。

由于生活中的概念漂移问题并不是孤立出现的，如某个气体传感器阵列上对多种气体的测定数据可能会同时漂移；相邻城市的天气情况具有一定的关联；相近街区的交通流量会相互影响等。对多个相关概念漂移问题同时建模，挖掘其他问题中的有效信息，能对建模起到有益的补充。共享矢量链支持向量机^[15](shared vector chain supported vector machines, SVC-SVM)方法通过对相关概念漂移问题协同建模，有效地提升了所得模型的泛化性能。但由于具有较高的算法时间复杂度，限制了其在数据量急剧增长的社会现状下的应用能力。

现在已进入大数据时代，各种社交和电子商务等信息量都越来越大，多任务概念漂移算法的时间复杂度也变得越来越重要。SVC-SVM方法可转化为核空间中的另一SVM问题，算法时间复杂度一般为 $O({n^{\rm{3}}})$ ，其中 $n$ 为样本容量。如采用SMO(sequential minimal optimization)^[16]方法来求解，其复杂度可降为 $O({n^{{\rm{2}}{\rm{.3}}}})$ ，但SVC-SVM方法仍然无法从容面对大规模概念漂移数据集。本文旨在寻找出一种新的概念漂移学习方法，除了能保持SVC-SVM方法良好的分类特性外，又能在面对多任务概念漂移大规模数据集时具有较好的算法时间性能。

结合前期在概念漂移领域的研究基础^[14-16]，本文提出了共享矢量链核心向量机(shared vector chain core vector machines, SVC-CVM)方法，并基于核心向量机^[17-19](core vector machine, CVM)理论给出了SVC-CVM方法的快速算法。所提SVC-CVM方法具有以下特点：

1)面对多任务概念漂移问题时，SVC-CVM方法优于独立求解单个概念漂移问题的TA-SVM及ITA-SVM方法；

2)SVC-CVM方法采用了与SVC-SVM方法相同的技巧，即假设多个概念漂移问题共享渐变的矢量链序列，因而在分类性能上，SVC-CVM方法与SVC-SVM方法相当；

3)SVC-CVM方法可以借鉴CVM理论^[17]设计出快速求解算法，以处理多任务概念漂移中数据量较大的问题，算法时间复杂度接近 $O(n)$ 。

1 概念漂移问题相关研究

在概念漂移研究方面，传统的研究是基本滑动窗算法，这是一类局部优化模式。TA-SVM和ITA-SVM方法对局部优化和全局优化进行了权衡，取得了良好的效果。

1.1 单任务概念漂移分类方法

TA-SVM^[13]方法及ITA-SVM^[14]方法针对的是传统的单任务概念漂移分类。假设有T个按时间顺序采集的子数据集，TA-SVM方法在优化各子分类器的同时，还假设子分类器应该能够光滑地变化，因此约束相邻子分类器之间的差异，其基本思想可由(1)式来表示。

$ \min \sum\limits_{t = 1}^T {{\rm{Risk}}\left( {{f_t}} \right)} + \lambda \sum\limits_{t = 1}^{T - 1} {d\left( {{f_{t + 1}},{f_t}} \right)} $

(1)

式中：第1项为局部优化项， ${f_t}$ 为第 $t$ 个子分类器；第2项为全局优化项， $d({f_{t + 1}},{f_t})$ 为相邻两个子分类器之间的差别，以保证子分类器能平稳变化； $\lambda $ 是对局部优化与全局优化进行权衡的因子。

1.2 SVC-SVM方法及其对偶

为了能进一步挖掘出相关概念漂移数据集中蕴含的有效信息，需要协同求解多个分类模型。假定现有K个相关概念漂移数据集，每个概念漂移数据集中的数据由T个按时间顺序采集的子数据集组成,每个子数据集中的数据量为m个。将所有数据合并记为数据集 $\left\{ {{\rm{(}}{{x}}{}_i{{,y}}{}_i{\rm{)|}}i = 1,2, \cdots ,n} \right\}$ ， $n = K \times $ $T \times m$ 。记 $f_{tk} $ 为第 $k(k = 1,2,\cdots, K)$ 个任务在第 $t(t = 1,2,\cdots, $ T)时刻的分类模型， ${{{w}}_t}$ 为第 $t$ 时刻的共享矢量， ${{{v}}_{\rm{tk}}}$ 表示在第 $t$ 时刻共享矢量与第 $k$ 个任务 $f_{\rm{tk}} $ 之间的差异。面向多任务概念漂移分类的共享矢量链支持向量机方法SVC-SVM的原理可通过式(2)来表示：

$\begin{aligned}&\min \frac{1}{{{\rm{2}}T}}\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2}} + \frac{\lambda }{{{{{\rm 2}T}}}}\sum\limits_{t = 1}^{T - 1} {{{\left\| {{{{w}}_{t + 1}} - {{{w}}_t}} \right\|}^2}} +\\ &\quad \frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {{{\left\| {{{{v}}_{\rm{tk}}}} \right\|}^2}} } + C\sum\limits_{i = 1}^n {L(f_{\rm{tk}} ,{{x}},y)} \end{aligned}$

(2)

式中： $\min \displaystyle\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2}} $ 为正则化项, $\min \displaystyle\sum\limits_{t = 1}^{T - 1} {{{\left\| {{{{w}}_{t + 1}} - {{{w}}_t}} \right\|}^2}} $ 通过约束相邻时刻共享矢量的差异使共享矢量链的变化尽量平稳， $\lambda $ 为约束各个模型平稳变化的参数； $\min \displaystyle\sum\limits_{t = 1}^T {\displaystyle\sum\limits_{k = 1}^K {{{\left\| {{{{v}}_{\rm{tk}}}} \right\|}^2}} } $ 是使各子任务在同一时刻的模型尽量相似，这是协同求解多个概念漂移问题的关键；权衡因子 $\gamma $ 表示多个任务间的相关程度； $L(f_{\rm{tk}} ,{{x}},y)$ 为损失函数。根据文献[15]的推导，可得到SVC-SVM方法的对偶形式：

$\mathop {\max }\limits_{\bf{\alpha }} {\rm{ }}{{{\alpha }}^{\rm{T}}}{\bf{1}} - \frac{1}{2}{{{\alpha }}^{\rm{T}}}{{H\alpha }} \begin{array}{*{20}{c}} {\rm{s.t.}}&{{{\alpha }} \geqslant 0} \end{array}$

(3)

式中：H为扩展核空间上的某个核函数，具体表达形式可以参见相关文献[15]。从式(3)可知，SVC-SVM方法对多个概念漂移问题同时建模，其对偶问题为核空间中的另一个支持向量机问题，当采用普通方法来求解此二次规划问题时，其算法时间复杂度为 $O({n^3})$ ，即便采用SMO^[16]方法来求解SVC-SVM的对偶问题，使其复杂度降为 $O({n^{2.3}})$ ，仍然是无法承受计算的代价，难以从容面对现实生活中数据规模较大的应用场景。

2 共享矢量链核心向量机及快速算法 2.1 共享矢量链核心向量机

鉴于SVC-SVM方法在针对多任务概念漂移大规模数据集时算法时间复杂度偏高，本文借鉴CVM^[17-19]的思路，提出了与SVC-SVM方法在分类性能相似，但在数据量较大的场景时又能进行快速处理的SVC-CVM方法。SVC-CVM方法借鉴了SVC-SVM方法的思想，为了能进一步用快速算法求解，本文按文献[17-18]的方法对SVC-SVM^[15]的目标函数稍作变化，采用平方损失函数，通过推导得到可以用CVM方法快速求解的对偶形式。

设数据集 $\left\{ {{\rm{(}}{{x}}{}_i{{,y}}{}_i{\rm{)|}}i{\rm{ = }}1{\rm{,}}2{\rm{,}} \cdots {\rm{,}}n} \right\}$ 中含有 $n$ 个样本点，其中包含K个数据流，每个数据流中的数据由T个按时间顺序采集的子数据集组成。在每个时刻引入某个共享矢量，记第 $t$ 时刻各个数据流共享某个矢量为 ${{{w}}_t}$ ,第 $t$ 时刻第 $k$ 个数据流的决策函数为 ${f_{\rm{ tk}}}$ ，并记决策函数与共享矢量之间的差为 ${{{v}}_{\rm{ tk}}}= $ ${f_{\rm{ tk}}}{\rm{ - }}{{{w}}_t}$ 。 ${{P}}$ 为 $T \times n$ 矩阵，用于标识第 $j$ 个点是否为第 $t$ 个时间段的数据， ${{{P}}_{tj}} = 1$ 当且仅当 $j \in {p_t}$ ，否则取值为0。 ${{R}}$ 为 ${\rm tk} \times n$ 矩阵，用于标识第 $j$ 个点是否属于第 ${\rm tk}$ 个子数据集，当且仅当 $j \in {r_{\rm{tk}}}$ 时 ${{{R}}_{{\rm{tk}},j}} = 1$ ，否则取值为0。 ${{Q}}$ 为指示各共享向量之间相关性的 $T \times T$ 矩阵，实际应用中只考虑直接相邻的各共享向量，即当且仅当 $\left| {s - t} \right| = 1$ 时有 $Q_{\rm{st}} = 1$ ，否则值为0。

SVC-CVM方法的目标函数为

$\begin{array}{c}\mathop {\min }\limits_{w,v,b,d} \displaystyle\frac{1}{{{{2T}}}}\displaystyle\sum\limits_{t = 1}^T {({{\left\| {{{{w}}_t}} \right\|}^2} + b_t^2)} + \\\displaystyle\frac{\lambda }{{{{4T}}}}\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {{Q_{ts}}({{\left\| {{{{w}}_t} - {{{w}}_s}} \right\|}^2}} } + {({b_t} - {b_s})^2}) + \\\displaystyle\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {({{\left\| {{{{v}}_{\rm{ tk}}}} \right\|}^2} + d_{\rm{ tk}}^2)} } - \rho + \displaystyle\frac{C}{2}\sum\limits_{i = 1}^n {\xi _i^2}\\ {\rm s.t.}\quad{y_i}\left( {{{({{{w}}_t} + {{ v}_{{\rm tk}(i)}})}^{\rm{T}}}\varphi ({{{x}}_i}) + ({b_t} + {d_{{\rm{tk}}(i)}})} \right) \geqslant \rho - {\xi _i}\\i = 1,2, \cdots ,n\end{array}$

(4)

式(4)中用记号 ${v_{{\rm{ tk}}(i)}}$ 、 ${d_{{\rm{ tk}}(i)}}$ 间接表示第 $i$ 个样本属于任务 $k$ 中的第 $t$ 个子数据集。下面求解式(4)的对偶问题：

$\begin{array}{c}J = \displaystyle\frac{1}{{{{2T}}}}\sum\limits_{t = 1}^T {({{\left\| {{{{w}}_t}} \right\|}^2} + b_t^2)} + \\\displaystyle\frac{\lambda }{{{{4T}}}}\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {{Q_{\rm{ ts}}}({{\left\| {{{{w}}_t} - {{{w}}_s}} \right\|}^2}} } + {({b_t} - {b_s})^2}) + \\\displaystyle\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {({{\left\| {{{{v}}_{\rm{ tk}}}} \right\|}^2} + d_{\rm{ tk}}^2)} } - \rho + \frac{C}{2}\sum\limits_{i = 1}^n {\xi _i^2} - \\\displaystyle\sum\limits_{i = 1}^n {{\alpha _i}\left( {{y_i}\left( {{{({{{w}}_t} + {{ v}_{{\rm{ tk}}(i)}})}^{\rm{T}}}\varphi ({{{x}}_i}) + ({b_t} + {d_{{\rm{ tk}}(i)}})} \right) - \rho + {\xi _i}} \right)} \end{array}$

(5)

由KKT条件，J取得极值时，有

$\frac{{\partial {{J}}}}{{\partial {\xi _i}}} = 0,\frac{{\partial {{J}}}}{{\partial \rho }} = 0,\frac{{\partial {{J}}}}{{\partial {{{w}}_t}}} = 0,$

$\frac{{\partial {{J}}}}{{\partial {b_t}}} = 0,\frac{{\partial J}}{{\partial {{{v}}_{\rm{tk}}}}} = 0,\frac{{\partial J}}{{\partial {d_{\rm{tk}}}}} = 0$

因此有：

$\begin{array}{c}\displaystyle\frac{{\partial J}}{{\partial {\xi _i}}} = 0 = C{\xi _i} - {\alpha _i} \Rightarrow {\xi _i} = {\alpha _i}/C\\\displaystyle\frac{{\partial {{J}}}}{{\partial \rho }} = 0 = - 1 + \sum\limits_{i = 1}^n {{\alpha _i} \Rightarrow } \sum\limits_{i = 1}^n {{\alpha _i} = 1} \end{array}$

(6)

将式(6)代入式(5)则有

$J{\rm{ = }}{J_{{w}}} + {J_{{v}}} + {J_b} + {J_d} - \frac{1}{{2C}}\sum\limits_{i = 1}^n {\alpha _i^2}$

(7)

式中：

$\begin{array}{c}{J_{{w}}}{\rm{ = }}\displaystyle\frac{1}{{{{2T}}}}\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2}} + \frac{\lambda }{{{{4T}}}}\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {{Q_{{\rm ts}}}{{\left\| {{{{w}}_t} - {{{w}}_s}} \right\|}^2}} } - \\\displaystyle\sum\limits_{i = 1}^n {{\alpha _i}{y_i}{{{w}}_{t(i)}}\varphi ({{{x}}_i})} \end{array}$

(8)

${J_{\bf{v}}}{\rm{ = }}\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {{{\left\| {{{{v}}_{\rm{tk}}}} \right\|}^2}} } - \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{{{v}}_{\rm{tk}}}{{_{(i)}} }\varphi ({{{x}}_i})}$

(9)

${J_b}{\rm{ = }}\frac{1}{{{{2T}}}}\sum\limits_{t = 1}^T {{{\left\| {{{{b}}_t}} \right\|}^2}} + \frac{\lambda }{{{{4T}}}}\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {Q_{{\rm ts}} {{\left\| {{{{b}}_t} - {{{b}}_s}} \right\|}^2}} } - \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{b_{t(i)}} }$

(10)

${J_d}{\rm{ = }}\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {d_{{\rm tk}}^2} } - \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{d_{{\rm tk}}}{{_{(i)}} }}$

(11)

又：

$\frac{{\partial {{J}}}}{{\partial {{{w}}_t}}} = 0 {\rm{ = }}\frac{1}{{{T}}}{{{w}}_t} + \frac{\lambda }{{{T}}}\sum\limits_{s = 1}^T {Q_{{\rm ts}} ({{{w}}_t} - {{{w}}_s})} - \sum\limits_{j \in {p_{{\rm tk}}}} {{\alpha _j}{y_j}\varphi ({{{x}}_j})}$

得：

$\frac{1}{{{T}}}\left( {{{{w}}_t} + \lambda \sum\limits_{s = 1}^T {Q_{\rm{ts}} ({{{w}}_t} - {{{w}}_s})} } \right) = \sum\limits_{j \in {p_{\rm{tk}}}} {{\alpha _j}{y_j}\varphi ({{{x}}_j})}$

若定义矩阵M为

${M_{{\rm{st}}}} = \left\{ \begin{array}{l}(1 + \lambda \sum\nolimits_k {{Q_{{\rm{tk}}}})} /T,\quad s = t\\ - \lambda {Q_{{\rm{ts}}}}/T,\!\quad\quad s \ne t\end{array} \right.$

因矩阵M可逆，则

${{{w}}_t} = \sum\limits_j {{{M}}_{{\rm tt}(j)}^{ - 1}} {\alpha _j}{y_j}\varphi ({{{x}}_j})$

(12)

因此有

$\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2} = \sum\limits_t {\sum\limits_{ij} {{{M}}_{{\rm{ tt}}(i)}^{ - 1}{{M}}_{{\rm{ tt}}(j)}^{ - 1}{\alpha _i}{\alpha _j}{y_i}{y_j}\varphi ({{{x}}_i})\varphi ({{{x}}_j})} } } $

由于

${\left( {{{{P}}^{\rm{T}}}{{{M}}^{ - 2}}{{P}}} \right)_{ij}} = \sum\limits_t {{{M}}_{{\rm{tt}}(i)}^{ - 1}{{M}}_{{\rm{tt}}(j)}^{ - 1}} $

则由(12)可得：

$\begin{aligned}\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2}}& = \sum\limits_{ij} {{{\left( {{{{P}}^{\rm{T}}}{{{M}}^{ - 2}}{{P}}} \right)}_{ij}}{\alpha _i}{\alpha _j}{y_i}{y_j}\varphi ({{{x}}_i})\varphi ({{{x}}_j})} = \\ & {{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 2}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }}\end{aligned}$

(13)

同时有

$\begin{array}{c} \displaystyle\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {Q_{{\rm ts}} {{\left\| {{{{w}}_t} - {{{w}}_s}} \right\|}^2}} } = \sum\limits_{{\rm ts}} {Q_{{\rm ts}} \sum\limits_{ij} {({{M}}_{{\rm tt}(i)}^{ - 1} - {{M}}_{{\rm ss}(i)}^{ - 1})} } \times \\({{M}}_{{\rm tt}(j)}^{ - 1} - {{M}}_{{\rm ss}(j)}^{ - 1}){\alpha _i}{\alpha _j}{y_i}{y_j}\varphi ({{{x}}_i})\varphi ({{{x}}_j}) = \\ \displaystyle\sum\limits_{ij} {2(\sum\limits_t {{{M}}_{{\rm tt}(i)}^{ - 1}{{M}}_{{\rm tt}(j)}^{ - 1}{{ D}_{\rm tt}}} - \sum\limits_{ts} {{{M}}_{{\rm tt}(i)}^{ - 1}{{M}}_{{\rm st}(j)}^{ - 1}Q_{{\rm ts}} } )} \times \\ {\alpha _i}{\alpha _j}{y_i}{y_j}\varphi ({{{x}}_i})\varphi ({{{x}}_j}) = \\2{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}({{D}} - {{Q}}){{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} \end{array} $

(14)

式中：Q是对称矩阵，且记对角矩阵D为

${D_{\rm{ts}}} = \left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_k {Q_{\rm tk} }, \begin{array}{*{20}{c}} {}&{t = s} \end{array}} \\ {\begin{array}{*{20}{c}} 0,&{\begin{array}{*{20}{c}} {}&{t \ne s} \end{array}} \end{array}} \end{array}} \right.$

将(12)、(13)代入(8)有

$\begin{gathered} {J_{{{ w}}}}{\text{ = }}\frac{1}{{{{2T}}}}\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_t}} \right\|}^2}} + \frac{\lambda }{{{{4T}}}}\sum\limits_{t = 1}^T {\sum\limits_{s = 1}^T {{Q_{{\rm ts}}}{{\left\| {{{{w}}_t} - {{{w}}_s}} \right\|}^2}} } - \\ \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{{{w}}_{t(i)}}\varphi ({{{x}}_i})} = \frac{1}{{{{2T}}}}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 2}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} + \\ \frac{\lambda }{{{{2T}}}}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}({{D}} - {{Q}}){{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right) \\ {{\alpha }} - {{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} = \\ - \frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} \end{gathered} $

(15)

则由(7)可知

$\begin{array}{c}J{\rm{ = }} - \displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} + \\{J_{{v}}} + {J_b} + {J_d} - \displaystyle\frac{1}{2}{{\rm{\alpha }}^{\rm{T}}}\left( {{{I}}/C} \right){{\alpha }}\end{array}$

(16)

下面求解 ${J_{{v}}}$ 。

${J_{\bf{v}}}{\rm{ = }}\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {{{\left\| {{{{v}}_{\rm{tk}}}} \right\|}^2}} } - \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{{{v}}_{\rm{tk}}}{{_{(i)}} }\varphi ({{{x}}_i})}$

由

$\frac{{\partial {{J}}}}{{\partial {v_{\rm{tk}}}}} = 0 \Rightarrow \gamma {v_{\rm{tk}}} - \sum\limits_{j \in {p_{\rm{tk}}}} {{\alpha _i}{y_i}\varphi ({{{x}}_i})} \\ \Rightarrow {v_{\rm{tk}}} = {1 /\gamma}\sum\limits_{j \in {p_{\rm{tk}}}} {{\alpha _i}{y_i}\varphi ({{{x}}_i})} $

得

$\begin{array}{l} {J_v}{\rm{ = }}\frac{\gamma }{2}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {{{\left\| {{v_{{\rm{tk}}}}} \right\|}^2}} } - \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{v_{{\rm{tk}}\left( i \right)}}} \varphi ({x_i}) = \\ - \frac{1}{{2\gamma }}\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {\sum\limits_{i,j \in {p_{{\rm{tk}}}}}^{} {{\alpha _{{\rm{tk}}(i)}}{\alpha _{{\rm{tk}}({\rm{j}})}}{y_{{\rm{tk}}(i)}}{y_{{\rm{tk}}(j)}}\varphi ({x_{{\rm{tk}}(i)}})\varphi ({x_{{\rm{tk}}(j)}})} } } = \\ - \frac{1}{2}{\alpha ^{\rm{T}}}\left( {({R^{\rm{T}}}R/{\lambda _2}) \otimes K \otimes Y} \right)\alpha \end{array}$

(17)

因此有

$\begin{array}{c}J{\rm{ = }} -\displaystyle \frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} - \\\displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{G}}/{\lambda _2}) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} + \\{J_b} + {J_d} - \displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {{{I}}/C} \right){{\alpha + }}{{{\alpha }}^{\rm{T}}}{\bf{1}}{\rm{ = }}\\ -\displaystyle \frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}} + {{G}}/\gamma ) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} + \\{J_b} + {J_d} - \displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {{{I}}/C} \right){{\alpha }}\end{array} $

又：

$\frac{{\partial {{J}}}}{{\partial {b_t}}} = 0 \Rightarrow \frac{1}{{{T}}}b_t + \frac{\lambda }{{{T}}}\sum\limits_{s = 1}^T {Q_{\rm{st}} ({b_s} - {b_t})} + \sum\limits_{j \in {p_{\rm{tk}}}} {{\alpha _j}{y_j}}$

$\frac{{\partial {{J}}}}{{\partial {d_{\rm{tk}}}}} = 0 \Rightarrow \gamma {d_{\rm{ tk}}} - \sum\limits_{j \in {p_{\rm{ tk}}}} {{\alpha _i}{y_i}} \Rightarrow {d_{\rm{ tk}}} = {1/\gamma}\sum\limits_{j \in {p_{{\rm tk}}}} {{\alpha _i}{y_i}}$

由此可得：

$\begin{array}{c}J{\rm{ = }} - \displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}} + {{{R}}^{\rm{T}}}{{R}}/\gamma ) \otimes {{K}} \otimes {{Y}}} \right){{\alpha }} - \\\displaystyle\frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}} + {{{R}}^{\rm{T}}}{{R}}/\gamma ) \otimes {{K}}} \right){{\alpha }} - \frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {{{I}}/C} \right){{\alpha }}\end{array}$

$J{\rm{ = }} - \frac{1}{2}{{{\alpha }}^{\rm{T}}}\left( {({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}} + {{{{{R}}^{\rm{T}}}{{R}}} / \gamma })} \right.\\ \otimes \left. {{{K}} \otimes ({{Y}} + {{E}}) + {{{I}} / C}} \right){{\alpha }}$

原始问题的对偶问题如下：

$\mathop {\max }\limits_{{\alpha }} {\rm{ }} - \frac{1}{2}{{{\alpha }}^{\rm{T}}}{{H\alpha }} \begin{array}{*{20}{c}} {\rm{s.t.}}&{{{\alpha }} \geqslant 0,{{{\alpha }}^{\rm{T}}}{\bf{1}} = 1} \end{array}$

(18)

式中：

${{H}} = ({{{P}}^{\rm{T}}}{{{M}}^{ - 1}}{{P}} + {{{{{R}}^{\rm{T}}}{{R}}} / \gamma })\\ \otimes {{K}} \otimes ({{Y}} + {{E}}) + {{{I}} / C}$

(19)

${{K}}$ 为核矩阵；

${{Y}} = {{{y}}^{\rm{T}}}{{y}}\;{{y}} = [{y_1}\;{y_2}\; \cdots \;{y_n}]$

${{E}} = {\bf{1}}{\text{×}}{{\bf{1}}^{\rm{T}}};{{1}} = {[{1_1}\;{1_2}\; \cdots \;{1_n}]^{\rm{T}}}$

由此，SVC-CVM方法中虽然包含了多个数据流，但其对偶问题仍相当于核空间中的另一个SVM问题，可以用常规方法来求解，其算法时间复杂度为 $O({n^3})$ ，在算法效率上并不具有优势。因此下文将介绍SVC-CVM的快速求解方法。

2.2 核心向量机

求解最小包含球(minimum enclosing ball, MEB)是一个数学问题，等价于求解一个二次规划问题^[17-19]，如式(20)所示：

$\mathop {\max }\limits_{{\alpha }} {{{\alpha }}^{\rm{T}}}{\rm{diag}}({{K}}) - {{{\alpha }}^{\rm{T}}}{{K\alpha }}\\\begin{array}{*{20}{c}} {\rm{s.t.}}&{\begin{array}{*{20}{c}} {{{\alpha }} \geqslant 0,}&{{{{\alpha }}^{\rm{T}}}{\bf{1}} = 1} \end{array}} \end{array}$

(20)

式中： ${{\alpha }} = {\left[ {{\alpha _1}\,\,{\alpha _2}\,\, \cdots \,\, {\alpha _n}} \right]^{\rm{T}}}$ 为Lagrange 乘子, ${{{K}}_{n \times n}} =$ $ [k({x_i},{x_j})] = [{{\phi}} {({x_i})^{\rm{T}}}{{\phi}} ({x_j})]$ 为核矩阵。 ${\rm{diag}}({{K}})$ 表示由核矩阵 ${{K}}$ 的主对角线元素组成的一维向量。

Tsang等在文献[17-18]中指出，形如式（20）的二次规划问题，如果核矩阵对角线元素为常量，则均等价于求解MEB问题。他们借助求解MEB问题时的近似包含球方法^[19]，提出了核心向量机(core vector machines, CVM),在处理大规模数据集时有接近线性的时间复杂度。对形如式(20)的二次规划问题，即使核矩阵对角线元素不为常量，也可以使用核心集方法进行求解，这时就需要给核空间中每个样本点 $\phi ({x_i})$ 都添加一个新的维度 ${\delta _i} \in R$ ,样本在新特征空间中表示为 $\tilde {{\phi}} ({x_i}) = {[\!\! \begin{array}{*{20}{c}} {\phi ({x_i})}&{{\delta _i}} \end{array}\!\!]^{\rm{T}}}$ ，然后求解在新特征空间中的最小包含球。该问题的形式如下：

$\begin{array}{c}\mathop {\max }\limits_{{\alpha }} {{{\alpha }}^{\rm{T}}}({\rm{diag}}{{K}} + {\rm{\Delta }}) - {{{\alpha }}^{\rm{T}}}{{K}}{{\alpha }}\\{\rm{s.t.}} \quad {{\alpha }} \geqslant 0, \quad {{{\alpha }}^{\rm{T}}}{\bf{1}} = 1\end{array}$

(21)

式中： ${\bf{\Delta }} = {\left[ {\delta _1^2 \,\, \delta _2^2 \,\, \cdots \,\, \delta _n^2} \right]^{\rm{T}}} \geqslant 0$ 是为了保证(20)式中 ${\bf{\alpha }}$ 的系数为常量。将式(21)进一步改写为如下形式：

$\begin{array}{l}\mathop {\max }\limits_{{\alpha }} {{{\alpha }}^{\rm{T}}}({\rm{diag}}{{K}} + {{\Delta }} - \eta {\bf{1}}) - {{{\alpha }}^{\rm{T}}}{{K\alpha }}\\{\rm{s.t.}} \quad {{\alpha }} \geqslant 0, \quad {{{\alpha }}^{\rm{T}}}{\bf{1}} = 1\end{array}$

(22)

式中： $\eta \in R$ 为用户自定义常数，目的是为了保证 ${\bf{\alpha }}$ 的系数为非负的。

2.3 SVC-CVM的快速算法

当使用普通方法来求解SVC-CVM时，其求解时间复杂度为 $O({n^3})$ ，对于多任务概念漂移大规模数据集来说，是相当大的计算开销。对比式(18)和式(22)，它们具有相似的形式，因此，SVC-CVM方法可以利用核心向量机技巧来求解。可以将式(18)等价地改写为

$\begin{array}{c}\mathop {\max }\limits_{{\alpha }} {{{\alpha }}^{\rm{T}}}({\rm{diag}}({{H}}) + {\bf{\Delta }} - \eta {\bf{1}}) - {{{\alpha }}^{\rm{T}}}{{K\alpha }}\\{\rm{s.t.}} \quad {{\alpha }} \geqslant 0, \quad {{{\alpha }}^{\rm{T}}}{\bf{1}} = 1\end{array}$

(23)

这是一个标准MEB问题，其中 ${\bf{\Delta }} = - {\rm{diag}}({{H}}) + \eta {\bf{1}}$ ，通过适当调节常数 $\eta $ 的值，可以保证 ${\bf{\Delta }} \geqslant {\rm{0}}$ 。

SVC-CVM算法的输入为多任务概念漂移大规模数据集S, 核心集逼近精度 $\varepsilon $ 、 $\eta $ 、 $\Delta $ 等参数；输出为核心集 ${S_t}$ 和权重系数 $\alpha $ 。下面给出实现步骤：

由于SVC-CVM算法是基于核心集理论的，因而在描述算法的时间与空间复杂度时，可以参考文献[17-18]，得到相关结论：

性质1 对于给定的误差 $\varepsilon $ ，由SVC-CVM算法求得的核心集数量的上界、算法迭代次数的上界、得到的支持向量数目上界都为 $O(1/\varepsilon )$ 。

输入　数据集S, 最小包含球近似精度；

1) 初始化核心集 ${S_0}$ ，最小包含球半径 ${R_0}$ 和中心 ${c_0}$ ，并设置初始迭代次数 $t = 1$ ;

2) 若所有点都包含在球 $B\left( {{c_t},(1 + \varepsilon ){R_t}} \right)$ 中,则转7);

3) 找到离中心 ${c_t}$ 最远的点 $x$ ,并将其加入核心集，即 ${S_{t + 1}}$ = ${S_t} \cup x$ ;

4) 对新的核心集进行求解，得到新的半径 ${R_{t + 1}}$ 和中心 ${c_{t + 1}}$ ，并更新权重系数 $\alpha $ ;

5) 计算新的中心到其他各点的距离 ;

性质2 对于给定的近似误差 $\varepsilon $ ，SVC-CVM算法时间复杂度上界应为 $O(N/{\varepsilon ^2} + 1/{\varepsilon ^4})$ 。

6) $t = t + 1$ ，转2 ;

7) 终止训练，返回求解的核心集 ${S_t}$ 及权重系数 $\alpha $ ;

输出　核心集 ${S_t}$ ，权重系数 $\alpha $ 。

3 实验研究和分析

本节将对SVC-CVM方法进行实验验证，实验将从SVC-CVM方法的分类准确率、SVC-CVM算法的时间性能两个方面展开。这里有必要首先验证其分类准确率。1)需要考察引入分类间隔 $\rho $ 及采用平方损失函数以后，SVC-CVM算法是否保持了良好的分类能力；2)因为SVC-CVM方法的有效性是其快速算法有效的必要条件。本文另外选取了在单任务概念漂移建模中取得良好效果的两个方法作为对比算法,作为对比算法的共有：1)TA-SVM方法^[13]；2)ITA-SVM方法^[14]；3)SVM-SVM方法^[15]。为了对比的客观性，本节实验中所使用的数据集及实验的设置都参照对比算法TA-SVM ^[13]。实验环境为MATLAB R2013a，操作系统为Windows7，8 GB内存及3.30 GHz奔腾处理器。

3.1 实验设置

实验中涉及的各方法与相应参数在表1中列出。

本文独立生成相同分布的训练集、验证集和测试集各10组，共进行10次重复实验，以获得比较客观的实验结果。实验分为参数优化和建模测试两个阶段，首先需要基于训练集，利用验证集获得各方法的最优参数；其次基于得到的优化参数对训练集建模，并利用测试集来获得各方法的性能。本文采用网格遍历法来寻找最优参数。

将旋转超平面数据集记为数据集DS₁中的第1个任务Task₁，Task₁数据集的样本量为500，采样于独立分布的2维立方体 ${[ - 1,1]^d}$ ，两类之间的边界是一个超平面，并绕原点缓慢旋转。设超平面的法向量为 ${{v}}$ ，Task₁的训练、验证、测试数据由式(24)生成：

$\begin{array}{c}{v_1}(i) = \cos (2\text{π} i/500),{v_2}(i) = \sin (2\text{π} i/500)\\{y_i} = {\rm{sign}}({{{x}}_i}{{v}}(i)),1 \leqslant i \leqslant 500\end{array}$

(24)

数据集DS₁中的第2个任务Task₂数据则由Task₁模型顺时针旋转一定的角度 $r$ ( $r \in \left\{ {2,4,6,8,10} \right\}$ )后随机生成，以体现出Task₂与Task₁模型的相关性。

将TA-SVM方法中所使用的高斯漂移数据集记为数据集DS₂中的第1个任务Task₁，数据集中包含两个类别，共含有 $n(n = 500)$ 个数据点，每个类别中数据的特征都在缓慢变化。Task₁的训练、验证、测试数据由式(25)取 $r = 0$ 时独立生成，DS₂中还包含另一个概念漂移数据集Task₂，其数据同样由(25)式生成，这时 $r \ne 0$ ，以体现任务之间的差异性。

${x_t} = {\frac{{2t\text{π} }}{n} - \text{π} + 0.2{y_t} + {\varepsilon _1},(1 - r){\rm{\times}}\sin (\frac{{2t\text{π}}}{n} -\text{π}+ 0.2{y_t}) + {\varepsilon _2}} $

(25)

式中： $t = 1,2, \cdots ,n$ ， ${\varepsilon _{1,2}}$ 服从于均值为0，方差为 $\sigma = 0.1$ 的正态分布， $ {y_{t2}} $ 、 $ {y_{t2}} $ 是 $ \pm 1$ 的随机序列，并保持正类负类个数的均衡。为体现出两个概念漂移数据集Task₁与Task₂的相关性及差异性，将Task₂的生成模型式(11)中的第二维数据作了适度的扰动，用参数 $r$ 来表示概念漂移数据Task₂较之Task₁的偏离程度，其中 $r \in \left\{ {0.05,0.1,0.2,0.3} \right\}$ 。

将DS₁、DS₂中的类别标签按一定比例随机替换以模拟噪音数据，得到数据集DS₃、DS₄，用于测试SVC-SVM方法在噪音条件下的分类能力。

数据集DS₅、DS₆由DS₁, DS₂逐步加大采样量分别得到，它们用于测试SVC-CVM方法的算法时间复杂度。实验所用数据集如表2所示。

3.2 SVC-SVM的分类性能

本子节基于数据集DS₁和DS₂来观察SVC-CVM方法的分类能力，并将在噪音数据集DS₃、DS₄上观察SVC-CVM方法在噪音条件下的性能。

针对数据集DS₁，依据文献[13]的策略，我们独立生成10组训练集、测试集及用于选择最优参数的验证集。根据前述的实验设置，实验分为优化参数和建模测试两个阶段。核函数选用最常用的线性核及高斯核。当两个概念漂移数据Task₁、Task₂呈现出不同的偏离程度 $r$ 时，求得各方法在两个概念漂移数据Task₁、Task₂上的分类精度及平均值Average。每个方法对各训练集共计10次运行后的平均分类精度及标准差记录在图1中。

由图1可以得到如下观察：

1)在数据集DS₁上，不管采用高斯核还是线性核，当多个任务呈不同偏移程度时，协同求解多个概念漂移问题的SVC-SVM、SVC-CVM方法在任务Task₁和Task₂上总是优于独立求解单个概念漂移问题的TA-SVM和ITA-SVM方法，显示了协同求解多任务概念漂移问题是有效的。

2)随着多个任务之间偏离程度的增加，相对于独立求解单个任务，协同求解方法的优势逐渐减弱。

3)不管是采用高期核还是线性核，也不管任务间的偏移程度，用普通方法求解的SVC-SVM与核心集技术求解的SVC-CVM的分类性能都非常接近。

对高斯漂移数据集DS₂，按照同样的实验流程，求得当两个任务Task₁、Task₂呈现出不同的偏离程度 $r$ 时，各方法的分类性能。每个方法对各训练集共计10次运行后的平均分类精度及标准差记录在表3及表4中。

由表3及表4可以得到如下观察：

1)在高斯漂移数据集DS₂上，不管是采用高斯核还是线性核，协同求解多个概念漂移问题的SVC-SVM、SVC-CVM方法总是优于独立求解单个概念漂移问题的TA-SVM方法及ITA-SVM方法，与数据集DS₁上的实验结果相似。

2)采用高期核或线性核时，不管任务间的偏移程度，SVC-CVM与SVC-SVM方法的分类性能是相当的。

下面继续评估SVC-CVM方法在噪音数据集DS₃和DS₄上的表现，以观察本文方法的抗噪能力。与文献[13]的实验设置相同，通过将DS₁和 DS₂上的类别标签随机变换来模拟噪音数据，噪音比例分别为2%～10%。在数据集DS₃和DS₄上，当含有不同噪音时各方法的实验结果记录在表5到表6中。

由表5及表6可知：

1) 在噪音数据集DS₃及DS₄上，不管采用高斯核或是线性核时，SVC-SVM和SVC-CVM方法相对于独立求解的TA-SVM方法及ITA-SVM方法，都有较大的优势。

2) SVC-CVM与SVC-SVM方法在噪音情况下的分类性能是相当的。

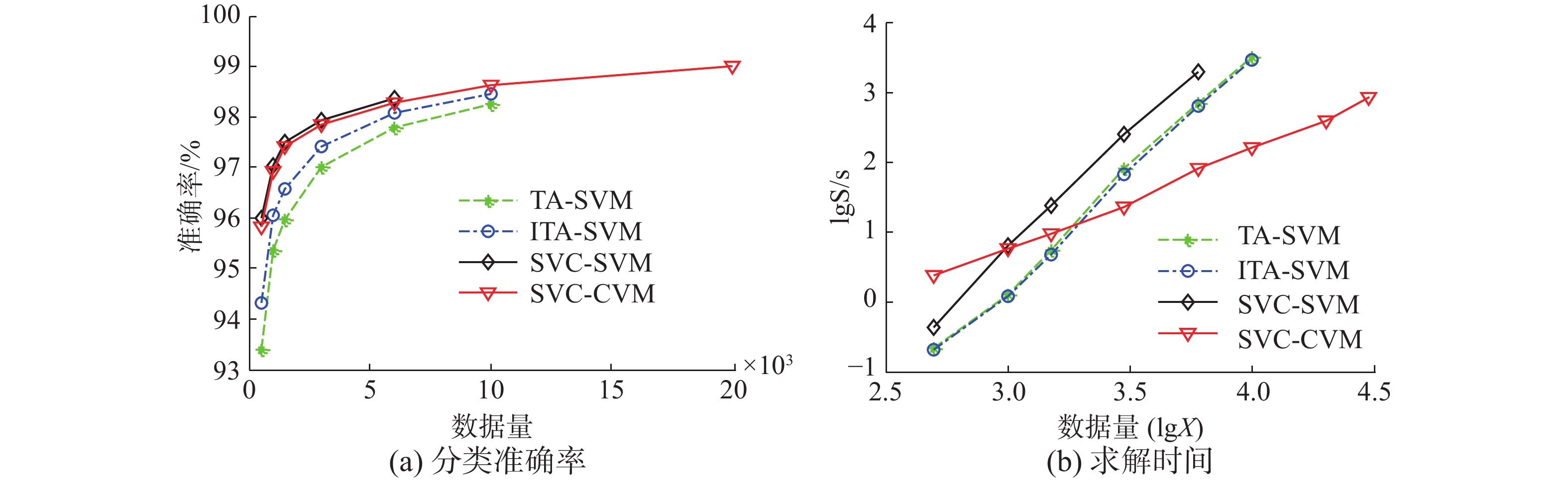
3.3 SVC-CVM方法的时间性能

本子节将以数据集DS₅、DS₆为基础来评估各方法的算法时间效率。各数据集的样本量从500缓慢增加到30 000个。对于数据集DS₅，独立生成10组训练集及测试集，并将各方法在取不同容量样本时的平均准确率及平均训练时间显示在图2中。随着数据量增加时，为了能更准确地观察各方法时间性能的量级，本文分别以 ${\log _{10}}n$ ( $n$ 为样本量)为横坐标，以 ${\log _{10}}S$ (S为运行时间，单位为s)为纵坐标描述各方法的时间性能图，将始的指数曲线转化为线性曲线，斜率代表运行时间的指数量级，如图2(b)所示。

由图2可以得到如下观察：

图2(a)可知，在数据集合DS₅上，随着训练数据量的加大，各方法的泛化性能稳定增加。同时SVC-SVM和SVC-CVM方法优于独立求解单个概念漂移问题的TA-SVM和ITA-SVM方法。由于用普通SVM方法求解时需要先求解相应方法的核矩阵，因此受硬件约束较大，当数据量较大时，相应方法无法继续求解。而SVC-CVM方法采用核心集技术求解，相应的支持向量逐个添加到核心集中，不需要预先计算核矩阵，因而能处理更大容量的数据，得到泛化能力更强的模型。

图2(b)可知，在数据集DS₅上，求解各方法所需时间与数据量之间呈现稳定的指数级关系，其中SVC-CVM方法所表示的准直线的斜率明显小于其他方法，显示了SVC-CVM方法在时间效率上远优于TA-SVM、ITA-SVM与SVC-SVM方法。

在数据集DS₆上，按相同的流程进行训练及测试，并将各方法在不同容量样本上的平均准确率和标准差、平均训练时间和标准差分别记录在表7及表8中(其中—表示在本文实验环境中无法得到相应结果)。

由表7及表8可以得到如下观察：

1) 从表7中可以看出，在数据集DS₆上，随着训练数据量的增加，各方法的分类性能逐渐增高，其中SVC-SVM和SVC-CVM的分类性能相当，都优于独立求解单个概念漂移问题的TA-SVM与ITA-SVM方法。

2) 从表8可以看出，在数据集DS₆上，当数据量较小时，SVC-CVM方法的求解时间上并不具有优势。当数据量的逐渐增加时，SVC-CVM方法求解时间的变化很缓慢，明显优于用普通二次规划方式进行求解。

在数据集DS₅和DS₆上的实验可知，当数据量不大时，SVC-SVM方法和SVC-CVM方法都优于独立求解的方法，且两者的分类性能相当。当数据量很大时，只有SVC-CVM方法能处理较大规模数据集，且在算法时间性能上保持近线性时间复杂度，因而具有较强的实用性。

4 结束语

本文提出了适用于对概念漂移大规模数据集快速求解的多任务核心向量机方法SVC-CVM。由于采用共享矢量链技术协同求解多个概念漂移问题，SVC-CVM方法在分类精度上等价于SVC-SVM方法，明显优于独立求解单个概念漂移问题的TA-SVM及ITA-SVM方法，且SVC-CVM算法在面对多个概念漂移大数集时仍然能够进行快速建模决策。当然SVC-CVM方法仍需要进一步研究，特别是多任务概念漂移大规模数据集的回归问题；多任务概念漂移大规模数据集的单类问题，将是更有意义的挑战。