随着生活水平的提高，人们对海参等海珍品的需求量越来越大。底播养殖是海参的主要养殖方式，即将海参苗播撒在海底进行养殖，待长成后再进行捕捞。由于海参无法采用拖网捕捞，主要以人工下潜作业的方式采捕，劳动强度大、产量低，养殖企业迫切需要自动化的装备以替代人工采捕^[1]。目前水下机器人广泛应用于水下检测、识别等海洋活动中^[2-4]，应用带有机器视觉的水下机器人进行海参采捕也是可行的方式，但由于水下光照、悬浮物、水对光线的吸收和散射等等原因，水下图像通常对比度低，质量差，因此应用机器视觉技术对海参目标进行识别和跟踪抓捕非常困难。

目前针对目标跟踪问题，已经提出了许多算法，主要分为生成式跟踪算法和判别式跟踪算法两类。生成式跟踪算法通过搜索与目标外观模型最相似的区域以实现跟踪。判别式跟踪算法将目标跟踪看作二值分类问题，通过对目标进行机器学习生成的分类器将视场中的目标和背景区分开，分类器置信度最大的位置就是目标位置。考虑到水下特殊的光学环境，判别式跟踪算法不需要生成准确的目标模型特征，因此更有优势。判别式算法中的相关滤波跟踪算法由于速度快、精度高，近年来成为目标跟踪领域的研究热点^[5-19]。David S.Bolme等^[6]首先将相关滤波方法应用到视觉跟踪领域，提出平方输出误差总和最小(MOSSE)的相关滤波器的追踪方法。Henriques等^[7]利用对单张目标图像循环移位的方法进行密集采样，并用核岭回归分析方法训练滤波器，即CSK滤波器，分类器的训练和检测都利用快速傅里叶变换转换到频域实现，追踪速度很快。在CSK基础上，Henriques等^[8]提出了核相关滤波方法(KCF)，引入了梯度方向直方图(HOG)特征,有效提升了算法性能。杨德东等^[9]在KCF的基础上，引入空间正则化和在线SVM分类器重定位组件，以解决KCF跟踪器在跟踪过程中目标因严重遮挡、相似目标干扰和移出视野等因素而造成的跟踪失败问题。Zhang等^[10]提出了STC方法，利用了置信图和快速傅里叶变换减少了图像中目标区域在图像模糊时对目标识别与定位的影响，提高了目标定位的准确度和追踪效率。张雷等^[11]通过对正则化最小二乘分类器学习获得位置和尺度核相关滤波器，并通过寻找位置和尺度核相关滤波器输出响应的最大值实现目标位置和尺度的检测。段伟伟等^[12]提出一种分块核化相关滤波跟踪算法，根据目标外观特性对目标进行子块划分，单独跟踪每个目标子块，并根据子块的跟踪结果确定整体的位置信息。邢运龙等^[13]提出了基于相位特征的高斯核相关算子增强算法对光照强度变化的适应能力，并融合kalman滤波器提高系统在目标遮挡时的准确性。

大多数的追踪方法，如MOSSE、CSK、KCF等都仅限于检测目标的移动，在检测目标尺度变化时，追踪目标的效果不好。虽然有少数的跟踪算法可以检测目标尺度变化^[14-16]，但是运行速度较慢，不能实现实时追踪要求。本文为实现利用水下机器人进行海参采捕的要求，在KCF算法的基础上，提出一种能够适应大尺度变化的海参目标跟踪算法，主要思想是通过跟踪两个头部位置计算出目标海参的中心位置，并进行尺度估计。实验表明本文提出的算法可以有效地提高跟踪的准确性和效率。

1 KCF跟踪方法

KCF算法(Kernel correlation filters)通过核化岭回归分析方法解决目标追踪问题。在相关滤波方法的基础上，利用基准样本的循环位移方法构造训练集训练分类器，而且在训练和检测时利用快速傅里叶变换将耗时的矩阵运算转换到频域求解，显著提高了跟踪精度和效率。

1.1 循环矩阵

按图1所示方法，将 $1 \times n$ 的基础向量 ${{x}}$ 循环移位可以得到 $n \times n$ 的循环矩阵 ${{C}}({{x}})$ ，即

${{X}} = {{C}}({{x}}) = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}&{{x_3}}& \cdots &{{x_n}} \\ {{x_n}}&{{x_1}}&{{x_2}}& \cdots &{{x_{n - 1}}} \\ {{x_{n - 1}}}&{{x_n}}&{{x_1}}& \cdots &{x{}_{n - 2}} \\ \vdots & \vdots & \vdots & & \vdots \\ {{x_2}}&{{x_3}}&{{x_4}}& \cdots &{{x_1}} \end{array}} \right]$

(1)

循环矩阵可以通过傅里叶变换对角化：

${{C}}({{x}}) = {{{F}}^{\rm{H}}}{\rm{diag}}\left( {\hat {{x}}} \right){{F}}$

(2)

式中： $\hat {{x}}$ 是基础向量的离散傅里叶变换； ${\rm{H}}$ 表示矩阵的共轭；F 是离散傅里叶变换矩阵(DFT)，该矩阵的性质为

$\left\{ \begin{array}{l} \hat {{x}} = {{F}}{{x}} \\ {{{F}}^ * } = {{{F}}^{\rm{H}}} = {{{F}}^{ - 1}} \\ {{F}} = {{{F}}^{\rm{T}}} \\ \end{array} \right.$

(3)

1.2 训练样本的建立

在视频第一帧图像中，在给出的目标位置选取大小为 $M \times N$ 的图像块 $x$ 作为基准输入样本，利用式(3)计算得到的相同大小高斯响应图像作为基准输出样本 $y$ ，如图2所示。

${y_{ij}} = \exp \,\, \left( - \frac{{{{(i - w)}^2} + {{(j - h)}^2}}}{{2\delta _p^2}}\right)$

(4)

把 $(x,y)$ 所有循环移位得到的图像块 $({x_i},{y_i})$ 作为训练样本，如图3所示。

1.3 跟踪算法

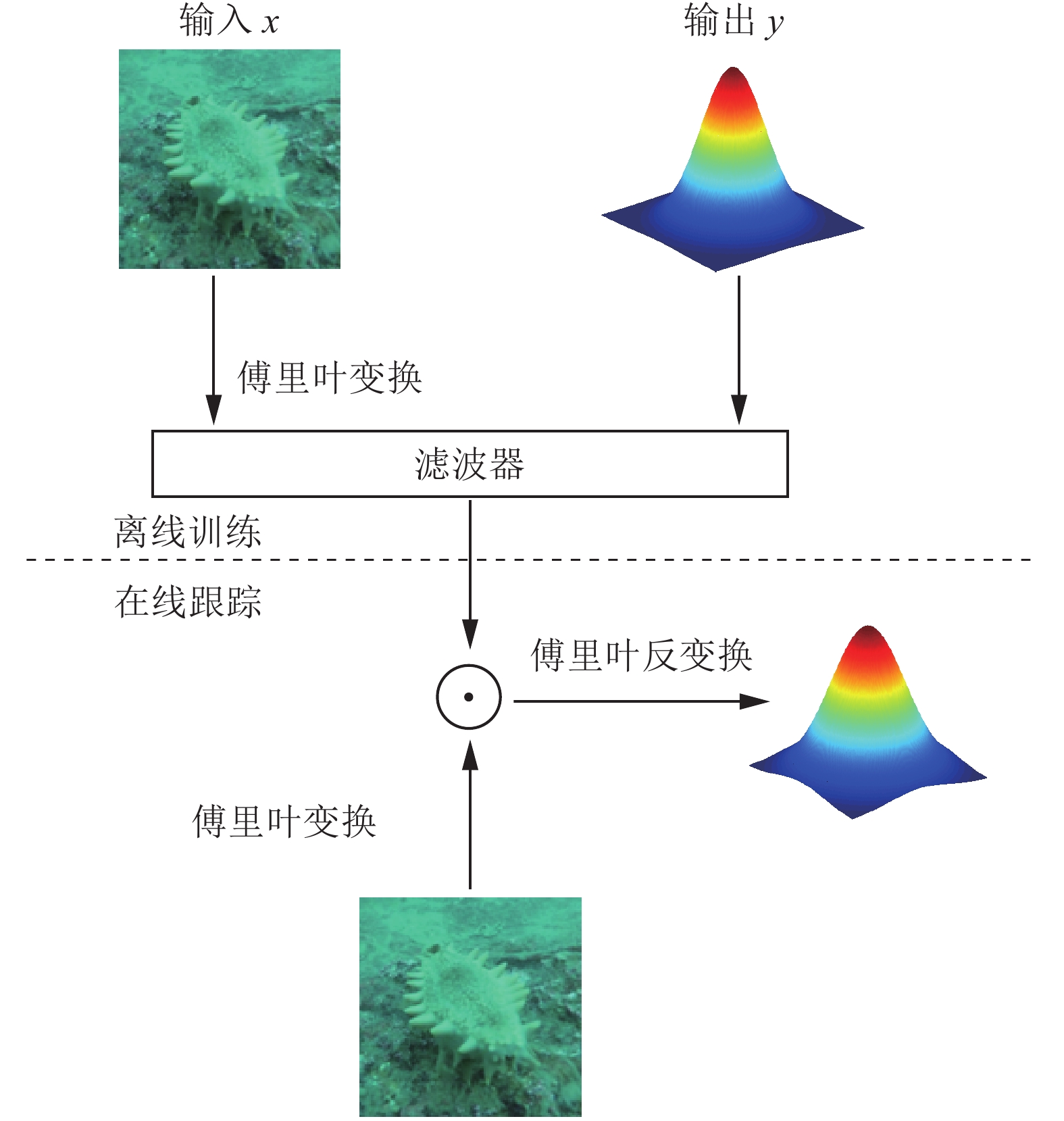
KCF算法的基本流程分为离线训练和在线检测两步。在训练时，以初始帧中给出的目标图像为输入信息，对应的高斯响应为输出信息，利用离散傅里叶变换转换到频域求解滤波器。在线跟踪检测时，用滤波器对包含目标的图像进行滤波可得到高斯型的响应面。响应面最大的位置就是目标位置。KCF算法的基本流程如图4所示。

离线训练的关键是求解分类器 $f({{{{z}}}}) = {{{w}}^{\rm{T}}}{{{{z}}}}$ ，使得在输入样本 ${x_i}$ 基础上计算得到的 $f({x_i})$ 与输出样本 ${y_i}$ 的均方差最小,即求解式(4)所示目标函数：

$\mathop {{\rm{min}}}\limits_w {\sum\limits_i {{{(f({x_i}) - {y_i})}^2} + {\textit{λ}} \left\| w \right\|} ^2}$

(5)

式中 ${\textit{λ}} $ 为控制过拟合的正则化系数。式(4)存在闭式解：

${{w}} = {{{X}}^{\rm{T}}}{({{X}}{{{X}}^{\rm{T}}} +{\textit{λ}} {{I}})^{ - 1}}{{Y}}$

(6)

式中 X 和 Y 分别是由输入样本 ${x_i}$ 和输出样本 ${y_i}$ 组成的循环矩阵。令

${{\alpha }} = {({{K}} + {\textit{λ}} {{I}})^{ - 1}}{{Y}}$

(7)

式中 ${{K}} = {{X}}{{{X}}^{\rm{T}}}$ ，则分类问题由求解 ${{w}}$ 转变为求解对偶解 $\alpha $ ，即

${{w}} = {{{X}}^{\rm{T}}}\alpha = \sum\limits_{i = 1}^n {{\alpha _i}{x_i}} $

(8)

利用核技巧，即采用映射函数 $x \to \varphi (x')$ ，以及用核函数代替内积 $\kappa (u,v) \to \varphi (u)\varphi (v)$ ，可在不显式给出映射函数 $\varphi ( \cdot )$ 的情况下，将训练样本 $x$ 映射到高维特征空间 $x'$ ，从而将线性分类问题推广为非线性分类问题。则式(6)中 ${{{K}}_{ij}} \!\!=\!\! {{{\phi}} ^{\rm{T}}}({x_i})\phi ({x_j}) \!\!=\!\! \kappa ({x_i},{x_j})$ ，即 K 转化为核矩阵，可以证明当 $\kappa $ 采用高斯核函数时 K 是循环矩阵,即 ${{K}} = {{C}}(\kappa (x,x))$ 。应用循环矩阵的性质即式(1)和式(2)可将式(6)对角化得到

${\hat \alpha ^ * } = \frac{{\hat {{y}}}}{{\hat \kappa ({{x}},{{x}}) + {\textit{λ}} }}$

(9)

式中x 和 y 分别是组成 X 和 Y 的基础向量。 $\hat \kappa (x,x')$ 为高斯核函数的傅里叶变换，按式(9)计算：

$\hat \kappa \left( {{{x}},{{x}}'} \right) = \exp \left( { - \frac{1}{{{\sigma ^2}}}{{\left( {\left\| {{x}} \right\|} \right)}^2} + {{\left( {\left\| {{{x}}'} \right\|} \right)}^2} - 2{F^{ - 1}}\left( {\hat {{x}} \odot \hat {{x}}'*} \right)} \right)$

(10)

式中： $ \odot $ 表示两向量间对应元素乘运算；符号 $ * $ 表示复共轭。

利用核技巧，对新输入的图像块 z，分类器的响应为

$\begin{aligned} f({{z}}) = & {\left( {\sum\limits_{i = 1}^n {{{{\alpha}} _i}{{\phi}} ({{{x}}_i})} } \right)^{\rm{T}}}{{\phi}} ({{{{z}}}}) = \sum\limits_{i = 1}^n {{{{\alpha}} _i}{{{\phi}} ^{\rm{T}}}({{{x}}_i})} {{\phi}} ({{{{z}}}}) = \\ & \sum\limits_{i = 1}^n {{{{\alpha}} _i}\kappa ({{{x}}_i},{{{{z}}}})} = {({{C}}(\kappa ({{x}},{{{{z}}}})))^{\rm{T}}}{{\alpha}} \end{aligned} $

(11)

应用循环矩阵的性质，即式(1)和式(2)，式(10)可进一步转换到频域计算：

$f = {{{F}}^{ - 1}}\left( {\hat \kappa {{({{x}},{{{{z}}}})}^ * } \odot \hat {{\alpha}} } \right)$

(12)

在响应 f 中定位极大值位置即为目标位置。式(11)中， $\hat {{\alpha}} $ 利用式(8)进行计算， $\hat \kappa ({{x}},{{{{z}}}})$ 按式(9)计算。在实际跟踪过程中，仅在第一帧图像中以式(8)计算滤波器 $\hat {{\alpha}} $ ，后续帧按式(12)在线更新滤波器模型：

${\hat {{\alpha}} _{t + 1}} = \left( {1 - \beta } \right){\hat {{\alpha}} _{t - 1}} + \beta {\hat {{\alpha}} _t}$

(13)

为适应目标的变化，对目标模型也需要在线更新：

${\hat {{x}}_{t + 1}} = \left( {1 - \beta } \right){\hat {{x}}_{t - 1}} + \beta {\hat {{x}}_t}$

(14)

式中： $\, \beta $ 为学习速率；t为帧数。

2 改进算法

在海参抓取过程中机器人相对目标位置不断变化，导致目标尺度发生较大变化，直接应用KCF算法跟踪精度将大幅下降，不能满足任务要求。对KCF算法进行改进，分别对两个头部位置进行局部跟踪，并利用两个头部之间的距离变化估计目标尺度，同时计算出目标的准确位置。

2.1 海参头部定位

海参在摄像机中显示的姿态可能有如图5所示的3种情况，不能简单地根据给定的目标中心位置确定两头部位置。将目标外包框等分成 $3 \times 3$ 共9个子图像，标记为 ${x_{ij}}$ ，其中 $i = 1,2,3$ 和 j = 1,2,3 分别表示图像块的行号和列号。由于海参各部分的颜色基本相同，且不论海参处于何种姿态，中心块 ${x_{22}}$ 都是海参的中部，因此可通过周围块与中心块的灰度偏差确定头部位置。两个头部位置 ${x_A}$ 和 ${x_B}$ 的可能组合有以下种情况(见图5)：

$({x_A},{x_B}) \in \left\{ {({x_{11}},{x_{33}}),({x_{12}},{x_{32}}),({x_{13}},{x_{31}}),({x_{21}},{x_{23}})} \right\}$

按式(14)计算各图像块组合与中心块的像素偏差，取偏差最小的组合为跟踪目标。

${D_{ij}} = \left\| {x_{ij}^{} - x_{22}^{}} \right\| + \left\| {x_{4 - i,4 - j}^{} - x_{22}^{}} \right\|$

(15)

式中符号 $\left\| \cdot \right\|$ 表示对应图像块像素灰度值之差的2-范数。

2.2 尺度和位置估计方法

由初始帧确定海参头部位置后开始跟踪，将第 $t$ 帧中两图像块中心分别记为 $p_A^t$ 和 $p_B^t$ ，如图6所示。

则海参中心位置 ${p^t}$ 为

$p_{}^t = \frac{{p_A^t + p_B^t}}{2}$

(16)

尺度因子 $S$ 为

$S = \frac{{\left\| {p_A^t - p_B^t} \right\|}}{{\left\| {p_A^1 - p_B^1} \right\|}}$

(17)

式中：上标“1”代表第1帧，上标t代表第t帧。

如图7(a)所示，目标尺寸变化大时KCF算法不能估计目标尺度，跟踪效果明显不好；如图7(b)所示，改进算法则可以准确跟踪目标海参的位置并正确检测其尺度。

2.3 改进算法流程

改进算法流程分为头部定位模块、训练模块、检测模块3个模块，如算法1所示。在头部定位模块中，首先将海参目标图像分块，然后计算各块与中心块像素灰度值的距离(即2-范数)，选取距离最小的两块作为目标；在训练模块中，分别用KCF方法计算两块的滤波器；在检测模块中，分别用KCF方法计算两块的位置,然后计算目标中心和尺度因子。

算法1　改进算法

输入　初始目标的定位模块 ${x_1}$ ， ${x_2}$ ；

输出　目标的中心位置 $p_{}^t$ ，目标的尺度因子 $s\text{。}$

1)当 $t = 1$ 时，根据初始条件计算目标位置 $p_A^1$ 和 $p_B^1$ ，并截取图像块 ${x_1}$ 、 ${x_2}$ ，通过式(3)计算得出基准输出样本 ${y_1}$ 、 ${y_2}$ ；通过式(9)求核函数的傅氏变换 $\hat \kappa \left( {{x_1},{x_1}} \right)$ 和 $\hat \kappa \left( {{x_2},{x_2}} \right)$ ，并求输出样本的傅氏变换 ${\hat y_1}$ 和 ${\hat y_2}$ 。通过式(8)分别求解滤波器 ${\hat \alpha _1}$ 和 ${\hat \alpha _2}$ 。

2)当 $t > 1$ 时，在当前帧图像位置 $p_A^{t - 1}$ 和 $p_B^{t - 2}$ 截取图像块 $\hat {\textit{z}}_1^t$ 和 $\hat {\textit{z}}_2^t$ ，并通过式(9)求核函数的傅氏变换 $\hat \kappa \left( {x_1^t,{\textit{z}}_1^t} \right)$ 和 $\hat \kappa \left( {x_2^t,{\textit{z}}_2^t} \right)$ ；通过式(11)计算响应面 $f_1^t$ 和 $f_2^t$ ，并求响应面最大值得到两跟踪目标位置 $p_A^t$ 和 $p_B^t$ ；通过式(14)求出目标的中心位置 $p_{}^t$ ，通过式(15)求出目标尺度因子 ${s^t}$ ；通过式(12)更新滤波器 $\hat \alpha _1^{t + 1}$ 和 $\hat \alpha _2^{t + 1}$ ，并通过(13)更新目标外观模型 $\hat x_1^{t + 1}$ 和 $\hat x_2^{t + 1}$ 。

3 实试验结果分析

在处理器为Intel Core i5-3317U CPU，主频 1.70 GHz，内存为4 GB RAM的笔记本上进行跟踪实验，采用MATLABR2014a软件编程。使用本文算法和4种性能优秀的相关滤波算法KCF^[8]、CSK^[7]、STC^[10]、DSST^[9]进行对比追踪测试，每种算法均使用作者提供的源代码和预设参数。实验所用视频为在海参养殖水域拍摄的7个水下监控视频具体参数如表1所示。

3.1 定性分析

5种对比算法中只有本文算法和DSST算法具有尺度估计环节，另外3种算法KCF、CSK和STC均采用固定尺度跟踪。图8中7组视频的共同特点是：目标尺度变化大，且由于水下特殊的成像环境导致图像质量较差。从跟踪结果可以看出：KCF、CSK和STC 3种算法追踪效果较差，而本文算法和DSST算法跟踪效果较好，可见对于尺度变化大的应用来说，尺度估计环节非常重要。图8中视频1~7代表7组视频系列实验比较结果。

3.2 定量分析

为了评测本文跟踪算法的性能，采用了本领域广泛应用的每秒运行帧数、距离精度和成功率3种评测指标^[5]。

1)跟踪速度

通过每秒跟踪帧数可以对比跟踪算法的运行速度。表2给出了5种算法的运算速度，其中下划线标出了最大的速度值。可见，在7个视频中，本文算法有5个视频跟踪速度最快，平均达到了111.44 f/s，较排第二位的STC算法高出了33.61 f/s。经分析，本文算法速度更快的原因在于：本文算法只取两个局部图像分别进行跟踪，计算量明显小于其他整体跟踪算法。DSST算法跟踪速度最慢，仅为3.84 f/s，原因是其尺度估计环节非常耗时。

2)距离精度

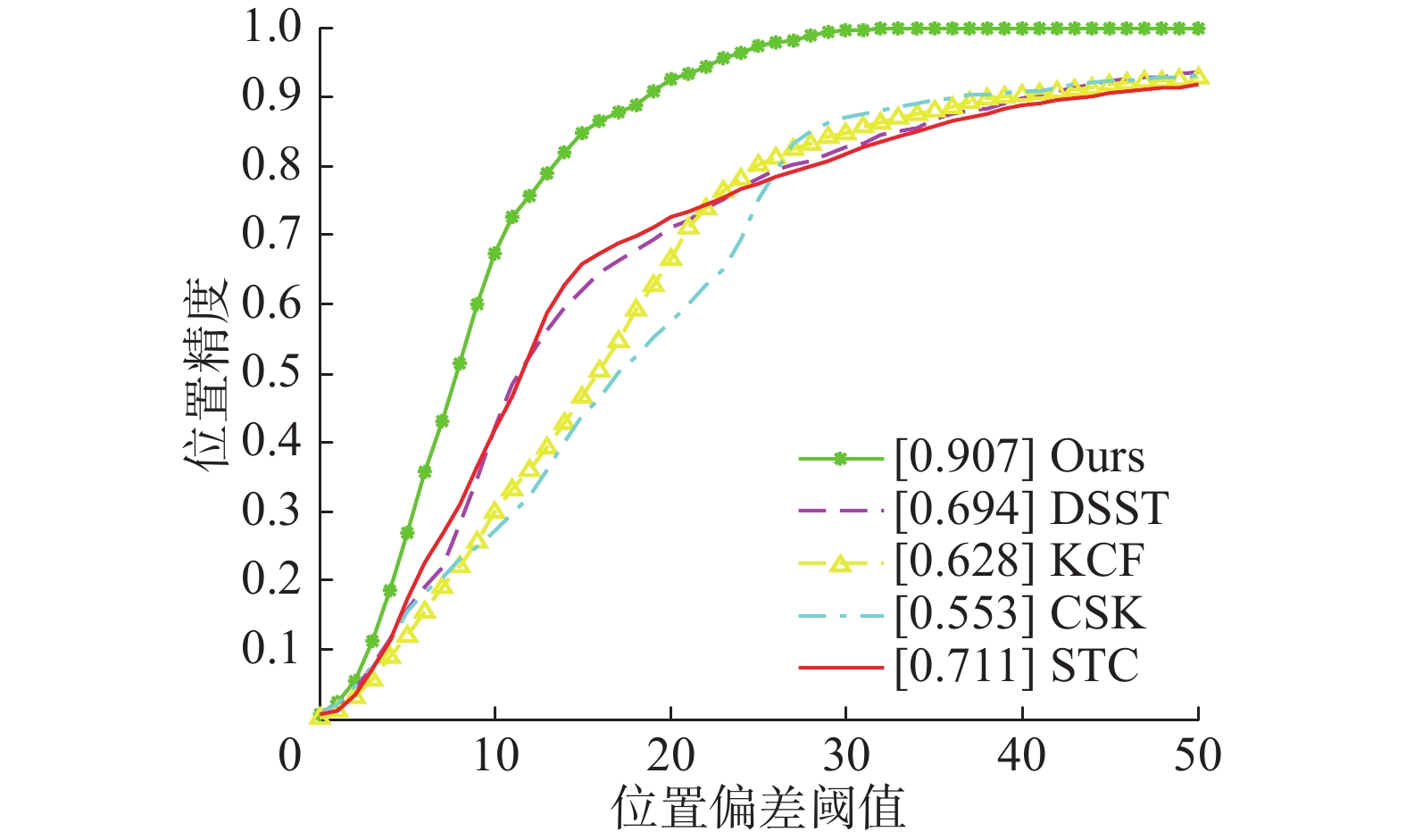
衡量跟踪中心准确性的指标是距离精度，即追踪到目标的中心偏离实际位置的距离 $d$ 小于预定阀值 ${d_0}$ 的帧数与视频总帧数 $n$ 的比值，即

$D = \frac{{n(d \leqslant {d_0})}}{n}$

(18)

图9是综合精确度曲线，表示随着阈值 ${d_0}$ 从0像素到50像素递增时算出的距离精度曲线。可见本文算法跟踪中心精度明显好于其他算法。

表3是阈值 ${d_0} = 20$ 像素时各算法的精度值，其中最后一行是各算法在所有视频上按帧数的加权平均值。从表3可见，本文算法在所有视频上平均精确度达到了90.7%，较排名第2位的DSST算法高出了27.6%。其原因在于：本文算法在选取的两个头部有比较明显的突起等特征，更容易实现准确跟踪，而其他算法直接以中心为跟踪目标。由于各算法为处理振铃效应对边界进行了平滑处理，导致边界部位的突起特征弱化。

3)跟踪成功率

成功率SR为重叠率s大于选定阀值 ${s_0}$ 的帧数与总视频帧数的比值，即

${\rm{SR}} = \frac{{n(s \geqslant {s_0})}}{n}$

(19)

其中重叠率s的计算方法为

$s = \frac{{{R_r} \cap {R_t}}}{{{R_r} \cup {R_t}}}$

(20)

式中：R_r为人工标定目标框内的像素总数，R_t为算法追踪到目标框内像素总数。式(19)中分子为两框重合区域内像素数量，分母是两框合并后总区域内像素数量。

图10是在7个视频上的综合成功率曲线，表示随着重合率阈值 ${s_0}$ 从0到1之间递增时，各算法的综合成功率相应的变化。可见，本文算法略好于DSST算法，但远好于其他3种算法。其原因在于：DSST和本文算法都能根据目标大小调整图像框大小，而其他算法采用固定图像框，因此重叠率受目标尺度变化影响较大。

表4是当阈值 ${s_0}$ 选定为0.5时各算法的成功率，其中最后一行是各算法在所有视频上按帧数的加权平均值。本文算法在所有视频上均取得了最高值，比DSST算法高4.4%，比排在第3位的STC算法高47.5%。虽然DSST算法跟踪成功率与本文算法接近，但由表2可见该算法速度很慢，在实时性要求较高的水下海参采捕中难以应用。

4 结束语

针对跟踪水下尺度变化的海参，在核相关滤波器基础上提出了一种可以追踪尺度变化海参的算法。首先把追踪模块合理地选择在海参的两头部；然后用KCF算法追踪两个头部，通过两个模块间距离来检测海参的尺度并计算出海参的中心。通过对比实验，本文算法的跟踪速度、精度和成功率均高于其他其他算法，能较好地处理尺度和旋转变化等问题。虽然DSST算法跟踪成功率与本文算法接近，但由于DSST算法跟踪速度很慢，不能满足对实时性要求较高的水下海参采捕的实际跟踪过程。下一步的工作：将算法应用到海参采捕水下机器人样机进行采捕实验，针对出现的问题进行更深入研究，以进一步提高跟踪算法的鲁棒性。