推荐系统的核心是推荐算法,根据算法的学习目的不同,主要分为评分预测推荐算法和排序预测推荐算法两大类。文献[1-2]研究指出,排序预测更符合TopN推荐的思想,排序预测比评分预测能更好地为用户进行TopN推荐。随着互联网信息的爆炸式增长,带来信息过载问题的同时,大量信息背后隐藏着用户潜在行为因子,而传统推荐算法包括业界运用成熟的协同过滤算法[3],并没有考虑挖掘用户的潜在行为过程。
文献[4-5]运用边缘化去噪自编码的深度学习方法学习出一种高效潜在表征方法,没有将用户潜在行为用于深度学习建模中;文献[6]将用户的点击行为与转化率联系在一起构建了动态集体矩阵分解模型,有效利用了用户的显性点击行为而没有关注用户隐性行为;文献[7]提出了一种基于本体论与时序模式挖掘的混合推荐算法以此来提高TopN推荐质量;文献[8-9]采用概率矩阵分解技术,将用户评分信息和社交网络信息整合,挖掘出额外信息可以很好地解决预测精度低的问题,未考虑到用户兴趣因子情况;文献[10]使用物品协变量和物品标签等个性化物品潜在的主题,提出了随机变分贝叶斯(SVB)框架和一种协变量为导向的多异性监督主题模型(CGHSTM);文献[11]考虑到用户对物品各个属性面的偏好,利用LDA模型挖掘用户K个属性面提出了一种SACF算法;文献[12]为了提高推荐多样性,将用户的主题模型和应用的主题模型与MF相结合的LDA_MF模型融合提出了一种混合推荐算法。上述几个模型有效缓解了可扩展性问题,提高了推荐多样性,而未考虑兴趣因子以及高效用因子等用户潜在行为因素。
综上,为有效挖掘用户兴趣偏好,本文考虑到用户的潜在行为过程,即用户评分和物品选择两个阶段。通过分析用户历史行为数据,采用用户topic模型进行训练,挖掘出用户潜在高效用因子和物品被靶向概率因子,提出了一种加权用户潜在高效用因子的两阶段混合推荐算法。
1 算法描述 1.1 用户topic模型考虑到一个用户不可能只对一种物品感兴趣,一种物品通常有多重属性,不仅归属于单一类型。一个用户不一定对所有物品评高分,而被评高分的物品通常不仅源自单一用户等情况。因此,本文选择LDA主题模型对用户历史动作特征进行训练,进而挖掘出用户潜在高效用因子与物品被靶向概率因子,LDA描述文档的生成概率为[13]
| $P(w\left| d \right.) = \sum\limits_{\textit{z}} {P({\textit{z}}\left| d \right.) \cdot P(w\left| {\textit{z}} \right.)} $ | (1) |
式中:

|
Download:
|
| 图 1 两种因子流程图 Fig. 1 Flowchart of two factors | |
图1中,
本文认为用户选择物品后并决定对该物品评分之前还要有一个动作,即衡量评分后这个物品会给用户自身带来多少潜在效用。然后根据这个效用再结合该物品是否符合用户兴趣选择物品给出具体评分值。
定义1 用户潜在高效用因子。在推荐系统中,用户在花销时间成本的条件下对物品进行评分时,不仅会考虑物品是否符合自己的兴趣,还会考虑评分给自身带来的效用,即用户满意度。显然效用直接决定用户评分值。而本文将这种效用定义为用户潜在效用因子(latent utility factor,LUF)。为避免抽取单个效用因子造成的偏置现象,本文抽取其中两个高概率因子进行累加,累加的结果称为用户潜在高效用因子(latent high utility factor,LHUF)。综上,可根据用户的历史评分行为来预测用户的潜在高效用因子。用户潜在高效用因子数学范式为
| ${\rm{h}}\_{\rm{pf}}(u) {\buildrel \Delta \over =} \sum\limits_{v \in [V - 1,V]}^u {P({r_v})} \leftarrow (U,I,V,{\{ {R_{u,i}}\} _{i \in I,u \in U}},{\{ P({r_v})\} _{v \in V}})$ | (2) |
式中:
受启发于LDA模型在文本挖掘中加入主题维度,在推荐系统用户−评分值二分关联关系中加入效用维度,则变为用户、效用、评分值三分关联关系。相应的用户打分值概率为
| $ \begin{array}{c} \hat P{({\rm{user}},{\rm{value}})_{{\rm{LDA}}}} = P({\rm{value}}\left| {{\rm{user}}} \right.) = \\ \displaystyle\sum\limits_{{\rm{benefits}}} {P({\rm{benefits}}\left| {{\rm{user}}} \right.) \cdot P({\rm{value}}|{\rm{benefits}})} \end{array} $ | (3) |
式中:
在上述过程中,一个观测数据
该过程为由已知隐含变量参数,生成观测数据的过程,为了充分挖掘这些信息,本文采用LDA模型训练数据。在LDA模型中的训练方法有变分法(varialtional inference)和Gibbs抽样法(gibbs sampling)[14]等,本文采用Gibbs抽样法。Gibbs用户效用抽样算法详细描述如下。
1)随机初始化:为所有用户评分行为中的具体评分值随机分配一个初始的效用。
2)重新扫描观测数据,对其中的每个评分过程进行记录,基于式(4)利用观测数据中的其他行为信息,估计其条件概率,重新采样该评分值的效用。同时更新模型参数。
| $P({\sigma _{u\xi }} \!=\! \sigma |{\mathop {{\sigma}} \limits_{\neg < u,\xi > }},\xi ) \propto \! \frac{{{{\rm{SV}}_{u\sigma ,\neg < u,\xi > }} \!+\! \delta }}{{\sum\limits_{k = 1}^{{T_p}} {{{\rm{SV}}_{uk,\neg < u,\xi > }}} \!+\! {T_p} \delta }} \! \cdot \! \frac{{{{\rm{SW}}_{\sigma \xi ,\neg < u,\xi > }} \!+\! \eta }}{{\sum\limits_{j = 1}^n {{{\rm{SW}}_{\sigma j,\neg < u,\xi > }}} \!+\! n \eta }}$ | (4) |
式中:
3)重复执行上述采样过程直到Gibbs抽样收敛。
4)统计Gibbs抽样收敛后的效用−分共存概率矩阵,利用式(5)和式(6)计算LDA模型的参数。
| ${{\textit{λ}} _{u\sigma }} = P(\sigma |u) = \frac{{{{\rm{SV}}_{u\sigma }} + \delta }}{{\sum\limits_{k = 1}^{{T_p}} {{{\rm{SV}}_{uk}}} + {T_p} \delta }}$ | (5) |
| ${\omega _{\sigma \xi }} = P(\xi |\sigma ) = \frac{{{{\rm{SW}}_{\sigma \xi }} + \eta }}{{\sum\limits_{j = 1}^n {{{\rm{SW}}_{\sigma j}}} + n \eta }}$ | (6) |
式中:
综上,预测用户user根据效用utility评价评分值为value的概率记为
| ${\mathop P\limits^\Delta } _{\rm{LDA}}^{\rm{LUF}} = \sum\limits_{v \in \left[ {V - 1,V} \right]}^{\rm{user}} {P\left( {{r_v}} \right)} $ | (7) |
| $P({r_v}) = \sum\limits_{\rm{utility}} {p({\rm{utility}}|{\rm{user}}) \cdot p({\rm{value}}|{\rm{utility}}) = \sum\limits_{\sigma = 1}^{{T_p}} {{{\textit{λ}} _{u\sigma }}} \cdot } {\omega _{\sigma \xi }}$ | (8) |
式中
根据用户的历史行为预测用户对每个物品感兴趣的概率。
定义2 物品被靶向概率因子。每个用户不可能对所有物品都有过评分行为,为挖掘用户潜在兴趣,根据用户历史数据预测用户对每个物品进行评价的概率,本文将此概率定义为物品被靶向概率因子。
物品被靶向概率因子数学范式为
| ${\rm{I}}\_{\rm{Tf}}(u) {\buildrel \Delta \over =} (U,I,{\{ {P_{u,i}}\} _{u \in U,i \in I}})$ | (9) |
式中:
| $P({{\textit{z}}_{ui}} \!=\! {\textit{z}}|{\mathop {{z}}\limits _{\neg < u,i > }},\mathop {{i}}) \propto \! \frac{{{{\rm{PT}}_{u{\textit{z}},\neg < u,i > }} \!\!+\! \mu }}{{\sum\limits_{k = 1}^M {{{\rm{PT}}_{uk,\neg < u,i > }}} \!\!+\! M \mu }} \! \cdot \! \frac{{{{\rm{PF}}_{{\textit{z}}i,\neg < u,i > }} \!\!+\! \psi }}{{\sum\limits_{j = 1}^n {{{\rm{PF}}_{{\textit{z}}j,\neg < u,i > }} \!\!+\! n \psi } }}$ | (10) |
| ${\ell _{u{\textit{z}}}} = P({\textit{z}}|u) = \frac{{{{\rm{PT}}_{u{\textit{z}},\neg < u,i > }} + \mu }}{{\sum\nolimits_{k = 1}^M {{{\rm{PT}}_{uk,\neg < u,i > }}} + M \mu }}$ | (11) |
| ${\tau _{{\textit{z}}i}} = P(i|{\textit{z}}) = \frac{{{{\rm{PF}}_{{\textit{z}}i,\neg < u,i > }} + \psi }}{{\sum\nolimits_{j = 1}^n {{{\rm{PF}}_{{\textit{z}}j,\neg < u,i > }} + n \psi } }}$ | (12) |
式中:
| ${P_{u,i}} = \sum\limits_{\textit{z}} {P({\textit{z}}|u) \cdot P(i|{\textit{z}}) = \sum\limits_{{\textit{z}} = 1}^M {{\ell _{u{\textit{z}}}}} \cdot } {\tau _{{\textit{z}}i}}$ | (13) |
根据定义1、2分别计算出用户潜在高效用因子与物品被靶向概率因子。用户是否评高分不仅取决于被推荐物品与兴趣吻合度,更取决于被推荐物品给用户带来满足程度,即用户潜在高效用。因此,本文认为用户根据兴趣选择高概率物品进行评分且具有高效用因子的情况下预测物品评分,推荐效果会更好。
算法时间复杂度分析如下:由式(7)知,用户潜在高效用因子采用topic模型抽样收敛后所获得的值为
本文将两种因子进行线性加权融合记为HRe_FP,作为两阶段推荐中的第一阶段。
| ${\rm{HRe}}\_{\rm{FP}} = \alpha \cdot {\mathop P\limits^\Delta } _{\rm{LDA}}^{\rm{LHUF}} + \beta \cdot {P_{u,i}}$ | (14) |
式中参数
推荐系统的核心问题是给用户推荐他最感兴趣的几个物品,而不仅仅是预测用户对物品的评分,将评分高的物品推荐给用户。为了更好地挖掘出用户兴趣,重视评分过程,本文将用户评分过程分为用户评分和物品选择两个阶段,将兴趣度排序值作为用户推荐的依据更符合推荐算法设计的初衷。同时为不显著增加算法的时间复杂度,本文将两阶段线性融合。
首先采用奇异值分解计算预测评分值
| $\mathop {{r_{ui}}}\limits^ \wedge = \mu + {b_i} + {b_u} + {{q}}_i^{\rm{T}}{{{p}}_u}$ | (15) |
| ${\rm{Re cOrderValue}}{_{\rm{u,i}}} = {\rm{HRe}}\_{\rm{FP}} \times \mathop {{r_{ui}}}\limits^ \wedge $ | (16) |
式中:
本文实验所用的数据集是Minnesota大学GroupLens小组开发的MovieLens数据集。实验所采用的数据集规模为943个用户对1 682部电影的10万条评分数据和6 040个用户对3 900部电影的100万条评分数据。
2.2 实验评价标准推荐算法的评价标准总体上来说一般有两种:一种是与顺序无关的评价标准,例如均方根误差、平均绝对误差、K-Call[15]等;另一种是与顺序相关的评价标准,例如归一化累计折损增益(normalized discounted cumulative gain,NDCG[16])。本文分别采用1-call(K=1时)和NDCG作为实验评价标准。具体描述为:K-Call表示TopN推荐结果中至少含有K个相关产品的用户所占有的比例。K-Call的公式为
| $K {\text-} {\rm{Call}}@N = \frac{1}{{\left| U \right|}}\sum\limits_{u \in U} {f(\left| {{L_N}(u)} \right| \geqslant K)} $ | (17) |
式中:
| ${\rm{DCG}}@N(u) = \sum\limits_{i = 1}^N {\frac{{{2^{R(u,i)}} - 1}}{{\log (1 + i)}}} $ | (18) |
| ${\rm{IDCG}}@N(u) = {\rm{Max}}({\rm{DCG}}@N(u))$ | (19) |
| ${\rm{NDCG}}@N = \frac{1}{{\left| U \right|}}\sum\limits_{u \in U} {\frac{{{\rm{DCG}}@N(u)}}{{{\rm{IDCG}}@N(u)}}} $ | (20) |
式中:
本小节主要是将本文提出的Htp_Uf算法与4种基线算法在两种评价标准下的对比,以及各个参数选取对Htp_Uf算法的影响。4种基线算法分别为:基于用户的协同过滤推荐(User_Based),基于物品的协同过滤推荐(Item_Based)[17]、SVD推荐算法[18]、主题模型和矩阵分解模型的混合推荐算法(HTMMF)[19]。
2.3.1 Htp_Uf算法与4种基线算法在NDCG评价标准下的对比实验中Htp_Uf算法各参数取值如下:
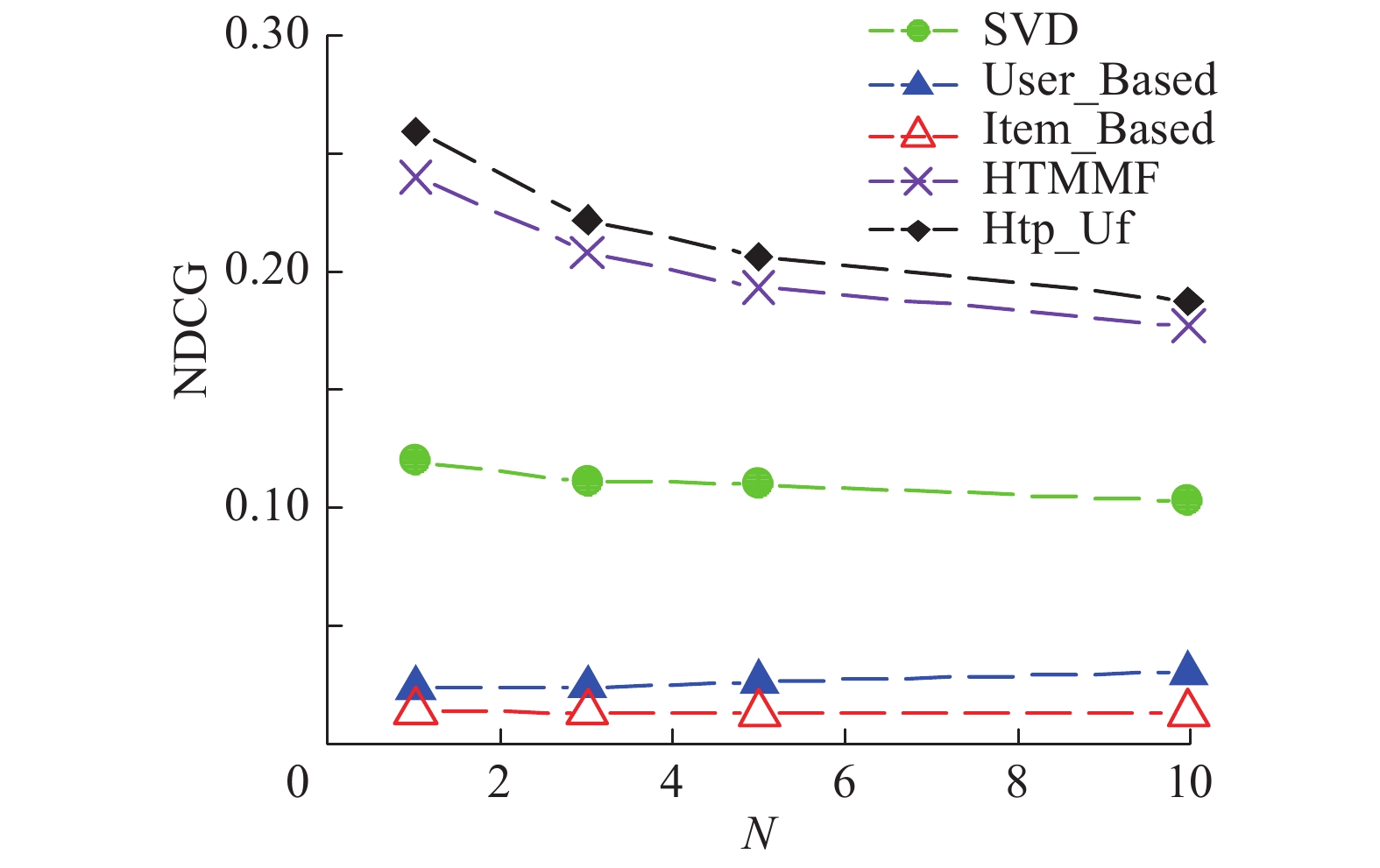
图2主要是将本文提出的Htp_Uf算法与基于用户的协同过滤算法(User_Based,近邻数为50),基于物品的协同过滤算法(Item_Based),奇异值分解(SVD),以及主题模型和矩阵分解模型的混合算法(HTMMF)在NDCG评价标准下进行的比较。
|
Download:
|
| 图 2 Htp_Uf与4种基线算法NDCG对比 Fig. 2 Diagram comparing performances of Htp_Uf and four baseline algorithms by NDCG | |
图2中,N表示推荐列表长度。对比发现Htp_Uf算法相比其他4种算法效果更好,特别是与User_Based和Item_Based相比,提升效果呈级数增长。其主要原因为:Htp_Uf算法将用户潜在高效用因子与物品被靶向因子用于推荐算法第一阶段,不仅预测用户对物品评分的概率,还考虑到用户潜在高效用情况,更适合进行TopN推荐,从而提升推荐算法性能。而HTMMF算法次之,原因是:HTMMF算法在第一阶段中考虑到用户对物品评分的概率,而没有考虑到用户潜在高效用因子情况。
由表1中数据知,Htp_Uf算法比Item_Based、User_Based、SVD、HTMMF这4种算法均有不同幅度的提高,HTMMF算法仅次于Htp_Uf算法,而对比Item_Based算法,Htp_Uf算法提升效果呈指数增长,验证了该算法的有效性。从侧面说明了Item_Based算法不适合TopN推荐,其主要原因是:Item_Based算法为了给用户推荐与该用户历史偏好物品相似的物品,而不一定是用户最感兴趣的物品。
| 表 1 Htp_Uf与4种基线算法NDCG提升率比较 Tab.1 Comparison of increasing rates by Htp_Uf and four baseline algorithms by NDCG % |
实验中Htp_Uf算法各参数取值为:
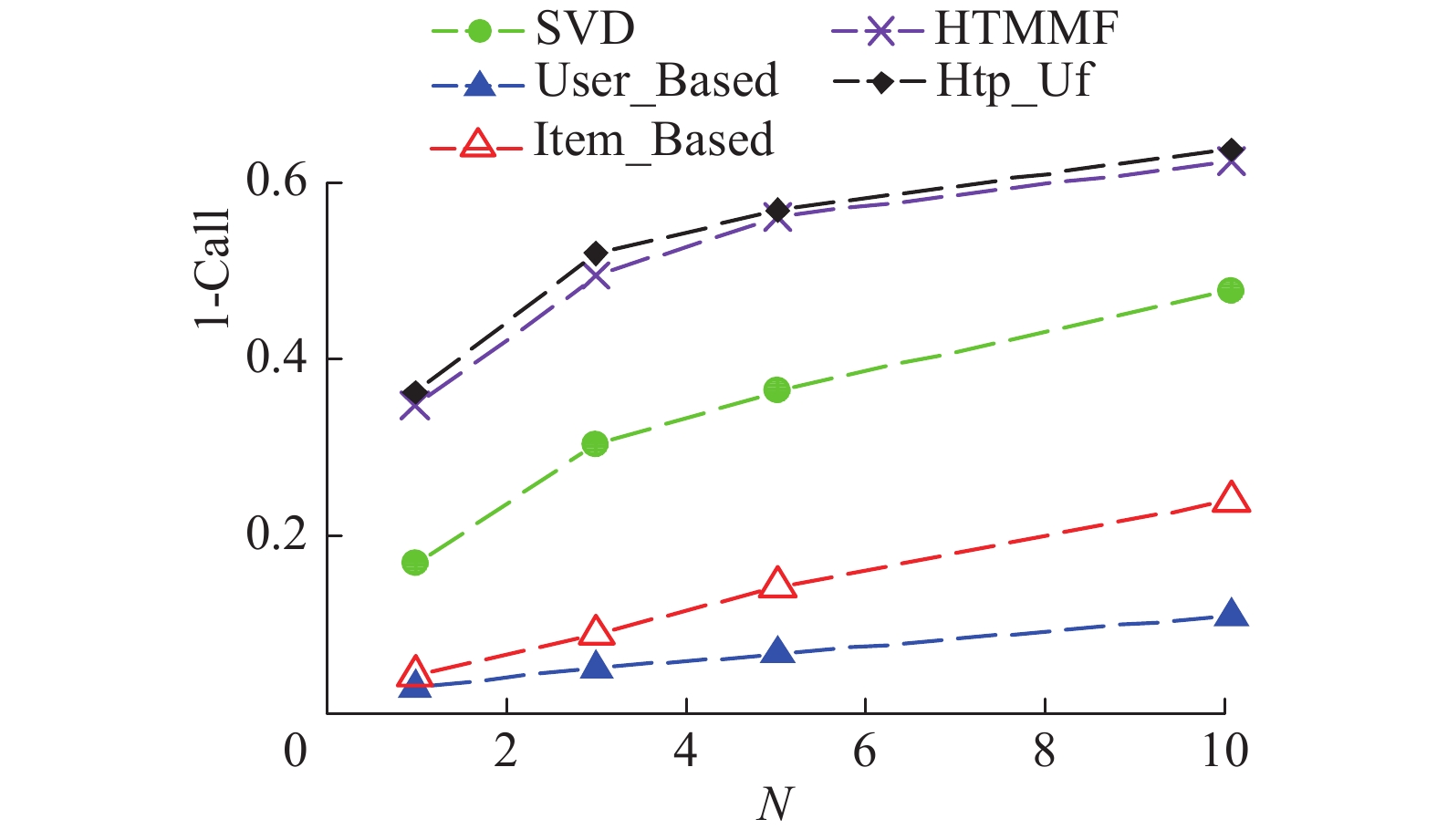
由图3对比可知,Htp_Uf算法在1-Call评价标准下,相比SVD算法至少提高33.12%,相比HTMMF算法提高5.8%,相比User_Based与Item_Based呈指数级地提升。综上,Htp_Uf算法在至少推荐一个相关物品的能力上性能更好,也验证了该算法的有效性。
|
Download:
|
| 图 3 Htp_Uf与4种基线算法1-call对比图 Fig. 3 Diagram comparing Htp_Uf and four baseline algorithms by 1-Call | |
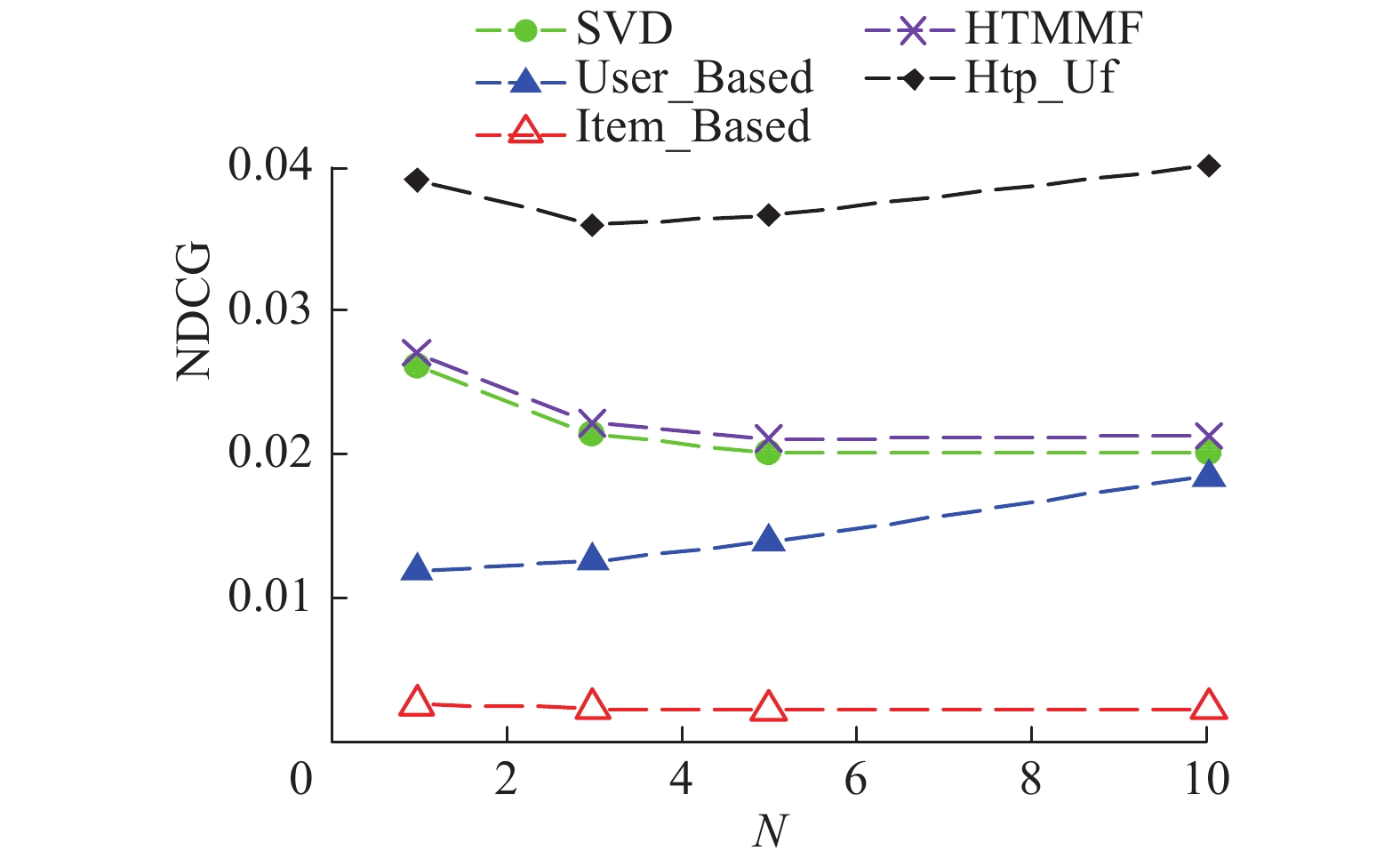
图4为在MovieLens 1M数据集上,Htp_Uf算法与其他4种算法在NDCG评价标准下效果对比图。该数据集包含6 040个用户对3 900个物品100万条评分记录,由图4知,Htp_Uf算法在NDCG评价标准下相比其他4种算法有显著提高。
|
Download:
|
| 图 4 Htp_Uf与4种基线算法NDCG对比图 Fig. 4 Diagram comparing Htp_Uf and four baseline algorithms by NDCG | |
由表2知,Htp_Uf算法在不同的推荐列表长度下,采用1-Call评价标准,相比其他4种基线算法均有不同程度的提高。由表1和表2联合说明,Htp_Uf算法在与顺序有关的评价标准下的提升率要明显高于顺序无关下的提升率,符合该算法的设计初衷。
| 表 2 Htp_Uf与4种基线算法1-Call提升率比较 Tab.2 Comparison of increasing rates for Htp_Uf and four baseline algorithms by 1-Call % |
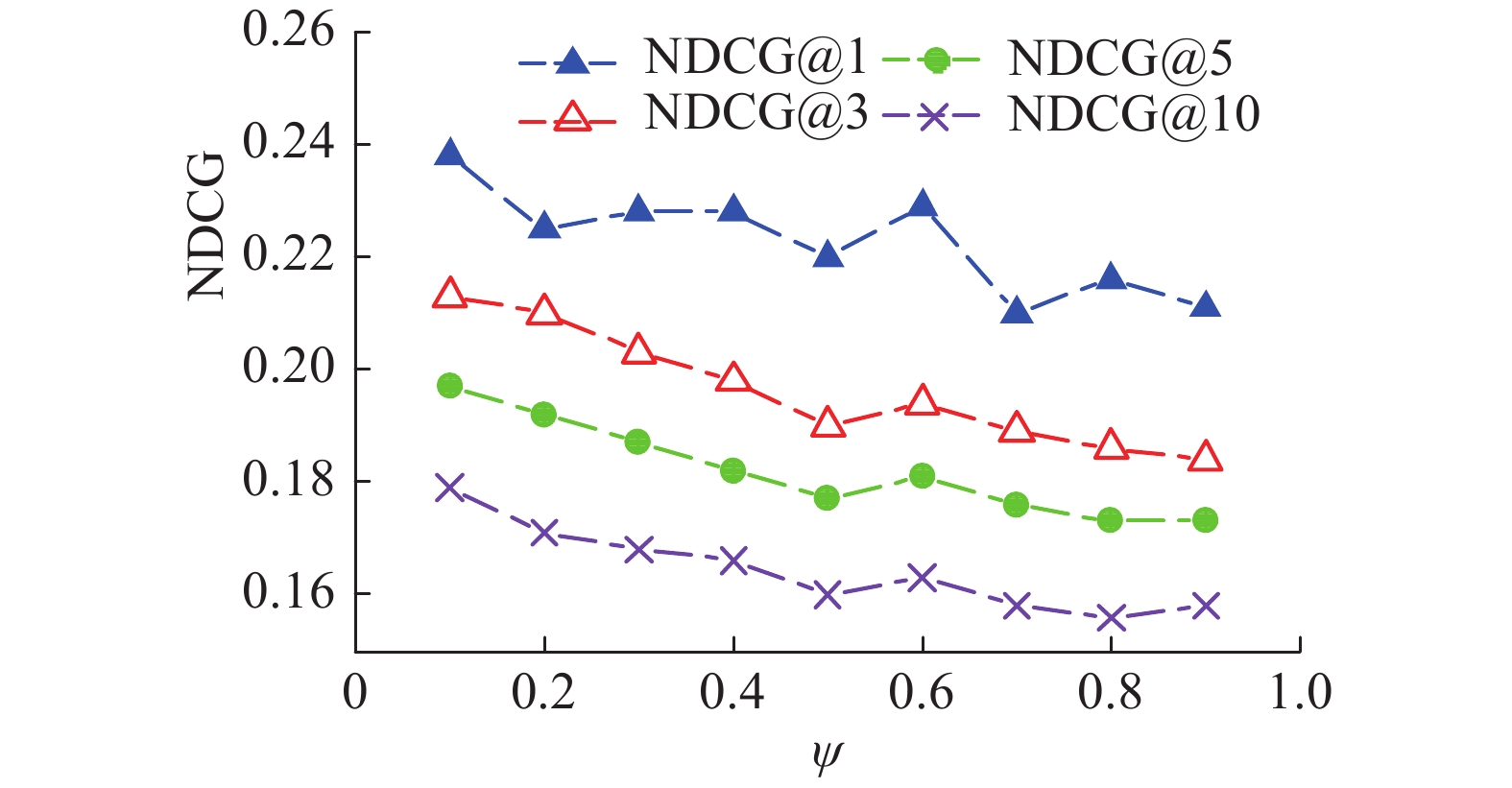
固定参数
由图5知,参数
|
Download:
|
|
图 5 参数
|
|
固定参数
由图6知,当推荐列表长度为1时,为使NDCG值最高,

|
Download:
|
|
图 6 参数
|
|
受经济学领域中效用函数的启发,同时考虑到用户对物品感兴趣但不一定评高分的情况,本文将用户评分过程分为用户评分和选择产品两个阶段。将用户评分行为中抽象出用户潜在高效用因子和物品被靶向概率因子,并且将这两种因子加权作为两阶段推荐的第一阶段,采用奇异值分解因子模型来预测具体评分值作为第二阶段,将两阶段融合形成一种加权高效用因子的两阶段混合推荐算法,实验结果表明该算法提高了TopN推荐质量。
本文提出的两阶段混合推荐算法在挖掘高效用因子和靶向物品概率因子计算方面,都不同程度地受到用户历史评分矩阵数据缺失的影响,也存在用户冷启动,物品冷启动,数据稀疏性等问题,这些问题将是我们未来研究工作的重点。
| [1] |
WEIMER M, KARATZOGLOU A, LE Q V, et al. COFIRANK maximum margin matrix factorization for collaborative ranking[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada: Curran Associates Inc., 2007: 1593–1600.
( 0) 0)
|
| [2] |
LIU N N, ZHAO Min, YANG Qiang. Probabilistic latent preference analysis for collaborative filtering[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management. Hong Kong, China: ACM, 2009: 759–766.
( 0) 0)
|
| [3] |
BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C]//Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence. Madison, Wisconsin: Morgan Kaufmann Publishers Inc., 1998: 43–52.
( 0) 0)
|
| [4] |
LI Sheng, KAWALE J, FU Yun. Deep collaborative filtering via marginalized denoising auto-encoder[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. Melbourne, Australia: ACM, 2015: 811–820.
( 0) 0)
|
| [5] |
KAŠŠÁK O, KOMPAN M, BIELIKOVÁ M. Personalized hybrid recommendation for group of users: Top-N multimedia recommender[J]. Information processing and management, 2016, 52(3): 459-477. DOI:10.1016/j.ipm.2015.10.001 ( 0) 0)
|
| [6] |
LI Sheng, KAWALE J, FU Yun. Predicting user behavior in display advertising via dynamic collective matrix factorization[C]//Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information. Santiago, Chile: ACM, 2015: 875–878.
( 0) 0)
|
| [7] |
TARUS J K, NIU Zhendong, YOUSIF A. A hybrid knowledge-based recommender system for e-learning based on ontology and sequential pattern mining[J]. Future generation computer systems, 2017, 72: 37-48. DOI:10.1016/j.future.2017.02.049 ( 0) 0)
|
| [8] |
KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30-37. DOI:10.1109/MC.2009.263 ( 0) 0)
|
| [9] |
MA Hao, ZHOU Dengyong, LIU Chao, et al. Recommender systems with social regularization[C]//Proceedings of the 4th ACM International Conference on Web Search and Data Mining. Hong Kong, China: ACM, 2011: 287–296.
( 0) 0)
|
| [10] |
ANSARI A, LI Yang, ZHANG J Z. Probabilistic topic model for hybrid recommender systems: a stochastic variational Bayesian approach[D]. New York: Columbia Business School, 2017.
( 0) 0)
|
| [11] |
彭敏, 席俊杰, 代心媛, 等. 基于情感分析和LDA主题模型的协同过滤推荐算法[J]. 中文信息学报, 2017, 31(2): 194-203. PENG Min, XI Junjie, DAI Xinyuan, et al. Collaborative filtering recommendation based on sentiment analysis and LDA topic model[J]. Journal of Chinese information processing, 2017, 31(2): 194-203. (  0) 0)
|
| [12] |
黄璐, 林川杰, 何军, 等. 融合主题模型和协同过滤的多样化移动应用推荐[J]. 软件学报, 2017, 28(3): 708-720. HUANG Lu, LIN Chuanjie, HE Jun, et al. Diversified mobile app recommendation combining topic model and collaborative filtering[J]. Journal of software, 2017, 28(3): 708-720. (  0) 0)
|
| [13] |
BLEI D M, NG A Y, JORDAN M I, et al. Latent dirichlet allocation[J]. Journal of machine learning research, 2003, 3(4/5): 993-1022. ( 0) 0)
|
| [14] |
GRIFFITHS T L, STEYVERS M. Finding scientific topics[J]. Proceedings of the national academy of sciences of the United States of America, 2004, 101(S1): 5228-5235. ( 0) 0)
|
| [15] |
SHI Yue, KARATZOGLOU A, BALTRUNAS L, et al. CLiMF: learning to maximize reciprocal rank with collaborative less-is-more filtering[C]//Proceedings of the 6th ACM conference on recommender systems. Dublin, Ireland: ACM, 2012: 139–146.
( 0) 0)
|
| [16] |
JÄRVELIN K, KEKÄLÄINEN K. Cumulated gain-based evaluation of IR techniques[J]. ACM transactions on information systems (TOIS), 2002, 20(4): 422-446. DOI:10.1145/582415.582418 ( 0) 0)
|
| [17] |
LINDEN G, SMITH B, YORK J. Amazon. com recommendations: item-to-item collaborative filtering[J]. IEEE internet computing, 2003, 7(1): 76-80. DOI:10.1109/MIC.2003.1167344 ( 0) 0)
|
| [18] |
SYMEONIDIS P. Content-based dimensionality reduction for recommender systems[M]//PREISACH C, BURKHARDT H, SCHMIDT-THIEME L, et al. Data Analysis, Machine Learning and Applications. Berlin, Heidelberg: Springer, 2008: 619–626.
( 0) 0)
|
| [19] |
ZHAO Xiangyu, NIU Zhendong, CHEN Wei, et al. A hybrid approach of topic model and matrix factorization based on two-step recommendation framework[J]. Journal of intelligent information systems, 2015, 44(3): 335-353. DOI:10.1007/s10844-014-0334-3 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


