在机器学习^[1]领域中，半监督学习^[2-3]和集成学习^[4]是当前的研究热点。它们被广泛应用于智能信息处理^[5]、图像处理^[6]、生物医学^[7]等领域。在许多大数据场景中，样本属性的获取容易且廉价，而其标签的获取则困难且昂贵^[8]。如果只使用少量已标记样本进行学习，那么训练得到的分类模型通常会造成过度拟合^[9]。为此，Merz等^[10]于1992年提出半监督分类，它不依赖外界交互，充分利用未标记样本，有效提高分类模型的稳定性和精度。

集成学习是指先构建多个学习器，再采用某种集成策略进行结合，最后综合各个学习器的结果输出最终结果。集成学习中的多个学习器可以是同种类型的弱学习器，也可以是不同类型的弱学习器，基于这些弱学习器进行集成后获得一个精度更高的“强学习器”^[11-12]。

基于聚类的分类算法是指先进行数据聚类^[13]，然后根据类簇和标签信息进行分类。其优点是需要的标签较少，但单一算法的聚类效果不稳定或不符合类标签分布时，分类效果受到严重影响。2002年Strehl等^[14]提出“聚类集成”，使用不同类型的聚类算法构造不同的学习器，结合这些学习器可得到更可靠更优的聚类结果；Fred等^[15]提出通过对同一种聚类算法选取不同参数来构造学习器；Zhou^[16]利用互信息设定权重，采用基于投票、加权投票进行聚类集成学习；Zhang^[17]提出一种无标签数据增强集成学习的方法UDEED，能够同时最大化基分类器在有标签数据上的精度和无标签数据上的多样性。

本文针对名词型数据分类问题，在半监督学习的框架之下，融合聚类和集成学习技术，提出一种新的半监督分类算法(semi-supervised binary classification based on clustering ensemble，SUCE)。通过在UCI 4个数据集上的实验表明，该方法比传统的ID3、kNN、C4.5等算法的分类效果要好。而且，当标签较少时，其分类优势更为明显。

1 基本概念

分类问题的基础数据为决策系统。

定义1^[18] 　决策系统S为一个三元组：

$S = \left( {U,C,d} \right)$

(1)

式中：U是对象集合也称为论域；C是条件属性集合；d是决策属性。本文只研究名词型数据的二分类问题，所以决策属性只有两个属性值即|V_d|=2。一般假设所有的条件属性值已知，而仅有部分样本决策属性值已知。这些对象构成了训练集U_r，而U_t=U–U_r构成了测试集。实际上，在半监督学习中，测试集的对象也参与了训练模型的构建。

 

聚类问题不涉及决策属性d。聚类集成是指关于一个对象集合的多个划分组合成为一个统一聚类结果的方法，目标就是要寻找一个聚类，使其对于所有的输入聚类结果来说，尽可能多地符合^[19]。

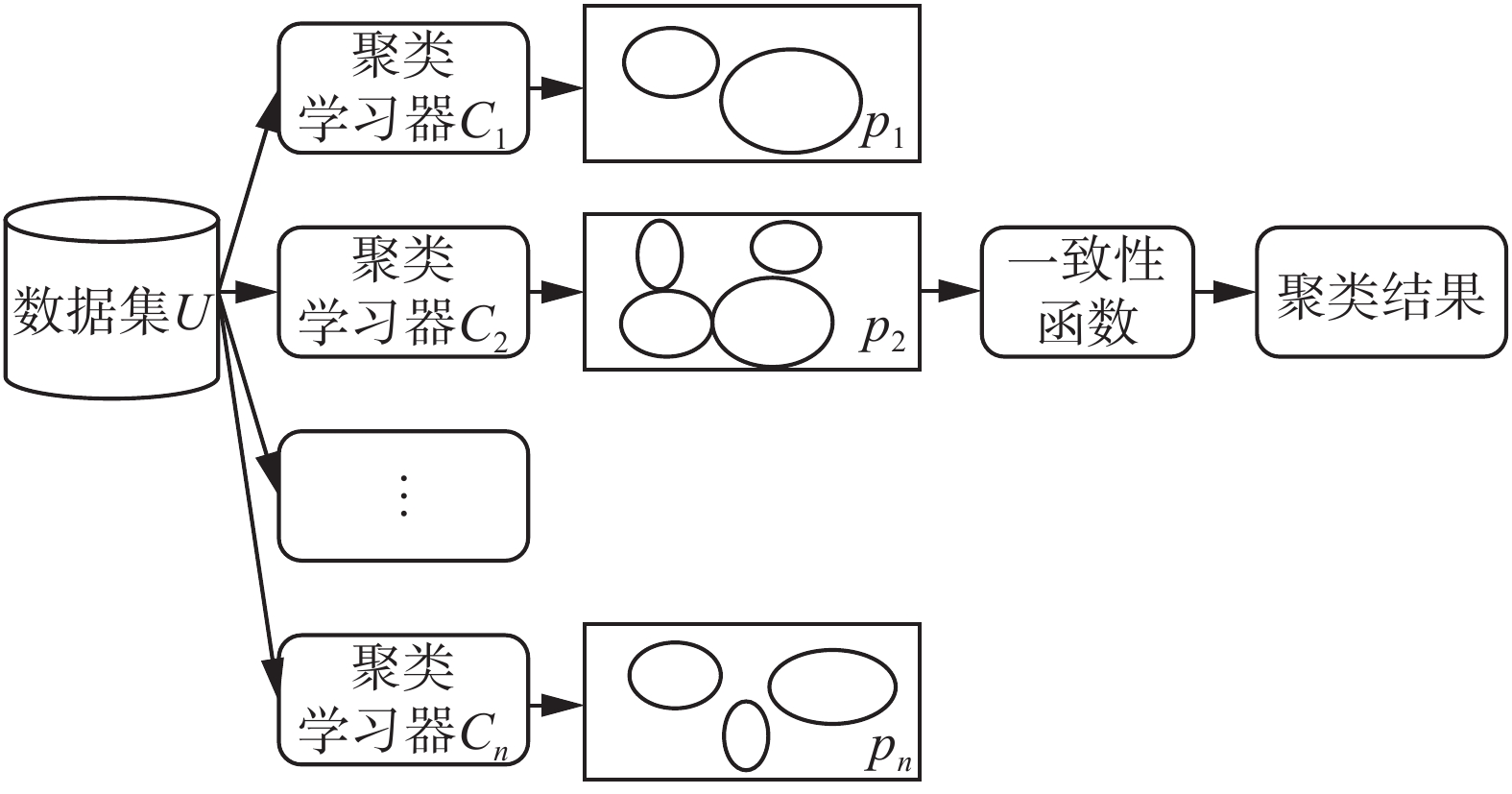
如图1所示，聚类集成的过程为：首先对 $U = $ $ \left\{ {{x_1},{x_2}, \cdots ,{x_m}} \right\}$ ，通过集成学习器集合 ${\mathbb{C}} = \left\{ {{C_1},{C_2}, \cdots ,{C_k}} \right\}$ ，得到 $P = \left\{ {{p_1},{p_2}, \cdots ,{p_k}} \right\}$ ，其中 ${p_i}\left( {i = 1,2, \cdots ,k} \right)$ 为第i个聚类学习器得到的聚类结果。最后通过一致性函数对x∈U_t的k个预测标签进行集成，得到一个统一的集成标签h(x)。

集成学习中，学习器之间的差异性被认为是影响集成结果的关键因素之一^[20]。聚类集成的第一步是通过不同类型聚类基学习器产生多个聚类结果，从不同的方面反映数据集的结构，有利于集成^[21]。在本文中，k-Means^[22]、EM^[23]、FarthestFirst^[24]和HierarchicalClusterer^[25]4个聚类算法将作为聚类集成的基础学习算法，并且每次运行都设置不同的参数。k-Means原理简单运行速度较快，但依赖于初始参数设置使得聚类结果存在不稳定性，并且不能有效针对非凸形状分布数据聚类。EM不需要事先设定类别数目，计算结果稳定、准确，但算法相对复杂，收敛较慢不适用于大规模数据集和高维数据。HierarchicalClusterer没有任何目标函数，簇合并后不可逆转，将局部最优作为全局最优解，聚类结果依赖于主观获得。FarthestFirst在迭代过程中减少待聚类样本数和类别数，具有精简聚类结果的效果。每个算法各有优劣，适用的场景不同；因此需要对它们进行集成化来实现优势互补。因为本文只研究名词型数据的二分类问题，所以在聚类时，聚簇的数量直接设为类别数量，在实验中，本文将所有聚类算法的聚簇数量设定为2。

聚类效果的主要评价指标有JC系数、FM指数、DB指数和DI指数等。本文通过聚类方法研究二分类问题，使用U_r的聚类纯度对聚类结果进行评估。通常来说，聚类纯度越高则表明聚类效果越好。

定义2　聚类纯度(purity of cluster, PC)

设数据集U=U_t∪U_r，对于任意聚类学习器 $C \in {\mathbb{C}}$ 的聚类结果 ${{t}}\left( U \right) = \left[ {{{t}}\left( {{U_t}} \right)\;{{t}}\left( {{U_r}} \right)} \right]$ ，其中 ${{t}}\left( {{U_r}} \right) = $ $ \left[ {t\left( {\!{x_1}} \right)\;t\left( {\!{x_2}} \right)\; \cdots \;t\left( {{x_{\left| {{U_r}} \right|}}} \right)} \right]$ ，用 ${ d}\left( {{U_r}} \right) \!=\! \left[ {d\left( {\!{x_1}} \right)\;d\left( {\!{x_2}} \right)\; \cdots\;d\left( {{x_{\left| {{U_r}} \right|}}} \right)} \right]$ 表示x_i∈U_r的真实标签。

那么基学习器C对于U_r的聚类纯度可表示为

${\rm PC}\left( {{U_r}} \right) = \frac{1}{{\left| {{U_r}} \right|}}\mathop \sum \limits_{i = 1}^{\left| {{U_r}} \right|} \sigma \left( {t\left( {{x_i}} \right),d\left( {{x_i}} \right)} \right)$

(2)

式中：

$\sigma \left( {a,b} \right) = \left\{ {\begin{array}{*{20}{c}}{1,\;\;\;\;\;\;a = b}\\{0,\;\;\;\;\;\;{\text{其他}}}\end{array}} \right.$

(3)

另外，聚类集成学习存在一个必须要解决的问题：簇标签与真实标签的对应。

定义3　(标签对应)任意聚类基学习器 $C \in {\mathbb{C}}$ ，根据对训练集U_r上的聚类纯度PC(U_r)，得到x∈U_t中样本的聚类标签。标签对应函数 $A $ (U_t)可定义为

$A\left( {{U_t}} \right) = \left\{ \begin{array}{l}{\bf normal}\left( {{U_t}} \right),\;\;\;\;{\rm PC}\left( {{U_r}} \right) > \theta \\{\bf covert}\left( {{U_t}} \right),\;\;\;\;{\rm PC}\left( {{U_r}} \right) < 1 - \theta \\{\rm reset}\left( {{U_t}} \right),\;\;\;\; 1 - \theta < {\rm PC}\left( {{U_r}} \right) < \theta \end{array} \right.$

(4)

式中： $ \begin{array}{c}{\bf{normal}}\left( {{U_t}} \right) = \left[ {\sigma \left( {d'\left( {{x_1}} \right)\;t\left( {{x_1}} \right)} \right)\; \cdots \;\sigma \left( {d'\left( {{x_{\left| {{U_t}} \right|}}} \right)\;t\left( {{x_{\left| {{U_t}} \right|}}} \right)} \right)} \right],\\\!\!\!\!{\bf{convert}}\left( {{U_t}} \right) = \left[ {\sigma \left( {d'\left( {{x_1}} \right)\;1 - t\left( {{x_1}} \right)} \right)\; \cdots \;\sigma \left( {d'\left( {{x_{\left| {{U_t}} \right|}}} \right)\;1 - t\left( {{x_{\left| {{U_t}} \right|}}} \right)} \right)} \right],\end{array}$ 　　 $ \begin{array}{c}{\rm reset}\left( {{U_t}} \right) = - {1_{{U_t} \times 1}},{\text{且}}{\rm{}}{x_{\rm{i}}} \in {U_t},i = 1,2, \cdots ,\left| {{U_t}} \right|\end{array}$ 。

本文用t(x)和d'(x)分别表示样本x∈U_t的聚类标签和预测标签。θ是用户设置的阈值，当PC(U_r)>θ时，即表示聚类标签与类标签相匹配，将调用normal(U_t)函数，并直接把聚类标签作为预测标签；当PC(U_r)>θ时，即表示聚类标签与类标签相反，将调用covert(U_t)函数，把聚类标签取反后作为预测标签；当PC(U_r)介于1−θ和θ之间，即认为聚类结果不适于指导标签预测，调用reset(U_t)函数，用−1表示x∈U_t的预测标签。

例1　对 ${U_r} \!=\! \left\{ {{x_1},{x_2},{x_3}} \right\}$ ， ${U_t} \!=\! \left\{ {{y_1},{y_2}} \right\}$ ，有 $U = {U_r} \cup {U_t}$ ，且 ${{d}}\left( {{U_r}} \right) = \left[ {1\;0\;1} \right]$ ，θ=0.9。

1) 如果t(U)=[1 0 1 10], PC(U_r)=1>θ，所以 ${{d}}'\left( {{U_t}} \right) = {\bf normal}\left( {{U_t}} \right) = \left[ {1\;{\rm{}}0} \right]$ ；

2) 如果t(U)=[0 1 0 0 1]，PC(U_r)=0<1−θ，所以 ${{d}}'\left( {{U_t}} \right) = {\bf convert}\left( {{U_t}} \right) = \left[ {1\;{\rm{}}0} \right]$ ；

3) 如果t(U)=[0 0 0 0 1]，1-θ<PC(U_r)=0<1−θ，所以 ${{d}}'\left( {{U_t}} \right) = {\rm reset}\left( {{U_t}} \right) = \left[ { - 1\;{\rm{}} - 1} \right]$ 。

聚类学习器集合 ${\mathbb{C}}$ 将给样本x∈U_t标记| ${\mathbb{C}}$ |个聚类标签，并根据定义(2)和定义(3)得到| ${\mathbb{C}}$ |个预测标签。

定义4　(一致性)聚类学习器 ${C_i} \in {\mathbb{C}}$ 对x∈U_t上的预测标签 ${d_i}'\left( x \right)$ ，且 ${d_i}'\left( x \right) \in \left\{ {0,1} \right\}$ ，那么集成标签h(x)的值为

$h\left( x \right) = \left\{ {\begin{aligned}&{d'\left( x \right),\;\;\;\displaystyle\mathop \sum \limits_{i = 1}^{\left| {\mathbb{C}} \right|} {d_i}'\left( x \right) = \left| C \right|\;{\rm{or}}\;\mathop \sum \limits_{i = 1}^{\left| {\mathbb{C}} \right|} {d_i}'\left( x \right) = 0}\\&{ - 1,\;\;\;\;\;\;\;{\text{其他}}}\end{aligned}} \right.$

(5)

例2　采用与例1中相同的U_t和U_r，且| ${\mathbb{C}}$ |=3，若C₁的预测标签 ${{{d}}_1}'\left( {{U_t}} \right) = \left[ {1\;0} \right]$ ，若C₂的预测标签 ${{{d}}_2}'\left( {{U_t}} \right) = \left[ {1\;1} \right]$ ，若C₃的预测 ${{{d}}_3}'\left( {{U_t}} \right) = \left[ {1\;0} \right]$ 。

对 ${U_t} = \left\{ {{y_1},{y_2}} \right\}$ 的结果为

因为 $\displaystyle\mathop \sum \limits_{i = 1}^3 d_i'\left( {{y_1}} \right) = \left| {\mathbb{C}} \right| = 3$ ，所以h(y₁)=1；

因为 $\displaystyle\mathop \sum \limits_{i = 1}^3 d_i'\left( {{y_2}} \right) = 2$ ，所以h(y₂)=−1。

2 算法设计与分析

本节首先描述算法的总体框架，然后进行算法伪代码描述，最后分析算法复杂度。

2.1 算法总体方案

基于集成的半监督分类方法主要是通过集成学习控制无标记样本的标注过程来减少未标记的不确定性^[12]。然而，目前在利用集成学习辅助半监督学习方面的方法研究较少，主要是存在如下矛盾：半监督学习适用于标记样本不足的情况，然而传统的集成学习本身就需要大量的标记样本进行训练^[12]。针对上述问题，SUCE综合聚类集成与半监督学习，在已知标签较少的情况下，有效提高分类器的精度。

如图2所示，基于聚类集成的半监督分类过程为：第1个分图说明，首先通过聚类集成，将B中部分没有类别样本C的类标签预测出来；达到“扩大”有类别的样本集合(A变成了A+C)，“缩小”了未标记类别集合(B变成了B')。第2个分图说明，对于扩大后的集合(A+C)利用分类模型，完成预测没有类别的样本B'。

2.2 算法描述

在训练阶段，本算法将依次对数据集进行4步处理，从而生成分类器：

1) 通过getLabel(U_r)获取训练集U_r的标签 $ {{{{L}}_{{U_r}}}} $ 。然后，利用remove(U_r)对U_r去标签得到U_r′；并将U_r′∪U_t得到无标签U。

2) 通过多个基于EM、K-Means、FarthestFirst和HierarchicalClusterer等聚类算法的个体学习器对U进行全局聚类。根据已获取的 ${{{L}}_{U_r}} $ ，计算第i个聚类学习器 $ {{{L}}_l} $ 在U_r上的聚类纯度PC(i)。如果PC(i)高于阈值θ， $ {{{L}}_l} $ 将继续参加集成学习，并将 $ {{{L}}_l} $ 移入到学习器集合E中即E∪ $ {{{L}}_l} $ 。

3) 对测试集的预测标签进行集成学习。通过h(x)一致性函数依次对测试集每个样本x∈U_t的预测标签进行一致性处理。如果E中所有学习器对x的预测标签均一致，将预测标签d'(x)赋给x得到x'=(x, d'(x))。x'移入到训练集U_r∪{x'}，同时在测试集中将其删除U_t-{x}。

4) 对扩大规模后的U_r进行学习，再对缩减规模后的U_t进行分类 $ {{{{L}}_{{U_t}}}} $ =classifier(U_r, U_t)得到U_t的类标签 $ {{{{L}}_{{U_t}}}} $ ；然后，获取U_r的标签 $ {{{{L}}_{{U_r}}}} $ =getLabel(U_r)。最终得到U类标签 $ {{{{L}}_{{U}}}}$ =combine( $ {{{{L}}_{{U_t}}}} $ , $ {{{{L}}_{{U_r}}}} $ )。

SUCE：基于集成聚类的半监督分类算法

算法　SUCE

输入　训练集U_r，测试集U_t，阈值；

输出　 U_t的类标签向量 $ {{{{L}}_{{U_t}}}} $ 。

优化目标：最大化分类精度；

1）U=Ø，E=Ø；//初始化

2） $ {{{{L}}_{{U_r}}}} $ =getLabel(U_r) //获取U_r类标签

3） $U_r' = {\rm remove}\left( {{U_r}} \right)$ ；//隐藏U_r类标签

4） $U = U_r' \cup {U_t}$ ；

5） $ {{{{L}}_1}} = {\rm KMeans}\left( U \right)$ ；

6） $ {{{{L}}_2}} = {\rm EM}\left( U \right)$ ；

7） $ {{{{L}}_3}} = {\rm FarthestFirst}\left( U \right)$ ；

8） $ {{{{L}}_4}} = {\rm HierarchicalCluster}\left( U \right)$ ；

9）for (i=0; i<4;i++) do //筛选基学习器

10）　if (PC(i)>θ) then

11）E∪ $ {{{{L}}_{l}}} $

12）end if

13）end for

14）for (each x∈U_t) do //标签一致性处理

15）if ( $h\left( x \right) = d'\left( x \right)$ ) then

16） $ {{{{L}}_{{U_t}\left( x \right)}}} = d'\left( x \right)$ ；

17）else then

18） $ {{{{L}}_{{U_t}\left( x \right)}}} = -1$ ；

19）end if

20）end for

21）for (each x∈U_t) do //扩充训练集

22）if ( $ {{{{L}}_{{U_t}\left( x \right)}}} ! = - 1$ ) then

23）x'=(x, d'(x))

24）U_r∪{x'};

25）U_t-{x};

26）end if

27）end for

28） $ {{{{L}}_{{U_t}}}} $ =classifier(U_r, U_t)；//分类

29） $ {{{{L}}_{{U_r}}}}$ =getLabel(U_r)；

30） $ {{{{L}}_{{U}}}}\ $ =combine( $ {{{{L}}_{{U_t}}}} $ , $ {{{{L}}_{{U_r}}}} $ )；

2.3 复杂度分析

为方便讨论，假设训练集U_r的对象数量为n，条件属性数量为c，测试集U_t的对象数量为m。基学习器数量为|E|，迭代次数为t、聚类簇数为k。SUCE算法细分为以下4个阶段。

1) 对数据集进行去标签化预处理。在隐藏U_r类标签之前，需先记录其真实类标签，如第2)行所示再隐藏U_r中的类标签，如第(3)行所示。至此，需要对U_r进行两次遍历，共执行2n次计算。接下来是合并去标签后的U_r和U_t，构建无标签论域U。第1阶段，计算机将共执行3n+m次运算，故该阶段的时间复杂度为O(n+m)。

2) 分别通过基于K-Means、EM、FarthestFirst和HierarchicalClusterer基学习器对U进行全局聚类，如第5)~8)行所示。其时间复杂度分别为O(kt(n+m))、O(ct(n+m))、O(k(n+m))、O((n+m)²lg(n+m))，然后计算基学习器的聚类纯度，并对其进行筛选，共执行n×|E|次运算，如第9)~13)行所示。所以，第2阶段的时间复杂度为 $O\left( {\left( {n + m} \right)\left( {ct + \left( {n + m} \right)} \right.} \right.$ $\left. {\left. {\lg \left( {n + m} \right)} \right)} \right)$ 。

3) 对U_t中的对象进行一致化处理。遍历U_t中对象，共执行m次处理，如第14)-20)行所示。然后将U_t中置信度高的对象移入到U_r，如第21)~27)行所示，共执行2m次计算，故时间复杂度为O(m)。

4) 对扩展后的U_r进行学习，并对U_t进行分类。该阶段的时间复杂度根据所采用的具体分类算法变化而变化。

综上，因为第1、3、4阶段的时间复杂度远小于第2阶段。所以，SUCE的时间复杂度为 $O\left( {\left( {n + m} \right)\left( {ct + \left( {n + m} \right)\lg \left( {n + m} \right)} \right)} \right)$ 。为方便表述，数据集规模n+m改写成|U|，SUCE的时间复杂度为 $O\left( {\left| U \right|\left( {ct + \left| U \right|\lg \left( {\left| U \right|} \right)} \right)} \right)$ 。

3 实验及分析

本节通过实验回答以下3个问题：1) 如何设置合适的θ阈值；2) SUCE应用于哪些基础算法效果更好；3) 相比于流行的分类算法，SUCE能否提高分类器的精度。

3.1 实验设置

实验采用了UCI数据库中的Sonar、Ionosphere、Wdbc和Voting4个数据集。Sonar、Wdbc是连续型数据，因此通过Weka应用默认方法对其进行离散化处理。

根据UCI数据集的样本数量，实验设置的训练集规模分别为2%、4%、6%、8%、10%、12%、14%和16%。在测试集中，样本标签不可见，直到所有的未分类样本都得到预测标签。为减小实验随机误差，每个结果均为200次相同实验的平均值。所有(对比)实验均采用上述相同的实验参数，如表1所示。

3.2 实验结果与分析

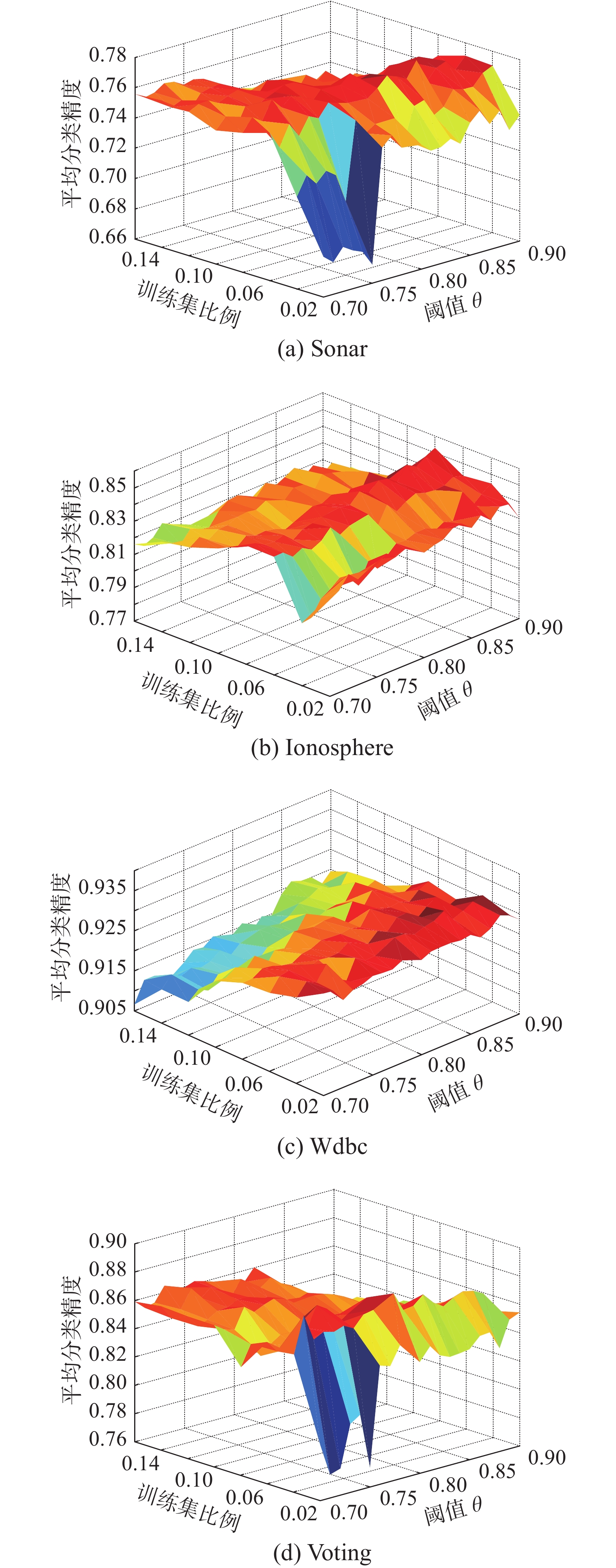
图3显示了Sonar、Wdbc、Ionosphere和Voting数据集在不同阈值θ和训练集规模下的平均分类精度变化。通过实验数据观察发现，θ=0.8左右时，SUCE在4个数据集上均能取得最好的分类效果。在Sonar和Voting数据集上，对于不同的θ取值，随着训练集规模的扩大，平均分类精度会呈现出先增加后趋于稳定的趋势。因为随着阈值θ的提高，筛选过后还保留的个体学习器通常会变得更少，所以获得的样本标签并没有提高，从而导致分类效果没有提升。对于Ionosphere和Wdbc，训练集规模并不太影响平均分类精度。

表2显示了SUCE作用在ID3、J48、Bayes、kNN、Logistic、OneR等基础算法上，并对Sonar、Wdbc、Ionosphere和Voting数据集进行半监督分类的分类结果。实验参数设置为：θ=0.8，训练集比例=4%。Win值的计算如下：在某一数据集上，如果某种算法效果比其对比算法精度高1%以上，则该算法得1分；否则两种算法效果相当且均不得分。

通过表2可以统计发现，SUCE获胜14次，打平5次，失败5次。在Sonar、Wdbc和Ionosphere数据集上的分类效果要优于基础算法。但SUCE在Voting数据集上对基础算法分类效果的提升不明显。

SUCE更适用于ID3、C4.5、OneR等基础算法。例如，在Sonar数据上，SUCE-C4.5获得了高达14%的精度提升。然而，SUCE对Naive Bayes算法的改进不明显。

现在可以回答本节提出的问题。1)取为0.8左右较合适；2) SUCE应用于ID3、C4.5、OneR等基础算法效果更好；3)相比基础算法，SUCE通常可以提高分类器的精度。

4 结束语

本文提出的基于集成聚类的半监督二分类算法SUCE解决了样本过少情况下的分类效果较差的问题。优点在于通过集成聚类的学习充分挖掘大量未标记样本中的重要信息，而不需要去求助外界来解决，降低了学习的成本。在未来的工作中，进一步研究以下3个方向：1)由目前只能解决二分类问题过渡到多分类问题；2)加入更多学习能力强的聚类算法，扩大集成学习个体学习器的规模；3)引入代价敏感，增强集成学习的能力。