在云计算提供强大服务的背后，存在集群资源使用率偏低的现象：Bohrer^[1]指出集群节点的使用率一般仅为11%~50%，大量资源处于闲置状态，资源浪费严重。Barrsos等^[2]通过统计分析近5 000台主机近半年的运行状况，节点的使用率仅有10%~50%。因此，如何准确有效地分配云资源，提高集群资源利用率是云计算的一个重要研究内容。

在云计算的研究中，通过对Google cluster trace分析发现^[3-4]，云任务可分为即时响应的应用与批处理任务，其服务特征、资源需求具有多样性。多数研究通过分析任务作业时长，资源使用特性等，对任务进行聚类^[5-10]，以此描述任务的异构性特征，并根据聚类后各类簇的特性设置调度函数，其实验结果表明聚类调度对任务响应时间与集群资源使用有显著改善。但任务聚类通常并不完全是非此即彼的类别划分，也可能出现中间态模糊集。针对此类问题，三支决策聚类通过定义边缘域概念拓展了传统的二支聚类算法，并根据对象属性对兼具多标签对象作出进一步的划分，其中，三支决策理论源于Yao对概率粗糙集和决策粗糙集3个域的合理解释^[11-13]，是一种更为一般，有效的决策方法。本文将其引入云计算，为任务调度问题提供新的解决方案。

1 相关工作

作为一种有效的问题解决手段，三支决策的基本思想是通过一对阈值 $(\alpha ,\beta )$ 将一个全集 $U$ 划分成3个独立的部分，然后针对各个区域设置相应的策略。其特征是使用三支方法进行问题解决和信息处理。三支决策基于启发式方法，将复杂问题利用分治策略转化为简单问题，其定义为

${c_{(\alpha ,\beta )}}:\tau :U \to \{ {S_1},{S_2},{S_3}\} $

(1)

式中：基于条件集 $C$ ，三支决策通过映射 $\tau $ 将实体集 $U$ 分成3个两两互不相交的 ${S_1}\text{、}{S_2}\text{、}{S_3}$ ,然后根据3个区域的特点，有针对性的设计策略和动作，以期达到某种收益的最大化。关于三支决策的理论，模型与应用研究已经取得了较大进展，如垃圾邮件过滤研究^[14]、代价敏感的三支决策模型研究^[15]、三支决策和博弈论^[16]、多粒度三支决策^[17]、序列三支决策^[18]、动态三支决策^[19]、三支决策与逻辑^[20]等。

作为三支决策在聚类算法方面的有效应用，三支聚类^[21-22]拓展了对象与集合的隶属关系。给定对象集合 $U = \{ {x_1},{x_2}, \cdots ,{x_n}\} $ ， $n$ 表示对象数。以二支聚类的思想判定，对象 ${x_i}$ ，要么属于集合 $c{s_i}$ ，要么不属于集合 $c{s_i}$ ，其聚类的结果为 $CS \!=\! \{ c{s_1}, c{s_2}, \cdots c{s_k}\} $ ， $k$ 为类别数。而以三支的角度观察，对象 ${x_i}$ 与集合 $c{s_i}$ 的所属关系有： ${x_i}$ 属于 $c{s_i}$ ， ${x_i}$ 可能属于 $c{s_i}$ ， ${x_i}$ 不属于 $c{s_i}$ ，因此集合 $c{s_i}$ 被划分为互不相交的 $L$ 域、 $M$ 域和 $R$ 域，其中 $L$ 域表示该类簇的核心对象集合， $M$ 域为边缘对象集合。其聚类结果为 $CS = \{ (L(c{s_1}),$ $M(c{s_1})),(L(c{s_2}),M(c{s_2})), \cdots ,(L(c{s_k}),M(c{s_k}))\} $ 。三支聚类算法根据簇间离散度与簇内聚合度，对类中对象之间的紧密程度作进一步划分。

传统的二支聚类算法在云计算中被广泛应用。文献[5]使用k-means算法将任务聚类为计算、存储与网络类型，引入权重因子调整属性间优先级，根据任务类型调度任务。刘家志^[6]将FCM算法引入到任务调度中，根据CPU、内存、IO与带宽等属性为任务建模并聚类，根据类簇特征为任务设置调度函数。文献[7]根据集群资源的多维属性定义资源可见度，通过静态阈值划分可见度等级，在PSO调度中以该等级与任务执行时间作为适应性函数，提高集群负载均衡度。张以利等^[8]根据作业长短及重要性聚类任务，构建LPM模型，追求最大化的任务完成数，文献[9]采用层级聚类对云任务进行预处理，以最小化任务完成时间为目标函数调度任务，兼顾资源负载与系统吞吐量，在满足服务质量的同时，缩短任务完成时间。高正九等^[10]提出了一种基于任务分类的延迟调度算法，根据任务长度聚类，并依据该类别调整任务等待时间阈值。相比于DS、FIFO算法，该算法有效缩短了任务响应时间。

三支决策理论体系的引入，将对任务调度提供新思路。本文提出的三支聚类评分(three-way clustering weight，TWCW)算法，对任务进行三支聚类划分，追求最大化资源使用，根据聚类结果中核心态与模糊态任务偏好设置调度策略。

2 TWCW算法 2.1 任务模型

在2011公布的Google Cluster Trace中，作业由一个或多个任务构成，与任务相关的属性有优先级、资源请求(resource request)与限制条件等^[3]。从任务优先级的角度观察，Google设置了任务的12个优先级，并将其依次划分为高优先级(9-11)、中优先级(2-8)与低优先级(0-1)三类。优先级越高，意味着成功调度的几率更大，拥有更高的服务质量。且各优先级作业，其运行时长，资源使用特征存在异构性。在资源请求的维度上，任务请求的资源主要有CPU与内存空间，通过对CPU与内存在请求率上的回归分析得出，两者存在关联，但关联性较弱( $R \approx 0.14$ )。在任务的限制条件中，通常是由用户为作业指定主机性能或是其他关联性任务，限制条件数量与任务的延迟调度并不存在明显关联关系，例如，对于只有一个限制条件的任务集合，与同时拥有6个限制条件的任务集合，其平均调度延迟差值较小。

在trace数据中，作业可分为面向用户的交互式作业与批处理作业，它们对资源的请求存在多样化特性，且主要体现为对计算、内存与带宽资源的请求。因此本文选择在资源请求的维度为任务建模，以 ${\rm (id,mips,mem,bw)}$ 元组的形式描述任务的资源请求，其中， ${\rm id}$ 表示任务标识， ${\rm mips}$ 表示任务请求的计算资源，执行任务指令。 ${\rm mem}$ 表示任务请求的内存资源，用于构建程序数据结构， ${\rm bw}$ 表示请求的带宽资源，用于访问任务链接的外部资源。

2.2 调度模型

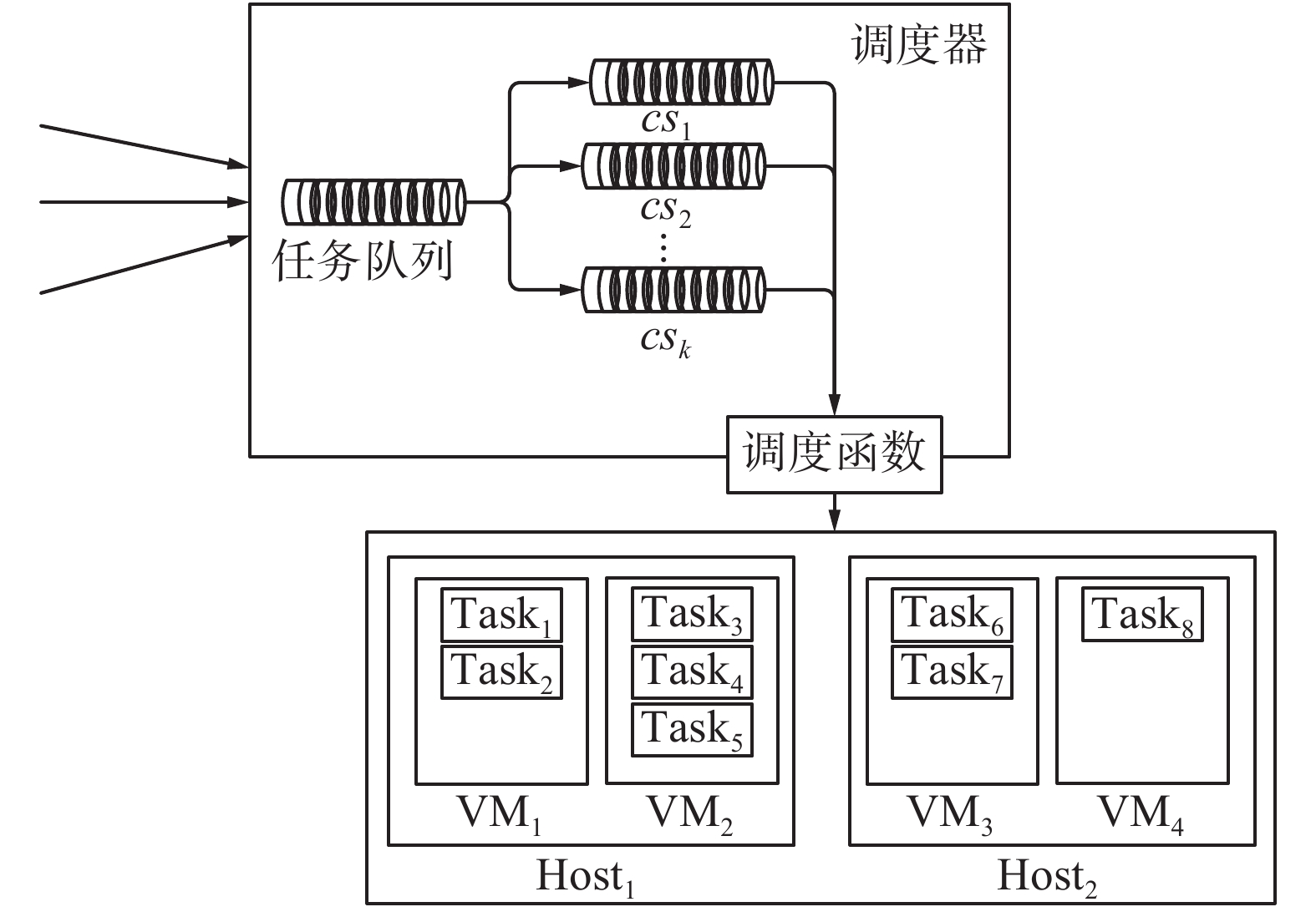
调度器是集群的核心，负责任务的调度与资源的合并、迁移，其调度方式与效率将极大影响集群的性能输出。本文建立的调度模型如图1所示，其主要模块和功能如下：

1)调度器(Scheduler)：聚类调度，为任务选择合适节点。

2)计算节点(Host)：物理机节点，承载虚机。

3)虚机(VM)：资源分配的基本单元，执行请求任务。

如图1所示，用户任务(Task)进入任务队列(Task queue)，调度器(Scheduler)首先提取Task queue中的任务集合，根据任务属性将其聚类划分为 $\{ c{s_1},c{s_2}, \cdots ,c{s_k}\} $ ，然后通过调度函数(Strategies)为各类簇任务选择目标主机(Host)，由Host中的虚机(VM)执行该任务，将结果返回。

2.3 算法描述

给定任务集合 $T = \{ {t_1},{t_2}, \cdots ,{t_n}\} $ ，其中 ${t_i} = \{ {\rm id},{\rm mip}{s_i},$ ${\rm me{m}_i},{\rm b{w}_i}\} $ ，分别表示任务i标志，请求的计算、内存、带宽资源。设有主机列表 $H = \{ {h_1},{h_2}, \cdots ,{h_m}\} $ ,其中 ${h_i} = \{ ({P_i},{p_i}),({M_i},{m_i}),({B_i},{b_i})\} $ , ${P_i}{\text 、}{M_i}{\text 、}{B_i}$ 分别表示h_i最大可分配的计算、内存与带宽资源， ${p_i}{\text 、}{m_i}{\text 、}{b_i}$ 则分别表示 ${h_i}$ 已分配的计算、内存、带宽资源。TWCW算法由聚类，评分与调度3部分组成。

2.3.1 聚类

基于三支聚类算法，提出任务类簇的三支表示形式：

$c{s_i} = (L(c{s_i}),M(c{s_i}))$

(2)

式中： $L(c{s_i}) \subseteq T$ 且 $M(c{s_i}) \subseteq T$ 。设 $R(c{s_i}) = T - L(c{s_i}) - $ $M(c{s_i})$ ，则 $L(c{s_i}){\text 、}M(c{s_i}){\text 、}R(c{s_i})$ 构成了类簇 $c{s_i}$ 的核心域、边缘域和琐碎域，它们满足如下性质：

$T = L(c{s_i}) \cup M(c{s_i}) \cup R(c{s_i})$

(3)

$\begin{gathered} L(c{s_i}) \cap M(c{s_i}) = \text{Ø} \\ L(c{s_i}) \cap R(c{s_i}) = \text{Ø} \\ M(c{s_i}) \cap R(c{s_i}) = \text{Ø} \\ \end{gathered} $

(4)

若任务 $t \in L(c{s_i})$ ，则 $t$ 属于类簇 $c{s_i}$ ；若任务 $t \in R(c{s_i})$ ，则 $t$ 不属于类簇 $c{s_i}$ ；若任务 $t \in M(c{s_i})$ ，则 $t$ 可能属于类簇 $c{s_i}$ 。其聚类结果为 $= \{ (L(c{s_1}),$ $ CSM(c{s_1})), \cdots ,(L(c{s_k}),M(c{s_k}))\} $ 。三支聚类算法包括寻找最佳聚类数与确定类簇域对象两个子步骤，其基本思想如下：

1) 寻找最佳聚类数，使用聚类算法(如k-means)聚类任务集合 $T$ ，根据类簇间离散度与类簇内聚合度择优确定最佳聚类结果；

2) 确定类簇域对象，首先通过近邻域确定类簇 $M$ 域对象，然后使用差值排序进一步划分类簇 $L$ 域与 $M$ 域对象，其具体内容如下：对于类簇 $c{s_k}$ ，任务 ${t_i}$ 、 ${t_j}$ 与近邻域 ${\rm Nei{g}_q}({t_i})$ ，其中，类簇 $c{s_k}$ 存在中心点 ${\rm centroi{d}_k}$ ， ${\rm Nei{g}_q}({t_i})$ 表示在欧式距离上离 ${t_i}$ 最近的 $q$ 个任务，当 ${t_i} \notin c{s_h}$ ， ${t_j} \in Nei{g_q}({t_i})$ 时，若 ${t_j} \in c{s_h}$ ，则确定 ${t_i}$ 为 $M(c{s_h})$ 对象，然后根据类簇 $c{s_h}$ 内任务集合 ${t_1},{t_2}, \cdots ,{t_l}$ 与中心点 ${\rm centroi{d}_h}$ 的欧式距离差值排序，确定差值最大的任务对 ${t_{p - 1}}$ 和 ${t_p}$ ，将 ${t_1},{t_2}, \cdots ,{t_{p - 1}}$ 划分到 $L(c{s_h})$ 中， ${t_p},{t_{p + 1}}, \cdots ,{t_l}$ 划分给 $M(c{s_h})$ 。其算法描述如下：

输入　任务集合 $T$ ，近邻数 $q$ 。

输出　 $CS = \{ (L(c{s_1}),M(c{s_1})), \cdots ,(L(c{s_k}),M(c{s_k}))\} $

1) 初始化， $k = 2$ ；

2) 随机选取 $k$ 个聚类中心 ${v_1},{v_2}, \cdots ,{v_k}$ ；

3) 对于每个任务 ${t_i}$ ，计算其到每个聚类中心 ${v_i}$ 的距离，将其划分到距离最小的类中；

4) 更新聚类中心 $v = \{ v_1', v_2',\cdots ,v_k'\} $ ;

5) 如果聚类中心不发生变化至6)；否则转至3)；

6) 计算 ${\rm CVIN}(CS)$ ，如果 $k \leqslant \sqrt N $ ,那么 $k = k + 1$ ，转至2)；否则转至7)；

7) 考查任务 ${t_i}$ 和类 $cs$ ，其中 ${t_i} \in cs,{t_j} \in {\rm Nei{g}_q}(t)$ 。如果 ${t_j} \in cs$ ，那么把 ${t_i}$ 划分到 $M(cs)$ ；

8) 对于类中剩余非 $M$ 域中对象，根据差值排序法，找到第一个距离差值最大的对象对 ${t_{i - 1}}$ 和 ${t_i}$ ，把 ${t_i}$ 及其后的对象划分到 $M(cs)$ ；

9) 算法结束，输出结果 $CS = \{ (L(c{s_1}),M(c{s_1})), \cdots ,$ $(L(c{s_k}),M(c{s_k}))\} $ 。

2.3.2 评分

在对任务集合T进行三支聚类后得到聚类结果 $CS = \{ (L(c{s_1}),M(c{s_1})), \cdots ,(L(c{s_k}),M(c{s_k}))\} $ ，其中，类簇 $c{s_i}$ 的类簇中心 ${\rm centroi{d}_i} = \{ {\rm mips},{\rm mem},{\rm bw}\} $ 。通过比较类簇中心 ${\rm centroid}$ 间属性大小确定类簇间属性比重与类簇内属性偏好，以评分矩阵的形式记录评分结果。

定义1　类簇评分矩阵 ${{ W}_{NxM}}$ ，如式(5)所示。

${{ W}_{N{\text ×}M}} = \left[ {\begin{array}{*{20}{c}} {{w_{1,1}}}&{{w_{1,2}}}& \cdots &{{w_{1,M}}} \\ {{w_{2,1}}}&{{w_{2,2}}}& \cdots &{{w_{2,M}}} \\ \vdots & \vdots &{}& \vdots \\ {{w_{N,1}}}&{{w_{N,2}}}& \cdots &{{w_{N,M}}} \end{array}} \right],\;N = 3,M = k$

(5)

式中： ${w_{i,j}}$ 表示类簇 $j$ 第 $i$ 维属性得分值；矩阵的行向量 ${{ w}_i} = [{w_{i,1}}\,\,{w_{i,2}}\,\, \cdots \,\,{w_{i,M}}]$ 表示各类簇中心在第 $i$ 维资源上的评分值，记录类簇间资源请求的比重；矩阵的列向量 ${{ w}_j} = {[{w_{1,j}}\,\,{w_{2,j}}\,\, \cdots \,\,{w_{N,j}}]^{\rm{T}}}$ 表示类簇 $j$ 资源请求偏好。评分函数通过排序算法比较 ${\rm centroi{d}_1},$ ${\rm centroi{d}_2}, \cdots ,{\rm centroi{d}_k}$ 间第 $i$ 维属性，确定行向量 ${ w} = [{w_{i,1}}\,\,{w_{i,2}}\,\, \cdots \,\,{w_{i,M}}]$ 。假设评分矩阵为

${{ W}_{3 \times 4}} = \left[ {\begin{array}{*{20}{c}} 4&3&2&1 \\ 3&1&4&2 \\ 2&4&1&3 \end{array}} \right]$

观察 ${ W}$ 行向量可知，对于请求的 ${\rm mips}$ 资源， ${\rm centroi{d}_1} > {\rm centroi{d}_2} > {\rm centroi{d}_3} > {\rm centroi{d}_4}$ ，所以 ${w_{1,1}}$ 的得分最高， ${w_{1,2}}$ 次之。接着观察其列向量，以列向量 ${{ w}_1} = {[4\,\,3\,\,2]^{\rm{T}}}$ 为例，类簇 $c{s_1}$ 中的任务请求4单位的 ${\rm mips}$ ，3单位的 ${\rm mem}$ 与2单位的 ${\rm bw}$ 。任务偏好为4:3:2。

2.3.3 调度

在完成对任务的聚类、评分后，根据聚类结果 $CS$ 与评分矩阵 ${ W}$ ，分别对 $c{s_i}$ 的 $L$ 域、 $M$ 域任务设置调度函数。TWCW算法追求最大化的资源使用，因此调度函数需充分利用闲置资源，均衡集群负载。通过定义主机 ${{\rm hos{t}}_i}$ 资源剩余可分配空间表示其资源空闲度。

定义2　主机 ${{\rm hos{t}}_i}$ 的第 $j$ 维资源剩余可分配空间 ${{\rm spac{e}}_{i,j}}$ ，如式(6)所示。

${{\rm spac{e}}_{i,j}} = ({{{{\rm allocabl{e}}_{i,j}} - {{\rm allocate{d}}_{i,j}})}/{{{\rm allocabl{e}}_{i,j}}}}$

(6)

式中： ${{\rm allocabl{e}}_{i,j}}$ 表示 ${{\rm hos{t}}_i}$ 最大可分配的 $j$ 维资源， ${{\rm allocate{d}}_{i,j}}$ 表示 ${{\rm hos{t}}_i}$ 已分配的 $j$ 维资源。

定义3　主机 ${{\rm hos{t}}_i}$ 的资源剩余可分配空间，如式(7)所示。

${S_i} = \sum\limits_{j = 1}^N {{\mu _j} \cdot {{\rm spac{e}}_{i,j}},\;N = 3} $

(7)

式中 ${\mu _j}$ 表示主机 ${{\rm hos{t}}_i}$ 的第 $j$ 维资源的权重。

TWCW算法可最大限度的利用空闲资源，根据任务属性评估节点列表 $H$ 的剩余可分配空间 ${S_i}$ ，选择资源可分配空间最大的主机作为目标节点，如式(8)所示。

${h_{\rm{target}}} = \max (\sum\limits_{j = 1}^N {{\mu _j}{\rm spac{e}}}_{i,j} ),\;N = 3,i = 1,2, \cdots ,m$

(8)

TWCW算法可最大限度的利用空闲资源，根据任务属性评估节点列表 $H$ 的剩余可分配空间 ${S_i}$ ，选择资源可分配空间最大的主机作为目标节点，如式(8)所示。

对于 $L({C_i})$ 域的任务，通过归一化评分矩阵 ${ W}$ 列向量确定权重因子 ${\mu _j}$ ，如式(9)所示。

${\mu _j} = \frac{{{w_{j,i}}}}{{\displaystyle\sum\limits_{j = 1}^N {{w_{j,i}}} }},N = 3$

(9)

对于 $M({C_i})$ 域的任务，根据任务请求的资源在集群资源中的所占比确定该任务请求的主资源，将多维属性映射到单维空间，从而确定权重因子 $\mu $ ，其算法描述如下。

输入　任务 $t$ ；

输出　权重因子 $\mu $ 。

1) 初始化权重因子 $\mu $ ；

2) 获取集群资源resource，初始化迭代变量i=0；

3) 计算在第 $i$ 维属性中，任务 $t$ 在资源resource中的比重prop_i=t.attr_i/resource_i；

4) 如果 $i < N$ ， $i = i + 1$ ，转至步骤3)。否则转至5)；

5) 确定prop_i中比重最大的第 $l$ 维属性，将 ${\mu _l}$ 置为1，算法结束。

2.3.4 时间复杂度分析。

TWCW算法包括了任务聚类、评分与调度，其中：

1) 三支聚类时间复杂度分析。设任务集合的任务数为 $n$ ，聚类分支数为 $k$ ，近邻数为 $q$ ，k- ${\rm means}$ 的迭代次数为 $I$ ，寻找最佳聚类数目的时间复杂度为 $O({n^2}I + {n^2}q)$ ，确定分支域对象的时间复杂度为 $O(n\log n + knq)$ ^[21]。

2) 类簇评分时间复杂度分析。设聚类分支数为 $k$ ，确定类簇中心在单个属性的排序算法的时间复杂度为 $O(k\log k)$ 。

3) 选择目标主机时间复杂度分析。设任务集合的任务数为 $n$ ，主机列表的节点数为 $m$ ，对于单个任务选择目标节点的时间复杂度为 $O(m)$ ，那么选择目标主机的时间复杂度为 $O(nm)$ 。

3 实验及数据分析 3.1 实验环境与参数设置

本文采用cloudsim3.0进行实验。实验模拟1 000个节点，主机均为四核的，单核处理能力为37 274 MIPS。主机 RAM为8 GB，硬盘容量为1 TB，带宽1 Gb/s。随机生成一系列虚拟请求构成的任务(请求序列)。任务的相关参数如表1所示。

实验采用了两个指标来评估TWCW算法的性能：平均响应时间和系统资源利用率。其中，平均响应时间包括等待时间和处理时间，系统资源利用率为主机集合的平均使用率。实验同时实现了k-means^[5]和FCM^[6]聚类调度算法，观察它们在上述性能方面的表现。

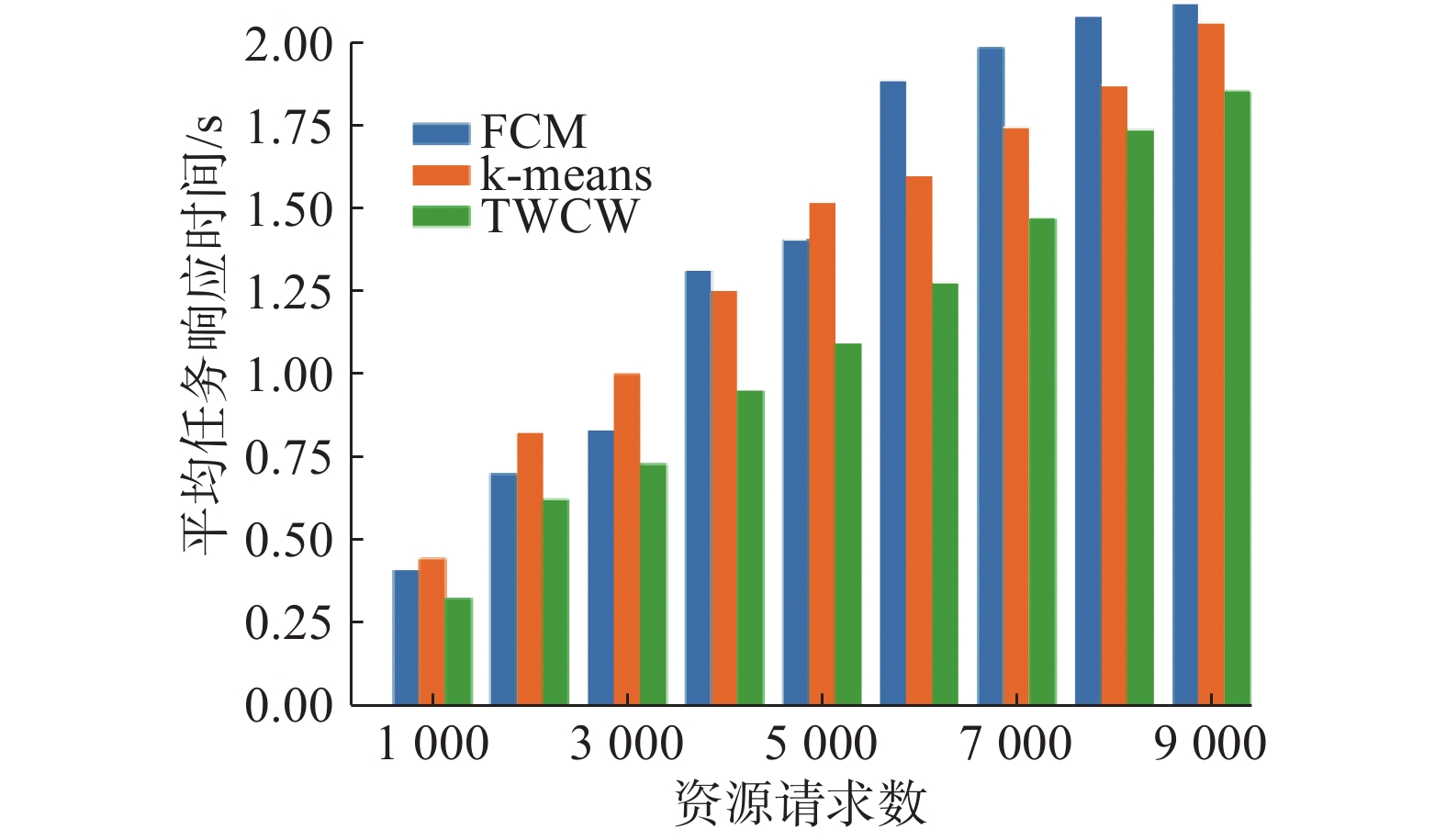
3.2 任务平均响应时间比较实验

评估了TWCW聚类调度在任务响应时间的表现。实验分别实现了TWCW、k-means和FCM算法来验证聚类方式的改变对任务响应时间的影响，实验结果分别如图2所示。

由图2可以看出TWCW算法比k-means或FCM在任务响应时间上有一定下降。说明TWCW在对任务更细粒度聚类划分后，为任务选择偏好属性更充足的节点，使其能够更快地完成计算操作返回结果从而减少任务运行时间。经统计TWCW算法任务的平均响应时间，相比于FCM与k-means算法减少了约7%。

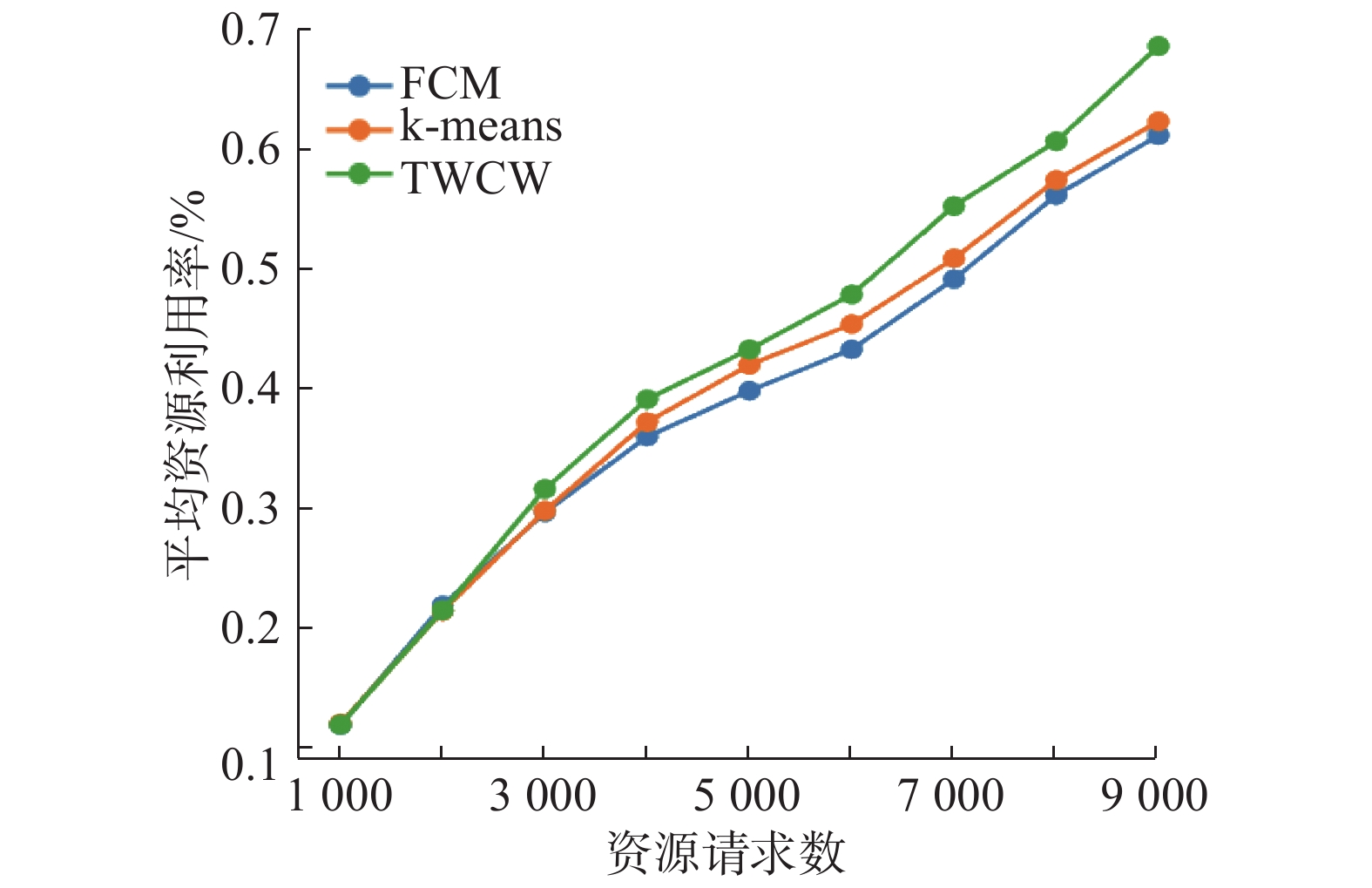
3.3 集群资源利用率比较实验

验证了TWCW算法在资源利用率方面的优化效果。实验分别评估了TWCW、k-means和FCM算法在集群资源利用率方面的表现。实验结果分别如图3~4所示。

由图3可知，集群资源使用率随着负载的增加而增加，可以看出，在资源请求为1 000~2 000个时3种算法的差别不大，而在请求幅度继续增大时，TWCW算法的优化效果较为明显，相对其他算法最高有近11.3%的改善。

图4中四分位区间内的实线表示资源利用率的中位数。可以观察到，TWCW算法四分位区间相对集中且利用率中位数均高于其他算法，说明相比于k-means或FCM需提前设置聚类分支，TWCW聚类类簇的三支划分与域对象的分类调度能细粒度地将任务匹配给合适资源，避免了节点的过量负载与资源闲置，从而能更有效地平滑集群负载，提高资源使用率。

4 结束语

本文在云任务调度中，引入三支聚类评分算法，以提高资源利用率为目标，利用任务的多样化特性，对任务集合进行三支聚类，通过类簇评分调度，实现资源的合理分配。并在试验中实现并比较了k-means和FCM聚类调度算法，考察它们在上述性能方面的表现，实验结果表明：对任务集合细粒度的类簇划分与对象的针对性调度，有利于集群资源利用率与负载均衡。

在未来的工作中，将对任务进行更细化的分类建模，改进任务与资源的匹配模型，且基于节能角度的考虑，对资源负载进行动态迁移，确定虚机迁移阈值的在线学习方案，设计评价函数动态调整阈值区间等。