无线传感器网络(wireless sensor network, WSN)是一种能够在未知环境中对特定的未知区域检测、采集和传输信息的一种新兴的技术。目前在国防、医疗卫生以及日常生活等领域扮演着越来越重要的角色。WSN节点位置信息在很多WSN的应用场合都是极其重要的。WSN所收集的数据信息都是建立在已知节点位置信息的基础上展开的^[1]。

由于在现实的使用过程中为了节省成本，所以不适合在所有的WSN节点中装载全球定位系统模块（global positioning system，GPS）^[2]。现在的WSN节点定位方法中有蒙特卡洛法、DV-HOP法和三边定位法等^[3-5]。文献[6]针对三维DV-HOP WSN定位算法在实际地形中定位时误差较大的问题，提出了一种非测距定位算法，实验表明该算法减小了定位误差。文献[7]针对WSN中传感器节点的初始位置未知的问题，提出了一种通信损耗小，设计简单的三维定位算法，最后的仿真结果表明，该算法具有较小的节点定位误差。文献[8]针对标准粒子群算法进化后期收敛速度，容易陷入局部极小点等问题，提出了一种农业WSN三维定位算法。仿真结果表明，该方法的稳定性和定位精度均优于标准粒子群算法。文献[9]针对目前WSN三维空间定位算法精度不高，稳定性差等问题，创建了一种三维定位算法3D-LE-LPCCA。最后的仿真结果表明，该算法有良好的定位精度和稳定性。文献[10]提出了一种基于移动信标的加权最小二乘距离估计法。仿真结果表明，该方法提高了定位精度。

文献[11]通过神经网络来对未知节点进行定位，实验表明RBF神经网络具有较好的定位精度，MLP神经网络具有最佳的计算和存储资源。文献[12]提出了一种新的目标跟踪双分布式传感器定位系统，结果表明在一定程度上提高了定位精度。文献[13]通过一种基于共面度单位的三维定位算法来实现定位的准确性。文献[14]通过不相似矩阵来表示每个节点到其他节点的距离，最后的仿真结果证明了算法的有效性。文献[15]通过引入3D Voronoi图来划分3D位置空间，构建虚拟信标节点的秩序来实现定位。仿真实验表明，它可以提高复杂三维空间节点的定位精度，减少测量和计算成本。文献[16]通过使用模糊逻辑系统(FLS)对接收信号强度（RSS）和距离之间的非线性进行建模以降低计算复杂度，并通过混合粒子群算法（HPSO）和基于生物地理学优化(BBO)进一步优化，从而最大限度的减少误差。文献[17]为了提高未知节点的定位精度，提出了一种基于CKF的无线传感器网络分布式节点定位算法。仿真结果表明，该算法具有优良的定位性能。

本文借鉴孙尧^[18]所提出的用无人机作为辅助工具，结合一定的算法给WSN节点进行室外的精确定位。利用无人机在三维空间灵活的机动性和强大的计算能力，将一般利用信标节点−节点之间进行定位的方式变成了无人机−节点协作的定位方式。由于无人机的引入，会产生一定的过程噪声，为避免滤波的发散和鲁棒性的降低。本文对文献[17]的算法进行了改进，增加了阈值选择的更新策略。提出了一种改进的SR-CKF滤波算法。由此形成了一种在无人机协助下，利用SR-CKF对WSN节点进行精确定位的模式。

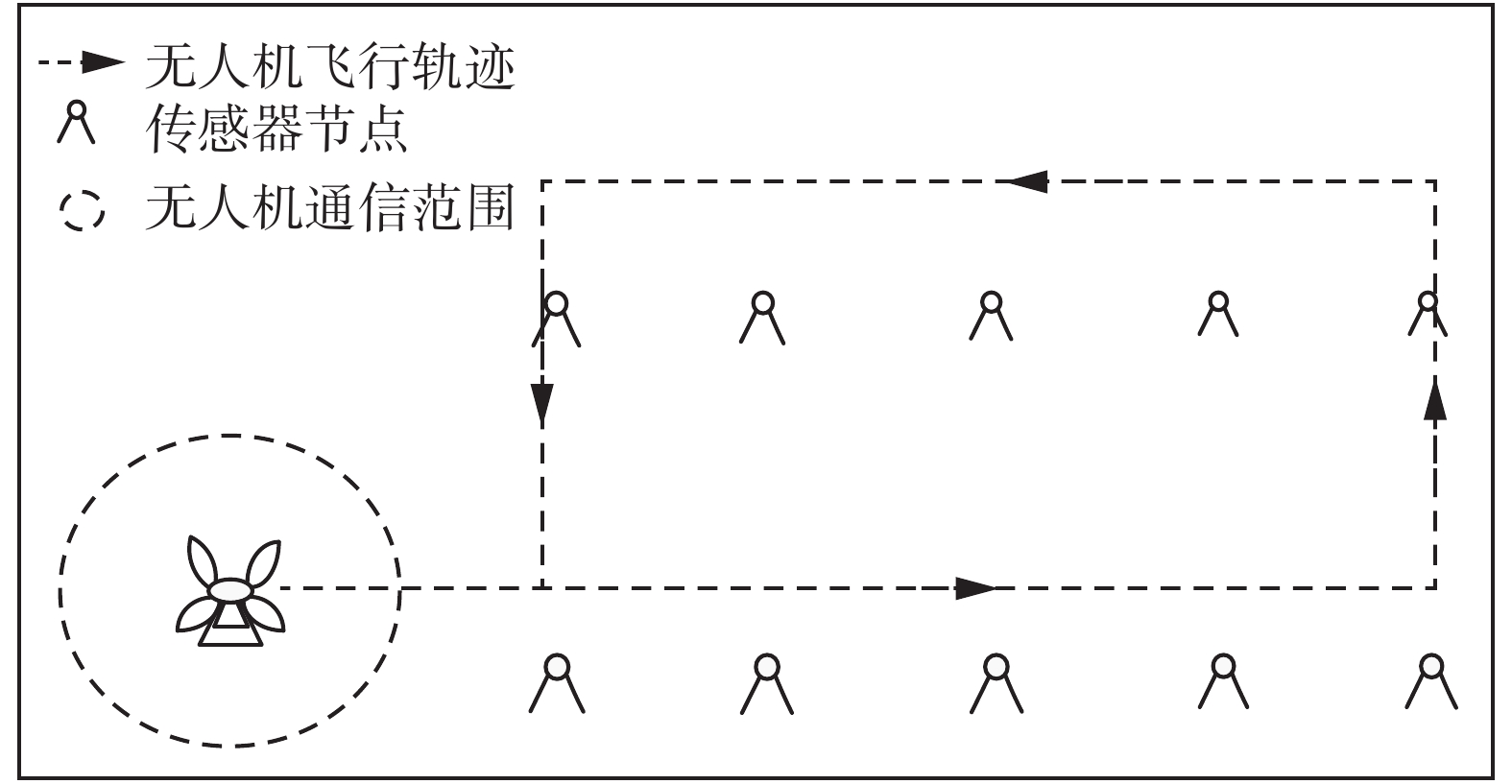
1 初步定位模型

在初步定位模型中，UAV携带GPS定位系统在三维空间中以一个固定的高度、轨迹和速度飞行。作为一个移动的信标节点，UAV在和未知节点建立互相通信的同时，可以周期性的发射自身的位置数据，通过RSSI测距数学模型来获取UAV和m个未知节点之间的相对距离数据，最后未知节点的初步定位数据可以通过极大似然估计法（maximum likelihoodestimation，MLE）来获取，初步定位系统模型如图1所示。

1.1 RSSI测距系统模型的建立

RSSI测距数学模型的建立需要将UAV和未知节点之间互相通信，UAV作为一个三维空间的移动信标，可以假设它的最大通信范围为R。在通信范围内，UAV周期性的发射虚拟信标信息，未知节点接收信息。计算出UAV和未知节点之间的相对距离信息 $l$ ，并满足 $l \leqslant R$ ，根据传播损耗模型建立的测距模型可表示为：

${P_r}\left( d \right) = {P_i}\left( {{d_i}} \right) - 10\gamma \lg \left( {\frac{d}{{{d_i}}}} \right) + {W_\delta }$

(1)

式中： $d$ 表示发射器和接受器之间的相对测量距离； $ P_{r}(d)$ 为接收器接收到的实际信号强度； $d_i$ 为近地的参考距离； $P_i(d_i)$ 为在 $d_i$ 处接收到的信号强度； $\gamma $ 为信号在路径中的衰减因子，它的大小取决于信号传播的具体环境； ${W_\delta }$ 为一个正态分布的高斯随机变量。通过此模型来计算出无人机与未知节点之间的相对距离。

1.2 基于RSSI测距的极大似然法位置估计模型

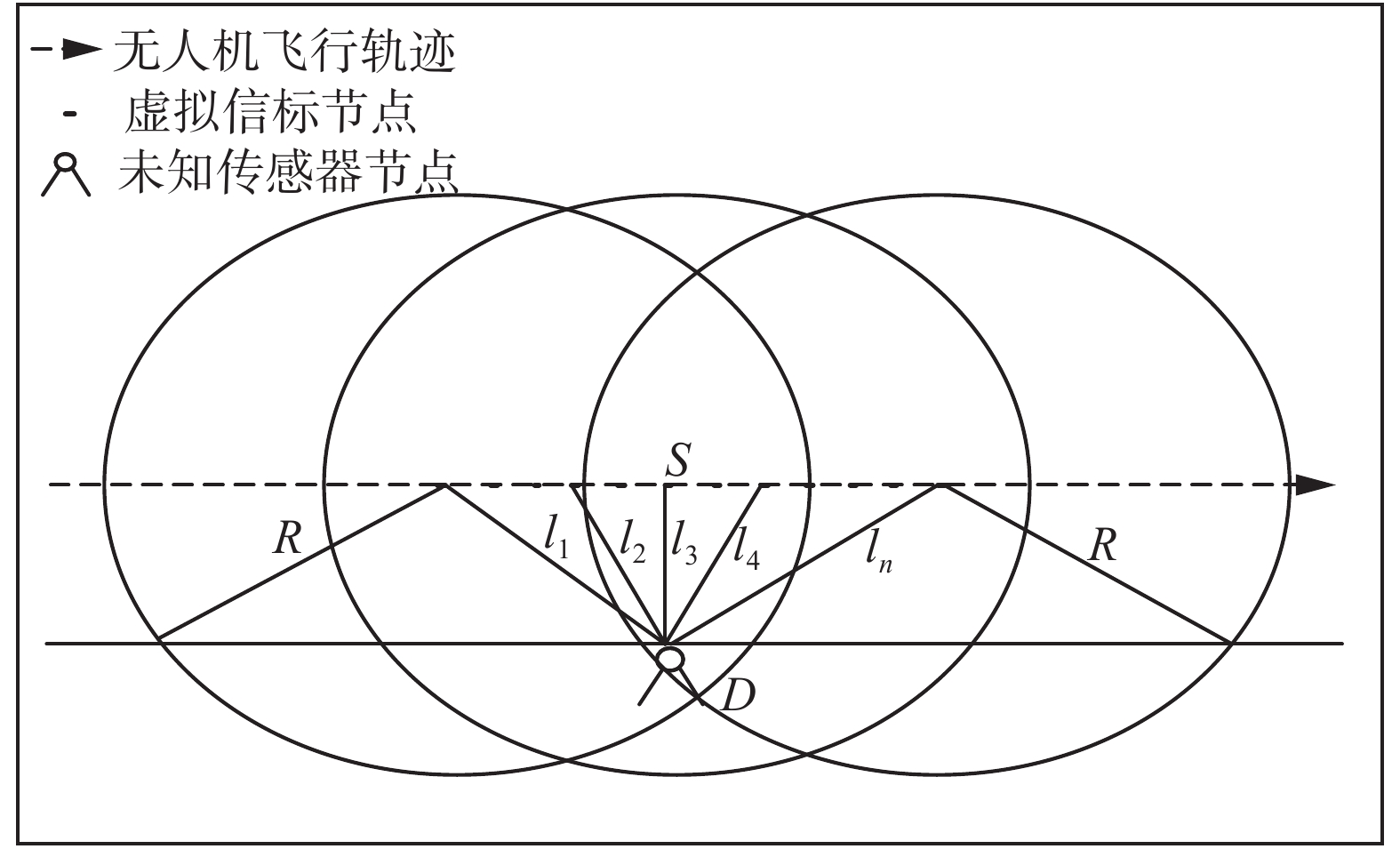
当无人机飞行到未知传感器节点区域时，无人机以设定好的高度 z 和速度 $v$ 在未知传感器垂直上方移动，如图2所示。

图2中 $R$ 为无人机的通信半径，其通信半径的大小取决于信号发射器功率的大小和具体环境。令无人机每隔固定的周期T广播自身的位置信息，即每经过周期T无人机产生一个虚拟信标。 $S$ 为无人机广播虚拟信标过程中所飞行的距离，虚拟信标包含无人机在该时刻的实际位置。从图中可以看出，所有的虚拟信标的通信范围都满足它的通信半径不小于虚拟信标到未知传感器之间的相对距离，即 $l \leqslant R$ 。假设无人机经过 $n$ 个虚拟信标，即设为 $\left\{ {M_1,M_2, \cdots, M_n} \right\}$ 。则无人机在每个虚拟信标对应未知传感器节点的垂直坐标为 $\left( {{x_1},{y_1},{z_1}} \right),\left( {{x_2},{y_2},{z_2}} \right), \cdots, \left( {{x_n},{y_n},{z_n}} \right)$ 。由图中可以看出 ${l_1},{l_2}, \cdots, {l_n}$ 为虚拟信标到未知传感器之间的相对距离。通过1.1节的RSSI测距模型可以测得它们的相对距离。由于无人机机载GPS模块在未知传感器节点上空飞行，无人机在未知传感器节点的垂直坐标 $\left( {{x_1},{y_1},{z_1}} \right),\left( {{x_2},{y_2},{z_2}} \right),$ $ \cdots, $ $ \left( {{x_n},{y_n},{z_n}} \right)$ 是已知的。另外可知当无人机在未知传感器节点正垂直上空所产生的虚拟信标到未知传感器节点之间的距离 ${l_3}$ 是已知的。假设未知传感器节点的坐标为 $(x,y,{z_0})$ ，由于无人机的垂直海拔高度 ${z_1}$ 是已知的，则未知传感器节点的高度 ${z_0}$ 是已知的，即为 ${z_0} = {z_1} - {l_3}$ 。其他未知传感器节点的高度也可依此推出。只需要求得未知传感器节点的 $(x,y)$ 坐标就可以确定未知传感器节点的初步位置。经过RSSI测距后，令无人机和未知传感器节点D的相对距离分别是 ${d_1},{d_2}, \cdots, {d_n}$ ，根据欧氏距离公式有如下关系式：

$\left\{ {\begin{array}{*{20}{c}} {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2} = d_1^2} \\ {{{\left( {{x_2} - x} \right)}^2} + {{\left( {{y_2} - y} \right)}^2} = d_2^2} \\ \vdots \\ {{{\left( {{x_n} - x} \right)}^2} + {{\left( {{y_n} - y} \right)}^2} = d_n^2} \end{array}} \right.$

(2)

式（2）可将其表示为线性方程 ${{AX}}={{b}}$ ，其中：

${{A}} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1} - {x_n}} \right)}&{2\left( {{y_1} - {y_n}} \right)}\\ {2\left( {{x_2} - {x_n}} \right)}&{2\left( {{y_2} - {y_n}} \right)}\\ \vdots & \vdots \\ {2\left( {{x_{n - 1}} - {x_n}} \right)}&{2\left( {{y_{n - 1}} - {y_n}} \right)} \end{array}} \right]$

(3)

$ {{b}} = \left[ {\begin{array}{*{20}{c}} {x_1^2 - x_n^2 + y_1^2{\rm{ - }}y_n^2{\rm{ + }}d_n^2{\rm{ - }}d_1^2}\\ {x_2^2 - x_n^2 + y_2^2{\rm{ - }}y_n^2{\rm{ + }}d_n^2{\rm{ - }}d_2^2}\\ \vdots \\ {x_{n - 1}^2 - x_n^2 + y_{n - 1}^2{\rm{ - }}y_n^2{\rm{ + }}d_n^2{\rm{ - }}d_{n - 1}^2} \end{array}} \right],{{X}} = \left[ \begin{array}{l} x\\ y \end{array} \right] $

(4)

对以上的公式（3）、（4）用最小均方差估计法，未知传感器节点D的位置二维坐标可表示为： $\mathop {{X}}\limits^ \wedge = $ $ {\left( {{{{A}}^{\rm{T}}}{{A}}} \right)^{ - 1}}{{{A}}^{\rm{T}}}{{b}}$ ，三维初步定位的坐标可表示为 $\left( {\hat {{X}},{z_0}} \right)$ 。

2 基于SR-CKF的节点精确定位算法 2.1 容积卡尔曼定位算法

容积卡尔曼滤波器(CKF)是一种新型的非线性高斯滤波算法，它的核心思想是通过时间更新和量测更新2个基本步骤来达到后验概率密度的不断更新。

2.2 SR-CKF滤波算法

通过在第1节中用无人机和未知节点之间建立的模型对未知节点的位置进行粗略的估计，本节在未知节点初步定位的基础上通过平方根容积卡尔曼滤波算法对未知节点的位置进行更加精确的定位。在定位系统中设有 $M\left( {i = 1,2, \cdots ,10} \right)$ 个未知WSN节点，则可考虑该离散非线性系统模型为

$\left\{ \begin{array}{l} {x_k} = f\left( {{x_{k - 1}}} \right) + {W_{k - 1}} \\ {{\textit{z}}_k} = h\left( {{x_k}} \right) + {V_k} \\ \end{array} \right.$

(5)

式中： ${x_k}$ 为 $k$ 时刻系统所在的状态向量； ${{\textit{z}}_k}$ 为 $k$ 时刻系统状态所在的量测值； $f( \cdot )$ 为非线性系统所在的状态方程； $h( \cdot )$ 为非线性系统的量测方程。 ${W_{k - 1}}\sim N(0,R)$ 和 ${V_k}\sim N(0,R)$ 分别为系统噪声和观测噪声。

则SRCKF算法的具体实现步骤可表示如下^[19]：

时间更新阶段，可令 ${{p}}\left( {{x_{k - 1}}} \right) = {{N}}\left( {{{\hat x}_{k - 1\left| {k - 1} \right.}},{{{P}}_{k - 1\left| {k - 1} \right.}}} \right)$ 为已知，分解因式 ${{{S}}_{k - 1\left| {k - 1} \right.}} = {\rm{chol}}\left( {{{{P}}_{k - 1\left| {k - 1} \right.}}} \right)$ ，式中 ${\rm{chol}}$ 为 ${\rm{Cholesky}}$ 分解函数。计算 ${\rm{cubature}}$ 点 ${{{X}}_{i,k - 1\left| {k - 1} \right.}} = $ $ {{{S}}_{k - 1\left| {k - 1} \right.}}{\xi _i} + {\hat x_{k - 1\left| {k - 1} \right.}}$ ，通过非线性状态方程传播 cubature 点 ${{X}}_{i,k\left| {k - 1} \right.}^ {*} \!\!= f\left( {{X_{i,k - 1\left| {k - 1} \right.}}} \right)$ ，状态预测为 ${\hat {{x}}_{k\left| {k - 1} \right.}} \!=\! \displaystyle\frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {{{X}}_{i,k\left| {k - 1} \right.}^ {*} } $ ，计算估计预测误差协方差矩阵的平方根为

${{\chi}} _{k\left| {k - 1} \right.}^ {*} = \frac{1}{{\sqrt {2n} }}\left[ {{{X}}_{1,k - 1}^ {*} - {{\hat {{x}}}_{k\left| {k - 1} \right.}}, \cdots ,{{X}}_{2n,k\left| {k - 1} \right.}^ {*} - {{\hat {{x}}}_{k\left| {k - 1} \right.}}} \right]$

(6)

${{{S}}_{k\left| {k - 1} \right.}} = qr\left\{ {\left[ {{{\chi}} _{k\left| {k - 1} \right.}^ {*} ,\sqrt {{Q_{K - 1}}} } \right]} \right\}$ ，其中 $qr( \cdot )$ 为 ${\rm{QR}}$ 的分解函数。

量测更新阶段，计算 ${\rm{cubature}}$ 点 ${{{X}}_{i,k\left| {k - 1} \right.}} = $ $ {{{S}}_{k\left| {k - 1} \right.}}{\xi _i} + {\hat x_{k\left| {k - 1} \right.}}$ ，传播 ${\rm{cubature}}$ 点 ${{Z}}_{i,k\left| {k - 1} \right.}^ {*} = h\left( {{{{X}}_{i,k\left| {k - 1} \right.}}} \right)$ ，计算量测预测值 ${\hat {{z}}_{k\left| {k - 1} \right.}} = \displaystyle\frac{1}{{2n}}\sum\limits_{i = 1}^{2n} {{{Z}}_{i,k\left| {k - 1} \right.}^ {*} } $ ，计算信息协方差矩阵的平方根为 ${{{\eta}} _{k\left| {k - 1} \right.}} = \displaystyle\frac{1}{{\sqrt {2n} }}\left[ {{{Z}}_{1,{\rm{k}}\left| {k - 1} \right.}^ {*} - {{\hat {\textit{z}}}_{k\left| {k - 1} \right.}}, \cdots ,{{Z}}_{2n,k\left| {k - 1} \right.}^ {*} - {{\hat {\textit{z}}}_{k\left| {k - 1} \right.}}} \right]$ ，

计算互协方差矩阵的平方根为：

$ \begin{split} & {{{\chi}} _{k\left| {k - 1} \right.}} = \frac{1}{{\sqrt {2n} }}\left[ {{{{X}}_{1,k\left| {k - 1} \right.}} - {{\hat x}_{k\left| {k - 1} \right.}}, \cdots ,{{{X}}_{2n,k\left| {k - 1} \right.}} - {{\hat x}_{k\left| {k - 1} \right.}}} \right]\\ & {{{P}}_{x{\textit{z}},k\left| {k - 1} \right.}} = {\chi _{k\left| {k - 1} \right.}}\eta _{k\left| {k - 1} \right.}^{{\rm{T}}}\end{split}$

(7)

估计卡尔曼滤波增益为 $\left( {{{{P}}_{x{\textit{z}},k\left| {k - 1} \right.}}/{{S}}_{{\textit{z}}{\textit{z}},k\left| {k - 1} \right.}^T} \right)/$ ${{{S}}_{{\textit{z}}{\textit{z}},k\left| {k - 1} \right.}}$ ，状态估计值为 ${\hat {{x}}_{k\left| k \right.}} = {\hat {{x}}_{k\left| {k - 1} \right.}} + {K_k}\left( {{{\textit{z}}_k} - {{\hat {\textit{z}}}_{k\left| {k - 1} \right.}}} \right)$ 。最后计算状态误差协方差矩阵平方根为

${S_{k\left| k \right.}} = qr\left\{ {\left[ {{\chi _{k\left| {k - 1} \right.}} - {K_k}{\eta _{k\left| {k - 1} \right.}},{K_k}\sqrt {{R_k}} } \right]} \right\}$

(8)

最后通过公式（8）可以得到未知节点的观测更新，由于引入了UAV作为信号发射源，因此会产生一定的高斯噪声，为了保证整个系统中未知节点的定位精度，因此加入了一种基于阈值选择的更新策略，即将公式（6）中 ${{\chi}} _{k\left| {k - 1} \right.}^ {*} $ 上的值在更新时设置一个阀值 $\alpha $ ，当 ${{\chi}} _{k\left| {k - 1} \right.}^ {*} $ 上的值设为 ${D_j}$ ，当 ${D_j} \geqslant \alpha $ 时，可令该数值保留，继续更新。当 ${D_j} < \alpha $ ，则令 ${D_j} = 0 $ ，即对 ${{\chi}} _{k\left| {k - 1} \right.}^ {*} $ 上的值不进行更新。通过加入这种策略，有效的减少了算法运算时间，提高了未知节点定位精度和可靠性。

2.3 SR-CKF的WSN协作定位

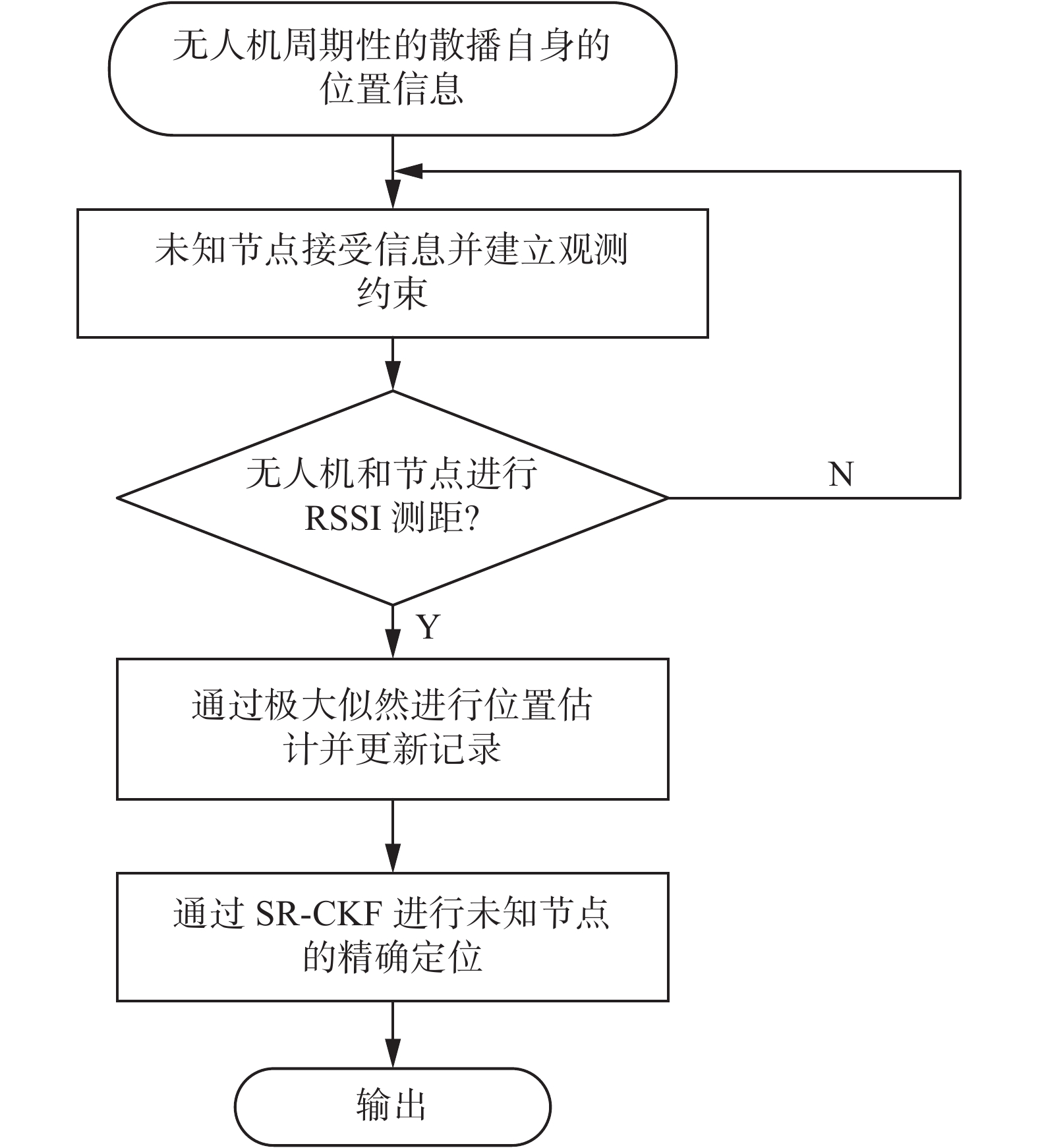
当无人机以设定好的航迹、速度和高度飞行并周期的广播自身的位置信息，从而和未知节点之间建立起足够多的观测约束，通过RSSI测距和极大似然估计获得未知节点的近似位置，再通过SR-CKF滤波算法对未知节点进行精确定位。算法流程图如图3所示。

3 仿真结果及分析 3.1 MLE、CKF、SR-CKF定位算法的比较

通过平均定位误差(mean positioning error, MPE)对未知传感器节点的定位精度进行相关的分析：

${\rm{MPE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\sqrt {{{\left( {{x_i} - {{\overline x }_i}} \right)}^2} + {{\left( {{y_i} - {{\overline y }_i}} \right)}^2}} } $

(9)

式中：n为未知传感器节点的个数； $\left( {{x_i},{y_i}} \right)$ 为未知节点的实际位置； $\left( {{{\overline x }_i},{{\overline y }_i}} \right)$ 为未知传感器节点的估计位置。图4分别仿真了MLE、CKF、SR-CKF3种算法，从图中的结果可以看出CKF的定位精度明显优于MLE，而SR-CKF的定位精度优于CKF。

3.2 无人机环境下的算法仿真结果分析

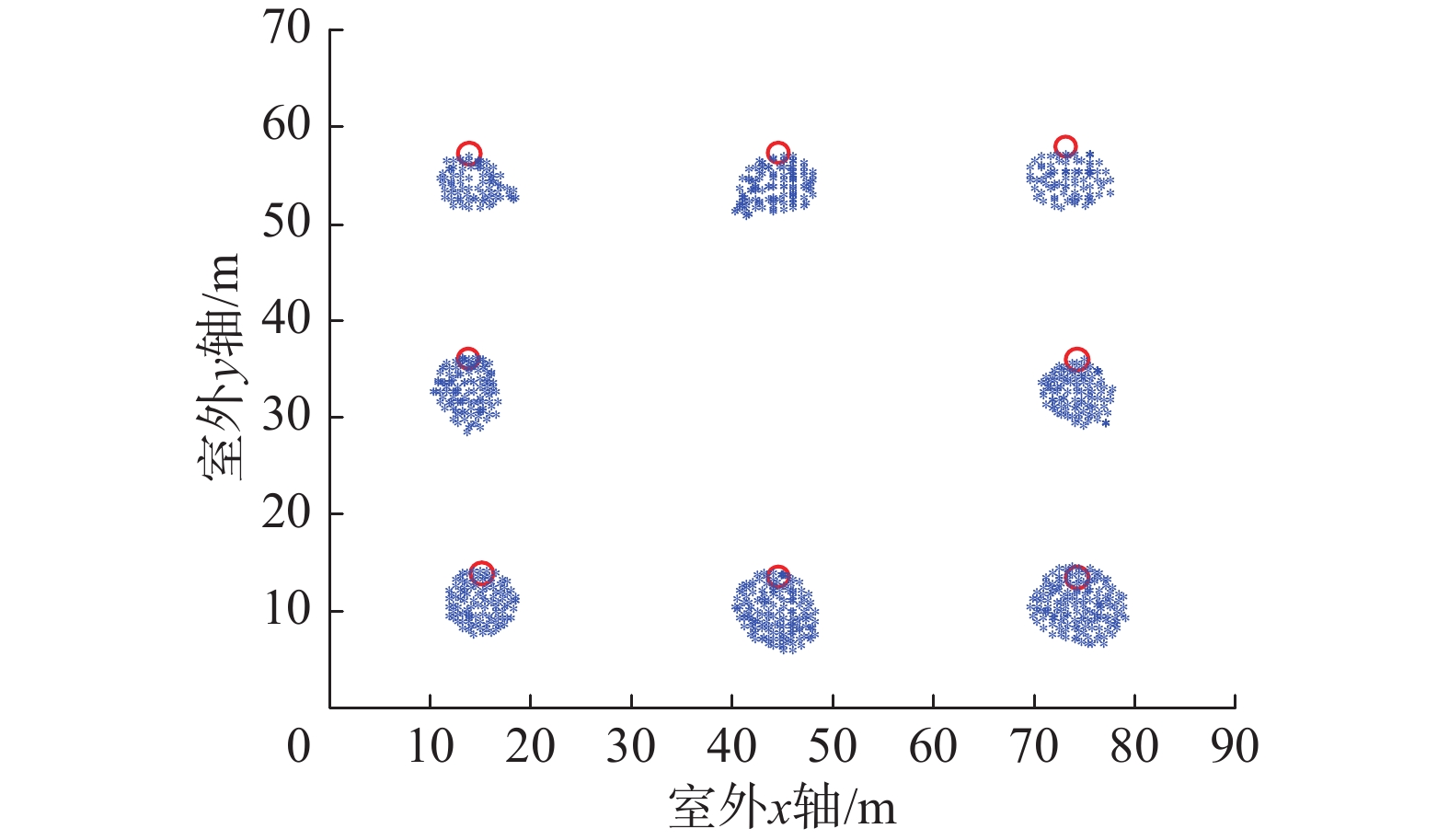
本文的仿真环境为90 m×70 m的室外环境，在这个环境中随机的部署8个未知传感器节点，无人机以1 m/s的速度，10 m的高度垂直在未知传感器节点的上空移动，无人机每隔1 s的周期散播自身的位置信息，并和未知节点进行通信。其中测距误差为 $\left[ {r - s \cdot r,r + s \cdot r} \right],s = 0.15$ ，图5仿真了在无人机协助下通过极大似然法对未知传感器节点进行定位(UAV-WSN-MLE)，其中“ ”表示未知节点的实际位置,“ ”表示未知节点每次采样的估计位置。

图6仿真了在WSN节点初步定位的基础上，引入CKF对未知节点精确定位（UAV-WSN-MLE-CKF），其中星号“ ”是作为CKF算法不同迭代次数的状态位置估计。因此从图6中可以观察出在相同参数下与仿真图5中UAV-WSN-MLE算法相比，图6中未知节点位置与实际位置的距离更小。

图7在相同仿真参数的情况下引入了阈值选择的更新策略，并采用了SR-CKF算法对未知节点进行了更加精确的定位(Unmanned Aerial Vehicle-Wireless Sensor Network-Maximum Likelihood Estimation-Square Root Cubature Kalman Filtering，UAV-WSN-MLE-SRCKF)。从仿真图中可以观察到，该算法的定位精度高于前两者的定位精度。

3.3 算法的对比分析

通过对定位均方误差进行分析，对以上3种方法在相同的仿真条件下进行了定位均方误差的对比。

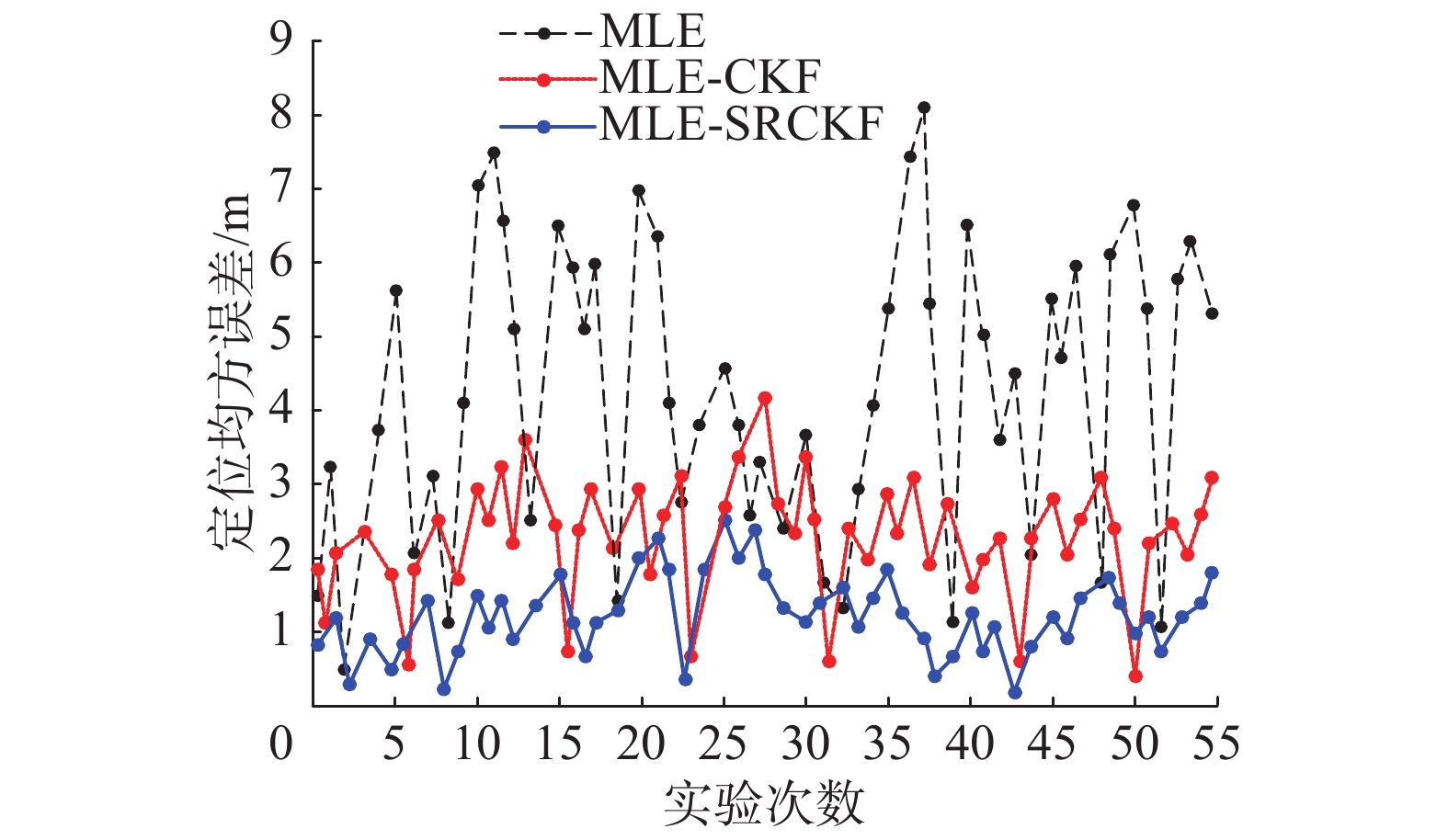
图8仿真了3种算法以无人机作为移动信标节点，其中测距误差为S=0.15的情况下获得的8个未知节点定位误差的55次蒙特卡罗实验的对比图，其中 为MLE(单纯的极大似然估计)的定位均方误差，为MLE-CKF(极大似然估计初定位下的容积卡尔曼)定位均方误差，为MLE-SRCKF(极大似然初定位下的平方根容积卡尔曼)定位均方误差。从图8中可以看出来MLE-SRCKF的定位均方误差均要小于MLE-CKF和MLE，其中MLE-CKF的定位均方误差要小于MLE。

4 结束语

本文提出了一种无人机协助下对未知传感器节点的定位方法，充分地利用了无人机在三维空间灵活的机动性和强大的计算能力，为三维复杂地形下实现无线传感器网络节点定位提供了很大可能。另一方面，采用阈值选择的更新策略，进一步减小了非线性因素的影响。仿真实验表明所采用的UAV-WSN-MLE-SRCKF算法有效地解决了无线传感器网络节点在三维地形的定位问题，大量减少了装载GPS模块所带来的成本，所用到的平方根容积卡尔曼滤波算法不但增强了数值的鲁棒性，确保了状态协方差矩阵的正定性，减小了系统滤波发散导致的误差，也同时提高了定位的精度。

本文目前只是在仿真上验证了该算法在三维地形中实现无线传感器网络节点定位的合理性与可行性。在实际应用中，验证本文所述算法，是接下来的重点工作，正在深入研究中。