2. 天津市智能机器人重点实验室,天津 300350
2. Key Laboratory of Intelligent Robotics of Tianjin, Tianjin 300350, China
时滞系统广泛存在于现代过程控制工业中,例如冶金、化工、炼油等工业。一般认为纯迟延时间
20世纪80年代末,韩京清研究员提出了自抗扰技术,由于能够实时估计和补偿扰动,受到了控制领域的广泛关注,并成功应用于各种不确定系统。针对时滞系统,韩京清[11]研究员提出了无视时滞法、一阶惯性环节近似法、输入预测法和输出预测4种方法,但是随着时滞增大控制效果变差。由于自抗扰技术的各种实用优点和需调参数太多等原因,美国克利夫兰州立大学的高志强教授[12]提出了线性自抗扰方法,大大简化了调参工作量,而且线性自抗扰的分析相对容易,现在已经有很多文献对此进行了理论分析[13-16]。
因此,将具有实时估计补偿扰动能力的线性自抗扰技术与解决纯时滞问题的Smith预估器相结合,来解决大时滞系统的控制问题。已有学者进行了一些相关研究,文献[17]在模型大约已知的条件下,将ADRC-Smith与基于时滞的扰动补偿观测器、PI-Smith在鲁棒性能和抗扰能力方面进行了比较,并进行频域分析,说明了ADRC-Smith控制性能更好,并对化学反应器浓度控制进行了仿真测试,对锅炉的氧浓度控制进行了仿真测试和实际结果的对比;文献[18]分析了ADRC-Smith的性能,并通过改进差分算法整定控制参数,最后与ADRC、PI-Smith、PI 3种控制器进行仿真比较。
在上述基础上,本文研究了在被控对象准确已知和大约已知两种情况下,LADRC-Smith控制方法的稳定条件和Smith预估器参数选择问题,通过MATLAB仿真进行了验证,并仿真分析了参数摄动对系统各个性能指标的影响。
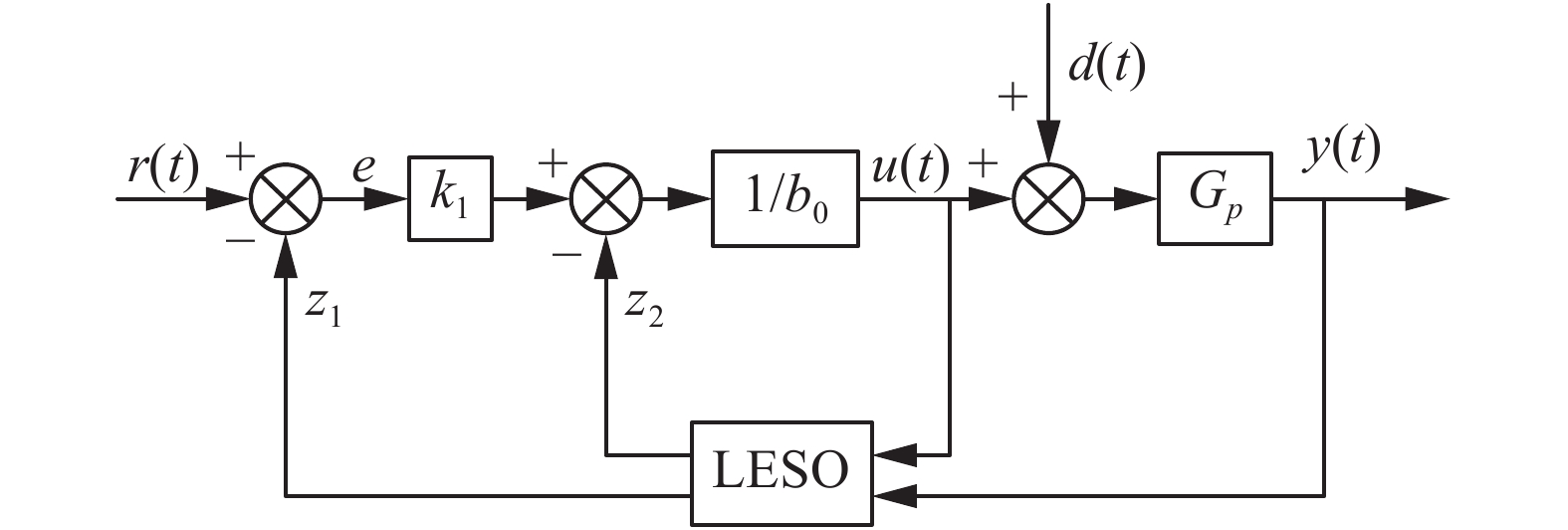
1 线性自抗扰的基本原理线性自抗扰以线性扩张状态观测器(linear extended state observer,LESO)为核心,包含了状态和扰动估计、误差反馈和扰动补偿几部分,结构如图1所示。
|
Download:
|
| 图 1 一阶系统线性自抗扰控制结构 Fig. 1 Diagram of LADRC for first-order systems | |
下面以一阶系统为例,假定不含时滞的一阶被控对象用微分方程表示为
| $\dot y = f(y,d) + bu$ | (1) |
式中:
式(1)所描述系统的状态方程为
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot X}} = {{AX}} + {{B}}u + {{E}}\dot f} \\ {y = {{CX}}} \end{array}} \right.$ | (2) |
根据式(2)设计的线性扩张状态观测器为
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot Z}} = {{AZ}} + {{B}}u + {{L}}(y - \hat y)} \\ {\hat y = {{CZ}}} \end{array}} \right.$ | (3) |
式中:
控制量
| $u = \frac{{{k_1}(r - {z_1}) - {z_2}}}{{{b_0}}}$ | (4) |
式中:
| ${{L}} = {\left[ {\begin{array}{*{20}{c}} {{\beta _1}}&{{\beta _2}} \end{array}} \right]^{\text{T}}} = {\left[ {\begin{array}{*{20}{c}} {2{w_o}}&{w_o^2} \end{array}} \right]^{\text{T}}},{\text{ }}{k_1} = {w_c}$ | (5) |
通常,一阶大时滞被控对象的数学模型为
| ${G_p}(s) = \frac{K}{{Ts + 1}}{{\text{e}}^{ - \tau s}}, \,\, K,T,\tau > 0$ | (6) |
式中:
| $\dot y = f(y,d) + bu(t - \tau )$ | (7) |
可以看出,由于时滞的存在,进入LESO的输出量
| ${G_m}(s) = \frac{{{K_m}}}{{{T_m}s + 1}}(1 - {{\text{e}}^{ - {\tau _m}s}})$ | (8) |
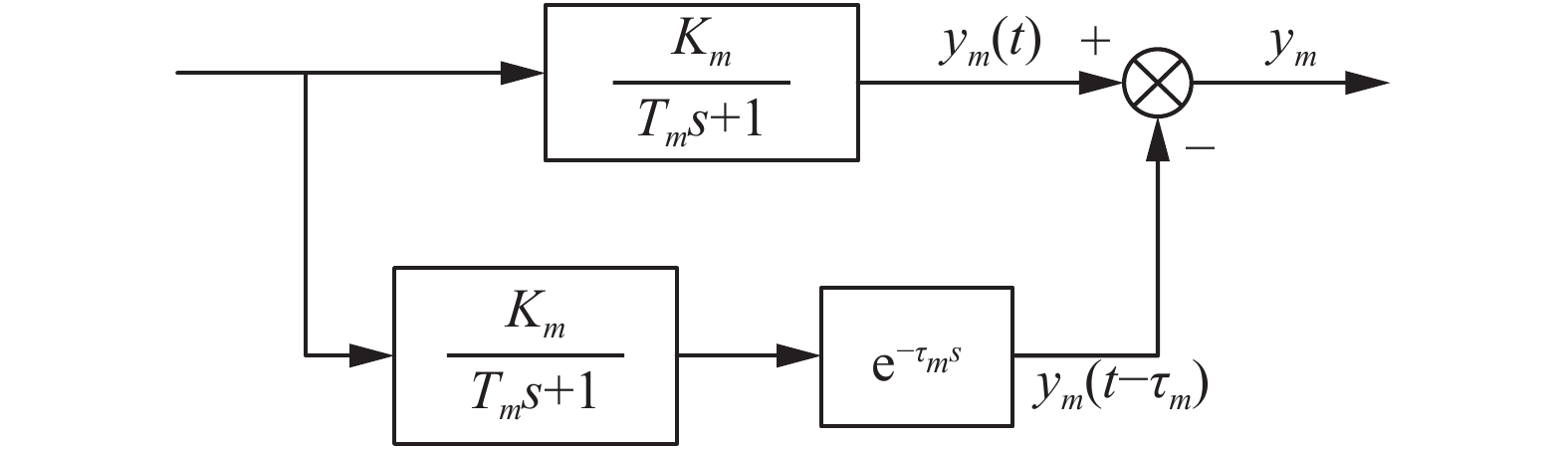
Smith 预估器原理结构图如图2所示。
|
Download:
|
| 图 2 Smith预估器结构 Fig. 2 Diagram of Smith predictor | |
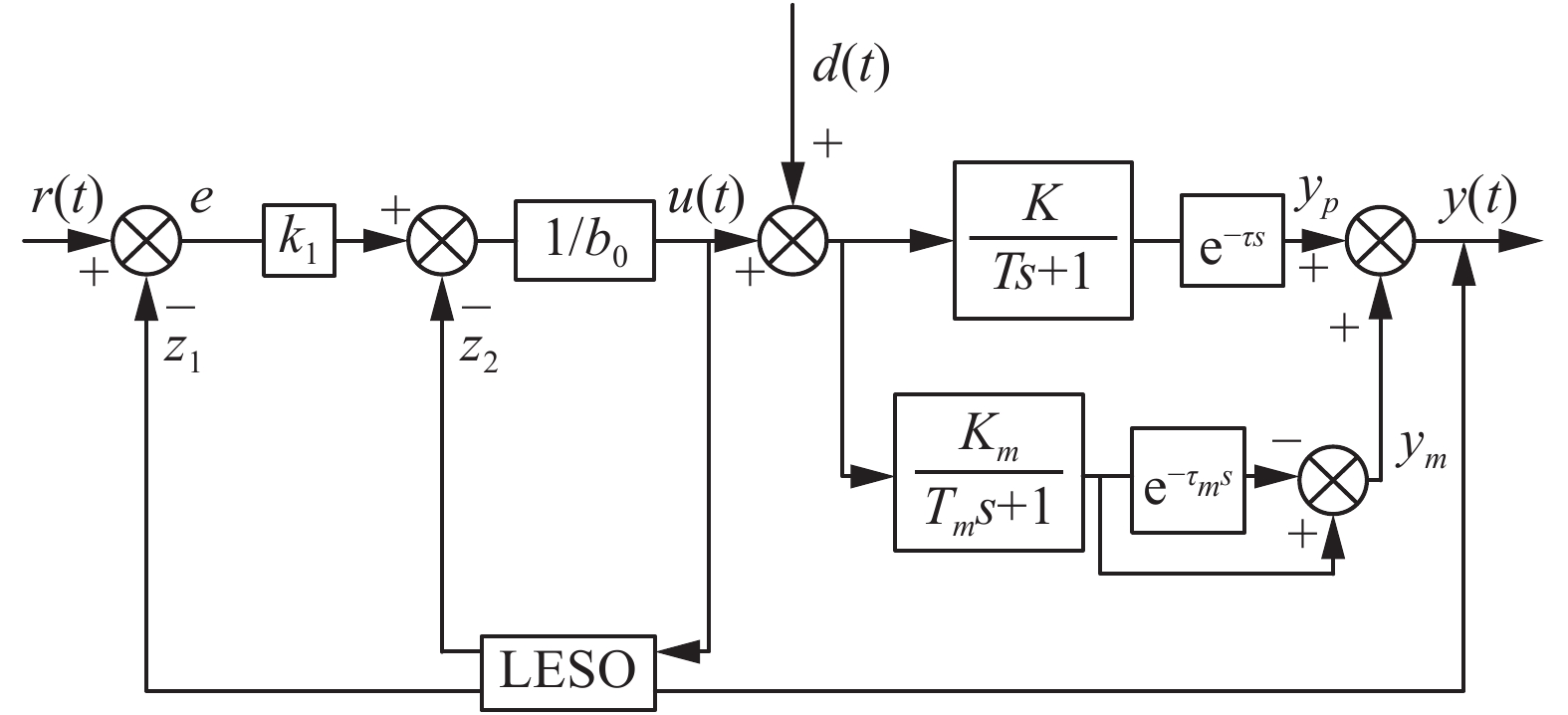
这样,当Smith预估器参数与被控对象相同时,进入LESO的被控输出
|
Download:
|
| 图 3 LADRC-Smith系统结构 Fig. 3 Diagram of the LADRC-Smith system | |
根据式(3)和式(5),可以得到表达式:
| $\left\{ {\begin{array}{*{20}{l}} {s{z_1} = {z_2} + {b_0}u + 2{w_o}(y - {z_1})} \\ {s{z_2} = w_o^2(y - {z_1})} \end{array}} \right.$ | (9) |
求解式(9),可以得到估计状态
| $\left\{ {\begin{array}{*{20}{l}} {{z_1}\left( s \right) = \displaystyle\frac{{2{w_o}s + w_o^2}}{{{{(s + {w_o})}^2}}}y + \frac{{{b_0}s}}{{{{(s + {w_o})}^2}}}u(s)} \\ {{z_2}(s) = {{(\displaystyle\frac{{{w_o}}}{{s + {w_o}}})}^2}sy - {{(\displaystyle\frac{{{w_o}}}{{s + {w_o}}})}^2}{b_0}u(s)} \end{array}} \right.$ | (10) |
结合状态误差反馈控制率式(4),可以得到系统的典型单回路反馈控制结构框图如图4。

|
Download:
|
| 图 4 LADRC-Smith单回路结构 Fig. 4 The single loop diagram of LADRC-Smith | |
其中:
| $\begin{array}{c} C(s) = {k_1}{(s + {w_o})^2} \cdot \{ {b_0}\left[ {{s^2} + (2{w_o} + {k_1})s} \right] + {\text{ }}\left[ {(2{k_1}{w_o} + w_o^2)s + {k_1}w_o^2} \right]{G_m}(s){\} ^{ - 1}} H(s) \\ = \displaystyle\frac{{(2{k_1}{w_o} + w_o^2)s + {k_1}w_o^2}}{{{k_1}{{(s + {w_o})}^2}}} \end{array} $ | (11) |
从而可以得到系统的开环和闭环传递函数:
| $\begin{array}{c} {G_{ol}} = C(s)H(s){G_p}(s) = \\[3pt] {\text{ }}[(2{k_1}{w_o} + w_o^2)s + {k_1}w_o^2]{G_P}(s) \cdot \\[3pt] {\text{ }}\{ {b_0}[{s^2} + (2{w_o} + {k_1})s]{\text{ + }} \\[3pt] {\text{ }}[(2{k_1}{w_o} + w_o^2)s + {k_1}w_o^2]{G_m}(s){\} ^{ - 1}}\end{array} $ | (12) |
| $\begin{array}{c} {G_{cl}} = \displaystyle\frac{{C(s){G_p}(s)}}{{1 + C(s)H(s){G_p}(s)}} = \\[5pt] {\text{ [}}{k_1}{(s + {w_o})^2}{G_p}(s){\text{]}} \cdot {\text{\{ }}{b_0}[{s^2} + \\[3pt] {\text{ }}(2{w_o} + {k_1})s] + [(2{k_1}{w_o} + w_o^2)s + \\[3pt]{k_1}w_o^2][{G_m}(s) + {G_p}(s)]{{\text{\} }}^{ - 1}}\end{array} $ | (13) |
下面从被控对象模型准确已知和大约已知两个方面分析LADRC-Smith的条件稳定性。
3.1.1 被控模型准确已知命题1 当被控对象模型准确已知时,Smith预估器与被控模型参数完全相同,只要3个控制参数为正,系统输出是稳定的。
证明
此时,将
| $\begin{array}{c} {G_{cl}} = {w_c}{(s + {w_o})^2}K{{\text{e}}^{ - \tau s}} \cdot \\[3pt] {\text{ }}\{ {b_0}(Ts + 1)[{s^2} + (2{w_o} + {w_c})s] + \\[3pt] {\text{ }}K[(2{w_c}{w_o} + w_o^2)s + {w_c}w_o^2]{\} ^{ - 1}}\end{array} $ | (14) |
只有分子中包含时滞,不会影响系统的最终稳定性,因此可以利用劳斯判据对系统特征方程进行稳定性分析[19]。
| $D(s) = {a_3}{s^3} + {a_2}{s^2} + {a_1}s + {a_0}$ | (15) |
式中:
可以看出:
| $\begin{array}{c} {a_1}{a_2} - {a_0}{a_3} = \\[3pt] {b_0}[{b_0}(2{w_o} + {w_c}) + K(2{w_c}{w_o} + w_o^2)](1 + 2T{w_o} + T{w_c}) - \\[3pt]{b_0}KT{w_c}w_o^2 = \\[3pt] {b_0}\{ (2{b_0}{w_o} + {b_0}{w_c} + 2K{w_c}{w_o})[(1 + 2T{w_o}) + T{w_c}] + \\[3pt]Kw_o^2(1 + 2T{w_o})\} > 0 \end{array} $ |
证毕。
3.1.2 被控模型大约已知假设:
| ${K_m} = \alpha K,{T_m} = \beta T,{\tau _m} = \gamma \tau ,\frac{{{\tau _m}}}{{{T_m}}} = \lambda (\alpha ,\beta ,\gamma ,\lambda > 0)$ |
命题2 当被控对象模型大约已知,时间常数
1)
2) 2α
3)
证明
闭环特征方程为
| $\begin{array}{*{20}{c}}{D(s) = {b_0}[{s^2} + (2{w_o} + {k_1})s] + [(2{k_1}{w_o} + w_o^2)s + {k_1}w_o^2] \cdot }\\{\left[ {\displaystyle\frac{K}{{Ts + 1}}{{\rm{e}}^{ - \tau s}} + (1 - {{\rm{e}}^{ - {\tau _m}s}})\frac{{{K_m}}}{{{T_m}s + 1}}} \right]}\end{array}$ | (16) |
对被控系统特性进行仿真发现,针对大惯性环节,当时间常数T摄动较小时(即
| ${{\text{e}}^{ - \tau s}} = \frac{{2 - \tau s}}{{2 + \tau s}},{{\text{e}}^{ - (\gamma - 1)\tau s}} = 1 - (\gamma - 1)\tau s,T \approx {T_m} = \beta T$ |
则
| $\begin{array}{c} {G_p} + {G_m} \approx \displaystyle\frac{K}{{\beta Ts + 1}} \cdot \frac{{2 - \tau s}}{{2 + \tau s}} + \\[8pt] \displaystyle\frac{{\alpha K}}{{\beta Ts + 1}}[1 - \displaystyle\frac{{2 - \tau s}}{{2 + \tau s}}(1 - (\gamma - 1)\tau s)] \end{array} $ | (17) |
从而,式(16)可以转化为
| $D(s) = {a_4}{s^4} + {a_3}{s^3} + {a_2}{s^2}{\text{ + }}{a_1}{s^1} + {a_0}$ | (18) |
式中
| $\begin{array}{c} {a_4} = \beta {b_0}T\tau \\[4pt] {a_3} = {b_0}[\beta T\tau (2{w_o} + {w_c}) + (2\beta T + \tau )] - \\[4pt] K(2{w_c}{w_o} + w_o^2)\alpha (\gamma - 1){\tau ^2} \\[4pt] {a_2} = {b_0}[(2{w_o} + {w_c})(2\beta T + \tau ) + 2] +\\[4pt] {\text{ }}K[(2{w_c}{w_o} + w_o^2)(2\alpha \gamma - 1)\tau - {w_c}w_o^2\alpha (\gamma - 1){\tau ^2}] \\[4pt] {a_1} = 2{b_0}(2{w_o} + {w_c}) + K[{w_c}w_o^2(2\alpha \gamma - 1)\tau + \\[4pt] 2(2{w_c}{w_o} + w_o^2)] \\[4pt] {a_0} = 2K{w_c}w_o^2\end{array}$ |
根据劳斯判据,定性得到了一个近似的稳定充分条件:
1)
2)
3)
证毕。
3.2 仿真验证被控对象为[18]:
由图5可以看出,当Smith预估器的参数与被控对象完全相同时,只要3个被调参数为正,系统输出最终是稳定的,但是动态过程跟参数选择十分密切,参数调节与性能关系将在下面讨论。
3.2.2 Smith预估器参数与被控对象不同当Smith预估器参数与被控对象参数不相同时,按照命题2的近似充分条件选择Smith预估器参数,控制参数随意给定,然后进行仿真验证,如图6所示。

|
Download:
|
| 图 5 被控对象准确已知时的阶跃响应 Fig. 5 Step response when plant is accurately known | |

|
Download:
|
| 图 6 被控对象大约已知时的阶跃响应 Fig. 6 Step response when plant is approximately known | |
可以看出,当Smith预估器参数与被控对象不相同时,根据命题2选择参数,由于是近似条件,系统最终可能不稳定,与控制参数选择也相关,所以,命题2有一定的局限性,但也有一定的参考意义,控制参数与性能的关系将在下面分析。
4 参数分析与设计原则同样,选择一阶系统:
系统的动态性能指标中比较重要的是最大超调量
Smith预估器参数为
| ${K_m} = 0.85,{T_m} = 1\;200,{\tau _m} = 1\;800 ;$ |
控制参数为

|
Download:
|
| 图 7 LADRC-Smith奈氏曲线图 Fig. 7 Nyquist diagram of LADRC-Smith | |
| 表 1 被控对象参数摄动的稳定边界值 Tab.1 Stable boundary when parameters perturbation |
1) 与
2) 随着
3) 随着
4) 随着
所以,相对于
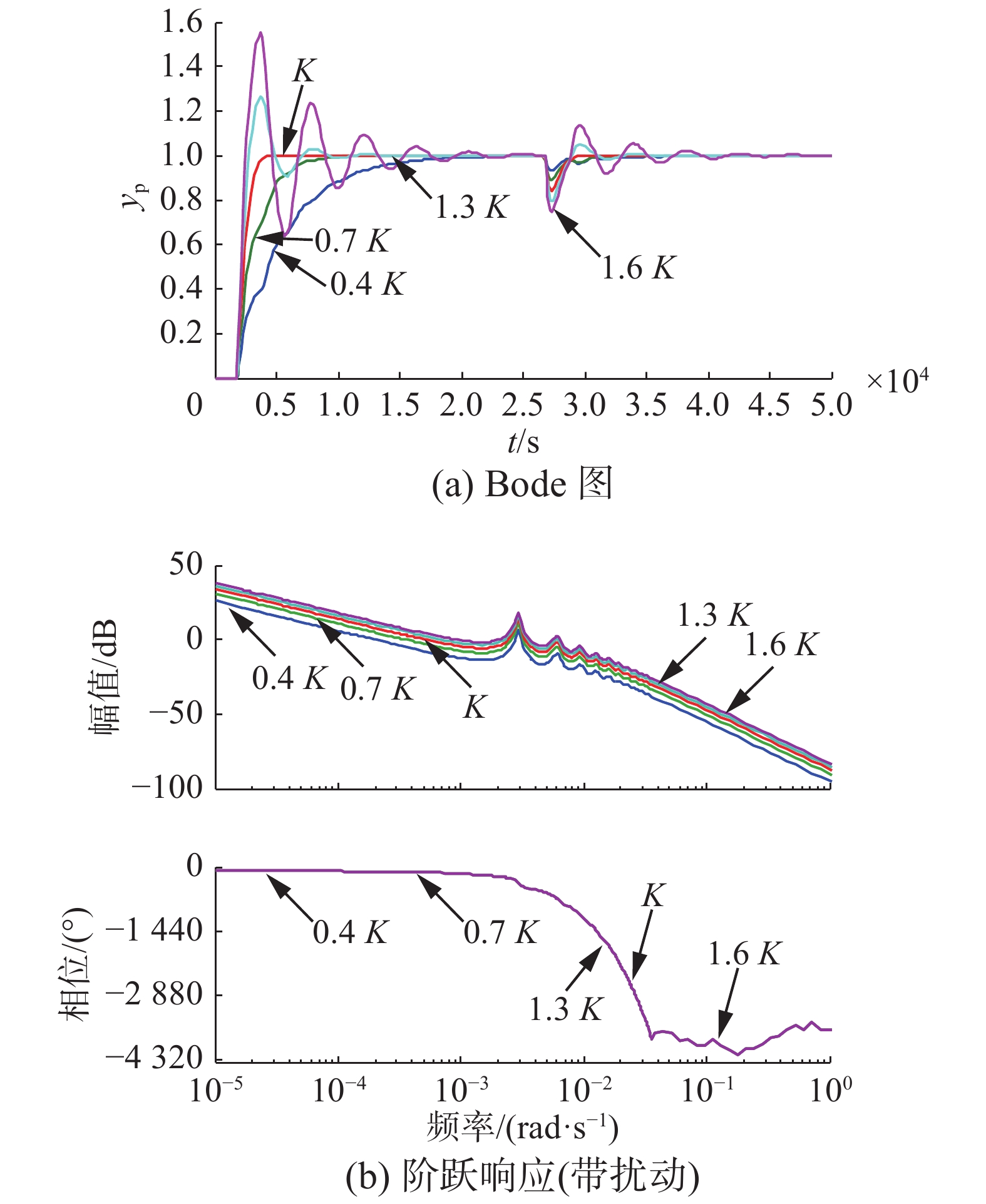
| 表 2 K变化的性能指标 Tab.2 Performance index when K changes |
|
Download:
|
| 图 8 K变化的阶跃响应(带扰动)和Bode图 Fig. 8 Step response with disturbance and Bode diagram for K | |
1) 相对于
2) 随着
3) 随着
4) 随着
所以,相对于
| 表 3 T变化的性能指标 Tab.3 Performance index when T changes |

|
Download:
|
|
图 9 |
|
1)
2) 随着
3) 随着
4) 与
所以,相对于
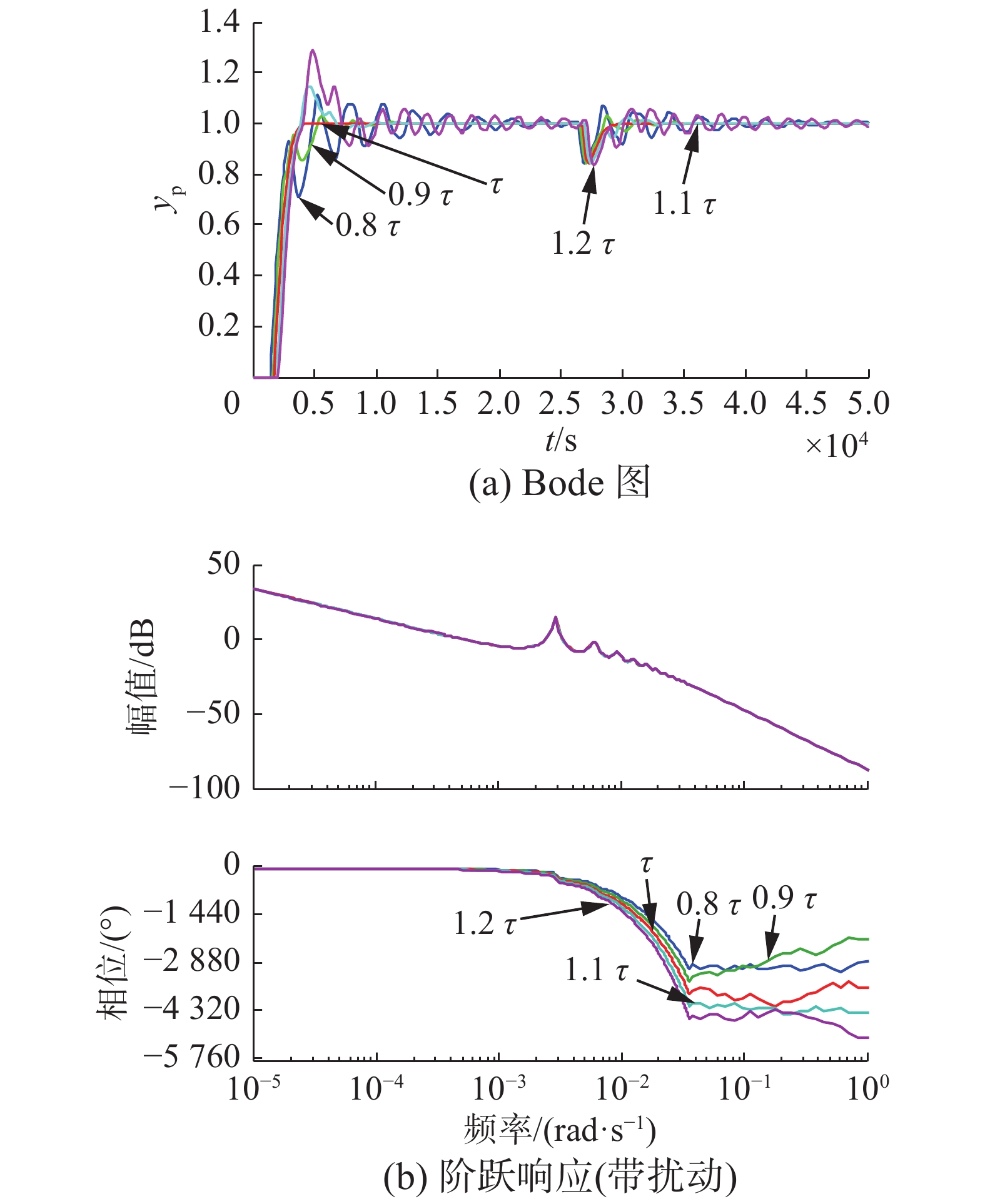
| 表 4 |
|
Download:
|
|
图 10 |
|
综上,进行Smith设计时,
下面进行验证,对如上同一被控对象,选择同一控制参数设计3个Smith预估器
| $\begin{array}{c} {G_{m1}}:{K_{m1}} = 1.1K,{T_{m1}} = 0.9T,{\tau _{m1}} = 1.1\tau {G_m}:{K_m} = K,{T_m} = T,{\tau _m} = \tau {G_{m2}}:{K_{m2}} = 0.9K,{T_{m2}} = 1.1T,{\tau _{m2}} = 0.9\tau \end{array} $ |
进行时域和频域分析,如图11所示。
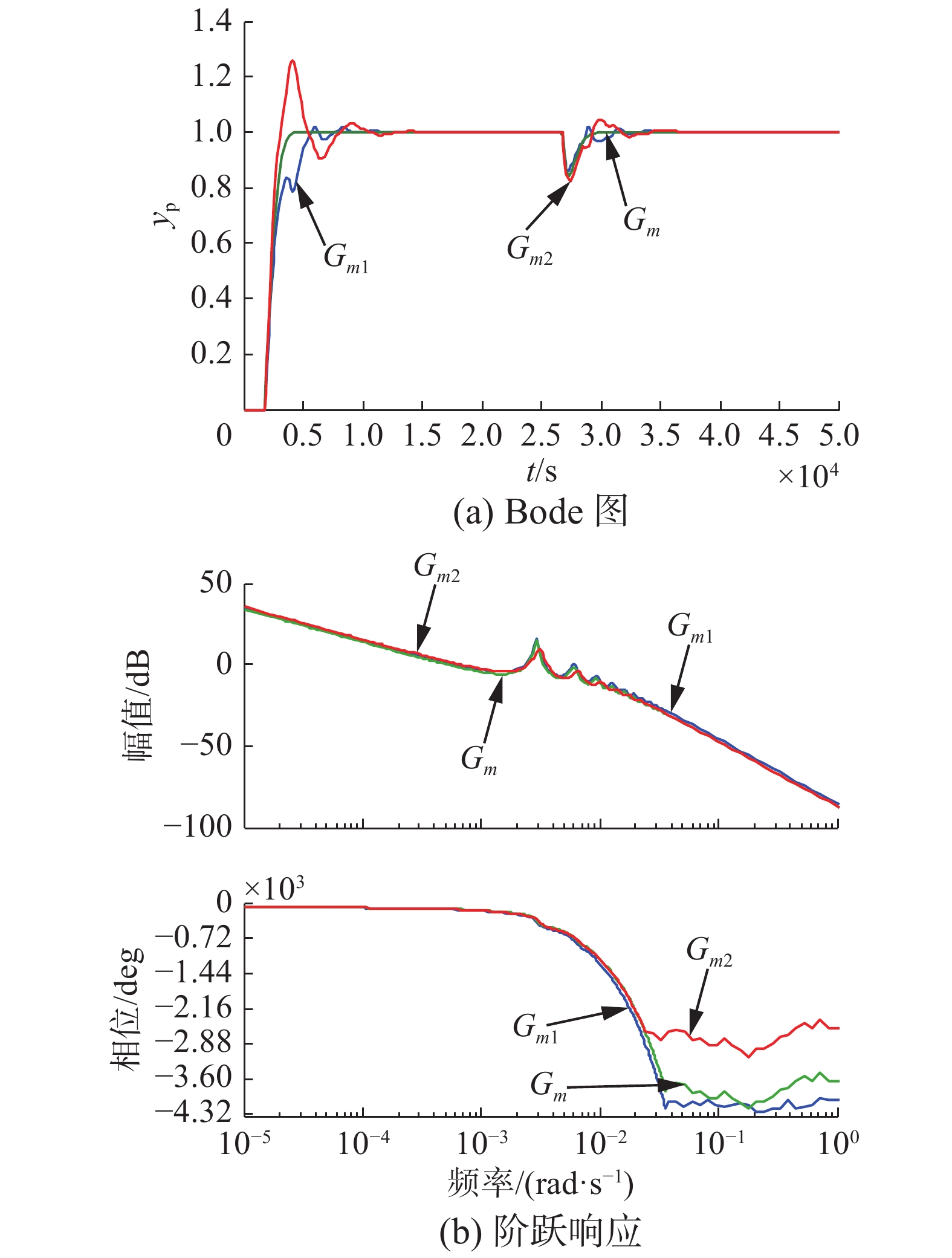
如表5和图11可以看出,
| 表 5 不同Smith预估器的性能指标 Tab.5 Performance index for different Smith predictors |
|
Download:
|
| 图 11 不同预估器的阶跃响应和Bode图 Fig. 11 Step response and Bode diagram for different predictors | |
控制

|
Download:
|
|
图 12 |
|
| 表 6 |
可以看出:随着
1) 系统响应变慢,振荡消失,出现了超调;
2) 当扰动出现时,扰动偏离量和扰动恢复时间增加,抗扰性能变弱;
3) 增益裕度先减小后增加,相角裕度减小,时滞裕度增加,穿越频率减小。
所以,选取
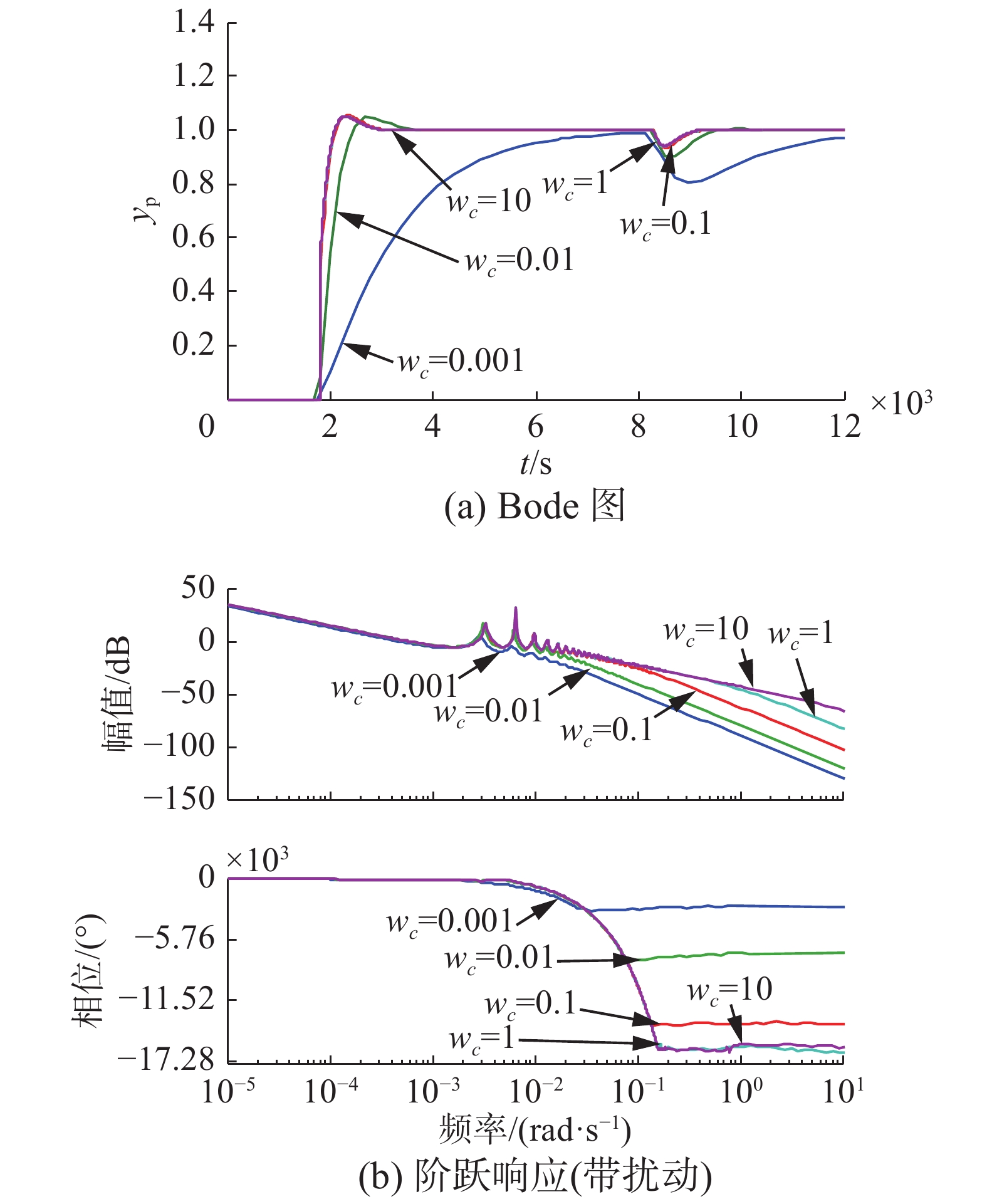
控制
|
Download:
|
|
图 13 |
|
| 表 7 |
可以看出:随着控制器带宽增加,1) 系统响应变快,出现了超调;2) 抗扰性能增强,扰动偏离量和扰动恢复时间减小;3) 增益裕度和相角裕度先减小后增加,时滞裕度减小,穿越频率增加。
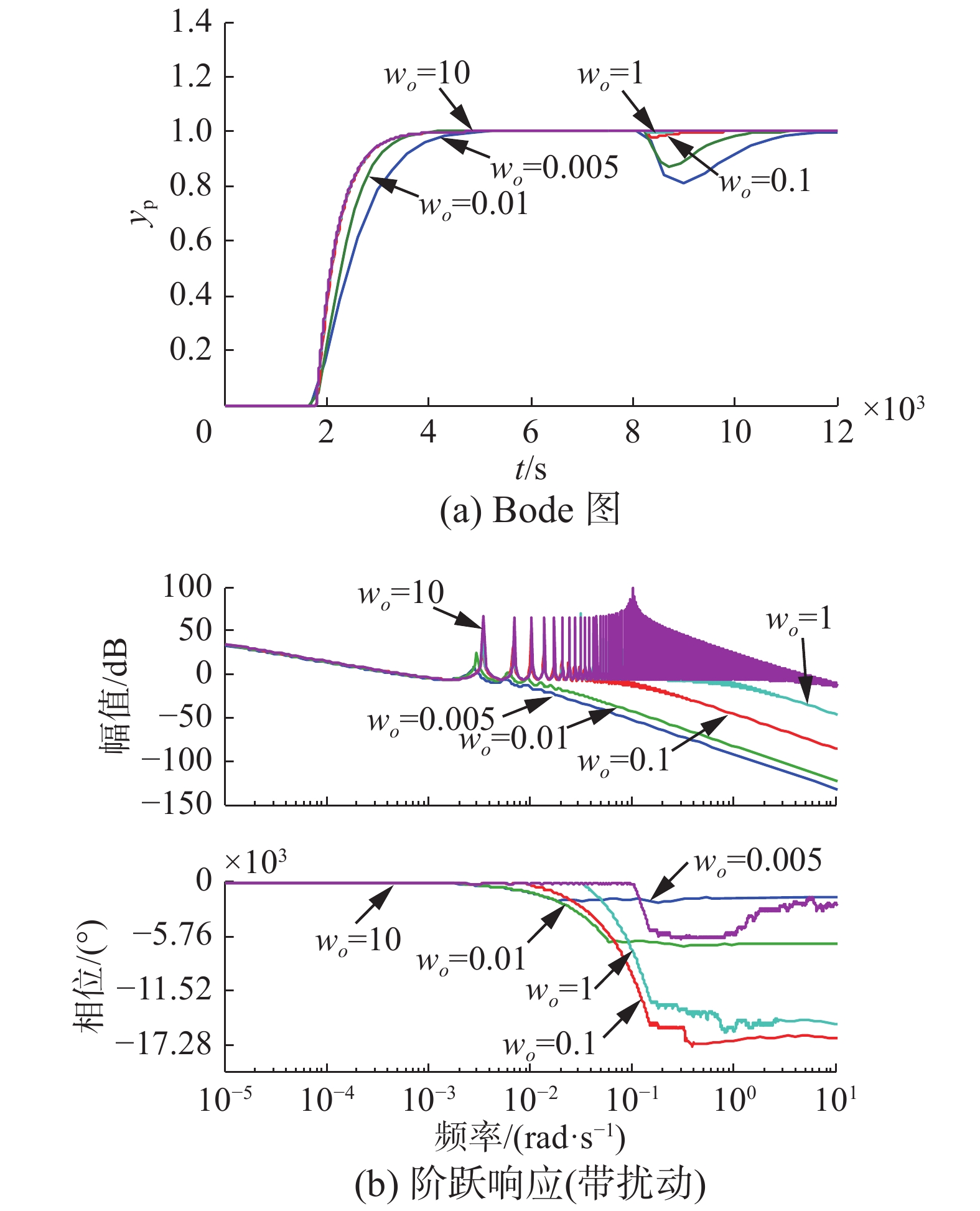
4.2.3控制
|
Download:
|
|
图 14 |
|
| 表 8 wo变化的性能指标 Tab.8 Performance index when wo changes |
可以看出:随着观测器带宽增加
1) 系统响应变快,调节时间变短;
2) 抗扰性能增强,扰动偏离量和扰动恢复时间减小;
3) 增益裕度和相角裕度先减小后增加,时滞裕度减小,穿越频率增加。
综上,可以得到如下控制参数调节规则:
1) 当系统响应慢、需要较强抗扰能力时,减小
2) 当系统开始振荡时,增大
3) 当系统有超调、需要较大时滞裕度时,增大
4) 需要较大相角裕度时,减小
5) 需要较大增益裕度时,从小到大调节
本文针对大时滞系统,研究了基于Smith预估器的线性自抗扰控制的稳定条件,通过MATLAB仿真进行验证,并分析了系统参数和控制参数对系统的影响,得出以下结论:
1) 当被控对象准确已知,Smith预估器参数与被控对象相同时,系统是稳定的。当被控对象大约已知时,根据稳定的近似充分条件选择Smith预估器参数进行设计,根据性能需要适当调节参数,系统更易稳定。
2) 当被控对象摄动,系统参数
3) 本文分析建立在被控对象大约已知的基础上,限制了实际应用,而且Smith预估器参数与被控对象不同时的近似充分条件并不能保证系统一定稳定,有一定局限性。所以对模型未知情况下的系统控制和稳定性证明需要进一步探索。
| [1] |
SMITH O J M. Closer control of loops with dead time[J]. Chemical engineering progress, 1957, 53(5): 217-219. ( 0) 0)
|
| [2] |
贾飚. Smith预估器在纯滞后矿仓料位控制中的应用[J]. 自动化仪表, 2004, 25(5): 39-41. JIA Biao. Application of smith predictor in ore silo material level control with dead time characteristic[J]. Process automation instrumentation, 2004, 25(5): 39-41. (  0) 0)
|
| [3] |
刘启辉, 文云, 张云龙. 基于一阶时滞系统的Smith预估器控制研究[J]. 自动化技术与应用, 2014, 33(9): 11-13, 17. LIU Qihui, WEN Yun, ZHANG Yunlong. Research of smith predictor controller based on first-order dynamics plus dead time[J]. Techniques of automation and applications, 2014, 33(9): 11-13, 17. (  0) 0)
|
| [4] |
任雪梅. 非线性时滞系统的稳定自适应控制[J]. 智能系统学报, 2007, 2(5): 84-90. REN Xuemei. Stable adaptive neural network control of nonlinear time delay systems[J]. CAAI transactions on intelligent systems, 2007, 2(5): 84-90. (  0) 0)
|
| [5] |
罗小元, 朱志浩, 关新平. 不确定非线性时滞系统的自适应滑模控制[J]. 智能系统学报, 2010, 5(4): 332-335. LUO Xiaoyuan, ZHU Zhihao, GUAN Xinping. Adaptive sliding mode control for uncertain nonlinear time-delay systems[J]. CAAI transactions on intelligent systems, 2010, 5(4): 332-335. (  0) 0)
|
| [6] |
蒋朝辉, 李学明, 桂卫华. 大时滞系统全参数自适应预测控制策略[J]. 中南大学学报: 自然科学版, 2012, 43(1): 195-201. JIANG Zhaohui, LI Xueming, GUI Weihua. All parameters adaptive predictive control strategy for long time-delay system[J]. Journal of central south university: science and technology, 2012, 43(1): 195-201. (  0) 0)
|
| [7] |
MANFRED M, SKOGESTAD S, RIVERA D F. Implications of internal model control for PID controllers[C]//Proceedings of 1984 American Control Conference. San Diego, USA, 1984: 661–666.
( 0) 0)
|
| [8] |
邓九英, 王钦若, 叶宝玉. 一种纯时滞系统的鲁棒控制优化设计方法[J]. 信息与控制, 2011, 40(1): 1-7. DENG Jiuying, WANG Qinruo, YE Baoyu. Robust control optimization design method of a system with pure-delay[J]. Information and control, 2011, 40(1): 1-7. (  0) 0)
|
| [9] |
达飞鹏, 宋文忠. 大时滞系统的智能控制研究[J]. 中国电机工程学报, 2003, 23(9): 186-188. DA Feipeng, SONG Wenzhong. Intelligent controller design for systems of long time delay[J]. Proceedings of the CSEE, 2003, 23(9): 186-188. (  0) 0)
|
| [10] |
ZHOU Ling, CHEN Jie, XU Lixin. An intelligent control scheme of time delay system[C]//Proceedings of 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application. Wuhan, China, 2008: 446–448.
( 0) 0)
|
| [11] |
韩京清, 张文革. 大时滞系统的自抗扰控制[J]. 控制与决策, 1999, 14(4): 67-71. HAN Jingqing, ZHANG Wen’ge. ADRC control for large time-delay systems[J]. Control and decision, 1999, 14(4): 67-71. (  0) 0)
|
| [12] |
GAO Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of 2003 American Control Conference. Denver, USA, 2003: 4989–4996.
( 0) 0)
|
| [13] |
TIAN Gang, GAO Zhiqiang. Frequency response analysis of active disturbance rejection based control system[C]//Proceedings of 2007 IEEE International Conference on Control Applications. Singapore, 2007: 1595–1599.
( 0) 0)
|
| [14] |
陈增强, 孙明玮, 杨瑞光. 线性自抗扰控制器的稳定性研究[J]. 自动化学报, 2013, 39(5): 574-580. CHEN Zengqiang, SUN Mingwei, YANG Ruiguang. On the stability of linear active disturbance rejection control[J]. Acta automatica sinica, 2013, 39(5): 574-580. (  0) 0)
|
| [15] |
ZHANG Dongyang, YAO Xiaolan, WU Qinghe. Frequency-domain characteristics analysis of linear active disturbance rejection control for second-order systems[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015: 53–58.
( 0) 0)
|
| [16] |
HUANG Congzhi, GAO Zhiqiang. On transfer function representation and frequency response of linear active disturbance rejection control[C]//Proceedings of the 32nd Chinese Control Conference. Xi’an, China, 2013: 72–77.
( 0) 0)
|
| [17] |
ZHENG Qinling, GAO Zhiqiang. Predictive active disturbance rejection control for processes with time delay[J]. ISA transactions, 2014, 53(4): 873-881. DOI:10.1016/j.isatra.2013.09.021 ( 0) 0)
|
| [18] |
唐德翠, 高志强, 张绪红. 浊度大时滞过程的预测自抗扰控制器设计[J]. 控制理论与应用, 2017, 34(1): 101-108. TANG Decui, GAO Zhiqiang, ZHANG Xuhong. Design of predictive active disturbance rejection controller for turbidity[J]. Control theory and applications, 2017, 34(1): 101-108. (  0) 0)
|
| [19] |
杨瑞光. 线性自抗扰控制的若干问题研究[D]. 天津: 南开大学, 2011: 65–67. YANG Ruiguang. On linear active disturbance rejection control[D]. Tianjin: Nankai University, 2011: 65–67. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


