2. 计算智能与智能系统北京市重点实验室,北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China
自从Hopfiled和Tank用提出的Hopfiled网络(Hopfiled neural network, HNN)开创性成功解决旅行商(traveling salesman problem, TSP)问题以来,神经网络在解决优化问题中开始得到广泛关注和应用[1]。由于HNN的算法依然采用传统的梯度下降算法,极易陷入局部极小点,导致无法找到最优解[2]。Chen等[3]在Hopfield网络基础上引入自反馈,并加入模拟退火(simulated annealing, SA)机制,提出暂态混沌神经网络(transient chaotic neural network, TCNN),通过混沌的遍历性和伪随机性克服了HNN局部极小问题。混沌神经网络(chaotic neural network, CNN)被证明是解决优化问题的有效工具[3-7]。随后,Zhang等[4]采用小波函数作为激励函数,提出了WCNN模型,用来解决函数优化问题;Liu等[5]在混沌神经元模型中加入迟滞动力,提出了HCNN模型,并应用于TSP问题中;Zhao等[6]引入高斯自反馈项,提出了CNNW模型,成功应用于组合优化问题。以上学者提出的CNN模型,虽然都在一定程度上提高了全局寻优能力,但是大都缺乏一定的生物学机制,无法表征神经元激励与响应的频幅关系,不能充分体现出复杂多变脑部活动的非线性动力学特征和具有更加丰富的混沌全局搜索性能。因此,Hu等[7]基于脑电波的生物机制,将变频正弦函数(frequency conversion sinusoidal, FCS)与Sigmoid函数加权和组成非单调激励函数,提出了变频正弦混沌神经网络(frequency conversion sinusoidal chaotic neural network, FCSCNN) 模型,进一步提高了TCNN的混沌动力学特性和全局寻优性能,更准确地解决了函数优化及TSP问题,验证了模型有效性和可行性。
而人们研究TCNN的优化计算方法,归根结底是希望能够看到其在硬件上的实现,进而观察和研究混沌神经元的状态和响应,最终制造出混沌计算机[8]。但是,由于电子元器件或电路的不稳定性,在一定情况下,不可避免地会出现不同程度的扰动,这会对FCSCNN性能产生影响,所以对该模型的抗扰动能力进行实验、评估、比较是很有必要的。因此,本文针对FCSCNN模型,通过引入不同程度的周期和非周期扰动,将其应用到函数优化和组合优化问题上,分析其抗扰动能力,仿真实验证明了FCSCNN具有较强的鲁棒性和抗扰动能力。
1 带扰动的变频正弦混沌神经元模型TCNN多采用Sigmoid函数作为激励函数,而非单调激励函数比单调(Sigmoid)激励函数更容易产生混沌,在寻优过程中具有更好的全局搜索性能[9-10]。基于以上理论以及脑电波的生物机制,FCSCNN模型获得了较好的优化效果[7, 11]。由于来自外界的扰动有周期的和非周期的,因此本文分别用代表周期扰动的三角函数和非周期扰动的小波函数来进行研究,在FCS神经元模型的基础上加入扰动项,来分析模型的抗扰动能力。建立如下带扰动的FCS混沌神经元模型:
| $x\left( t \right) = f\left( {y\left( t \right)} \right)$ | (1) |
| $y\left( {t + 1} \right) = ky\left( t \right) + \gamma \cdot D\left( {y\left( t \right)} \right) - z\left( t \right)\left( {x\left( t \right) - {I_0}} \right)$ | (2) |
| $z\left( {t + 1} \right) = \left( {1 - \beta } \right)z\left( t \right)$ | (3) |
| $f\left( u \right) = {S_1}\left( {u,{\varepsilon _1}} \right) + c \cdot {S_2}\left( {u,{\varepsilon _2}} \right)$ | (4) |
| ${S_1}\left( {u,{\varepsilon _1}} \right) = 1/\left[ {1 + \exp \left( { - u/{\varepsilon _1}} \right)} \right]$ | (5) |
| ${S_2}(u,{\varepsilon _2}) = A \cdot \sin (u/{\varepsilon _2})$ | (6) |
| ${D_1}\left( {v,{\varepsilon _3}} \right) = \cos \left( {v/{\varepsilon _3}} \right)$ | (7) |
| ${D_2}\left( {v,{\varepsilon _3}} \right) = {\text{exp}}\left[ { - {{\left( {v/{\varepsilon _3}} \right)}^2}/2} \right]\cos \left( {5v/{\varepsilon _3}} \right)$ | (8) |
式中:
神经元的倒分岔图和最大Lyapunov指数可以直观体现出神经元的动力学特性。Lyapunov指数大于零(非正无穷),证明模型具有混沌行为,并且值越大表明混沌程度越强[5]。Lyapunov指数定义为
| $\lambda = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\log \left| {\frac{{{\rm{d}}y\left( {t + 1} \right)}}{{{\rm{d}}y\left( t \right)}}} \right|} $ | (9) |
则对于带扰动的FCS混沌神经元模型有
| $\begin{array}{c}\displaystyle\frac{{{\rm{d}}y\left( {t + 1} \right)}}{{{\rm{d}}y\left( t \right)}} = k - z\left( t \right)\frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}y\left( t \right)}} + \gamma \cdot \frac{{{\rm{d}}D(y(t))}}{{{\rm{d}}y(t)}} = k - z\left( t \right)\left[ {\displaystyle\frac{{{\rm{d}}{S_1}\left( {y\left( t \right)} \right)}}{{{\rm{d}}y\left( t \right)}} + c\frac{{{\rm{d}}{S_2}\left( {y\left( t \right)} \right)}}{{{\rm{d}}y\left( t \right)}}} \right] + \gamma \cdot \displaystyle\frac{{{\rm{d}}D(y(t))}}{{{\rm{d}}y(t)}}\end{array}$ | (10) |
式(10)中第2项表达式同文献[7],第3项如下:
| $\frac{{{\rm{d}}{D_1}(y(t))}}{{{\rm{d}}y(t)}} = - \frac{1}{{{\varepsilon _3}}}\sin (y(t)/{\varepsilon _3})$ | (11) |
| $\begin{array}{c}\displaystyle\frac{{{\rm{d}}{D_2}(y(t))}}{{{\rm{d}}y(t)}} = - \frac{{y(t)}}{{\varepsilon _3^2}}\exp [ - 0.5{(\frac{{y(t)}}{{{\varepsilon _3}}})^2}]\cos (\frac{{5y(t)}}{{{\varepsilon _3}}}) - \displaystyle\frac{5}{{{\varepsilon _3}}}\exp [ - 0.5{(\frac{{y(t)}}{{{\varepsilon _3}}})^2}]\sin (\frac{{5y(t)}}{{{\varepsilon _3}}})\end{array}$ | (12) |
由文献[7]可知,相同模型参数下,提出的FCS混沌神经元比标准的暂态混沌神经元具有更复杂和更丰富的混沌动力学行为,具有更多的正值Lyapunov指数,并且混沌搜索的时间更长,这都为混沌全局寻优提供了良好的动力学基础。证实了提出的新的混沌神经元模型的有效性和可行性。
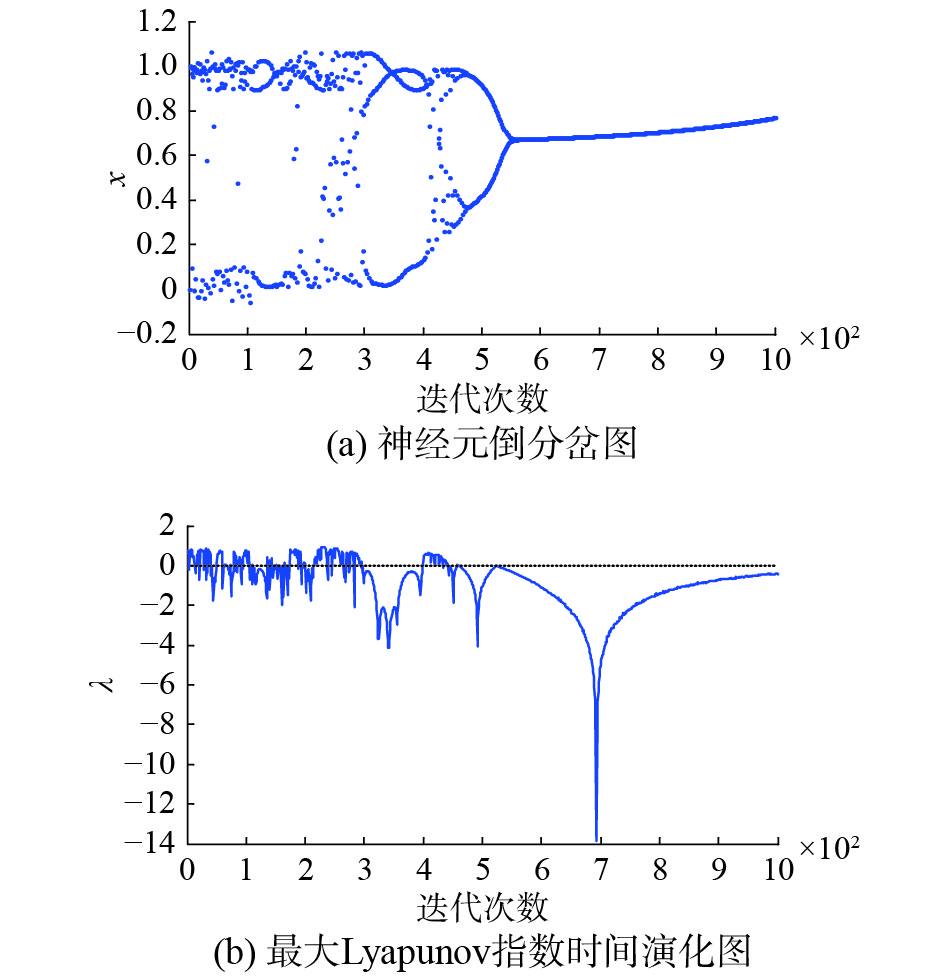
进而,为了验证FCS混沌神经元模型的鲁棒性和抗扰动能力,当设置扰动项为三角函数扰动时,当选取参数k=1, β=0.004, ε1=0.02, I0=0.65, z(0)=0.9, A(0)= 0.6, ε2(0)=0.02, a=6, b=1, c=0.25, ε3=0.1固定不变时,分别取γ=0.002和γ=0.02时,FCS神经元的倒分岔图和最大Lyapunov指数时间演化图分别如图1~2所示。
|
Download:
|
| 图 1 带三角函数扰动(γ=0.002)的FCS神经元倒分岔图和最大Lyapunov指数图 Fig. 1 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within trigonometric function disturbance (γ=0.002) | |
|
Download:
|
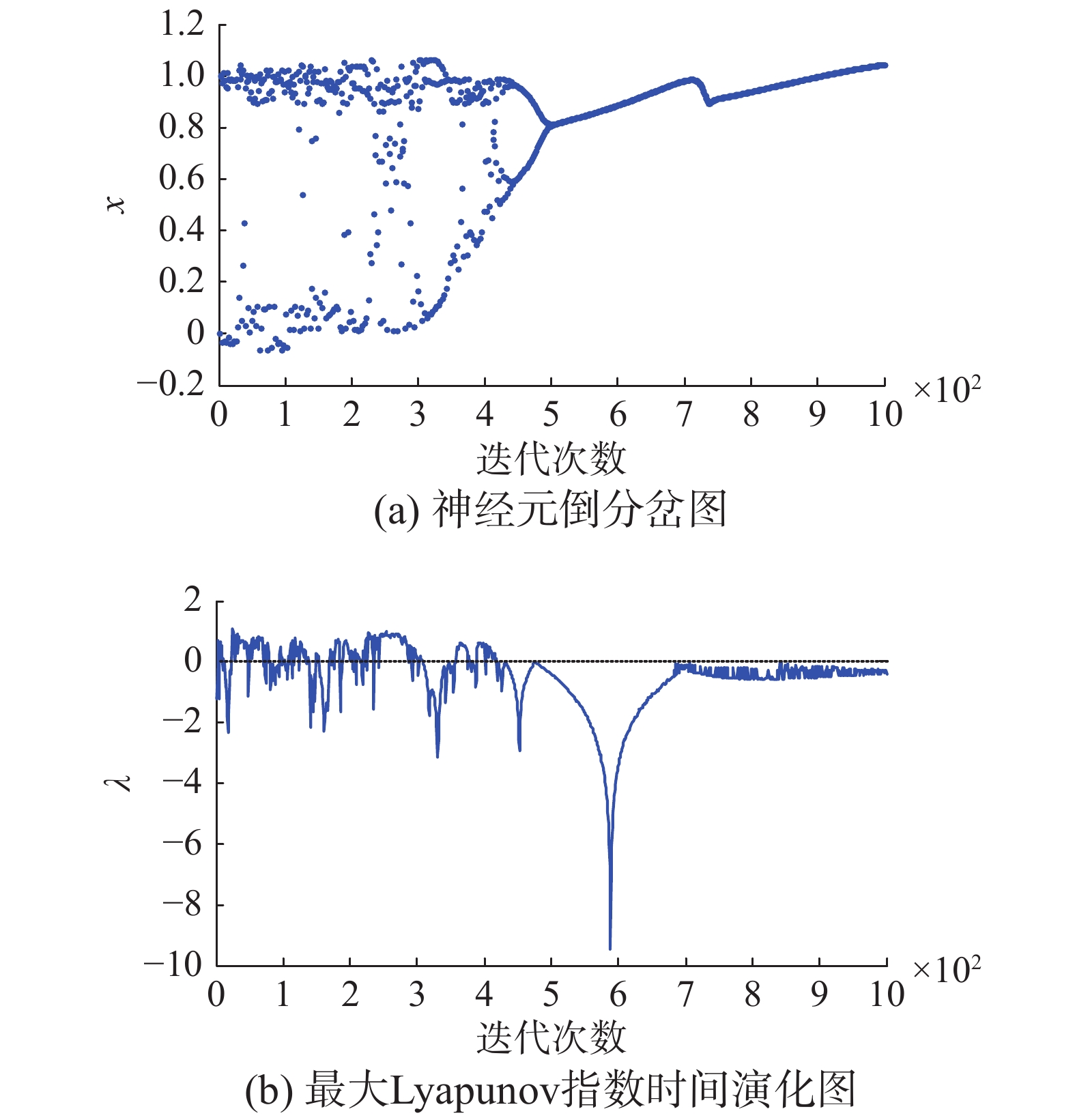
| 图 2 带三角函数扰动(γ=0.02)的FCS神经元倒分岔图和最大Lyapunov指数图 Fig. 2 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within trigonometric function disturbance (γ=0.02) | |
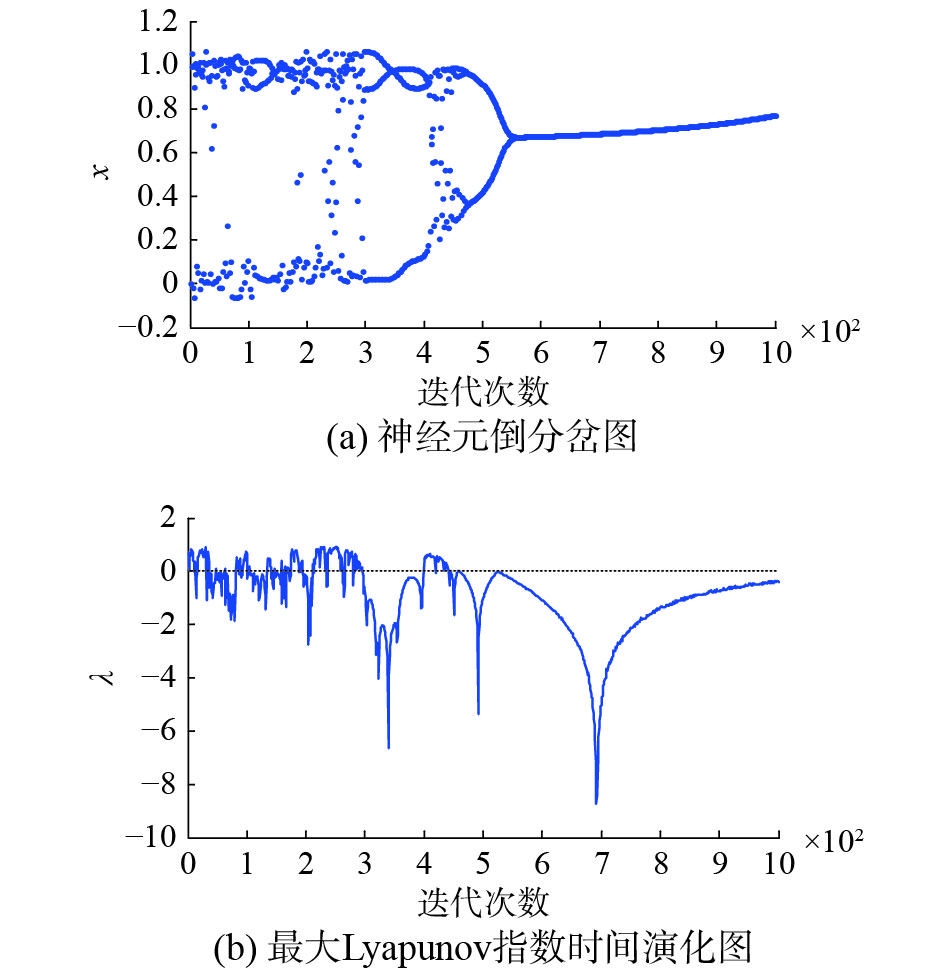
当扰动为Morlet小波函数时,选取参数k=1, β=0.004, ε1=0.02, I0=0.65, z(0)=0.9, A(0)=0.6, ε2(0)=0.02, a=6, b=1, c=0.25, ε3=2.5固定不变时,分别取γ=0.002和γ=0.02时,FCS神经元的倒分岔图和最大Lyapunov指数时间演化图如图3、图4所示。
|
Download:
|
| 图 3 带Morlet小波扰动(γ=0.002)的FCS神经元倒分岔图和最大Lyapunov指数图 Fig. 3 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within Morlet function disturbance (γ=0.002) | |

|
Download:
|
| 图 4 带Morlet小波扰动(γ=0.02)的FCS神经元倒分岔图和最大Lyapunov指数图 Fig. 4 The reversed bifurcation and the time evolution of the maximal Lyapunov exponent of the FCS neuron within Morlet function disturbance (γ=0.02) | |
由图1~4可知,在神经元内部加入三角函数或小波函数扰动项,进行动力学特性对比分析。在扰动系数γ为0.002时,两类不同的扰动下,神经元的动力学特性都只是发生微小的变动,并没有发生明显的改变。在扰动系数γ为0.02时,两类不同的扰动下,神经元的动力学特性都发生了较明显的变化,随着扰动系数的增大,动力学特性变动更加剧烈,动力学演变过程开始受到影响,但是整体的倒分岔特点和混沌程度并没有受到本质改变,依旧保持原有形态。证明了在一定程度扰动项作用下,FCS混沌神经元模型具有一定鲁棒性和抗扰动能力。
2 带扰动的FCS混沌神经网络模型利用上述带扰动的FCS混沌神经元模型,构建得到了如下带扰动的FCSCNN模型:
| ${x_i}\left( t \right) = f\left( {{y_i}\left( t \right)} \right)$ | (13) |
| $\begin{array}{c}{y_i}\left( {t + 1} \right) = k{y_i}\left( t \right) + \gamma \cdot D\left( {{y_i}\left( t \right)} \right) + \\\alpha \left[ {\displaystyle\sum\limits_{j = 1,j \ne i}^N {{w_{ij}}{x_j}\left( t \right) + {I_i}} } \right] - {z_i}\left( t \right)\left[ {{x_i}\left( t \right) - {I_0}} \right]\end{array}$ | (14) |
| ${z_i}\left( {t + 1} \right) = \left( {1 - \beta } \right){z_i}\left( t \right)$ | (15) |
| $f\left( u \right) = {S_1}\left( {u,{\varepsilon _1}} \right) + c \cdot {S_2}\left( {u,{\varepsilon _2}} \right)$ | (16) |
| ${S_1}\left( {u,{\varepsilon _1}} \right) = 1/\left[ {1 + \exp \left( { - u/{\varepsilon _1}} \right)} \right]$ | (17) |
| ${S_2}(u,{\varepsilon _2}) = A \cdot \sin (u/{\varepsilon _2})$ | (18) |
| ${D_1}\left( {v,{\varepsilon _3}} \right) = \cos \left( {v/{\varepsilon _3}} \right)$ | (19) |
| ${D_2}\left( {v,{\varepsilon _3}} \right) = {\text{exp}}\left[ { - {{\left( {v/{\varepsilon _3}} \right)}^2}/2} \right]\cos \left( {5v/{\varepsilon _3}} \right)$ | (20) |
式中:α为正比例参数,wij为神经元i和神经元j间的连接权值(wij=wji, wii=0),Ii是第i个神经元阈值,其他参数定义同带扰动的FCS神经元模型。
FCSCNN采用传统的Hopfield网络的优化机制[12]。由于自反馈的存在,网络会表现出混沌特性。在演化初期,选择合适的网络参数,并且具有较大的自反馈连接权重初值z(0),利用混沌的遍历性和伪随机性在相空间内按照一定“分形”结构进行“自抑制”的不重复全局搜索,避免陷入局部极小[13]。根据式(15),随着退火衰减因子β的作用,z值不断进行减小,网络随之从混沌态经历倒分岔过程过渡到稳态,直至完全退化为Hopfield网络,收敛到优化值。FCSCNN模型中动力学特性和优化能力敏感的依赖于网络参数(k, α, z, β, ε1, ε2, I0)的选择。k表征记忆保留或遗忘内部状态的能力;α表征能量函数对混沌动力学特性的影响,决定着网络演化和混沌动力的比例;β表征自反馈项的退火速度,决定着混沌特性的退化快慢。参数之间相互影响,需要选择合理的搭配才能获得好的优化效果。反之,则无法得到最优解甚至失去优化能力。
当加入扰动后,从图1~4的神经元动力学特性仿真分析可知,扰动的影响会随着扰动系数增大而增加,当扰动过大,会改变甚至会完全破坏FCS神经元模型的混沌动力学特性。这将影响FCS模型混沌搜索遍历性和伪随机性的动力学特性,不能很好利用自身的自抑制进行全局搜索。因此,要保持良好的寻优能力,除了选择合适的网络参数外,还需要控制扰动在适当的范围内。对于在扰动条件下能否依然较好地解决优化问题,将在不同程度的扰动项作用下,采用FCSCNN模型解决函数优化和组合优化问题,进一步验证模型的抗扰动能力。
3 带扰动的FCSCNN模型在优化问题中的应用根据Hopfield的优化机制有如下规则[14]:
| $\frac{{{\rm{d}}{y_i}}}{{{\rm{d}}t}} = \sum\limits_{j = 1,j \ne i}^N {{w_{ij}}{x_j}\left( t \right) + {I_i}} = - \frac{{\partial E}}{{\partial {x_i}}}$ | (21) |
在设置好模型参数后,将问题的目标函数映射为网络的能量函数,将网络的动力学演化过程视为目标函数的寻优过程,当网路收敛到稳定点时,对应的神经元输出即为所要求得优化问题的解。
3.1 在函数优化中的应用优化函数1:
| $\begin{array}{c}f\left( {{x_1},{x_2}} \right) = {\left( {{x_1} - 0.7} \right)^2}\left[ {{{\left( {{x_2} + 0.6} \right)}^2} + 0.1} \right] + \\{\left( {{x_2} - 0.5} \right)^2}\left[ {{{\left( {{x_1} + 0.4} \right)}^2} + 0.15} \right]\end{array}$ | (22) |
函数f的最小值为0,最小值点为(0.7,0.5);局部极小点为(0.6,0.4), (0.6,0.5)和(0.7,0.4)。在FCSCNN模型中,选取参数如下:k=1, α=0.1, β=0.2, ε1=0.08, I0=0.56, z1(0)=z2(0)=0.1, A(0)=0.4, ε2(0)= 0.08, a=6, b=1, c=0.25。随机初始化神经元输出x1, x2的值,扰动系数γ分别取0.002, 0.02和0.2。对比FCSCNN模型在不同扰动和不同扰动系数下的函数优化能力,进行10次独立实验取均值,每次网络演化50步,实验结果如表1所示。
| 表 1 带扰动FCSCNN求解函数1优化问题结果 Tab.1 The optimization results of the FCSCNN with disturbances for function 1 |
优化函数2:
| $f\left( {{x_1},{x_2}} \right) = 100{\left( {x_1^2 - {x_2}} \right)^2} + {\left( {{x_1} - 1} \right)^2}$ | (23) |
函数f的最小值为0,最小值点为(1, 1)。最优解位于一个平滑、狭长的抛物线形山谷内,函数为优化算法提供的信息比较有限。传统梯度下降法方向几乎与最小值的最佳方向垂直,很难辨别搜索方向,查找最优解变得十分困难。在FCSCNN模型中,选取参数如下:k=1, α=1.0×10–5, β=0.01, ε1=8.0×10–4, I0=0.65, z1(0)=z2(0)=0.8, A(0)=0.4, ε2(0) =0.08, a=6, b=1, c=0.25。随机初始化神经元输出x1、x2的值,扰动系数γ分别取0.002、0.02和0.2。对比FCSCNN模型在不同扰动和不同扰动系数下的函数优化能力,进行10次独立实验取均值,每次网络演化5 000步,实验结果如表2所示:
| 表 2 带扰动FCSCNN求解函数2优化问题结果 Tab.2 The optimization results of the FCSCNN with disturbances for function 2 |
由表1、2仿真实验可知,当扰动系数γ为0(无扰动)时,FCSCNN模型均具有很好的全局寻优性能,找到了全局最优解;当扰动系数γ为0.002时,模型依然保持了较好的全局搜索能力,能够比较接近全局最优解;当扰动系数γ为0.02时,模型的寻优能力均出现明显下降。由于扰动系数γ的增大,扰动项对模型的动力学演化过程和混沌全局性能的影响越大。适当(γ≤0.002)的扰动系数下,网络可以保持全局寻优能力,当扰动项过大(γ≥0.2),会影响甚至破坏模型的寻优水平。为了更好地验证实验结果,选择复杂的组合优化问题进一步实验分析。
3.2 在组合优化中的应用旅行商(traveling salesman problem, TSP)问题描述如下:
假定有N个城市,给出它们的位置和相互距离,要求寻找一条闭合路径,每个城市仅且被访问一次,回到起始城市,要求这条路径的距离最短。
问题对应的目标函数[14]为
| $\begin{array}{c}E = \displaystyle\frac{{{W_1}}}{2}\left[ {\sum\limits_{i = 1}^N {{{\left( {\sum\limits_{j = 1}^N {{x_{ij}} - 1} } \right)}^2} + \sum\limits_{j = 1}^N {{{\left( {\sum\limits_{i = 1}^N {{x_{ij}} - 1} } \right)}^2}} } } \right] + \\\displaystyle\frac{{{W_2}}}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\sum\limits_{k = 1}^N {\left( {{x_{k,j + 1}} + {x_{k,j - 1}}} \right){x_{ij}}{d_{ik}}} } } {\kern 1pt} {\kern 1pt} \end{array}$ | (24) |
式中:xij为神经元的输出,它表示城市i于第j个被访问;W1和W2分别为与约束和关于路径长度的代价函数对应的耦合系数;dij为城市i和城市j之间的距离。
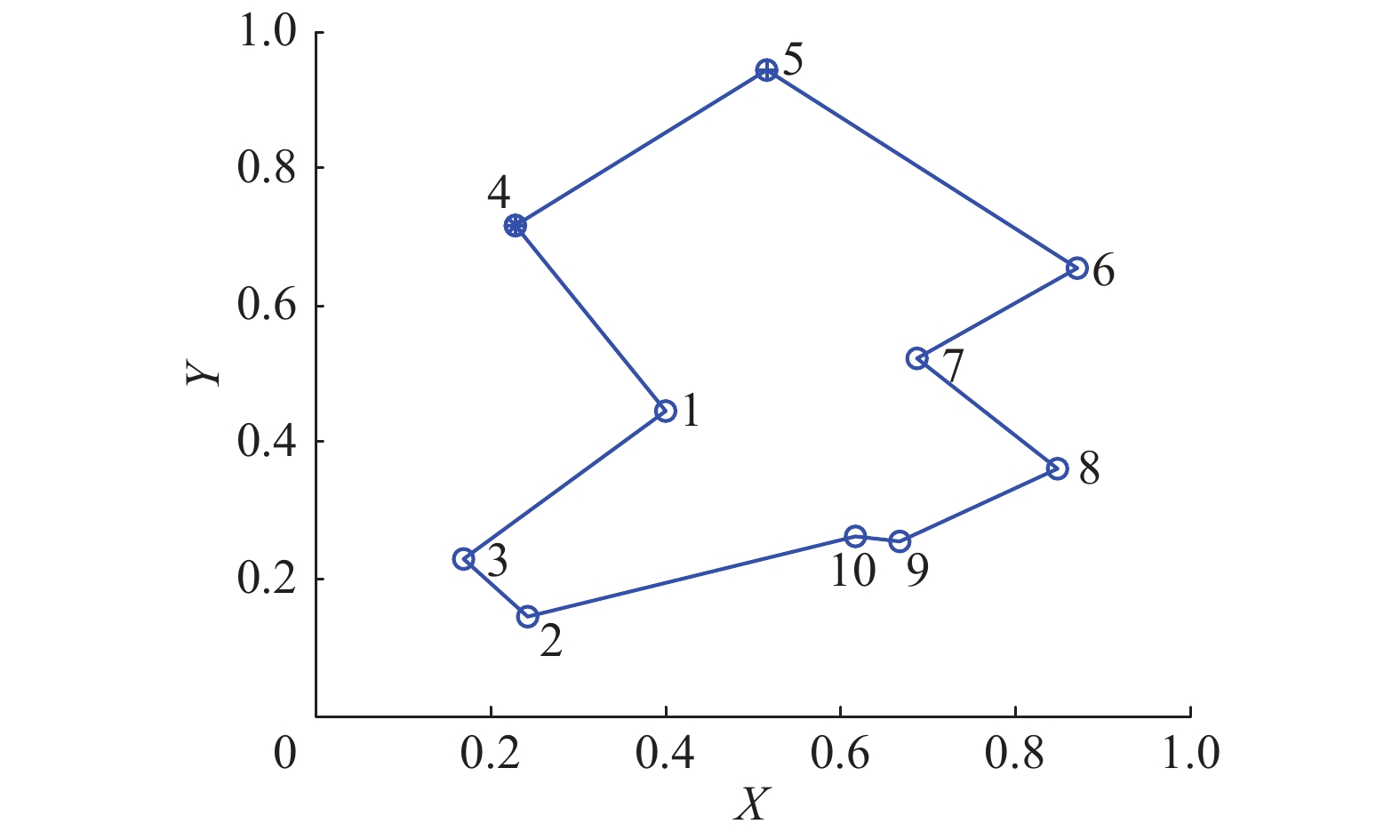
选取10个城市归一化后的坐标,取值分别为:(0.400 0, 0.443 9),(0.243 9, 0.146 3),(0.170 7, 0.229 3),(0.229 3, 0.716 0),(0.517 1, 0.941 4),(0.873 2, 0.653 6),(0.687 8, 0.521 9),(0.848 8, 0.360 9),(0.668 3, 0.253 6),(0.619 5, 0.263 4)。该10个城市TSP问题满足条件最短路径长度为2.677 6[14],最优路径如图5所示。
|
Download:
|
| 图 5 10城市TSP问题的最短路径 Fig. 5 The optimal distance of 10 city TSP | |
在FCSCNN模型中,选取参数如下:k=1, α=0.05, β=0.05, ε1=0.05, I0=0.65, z(0)=0.8, A(0)=0.4, ε2(0)=0.08, a=6, b=1, c=0.25, W1=1, W2=1。随机初始化神经元输出xij的值,对比FCSCNN模型在不同扰动和不同扰动系数下的组合优化能力,进行500次独立实验,每次网络演化1 000步,实验结果如表3所示:
由表3可知,带扰动的FCSCNN模型在解决10城市旅行商问题时:三角扰动系数γ小于0.005的情况下,合法路径比率均在95%以上,最优路径比率均在88%以上;小波扰动系数γ小于0.01的情况下,合法比均在96%以上,最优比均在90%以上。可认为适当的扰动对网络模型的混沌全局寻优能力影响不大。但是随着扰动系数的增大,合法比和最优比均呈下降趋势,扰动项的影响过大时,甚至失去寻优能力。同时,当前的扰动参数下,FCSCNN模型对Morlet小波扰动的鲁棒性比三角函数扰动要好。
| 表 3 带扰动FCSCNN求解10城市TSP问题结果 Tab.3 The optimization results of the FCSCNN with disturbances for 10 city TSP |
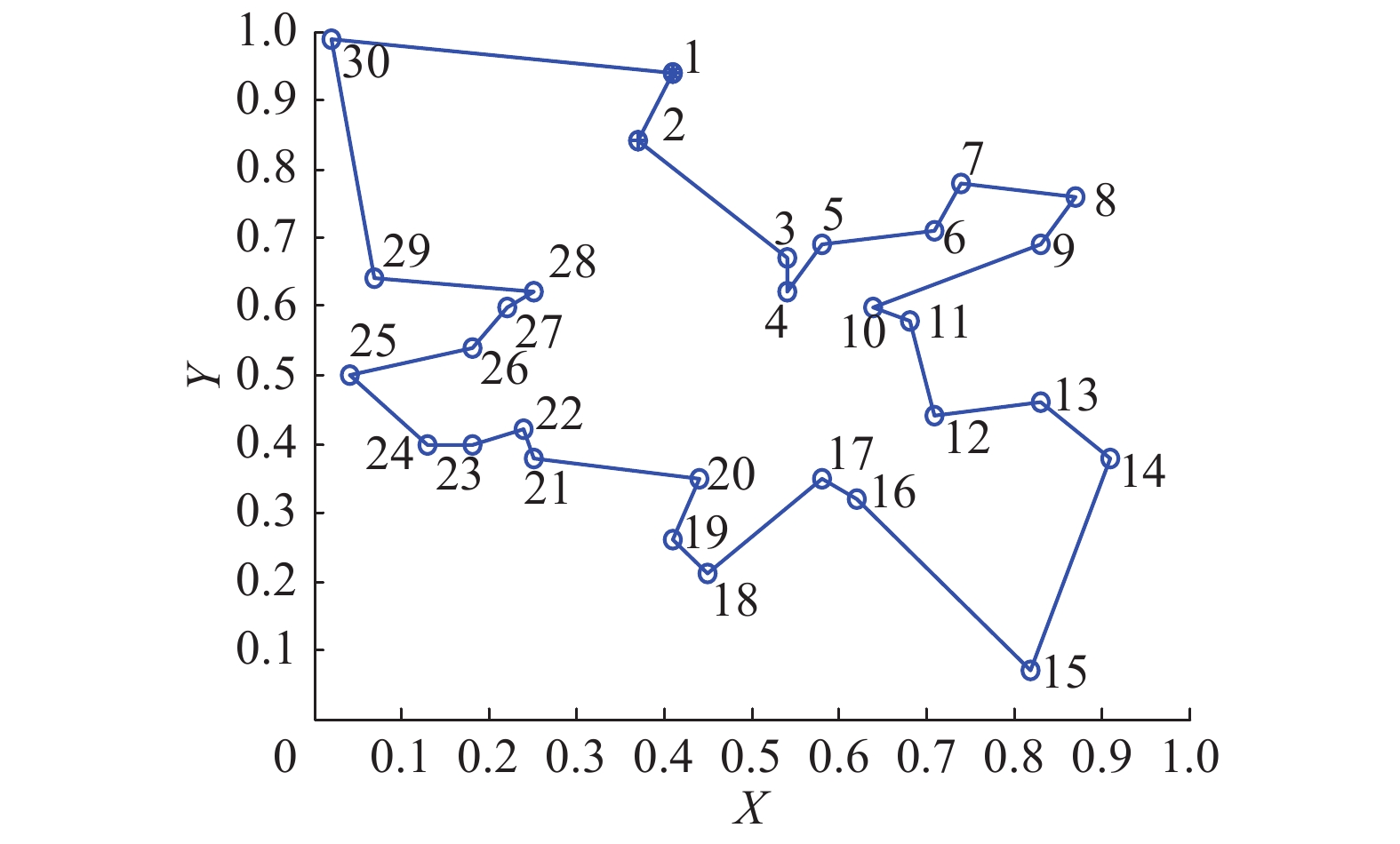
选取30个城市归一化后的坐标,取值分别为:(0.41, 0.94),(0.37, 0.84),(0.54, 0.67),(0.25, 0.62),(0.07, 0.64),(0.02, 0.99),(0.68, 0.58),(0.71, 0.44),(0.54, 0.62),(0.83, 0.69),(0.64, 0.60),(0.18, 0.54),(0.22, 0.60),(0.83, 0.46),(0.91, 0.38),(0.25, 0.38),(0.24, 0.42),(0.58, 0.69),(0.71, 0.71),(0.74, 0.78),(0.87, 0.76),(0.18, 0.40),(0.13, 0.40),(0.82, 0.07),(0.62, 0.32),(0.58, 0.35),(0.45, 0.21),(0.41, 0.26),(0.44, 0.35),(0.04, 0.50)。该30个城市TSP问题满足条件最短路径长度为4.237 406[6],最优路径如图6所示。
|
Download:
|
| 图 6 30城市TSP归一化坐标的最短路径 Fig. 6 The optimal distance of 30 city TSP | |
在FCSCNN模型中,选取参数如下: k=1, α= 0.006, β=0.001, ε1=0.04, I0=0.65, z(0)=0.8, A(0)=0.4, ε2(0) =0.08, a=6, b=1, c=0.25,W1=1,W2=1。随机初始化神经元输出xij的值,对比FCSCNN模型在不同扰动和不同扰动系数下的组合优化能力,进行200次独立实验,每次网络演化10 000步,实验结果如表4所示:
| 表 4 带扰动FCSCNN求解30城市TSP问题结果 Tab.4 The optimization results of the FCSCNN with disturbances for 30 city TSP |
由表4可知,30城市的旅行商问题具有更高的复杂度,需要更多的演化步数,这也是TCNN类模型在解决不同问题时需要不同的参数搭配的原因。三角扰动系数γ小于0.002的情况下,合法路径比率均在70%以上,最优路径比率均在25%以上;小波扰动系数γ小于0.005的情况下,合法比均在65%以上,最优比均在20%以上。同样的可认为较小的扰动对网络模型的混沌全局寻优能力影响不大。在适当扰动强度内,网络表现出一定的抗扰动能力。
4 结束语为了验证的具有非线性激励函数且比标准的暂态混沌神经元模型具有更丰富混沌动力学特性的新型混沌神经网络模型—FCSCNN的抗扰动能力,在该模型内部状态中分别引入三角函数和小波函数扰动项,分析带扰动的FCS混沌神经元模型的动力学特性。通过神经元倒分岔图和最大Lyapunov指数图可知,扰动的引入会影响网络模型的动力学演化过程,进而会对全局寻优性能产生影响。通过函数优化和组合优化问题的仿真实验,证实了这种影响会随着扰动系数的增大而增加,但一定范围内,FCSCNN模型对三角扰动和Morlet扰动均具有一定鲁棒性和抗扰动能力,选取合适的模型参数,依然可以保持较好的全局搜索能力,获得最优解。
| [1] |
HOPFIELD J J, TANK D W. " Neural” computation of decisions in optimization problems[J]. Biological cybernetics, 1985, 52(3): 141-152. ( 0) 0)
|
| [2] |
WANG Jiahai, CAI Yiqiao, YIN Jian. Multi-start stochastic competitive Hopfield neural network for frequency assignment problem in satellite communications[J]. Expert systems with applications, 2011, 38(1): 131-145. DOI:10.1016/j.eswa.2010.06.027 ( 0) 0)
|
| [3] |
CHEN Luonan, AIHARA K. Chaotic simulated annealing by a neural network model with transient chaos[J]. Neural networks, 1997, 8(6): 915-930. ( 0) 0)
|
| [4] |
ZHANG Jiahai, XU Yaoqun. Wavelet chaotic neural networks and their application to continuous function optimization[J]. Natural science, 2009, 1(3): 204-209. DOI:10.4236/ns.2009.13027 ( 0) 0)
|
| [5] |
LIU Xiangdong, XIU Chunbo. A novel hysteretic chaotic neural network and its applications[J]. Neurocomputing, 2007, 70(13/14/15): 2561-2565. ( 0) 0)
|
| [6] |
ZHAO Lin, SUN Ming, CHENG Jianhua, et al. A novel chaotic neural network with the ability to characterize local features and its application[J]. IEEE transactions on neural networks, 2009, 20(4): 735-742. DOI:10.1109/TNN.2009.2015943 ( 0) 0)
|
| [7] |
胡志强, 李文静, 乔俊飞. 变频正弦混沌神经网络及其应用[J]. 物理学报, 2017, 66(9): 090502. HU Zhiqiang, LI Wenjing, QIAO Junfei. Frequency conversion sinusoidal chaotic neural network and its application[J]. Acta physica sinica, 2017, 66(9): 090502. (  0) 0)
|
| [8] |
HSU C C, GOBOVIC D, ZAGHLOUL M E, et al. Chaotic neuron models and their VLSI circuit implementations[J]. IEEE transactions on neural networks, 1996, 7(6): 1339-1350. DOI:10.1109/72.548163 ( 0) 0)
|
| [9] |
SHUAI Jianwei, CHEN Zhenxiang, LIU Riutang, et al. Self-evolution neural model[J]. Physics letters A, 1996, 221(5): 311-316. DOI:10.1016/0375-9601(96)00594-4 ( 0) 0)
|
| [10] |
POTAPOV A, ALI M K. Robust chaos in neural networks[J]. Physics letters A, 2000, 277(6): 310-322. DOI:10.1016/S0375-9601(00)00726-X ( 0) 0)
|
| [11] |
SIH G C, TANG K K. Sustainable reliability of brain rhythms modeled as sinusoidal waves with frequency–amplitude trade-off[J]. Theoretical and applied fracture mechanics, 2012, 61: 21-32. DOI:10.1016/j.tafmec.2012.08.003 ( 0) 0)
|
| [12] |
韩广, 乔俊飞, 韩红桂, 等. 基于Hopfield神经网络的污水处理过程优化控制[J]. 控制与决策, 2014, 29(11): 2085-2088. HAN Guang, QIAO Junfei, HAN Honggui, et al. Optimal control for waste-water treatment process based on Hopfield neural network[J]. Control and decision, 2014, 29(11): 2085-2088. (  0) 0)
|
| [13] |
CHEN S S. Chaotic simulated annealing by a neural network with a variable delay: design and application[J]. IEEE transactions on neural networks, 2011, 22(10): 1557-1565. DOI:10.1109/TNN.2011.2163080 ( 0) 0)
|
| [14] |
GARCÍA L, TALAVÁN P M, YÁÑEZ J. Improving the Hopfield model performance when applied to the traveling salesman problem[J]. Soft computing, 2017, 21(14): 3891-3905. DOI:10.1007/s00500-016-2039-8 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


