无源定位技术一直备受科研人员的关注，广泛应用于雷达、声纳、导航、监测、无线通信、传感器网络等领域^[1-2].目标定位常用到达时间、到达时间差(TDOA, time difference of arrival)和到达频率差(FDOA, frequency difference of arrival)^[3-4]等测量技术.定位目标时微小的传感器位置误差将导致较大的估计误差，故定位目标时应考虑传感器位置误差的影响. Ho等^[5]提出了两步加权最小二乘(TSWLS, two-stage weighted least squares)算法定位多目标；Li等^[6]结合传感器的位置误差和TSWLS算法定位多目标；陈少昌等^[7]利用约束总体最小二乘(CTLS, constrained total least squares)算法定位目标，但CTLS算法仅对静止目标有效.笔者基于文献[5]和文献[7]提出了改进的CTLS (ICTLS, improved CTLS)算法定位多个运动目标，引入拉格朗日乘子和拟牛顿迭代公式求解带约束条件的定位方程.实验结果表明，该方法比TSWLS算法有较好的定位性能，能有效地减小定位偏差，在噪声误差较大的情况下也能达到克拉美罗下界.

1 定位场景

三维空间中随机分布K个运动目标，设第i个目标的真实位置和速度分别为u_i和${{\mathit{\boldsymbol{\dot u}}}_i}$，i=1, 2, …, K. K个目标由空间中M个传感器进行位置估计.传感器的真实位置和速度分别为${\mathit{\boldsymbol{s}}^0} = {[\mathit{\boldsymbol{s}}_1^{0{\rm{T}}},\mathit{\boldsymbol{s}}_2^{0{\rm{T}}}, \cdots ,\mathit{\boldsymbol{s}}_M^{0{\rm{T}}}]^{\rm{T}}}$和${{\mathit{\boldsymbol{\dot s}}}^0} = {[\mathit{\boldsymbol{\dot s}}_1^{0{\rm{T}}},\dot s_2^{0{\rm{T}}}, \cdots ,\mathit{\boldsymbol{\dot s}}_M^{0{\rm{T}}}]^{\rm{T}}}$，其中$\mathit{\boldsymbol{s}}_j^0$和$\mathit{\boldsymbol{\dot s}}_j^0$(j=1, 2, …, M)分别为第j个传感器的真实位置和速度，[·]⁰为[·]的真实值，[·]^T为[·]的转置，且$\mathit{\boldsymbol{s}}_j^0$和$\mathit{\boldsymbol{\dot s}}_j^0$未知，而带有位置误差的位置s_j和${{\mathit{\boldsymbol{\dot s}}}_j}$已知. $\mathit{\boldsymbol{s}} = {[\mathit{\boldsymbol{s}}_1^{\rm{T}},\mathit{\boldsymbol{s}}_2^{\rm{T}}, \cdots \mathit{\boldsymbol{s}}_M^{\rm{T}}]^{\rm{T}}} = {\mathit{\boldsymbol{s}}^0} + \Delta \mathit{\boldsymbol{s}}$为已知的位置向量，已知的速度向量为$\mathit{\boldsymbol{\dot s}} = {[\mathit{\boldsymbol{\dot s}}_1^{\rm{T}},\mathit{\boldsymbol{\dot s}}_2^{\rm{T}}, \cdots \mathit{\boldsymbol{\dot s}}_M^{\rm{T}}]^T} = {{\mathit{\boldsymbol{\dot s}}}^0} + \Delta \mathit{\boldsymbol{\dot s}}$，Δs和$\Delta \mathit{\boldsymbol{\dot s}}$分别为位置和速度的误差向量.传感器真实位置向量为${\mathit{\boldsymbol{\beta }}^0} = {[{\mathit{\boldsymbol{s}}^{0{\rm{T}}}},{{\mathit{\boldsymbol{\dot s}}}^{0{\rm{T}}}}]^{\rm{T}}}$，而带有误差的位置向量为$\mathit{\boldsymbol{\beta }} = {[{\mathit{\boldsymbol{s}}^{\rm{T}}},{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}]^{\rm{T}}} = {\mathit{\boldsymbol{\beta }}^0} + \Delta \mathit{\boldsymbol{\beta }},\Delta \mathit{\boldsymbol{\beta }} = {[\Delta {\mathit{\boldsymbol{s}}^{\rm{T}}},\Delta {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}]^{\rm{T}}}$为传感器位置误差向量，假定误差向量为零均值的高斯随机过程且协方差矩阵为Q_β.通常把传感器j=1作为参考传感器，因此目标i和传感器j之间的真实距离为

$ \mathit{r}_{j,i}^0 = {\left\| {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_j^0} \right\|_2} = \sqrt {{{\left( {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_j^0} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_j^0} \right)} $

(1)

其中‖·‖₂表示2范数.故目标i到传感器1和j的距离差的真实值和测量值分别为

$ r_{j1,i}^0 = r_{j,i}^0 - r_{1,\mathit{i}}^0 $

(2)

$ {r_{j1,i}} = r_{j1,i}^0 + {\rm{\Delta }}{r_{j1,i}} $

(3)

其中Δr_{j1, i}为测量误差.目标i的TDOA测量向量为

$ {\mathit{\boldsymbol{r}}_i} = {\left[ {{r_{21,i}},{r_{31,i}}, \cdots ,{r_{\mathit{M}1,i}}} \right]^{\rm{T}}} = \mathit{\boldsymbol{r}}_i^0 + {\rm{\Delta }}{\mathit{\boldsymbol{r}}_\mathit{i}} $

(4)

其中$\Delta {r_i} = {[\Delta {r_{21,i}},\Delta {r_{31,i}}, \cdots \Delta {r_{M1,i}},]^{\rm{T}}}$为测量误差向量.

当目标相对于传感器发生运动时，参照式(2) 和式(3) 得到FDOA测量值：

$ {{\dot r}_{j1,\mathit{i}}} = \dot r_{j1,i}^0 + {\rm{\Delta }}{{\dot r}_{j1,i}} = \dot r_{j,i}^0 - \dot r_{1,i}^0 + {\rm{\Delta }}{{\dot r}_{j1,\mathit{i}}} $

(5)

其中$\dot r_{j,i}^0$为目标i与传感器j之间真实距离变化率，且$\dot r_{j,i}^0 = \mathit{\boldsymbol{\rho }}_{{u_i},s_J^0}^{\rm{T}}({{\mathit{\boldsymbol{\dot u}}}_i} - \mathit{\boldsymbol{\dot s}}_j^0)({\mathit{\boldsymbol{\rho }}_{a,b}} = (\mathit{\boldsymbol{a}} - \mathit{\boldsymbol{b}})/\left\| {\mathit{\boldsymbol{a}} - \mathit{\boldsymbol{b}}} \right\|$表示由b指向a的单位向量)，同理得到FDOA测量向量${{\mathit{\boldsymbol{\dot r}}}_i} = {[{{\dot r}_{21,i}},{{\dot r}_{31,i}}, \cdots ,{{\dot r}_{M1,i}},]^{\rm{T}}} = \mathit{\boldsymbol{\dot r}}_i^0 + \Delta {{\mathit{\boldsymbol{\dot r}}}_i}$.

为了方便表述，通常把TDOA和FDOA测量向量表示为单一的向量方程.目标i的测量向量为${\mathit{\boldsymbol{\alpha }}_i} = {[\mathit{\boldsymbol{r}}_i^{\rm{T}},\mathit{\boldsymbol{\dot r}}_i^{\rm{T}}]^{\rm{T}}} = \mathit{\boldsymbol{\alpha }}_i^0 + \Delta {\mathit{\boldsymbol{\alpha }}_i}$，且$\Delta {\mathit{\boldsymbol{\alpha }}_i} = {[\Delta \mathit{\boldsymbol{r}}_i^{\rm{T}},\Delta \mathit{\boldsymbol{\dot r}}_i^{\rm{T}}]^{\rm{T}}}$.因此，测量方程$\mathit{\boldsymbol{\alpha }} = {[{\mathit{\boldsymbol{\alpha }}_1},{\mathit{\boldsymbol{\alpha }}_2}, \cdots {\mathit{\boldsymbol{\alpha }}_K}]^{\rm{T}}} = {\mathit{\boldsymbol{\alpha }}^0} + \Delta \mathit{\boldsymbol{\alpha }}$的维数为2K(M－1)×1.测量误差向量Δα为零均值的高斯随机过程且协方差矩阵为Q_α，假设位置误差向量Δβ与测量误差向量Δα相互独立.

2 基于CTLS的优化算法

为了估算运动目标的位置和速度，需要建立关于目标和传感器的TDOA和FDOA定位方程组.引入辅助变量$r_{1,i}^0 = {\left\| {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_1^0} \right\|_2}$，把$r_{1,i}^0$和$r_{j,i}^0$代入式(2) 两边平方整理后得到TDOA方程组：

$ \begin{array}{l} {\left( {r_{_{j1,i}}^0} \right)^2} + 2r_{_{j1,i}}^0r_{1,i}^0 = \\ {\left( {\mathit{\boldsymbol{s}}_j^0 - \mathit{\boldsymbol{s}}_1^0} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{s}}_j^0 - \mathit{\boldsymbol{s}}_1^0} \right) - 2{\left( {\mathit{\boldsymbol{s}}_j^0 - \mathit{\boldsymbol{s}}_1^0} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_1^0} \right) \end{array} $

(6)

由于$r_{1,i}^0 = {\left\| {{\mathit{\boldsymbol{u}}_i} - \mathit{\boldsymbol{s}}_1^0} \right\|_2}$包含参考传感器$\mathit{\boldsymbol{s}}_1^0$的位置坐标参数，将$r_{1,i}^0$在s₁带噪声位置处做一阶泰勒级数展开，忽略二阶以上的高次项，整理得到

$ r_{1,i}^0 \approx {\left\| {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right\|_2} + \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}_i},{\mathit{\boldsymbol{s}}_1}}^{\rm{T}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_1} = {{\hat r}_{1,i}} + \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}_i},{\mathit{\boldsymbol{s}}_1}}^{\rm{T}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_1} $

(7)

其中${{\hat r}_{1,i}} = {\left\| {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right\|_2}$为$r_{1,i}^0$的估计值，且设${\mathit{\boldsymbol{d}}_{1,i}} = \mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}_i},{\mathit{\boldsymbol{s}}_1}}^{\rm{T}}.$把式(7) 和${\mathit{\boldsymbol{s}}_1} = \mathit{\boldsymbol{s}}_1^0 + \Delta {\mathit{\boldsymbol{s}}_1}$代入式(6) 整理得到

$ \begin{array}{l} 2{\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right) + 2{r_{j1,i}}{{\hat r}_{1,i}} - \\ 2{\left( {{\rm{\Delta }}{\mathit{\boldsymbol{s}}_j} - {\rm{\Delta }}{\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right) - 2{\rm{\Delta }}{r_{j1,i}}{{\hat r}_{1,i}} = \\ {\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right) + 2{r_{j1,i}}{\rm{\Delta }}{r_{j1,i}} - \\ 2{\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_j} - 2{r_{j1,i}}{\mathit{\boldsymbol{d}}_{1,i}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_1} - {\left( {{r_{j1,i}}} \right)^2} \end{array} $

(8)

将式(8) 对时间求微分得到FDOA方程组：

$ \begin{array}{l} {\left( {{{\mathit{\boldsymbol{\dot s}}}_j} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right) + {{\dot r}_{j1,i}}{{\hat r}_{1,i}} + {\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\dot u}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right) + \\ {r_{j1,i}}{{\hat {\dot r}}_{1,i}} - {\left( {{\rm{\Delta }}{{\mathit{\boldsymbol{\dot s}}}_j} - {\rm{\Delta }}{{\mathit{\boldsymbol{\dot s}}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right) - \\ {\rm{\Delta }}{{\dot r}_{j1,i}}{{\hat r}_{1,i}} - {\left( {{\rm{\Delta }}{\mathit{\boldsymbol{s}}_j} - {\rm{\Delta }}{\mathit{\boldsymbol{s}}_1}} \right)^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\dot u}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right) - \\ {\rm{\Delta }}{r_{j1,i}}{{\hat {\dot r}}_{1,i}} = {\left( {{{\mathit{\boldsymbol{\dot s}}}_j} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right) - {r_{j1,i}}{{\dot r}_{j1,i}} + \\ {{\dot r}_{j1,i}}{\rm{\Delta }}{r_{j1,i}} + {r_{j1,i}}{\rm{\Delta }}{{\dot r}_{j1,i}} - {\left( {{{\mathit{\boldsymbol{\dot s}}}_j} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)^{\rm{T}}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_j} - \\ {\left( {{\mathit{\boldsymbol{s}}_j} - {\mathit{\boldsymbol{s}}_1}} \right)^{^{\rm{T}}}}{\rm{\Delta }}{{\mathit{\boldsymbol{\dot s}}}_j} - \mathit{\boldsymbol{d}}_{2,i}^{\rm{T}}{\rm{\Delta }}{\mathit{\boldsymbol{s}}_1} - \mathit{\boldsymbol{d}}_{1,i}^{\rm{T}}{\rm{\Delta }}{{\mathit{\boldsymbol{\dot s}}}_1} \end{array} $

(9)

其中${\mathit{\boldsymbol{d}}_{2,i}} = \frac{{({{\mathit{\boldsymbol{\dot u}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1})}}{{{{\hat r}_{1,i}}}} - \frac{{({{\mathit{\boldsymbol{\dot u}}}_i} - {{\mathit{\boldsymbol{\dot s}}}_1})}}{{{{\hat r}_{1,i}}}}{\mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}_i},{\mathit{\boldsymbol{s}}_1}}}\mathit{\boldsymbol{\rho }}_{{\mathit{\boldsymbol{u}}_i},{\mathit{\boldsymbol{s}}_1}}^{\rm{T}}$.联合式(8) 和式(9) 得到矩阵形式的方程组

$ \left( {\mathit{\boldsymbol{A + }}{\rm{\Delta }}\mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{\theta = b + }}{\rm{\Delta }}\mathit{\boldsymbol{b}} $

(10)

其中：$\mathit{\boldsymbol{\theta }} = {[{\mathit{\boldsymbol{w}}^{\rm{T}}},{\widehat r_{1,i}},{\mathit{\boldsymbol{\dot w}}^{\rm{T}}},{\widehat {\dot r}_{1,}}_i]^{\rm{T}}}$, $\mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}$，$\mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_i}$；而A、ΔA、b、Δb与文献[7]中的表达式形式一致.

当目标靠近参考传感器时有u_i－s₁≈0，在式(8)、式(9) 和式(10) 中求解位置的参量趋于零，此时目标估计位置误差较大.为此，首先利用TSWLS算法的第1步粗略估计出目标u_i的位置，然后选取离目标u_i最远的传感器作为新的参考传感器^[8]，根据新的参考传感器重新建立坐标系.在新坐标系下再次估计目标位置，由于TSWLS仅考虑了部分定位方程系数矩阵的误差，造成目标估计位置误差增大；另外，TSWLS没有考虑辅助变量${{\hat r}_{1,i}}$和${\widehat {\dot r}_{1,i}}$与w和${\mathit{\boldsymbol{\dot w}}}$之间的约束关系，从而造成定位模型的失真.因此，笔者全面考虑定位方程中所有系数矩阵的误差，结合附加变量${{\hat r}_{1,i}}$和${\widehat {\dot r}_{1,i}}$与w和${\mathit{\boldsymbol{\dot w}}}$之间的约束关系，利用CTLS算法估计目标位置.向量θ的价值函数为

$ J\left( \mathit{\boldsymbol{\theta }} \right) = {\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right) $

(11)

其中W_θ为加权矩阵，具体表达式见附录中式(37).故待求向量θ的最小二乘解为

$ \mathit{\boldsymbol{\hat \theta = }}{\rm{arg}}\;\mathop {{\rm{min}}}\limits_{\tilde \theta } {\left( {\mathit{\boldsymbol{A\tilde \theta }} - \mathit{\boldsymbol{b}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_{\tilde \theta }}\left( {\mathit{\boldsymbol{A\tilde \theta }} - \mathit{\boldsymbol{b}}} \right) $

(12)

其中：${\mathit{\boldsymbol{\hat \theta }}}$是θ的估计值，${\mathit{\boldsymbol{\tilde \theta }}}$是θ的优化值.因辅助变量${{\hat r}_{1,i}}$和${\widehat {\dot r}_{1,i}}$与w和${\mathit{\boldsymbol{\dot w}}}$有一定的约束关系，

求解式(12) 应考虑此约束条件.结合式(1) 和式(5) 约束条件为

$ \left. \begin{array}{l} {{\hat r}_{1,i}} = \sqrt {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}} \\ {{\hat {\dot r}}_{j,i}} = {{\mathit{\boldsymbol{\dot w}}}^{\rm{T}}}\mathit{\boldsymbol{w}}/{{\hat r}_{1,i}} \end{array} \right\} $

(13)

将式(13) 变形整理代入式(11)，整理得到矩阵形式的约束条件：

$ \left. \begin{array}{l} {\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1}\mathit{\boldsymbol{\theta }} = 0\\ {\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}\mathit{\boldsymbol{\theta }} = 0 \end{array} \right\} $

(14)

其中：${\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{11}}}&\mathit{\boldsymbol{O}}\\ \mathit{\boldsymbol{O}}&\mathit{\boldsymbol{O}} \end{array}} \right]$，${\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2} = \left[ {\begin{array}{*{20}{c}}\mathit{\boldsymbol{O}}&{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{12}}}\\{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{21}}}&\mathit{\boldsymbol{O}}\end{array}} \right]$，O为4×4的全0矩阵，${\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{11}} = {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{12}} = {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{22}} = {\rm{diag}}\left( {1,1,1, - 1} \right)$.因此θ的总体最小二乘解变为CTLS解：

$ \begin{array}{l} \mathit{\boldsymbol{\hat \theta }}\mathit{ = }\arg \;min{(\mathit{\boldsymbol{A\tilde \theta }} - b)^{\rm{T}}}{\mathit{\boldsymbol{W}}_{\mathit{\tilde \theta }}}(\mathit{\boldsymbol{A\tilde \theta }} - b)\\ {\begin{array}{*{20}{c}} {{\rm{s}}.}&{{\rm{t}}.}&{{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}} \end{array}_1}\mathit{\boldsymbol{\theta }} = 0,{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}\mathit{\boldsymbol{\theta }} = 0 \end{array} $

(15)

求解式(15) 约束优化最小值问题时，引入拉格朗日乘子，则θ的价值函数式(11) 变为

$ \begin{array}{l} L\left( {\mathit{\boldsymbol{\theta }},{\mathit{\lambda }_1},{\mathit{\lambda }_2}} \right) = \\ {\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right) + {\mathit{\lambda }_1}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1}\mathit{\boldsymbol{\theta + }}{\mathit{\lambda }_2}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}\mathit{\boldsymbol{\theta }} \end{array} $

(16)

其中λ₁和λ₂为拉格朗日乘子.式(16) 变为二次约束的非凸优化问题.将式(16) 对θ求偏微分，然后令$\partial $L[θ, λ₁, λ₂]/$\partial $θ=0，整理得到

$ \begin{array}{l} 2\left[ {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{D}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\mathit{\boldsymbol{A + }}{\mathit{\lambda }_1}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1} + {\mathit{\lambda }_2}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}} \right]\mathit{\boldsymbol{\theta }} - \\ 2{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{D}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\mathit{\boldsymbol{b = 0}} \end{array} $

(17)

其中D=[$\mathit{\boldsymbol{EQF}}_1^{\rm{T}}$W_θ(Aθ－b), …, $\mathit{\boldsymbol{EQF}}_{L + 1}^{\rm{T}}$W_θ(Aθ－b)]，L=8为向量θ的维数，E=$\sum\limits_{l = 1}^{L + 1} {} $θ_lF_l－F_L+1，Q=E(nn^T)为初始加权矩阵且n=[Δβ^T, Δα^T]^T为随机噪声, F₁, …, F_L为扰动矩阵ΔA、Δb的系数矩阵，具体表达式见附录.向量θ的最终估计值为

$ \mathit{\boldsymbol{\hat \theta = }}{\left[ {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{D}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\mathit{\boldsymbol{A + }}{\mathit{\lambda }_1}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1} + {\mathit{\lambda }_2}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}} \right]^{ - 1}}{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{D}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\mathit{\boldsymbol{b}} $

(18)

把式(18) 代入约束条件式(14) 得到

$ \left. \begin{array}{l} {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1}\mathit{\boldsymbol{\hat \theta }} = 0\\ {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}\mathit{\boldsymbol{\hat \theta = }}0 \end{array} \right\} $

(19)

式(19) 组成了关于λ₁和λ₂的2个高阶多项式方程组，求此方程组得到λ₁和λ₂并代入式(18) 得到目标的估计位置.改写式(19) 为

$ {f_k}\left( {{\mathit{\lambda }_1},{\mathit{\lambda }_2}} \right) = {\mathit{\boldsymbol{p}}^{\rm{T}}}\mathit{\boldsymbol{G}}_f^{ - {\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k}\mathit{\boldsymbol{G}}_f^{ - {\rm{1}}}\mathit{\boldsymbol{p}} = 0,k = 1,2 $

(20)

其中：G_f=(A－D)^TW_θA+λ₁Σ₁+λ₂Σ₂，p=(A－D)^TW_θb.定义λ=[λ₁, λ₂]^T，f=[f₁, f₂]^T.利用拟牛顿迭代公式求解λ：

$ {\mathit{\boldsymbol{\lambda }}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{\lambda }}^{\left( k \right)}} - {\alpha ^{\left( k \right)}}{\mathit{\boldsymbol{H}}^{\left( k \right)}}{g^{^{\left( k \right)}}} $

(21)

其中：λ^(k)为第k次迭代结果，g^(k)=∇f(λ^(k))，α^(k)为步长，H^(k)为相应维数的对称矩阵且由BFGS (Broyden Fletcher Goldfarb Shanno)公式(式(22))更新.

$ \begin{array}{l} {\mathit{\boldsymbol{H}}^{^{\left( {k + 1} \right)}}} = {\mathit{\boldsymbol{H}}^{^{\left( k \right)}}} - \\ \frac{{{\mathit{\boldsymbol{H}}^{^{\left( k \right)}}}{\mathit{\boldsymbol{y}}^{^{\left( k \right)}}}{\mathit{\boldsymbol{y}}^{^{\left( k \right){\rm{T}}}}}{\mathit{\boldsymbol{H}}^{^{\left( k \right)}}}}}{{{\mathit{\boldsymbol{y}}^{^{\left( k \right){\rm{T}}}}}{\mathit{\boldsymbol{H}}^{^{\left( k \right)}}}{\mathit{\boldsymbol{y}}^{^{\left( k \right)}}}}} + \frac{{{\mathit{\boldsymbol{s}}^{\left( k \right)}}{\mathit{\boldsymbol{s}}^{\left( k \right){\rm{T}}}}}}{{{\mathit{\boldsymbol{y}}^{^{\left( k \right){\rm{T}}}}}{\mathit{\boldsymbol{s}}^{\left( k \right)}}}} + {\mathit{\boldsymbol{w}}^{\left( k \right)}}{\mathit{\boldsymbol{w}}^{\left( k \right){\rm{T}}}} \end{array} $

(22)

采用拟牛顿算法的BFGS公式迭代步骤如下：

1) 设定参数δ∈(0, 1)，σ∈(0, 0.5)，W_θ=Q^－1.置精度要求ε=10^－3，取初始点λ⁽¹⁾=[0, 0]^T，初始对称矩阵H⁽¹⁾为相应的单位阵I，k=0.

2) 计算g^(k)=∇f(λ^k)，若‖g^(k)‖≤ε则停止迭代，输出λ^(k)作为近似解.

3) 计算搜索方向p^(k)=－H^(k)g^(k).

4) 设m_k是满足下面不等式的最小非负整数m：f(λ^(k))+δ^mp^(k)≤f(λ^(k))+σδ^mg^(k)Tp^(k).

5) 由BFGS公式更新H^(k+1)，令k=k+1，转向步骤2).

最终通过拟牛顿算法获得λ^(k)的最优值代入式(18)，得到θ的最优估计值.

3 仿真实验及分析

仿真实验采用文献[5]中的方案，假定有6个传感器，其位置和速度如表 1所示.

在多目标定位中以2个目标为例进行仿真实验，2个待定目标的位置和速度分别为$\mathit{\boldsymbol{u}}_1^0$=[600, 650, 550]^T，$\mathit{\boldsymbol{\dot u}}_1^0$=[－20, 15, 40]^T和$\mathit{\boldsymbol{u}}_2^0$=[310, 480, 245]^T，$\mathit{\boldsymbol{\dot u}}_2^0$=[40, 15, －20]^T.设传感器的位置误差为零均值的高斯白噪声，其协方差矩阵为Q_β=diag($\sigma _s^2$R(m²), $\dot \sigma _s^2$R(m·s^-1)²)，其中$\sigma _s^2$和$\dot \sigma _s^2$分别为传感器位置和速度误差方差，且$\dot \sigma _s^2$=0.1$\sigma _s^2$，矩阵R= diag (1, 1, 1, 2, 2, 2, 10, 10, 10, 40, 40, 40, 20, 20, 20, 3, 3, 3). TDOA和FDOA测量误差均为零均值的随机向量，其协方差矩阵Q_α=diag($\sigma _t^2$J(m²), $\sigma _f^2$J(m·s^-1)²)，其中$\sigma _t^2$和$\sigma _f^2$分别为时差和频差方差，令$\sigma _t^2$=10^－4(m²)，$\sigma _f^2$=10^－6(m·s^-1)²，J为一个主对角线元素为1其他元素为0.5的(M－1)×(M－1) 方阵.利用计算机进行10 000次蒙特卡罗实验，对比ICTLS算法与TSWLS和CTLS方法对目标位置和速度估计的均方根误差(RMSE, root mean square error). RMSE定义如下：

$ {P_{{\rm{RMSE}}}}\left| {{V_{{\rm{RMSE}}}}} \right.\left( {{\mathit{\boldsymbol{u}}_i}} \right) = \sqrt {\frac{{\sum\limits_{\iota = 1}^{10000} {\left\| {{{\mathit{\boldsymbol{\tilde u}}}_i}\left( \iota \right) - \mathit{\boldsymbol{u}}_i^0} \right\|_2^2} }}{{10000}}} $

(23)

其中：P_RMSE和V_RMSE分别为位置和速度估计值的RMSE，${{\mathit{\boldsymbol{\tilde u}}}_i}$(l)为第l次蒙特卡罗实验位置和速度的估计结果.考虑3种定位场景：① 利用TDOA/FDOA测量值对单一目标定位，目标的真实位置和速度分别为$\mathit{\boldsymbol{u}}_1^0$=[600, 650, 550]^T和$\mathit{\boldsymbol{\dot u}}_1^0$=[－20, 15, 40]^T；② 对2个目标定位，在目标$\mathit{\boldsymbol{u}}_1^0$基础上另加1个目标，其真实位置和速度分别为$\mathit{\boldsymbol{u}}_2^0$=[310, 480, 245]^T和$\mathit{\boldsymbol{\dot u}}_2^0$=[40, 15, －20]^T；③ 假定目标$\mathit{\boldsymbol{u}}_1^0$和$\mathit{\boldsymbol{u}}_2^0$速度为零，且选择靠近$\mathit{\boldsymbol{u}}_2^0$的传感器$\mathit{\boldsymbol{s}}_3^0$为参考传感器，定位2个静止目标位置.实验中目标和传感器位置分布如图 1所示.

图 2分别展现了TSWLS、CTLS和ICTLS算法的位置估计精度，以及位置与速度估计值的RMSE与克拉美罗下界(CRLB, Cramér-Rao lower bound)的对比结果.由图 2可知：① 位置估计，当10lg($\sigma _s^2$)≤5 dBm²时，3种算法的定位精度都能达到CRLB. TSWLS、CTLS和ICTLS算法的RMSE分别在10 lg ($\sigma _s^2$)≥5 dBm², 10 dBm², 12.5 dBm²时开始高于CRLB，这3个值分别称作各自算法的阈值，在3种算法中传感器的位置误差方差一旦高于各自的阈值，相应算法的RMSE均将高于CRLB.造成3种定位方法出现不同阈值的主要原因是TSWLS算法中第1步加权最小二乘结果偏差随噪声误差的增大而增大，导致最终的定位精度对测量噪声的适应能力较差；CTLS方法虽然整体考虑了传感器位置误差和测量误差等因素，但由于没有考虑附加变量与目标位置的关系以及噪声间的相关性而不能达到最优解；ICTLS算法在CTLS的基础上既考虑了噪声间的相关性，又在引入附加变量时做了近似处理减小了偏差，考虑了附加变量与目标位置的约束关系，因此ICTLS算法在3种定位算法中定位性能最优. ② 速度估计，当10lg($\sigma _s^2$)≤2.5 dBm²时3种定位算法的速度估计精度均能达到CRLB. TSWLS、CTLS和ICTLS算法的阈值分别为2.5 dBm²、5 dBm²和7.5 dBm²，3种算法的位置阈值分别大于其速度阈值.由此可见，定位运动目标时速度估计适应噪声的能力比位置估计适应噪声的能力差，且误差的随机性也增大.

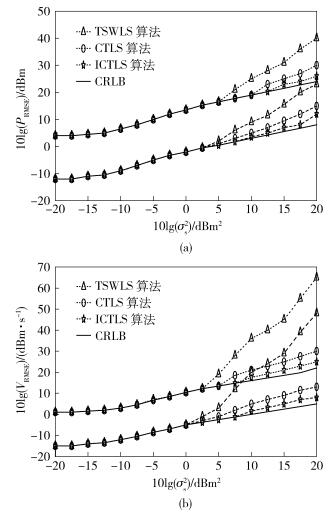
图 3给出了TSWLS、CTLS和ICTLS算法对2个目标定位时各自算法定位精度的RMSE与CRLB的吻合情况.在位置和速度估计结果的RMSE曲线中，上方曲线为目标$\mathit{\boldsymbol{u}}_1^0$的RMSE曲线，下方曲线为目标$\mathit{\boldsymbol{u}}_2^0$的RMSE曲线.由图 3可知，对$\mathit{\boldsymbol{u}}_1^0$和$\mathit{\boldsymbol{u}}_2^0$进行定位时无论位置还是速度，ICTLS算法总比其他2种算法具有更高的精度和更强的噪声适应能力，在较大的误差下也可以达到CRLB.需要指出的是，TSWLS和CTLS方法在定位近场目标$\mathit{\boldsymbol{u}}_2^0$时，无论是位置还是速度的估计中出现的噪声误差阈值都要比远场目标$\mathit{\boldsymbol{u}}_1^0$的噪声误差阈值要小，这说明TSWLS和CTLS方法在定位近场目标时性能较差，主要是没有考虑各噪声误差的相关性，而近场目标间的噪声相互影响较大而造成的.

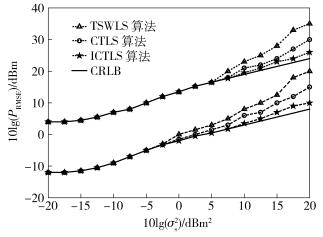
图 4描绘了TSWLS、CTLS和ICTLS算法定位2个固定目标时估计位置的RMSE与CRLB的比较结果.由图 4可知，对于目标$\mathit{\boldsymbol{u}}_1^0$，当10lg($\sigma _s^2$)≤5 dBm²时3种定位算法均能达到CRLB，即使噪声功率10lg($\sigma _s^2$)>5 dBm²之后，3种算法虽然都随着噪声功率的增加RMSE增大，但在同样噪声功率增加量的条件下比图 3中的RMSE增加量较小，这说明定位固定目标时缺少了速度频率等参量，缩减了参与运算参量之间的相互影响，在很大程度上提高了计算效率和定位精度.从图 4中同样可以看出，ICTLS算法抗噪声性能最好，即使在较大的噪声功率下也能逼近CRLB.然而，定位离参考传感器较近的目标$\mathit{\boldsymbol{u}}_2^0$时，TSWLS和CTLS算法的噪声阈值明显要比目标$\mathit{\boldsymbol{u}}_1^0$的噪声阈值要小得多，这2种方法在定位靠近参考传感器的目标时误差较大.由于ICTLS算法中重新选择了参考传感器，并且考虑传感器位置误差和测量误差之间的关系以及引入的变量与目标之间的约束关系，增加了计算的复杂程度，故ICTLS算法比TSWLS和CTLS算法对目标定位用时较长，显然定位精度的提高是以牺牲计算时间为代价的.

4 结束语

针对多个动态目标定位问题，提出了ICTLS的无源定位算法. ICTLS方法避免了TSWLS算法中的2个不足：① 第1步的加权最小二乘结果偏差随噪声误差的增大而增大；② 第2步引入的非线性运算降低算法精度.所提算法修正了CTLS算法中未考虑目标离参考传感器较近以及引入变量与目标之间的关系，建立了全局约束条件；同时，求解定位方程时引入了拉格朗日乘子技术，通过拟牛顿法的BFGS迭代公式进行求解，避免了Hessian矩阵的计算，加快了收敛速度.仿真实验表明传感器误差和测量误差适度的情况下，ICTLS算法比TSWLS和CTLS算法具有更低的RMSE，展现出了较强的鲁棒性和较高的定位精度.

附录

设C=[A b]，ΔC=[ΔAΔb]，则式(10) 变为

$ \left( {\mathit{\boldsymbol{C}} + \Delta \mathit{\boldsymbol{C}}} \right){\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\theta }}&{ - 1} \end{array}} \right]^{\rm{T}}} = 0 $

(24)

方程式(24) 的CTLS解为约束最优化问题：

$ \begin{array}{l} \mathop {\min }\limits_{\Delta C,\theta } \left\| {\Delta \mathit{\boldsymbol{C}}} \right\|_{\rm{F}}^2\\ {\rm{s}}{\rm{.}}\;\;{\rm{t}}{\rm{.}}\;\;\left( {\mathit{\boldsymbol{C}} + \Delta \mathit{\boldsymbol{C}}} \right){\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\theta }}&{ - 1} \end{array}} \right]^{\rm{T}}} \end{array} $

(25)

其中‖·‖_F表示对矩阵求Frobenius范数，即‖H‖_F=tr(H^TH).设n=[Δs^T, $\Delta {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}$, Δr^T, $\Delta {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}$]^T，且ΔC可以表示为C=[C₁, C₂, …, C_L+1]，其中L=8.因此C的各列可以表示为

$ \Delta {\mathit{\boldsymbol{C}}_\iota } = {\mathit{\boldsymbol{F}}_{1n}},\iota = 1,2, \cdots ,\mathit{L + }{\rm{1}} $

(26)

当n不是白噪声的随机向量时，需要使向量n白化.假设Q=E(nn^T)=PP^T是矩阵Q的Cholesk分解，然后利用e=P^－1n将n变为白噪声向量e，故C_l可改写为

$ \Delta \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{F}}_1}\mathit{\boldsymbol{Pe,}}\iota = 1,2, \cdots ,\mathit{L + }{\rm{1}} $

(27)

式(24) 的CTLS解变为

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\;\;\min }\limits_{e,\theta } \left\| \mathit{\boldsymbol{e}} \right\|_{\rm{F}}^2\\ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.}}\;\;{\rm{t}}{\rm{.}}\;}&{\left( {\mathit{\boldsymbol{C + }}\left[ {{\mathit{\boldsymbol{F}}_1}\mathit{\boldsymbol{Pe,}}{\mathit{\boldsymbol{F}}_2}\mathit{\boldsymbol{Pe,}} \cdots \mathit{\boldsymbol{,}}{\mathit{\boldsymbol{F}}_{L + 1}}\mathit{\boldsymbol{Pe}}} \right]} \right)} \end{array} \times \\ \;\;\;\;\;\;\;\;\;\;{\left[ {\theta ,\;\; - 1} \right]^{\rm{T}}} = 0\; \end{array} $

(28)

而约束条件可变为

$ \begin{array}{l} \left[ {{\mathit{\boldsymbol{F}}_1}\mathit{\boldsymbol{Pe,}}{\mathit{\boldsymbol{F}}_2}\mathit{\boldsymbol{Pe,}} \cdots \mathit{\boldsymbol{,}}{\mathit{\boldsymbol{F}}_{L + 1}}\mathit{\boldsymbol{Pe}}} \right]{\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\theta ,}}}&{ - 1} \end{array}} \right]^{\rm{T}}} = \\ \;\;\;\left( {\sum\limits_{\iota = 1}^L {{\mathit{\boldsymbol{\theta }}_\iota }{\mathit{\boldsymbol{F}}_\iota }\mathit{\boldsymbol{P}} - {\mathit{\boldsymbol{F}}_{L + 1}}\mathit{\boldsymbol{Pe}}} } \right)\mathit{\boldsymbol{e}}\; = \mathit{\boldsymbol{EPe = }}{\mathit{\boldsymbol{G}}_\theta }\mathit{\boldsymbol{e}}\; \end{array} $

(29)

其中：

$ \begin{array}{l} \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_1}}&{{\mathit{\boldsymbol{E}}_2}} \end{array}} \right] = \sum\limits_{\iota = 1}^{L + 1} {{\mathit{\boldsymbol{\theta }}_\iota }{\mathit{\boldsymbol{F}}_\iota } - {\mathit{\boldsymbol{F}}_{L + 1}}} \\ {\mathit{\boldsymbol{E}}_1} = 2\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1} \otimes {{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{B}}_2}}&{{\mathit{\boldsymbol{O}}_{\left( {M - 1} \right) \times 3M}}}\\ {{\mathit{\boldsymbol{B}}_1} \otimes {{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{B}}_3}}&{{\mathit{\boldsymbol{B}}_1} \otimes {{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{s}}_i}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{B}}_2}} \end{array}} \right] \end{array} $

(30)

$ {\mathit{\boldsymbol{E}}_2} = 2\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{D}}&{{\mathit{\boldsymbol{O}}_{\left( {M - 1} \right) \times \left( {M - 1} \right)}}}\\ {\mathit{\boldsymbol{\dot D}}}&\mathit{\boldsymbol{D}} \end{array}} \right] $

(31)

$ \left. \begin{array}{l} \mathit{\boldsymbol{D}} = {\rm{diag}}\left( {r_2^0,r_3^0, \cdots ,r_M^0} \right)\\ \mathit{\boldsymbol{\dot D}} = {\rm{diag}}\left( {\dot {r_2^0,\dot {r_3^0, \cdots ,r_M^0}}} \right) \end{array} \right\} $

(32)

$ {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} { - 1}&1&0& \cdots &0\\ { - 1}&0&1& \cdots &0\\ { - 1}& \vdots & \vdots & \cdots & \vdots \\ { - 1}&0&0& \cdots &1 \end{array}} \right] $

(33)

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}_2} = \\ \left[ {\begin{array}{*{20}{c}} {{r_{21}}{\mathit{\boldsymbol{d}}_1}}&{{{\left( {{\mathit{\boldsymbol{s}}_2} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}}&{{{\rm{0}}^{\rm{T}}}}& \cdots &{{0^{\rm{T}}}}\\ {{r_{31}}{\mathit{\boldsymbol{d}}_1}}&{{{\rm{0}}^{\rm{T}}}}&{{{\left( {{\mathit{\boldsymbol{s}}_3} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}}& \cdots &{{0^{\rm{T}}}}\\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {{r_{M1}}{\mathit{\boldsymbol{d}}_1}}&{{0^{\rm{T}}}}&{{0^{\rm{T}}}}& \cdots &{{{\left( {{\mathit{\boldsymbol{s}}_M} - {\mathit{\boldsymbol{s}}_1}} \right)}^{\rm{T}}}} \end{array}} \right] \end{array} $

(34)

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{B}}_3} = \\ \left[ {\begin{array}{*{20}{c}} {{r_{21}}{\mathit{\boldsymbol{d}}_{2 + }}{{\dot r}_{21}}{\mathit{\boldsymbol{d}}_1}}&{{{\left( {{{\mathit{\boldsymbol{\dot s}}}_2} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)}^{\rm{T}}}}&{{{\rm{0}}^{\rm{T}}}}& \cdots &{{0^{\rm{T}}}}\\ {{{\dot r}_{31}}{\mathit{\boldsymbol{d}}_2} + {{\dot r}_{31}}{\mathit{\boldsymbol{d}}_1}}&{{{\rm{0}}^{\rm{T}}}}&{{{\left( {{{\mathit{\boldsymbol{\dot s}}}_3} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)}^{\rm{T}}}}& \cdots &{{0^{\rm{T}}}}\\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {{{\dot r}_{M1}}{\mathit{\boldsymbol{d}}_2} + {{\dot r}_{M1}}{\mathit{\boldsymbol{d}}_1}}&{{0^{\rm{T}}}}&{{0^{\rm{T}}}}& \cdots &{{{\left( {{{\mathit{\boldsymbol{\dot s}}}_M} - {{\mathit{\boldsymbol{\dot s}}}_1}} \right)}^{\rm{T}}}} \end{array}} \right] \end{array} $

(35)

因此，式(28) 中的约束条件变为

$ \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\theta }}&{ - 1} \end{array}} \right] + {\mathit{\boldsymbol{G}}_\theta }\mathit{\boldsymbol{e = }}{\rm{0}} $

(36)

因为G_θ是一个行满秩矩阵，G_θ的广义逆矩阵为其右伪逆矩阵$\mathit{\boldsymbol{G}}_\theta ^† = \mathit{\boldsymbol{G}}_\theta ^{\rm{T}}{({\mathit{\boldsymbol{G}}_\theta }\mathit{\boldsymbol{G}}_\theta ^{\rm{T}})^{ - 1}}$，故设加权矩阵：

$ \begin{array}{l} {\mathit{\boldsymbol{W}}_\theta } = {\left( {{\mathit{\boldsymbol{G}}_\theta }\mathit{\boldsymbol{G}}_\theta ^{\rm{T}}} \right)^{ - 1}} = {\left( {\mathit{\boldsymbol{EQE}}} \right)^{ - 1}} = \\ {\left( {{\mathit{\boldsymbol{E}}_1}{\mathit{\boldsymbol{Q}}_\beta }\mathit{\boldsymbol{E}}_1^{\rm{T}} + {\mathit{\boldsymbol{E}}_2}{\mathit{\boldsymbol{Q}}_\alpha }\mathit{\boldsymbol{E}}_2^{\rm{T}}} \right)^{ - 1}} \end{array} $

(37)

由此得到CTLS的价值函数为

$ J\left( \mathit{\boldsymbol{\theta }} \right) = {\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_\theta }\left( {\mathit{\boldsymbol{A\theta }} - \mathit{\boldsymbol{b}}} \right) $

(38)