0 引言
苏锡常地区地面沉降始于20世纪70年代中期,由于规模化开采地下水,地下水位不断下降,地面沉降现象逐渐显现;20世纪80—90年代,地下水位漏斗面积不断增大,地面沉降范围由中心城区逐渐扩大至外围区域;20世纪90年代实行地下水限采措施以来,地下水环境改善效果显著,大部分地区地下水位回升幅度明显[1-2],地面沉降得到有效控制,地面沉降速率大幅减小。地面沉降的成因是多方面综合作用的结果,地下水资源超采是前期地面沉降发展的主因[3]。但是苏州吴江盛泽地区由于近年来城镇化的快速发展,一方面建筑荷载短期内急剧增加,由建筑物基础桩的负摩擦力引发的地面沉降已成为一个不可忽视的重要因素,另一方面还存在较大的地下水位降落漏斗,地面沉降仍在发展之中。目前,地面沉降速率仍高于15 mm/a,成为苏锡常沉降速率最大的地区之一[4]。因此,全面分析地面沉降的影响因素,对地面沉降发展趋势进行准确模拟预测,为科学防治地面沉降提供有效的解决方案已成为当务之急。
目前,国内外关于地面沉降模拟和预测研究的热点集中以地下水开采为主因[5-9],对于地面荷载引起的地面沉降研究处于初级阶段[10-12],针对此方面的研究较少。已有的研究都是将高层建筑荷载和地下水开采作为独立事件进行分析,未考虑两者间存在的耦合效应对地面沉降的影响[13]。本文基于比奥固结理论[14-15],建立了吴江盛泽地区建筑荷载和地下水开采与地面沉降三维全耦合模型,模拟预测了建筑荷载单独作用、地下水开采单独作用及建筑荷载和地下水开采叠加作用下盛泽地区地面沉降发展趋势,分析二者对地面沉降造成的影响,以期为吴江盛泽地区地面沉降的科学防控提供决策依据。
1 研究区概况地处江苏省苏州市吴江区南部的盛泽位于30°50′35″N—30°57′52″N,120°30′37″E—120°40′13″E,为江、浙、沪交界处,包括南麻、坛丘等,行政总面积150 km2。区内第四纪沉积层一般厚度为140~200 m,主要为河湖相、河口相沉积。主要含水层为全新统孔隙潜水含水层、上更新统第Ⅰ孔隙承压含水层、中更新统第Ⅱ孔隙承压含水层、下更新统第Ⅲ孔隙承压含水层,主采层为第Ⅰ承压含水层。含水层组分布详见表 1。
| 孔隙含 水层组 |
含水岩(层)组 | 分布特征 | ||
| 地层时代 | 岩性 | 厚度/m | ||
| 潜水含 水层 |
Q4 | 粉砂、粉土、 粉质黏土 |
1~3 | 广泛 分布 |
| 第Ⅰ承压 含水层 |
Q3 | 粗砂、中细砂、粉细砂 | 10~20 | |
| 第Ⅱ承压 含水层 |
Q2 | 中细砂、细砂、粉细砂 | 10~15 | |
| 第Ⅲ承压 含水层 |
Q1 | 中粗砂、中细砂、细砂、粉细砂 | 10~20 | |
区内浅部地层中由高压缩性土层构成的软土相对发育,厚度一般为25~30 m,岩性、岩相变化不稳定,工程地质条件较差。
2 地质概念模型 2.1 边界条件研究区积累了多年的钻孔勘探资料和地下水动态观测资料,根据地下水动态及渗流场特征,将研究区的侧向边界概化为流量边界。研究区的顶部主要接受大气降雨的补给,是补给边界,同时地下水又通过其蒸发,故顶部也是排泄边界。研究区的底部为一固结黏土层,概化为隔水边界。图 1为研究区水文地质剖面布置图。

|
| 图 1 盛泽地区水文地质剖面布置图 Fig. 1 Arrangement diagram of hydrogeological section in Shengze area |
|
|
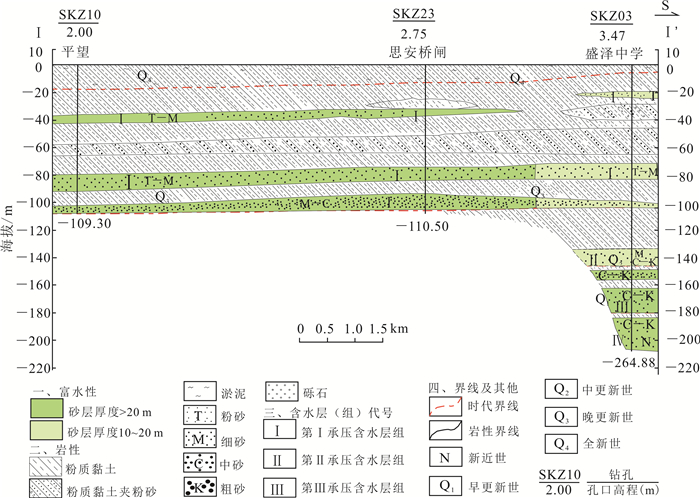
研究区第四纪地层厚度一般为140~200 m,垂向上为砂层和黏土层互层,平面上各土层的颗粒结构也极不均匀,水力学性质和土力学性质存在较大的差异,为非均质各向异性。图 2为Ⅰ-Ⅰ′南北向水文地质剖面略图。
|
| 图 2 研究区Ⅰ-Ⅰ′南北向水文地质剖面略图 Fig. 2 Hydrogeological profile of Ⅰ-Ⅰ′ in north-south in the study area |
|
|
由于早年间研究区不加节制地开采地下水,各含水层垂向产生较为强烈的水力联系,并形成降落漏斗。加之地下水开采和大气降雨季节性的影响,地下水位也发生强烈的波动,由此将地下水流态概化为三维非稳定流。
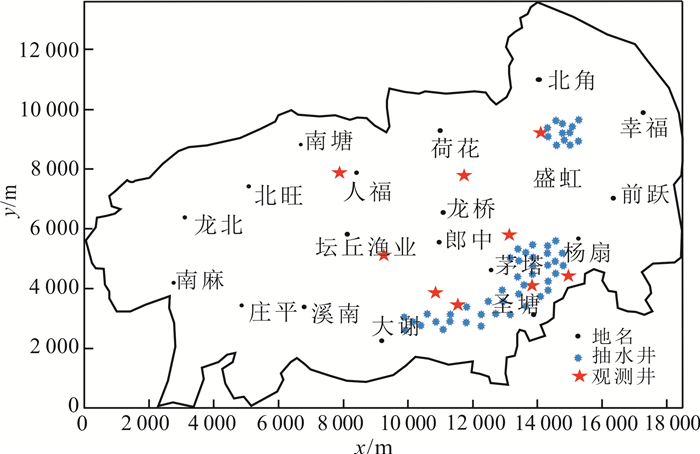
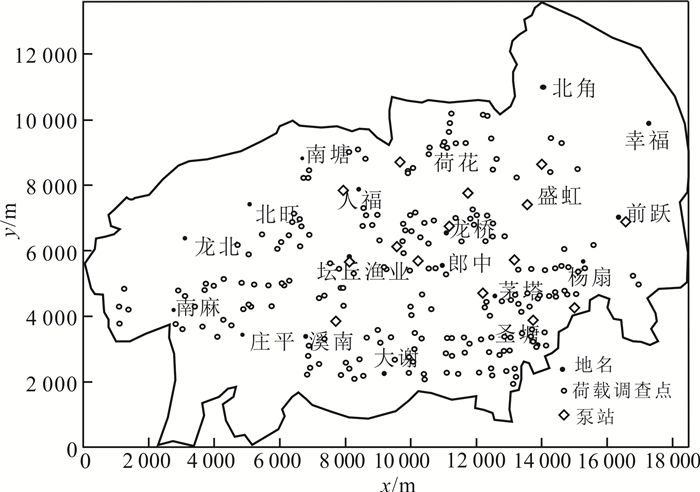
2.4 源汇项和建筑荷载研究区的源汇项主要是地下水开采、大气降雨入渗补给与地下水蒸发排泄。地下水开采概化为大井,大气降雨入渗补给和地下水蒸发排泄分别概化为入渗补给强度和蒸发排泄强度,并结合在一起综合处理。将地面建筑荷载概化为点荷载处理。研究区井位分布情况见图 3,主要地面建筑荷载分布见图 4。
|
| 图 3 盛泽地区井位分布 Fig. 3 Distribution of wells in Shengze area |
|
|
|
| 图 4 盛泽地区主要地面荷载分布 Fig. 4 Distribution of main ground building loads in Shengze area |
|
|
本次研究以三维比奥固结方程为基础,建立了盛泽地区建筑荷载和地下水开采与地面沉降三维全耦合数学模型:
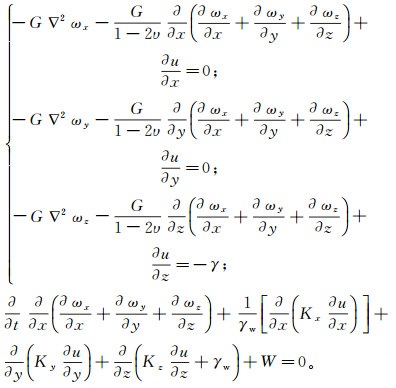 (1)
(1) 式中:G为剪切模量;▽为拉普拉斯算子;ωx、ωy、ωz分别为x、y、z方向的位移;υ为泊松比;u为超静孔隙水压力;γ为土的重度;t为时间;Kx、Ky、Kz分别为x、y、z方向的渗透系数;γw为水的重度;W为源汇项。
式(1)可以简写成:
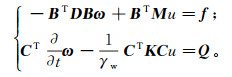
式中:ω=[ωx, ωy, ωz]T;D为应力应变关系矩阵;f=[fx,fy,fz]T,fx,fy,fz分别为体积力在x, y, z方向上的分量;M=[1, 1, 1, 0, 0, 0]T;Q为计算点的等效流量;C为弹性柔度矩阵;B为应变位移矩阵;K为固体刚度矩阵。
3.2 土体本构关系根据土体的流变特性,将土体本构关系拓展到黏弹塑性,则该土体的任一点在任一时刻的应变增量[16]可表示为

式中:dε为总应变增量;dεep为弹塑性应变增量;dεve为黏弹性应变增量;dεvp为黏塑性应变增量。
3.3 定解条件 3.3.1 初始条件1) 孔隙水压力初始条件
孔隙水压力初始条件为
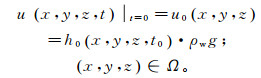
式中:u0(x, y, z)为初始孔压;h0(x, y, z, t0)为初始水头值;ρw为水的密度;g为重力加速度;Ω为整个研究区域。2014-09-01各含水层组的初始流场为该模型的初始水位值。
2) 地应力初始条件
已知土体的自重应力,可以估算土体的初始应力:

式中:σx、σz为土体的初始水平向和垂向应力;z′为各层计算点深度;k1为静止侧压力系数。
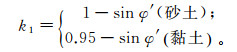
式中,φ′为有效内摩擦角。
3) 位移初始条件
模型的位移初始条件为2014-09-01各含水层的初始位移值,初始位移值设为0。

1) 流量边界条件Γ2:

式中:K为渗透系数;H为水位;n为孔隙度;qL为边界Γ2上的已知单位面积流量。
2) 自由面边界条件Γ3:

式中:μ为土体给水度;θ为自由面外法线方向与垂线的交角;q为通过自由面边界Γ3的单位面积流量;Z为自由面所在的海拔高度。
3) 位移边界条件Γ4:

式中:
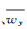

建筑荷载和地下水开采作用下产生孔隙水应力消散,土体骨架应力进而重新分布,土体固结变形为其宏观表现。基于比奥固结理论,结合孔隙度相关定义和Kozeny-Carman方程,得到渗透系数K和孔隙度n之间的关系式[17]:
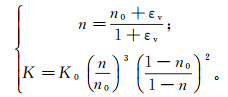
式中:n0为初始孔隙度;K0为初始渗透系数;εv为体应变, 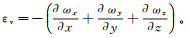
根据Duncan-Zhang提出的非线性模型,将土体本构关系推广到非线性,应力应变关系矩阵D的弹性常数E和υ为随应力状态改变的变量,则切线弹性模量Et和切线泊松比υt的表达式为:
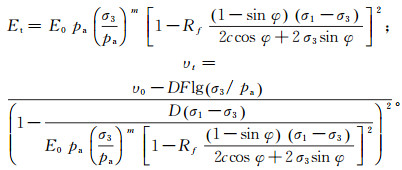
式中:pa为大气压强;σ1为第一主应力;σ3为第三主应力;Rf为破坏比;φ为内摩擦角;c为黏聚力;v0为围压为100 kPa时的初始泊松比;E0为σ3=100 kPa时的初始弹性模量;F为试验常数,本文F=0.04;m为弹性模量与固结压力曲线的斜率;D为土体试验参数,D=3。
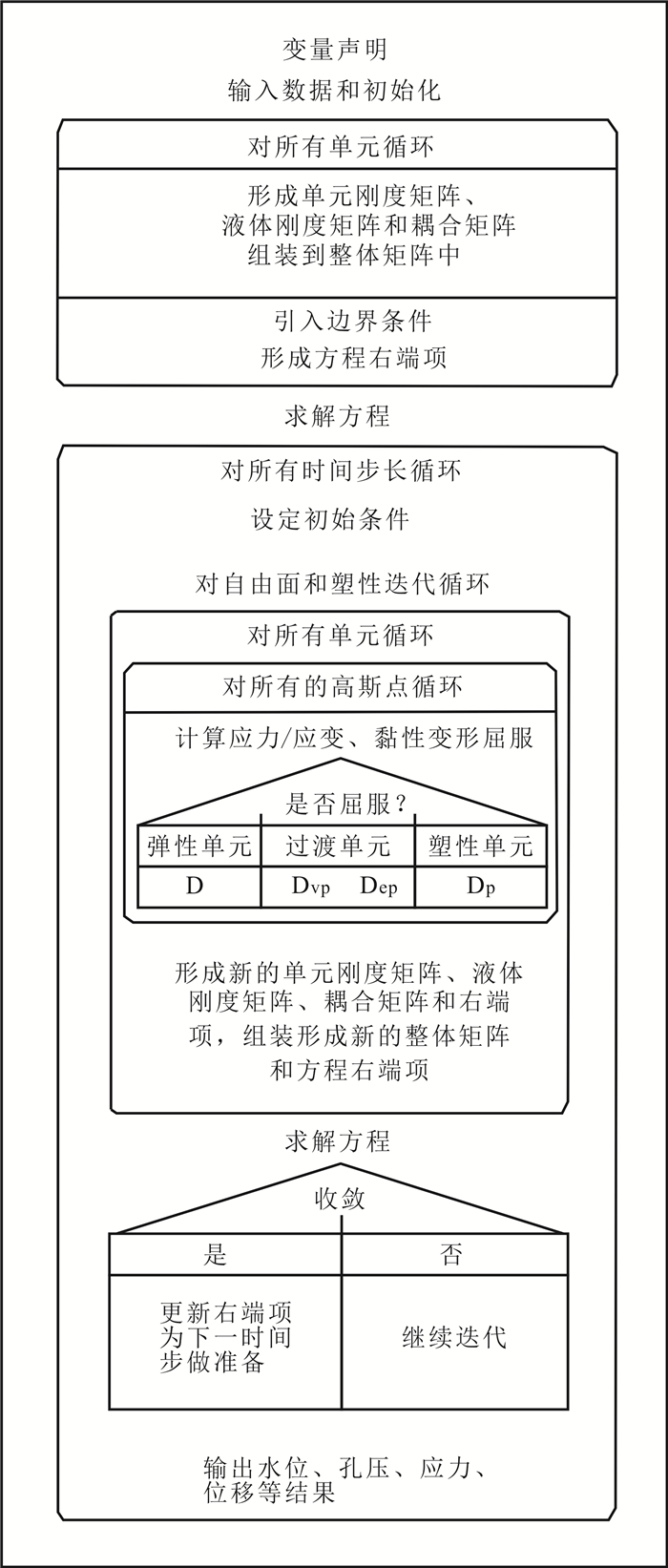
4 模型求解与校正根据前述数学模型,运用伽辽金有限元方法求解,采用Fortran95语言编制了建筑荷载和地下水开采与地面沉降三维全耦合数值分析程序[18],如图 5所示。
|
| D为弹性单元;Dvp,Dep,Dp分别为黏塑性单元、弹塑性单元和塑性单元。 图 5 程序结构框图 Fig. 5 Program structure |
|
|
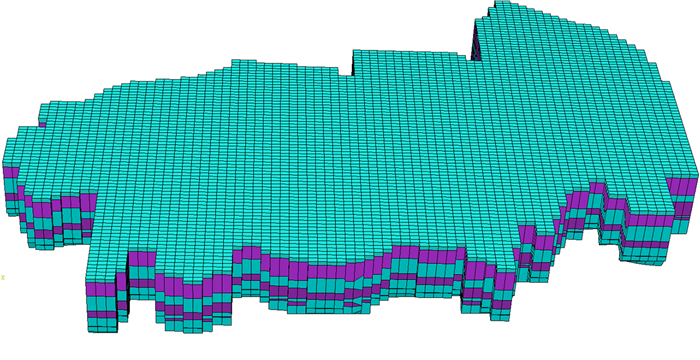
研究区平面上共计剖分成4 635个矩形网格,垂向上剖分成7个层位,平面尺度为18 481 m×13 578 m,垂向深度为140~200 m,面积约为150 km2。经过离散的模型中共有节点38 888个,单元32 445个。三维剖分网格见图 6。选取为期1 a(2014-09-01— 2015-08-31)的观测资料为研究基础,对模型参数进行反演计算,以每月作为1个应力期,1个应力期对应1个时间步长,共12个应力期。
|
| 图 6 研究区三维网格剖分图 Fig. 6 Three-dimensional mesh of simulation field in the study area |
|
|
根据盛泽地区的具体情况,降雨量采用年平均降雨量,经模型调试,扣除蒸发量以后的有效降雨入渗补给系数确定为0.014,有效入渗面积为72.27 km2。研究区共有41口井,地下水开采量在调查统计的基础上,结合现有地下水位降落漏斗形态特征,经模型反演计算确定。单井日开采量为50~200 m3/d,日均抽水量约为5 710 m3/d,其中镇区中南部茅塔、杨扇、圣塘、大谢处日均抽水量约为4 150 m3/d,盛虹社区以北思安桥处日均抽水量约为1 560 m3/d。本程序中流量的计算原理为,从外部水源流入计算单元的水流量Q与外部水源的水头h2和该计算单元水头h1之差成正比,公式为
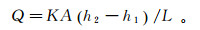
式中:A为过水断面面积;L为两单元中心之间的距离。结合各应力期边界上地下水进出量,经模型反演计算确定边界条件。
建筑荷载所产生的地面沉降量包括基础上部荷载产生的沉降量和相邻基础荷载因应力扩散产生的沉降量。根据实地调查的盛泽地区建筑物荷载分布特征情况确定建筑荷载,建筑荷载按每层自重1.2 t/m2、每层承重0.3 t/m2计算。将实际建筑荷载区域概化为矩形区域,计算概化后的矩形区域建筑荷载影响下的地基附加应力,得出影响范围内模型中各节点的附加应力。则矩形基础受垂直分布荷载作用下地基土中任意节点的竖向附加应力系数asr为:

其中:
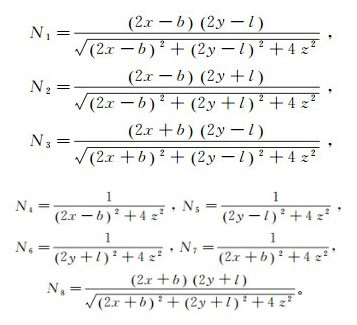
式中:l为矩形的长;b为矩形的宽;x、y、z为计算点坐标值。
则任意节点的附加应力为
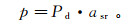
式中, Pd为高层建筑荷载。
全区有9口观测井进行水位拟合,结果见图 3。经调参、反演后,模型共7层38个分区。以第Ⅰ承压含水层为例,图 7为分区情况,各分区的水文地质参数值详见表 2。

|
| 图 7 研究区第Ⅰ承压含水层参数分区图 Fig. 7 Parameter partition of the first confined aquifer in the study area |
|
|
| 分区 | 主轴渗透系数/(m/d) | 变形模量/ MPa |
泊松比 | 黏聚力/ kPa |
摩擦角/ (°) |
膨胀角/ (°) |
重度/ (kN/m3) |
有效孔隙度 | ||
| Kx | Ky | Kz | ||||||||
| 10 | 0.178 | 0.178 | 0.015 | 42 | 0.480 | 34 | 18 | 0 | 19 | 0.454 |
| 11 | 0.487 | 0.487 | 0.040 | 45 | 0.480 | 32 | 16 | 0 | 20 | 0.452 |
| 12 | 0.800 | 0.800 | 0.080 | 41 | 0.470 | 30 | 18 | 0 | 19 | 0.439 |
| 13 | 0.150 | 0.150 | 0.020 | 48 | 0.470 | 35 | 15 | 0 | 21 | 0.445 |
| 14 | 0.300 | 0.300 | 0.050 | 43 | 0.470 | 32 | 17 | 0 | 19 | 0.446 |
| 15 | 0.400 | 0.400 | 0.040 | 43 | 0.460 | 34 | 18 | 0 | 19 | 0.446 |
| 16 | 0.200 | 0.200 | 0.010 | 47 | 0.480 | 36 | 19 | 0 | 20 | 0.453 |
| 17 | 0.500 | 0.500 | 0.050 | 43 | 0.470 | 34 | 14 | 0 | 19 | 0.450 |
| 18 | 0.600 | 0.600 | 0.030 | 42 | 0.470 | 35 | 15 | 0 | 19 | 0.449 |
| 19 | 0.450 | 0.450 | 0.045 | 44 | 0.47 | 34 | 16 | 0 | 18 | 0.451 |
模型识别计算所得的各含水层第12应力期的水均衡要素见表 3,可见地下水流入量和流出量基本相当。研究区各水准点2014-09—2015-08地面沉降拟合情况见表 4。以盛泽镇盛溪河泵站水位为例,其水位拟合图见图 8。由表 4和图 8可见,地面沉降量计算值与实测值拟合精度较高。累计地面沉降量计算值与实测值拟合图见图 9,可见累计地面沉降量计算值与实测值吻合程度较高,水准观测点沉降计算值和实测值模拟误差均小于10%。综上,模型收敛性及稳定性较好,模型识别所得结果可信,精度较高。
| 含水层 | 流入量/(m3/d) | 流出量/(m3/d) |
| 潜水含水层 | 76.84 | 76.88 |
| 第Ⅰ弱含水层 | 127.35 | 127.96 |
| 第Ⅰ承压含水层 | 16 875.84 | 16 875.70 |
| 第Ⅱ弱含水层 | 115.42 | 115.41 |
| 第Ⅱ承压含水层 | 844.83 | 844.82 |
| 第Ⅲ弱含水层 | 792.60 | 792.66 |
| 第Ⅲ承压含水层 | 806.88 | 806.91 |
| 总计 | 19 639.75 | 19 640.34 |
| 水准点 | 实测地面 沉降量/mm |
计算地面 沉降量/mm |
位置描述 | 经纬度 |
| B2 | 32.04 | 34.17 | 新安水利枢纽闸室东北角混凝土挡墙上的沉降监测钢筋 | 30.545 549°N, 120.355 277°E |
| B3 | 18.26 | 19.33 | 坛丘烧香港泵站东北角地上钢钉 | 30.534 339°N, 120.355 229°E |
| B4 | 11.93 | 10.97 | 坛丘港南闸西北角挡墙上的钢钉 | 30.524 519°N, 120.353 770°E |
| B5 | 18.41 | 16.82 | 坛丘社区坛丘村东港口泵站围墙大门门口地上钢钉 | 30.535 744°N, 120.365 266°E |
| B7 | 10.60 | 10.94 | 盛郎河闸门上最南侧的钢筋头 | 30.530 865°N, 120.382 598°E |
| B22 | 9.70 | 10.37 | 南草闸闸室东面桥西南角地上钢钉 | 30.544 820°N, 120.381 504°E |
| B24 | 22.21 | 20.64 | 革新泵站院子西面排水口混泥土上钢筋头 | 30.554 160°N, 120.375 213°E |
| B27 | 12.39 | 11.84 | 永兴桥泵站院子外地上的钢钉 | 30.543 466°N, 120.392 407°E |
| B12 | 22.15 | 23.56 | 前庄村镇南泵站闸室闸门混凝土柱上螺丝钉 | 30.524 969°N, 120.401 338°E |
| B14 | 23.46 | 21.41 | 东港村盛家港泵站闸室东南角地上螺丝钉 | 30.551 519°N, 120.394 176°E |
| B15 | 29.21 | 28.03 | 跃进村前跃泵站闸室西南角混凝土挡墙上螺丝钉 | 30.541 491°N, 120.411 388°E |
| B21 | 12.09 | 13.14 | 西白漾圩区目澜泵站闸室东面混凝土挡墙上螺丝钉 | 30.533 963°N, 120.390 705°E |

|
| 图 8 盛泽地区盛溪河地下水水位拟合情况 Fig. 8 Fitting condition of groungwater level in Shengxi River of Shengze area |
|
|

|
| 图 9 2014-09—2015-08累计地面沉降量计算值与实测值拟合图 Fig. 9 Fitting graph between calculated and measured values of accumulated land subsidence from September 2014 to August 2015 |
|
|
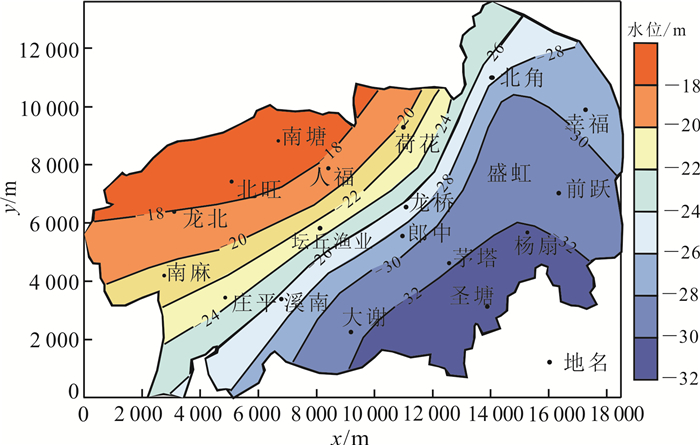
图 10为2015-08-31第Ⅰ承压含水层计算流场图,根据研究区建筑荷载和抽水井分布情况,结合图 8,可见模拟计算得到的地下水流场变化符合研究区内实际地下水流场的宏观流动变化规律。
|
| 图 10 2015-08-31研究区第Ⅰ承压含水层计算流场 Fig. 10 Computational Flow for the first confined aquifer in 2015-08-31 in the study area |
|
|
模型计算周期为2015-09-01—2030-08-31,以1 a作为1个应力期,每个应力期为1个时间步长,共15个应力期。分别模拟建筑荷载单独作用、地下水开采单独作用以及建筑荷载和地下水开采叠加情况下地面沉降趋势,根据不同情况下2015—2030年预测地面沉降量分布图,进行对比分析。
5.1 建筑荷载对地面沉降的影响在地下水禁采、地面建筑荷载单独作用下,2015-09-01—2030-08-31,盛泽地区从上至下的潜水含水层、3个承压含水层及其间的3个黏性土弱含水层共计7个层位中,除潜水含水层、第Ⅲ黏性土弱含水层部分地区水位下降外,其余含水层水位均呈现上升趋势。
停止地下水开采后,盛泽地区地下水位有一定程度的回升,但建筑荷载继续作用于各含水层,使其产生一定程度的压缩变形,从而引发地面沉降的发生。从2015-09-01—2030-08-31,盛泽地区从上至下7个层位的最大沉降量分别为27.99、190.28、87.97、74.10、27.28、24.63、9.86 mm,累计最大地面沉降量为442.11 mm。第Ⅰ黏性土弱含水层是建筑荷载引发土体变形的主压缩层,单层压缩量占比43.04%。
杨扇、龙桥、坛丘等建筑荷载较密集的地方为盛泽地区建筑荷载单独作用引发地面沉降的主要集中区域。远离建筑荷载及无建筑荷载分布的区域,地面沉降量逐渐减少,并趋近于0。此外,建筑荷载对土体变形的影响随着深度的增加也逐渐减弱。建筑荷载单独作用使盛泽地区出现漏斗状的地面沉降,以建筑物为中心向四周辐射。地面沉降量与影响范围与建筑荷载密集程度有关,建筑荷载分布越密集,地面沉降量越大,影响范围越广。建筑荷载单独作用下2015—2030年预测地面沉降量分布见图 11。

|
| 图 11 建筑荷载单独作用下2015—2030年研究区预测地面沉降量分布 Fig. 11 Prediction of land subsidence distribution from 2015 to 2030 with only building load in the study area |
|
|
假定第Ⅰ承压含水层作为开采层位,维持2014-09-01—2015-08-31单井开采量及开采布局不变。2015-09-01—2030-08-31,在不考虑建筑荷载,仅有地下水开采的情况下,盛泽地区从上至下7个层位中仅有潜水含水层、第Ⅲ承压含水层水位上升,其余层位水位均呈现下降趋势。地面沉降量最大的杨扇地区,2015—2030年地下水水位变化情况见图 12。由图 12可见, 杨扇地区2016年起地下水位进入平稳阶段,下降极其缓慢,说明地下水开采对地面沉降影响小于建筑荷载的影响。茅塔、杨扇、圣塘等纺织工厂分布较密集的地方为盛泽地区地下水开采单独作用引发的地面沉降主要集中区域,地下水开采单独作用引发的地面沉降漏斗分布范围与地下水位降落漏斗分布范围基本吻合,表现出了时间和空间的一致性。

|
| 图 12 2015—2030年杨扇地区第Ⅰ承压含水层水位变化情况 Fig. 12 Changes of water level in first confined aquifer of Yangshan from 2015 to 2030 |
|
|
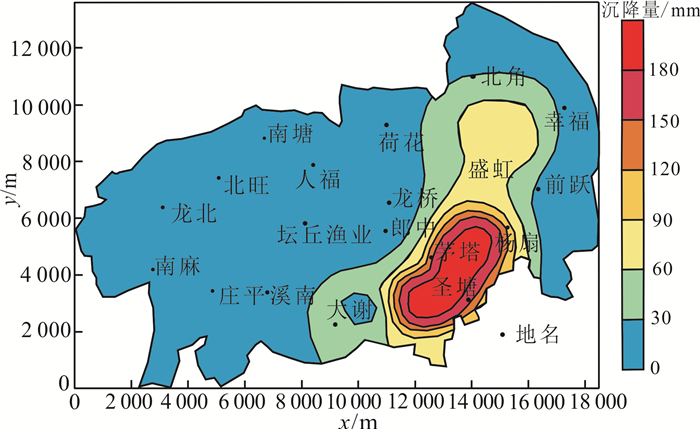
从2015-09-01—2030-08-31,茅塔社区从上至下7个层位的最大沉降量分别为9.74、32.97、101.74、28.32、8.11、4.47、2.84 mm,茅塔社区为各层最大沉降量产生区域,累计最大地面沉降量为188.19 mm。第Ⅰ承压含水层是地下水开采引发土体变形的主压缩层,单层压缩量占比54.06%。地下水开采单独作用下2015—2030年预测地面沉降量分布见图 13。
|
| 图 13 地下水开采单独作用下2015—2030年研究区预测地面沉降量分布 Fig. 13 Prediction of land subsidence distribution from 2015 to 2030 with only groundwater exploitation in the study area |
|
|
将现有建筑荷载和地下水开采的作用同时考虑,第Ⅰ承压含水层仍作为假定开采层位,保持2014-09-01—2015-08-31的假定开采布局及开采量不变。盛泽地区从上至下7个层位中仅有潜水含水层、第Ⅲ承压含水层水位上升,其余层位水位均呈现下降趋势。
从2015-09-01—2030-08-31,盛泽地区从上至下7个层位的最大沉降量分别为40.46、276.06、189.26、82.88、27.41、21.54、15.01 mm,累计最大地面沉降量为652.62 mm。第Ⅰ承压含水层及其上覆第Ⅰ黏性土弱含水层是建筑荷载和地下水开采叠加作用引发土体变形的主压缩层,二者压缩量之和占总压缩量的71.30%。
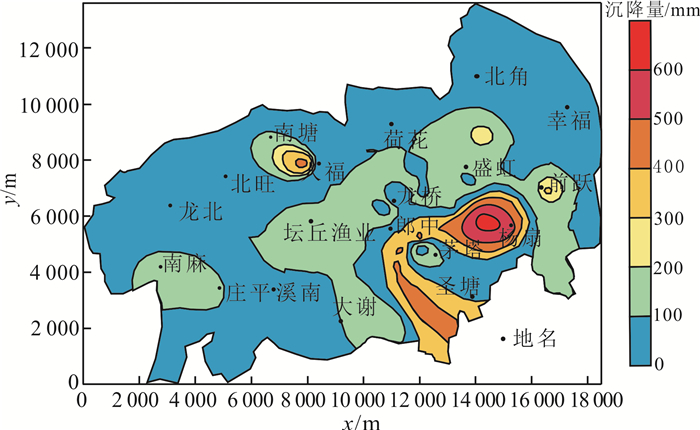
盛泽地区建筑荷载和地下水开采叠加作用下引发的地面沉降主要集中在杨扇、茅塔、圣塘等镇中南部区域,且形成了以杨扇社区为中心的沉降漏斗区,与建筑调查密集区和地下水位降落漏斗区分布一致。建筑荷载和地下水开采叠加作用下2015—2030年预测地面沉降量分布见图 14。
|
| 图 14 建筑荷载和地下水开采叠加作用下2015—2030年研究区预测地面沉降量分布 Fig. 14 Prediction of land subsidence distribution from 2015 to 2030 superposition of building load and groundwater exploitation in the study area |
|
|
盛泽部分地区不同条件下累计最大地面沉降量和地面沉降速率如表 5所示。根据表 5可知,除茅塔和圣塘外,盛泽地区建筑荷载引发的地面沉降量要大于地下水开采引发的地面沉降量,2015-09-01—2030-08-31,大部分区域建筑荷载和地下水开采对地面沉降的贡献比约为3.3:1,局部地段约为2.5:1,可知建筑荷载是造成盛泽地区地面沉降的主因,其次为地下水开采。此外,由表 5还可得出,盛泽地区建筑荷载和地下水开采单独作用下引发的地面沉降量的线性叠加之和大于二者叠加作用下引发的地面沉降量,说明建筑荷载和地下水开采叠加作用时产生地面沉降耦合效应。
| 区名 | 累计最大沉降量/mm | 最大地面沉降速率/(mm/a) | |||||||
| 建筑荷载 | 地下水开采 | 二者叠加作用 | 二者单独作用后线性叠加 | 建筑荷载 | 地下水开采 | 二者叠加作用 | 二者单独作用后线性叠加 | ||
| 杨扇 | 442.11 | 187.53 | 625.62 | 629.64 | 29.47 | 12.50 | 41.71 | 41.98 | |
| 盛虹 | 102.57 | 63.16 | 159.71 | 165.73 | 6.84 | 4.21 | 10.65 | 11.05 | |
| 茅塔 | 134.28 | 188.19 | 314.52 | 322.47 | 8.95 | 12.55 | 20.97 | 21.50 | |
| 前跃 | 246.14 | 28.47 | 272.46 | 274.61 | 16.41 | 1.90 | 18.16 | 18.31 | |
| 大谢 | 107.98 | 57.14 | 163.49 | 165.12 | 7.20 | 3.81 | 10.90 | 11.01 | |
| 北角 | 51.34 | 38.69 | 87.34 | 90.03 | 3.42 | 2.58 | 5.82 | 6.00 | |
| 圣塘 | 83.76 | 174.90 | 254.38 | 258.66 | 5.58 | 11.66 | 16.96 | 17.24 | |
以最大地面沉降速率为分析指标,由表 5可知,盛泽地区除茅塔和圣塘外,建筑荷载单独作用引发的地面沉降速率均大于地下水开采单独作用引发的地面沉降速率。建筑荷载和地下水开采单独作用下引发的地面沉降速率的线性叠加之和大于二者叠加作用下引发的地面沉降速率,这反映了建筑荷载和地下水开采叠加作用引发地面沉降时具有耦合效应。
6 结论1) 以比奥固结理论为研究基础,建立了盛泽地区建筑荷载和地下水开采与地面沉降三维全耦合模型,该模型对盛泽地区不同情况下地面沉降发展趋势的模拟结果较为准确,与实际情况相吻合。
2) 第Ⅰ黏性土弱含水层和第Ⅰ承压含水层分别为建筑荷载和地下水开采单独作用下的主压缩层,单层压缩量占比为43.04%和54.06%;第Ⅰ承压含水层及其上覆第Ⅰ黏性土弱含水层是建筑荷载和地下水开采叠加作用引发土体变形的主压缩层,二者的压缩量之和占总压缩量的71.30%。
3) 建筑荷载对盛泽地区地面沉降的影响大于地下水开采。从2015-09-01—2030-08-31,大部分区域建筑荷载和地下水开采对地面沉降的贡献比约为3.3:1,局部地段约为2.5:1。
4) 盛泽地区建筑荷载和地下水开采单独作用下引发的地面沉降量及地面沉降速率的线性叠加之和均分别大于二者叠加作用下引发的地面沉降量及地面沉降速率,叠加作用引发的地面沉降具有耦合效应。
| [1] |
赵文涛, 李亮. 苏锡常地区地面沉降机理及防治措施[J]. 中国地质灾害与防治学报, 2009, 20(1): 88-93. Zhao Wentao, Li Liang. The Mechanism of Land Subsidence and Its Prevention Measures in Suzhou-Wuxi-Changzhou Area[J]. The Chinese Journal of Geological Hazard and Control, 2009, 20(1): 88-93. DOI:10.3969/j.issn.1003-8035.2009.01.018 |
| [2] |
Shi Xiaoqing, Fang Rui, Wu Jichun, et al. Sustainable Development and Utilization of Groundwater Resources Considering Land Subsidence in Suzhou, China[J]. Engineering Geology, 2011, 124: 77-89. |
| [3] |
于军, 苏小四, 朱琳, 等. 苏锡常地区地面沉降地质结构三维可视化模型虚拟现实系统研究[J]. 吉林大学学报(地球科学版), 2007, 47(2): 393-399. Yu Jun, Su Xiaosi, Zhu Lin, et al. Research of 3D Visualized Strata Model Virtual Reality System of Land Subsidence in Suzhou-Wuxi-Changzhou Area[J]. Journal of Jilin University(Earth Sicence Edition), 2007, 47(2): 393-399. |
| [4] |
施小清, 冯志祥, 姚炳奎, 等. 苏锡常地区深层地下水禁采后土层变形特征分析[J]. 第四纪研究, 2014, 34(5): 158-167. Shi Xiaoqing, Feng Zhixiang, Yao Bingkui, et al. Analysis of Deformation Characteristics of Soil Layer After Deep Groundwater Withdrawal in Suzhou-Wuxi-Changzhou Area[J]. Quaternary Sciences, 2014, 34(5): 158-167. |
| [5] |
Zhu Juyan, Guo Haipeng. Relation Between Land Subsidence and Deep Groundwater Exploitation in Cang Zhou City[J]. Advanced Materials Research, 2013, 864/865/866/867: 2213-2217. |
| [6] |
Larson K J, Başaǧaoǧlu Mariño H M A. Prediction of Optimal Safe Groundwater Yield and Land Subsidence in the Los Banos-Kettleman City Area, California, Using a Calibrated Numerical Simulation Model[J]. Journal of Hydrology, 2001, 242(1/2): 25-43. |
| [7] |
Chen Xingxian, Luo Zujiang, Zhou Shiling. Influences of Soil Hydraulic and Mechanical Parameters on Land Subsidence and Ground Fissures Caused by Groundwater Exploitation[J]. Journal of Hydrody-namics:Series B, 2014, 26(1): 155-164. DOI:10.1016/S1001-6058(14)60018-4 |
| [8] |
孙晓涵, 彭建兵, 崔向美, 等. 山西太原盆地地裂缝与地下水开采、地面沉降关系分析[J]. 中国地质灾害与防治学报, 2016, 27(2): 91-98. Sun Xiaohan, Peng Jianbing, Cui Xiangmei, et al. Relationship Between Ground Fissures, Groundwater Exploration and Land Subsidence in Taiyuan Basin[J]. Chinese Journal of Geological Hazard and Control, 2016, 27(2): 91-98. |
| [9] |
熊小锋, 施小清, 吴剑锋, 等. 弹塑性变形条件下抽水引起的地面沉降三维数值模拟[J]. 水文地质工程地质, 2017, 44(2): 151-159. Xiong Xiaofeng, Shi Xiaoqing, Wu Jianfeng, et al. 3D Numerical Simulation of Elasto-Plastic Land Subsidence Induced by Groundwater Pumping[J]. Hydrogeology and Engineering Geology, 2017, 44(2): 151-159. |
| [10] |
Cui Zhendong, Tang Yiqun. Land Subsidence and Pore Structure of Soils Caused by the High-Rise Building Group Through Centrifuge Model Test[J]. Engineering Geology, 2010, 113(1): 1-4. |
| [11] |
赵悦文.集群建筑荷载在地面沉降中的作用研究[D].北京: 中国地质科学院, 2017. Zhao Yuewen.Study onthe Role of Cluster Land Subsidence[D].Beijing: Chinese Academy of Geological Sciences, 2017. http://cdmd.cnki.com.cn/Article/CDMD-82501-1017055344.htm |
| [12] |
付延玲, 骆祖江, 廖翔, 等. 高层建筑引发地面沉降模拟预测三维流固全耦合模型[J]. 吉林大学学报(地球科学版), 2016, 46(6): 1781-1789. Fu Yanling, Luo Zujiang, Liao Xiang, et al. A Three-Dimensional Full Coupling Model to Simulate and Predict Land Subsidence Caused by Hihg-Rise Buliding[J]. Journal of Jilin University (Earth Sicence Edition), 2016, 46(6): 1781-1789. |
| [13] |
丁德民, 马凤山, 张亚民, 等. 高层建筑物荷载与地下水开采叠加作用下的地面沉降特征[J]. 工程地质学报, 2011, 19(3): 433-439. Ding Demin, Ma Fengshan, Zhang Yamin, et al. Characteristics of Land Subsidence Due to Both High-Rise Building and Exploition of Groundwater in Urban Area[J]. Journal of Engineering Geology, 2011, 19(3): 433-439. DOI:10.3969/j.issn.1004-9665.2011.03.021 |
| [14] |
钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 水力水电出版社, 1996. Qian Jiahuan, Yin Zongze. Principle and Calculation of Geotechnics[M]. Beijing: Waterpower Press, 1996. |
| [15] |
骆祖江, 王琰, 田小伟, 等. 沧州市地下水开采与地面沉降地裂缝模拟预测[J]. 水利学报, 2013, 44(2): 198-204. Luo Zujiang, Wan Yan, Tian Xiaowei, et al. Simulating and Forecasting of Groundwater Exploitation, Land Subsidence and Ground Fissure in Cangzhou City[J]. Journal of Hydraulic Engineering, 2013, 44(2): 198-204. DOI:10.3969/j.issn.0559-9350.2013.02.011 |
| [16] |
陈崇希, 裴顺平. 地下水开采-地面沉降模型研究[J]. 水文地质工程地质, 2001, 28(2): 5-8. Chen Chongxi, Pei Shunping. Groundwater Pumping and Land Subsidence Model Research[J]. Hydrogeology and Engineering Geology, 2001, 28(2): 5-8. DOI:10.3969/j.issn.1000-3665.2001.02.002 |
| [17] |
陈兴贤, 骆祖江, 金玮泽, 等. 高层建筑荷载、地下水开采与地面沉降耦合研究[J]. 应用基础与工程科学学报, 2015, 23(2): 285-298. Chen Xingxian, Luo Zujiang, Jin Weize, et al. Study of High-Rise Building Load, Groundwater Seepage and Land Subsidengce[J]. Journal of Basic Science and Engineering, 2015, 23(2): 285-298. |
| [18] |
彭国伦. Fortan95程序设计[M]. 北京: 中国电力出版社, 2005. Peng Guolun. Fortran 95[M]. Beijing: China Electric Power Press, 2005. |


