0 引言
近年来,我国城市化进程发展很快,高层、超高层建筑逐渐增多;因高层建筑荷载应力场改变导致的地下水渗流场变化引发的区域地面沉降问题也愈来愈严重。严学新、唐益群等[1-4]进行了高层建筑群对地面沉降影响的模型试验研究,认为密集高层建筑群之间地表变形存在明显的沉降叠加效应,在高层建筑群作用下地面沉降曲线具有明显的突变特性。这不但影响了城市建筑的正常运营,也严重地制约着当地的经济发展。准确模拟预测由高层建筑荷载引起的应力场和渗流场变化,及其引发的地面沉降发生发展趋势,为地面沉降的科学防控提供依据已成为当务之急。
本文以河北省沧州市为例,基于比奥固结理论,将土体本构关系推广到黏弹塑性,并考虑了水力学及土力学参数随有效应力的动态变化,建立了沧州市高层建筑荷载、地下水渗流与土体变形三维全耦合模型,模拟预测了沧州市在地下水停采、仅加载高层建筑作用下的地面沉降发生发展趋势,为对地面沉降实现科学防控提供决策依据。
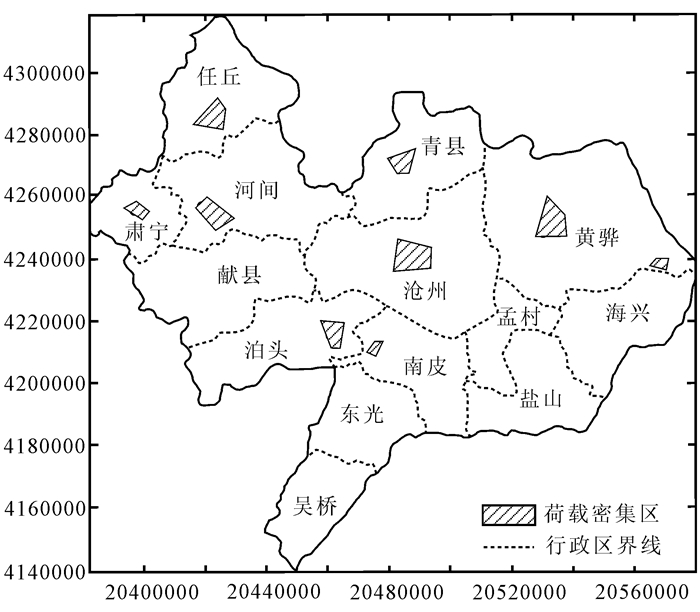
1 研究区概况沧州市地处河北省东南部,东临渤海,北靠京津,与山东半岛及辽东半岛隔海相望。地理坐标为115°42′N-117°58′N,37°28′N-38°57′N。东西长181 km,南北长165 km,总面积13 419 km2。区内第四纪沉积层厚度较大,最大达600 m左右。含水层以第四纪松散层孔隙水为主,根据沉积年代自上而下划分为:全新世第Ⅰ含水层组、晚更新世第Ⅱ含水层组、中更新世第Ⅲ含水层组、早更新世第Ⅳ含水层组。其中,第Ⅰ含水层组岩性主要为粉细砂、粉土、淤泥质亚黏土、黏土或泥炭,底面埋深为20~30 m;第Ⅱ含水层组岩性主要为粗中砂、中砂、细砂、含泥细砂、亚砂土、亚黏土,底面埋深为120~170 m;第Ⅲ含水层组岩性主要为黏土、亚黏土、粉砂、细砂、粗砂,底面埋深为250~350 m;第Ⅳ含水层组岩性主要为黏土、亚黏土、亚砂土,半固结状细砂、中细砂砾卵石层等,底面埋深为350~550 m,局部地区达600 m左右。高层建筑荷载主要分布在沧州市区、任丘市区、黄骅市区、青县市区、河间市区、泊头市区、肃宁市区、南皮市区等地,研究区高层建筑荷载分布如图 1所示。
|
| 图 1 研究区高层建筑荷载分布 Figure 1 Distribution of high-rise building load in the study area |
|
|
以平面行政区域为界,研究区面积为14 056 km2,第四纪松散沉积层深度约350 m,垂向上依次分为第Ⅰ、Ⅱ、Ⅲ、Ⅳ含水层组,在水力学和土力学上分别将其概化为非均质各向异性含水层。研究区四周在水力学上均概化为第二类流量边界;系统顶部接受大气降水及农业灌溉入渗的补给,其地下水又通过蒸发的方式排泄,因此其既是补给边界也是排泄边界;系统的底部为隔水边界。高层建筑荷载应力对土体变形压缩的影响范围有限,故在土力学上将研究区四周及底部概化为零位移边界。地下水开采作为研究区源汇项概化为大井处理,根据高层建筑荷载分布特征,分别将其概化为面荷载和点荷载处理。
3 数学模型建立与求解 3.1 比奥固结理论饱和土体(假定其土骨架变形为线弹性、微小变形,渗流符合达西定律,水不可压缩或微压缩)的三维比奥固结方程[5]如下:
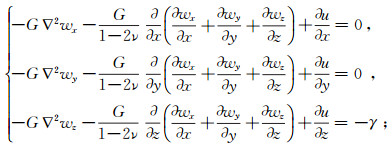 (1)
(1) 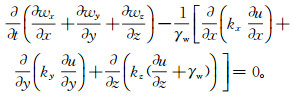 (2)
(2) 式中:G为剪切模量;ν为泊松比;wx、wy、wz分别为x、y、z方向上的位移分量;u为孔隙水压力;kx、ky、kz分别为x、y、z方向上的渗透系数;γ为土的重度;γw为水的重度;∇为拉普拉斯算子,∇2=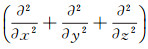
土的本构关系是土的力学特性,即应力、应变、强度、时间等关系的数学表达式。对于考虑流变特性的土体来说,其变形特征主要表现为变形的时间与应力水平有关,所显示的是具有弹性、塑性和黏滞性的黏弹塑性体。若将此类土体的总应变增量dε分为弹塑性应变增量dε ep、黏弹性应变增量dεve和黏塑性应变增量dεvp,则具有流变特性的土体中任意点在任意时刻的应变增量[6-8]为
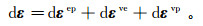 (3)
(3) 式(3)中各部分的应变增量可以由下述方法确定。
1)弹塑性应变增量
由土体的弹塑性本构模型可得
 (4)
(4) 式中:dεep=[dεx dεz dγxz]T,ε为应变,εx,εz为土体中一点在空间坐标系下沿x轴、z轴方向的应变分量,γxz为沿xz平面的应变分量;C为弹塑性柔度矩阵,C=[Dep]-1,Dep为土体的弹塑性应力应变矩阵;d σ ′=[dσx′ dσz′ dτxz]T,d σ ′为产生弹塑性应变增量所对应的有效应力增量,σx′为沿x轴方向有效应力,σz′为沿z轴方向有效应力,τxz为沿xz平面剪切应力。
2)黏弹性应变增量
由kelvin流变模型[9]E1 ε +Ke ε=σ (σ为产生黏弹性应变所对应的应力),可得应力不变时复杂应力状态下的黏弹性应变增量:
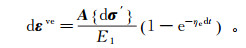 (5)
(5) 式中:E1为kelvin体黏弹性模量;Ke为黏滞系数;ηe=E1/Ke;A为应力矩阵,
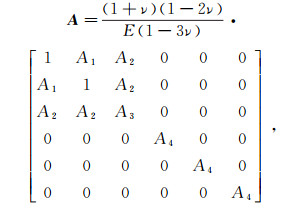
E为弹性模量,
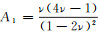
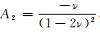
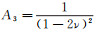
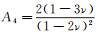
3)黏塑性应变增量
利用黏塑性法确定黏塑性应变增量,在方法中允许材料在有限“期间”内超越破坏准则(以破坏准则函数F的值大于0来表示)。在讨论土体的黏塑性应变而非塑性应变时,应变的变化率与超越量有关,即有以下关系式:
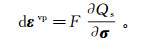 (6)
(6) 式中:F为破坏准则函数;Qs为塑性势函数;对于土体中的一点,应力σ=(σx, σy, σz, τxy, τyz, τzx)T,即有3个正应力分量σx、σy、σz和3个剪应力分量τxy、τyz、τzx。
对于摩尔-库伦材料来说,
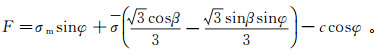
其中:φ为内摩擦角;c为黏聚力;σm=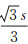

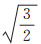

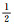

如果将黏塑性应变率与一个伪时间步相乘,就可以得到累加到下一个时间步的黏塑性应变增量,于是有
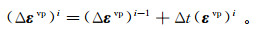 (7)
(7) 式中:i为迭代次数;Δt为时间步。对于摩尔-库伦材料,
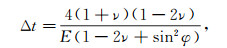 (8)
(8) 数值计算与绝对稳定的时间步和假定的破坏准则有关。
塑性势函数对应力的偏导数可以表示为
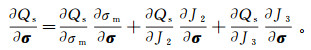 (9)
(9) 其中:J2=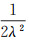
所以,应用摩尔-库伦准则的土体黏塑性应变增量可以表示为
 (10)
(10) 其中: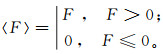
将式(4)、(5)、(10)代入式(3),可求得弹塑-黏弹-黏塑性体的应变增量[10-12]为
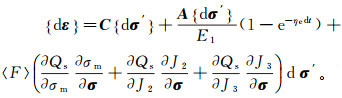 (11)
(11) 式(11)即为土体的黏弹塑性本构方程。
3.3 比奥固结有限元方程利用伽辽金加权余量法离散方程,考虑到土体的非线性特性,取Δt时间内的位移增量来代替位移,将式(1)、(2)离散成增量形式[13]:
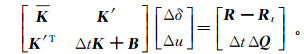 (12)
(12) 式中:K为固体刚度矩阵;K′为应力-渗流耦合项矩阵;K为渗透流量矩阵;B为自由面的积分矩阵;Δδ为结点位移增量;Δu为结点孔隙压力增量;R为等效节点荷载,当存在高层建筑荷载时,R为包括高层建筑荷载引起的附加应力值;R t为t时刻已经发生的位移所平衡了的那部分荷载;Δ Q为流量增量矩阵。
因为渗流取决于孔隙压力全量的分布,而不是取决于时间内孔隙压力增量,所以孔压要用全量的形式表示。记时刻tn和tn+1时单元节点i的孔压全量分别为ui(n)和ui(n+1),且Δui=ui(n+1)-ui(n),则式(12)可变换为
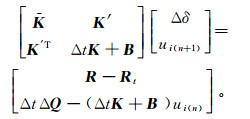 (13)
(13) 式(13)即为三维比奥固结有限元方程。
3.4 参数动态变化模型 3.4.1 孔隙度与渗透系数的非线性流固耦合问题实际上是孔隙应力消散引起土体骨架变形,导致渗透系数变化,从而影响土体的渗透性,宏观上表现为土体的固结变形。在比奥固结的假定条件下,根据孔隙度的相关定义和渗流力学Kozeny-Carman方程推得孔隙度n和渗透系数k的动态表达式[14]:
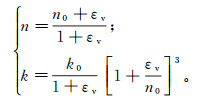 (14)
(14) 式中:n0为初始孔隙度;k0为初始渗透系数;εv为体应变,
采用邓肯-张非线性模型,将土体的本构关系推广到非线性,则本构关系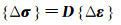
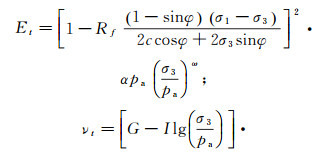 (15)
(15) 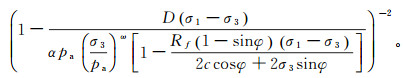 (16)
(16) 式中:Rf为破坏比,Rf=0.8;σ1为第一主应力;σ3为第三主应力;ω=0.5,为弹性模量与固结压力曲线的斜率;α为参数,可通过lgα反算得出, lgα为土体常规三轴压缩实验结果所绘曲线截距;G=0.35、I=0.04和D=3均为土体常规三轴试验常数;pa为大气压强。
3.5 定解条件 3.5.1 初始条件1)地应力初始条件:
采用土体的自重应力估算土体的初始应力:
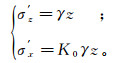 (17)
(17) 式中:σx′、σz′土体的初始水平向和垂向应力;z为计算点深度;K0为静止侧压力系数,K0=
2)位移初始条件:
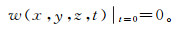 (18)
(18) 3)孔隙水压力初始条件:
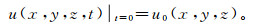 (19)
(19) 式中:u0(x, y, z)为研究区域内已知初始孔隙水压力。
3.5.2 边界条件1)孔隙水压力边界条件Γ1:
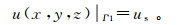 (20)
(20) 式中:us为水头边界Γ1上的已知孔隙水压力。
2)流量边界条件Γ2:
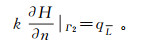 (21)
(21) 式中:H为某点处的水头;
3)自由面边界条件Γ3:
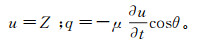 (22)
(22) 式中:μ为土体给水度;θ为自由面外法线方向与垂线的交角;q为通过自由面边界Γ3的单位面积流量;Z为自由面所在的高程。
4)位移边界条件Γ4:
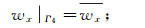
 (23)
(23) 式中:
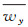
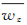
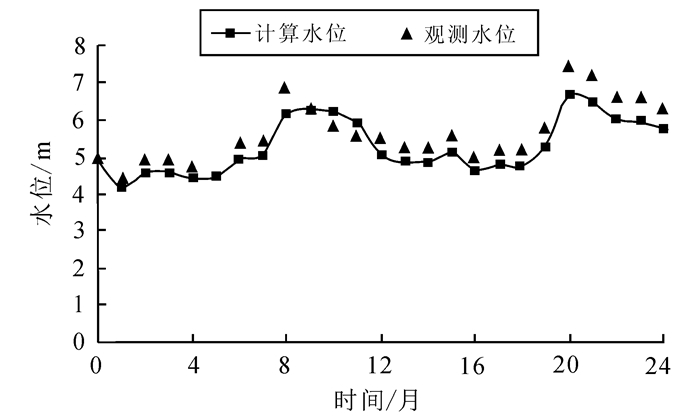
上述比奥固结有限元方程结合定解条件和水力学参数及土力学参数动态变化模型即可运用Fortran语言编制相应的有限元程序进行求解[5, 17]。
4 模型识别与验证采用八节点六面体单元对整个研究区进行离散,在平面上剖分成8 948个矩形网格单元,剖面上按地层岩性剖分成4层。单元总数为35 792个,节点总数为46 430个。研究区三维网格剖分如图 2所示。
|
| 图 2 三维网格剖分图 Figure 2 Three-dimensional mesh of simulation field |
|
|
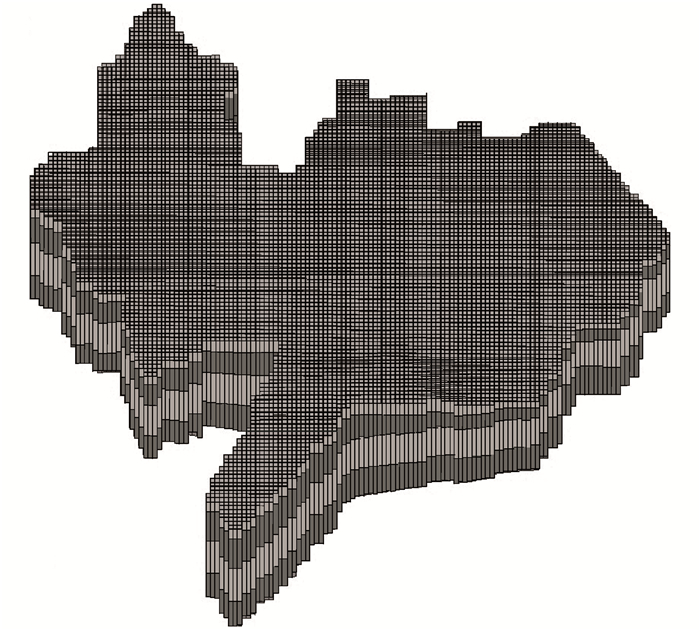
上述高层建筑物荷载、地下水渗流与土体变形三维全耦合模型必须经识别、验证后才能用于模型预测。根据观测资料,选取2008年12月31日至2010年12月31日作为模型识别、验证的时段,将其离散成24个应力期,每个月作为1个应力期,每个应力期为1个时间步长。全区共52口观测井对模型进行水位拟合,通过反演计算求得各含水层水文地质参数,整个模型共计41个参数分区,第Ⅲ含水层组参数分区和各分区的参数值详见图 3和表 1。部分观测井地下水位拟合见图 4、图 5,研究区地面沉降值拟合如图 6所示。
| 参数 分区 |
主轴方向渗透系数/(m/d) | 弹性模量/ Mpa |
泊松比 | 黏聚力/ kPa |
摩擦角/ (°) |
膨胀角/ (°) |
重度/ (kN/m3) |
有效 孔隙度 |
||
| x | y | z | ||||||||
| 1 | 11.0 | 11.0 | 0.020 00 | 23.55 | 0.46 | 6 | 23 | 0 | 20.74 | 0.345 |
| 2 | 11.0 | 11.0 | 0.001 00 | 23.54 | 0.46 | 6.2 | 20 | 0 | 20.62 | 0.346 |
| 3 | 8.5 | 8.5 | 0.001 50 | 23.55 | 0.45 | 6.0 | 20 | 0 | 20.68 | 0.345 |
| 4 | 8.0 | 8.0 | 0.090 00 | 22.54 | 0.46 | 7.0 | 19 | 0 | 20.74 | 0.345 |
| 5 | 8.0 | 8.0 | 0.002 50 | 23.53 | 0.47 | 7.5 | 20 | 0 | 20.91 | 0.344 |
| 6 | 7.0 | 7.0 | 0.000 45 | 23.49 | 0.47 | 6.0 | 19 | 0 | 20.74 | 0.341 |
| 7 | 9.0 | 9.0 | 0.000 01 | 23.48 | 0.47 | 6.5 | 21 | 0 | 20.68 | 0.340 |
| 8 | 5.0 | 5.0 | 0.015 00 | 23.51 | 0.47 | 6.0 | 18 | 0 | 20.71 | 0.342 |
| 9 | 5.0 | 5.0 | 0.048 00 | 23.51 | 0.47 | 6.0 | 20 | 0 | 20.74 | 0.340 |
| 10 | 6.0 | 6.0 | 0.015 00 | 23.50 | 0.47 | 6.2 | 20 | 0 | 20.84 | 0.339 |
| 11 | 3.0 | 3.0 | 0.001 00 | 23.14 | 0.48 | 6.0 | 17 | 0 | 20.74 | 0.334 |
| 12 | 5.0 | 5.0 | 0.000 30 | 23.22 | 0.48 | 6.0 | 20 | 0 | 21.14 | 0.329 |
| 13 | 4.0 | 4.0 | 0.000 60 | 23.02 | 0.48 | 7.0 | 18 | 0 | 21.04 | 0.328 |
| 14 | 8.0 | 8.0 | 0.012 00 | 23.30 | 0.48 | 6.5 | 20 | 0 | 21.24 | 0.330 |
|
| 图 3 第Ⅲ含水层组参数分区 Figure 3 Parameters of the third aquifer |
|
|

|
| 图 4 海卤2地下水位拟合图 Figure 4 Groundwater level fitting map of Hailu2 |
|
|
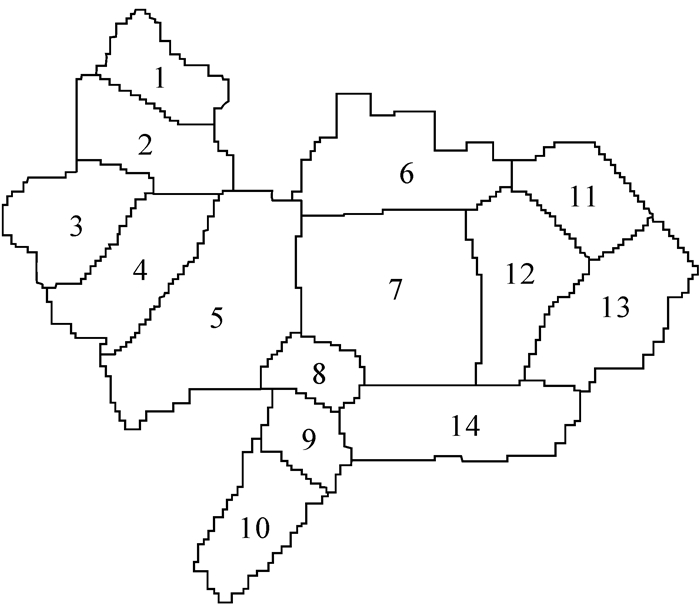
|
| 图 5 沧试7井地下水位拟合图 Figure 5 Groundwater level fitting map of Cangshi7 |
|
|
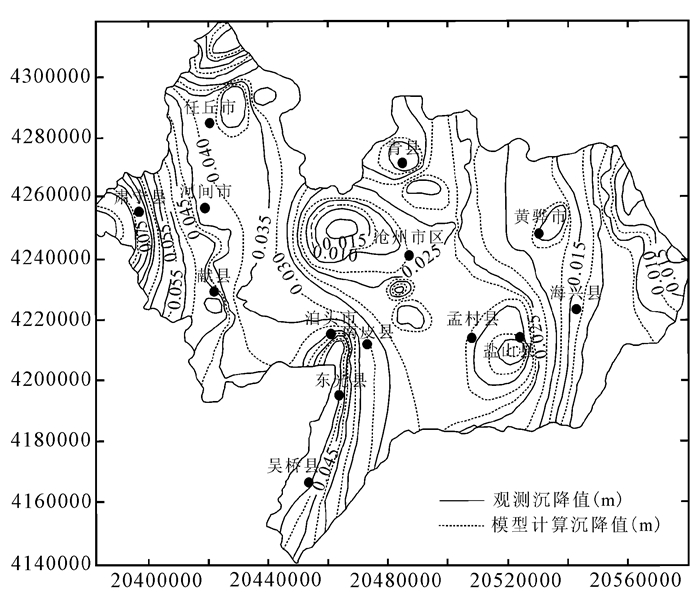
|
| 图 6 2010年地面沉降计算值与观测值对比 Figure 6 The 2010 land subsidence compared between the calculated and observed values |
|
|
根据实地调查的沧州建筑物荷载分布特征情况,结合《沧州市城市总体规划(2008-2020年)》[18],利用已经识别和验证的高层建筑物荷载、地下水渗流与土体变形三维全耦合模型,模拟预测了研究区在地下水停采、仅存在高层建筑荷载影响下,从2010年12月31日至2025年12月31日各含水层组的地下水流场变化特征和地面沉降发展趋势。模型计算得出,在单独存在高层建筑荷载的条件下,沧州地下水位降落漏斗中心水位出现回升。
以第Ⅲ含水层组为例:从2010年12月31日至2025年12月31日,任丘市最低水位由-46.65 m升至-32.81 m;河间市最低水位由-44.67 m升至-41.34 m;肃宁县最低水位由-31.23 m升至-30.53 m;献县最低水位由-42.75 m升至-41.87 m;泊头市最低水位由-46.78 m升至-46.37 m;青县最低水位由-60.70 m升至-58.03 m;南皮县最低水位由-59.81 m升至-58.31 m;东光县最低水位由-60.32 m升至-50.38 m;吴桥县最低水位由-61.42 m升至-51.48 m;孟村县最低水位由-61.58 m升至-52.10 m;盐山县最低水位由-50.13 m升至-48.01 m;黄骅市最低水位由-61.80 m升至-60.73 m;海兴县最低水位由-48.80 m升至-45.03 m;沧县最低水位由-84.62 m升至-63.23 m;沧州市区最低水位由-84.82 m升至-62.31 m。图 7为2025年12月底第III含水层组现状荷载下预测流场。
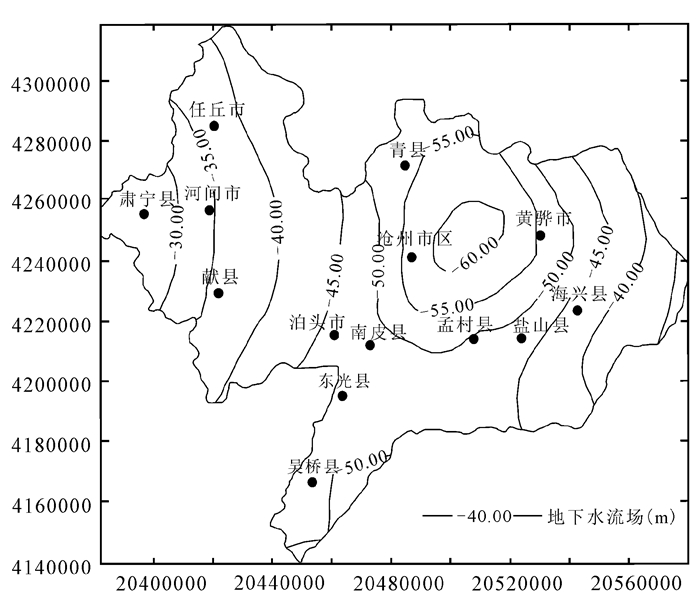
|
| 图 7 2025年12月底第Ⅲ含水层组现状荷载下预测流场 Figure 7 Forecast contour map of groundwater level in the third aquifers in late Dcember 2025 |
|
|
由于高层建筑荷载的作用,尽管地下水停采后,地下水位开始回升,但沧州市各含水层均会产生一定程度的压缩变形,沧州市由高层建筑荷载引发的最大地面沉降量为40.57 mm,最大地面沉降速率为2.70 mm/a,位于沧州市区。沧州地区各县市预测最大地面沉降量及最大沉降速率见表 2。图 8为2025年12月31日预测地面沉降等值线图。

|
| 图 8 2025年12月底预测地面沉降量等值线图 Figure 8 Forecast contour map of land subsidence in late December 2025 |
|
|
| 地区 | 最大地面沉降量/ mm |
最大沉降速率/ (mm/a) |
| 肃宁县 | 22.51 | 1.50 |
| 任丘市 | 35.16 | 2.34 |
| 河间市 | 30.42 | 2.03 |
| 献县 | 32.38 | 2.16 |
| 泊头市 | 30.21 | 2.01 |
| 青县 | 31.08 | 2.07 |
| 南皮县 | 31.50 | 2.10 |
| 东光县 | 15.53 | 1.04 |
| 吴桥县 | 16.31 | 1.09 |
| 黄骅市 | 17.61 | 1.17 |
| 盐山县 | 21.35 | 1.42 |
| 孟村县 | 21.26 | 1.42 |
| 海兴县 | 21.52 | 1.43 |
| 沧县 | 35.21 | 2.35 |
| 沧州市区 | 40.57 | 2.70 |
从计算结果可以看出,沧州市建筑物荷载引发的地面沉降中心主要集中在高层建筑荷载较密集的地方;而平面上远离高层建筑荷载的地方,地面沉降值逐渐减少并趋近于0,基本不受建筑荷载影响。由建筑物荷载引起的地面沉降呈现漏斗状,以高层建筑中心点为漏斗中心,高层建筑荷载越密集荷载越大的地方,地面沉降量越大,影响的范围也越广。
6 结论1)以比奥固结理论为基础,利用土体非线性流变理论,将比奥固结理论中的本构关系推广到黏弹塑性,同时考虑了水力学参数以及土力学参数随有效应力的动态变化建立的高层建筑荷载、地下水渗流与土体变形三维全耦合数学模型;其较好地刻画了由地面荷载增加引起的应力场和渗流场变化,从而引发地面沉降的机理,可以用来模拟预测由地面荷载增加引发的地面沉降发生发展趋势。
2)在地下水停采、仅存在高层建筑荷载作用下,预测从2010年12月31日到2025年12月31日,沧州市最大地面沉降量为40.57 mm,最大地面沉降速率为2.70 mm/a,位于沧州市区。地面沉降对应高层建筑荷载密集区呈漏斗状分布。
| [1] | 严学新, 沈国平. 上海城区建筑密度与地面沉降关系分析[J]. 水文地质工程地质, 2002, 29 (6) : 21-25. Yan Xuexin, Shen Guoping. Relationship Between Building Density and Land Subsidence in Shanghai Urban Zone[J]. Hydrogeology and Engineering Geology, 2002, 29 (6) : 21-25. |
| [2] | 唐益群, 宋寿鹏, 陈斌, 等. 不同建筑容积率下密集建筑群区地面沉降规律研究[J]. 岩石力学与工程学报, 2010, 29 (A01) : 3425-3431. Tang Yiqun, Song Shoupeng, Chen Bin, et al. Study of Land Subsidence Rule of Dense Buildings Under Different Floor Area Ratios[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29 (A01) : 3425-3431. |
| [3] | 龚士良. 上海城市建设对地面沉降的影响[J]. 中国地质灾害与防治学报, 1998, 9 (2) : 110-113. Gong Shiliang. Urban Construction's Impact on Land Subsidence in Shanghai[J]. The Chinese Journal of Geological Hazard and Control, 1998, 9 (2) : 110-113. |
| [4] | 张桂平, 洪万才. 沧州市地面沉降初探[J]. 水资源保护, 2003 (2) : 54-55. Zhang Guiping, Hong Wancai. The Study of Land Subsidence in Cangzhou[J]. Water Resources Protection, 2003 (2) : 54-55. |
| [5] | 钱家欢, 殷宗泽. 土工原理与计算 [M]. 北京: 水利水电出版社, 1996 . Qian Jiahuan, Yin Zongze. Principle and Calculation of Geotechnics [M]. Beijing: China Waterpower Press, 1996 . |
| [6] | Luo Zujiang, Zeng Feng. Finite Element Numerical Si-mulation of Land Subsidence and Groundwater Exploitation Based on Visco-Elastic-Plastic Biot's Consolidation Theory[J]. Journal of Hydrodynamics, 2011, 23 (5) : 615-624. DOI:10.1016/S1001-6058(10)60157-6 |
| [7] | 维亚诺夫C C.土力学的流变学原理[M].杜余培译.北京:科学出版社, 1987. Vianov C C. The Principle of Rheology in Soil Mec-Hanics[M]. Translated by Du Yupei. Beijing: Science Press, 1987. http://www.oalib.com/references/16933779 |
| [8] | 陈晓平, 白世伟. 软黏土地基黏弹塑性比奥固结的数值分析[J]. 岩土工程学报, 2001, 23 (4) : 481-484. Chen Xiaoping, Bai Shiwei. The Numerical Analysis of Visco-Elastic-Plastic Biot's Consolidation for Soft Clay Foundation[J]. Chinese Journal of Geotechnical Engineering, 2001, 23 (4) : 481-484. |
| [9] | 年廷凯, 余鹏程, 柳楚楠, 等. 吹填粉砂土固结蠕变试验及模型[J]. 吉林大学学报(地球科学版), 2014, 44 (3) : 918-924. Nian Tingkai, Yu Pengcheng, Liu Chunan, et al. Consolidation Creep Test an Creep Model of Dredger Fill Silty Sand[J]. Journal of Jilin University (Earth Science Edition), 2014, 44 (3) : 918-924. |
| [10] | 姚仰平, 候伟. 土的基本力学特性及其弹塑性描述[J]. 岩土力学, 2009, 30 (10) : 2881-2902. Yao Yangping, Hou Wei. Basic Mechanical Behavior of Soils and Their Elasto-Plastic Modeling[J]. Rock and Soil Mechanics, 2009, 30 (10) : 2881-2902. |
| [11] | 殷宗泽, 周建, 赵仲辉, 等. 非饱和土本构关系及变形计算[J]. 岩土工程学报, 2006, 28 (2) : 137-146. Yin Zongze, Zhou Jian, Zhao Zhonghui, et al. Constitutive Relations and Deformation Calculation for Uns-Aturated Soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28 (2) : 137-146. |
| [12] | 缪林昌. 非饱和土的本构模型研究[J]. 岩土力学, 2007, 28 (5) : 855-860. Miao Linchang. Research of Constitutive Model of Unsaturated Soil[J]. Rock and Soil Mechanics, 2007, 28 (5) : 855-860. |
| [13] | 李医民, 周凤燕. 一类三维偏微分方程边值问题的解法[J]. 江苏大学学报(自然科学版), 2004, 25 (4) : 328-331. Li Yimin, Zhou Fengyan. Solution to a Class of Boundary Value Problem of Three Dimensional Partial Differential Equation[J]. Journal of Jiangsu University (Natural Science Journal of Earth Sciences and Environment Edition), 2004, 25 (4) : 328-331. |
| [14] | 田杰, 刘先贵, 尚根华. 基于流固耦合理论的套损力学机理分析[J]. 水动力学研究与进展: A辑, 2005, 20 (2) : 221-225. Tian Jie, Liu Xiangui, Shang Genhua. Casing Damage Mechanism Based on Theory of Fluid-Solid Coupling Flow Through Underground Rock[J]. Journal of Hydrodynamics: A, 2005, 20 (2) : 221-225. |
| [15] | 陈兴贤, 骆祖江, 安晓宇, 等. 深基坑降水三维变参数非稳定渗流与地面沉降耦合模型[J]. 吉林大学学报(地球科学版), 2013, 43 (5) : 1572-1578. Chen Xingxian, Luo Zujiang, An Xiaoyu, et al. Coupling Model of Groundwater Three Dimensional Variable Parametric Non-Steady Seepage and Land-Subsidence[J]. Journal of Jilin University (Earth Science Edition), 2013, 43 (5) : 1572-1578. |
| [16] | 罗刚, 张建民. 邓肯-张模型和沈珠江双屈服面模型的改进[J]. 岩土力学, 2004, 25 (6) : 887-890. Luo Gang, Zhang Jianmin. Improvement of Duncan-Chang Nonlinear Model and Shen Zhujiang's Elastoplastic Model for Granular Soils[J]. Rock and Soil Mechanics, 2004, 25 (6) : 887-890. |
| [17] | Smith I M, Griffiths D V.有限元方法编程[M].第3版.王菘, 周坚鑫, 王来, 等译.北京:电子工业出版社, 2003. Smith I M, Griffiths D V. Programming the Finite Element Method[M].3rd ed. Translated by Wang Song, Zhou Jianxin, Wang Lai, et al. Beijing: Electronic Industry Press, 2003. |
| [18] | 沧州市城乡规划局.沧州市城市总体规划(2008-2020年)[R].沧州:沧州市城乡规划局, 2014. Urban and Rural Planning Bureau of Cangzhou City. Urban Master Planning of Cangzhou City (2008-2020)[R]. Cangzhou: Urban and Rural Planning Bureau of Cangzhou City, 2014. |


