海洋环境中波浪在传播过程往往伴随风与海流存在,三者在交互运动中存在复杂的能量传递,从而改变各自的传播特性。波浪传播发生折射导致流场的波浪要素和水质点速度分布特性发生改变。这对海工结构物的设计与安全运行造成严峻挑战。因此,准确模拟风、流与浪耦合作用下的海洋环境,探讨波浪传播的时空演化规律以及流场耦合机理具有重要现实意义。
现有针对波浪传播演化的研究方法主要包括解析法、模型试验法和数值模拟法。文献[1-2]从理论出发推导出波流同向与逆向作用下对波形参数与流速分布的影响,并从波能角度解释了波浪流速变化的原因;文献[3-4]利用多功能水池进行了波浪的缩尺模型试验,但缩尺比下傅氏数与雷诺数不匹配,试验模型与原型之间准确转换较困难,使得物理模型实验面临诸多挑战。数值模拟凭借建模灵活、不受缩尺效应影响等优势,成为了当前波浪研究的重要手段。文献[5]构建高精度数值波浪水池并开展规则波的数值模拟重点探究网格大小和时间步长等因素对波浪传播过程的影响;文献[6-7]进行了风-浪-流耦合流场的数值模拟,但均忽略了波浪水质点在入口边界速度的反复性,导致波高出现反常衰减。且尚未见相关文献对风、流与浪耦合工况下波浪传播演化机理的全面对比分析。
当波浪场存在结构物时,结构壁面附近波浪会出现反射、绕流、散射与绕射等效应,此时波浪场的运动规律会因结构发生改变。因此,研究此类问题时,须采用三维数值水池。然而,三维工况计算成本巨大,当研究重点放在波浪传播演变特性时,采用二维计算可保证计算结果正确性的同时,节省上百倍计算时间。
鉴于此,以不可压缩Navier-Stokes方程为控制方程,采用Fluent构建了二维数值水池,改进了传统边界造波法自由液面处风与水质点速度方向的一致性,并在风-浪场中进行了对比验证;在此基础上,进一步研究了各工况波浪传播的时空演化规律;最后分析了水质点水平/竖向速度、速度流线与加速度的空间分布,并提炼出流场耦合机理。
1 风-浪模拟及耦合改进 1.1 数值水池建立及网格划分在数值波浪水池建立中,将流动作为包含水和空气的两相流处理,水和空气均采用不可压缩、粘性流体假设。取水平方向为x轴(向右为正),垂直方向为y轴(向上为正),则二维Navier-Stokes连续方程为:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0 $ | (1) |
为防止波形反射干扰流场,在数值水池尾部添加动量源阻尼以实现消波[8],添加阻尼项后的动量方程为:
| $ \left\{ {\begin{array}{*{20}{r}} {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + }\\ {\lambda \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) - \mu (x)u}\\ {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial y}} + }\\ {\lambda \left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) + {g_y} - \mu (x)v}\\ {\mu (x) = \alpha \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)} \end{array}} \right. $ | (2) |
式中:u、v分别为x、y方向速度分量;P为流体压力;ρ为流体的密度;λ为动力学粘性系数;gy为重力加速度;μ(x)为消波系数;x1为消波区起始坐标;x2为消波区末端坐标;α为经验系数。
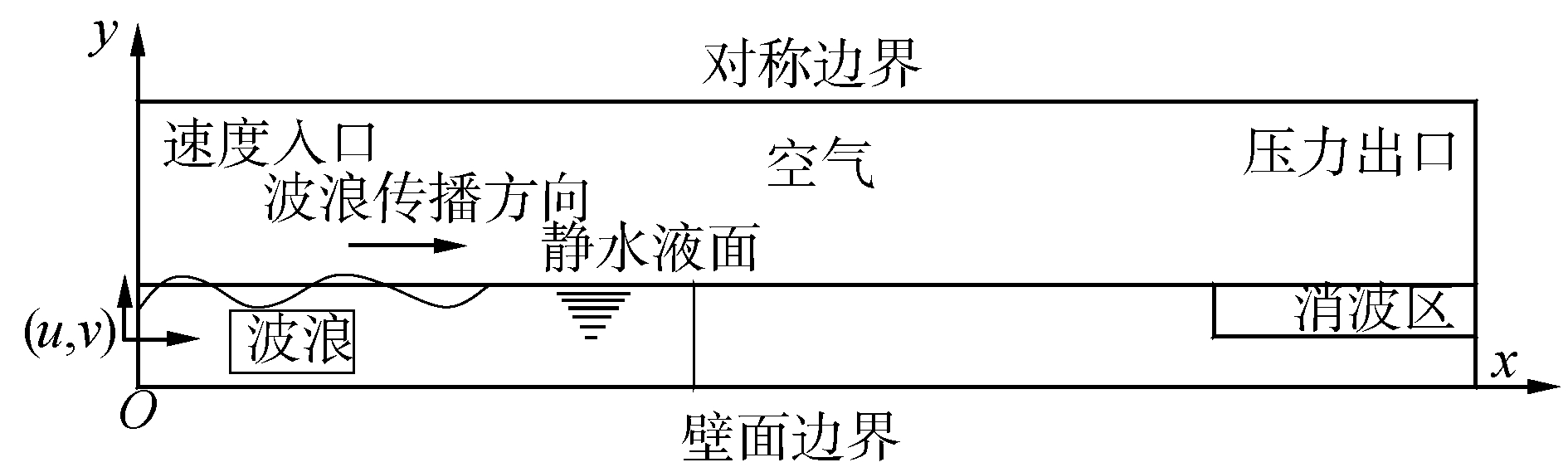
图 1给出了二维数值水池模型示意图。上部为空气,下部为水,水池尺寸为120 m×20 m (x×y),消波区尺寸为40 m×1.1 m (x×y)。边界条件设置为:左边界为入射波速度入口,右边界设为静水压力出口,上边界设为对称边界,下边界设为无滑移壁面。模拟过程采用Fluent中二维非定常分离隐式求解器,压力方程选用加权体积力格式,湍流模型选用RNG k-ε,压力方程与动量方程解耦采用压力隐式分割算法(pressure-implicit with splitting of operators, PISO)算法,空间离散采用二阶迎风格式,自由面重构方法采用改进的高分辨率界面捕获(High Resolution Interface Capturing, Modified HRIC),计算过程中采用流体体积分数法(volume of fluid, VOF) 技术对自由液面进行追踪处理,时间子步取为0.005 s。
|
Download:
|
| 图 1 波浪场数值模型 Fig. 1 Schematic diagram of numerical model of wave field | |
波浪属于典型的非定常流动问题,模拟精度对网格分辨率的依赖程度极大。表 1给出了不同网格方案下参数对比,由表可知:随着网格数的增加,波高误差逐渐减小。方案4和方案5的波高误差极小。综合考虑计算精度与效率的平衡,选取网格方案4。
| 表 1 网格独立性验证 Table 1 Grid independence verification |
图 2给出了二维数值水池网格划分示意图,波浪传播方向网格尺度取为Δx=L/120,Δy=H/5(L为波长,H为波高),自由液面附近与入口附近网格加密一倍,消波区网格尺寸逐渐稀疏,网格单元最大长宽比为4。

|
Download:
|
| 图 2 网格划分 Fig. 2 Schematic diagram of grid division | |
数值波浪的模拟方法主要有仿物理造波[9]、源项造波[10]和边界造波[11],其中仿物理造波依赖动网格技术,带来网格数量急剧上升和计算效率下降,源项造波受到造波源的扰动干扰,波形稳定性相对较差,且对波浪品质影响较高的造波源位置不好控制,而边界造波法适用于多场耦合模型同时具有较高的模拟精度和计算效率。选用的二阶Stokes波存在质点漂移和质量前移,比线性波更为接近实际海况,其速度势函数φ(x, y, t)为:
| $ \begin{array}{l} \;\;\varphi = \frac{{HL}}{{2T}}\frac{{\cosh (y + d)}}{{\sinh (kd)}}\sin (kx - \omega t) + \\ \frac{{3{\rm{ \mathsf{ π} }}{H^2}}}{{16T}}\frac{{\cosh (2k(y + d))}}{{{{\sinh }^4}(kd)}}\sin (2(kx - \omega t)) \end{array} $ | (3) |
波高方程η(x, t)为:
| $ \begin{array}{l} \eta = \frac{H}{2}\cos (kx - \omega t) + \frac{{{\rm{ \mathsf{ π} }}{H^2}}}{{8L}}\frac{{\cosh (kd)}}{{{{\sinh }^3}(kd)}}.\\ \;\;\;\;\;\cos 2(kx - \omega t)(\cosh (2kd + 2)) \end{array} $ | (4) |
式中:T、d分别为波浪的周期、静水水深;k为波数(k=2π/L);ω为波浪圆频率(ω=2π/T)。
波浪在x方向流速u:
| $ \begin{array}{l} \;\;\;\;\;\;\;u = \frac{{{\rm{ \mathsf{ π} }}H}}{T}\frac{{\cosh (k(y + d))}}{{\sinh (kd)}}\cos (kx - \omega t) + \\ 0.75\frac{{{\rm{ \mathsf{ π} }}H}}{T}\left( {\frac{{{\rm{ \mathsf{ π} }}H}}{L}} \right)\frac{{\cosh (2k(y + d))}}{{{{\sinh }^4}kd}}\cos (2(kx - \omega t)) \end{array} $ | (5) |
波浪在y方向流速v:
| $ \begin{array}{l} \;\;\;\;\;\;v = \frac{{{\rm{ \mathsf{ π} }}H}}{T}\frac{{\sinh (k(y + d))}}{{\sinh (kd)}}\sin (kx - \omega t) + \\ 0.75\frac{{{\rm{ \mathsf{ π} }}H}}{T}\left( {\frac{{{\rm{ \mathsf{ π} }}H}}{L}} \right)\frac{{\sinh 2k(y + d)}}{{{{\sinh }^4}(kd)}}\sin 2(kx - \omega t) \end{array} $ | (6) |
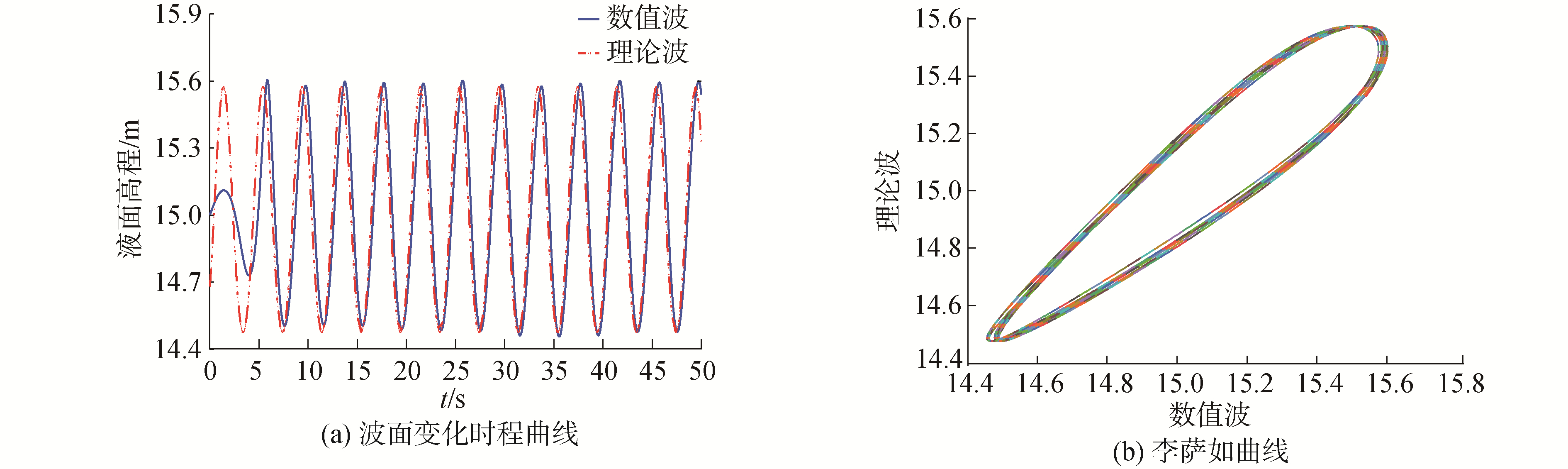
波浪的波形参数取波高1.1 m,静水深度15 m,周期4 s,波长25.5 m,波形要素满足弥散关系[12],图 3给出了数值波与理论波对比示意图,由图 3可知:数值波与理论波形锲合度较高,李萨如曲线呈现稳定、封闭的图形,验证了造波程序正确。
|
Download:
|
| 图 3 数值波与理论波对比 Fig. 3 Comparison of numerical and theoretical waves | |
波面以上的风速依《建筑结构荷载规范》[13]采用指数率梯度风进行定义,即:
| $ {U_{wx}} = {U_{10}}{\left( {\frac{{y - \eta }}{{10}}} \right)^\alpha } $ |
式中:U10为基本风速(30 m/s),α为粗糙度指数(α=0.12)。
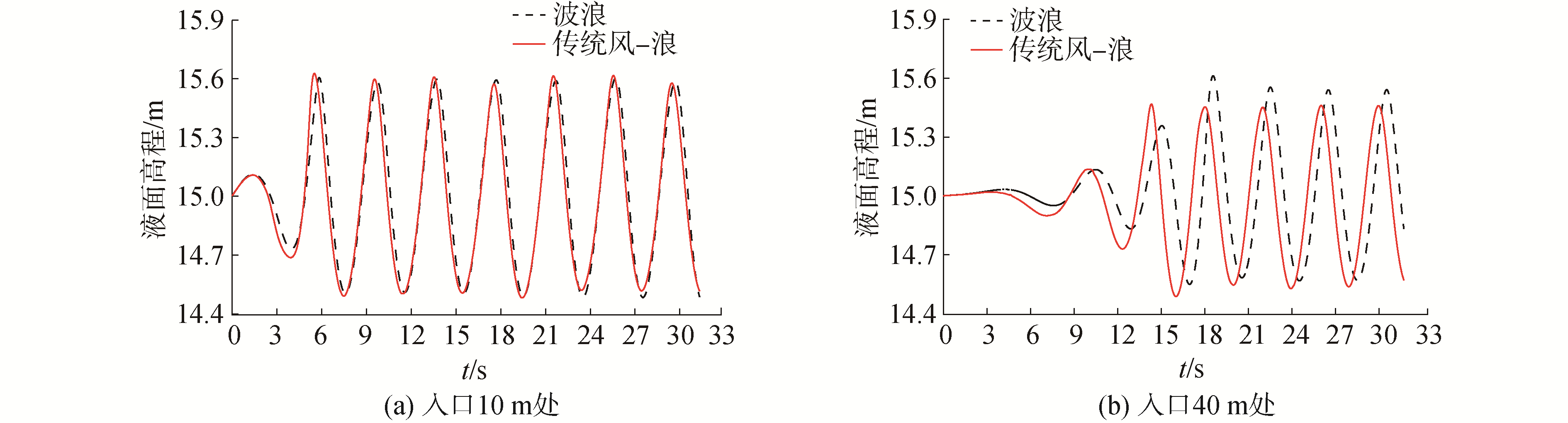
图 4给出了传统风-浪耦合场波形变化示意图,由图可得:传统风-浪耦合场在近端区域(距入口10 m)的波形与单纯波浪场基本吻合,在远端区域(距入口40 m)波峰波谷均有降低,波浪振幅略有减小。这有悖于风浪发育成长的运动过程[14],究其原因:波浪水质点的速度方向存在周期性的正负交替。倘若在造波边界波面以上区域加入定向风,当风速与波浪质点方向相同时,高速风场对波浪输入能量;反之高速风场与波浪之间存在能量抵消并导致波浪振幅衰减。
|
Download:
|
| 图 4 传统风-浪耦合场波形变化 Fig. 4 Diagram of waveform change of traditional wind-wave coupling field | |
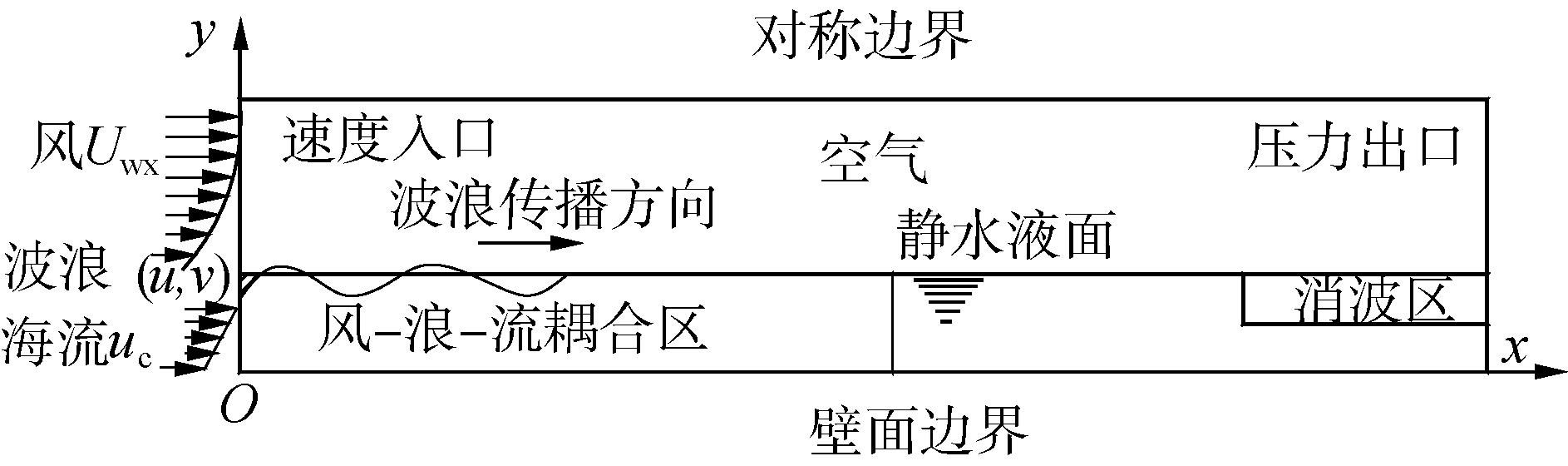
图 5给出了风-浪-流耦合场数值模型示意图,定义入口边界波面以上波峰以下区域的用户自定义函数,将波浪水质点速度化作单位矢量代入风剖面公式之中,从而保证风-浪耦合边界自由液面处风与水质点速度方向的一致性,同时可获得更好的计算收敛性。流场入口边界水平方向速度公式为:
| $ U = \left\{ {\begin{array}{*{20}{l}} {u, }&{y \le \eta }\\ {\left( {{U_{10}}\frac{u}{{|u|}}} \right){{\left( {\frac{{y - \eta }}{{10}}} \right)}^\alpha }, }&{\eta < y \le d + \frac{H}{2}}\\ {{U_{10}}{{\left( {\frac{{y - \eta }}{{10}}} \right)}^\alpha }, }&{y > d + \frac{H}{2}} \end{array}} \right. $ | (7) |
|
Download:
|
| 图 5 风-浪-流耦合场数值模型 Fig. 5 Schematic diagram of wind-wave-flow coupling field | |
海流水平速度沿水深分布剪切流定义,即:
| $ {u_c} = 0.04y $ | (8) |
水质点水平运动速度根据波流共同作用下流速场理论[15]进行定义,即:
| $ {u_x} = u{\rm{ }} + {u_c} $ | (9) |
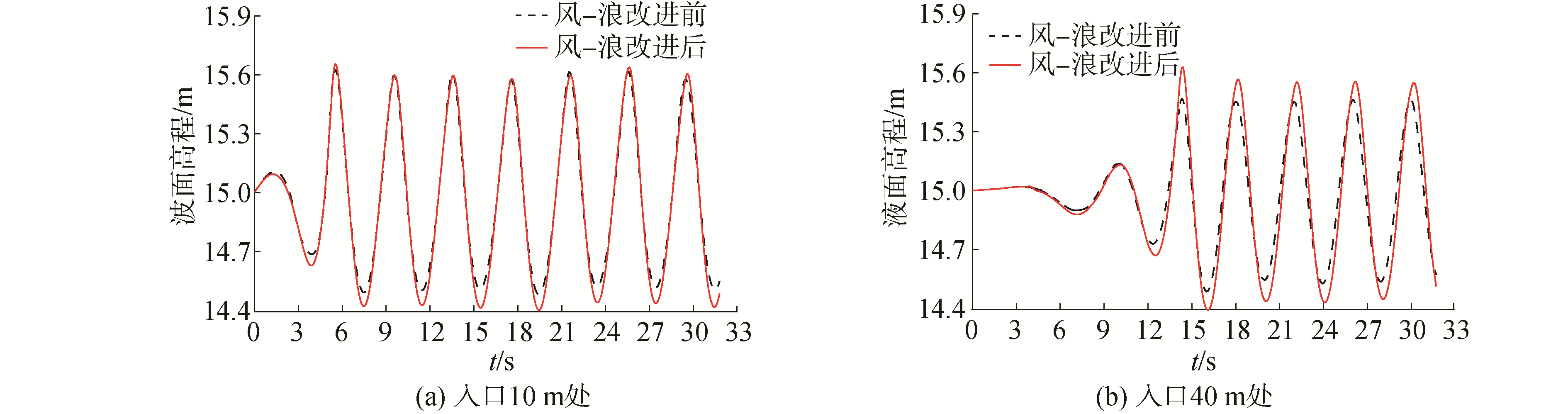
图 6给出了2种风-浪耦合模拟结果对比图,由图 6可知:改进前后风-浪耦合场波形差异明显。在近端(10 m) 波谷明显下降,波浪起伏增大约10%,伴随耦合距离增大,远端(40 m)波峰抬升、波谷下降,波浪起伏增大约20%,体现出风对波浪的能量传递。改进后的风-浪耦合场在长时间的演化计算中能够保持质量和动量守恒,未出现波形突变。
|
Download:
|
| 图 6 2种风-浪耦合技术模拟结果对比 Fig. 6 Comparison of simulation results of two wind-wave coupling technologies | |
图 7给出了风-浪耦合场压力分布示意图,对比分析可知:传统风-浪耦合场中无明显的压差区域,而改进后风-浪耦合场波峰两侧压力不对称,迎风面压力大于背风面,导致压差环境形成,风浪得以成长。同时解释了风浪发育成型的"遮拦机制"[16],也验证了风-浪耦合改进方法的有效性。

|
Download:
|
| 图 7 风-浪耦合场压力分布 Fig. 7 Schematic diagram of pressure distribution in the coupled wind-wave field | |
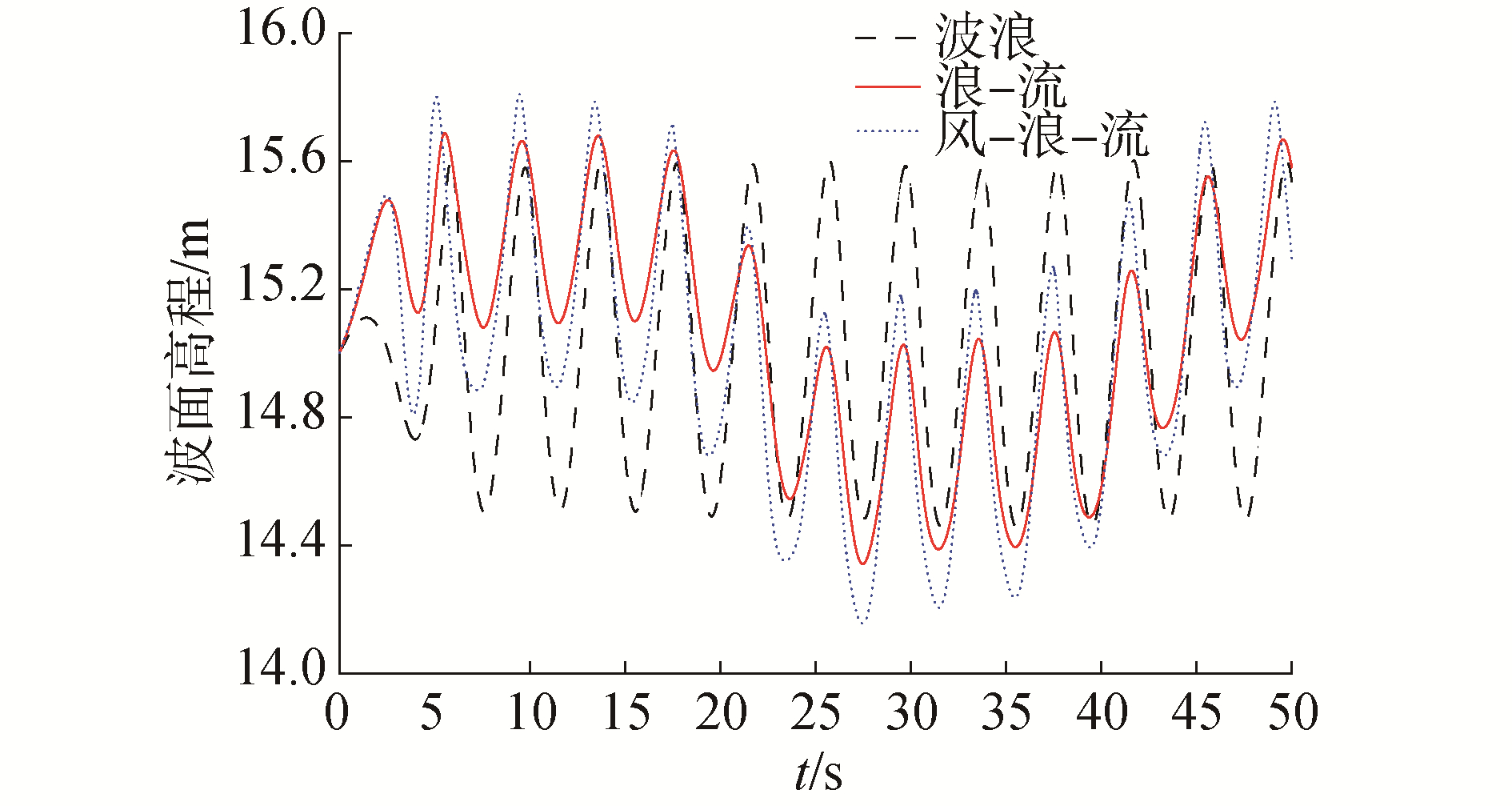
图 8给出了多耦合场中波形变化时程示意图,由图可知:海流的加入使波浪场的波高降低约50%,随流场的演化在20 s时出现波群现象,波群周期约为40 s;在波群前半周期波波谷抬升至静水液面高度处峰而后半周期波峰下沉至静水液面高度处;风对浪-流场的耦合效应相比波浪场更加显著,波群出现后会改变其上方的风结构,从而致使大量的能量由风向海浪转移[17],导致浪-流场的波峰抬升、波谷下沉,波高增大接近一倍;剪切海流和风场的加入对波浪周期的影响很小。
|
Download:
|
| 图 8 多耦合场中波形变化时程 Fig. 8 Schematic diagram of time history of waveform change in multi-coupling field | |
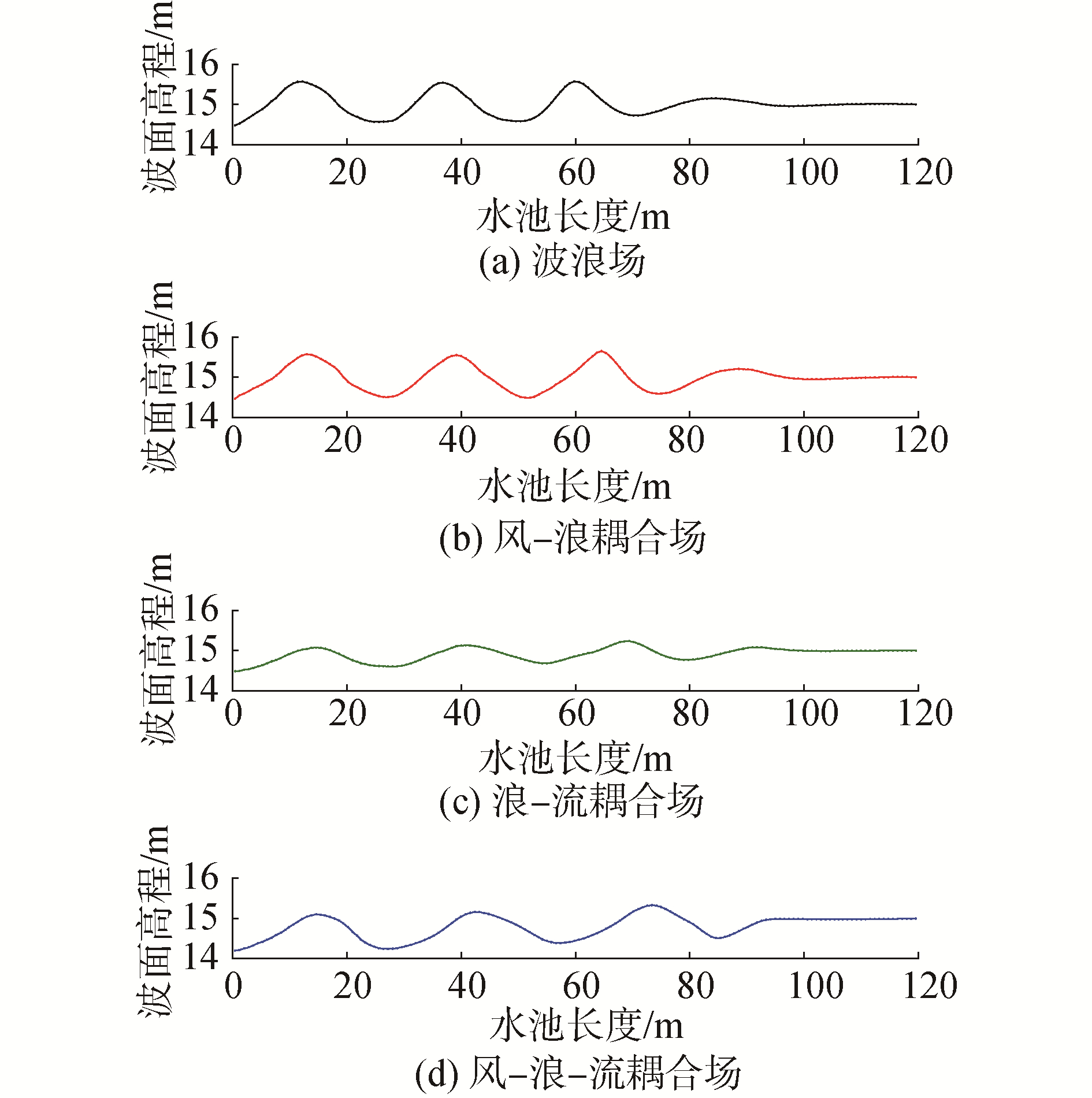
为了对比分析风、流与浪耦合作用对波浪传播空间演化规律带来的影响,图 9给出了稳定状态下(t = 26 s)各工况中波形变化空间示意图。
|
Download:
|
| 图 9 多耦合场中波形变化空间(t=26 s) Fig. 9 Spatial diagram of waveform variation in multiple coupling fields (t=26 s) | |
由图 9可知:风、流与浪的耦合作用对波浪场传播呈现显著的拉伸效应,其中海流对波长的增大效果比风更为显著,风-浪-流场中波长最长;相比波浪场,浪-流耦合场中的波面较为平缓,同时导致波长变长、波陡变小;风场加入后,波峰变得更加陡峭,波谷下沉导致二阶stokes波不再保持"谷坦"的特征;当波浪到达消波区后波高逐渐衰减,最后呈现稳定的静水状态到达出口边界。
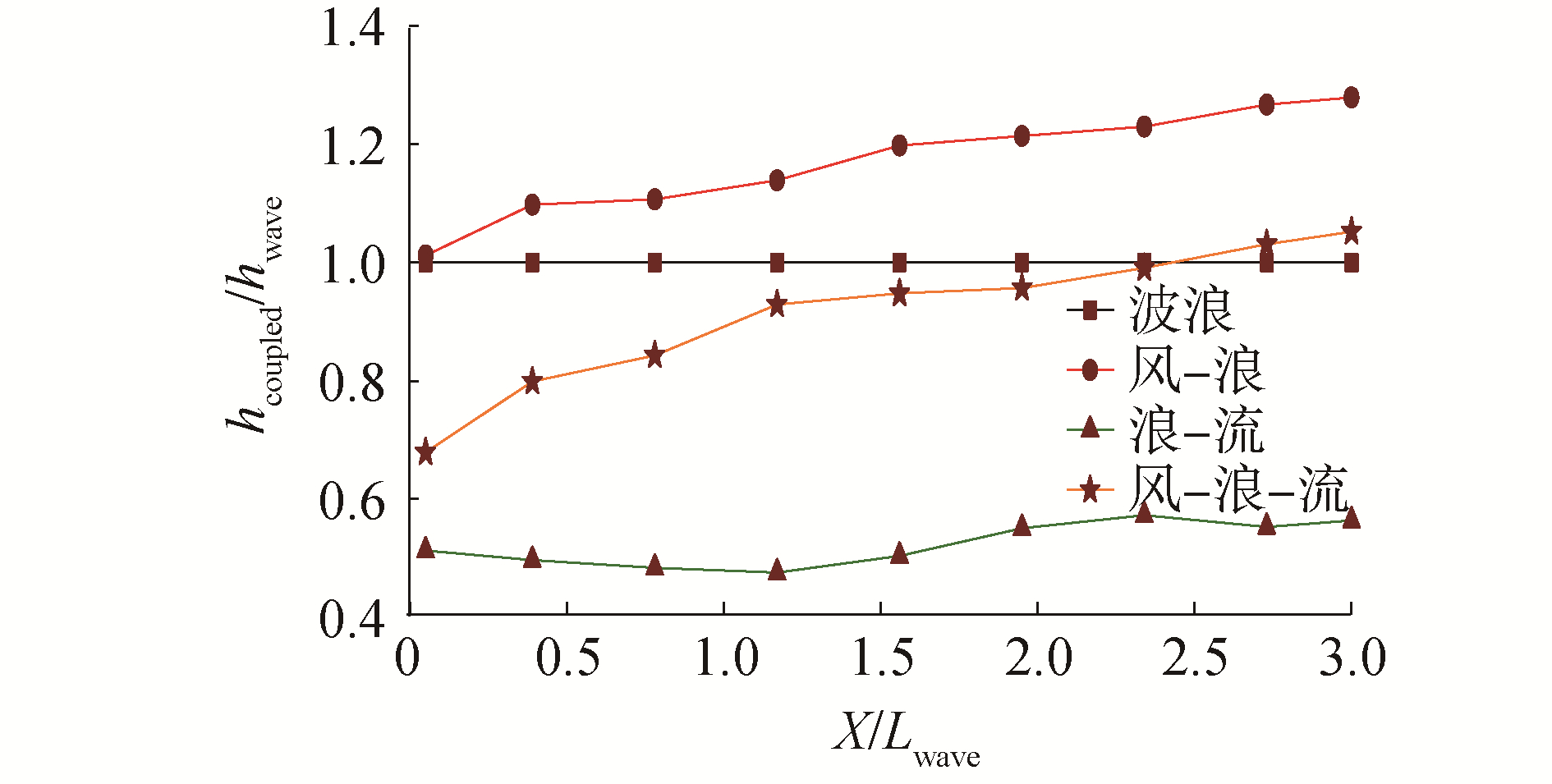
图 10给出了多耦合场作用下波高沿程变化示意图,其中横坐标为波浪传播距离与波长的比值,纵坐标为各耦合场与波浪场波高的比值。由图可知:因波群现象的存在,浪-流场波高沿程呈现出非单调的变化特性;风对波高有增益作用,且增益随耦合距离增加而增大,当耦合距离大于2倍波长时,波高增幅超过20%;风对浪-流场的波高影响更加显著,当耦合距离大于2.5倍波长时,风-浪-流场的波高超过波浪场,并呈现持续增长的趋势。
|
Download:
|
| 图 10 多耦合场作用下波高沿程变化 Fig. 10 Schematic diagram of wave height along the length of multi-coupling field | |
图 11给出了各工况流线空间分布示意图,由图可知:波浪流线由多组"U+V"型涡区间隔排序组成,其中波谷下部为顺时针旋转U型涡区,波峰下部为逆时针旋转V型涡区。风-浪场中,波面以上空气回流被正向风场破坏,风掠过波峰之后在波谷区域积聚旋转,风能向波浪能转移导致U型涡区增大、V型涡区减小,进而表现为波谷下沉;海流加入后,波浪场的涡系结构被破坏,水质点保持正向运动导致U型涡区消失,浪-流场上部流线以波峰为中心逆时针旋转,下部流线在水平方向上平直;风作用于浪-流场,波峰下部V型涡区与流线曲率同时增大,说明下部水体受风场的影响运动变得更加剧烈。

|
Download:
|
| 图 11 各工况流线空间分布 Fig. 11 Schematic diagram of spatial distribution of flow field line in each working condition | |
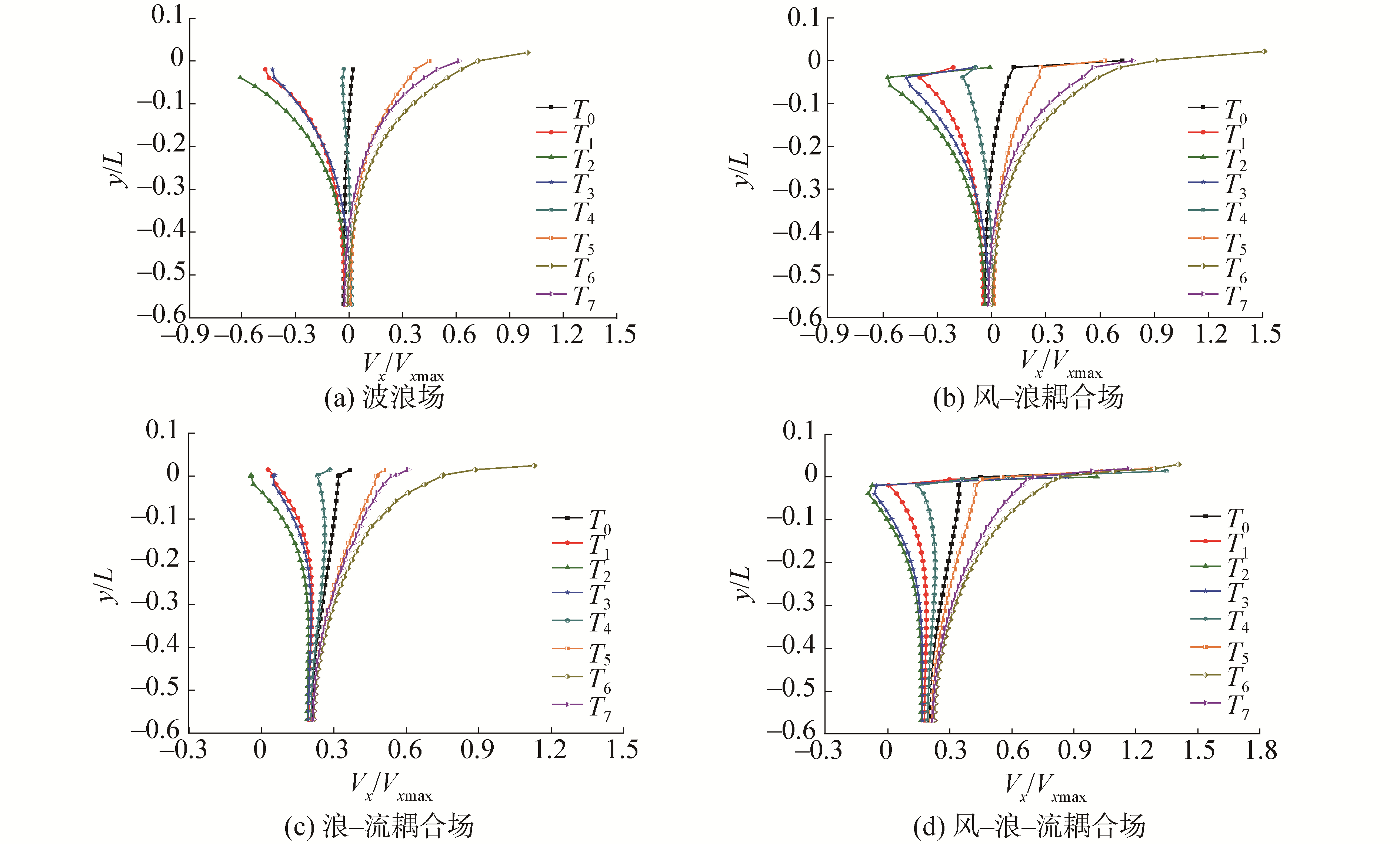
图 12给出了波浪周期相位示意图,定义波谷相位为T2、波峰相位为T6。图 13给出了距入口10 m处水质点水平速度分量沿水深变化示意图,其中Vxmax代表波浪场水质点在水平方向上速度的最大值,y/L为水深与波长的比值,由图可知:
|
Download:
|
| 图 12 波浪周期相位 Fig. 12 Schematic diagram of wave periodic phase | |
|
Download:
|
| 图 13 水质点水平速度分量沿水深变化 Fig. 13 Diagram of water quality point horizontal velocity component changing with water depth | |
1) 在波浪场中,水质点在波峰达到正方向运动速度极值,波谷达到负方向运动速度极值。各相位速度极值出现于气液交界面处,水平速度分量随水深变化曲线呈现"花束"形态。从T0开始,水质点x方向速度值大小呈现先减小后增大再减小的变化规律;
2) 剪切海流加入后,水质点的负方向速度被正流向海流抵消,水质点水平速度保持着正方向运动,导致波浪的波长显著增大;整个流场水质点的负方向速度变化幅值减小,"花束"整体向正方向倾斜并呈现"收束"形态;
3) 风场加入后,对深水区域的水质点水平速度影响不大,较大的水平风速导致气液交界面处的水平速度显著增加,速度变化曲线在近水面发生突变,波峰时刻速度增大约50%。
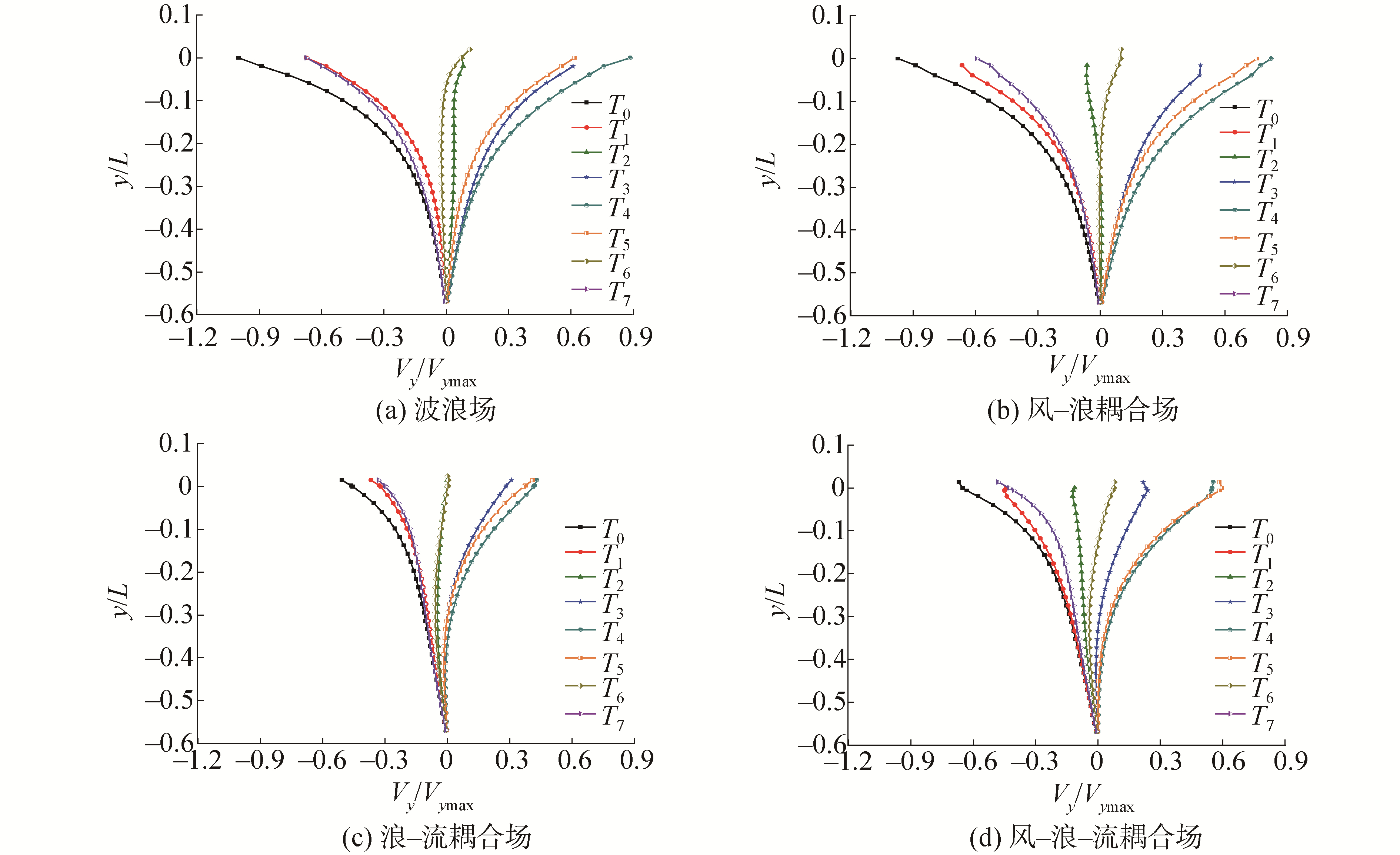
3.3 竖向速度分布图 14给出了水质点竖向速度分量沿水深变化示意图,由图可知:
|
Download:
|
| 图 14 水质点竖向速度分量沿水深变化 Fig. 14 Diagram of water quality point vertical velocity component changing with water depth | |
1) 波浪场各相位竖向的速度分布仍然呈现"花束"形态,波峰与波谷时刻水质点的竖向速度接近于零。从T0开始,水质点竖向速度数值大小呈现先增大后减小的变化规律。水质点向下运动时受到重力加速,负方向的速度变化幅值相对较大;
2) 剪切海流加入后,流场水质点正负2个方向的变化幅值均变小,"花束"曲线呈现"收束"形态,导致波浪场波高大幅度降低;
3) 风加入波浪场后,流场底部水质点的竖向运动幅度增大;风加入浪-流场后,正负2个方向的变化幅值均变大,"花束"曲线再次绽放,导致风-浪场中波高显著增大。
综合图 13和图 14可以发现:水平向和竖向的水质点沿水深增加运动幅值呈指数型递减,水平速度与竖向速度的运动规律相似且存在90°的相位差。流场上部区域水质点速度变化幅值较大,气液交界面处运动最为剧烈;水深0.5倍波长以下区域,水质点的速度变化幅值接近于0,海床附近波浪运动最为平静。
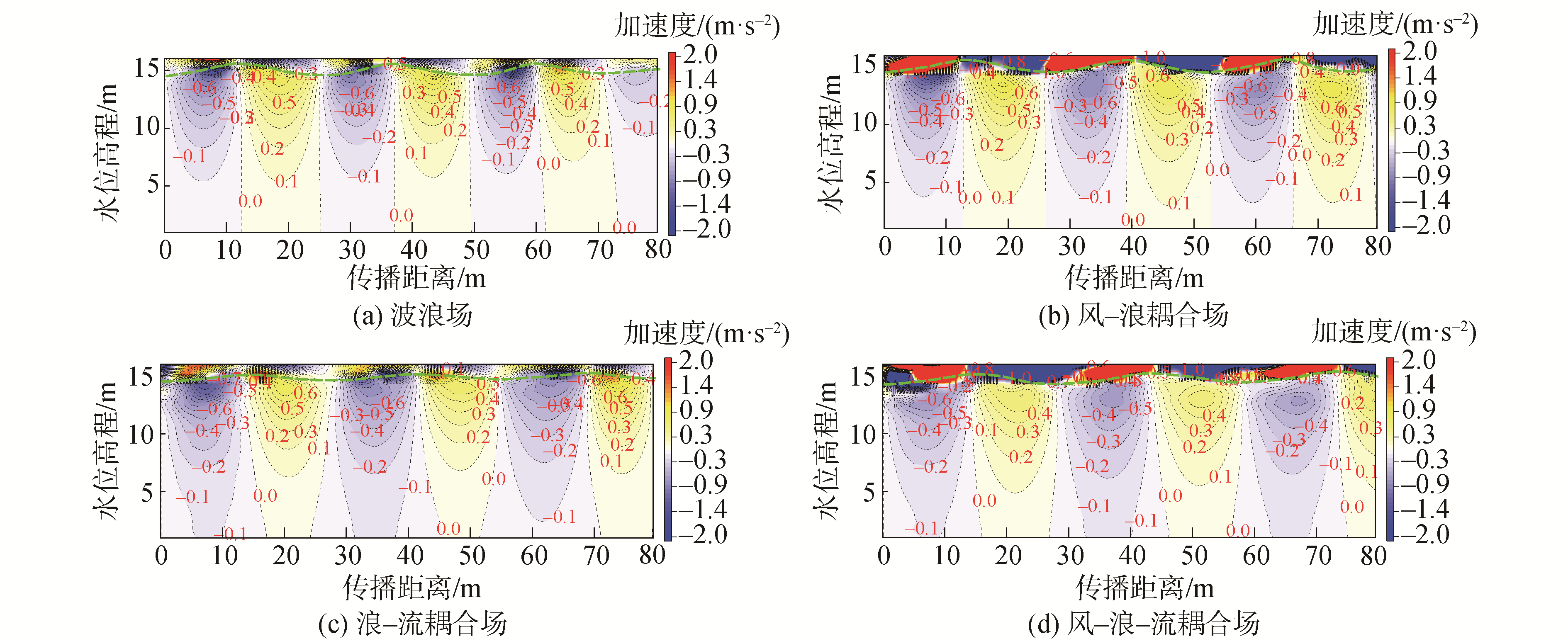
3.4 加速度分布图 15给出了各工况加速度空间分布示意图,由图可知:波浪场分别在T0、T4相位达到正向、负向加速度极值,且在波谷(T2)、波峰(T6)相位出现"加速度对流"现象;风-浪场下部水域的正负两方向加速度幅值增大,气液界面附近空气域以波峰波谷为界分为正负加速区域间隔分布,主要体现为波浪迎风面加速而背风面减速,同时导致波峰左右两侧形成压差环境。剪切海流加入后,波浪场负向加速区域增大而正向加速区域减小,且负向加速度数值明显增大;风-浪-流场相对浪-流场负向加速区域减小而正向加速区域增大。
|
Download:
|
| 图 15 各工况加速度空间分布(t=26 s) Fig. 15 Schematic diagram of spatial distribution of acceleration in each working condition (t=26 s) | |
1) 提出的改进边界风-浪耦合造波技术具有良好的稳定性和有效性,可提供风浪成长的压差环境,更好实现风对波浪场的能量传递,风对波高有增益作用,且增幅随耦合距离增加而增大;
2) 风、流与浪的耦合效果显著,海流使波浪的波长变长波陡变小,并伴随出现波群现象。风对波浪的波长影响较小,波高影响较大,风-浪耦合后波峰变得更加陡峭,波谷下沉导致二阶stokes波不再保持"谷坦"的特征;
3) 风、流与浪耦合后对流场的涡系结构影响显著,各耦合场在水平和竖向水质点的相位分布呈现花束状,速度幅值沿水深方向呈指数型变化规律;水质点分别在T2、T6相位达到水平方向速度极值和T0、T4相位达到竖向速度极值同时在T0、T4相位分别达到正向、负向加速度极值。
| [1] |
张卓, 宋志尧, 孔俊. 波流共同作用下流速垂线分布及其影响因素分析[J]. 水科学进展, 2010, 21(6): 801-807. ZHANG Zhuo, SONG Zhiyao, KONG Jun. Wave-current interaction effects on velocity profiles and influencing factor analysis[J]. Advances in water science, 2010, 21(6): 801-807. (  0) 0)
|
| [2] |
邱大洪. 波浪理论及其在工程上的应用[M]. 北京: 高等教育出版社, 1985. QIU Dahong. Wave theory and its application in engineering[M]. Beijing: Higher Education Press, 1985. (  0) 0)
|
| [3] |
CERMELLI C, AUBAULT A, RODDIER D, et al. Qualification of a semi-submersible floating foundation for multi-megawatt wind turbines[C]//Proceedings of 2010 Offshore Technology Conference. Houston, Texas, USA, 2010: 2.
(  0) 0)
|
| [4] |
GOUPEE A J, KOO B, KIMBALL R W, et al. Experimental comparison of three floating wind turbine concepts[C]//Proceedings of the ASME 31st International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, Brazil, 2012.
(  0) 0)
|
| [5] |
聂隆锋, 赵西增, 张志杭, 等. 基于VPM-THINC/QQ模型的波浪高保真模拟[J]. 力学学报, 2019, 51(4): 1043-1053. NIE Longfeng, ZHAO Xizeng, ZHANG Zhihang, et al. High-fidelity simulation of wave propagation based on VPM-THINC/QQ model[J]. Chinese journal of theoretical and applied mechanics, 2019, 51(4): 1043-1053. (  0) 0)
|
| [6] |
韦承勋. 风-浪-流联合作用场数值模拟及其对圆柱构件的作用研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. WEI Chengxun. Numerical simulation of combined actions of wind, wave and current and their actions on cylindrical component[D]. Harbin: Harbin Institute of Technology, 2012. (  0) 0)
|
| [7] |
刘红兵, 陈国明, 吕涛, 等. 海洋工程数值风-浪-流水池模拟及分析[J]. 中国海上油气, 2019, 31(6): 154-159. LIU Hongbing, CHEN Guoming, LYU Tao, et al. Ocean engineering numerical simulation and analysis in the wind-wave-current pool[J]. China offshore oil and gas, 2019, 31(6): 154-159. (  0) 0)
|
| [8] |
CHEN Qiang, KELLY D M, ZANG Jun. On the relaxation approach for wave absorption in numerical wave tanks[J]. Ocean engineering, 2019, 187: 106210. DOI:10.1016/j.oceaneng.2019.106210 (  0) 0)
|
| [9] |
赵西增, 聂隆锋, 殷铭简. 一种高保真超长黏性数值波浪水槽[J]. 水动力学研究与进展, 2020, 35(1): 23-30. ZHAO Xizeng, NIE Longfeng, YIN Mingjian. High fidelity extra-long viscosity numerical wave tank[J]. Chinese journal of hydrodynamics, 2020, 35: 23-30. (  0) 0)
|
| [10] |
马哲, 周婷, 孙家文, 等. 基于改进质量源造波方法的非线性波数值模拟[J]. 上海交通大学学报, 2020, 54(1): 60-68. MA Zhe, ZHOU Ting, SUN Jiawen, et al. Numerical simulation of nonlinear wave based on an improved source wave method[J]. Journal of Shanghai Jiao Tong University, 2020, 54(1): 60-68. (  0) 0)
|
| [11] |
TIAN Xiaojie, WANG Qingyang, LIU Guijie, et al. Numerical and experimental studies on a three-dimensional numerical wave tank[J]. IEEE access, 2018, 6: 6585-6593. DOI:10.1109/ACCESS.2018.2794064 (  0) 0)
|
| [12] |
夏国泽, 杨丹. 船舶流体力学[M]. 2版. 武汉: 华中科技大学出版社, 2018. XIA Guoze, YANG Dan. Ship fluid mechanics[M]. 2nd ed. Wuhan: Huazhong University of Science and Technology Press, 2018. (  0) 0)
|
| [13] |
中华人民共和国住房和城乡建设部. GB 50009-2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. GB 50009-2012, Load code for the design of building structures[S]. Beijing: China Building Industry Press, 2012. (  0) 0)
|
| [14] |
PHILLIPS O M. On the generation of waves by turbulent wind[J]. Journal of fluid mechanics, 1957, 2(5): 417-445. DOI:10.1017/S0022112057000233 (  0) 0)
|
| [15] |
李玉成. 波浪与水流共同作用下的流速场[J]. 海洋工程, 1983(4): 12-23. LI Yucheng. Velocity field for interacting waves and currents[J]. The ocean engineering, 1983(4): 12-23. (  0) 0)
|
| [16] |
BELCHER S E. Wave growth by non-separated sheltering[J]. European journal of mechanics-B/fluids, 1999, 18(3): 447-462. (  0) 0)
|
| [17] |
HUNT J C R, SAJJADI S G. Mechanisms and modelling of wind driven waves[J]. Procedia IUTAM, 2018, 26: 3-13. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


