2. 河海大学 港口海岸与近海工程学院, 江苏 南京 210098
2. College of Harbor, Coastal, and Offshore Engineering, Hohai University, Nanjing 210098, China
平板式结构物广泛应用于沿海和海洋工程中,但是由于海啸波的冲击和设计不当等原因,经常会导致结构物受损造成巨大的灾难。众所周知,孤立波是研究海啸波冲击海岸结构物时模拟海啸型波的理想选择,因此,孤立波作用下固定式水平板的水动力特性研究对于海洋工程结构物设计和人们的生产活动都有重要意义和参考价值。
关于板式结构物的研究已获得诸多成果,许多学者采用典型结构水平板为研究对象开展了一系列关于波浪作用于水下板[1-4]和水上板[5-7]的实验研究。近年来,随着计算流体力学(computational fluid dynamics, CFD)方法的发展,一些学者开始采用CFD的方法研究孤立波与水平板之间的相互作用问题[8-10]。You等[11]采用CIP的方法研究了孤立波作用于水下板的水动力特性。Hayatdavoodi等[12]利用Green-Naghdi方程研究了孤立波和椭圆余弦波作用下,波高、淹没深度和平板宽度等因素对水平板波散、透射系数和反射系数的影响。Seiffert等[13]基于OpenFOAM®中的interFoam求解器研究了波幅、淹没深度和水上高度等因素对平板波浪力的影响,但其研究只涉及到了3个净空高度且高度较小,和Xu等[14]一样未能全面地分析净空高度对波浪力的影响。综合来看,关于孤立波作用下水平板的水动力特性研究还不够全面,水上板的净空高度和板宽等因素对水平板的水动力特性的影响分析还不够全面,下文将根据水上板的净空高度和板宽2个因素对水平板水动力特性进行研究。
本文基于OpenFOAM®建立二维数值模型,以Navier-Stokes方程为控制方程,采用流体体积方法进行对自由面进行捕捉描述,运用waves2Foam进行造波和消波。应用该数值模型,先是对淹没固定平板上的波浪力、表面高程进行了数值验证,证明其计算波浪力结果和模拟波浪运动状态的准确性。进而对不同的板宽和相对净空比参数下平板上的波浪力和波面变化情况进行计算和分析,讨论了板宽和相对净空比对波浪力、透射系数和反射系数的影响规律。
1 数值模型描述本文求解器采用粘性流体求解器。基于OpenFOAM®多相求解器interFoam, 利用Jacobsen等[15]提出的基于松弛方法的波浪生成工具箱“waves2Foam”进行造波和消波。
1.1 控制方程数值模型采用连续性和Navier-Stokes方程求解水和空气两相流动的控制方程:
| $ \begin{gathered} \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \boldsymbol{u})=0 \end{gathered} $ | (1) |
| $ \begin{gathered} \frac{\partial \rho \boldsymbol{u}}{\partial t}+\nabla \cdot\left(\rho \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}\right)=-\nabla P-(\boldsymbol{g} \cdot \boldsymbol{x}) \nabla \rho+ \\ \nabla \cdot(\mu \nabla \boldsymbol{u})+\sigma_{t} k_{\alpha} \nabla \alpha \varphi_{\mathrm{air}} \end{gathered} $ | (2) |
式中:ρ为流动密度;
数值模型采用流体体积(VOF)方法对自由面进行捕捉。α为数值模型中每个计算单元的体积分数,其定义为:
| $ \alpha= \begin{cases}0, & \text { 气相 } \\ 0 <\alpha<1, & \text { 自由水面 } \\ 1, & \text { 液相 }\end{cases} $ | (3) |
α的分布满足对流输运方程:
| $ \frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot (\alpha \mathit{\boldsymbol{u}}) + \nabla \cdot \left[ {\alpha (1 - \alpha ){u_r}} \right] = 0 $ | (4) |
式中ur=uwater-uair表示为水和空气之间的相对速度。通过使用α,任何流体性质的空间变化φ(例如流体密度ρ和动态粘度μ)都可以通过加权平均法来表示:
| $ \varphi=\alpha \varphi_{\text {water }}+(1-\alpha) \varphi_{\text {air }} $ | (5) |
使用Jacobsen等[15]提出的“waves2Foam”工具箱在入口边界处进行造波,速度设置为入射波波速,波速为零。在入口和出口边界设置了2个松弛区,分别用来吸收反射波和透射波。在水平板的上部,边界条件设置为“大气”;水平板的底部和水槽箱的边界条件设置为“无滑移”;本模型为二维模型、三维墙上的边界条件设置为“空”。
基于有限体积法求解控制方程(1) 和(2) 以及对流输运方程(4),方程在每个时间步求解时,平板上的波浪力表示为:
| $ \boldsymbol{F}=\int_{\mathit{\Omega}}\left[P \boldsymbol{n}+\mu\left(\partial \boldsymbol{u}_{\tau} / \partial \boldsymbol{n}\right)\right] \mathrm{d} s $ | (6) |
式中:F表示波浪力的矢量;uτ表示切线速度分量;n表示单位法向矢量。
2 数值水槽图 1展示了本研究中使用的2-D数值波浪水槽的示意图,坐标系的定义、浪高仪的位置不按比例。波浪水槽长9 m,高0.292 m,宽(w) 0.149 m,坐标系原点位于左侧松弛消波区边界的端点位置。x轴定义为波浪传播的方向,z轴定义为垂直向上的方向,y方向的水槽厚度对应于一个单元。水平板放在波浪水槽的中间, 板长L=0.149 m,宽B=0.305 m,高d=0.012 7 m。水深定义为h=0.086 m,波高定义为A=0.025 m,ζ为自由面高程。
|
Download:
|
| 图 1 数值波浪水槽 Fig. 1 Sketch of numerical wave tank | |
实验进行了5组模拟,水平板板宽分别设置为B=0.305,0.400,0.500,0.600,0.800 m,每组的数值模拟中都考虑了6种相对净空比z*/h= 0,0.05,0.1,0.139,0.213,0.287(z*表示净空高度,即水平板的下表面到静水面的距离,z*/h=0时板下表面与静水面相平齐,z*/h = 0.139时板的上表面与波峰相平齐,z*/h = 0.287时板的下表面与波峰相平齐),共30个算例。设置了3个浪高仪,用G1~G3用来记录自由面高程,分别位于x=2.010,3.535,4.75 m处。在波浪水槽的入出口边界分别设置了2、2.245 m长的松弛区吸收反射波和入射波。
使用OpenFOAM®提供的内置网格生成程序“blockMesh”生成网格,B=0.305 m,z*/h=0工况下一个典型的计算网格如图 2所示,平板四周的网格区域分别对应水、空气两相环境。本数值实验采用非均匀网格,为了节省计算时间和准确地捕捉水和空气之间的界面,在平板周围使用分辨率更高的细网格。

|
Download:
|
| 图 2 计算域中典型网格的侧视图 Fig. 2 Side view of typical meshes in the computational domain | |
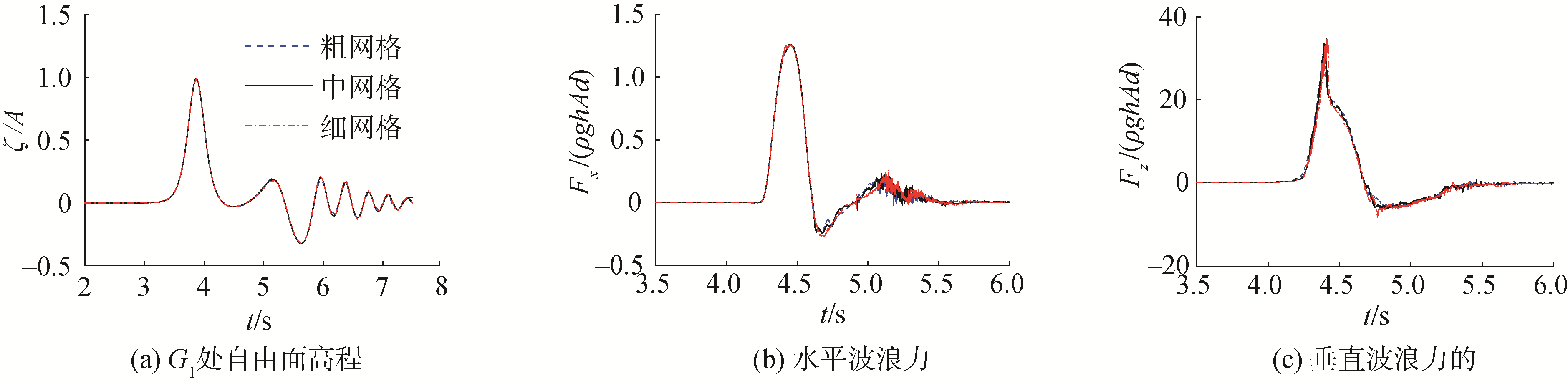
为了检验数值结果对网格分辨率的准确性,使用了3种不同分辨率的网格(即粗网格、中网格和细网格)进行数值模拟结果对比,网格单元数分别为164 510、370 215和658 040(见表 1)。计算的参数:h=0.086 m,A=0.025 m,B=0.305 m,z*/h=0.1。图 3显示了入射波作用于平板引起的G1处自由面变化和波浪力的时间历程情况。
| 表 1 网格参数 Table 1 Mesh parameters |
|
Download:
|
| 图 3 h=0.086 m,A=0.025 m,B=0.305 m,z*/h=0.1, 不同网格分辨率下时间历程 Fig. 3 h=0.086 m, A=0.025 m, B=0.305 m, z*/h= 0.1 time history at different grid resolutions | |
由图 3可以看出,3种不同网格分辨率下得到的自由表面高程、水平波浪力和垂直波浪力的时间历程曲线几乎吻合。考虑到与粗网格、细网格相比,中网格能更加精确地模拟入射波所引的波场和节省数据计算的时间,所以接下来的算例中均采用中网格的网格配置进行计算。
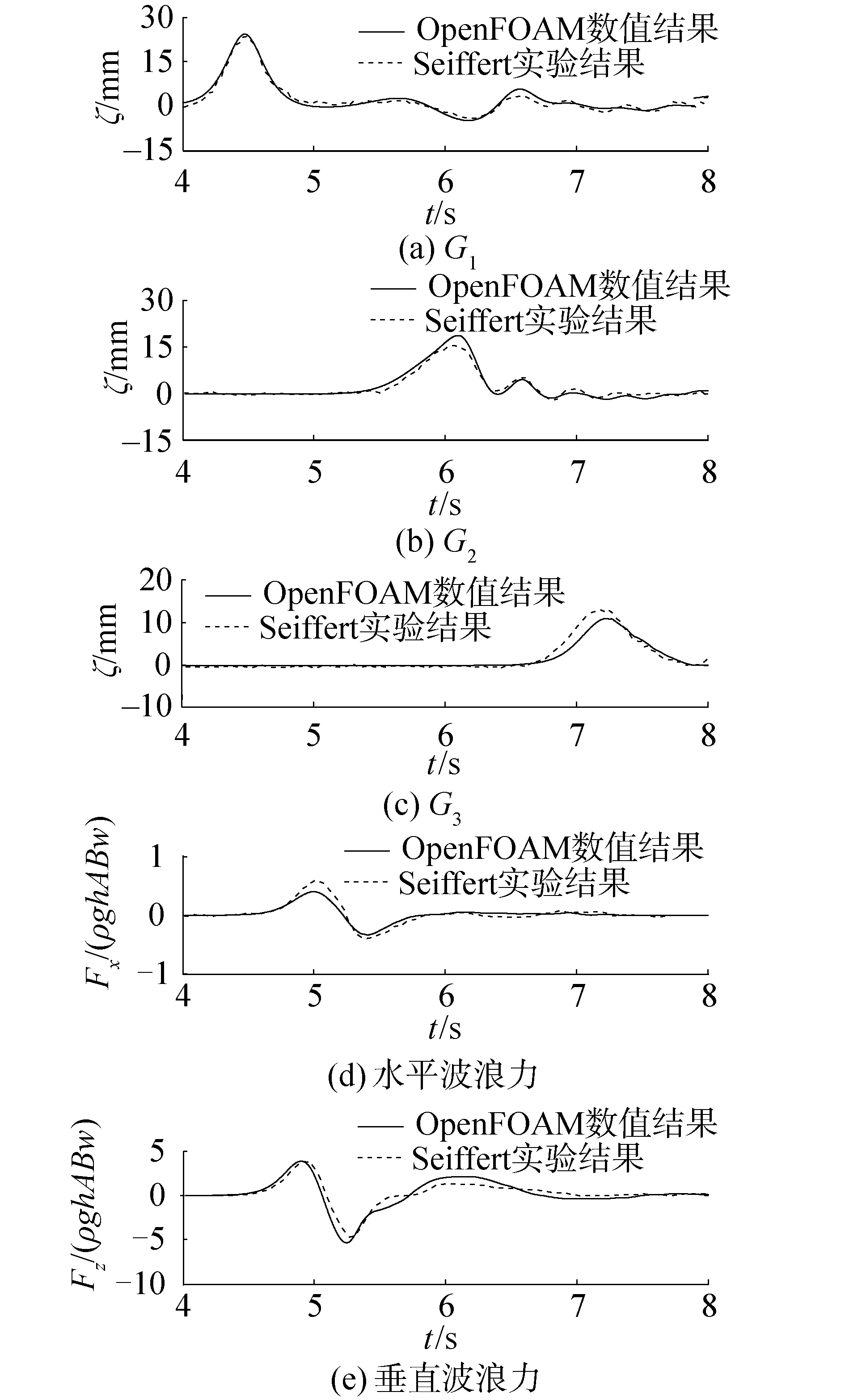
3 数值验证为了验证本文数值模型的可靠性以及得到的数值结果的准确性,将OpenFOAM®得到的计算结果与Seiffert等[13]的实验结果进行了比较。其实验模型与本文的数值模型大致相同(见图 1),板长L=0.149 m,宽B=0.305 m,高d=0.012 7 m,水深h=0.086 m,波高A=0.025 m,改变了水平板的位置,Seiffert等[13]实验模型的水平板位于水下z/h=0.2处(z/h表示水平板的淹没比,z表示水平板的上表面距静水面的垂直距离)。
通过图 4可以看到,通过OpenFOAM®模拟得到的G1~G3处的自由面变化情况、水平波浪力Fx和垂直波浪力Fz的时间历程情况与Seiffert等[13]得到的实验结果大致吻合。验证了本文数值模型对模拟孤立波作用于固定水平板得到的波面变化情况和提取波浪力的准确性。
|
Download:
|
| 图 4 OpenFOAM®计算和实验数据得到的自由面高程、波浪力的比较 Fig. 4 Comparison of free surface elevation and wave force from OpenFOAM® calculation and experimental data | |
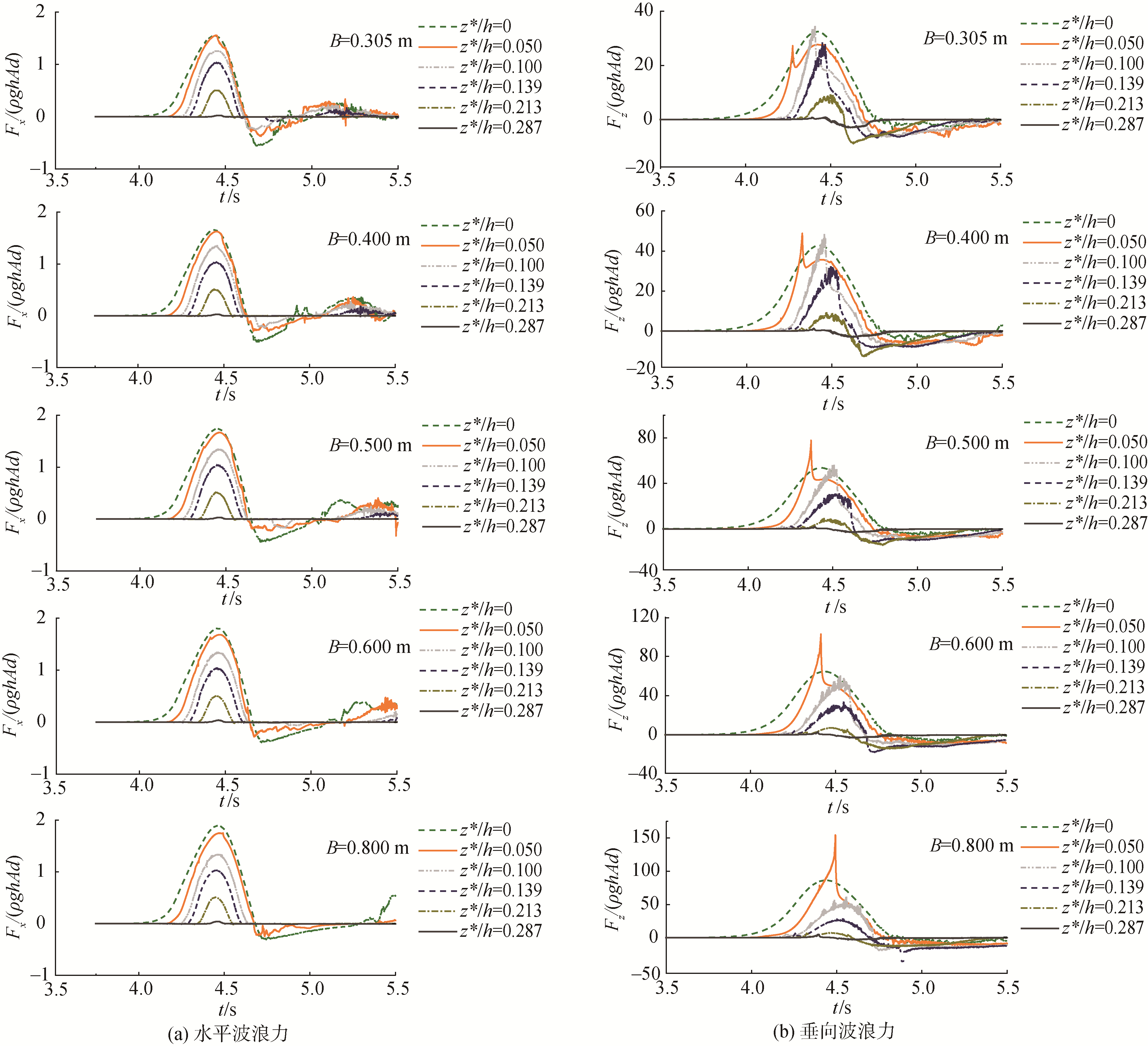
图 5展示了0.305≤B≤0.8 m, 0≤z*/h≤0.287工况下,孤立波作用于水平板上的水平波浪力和垂向波浪力的时间历程。对于水平波浪力Fx的时间序列(图 5(a)),图中的正值和负值分别指沿x轴正向和负向,随着板宽、相对净空比的增加, 水平波浪力在曲线形状上没有较为明显的差异, 随着孤立波的作用, 波浪力先增大后减小,后期由于波浪完整越过水平板,波板之间相互作用复杂,残余波的振荡引起板的力振荡。对于垂直波浪力Fz,随着相对净空比的增加,垂向波浪力的时间历程越来越复杂,垂向正向力明显大于反向力。从图 5(b)可以清楚地看到,z*/h=0.05工况下的垂向波浪力Fz较为明显地大于其他相对净空比状态下的力,结合图 6可知是由于其净空高度的原因,z*/h=0.05工况下的平板高于静水面,其下表面亦能全部受到波浪的作用,而当平板继续升高,相对净空比z*/h=0.1时,由于平板过高,波浪在上升的过程中发生破碎,能量逐渐减小,导致板的下表面不能全部受到波浪作用,当平板净空继续增大时,垂向波浪力变得更小;其垂向波浪力亦受板宽的影响,随着板宽的增加而增大。针对垂向波浪力Fz复杂的时间变化序列,下面将根据B=0.305 m,0≤z*/h≤0.213工况下的波浪力时间历程图(见图 7)进行具体描述。
|
Download:
|
| 图 5 B=0.305~0.800 m,z*/h=0~0.287工况下的波浪力时间历程图 Fig. 5 Time series of wave forces with B=0.305~0.800 m, z*/h=0~0.287 | |

|
Download:
|
| 图 6 B=0.8 m,z*/h=0,0.05和0.1垂向波浪力到达最大值时板周围的自由面情况 Fig. 6 Free surface around the plate when B=0.8 m, z*/h=0, 0.05 and 0.1 vertical wave force reach the maximum value | |

|
Download:
|
| 图 7 B=0.305 m,z*/h=0~0.13垂向波浪力的时间历程图 Fig. 7 Time series of vertical wave force with B=0.305 m, z*/h=0~0.213 | |
由图 7(a)可以看出,在整个阶段垂向波浪力只出现了一次正向极值,并随着孤立波的运动先增大后减小,后期由于残余波振荡的缘故,导致出现了时间较长的波浪力震荡现象。通过图 7可知,随着平板的相对净空比增大,垂向波浪力的时间历程阶段开始发生了较为明显的改变。图 7 (b)显示了平板开始离开静水面,在孤立波作用于平板的过程中发生了2次砰击,首先是当孤立波的波峰接近平板左侧时波浪对平板下端的冲击作用得到了一个极值,之后波浪主体发生破碎,一部分波浪在平板下方继续冲击向前,并向平板的下表面作用垂直向上的力,另一部分波浪受到平板左侧部分阻挡向上激起,落下后作用于平板的上表面,结合平板下表面所受的垂直向上的波浪力,再次得到了一个极值,从而得到了垂向波浪力的时间历程上具有2个正向极值的特点。这种垂向波浪力的变化情况也被Ren等[16]、Cuomo[17]提到过。随着平板的相对净空比继续增加(图 7(c)),当发生砰击取得第1次极值之后,波浪发生破碎,能量减少,不足以支撑板下的波浪继续作用于板的下表面,波浪逐渐削减,垂向波浪力逐渐减小,不能得到较为明显的第2次垂向极值波浪力。当平板的相对净空比继续增加,平板所受的垂向波浪力就变得更小(图 7(d))。
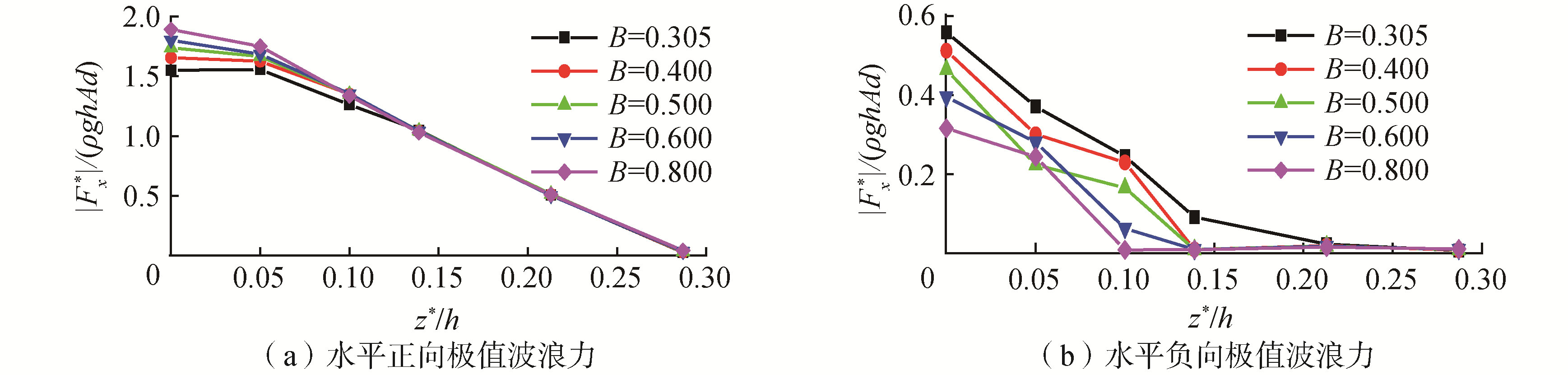
4.2 极值波浪力通过图 8可以看到,其正、负向水平极值波浪力整体呈规则性变化,正水平极值波浪力Fx*、负水平极值波浪力Fz*(后文提到的极值波浪力皆为极大值波浪力)随着相对净空比的增加皆呈逐渐减小的趋势,这是由于在运动过程中,波浪发生破碎,能量减少,极值波浪力也随之逐渐减小,并且在整个过程中正极值波浪力始终大于负极值波浪力。当平板相对净空比z*/h= 0时,平板的下表面贴于静水面,此时平板的左右面都能够最大程度上受到波浪作用,水平极值波浪力达到最大,随着净空高度的增加,平板所受的波浪作用越来越小,极值波浪力也随之逐渐减小。当平板处于0.139≤z*/h≤ 0.287时,此系列工况为波浪与平板接触的极限相对净空比(此时波浪的波峰处于平板下表面到上表面之间),由于净空高度板过高,导致只有平板的左面能受到波浪作用,则其负水平极值波浪力接近为0(图 8(b));板宽对水平极值波浪力的影响也随着相对净空比的增加逐渐减弱,最后趋于集中。
|
Download:
|
| 图 8 不同板宽条件下,正、负水平极值波浪力相对于相对净空比的变化 Fig. 8 Variation of positive and negative horizontal extreme wave forces with respect to relative clearance ratio under different plate width conditions | |
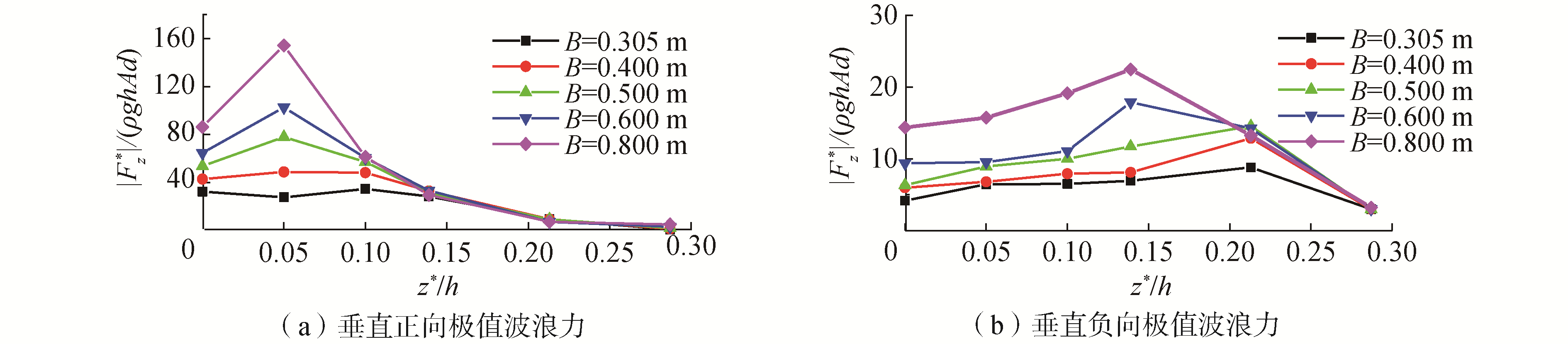
图 9显示了多组板宽条件下,正、负垂向极值波浪力相对于相对净空比的变化情况。由图 9 (a)可得知,随着相对净空比的增加,正垂向极值波浪力呈先增大后减小的趋势,0.5≤B≤0.8,z*/h=0.05工况下的平板,其正垂向极值波浪力达到最大,为整体变化趋势的转折点,并且随着板宽的增加这种现象更加明显,结合图 5和图 6自由面高程图了解到是由于净空高度和板宽的原因导致。当相对净空比一定时,正垂向极值波浪力随着板宽的增加而逐渐增加;当相对净空比大于0.139时(即波峰处于平板下表面到上表面之间),板宽变化对正垂向极值波浪力的影响逐渐减弱最后趋于集中,此情况与对正水平极值波浪力的影响一致(见图 8(a))。随着相对净空比的增加,负垂向极值波浪力亦呈先增大后减小的趋势(见图 9(b))。比较图 9 (a)和(b)可以发现正垂向极值波浪力均大于负极值波浪力,主要是因为波浪在作用于平板时,一部分波浪向上涌起发生破碎,导致负向的极值波浪力小于正向的极值波浪力。
|
Download:
|
| 图 9 不同板宽条件下,正、负垂向极值波浪力相对于相对净空比的变化 Fig. 9 Variation of wave forces with respect to the relative clearance ratio of positive and negative vertical extremum under different plate width conditions | |
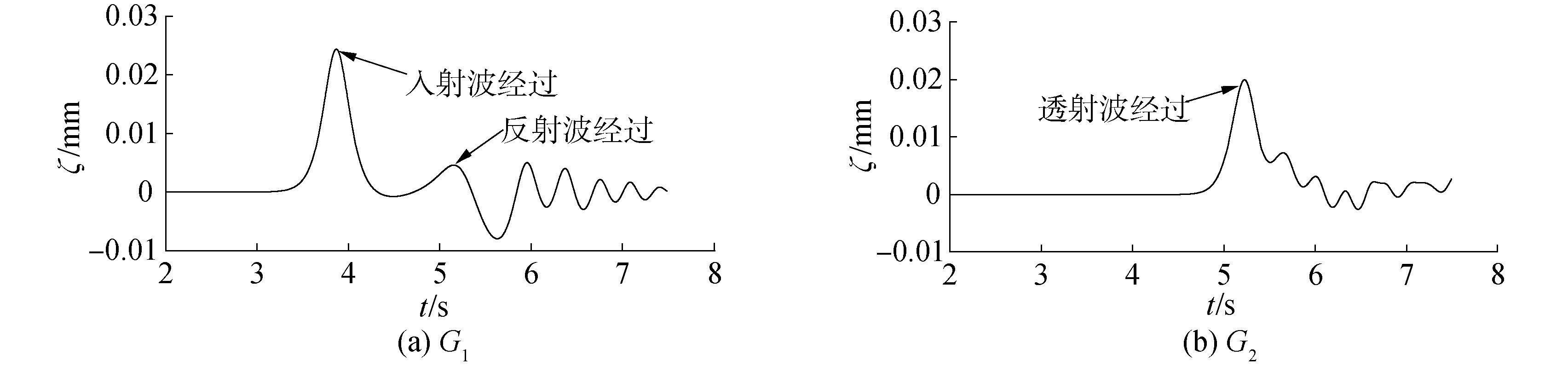
基于Ning等[18]中关于单孤立波的运动描述,反射波的形状由一个波峰和一个波谷组成,通过G1处的自由表面高程可获得入射波、反射波的波高(见图 1,图 10(a)),反射波的波高定义为波峰到波谷的垂直距离,反射系数Cr定义计算为反射波高与入射波高A的比值。透射波高可由G2处的自由面高程求得(见图 10(b)),透射系数Ct定义计算为透射波高与入射波高A的比值。相对净空比和板宽对反射系数Cr、透射系数Ct的影响如图 11所示。
|
Download:
|
| 图 10 G1,G2的自由面变化历程 Fig. 10 Free surface change course of G1 and G2 | |
|
Download:
|
| 图 11 不同板宽条件下,反射系数、透射系数相对于净空比的变化 Fig. 11 Variation of reflection coefficient and transmission coefficient with respect to clearance ratio under different plate width conditions | |
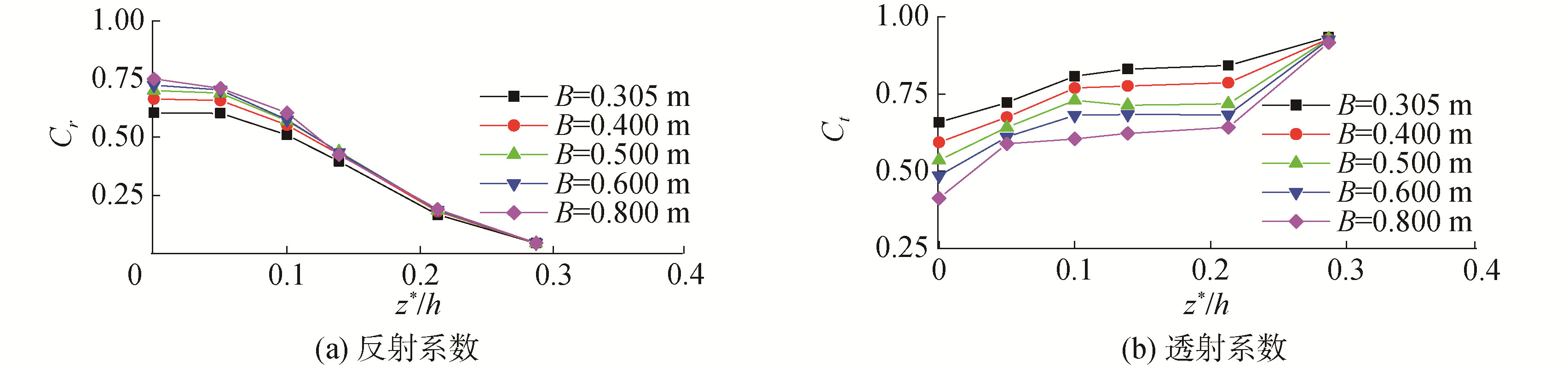
通过比较图 11 (a)和(b)可以发现,对于本文考虑的所有板宽参数,反射系数、透射系数随着相对净空比的增加具有不同的变化趋势。对于反射系数(图 11(a)),随着相对净空比的增加,不同板宽下的Cr呈逐渐减小的趋势;当相对净空比一定时,Cr随着板宽的增加而增加,且当相对净空比逐渐增大时,其随板宽增加对反射系数的影响逐渐减弱。相对净空比和板宽参数对反射系数变化特性的影响与对水平波浪极值力的影响非常相似(图 8(a))。对于透射系数(图 11(b)),Cr与Ct的变化趋势相反,在不同的板宽条件下,透射系数随着相对净空比的增加皆呈单调递增趋势;当相对净空比一定时,透射系数随着板宽的增加而逐渐减小。
5 结论1) 水平板板宽和相对净空比的变化对水平波浪力的变化趋势影响不大,对垂向波浪力的影响较为明显,且随着相对净空比的增加,其影响变得更加显著。
2) 随着相对净空比的增加,平板的水平极值波浪力逐渐减小,垂向极值波浪力先增大后减小;板宽变化对极值波浪力的影响随着相对净空比的增加逐渐减弱。
3) 透射、反射系数受相对净空比的影响,随着相对净空比的增加反射系数逐渐减小,透射系数逐渐增大,并且当平板的相对净空比处于0.139~0.287时(即波峰高度处于板的上下表面高度之间),板宽变化对反射系数的影响逐渐减弱,反射系数曲线逐渐趋于集中;当相对净空比一定时,随着板宽的增加,反射系数逐渐增大, 透射系数逐渐减小。
| [1] |
WANG Jiadong, HE Guanghua, YOU Rui, et al. Numerical study on interaction of a solitary wave with the submerged obstacle[J]. Ocean engineering, 2018, 158: 1-14. DOI:10.1016/j.oceaneng.2018.03.064 (  0) 0)
|
| [2] |
LIN Chang, HO T C, CHANG S C, et al. Vortex shedding induced by a solitary wave propagating over a submerged vertical plate[J]. International journal of heat and fluid flow, 2005, 26(6): 894-904. DOI:10.1016/j.ijheatfluidflow.2005.10.009 (  0) 0)
|
| [3] |
王千, 刘桦, 房詠柳, 等. 孤立波与淹没平板相互作用的三维波面和水动力实验研究[J]. 力学学报, 2019, 51(6): 1605-1613. WANG Qian, LIU Hua, FANG Yongliu, et al. An experimental study of 3-D wave surface and hydrodynamic loads for interaction between solitary wave and submerged horizontal plate[J]. Chinese journal of theoretical and applied mechanics, 2019, 51(6): 1605-1613. (  0) 0)
|
| [4] |
王佳东. 孤立波与板式结构物相互作用的数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2017. WANG Jiadong. Numerical simulation of interaction between a solitary wave and the plate structure[D]. Harbin: Harbin Institute of Technology, 2017. (  0) 0)
|
| [5] |
MCPHERSON R L. Hurricane induced wave and surge forces on bridge decks[D]. Texas: Texas A&M University, 2010.
(  0) 0)
|
| [6] |
孙家文, 孙昭晨, 梁书秀, 等. 随机波对水平板冲击作用实验研究[J]. 海洋工程, 2010, 28(4): 46-53. SUN Jiawen, SUN Zhaochen, LIANG Shuxiu, et al. Experimental study of random wave impact on a horizontal plate[J]. The ocean engineering, 2010, 28(4): 46-53. DOI:10.3969/j.issn.1005-9865.2010.04.007 (  0) 0)
|
| [7] |
JIN Feng. Simulation of irregular wave impact on horizontal plate structures[J]. Journal of ship mechanics, 2017, 21(6): 698-710. (  0) 0)
|
| [8] |
CARTER R W, ERTEKIN R C, LIN P. On the reverse flow beneath a submerged plate due to wave action[C]//Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering. Hamburg, 2006: 4-9.
(  0) 0)
|
| [9] |
LO H Y, LIU P L F. Solitary waves incident on a submerged horizontal plate[J]. Journal of waterway, port, coastal, and ocean engineering, 2014, 140(3): 04014009. DOI:10.1061/(ASCE)WW.1943-5460.0000236 (  0) 0)
|
| [10] |
HAYATDAVOODI M, ERTEKIN R C, VALENTINE B D. Solitary and cnoidal wave scattering by a submerged horizontal plate in shallow water[J]. AIP advances, 2017, 7(6): 065212. DOI:10.1063/1.4987024 (  0) 0)
|
| [11] |
YOU Rui, HE Guanghua, WANG Jiandong, et al. CIP-based analysis on strongly nonlinear interaction between solitary wave and submerged flat plate[J]. Ocean engineering, 2019, 176: 211-221. DOI:10.1016/j.oceaneng.2019.02.050 (  0) 0)
|
| [12] |
HAYATDAVOODI M, SEIFFERT B, ERTEKIN R C. Experiments and calculations of cnoidal wave loads on a flat plate in shallow-water[J]. Journal of ocean engineering and marine energy, 2015, 1: 77-99. DOI:10.1007/s40722-014-0007-x (  0) 0)
|
| [13] |
SEIFFERT B, HAYATDAVOODI M, ERTEKIN R C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part Ⅰ: Flat Plate[J]. Coastal engineering, 2014, 88: 194-209.
(  0) 0)
|
| [14] |
XU Bo, WEI Kai, QIN Shunquan, et al. Experimental study of wave loads on elevated pile cap of pile group foundation for sea-crossing bridges[J]. Ocean engineering, 2020, 197: 106896. DOI:10.1016/j.oceaneng.2019.106896 (  0) 0)
|
| [15] |
JACOBSEN N G, FUHRMAN D R, FREDSØE J. A wave generation toolbox for the open-source cfd library: openfoam®[J]. International journal for numerical methods in fluids, 2012, 70(9): 1073-1088. DOI:10.1002/fld.2726 (  0) 0)
|
| [16] |
REN Bing, WANG Yongxue. Experimental study of irregular wave impact on structures in the splash zone[J]. Ocean engineering, 2003, 30(18): 2363-2377. DOI:10.1016/S0029-8018(03)00104-5 (  0) 0)
|
| [17] |
CUOMO G, TIRINDELLI M, ALLSOP W. Wave-in-deck loads on exposed jetties[J]. Coastal engineering, 2007, 54(9): 657-679. DOI:10.1016/j.coastaleng.2007.01.010 (  0) 0)
|
| [18] |
NING Dezhi, SU Xiaojie, ZHAO Ming. Numerical investigation of solitary wave action on two rectangular boxes with a narrow gap[J]. Acta oceanologica sinica, 2016, 35(12): 89-99. DOI:10.1007/s13131-016-0967-x (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


