2. 武汉理工大学 能源与动力工程学院, 湖北 武汉 430063;
3. 湖北省海洋工程装备研究院有限公司, 湖北 武汉 430063
2. School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. Hubei Ocean Engineering Equipment Research Institute Co., Ltd., Wuhan 430063, China
近年来,受能源危机影响,极地的丰富能源成为各国争取的目标,全球环境的恶化使得北极地区的冰川出现大规模融化[1],为船舶在极地航行提供了便利[2]。与海洋航行不同,极地航行的条件非常恶劣,冰晶颗粒的大量存在使海水管道容易堵塞[3],若颗粒进入冷却系统,严重可使船舶动力系统停止工作。因此了解冰晶在管道中的特性对极地航行有着积极的意义。Kamyar等[4]研究了颗粒直径及入口速度对冰浆流动状态的影响,以及不同粒径和冰晶体积分数对管内压降的影响。徐爱祥等[5]建立CFD-PBM耦合模型,研究冰浆水平直管内非均匀流动下含冰率及流速对冰晶体积分数和粒径分布的影响。报道了含冰率越高时,冰晶体积分数及粒径越大;同时冰晶粒径增大,但增加速度逐渐降低。Tanveer等[6]采用多孔介质数值模拟方法分析纳米流体在弯曲通道中的流动特性,报道了通过修正的达西定律观察多孔介质,在弯角处速度保持非对称性质,且具有较大孔隙率的介质能够增加纳米流体的流速并降低其浓度。目前大多数两相流研究中管道处于静态, 实际情况中,船舶上存在低频振动[7],会对管内流体的流动进行干扰,且振动振幅、频率一直变化。针对以上问题,本文将引入振动波函数并将其简化为周期性正弦函数来进行模拟研究。
1 数值方法本文采用CFD商业软件FLUENT 17.0来研究冰晶的流动及传热特性,根据GB/T 151-2014极地船换热管设计规范[8],管道直径设置为25 mm,弯管的曲率半径R=100(R/D=4)。确定入口流入直管段1 500 mm,出口流出直管段为1 000 mm。三维管道网格如图 1所示。网格数量为799 740,网格质量大于0.65,符合仿真要求。

|
Download:
|
| 图 1 管道三维网格 Fig. 1 Pipe 3-D grid diagram | |
根据2013—2015年在北极实地航行的科学考察船“永盛轮”报告及极地研究资料可知,海水冰晶物性参数与海水盐度相关,本文研究选取盐度为35‰的北极夏季海水为研究对象[9],换热管路材质为碳钢结构。海水、冰晶两相流在标准大气压下,其热物性参数如表 1所示。
| 表 1 海水和冰晶的热物性参数 Table 1 Thermophysical parameters of seawater and ice crystals |
模型在非稳态下进行求解,设定时间步长为0.001 s,残差值设置为1.0×10-4,管道入口采用Velocity Inlet,管道出口设置为Pressure-out,管道壁面采用无滑移边界条件及标准壁面函数计算,速度-压力耦合采用Phase Coupled SIMPLE算法,其他均通过二阶迎风格式。振动模型通过Dynamic Grid块加载振动的UDF;并打开Energy方程开启热量传递,同时将传热传质模型UDF导入求解器,构建热量与质量传递。
2 数学模型本文流体被视为不可压缩流体,冰晶颗粒认为是光滑、非弹性球体,以颗粒动力学理论为基础,建立欧拉-欧拉双流体模型进行研究,湍流模型选用标准k-ε模型。
2.1 连续性方程| $ \frac{\partial}{\partial t}\left(\alpha_{i} \rho_{i}\right)+\nabla \cdot\left(\alpha_{i} \rho_{i} \boldsymbol{v}_{i}\right)=\dot{m}_{q i} $ | (1) |
式中:下标i=l、s分别表示液相海水与固相冰晶颗粒,下标q表示相反的相;α为相的体积分数,固相与液相体积分数满足关系式αs+αl=1;ρ为相的密度,kg/m3;v为相的速度,m/s1;
| $ \begin{gathered} \frac{\partial}{\partial t}\left(\alpha_{l} \rho_{l} \boldsymbol{v}_{l}\right)+\nabla \cdot\left(\alpha_{l} \rho_{l} \boldsymbol{v}_{l} \boldsymbol{v}_{l}\right)=-\alpha_{l} \nabla P+ \\ \nabla \cdot \boldsymbol{\tau}_{l}+\alpha_{l} \rho_{l} g+F_{s l}+\left(\dot{m}_{s l} \boldsymbol{v}_{s}-\dot{m}_{l s} \boldsymbol{v}_{l}\right) \end{gathered} $ | (2) |
| $ \begin{gathered} \tau_{s}=\left(-P_{s}+\xi_{s} \nabla \cdot \boldsymbol{v}_{s}\right) \boldsymbol{I}+ \\ \alpha_{s} \mu_{s}\left[-\frac{2\left(\boldsymbol{v}_{s}\right) \boldsymbol{I}}{3}+\nabla \cdot \boldsymbol{v}_{s}+\nabla \cdot \boldsymbol{v}_{s}^{\mathrm{T}}\right] \end{gathered} $ | (3) |
式中:Ps为颗粒流动力学理论推导出的固体压力,Pa;τs为固相冰晶颗粒的应力张量;ξs为冰晶颗粒的体积粘度,kg/(m·s);μs为冰晶颗粒的剪切粘度,kg/(m·s)。
体积粘度由Lun等[10]的模型计算;剪切粘度由文献[11]中的模型计算。
2.3 能量守恒方程| $ \begin{gathered} \frac{\partial}{\partial t}\left(\alpha_{i} \rho_{i} h_{i}\right)+\nabla \cdot\left(\alpha_{i} \rho_{i} h_{i} \boldsymbol{v}_{i}\right)=\tau_{i} \cdot \nabla \boldsymbol{v}_{i}+ \\ \nabla \cdot\left(\lambda_{\text {eff }, i} \nabla T_{i}\right)-h_{l s}\left(T_{i}-T_{q}\right)+\left(\dot{m}_{q i} h_{q}-\dot{m}_{i q} h_{i}\right) \end{gathered} $ | (4) |
式中:hi为各相的比焓,J/kg;λeff为海水与冰晶的导热系数,W/(m ·K);T为温度,K;hls为液相海水与固相冰晶的相间换热系数,W/(m2 ·K);
在本文中,采用编译传热传质模型的UDF(user-defined function)程序嵌入欧拉-欧拉双流体模型中,体积相间传热系数hv表达式为:
| $ h_{v}=\frac{6 \alpha_{s} \alpha_{l} h_{l s}}{d_{s}} $ | (5) |
式中hls为固体颗粒与液体之间的相间传热系数,采用Gunn模型。
固相冰晶颗粒融化为海水的传质率为:
| $ \dot{m}_{l s}=\frac{h_{v}\left(T_{l}-T_{s}\right)}{\Delta H} $ | (6) |
式中ΔH为冰晶颗粒的潜热,J/kg。
2.5 相间作用力本文中主要考虑拖曳力、升力和湍流扩散力,拖曳力在固-液两相流中起关键作用,表达式为[12]:
| $ F_{D}=\gamma_{s l}\left(\boldsymbol{v}_{q}-\boldsymbol{v}_{i}\right) $ | (7) |
式中:γsl表示相间动量交换系数,因固体颗粒浓度而改变表达式为:
| $ \gamma_{s l}=\left\{\begin{array}{l} \frac{3 C_{D} \alpha_{s} \alpha_{l} \rho_{l} \alpha_{l}^{-2.65}\left|\boldsymbol{v}_{l}-\boldsymbol{v}_{s}\right|}{4 d_{s}}, & \alpha_{s}<0.2 \\ \frac{1.75 \rho_{l} \alpha_{s}\left|\boldsymbol{v}_{l}-\boldsymbol{v}_{s}\right|}{d_{s}}+\frac{150 \mu_{l} \alpha_{s}^{2}}{\alpha_{l} d_{s}{ }^{2}}, & \alpha_{s} \geqslant 0.2 \end{array}\right. $ | (8) |
| $ C_{D}=\frac{24}{\alpha_{l} R e_{s}}\left[1+0.15\left(\alpha_{l} R e_{s}\right)^{0.687}\right] $ | (9) |
升力主要考虑staffman升力,表达式为:
| $ F_{L}=C_{L} \alpha_{s} \rho_{l}\left(\nabla \times \boldsymbol{v}_{l}\right) \times\left(\left|\boldsymbol{v}_{q}-\boldsymbol{v}_{i}\right|\right) $ | (10) |
式中: CL为升力系数,取值0.2[13];CD为拖曳力系数;Res为颗粒雷诺数;ds为冰晶颗粒直径。
湍流扩散力FTD由文献[14]的模型中获得。
2.6 颗粒动力学理论颗粒动力学理论是以气体分子动力学为基础,将固体颗粒看作致密气体分子。颗粒温度表达式为:
| $ \theta_{s}=\frac{1}{3} \overline{v_{s}^{\prime} v_{s}^{\prime}} $ | (11) |
式中:θs为颗粒相温度,m2/s2;vs为固体颗粒波动速度,m/s。颗粒相温度由颗粒的波动能量平衡方程求解[15],具体形式为:
| $ \begin{gathered} \frac{3}{2}\left[\nabla \cdot\left(\alpha_{s} \rho_{s} \boldsymbol{v}_{s} \theta_{s}\right)+\frac{\partial}{\partial t}\left(\alpha_{s} \rho_{s} \theta_{s}\right)\right]= \\ \nabla \cdot\left(k_{\theta_{s}} \nabla \theta_{s}\right)+\left(\tau_{s}-P_{s} I\right) \cdot \nabla \boldsymbol{v}_{s}+\boldsymbol{S}_{s l}-\psi_{\theta_{s}} \end{gathered} $ | (12) |
式中:
将振动函数简化为正弦函数,其圆管壁面振动方程表示为:
| $ y=A \sin (\omega t+\varphi) $ | (13) |
仿真数据的可靠性由实验数据验证,图 2为实验室台架的实物图,主要包括:制冰装置、运输及测试管道、储冰槽和数据测量装置。

|
Download:
|
| 图 2 实验台架实物图 Fig. 2 Physical drawing of test bench | |
实验制取的冰晶样本如图 3所示,实验过程中流动速度控制在1.5 m/s。

|
Download:
|
| 图 3 冰浆样本 Fig. 3 Ice slurry sample | |
实验主要测试了不同振动频率下冰浆流动过程中的压降结果、不同入口IPF下冰浆传热系数变化,并与CFD欧拉欧拉模型仿真结果作比较,如图 4、图 5所示。从图 4、5可以看出实验结果与仿真结果的变化趋势相同,最大相对误差在20%以内,说明使用的模型适合研究冰浆流动和传热特性。

|
Download:
|
| 图 4 不同频率下冰浆流动压降实验结果与计算结果比较 Fig. 4 Comparison of experimental results of flow pressure drop with different amplitude conditions and calculation results | |

|
Download:
|
| 图 5 不同入口IPF下传热系数实验结果与计算结果比较 Fig. 5 Comparison of experimental and calculated results of heat transfer coefficient under different inlet IPF | |
在振幅为0.5 mm、频率为20 Hz条件下研究管内流动参数如图 6所示,数据整体呈现二次函数型增长趋势,主要因为随着流速的增大,海水对冰粒的拖曳力增加,并且增强了冰粒及海水对壁面的碰撞,致使能量耗损严重。流速的增大及含冰率的升高造成冰晶颗粒沿管道横截面分布的不均匀性增加,同时壁面附近液体流向变化影响冰粒分布,导致壁面处剪切应力变化,这解释了随着流速及IPF的增加,压降增长越趋近于二次增长。

|
Download:
|
| 图 6 不同IPF下压降随入口速度变化的变化 Fig. 6 Variation of pressure drop with inlet velocity under variable IPF | |
如图 7为管道出口截面振幅对冰晶体积分数分布影响的云图。由图 7可见,由于海水密度大于冰晶密度,在流动过程中,冰晶受到的浮力大于重力,出现上浮,造成两相分层,施加振动后,冰晶颗粒的分布变化较大,振幅A从0 mm增加到1 mm,冰晶颗粒最大浓度则由13.8%降至12.5%。主要因为振动势能的不断增加,冰晶颗粒与海水间的粘性摩擦作用增强,同时壁面的粗糙度增大,颗粒与壁面碰撞增强,冰晶颗粒热交换量增加。

|
Download:
|
| 图 7 ω=20 Hz,IPF=15%,U=1.5 m/s,d=0.4 mm时不同振幅下冰晶体积分数分布云图 Fig. 7 ice crystal volume fraction cloud under different amplitude(ω=20 Hz, IPF=15%, U=1.5 m/s, d=0.4 mm) | |
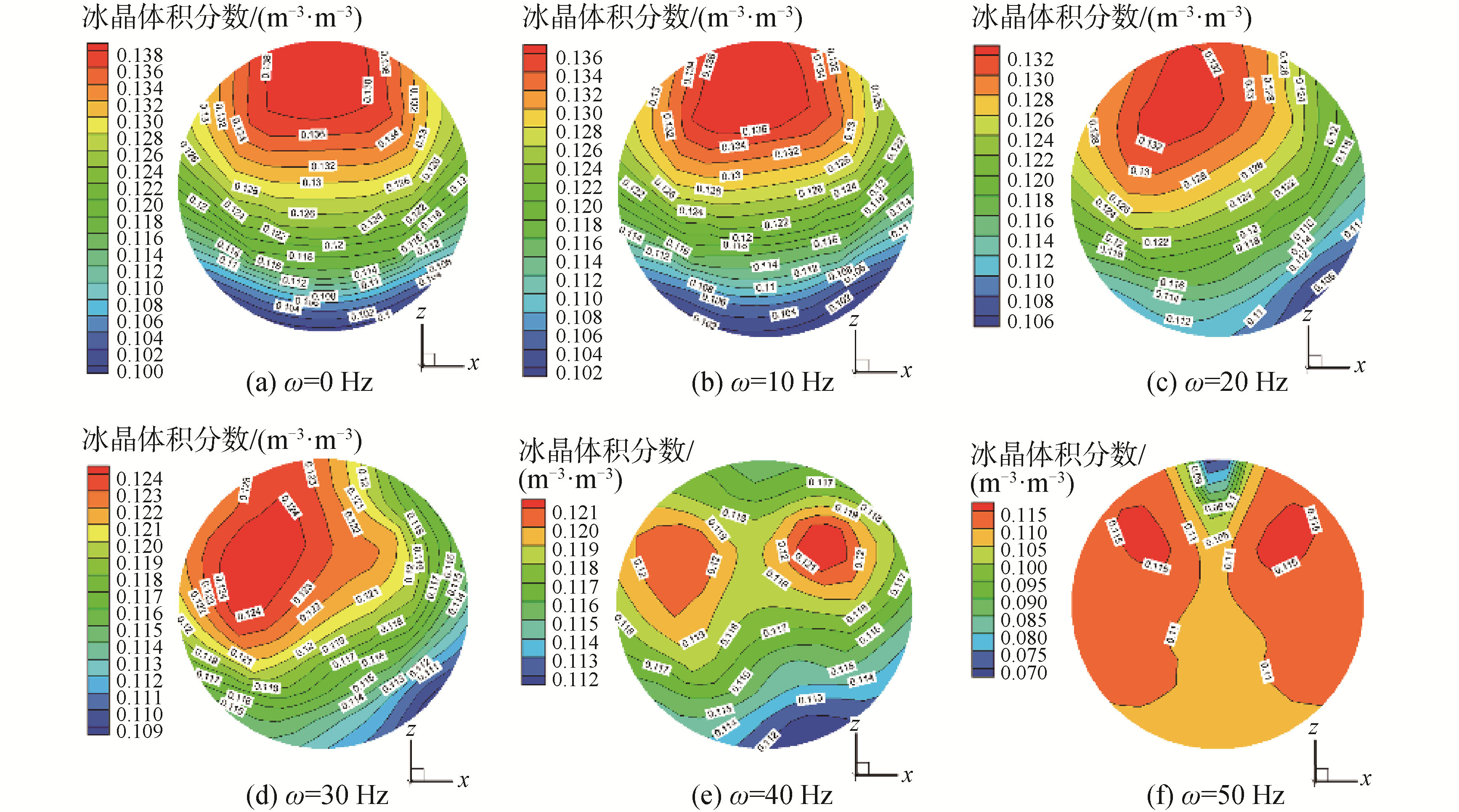
如图 8为出口截面冰晶体积分数分布随振动频率的变化云图。施加振动后,冰晶颗粒的振动现象较为显著,振幅A=0.5 mm时,随着振动频率ω从0 Hz增至50 Hz,冰晶颗粒最大体积分数从13.8%降至11.5%。这是因为振动频率的增加使冰晶运动,动能增加,冰粒与冰粒间的偶发性碰撞及冰粒与壁面的碰撞频率加快,能量损耗增大;同时,冰粒在较为频繁的换向运动中使得海水对其拖曳力增加,产生较大的摩擦损失,使冰粒融化。由图 8 (e)与(f)可知,在频率为40与50 Hz时,冰粒分布呈现在两侧聚集的趋势,因为频率增强了冰粒动能与势能之间的转换,在壁面碰撞、剪切应力及浮升力共同作用下往管内两侧上方运动。
|
Download:
|
| 图 8 A=0.5 mm,入口IPF=15%,U=1.5 m/s,d=0.4 mm时不同频率下冰晶体积分数分布 Fig. 8 Ice crystal volume fraction cloud under different frequency (A=0.5 mm, IPF=15%, U=1.5 m/s, d=0.4 mm) | |
在入口IPF=15%,入口平均流速1.5 m/s,冰晶粒径直径为0.4 mm,管壁加载恒定热流密为3.34 kW/m2下,改变参数振幅Dmm≤A≤1.0 mm研究振动工况下管内海水冰晶两相流沿程传热特性。
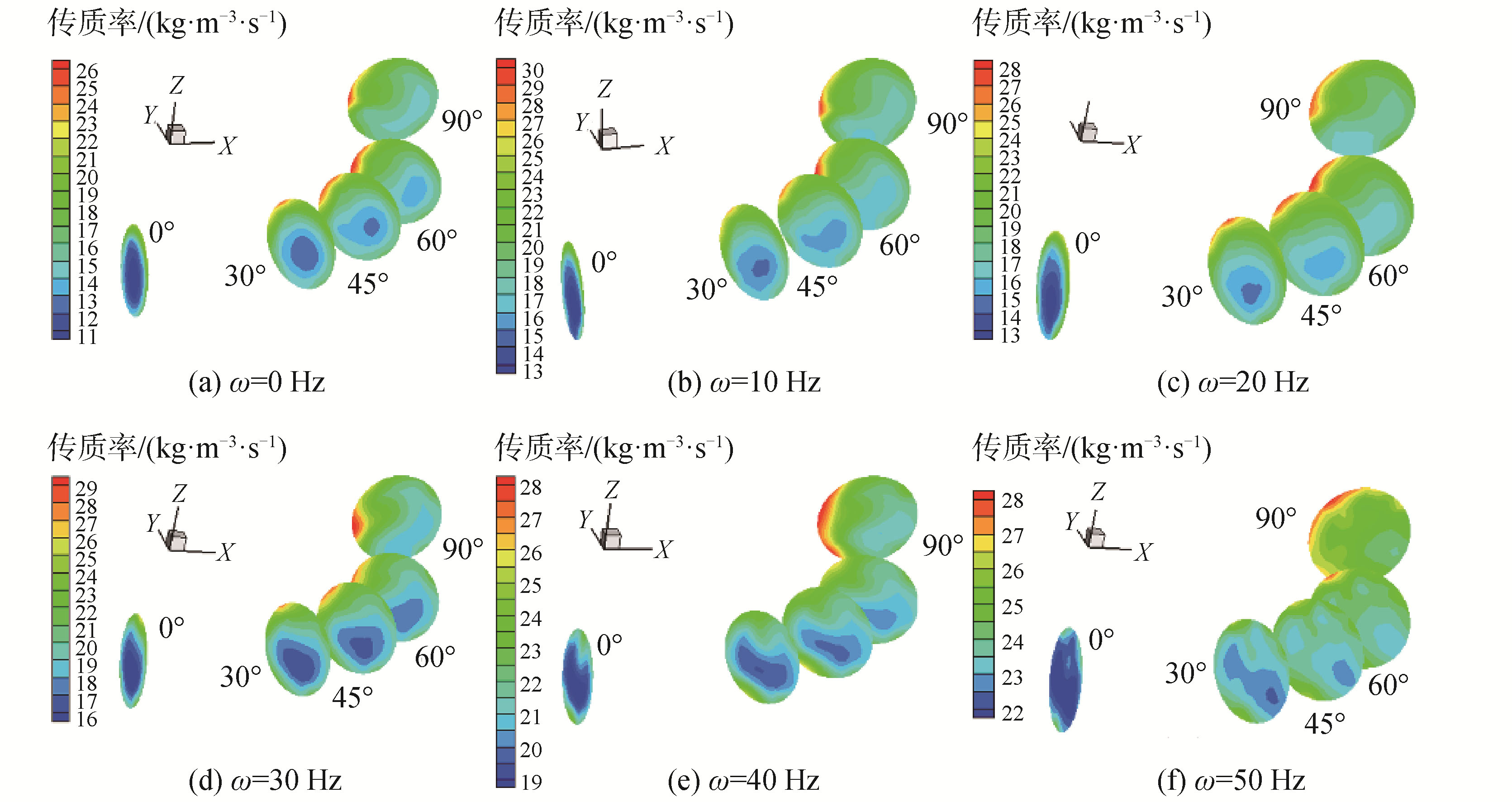
4.2.1 频率对弯角相间传质率的影响图 9可见,在壁面恒定热流密度作用下,管壁面附近存在明显的相变梯度,大量冰粒在壁面附近融化,且管内侧高于外侧面,在流动方向逐渐增加。在频率作用下传质率有了一定的提高,从0~50 Hz,其中心传质率持续增加,尤其在50 Hz条件下,90°截面基本趋近于均匀,因为高频率造成冰粒逐渐分布在垂直径向两侧,促成管内扰动剧烈,使作用在冰粒上的碰撞及摩擦显著,需提供更多热量弥补能量损失。
|
Download:
|
| 图 9 传质率随频率的变化而变化云图 Fig. 9 Mass transfer rate cloud under different frequency | |
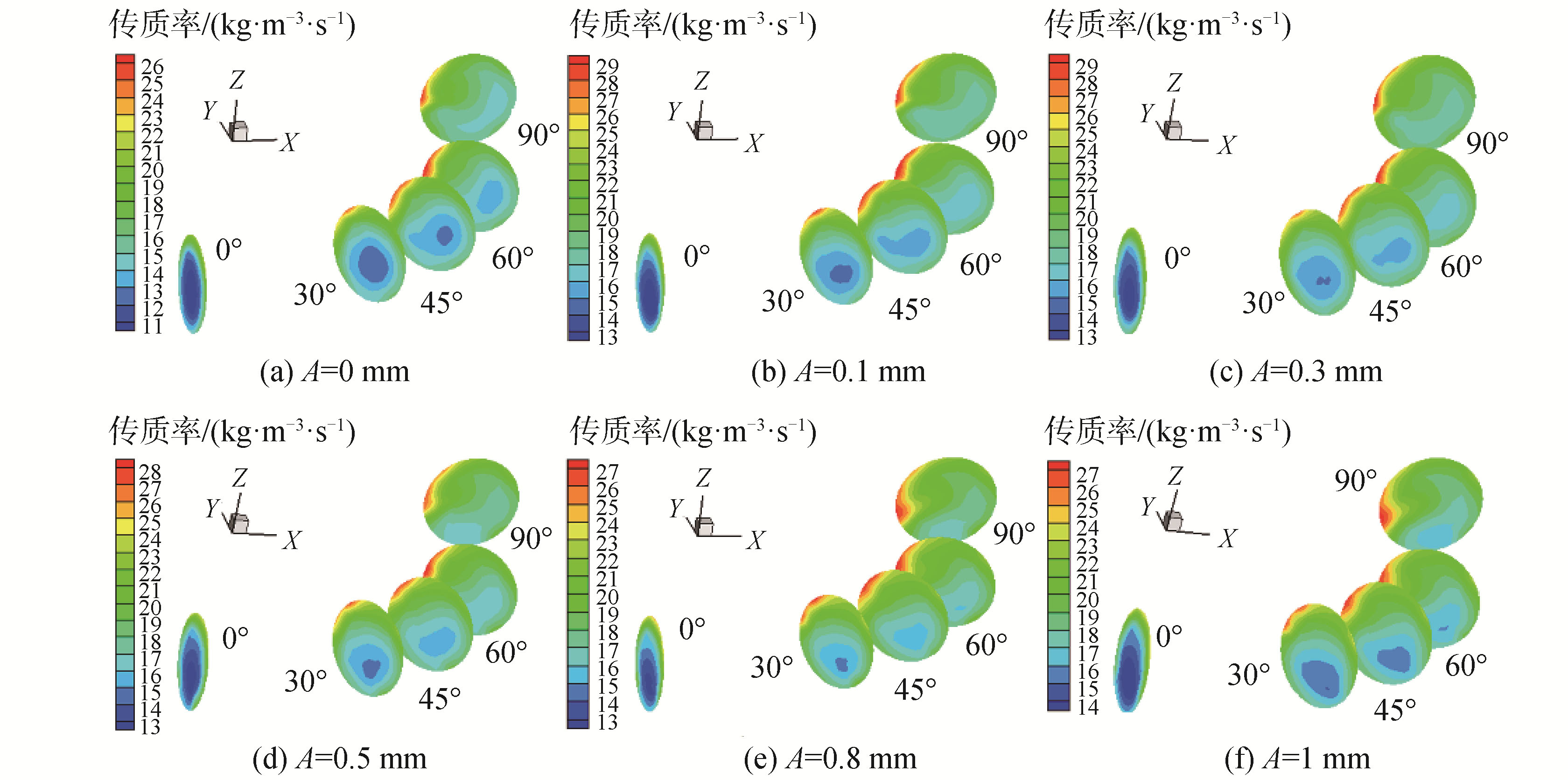
图 10可见,相间传质率在振幅及频率作用下有着明显的分层差异情况,弯管内侧传质率高于弯管外侧,因为在弯角内侧其热流传递面积较小,并且冰粒在弯角内侧偏上部分相对较大,热交换的现象更强烈,致使冰粒吸收更多潜热融化为海水。在沿程流动反向上,其传质率逐渐增大,因为二次流促使冰粒在管内的扰动,加快了冰粒的融化。图 10及11施加振幅后传质率明显增强,振幅的增大不仅加强了壁面与冰粒的碰撞,而且促进径向传热的发生,使得中心区域冰粒相变增大3 kg/(m3 ·s)。
|
Download:
|
| 图 10 振幅与弯角传质率分布云图 Fig. 10 Mass transfer rate cloud under different amplitude | |

|
Download:
|
| 图 11 弯角入口径向振幅与传质率曲线 Fig. 11 Change of mass transfer rate with amplitude in corner inlet diameter direction | |
1) 振动加载后,压降随着入口含冰率(5%~30%)及流速(0.5~3 m/s)的增加而逐渐增大,并且在流速改变时其压降增长趋势为二次增长趋势。
2) 振动频率及振幅增强管内扰动促进温度及相间传质率的升高。
3) 振动和振动频率的提高使最大冰晶颗粒浓度减少,并且在40 Hz与50 Hz时出现冰晶在两侧聚集趋势。
| [1] |
KEEN A, BLOCKLEY E. Investigating future changes in the volume budget of the Arctic sea ice in a coupled climate model[J]. The cryosphere, 2018, 12(9): 2855-2868. DOI:10.5194/tc-12-2855-2018 (  0) 0)
|
| [2] |
徐立, 江焕宝, 黄振飞, 等. 极地船海水管道海水-冰晶两相流的换热特性分析[J]. 哈尔滨工程大学学报, 2017, 38(6): 887-891. XU Li, JIANG Huanbao, HUANG Zhenfei, et al. Heat transfer characteristics analysis of seawater and ice two-phase flow in the polar vessel seawater pipeline[J]. Journal of Harbin Engineering University, 2017, 38(6): 887-891. (  0) 0)
|
| [3] |
徐陈芸. 冰浆在板式换热器中的流动与传热研究[D]. 武汉: 华中科技大学, 2012. XU Chenyun. The research on the ice slurry flow in plate heat exchangers[D]. Wuhan: Huazhong University of Science and Technology, 2012. (  0) 0)
|
| [4] |
KAMYAR A, AMINOSSADATI S M, LEONARDI C R, et al. Flow characterisation of monopropylene glycol ice slurry through a horizontal U-bend: a numerical approach[J]. European journal of mechanics-B/fluids, 2020, 82: 93-105. DOI:10.1016/j.euromechflu.2020.03.004 (  0) 0)
|
| [5] |
徐爱祥, 平仕昊, 徐丹, 等. 冰浆水平直管非均匀输运特性研究[J]. 湖南工业大学学报, 2018, 32(5): 6-11. XU Aixiang, PING Shihao, XU Dan, et al. Study on non-uniform transport properties of ice slurry horizontal straight tubes[J]. Journal of Hunan University of Technology, 2018, 32(5): 6-11. (  0) 0)
|
| [6] |
TANVEER A, HAYAT T, ALSAEDI A, et al. Numerical simulation for peristalsis of Carreau-Yasuda nanofluid in curved channel with mixed convection and porous space[J]. PLoS one, 2017, 12(2): e0170029. DOI:10.1371/journal.pone.0170029 (  0) 0)
|
| [7] |
FUKASAWA T, MUKAI K. On the effects of hull-girder vibration upon fatigue strength of a Post-Panamax container ship disaggregated by short-term sea state[J]. International journal of naval architecture and ocean engineering, 2014, 6(2): 431-441. DOI:10.2478/IJNAOE-2013-0190 (  0) 0)
|
| [8] |
张萌萌. 基于FLUENT的北极海冰三维温度场数值仿真和融化模拟[D]. 武汉: 武汉理工大学, 2013. ZHANG Mengmeng. Numerical simulation based on FLUENT for melting and three-dimensional temperature filed of arctic sea ice[D]. Wuhan: Wuhan University of Technology, 2013. (  0) 0)
|
| [9] |
赵庆爱. 永盛轮随船日记(上)[J]. 中国远洋航务, 2013(9): 36-42. ZHAO Qingai. Yongsheng shipping diary(1)[J]. Maritime China, 2013(9): 36-42. (  0) 0)
|
| [10] |
LUN C K K, SAVAGE S B, JEFFREY D J, et al. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield[J]. Journal of fluid mechanics, 1984, 140: 223-256. DOI:10.1017/S0022112084000586 (  0) 0)
|
| [11] |
ZEHNER P, SCHLUNDER E U. Wärmeleitfähigkeit von Schüttungen bei maessigen temperaturen[J]. Chemie ingenieur technik, 1970, 42(14): 933-941. DOI:10.1002/cite.330421408 (  0) 0)
|
| [12] |
GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. Boston: Academic Press, 1994: 314-315.
(  0) 0)
|
| [13] |
TOMIYAMA A. Drag, lift and virtual mass forces acting on a single bubble[C]//Proceedings of the Third International Symposium on Two-Phase Flow Modelling and Experimentation. Pisa, Italy, 2004: 22-24.
(  0) 0)
|
| [14] |
BURNS A D, FRANK T, HAMILL I, et al. The Favre averaged drag model for turbulent dispersion in eulerian multi-phase flows[C]//Proceedings of the 5th International Conference on Multiphase Flow. Yokohama, Japan, 2004.
(  0) 0)
|
| [15] |
JIN Tao, LI Yijian, WU Shuqin, et al. Numerical modeling for the flow and heat transfer of slush nitrogen in a horizontal pipe based on population balance equations[J]. Applied thermal engineering, 2017, 123: 301-309. DOI:10.1016/j.applthermaleng.2017.05.077 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


