2. 哈尔滨职业技术学院 汽车学院, 黑龙江 哈尔滨 150001
2. School of Automobile, Harbin Vocational and Technical College, Harbin 150001, China
目前,我国有近3 000万肢体存在运动障碍的患者,且只有30%左右的人能接受到不同程度的康复训练,但康复效果各不相同。
对人体运动生物力学的研究是康复医疗技术和康复设备研发的基础,目前,下肢存在运动障碍的人口数占比较大,且对下肢运动生物力学的相关研究报告也比较多:Deschamps等[1]通过动力学链的方法对下肢包括髋关节、膝关节和踝关节的下肢运动和关节力矩的变化进行研究,主要以将健康的运动员运动参数为例进行研究,但并没有考虑下肢肌肉力的变化规律。Hume等[2]建立了人体下肢缩比模型,研究了结构负载和关节力学的预测方法,对受伤患者、术后等下肢肌肉力和力矩负载的预测具有重要实际意义。在步行过程中,速度、步长、频率和不同坡度对下肢的运动学和动力学及肌肉力均有不同程度的影响[3-10],例如:大腿屈曲/伸展-大腿屈曲/伸展的vCRP(连续相对相位(continuous relative phase, CRP))值对人体运动速度很敏感,而且跑步的速度增加,下肢的协调性下降,相当于对下肢添加了一定的约束。另外,CRP值的减小是由于人体质心在垂直方向的运动所导致的,并非膝关节的屈曲角度[3]。Resende等[11]分析了单侧脚内旋可能造成的下肢伤害,对下肢康复和下肢矫正提供了的依据,但没有涉及下肢肌肉力的变化,无法从机理上研究下肢康复策略。Cheng等[12]分别针对健康青年、步态稳定老年人和步态不稳定的老年人在完成“坐到站”动作时肌肉功率的变化进行了分析,发现健康青年消耗的功率比老年人消耗的功率要大,且完成动作时间短。Koyama等[13]研究了在光脚和穿鞋的情况下进行向下跳跃运动的下肢力学特征和肌肉激活度,研究结果表明:在光脚和穿鞋2种情况下,下肢运动的关节角度差异较小,但在人体着地时,下肢肌肉激活度存在较大的差异。另外,在穿鞋的情况下向下跳跃是比较安全的。Carolina等[14]设计了一种混合神经的假肢用来实现下肢髋关节的康复训练,其中下肢运动关节力矩和运动数据在OpenSim软件环境中获取,基于上述数据研究了假肢的控制方法。
目前报道的文献未见单曲膝行走时下肢生物力学特性的研究,当人体下肢受伤后,所表现出来的保护性跛行的步态称之为单曲膝行走步态。因此,本文将针对青年正常行走步态和单曲膝病态行走下的运动学、动力学和下肢肌肉力及肌肉激活度进行分析,研究结果将为下肢康复医疗提供数据,以填补单曲膝下肢康复数据的空白。
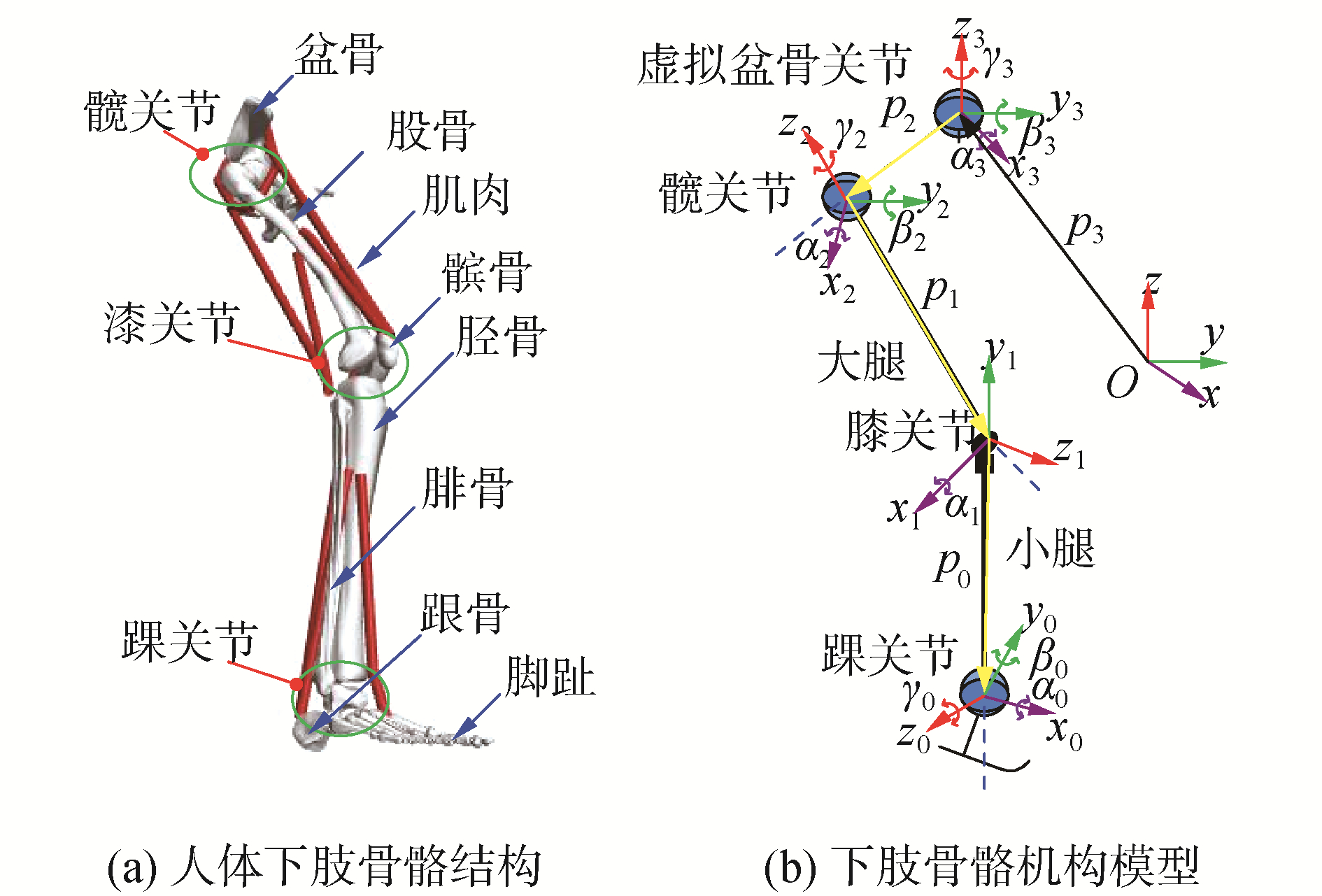
1 下肢运动学、动力学模型人体下肢的骨骼肌结构如图 1(a)所示,主要由盆骨、股骨、胫骨、腓骨、髌骨、足以及肌肉群构成,包含3个关节:髋关节、膝关节和踝关节,也包含盆骨的运动关节。根据人体实际运动情况,由于盆骨分别在矢状面、冠状面和水平面没移动,又可以绕垂直轴、矢状轴和冠状轴转动,因此可将骨盆处的运动关节假设为球形关节;髋关节和踝关节可以绕垂直轴、失状轴和冠状轴转动,其次将其简化为球形关节,而膝关节为可以绕冠状轴转动的关节,简化后的下肢骨骼机构模型如图 1(b)所示,并依次在各关节处建立了关节坐标系Oi-xiyizi(i=0, 1, 2, 3),[αi βi γi]为关节i相对于i-1关节坐标系的角位移,pi分别表示小腿、大腿和骨盆的位置向量,其中O-xyz为世界坐标系。
|
Download:
|
| 图 1 人体下肢骨骼结构及简化模型 Fig. 1 Skeleton structure and simplified model of human lower limb | |
根据下肢骨骼肌的机构特点,本文采用DH方法建立下肢的运动学模型,根据DH变换法则可知,Oi-xiyizi(i=0, 1, 2, 3)在世界坐标系O-xyz中的位置和姿态可以表示为AiO:
| $ \boldsymbol{A}_{i}^{O}=\boldsymbol{A}_{3}^{O} \boldsymbol{A}_{2}^{3} \cdots \boldsymbol{A}_{i}^{i+1} $ | (1) |
式中:Aii+1表示坐标系Oi-xiyizi相对于Oi+1-xi+1yi+1zi+1的位姿;A3O表示坐标系O3-x3y3z3相对于O-xyz的位姿,且有:
| $ \begin{array}{c} & \boldsymbol{A}_{i}^{i+1}= \\ &{\left[\begin{array}{cccc} \mathrm{c} \beta_{i} \mathrm{c} \gamma_{i} & -\mathrm{c} \beta_{i} \mathrm{~s} \gamma_{i} & \mathrm{~s} \beta_{i} & p_{i x} \\ \mathrm{c} \alpha_{i} \mathrm{~s} \gamma_{i}+\mathrm{s} \alpha_{i} \mathrm{~s} \beta_{2} \mathrm{c} \gamma_{i} & \mathrm{c} \alpha_{2} \mathrm{c} \gamma_{i}-\mathrm{s} \alpha_{i} \mathrm{~s} \beta_{i} \mathrm{~s} \gamma_{i} & -\mathrm{s} \alpha_{i} \mathrm{c} \beta_{i} & p_{i y} \\ \mathrm{~s} \alpha_{i} \mathrm{~s} \gamma_{i}-\mathrm{c} \alpha_{i} \mathrm{~s} \beta_{i} \mathrm{c} \gamma_{i} & \mathrm{~s} \alpha_{2} \mathrm{c} \gamma_{i}+\mathrm{c} \alpha_{i} \mathrm{~s} \beta_{i} \mathrm{~s} \gamma_{i} & \mathrm{c} \alpha_{i} \mathrm{c} \beta_{i} & p_{i z} \\ 0 & 0 & 0 & 1 \end{array}\right]} \end{array} $ | (2) |
式中:c=cos,s=sin,pi=[pix piy piz] T为Oi-xiyizi坐标系坐标原点在Oi+1-xi+1yi+1zi+1中的位置。
根据角速度叠加原理可知,下肢骨骼运动绝对角速度可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{\omega}_{3}^{O}=\left[\begin{array}{lll} \dot{\alpha}_{3} & \dot{\beta}_{3} & \dot{\gamma}_{3} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\omega}_{2}^{O}=\boldsymbol{\omega}_{3}^{O}+\left[\begin{array}{lll} \dot{\alpha}_{2} & \dot{\beta}_{2} & \dot{\gamma}_{2} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\omega}_{1}^{O}=\boldsymbol{\omega}_{2}^{O}+\left[\begin{array}{lll} \dot{\alpha}_{1} & 0 & 0 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\omega}_{0}^{O}=\boldsymbol{\omega}_{1}^{O}+\left[\begin{array}{lll} \dot{\alpha}_{0} & \dot{\beta}_{0} & \dot{\gamma}_{0} \end{array}\right]^{\mathrm{T}} \end{array}\right. $ | (3) |
式中:ωiO表示盆骨、大腿、小腿和脚的绝对角速度。
式(3)可进一步表达为:
| $ \boldsymbol{\omega}_{i-1}^{O}=\boldsymbol{\omega}_{i}^{O}+\dot{\boldsymbol{\theta}}{}_{i-1}^{i} \boldsymbol{e}_{i-1}^{i} $ | (4) |
式中ei-1i表示坐标系Oi-1在Oi坐标系中的单位向量变换矩阵。
对式(4)两边微分得到人体下肢骨骼运动绝对角加速度:
| $ \boldsymbol{\varepsilon}_{i-1}^{O}=\boldsymbol{\varepsilon}_{i}^{O}+\ddot{\boldsymbol{\theta}}{}_{i-1}^{i} \boldsymbol{e}_{i-1}^{i}+\dot{\boldsymbol{\theta}{}}_{i-1}^{i}\left(\boldsymbol{\omega}_{i}^{O} \times \boldsymbol{e}_{i-1}^{i}\right) $ | (5) |
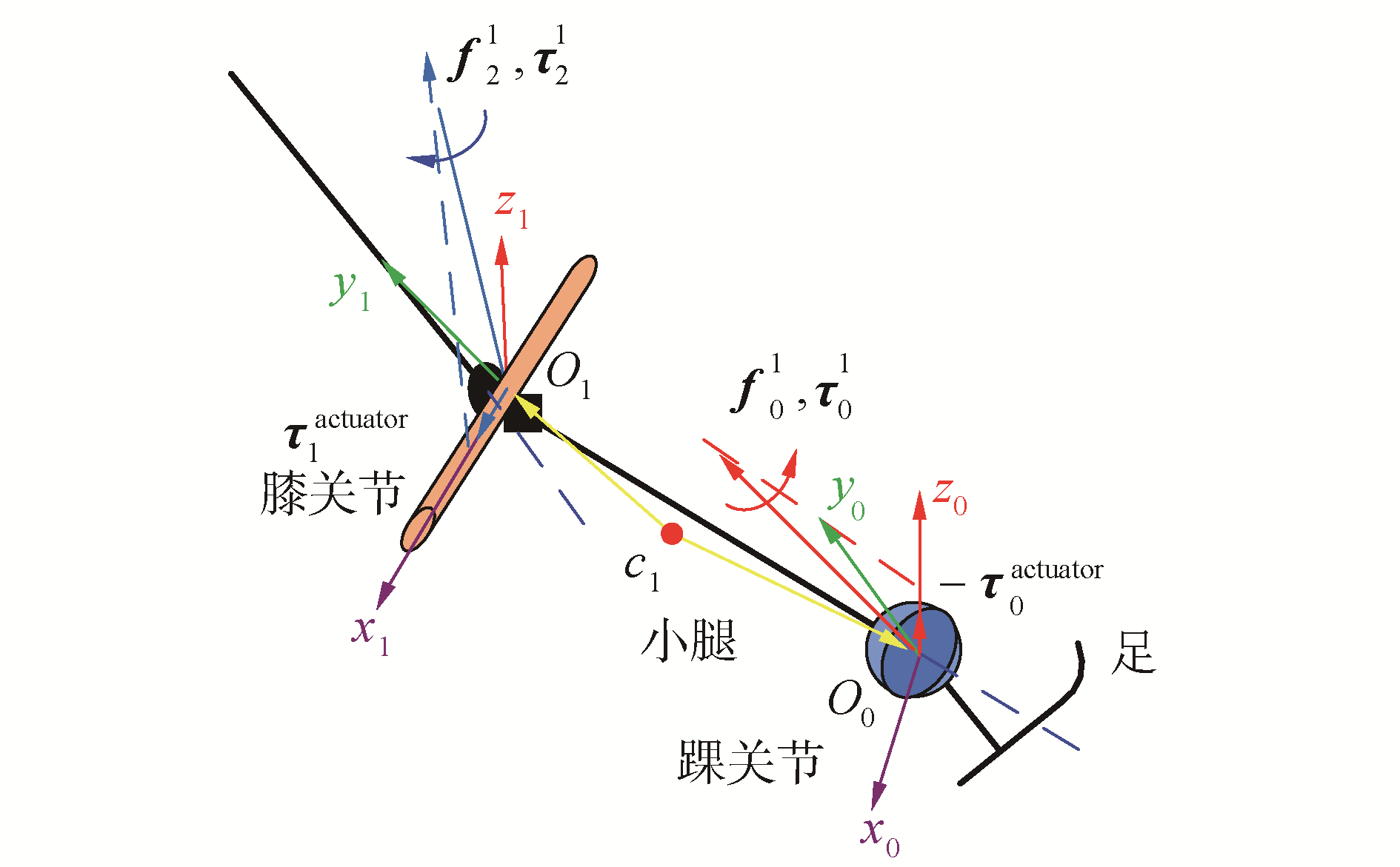
人体的运动是在肌肉通过力臂产生是关节运动的驱动力矩实现的,因此对下肢骨骼运动的动力学分析是合理制定下肢康复训练的重点。图 2为下肢小腿骨骼受力示意图,其中,f01、τ01与f21、τ21分别表示脚和大腿对小腿的关节约束力和力矩,τ1actuator和τ0actuator分别表示膝关节和踝关节的驱动力矩,c1表示小腿质心。
|
Download:
|
| 图 2 下肢小腿骨骼受力 Fig. 2 Schematic diagram of the force on the shank | |
对图 2所示的小腿骨骼受力进行分析,下肢其他骨骼受力和小腿受力一致,因此根据牛顿欧拉方程可得到人体下肢骨骼运动的动力学模型:
| $ \left\{\begin{array}{l} \boldsymbol{f}_{i+1}^{i}+\boldsymbol{f}_{i-1}^{i}+m_{i} \boldsymbol{g}=m_{i} \boldsymbol{a}_{c i} \\ l_{o, i+1}^{c i} \times \boldsymbol{f}_{i+1}^{i}+l_{o, i-1}^{c i} \times \boldsymbol{f}_{i-1}^{i}+\boldsymbol{\tau}_{i+1}^{i}+\boldsymbol{\tau}_{i-1}^{i}= \\ \ \ \ \ \ \ \ \ \ \ \ \ \boldsymbol{X}_{i} \boldsymbol{\varepsilon}_{i}^{O}+\boldsymbol{\omega}_{i}^{O} \times\left(\boldsymbol{I}_{i} \boldsymbol{\omega}_{i}^{O}\right) \end{array}\right. $ | (6) |
式中:fi+1i、fi-1i表示i+1骨骼和i-1对i骨骼形成运动关节的约束力;mi和aci表示i骨骼的质量和质心处线性加速度;g为重力加速度;lo, i+1ci和lo, i-1ci表示fi+1i、fi-1i作用i骨骼的力臂;τi+1i、τi-1i表示关节驱动力矩;Xi为i骨骼的惯性矩阵。
且关节力约束力和力矩之间存在关系:
| $ \left\{\begin{array}{l} \boldsymbol{f}_{i+1}^{i}=-\boldsymbol{f}_{i}^{i+1} \\ \boldsymbol{\tau}_{i+1}^{i}=-\boldsymbol{\tau}_{\mathrm{i}}^{\mathrm{i}+1} \end{array}\right. $ | (7) |
下肢骨骼运动的动力学模型(6)可进一步表示为:
| $ \boldsymbol{\tau}=\boldsymbol{X} \ddot{\boldsymbol{\theta}}+\boldsymbol{B} \dot{\boldsymbol{\theta}}+\boldsymbol{f L}+\boldsymbol{G} $ | (8) |
式中:τ为关节驱动力矩;X为下肢骨骼广义质量矩阵;B为Coriolis力和离心力;f、L分别表示肌肉力映射的广义力矩阵和对应的力臂矩阵;G为重力产生的广义力矩阵。
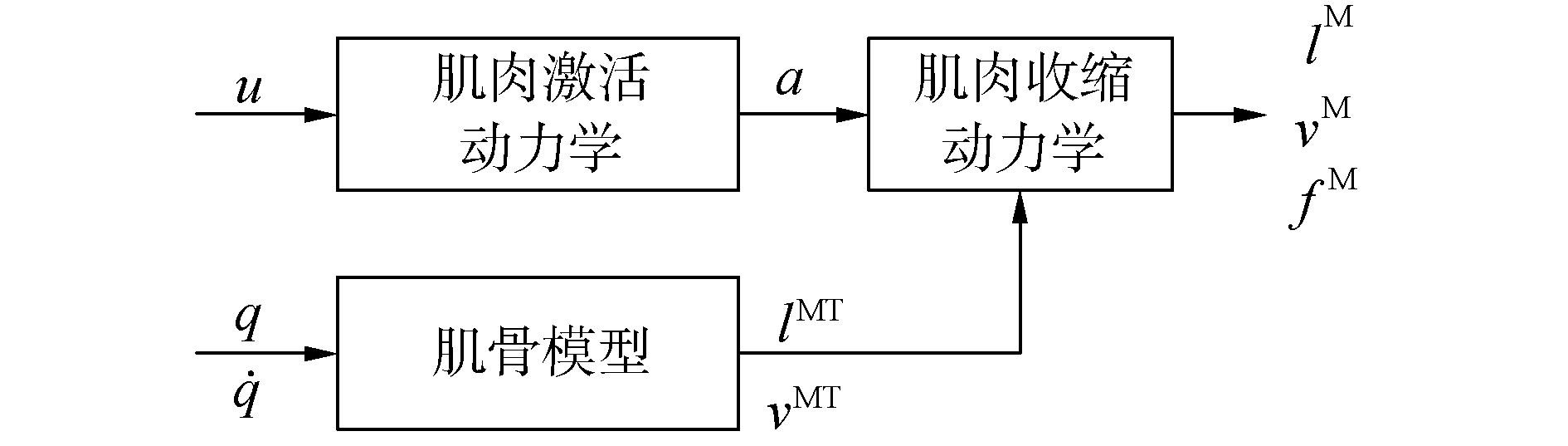
1.3 肌肉力力学分析生物肌肉和肌肉力的产生过程都很复杂,肌肉纤维受到运动神经信号的刺激,会产生收缩运动,肌肉力产生不仅和肌肉激活度a有关,而且还与肌肉腱速度vMT和长度lMT有关,其过程如图 3所示,主要包括3个模型:从神经刺激到肌肉激活度的产生模型(激活动力学)、由生成坐标q和速度
|
Download:
|
| 图 3 肌肉力驱动模型 Fig. 3 Muscle-driven simulations model | |
肌肉的激活和神经信号的刺激之间存在一定滞后,因此,采用简化的一阶微分方程表示激活度和神经刺激之间的关系[15]:
| $ \hat{a}=\frac{a-a_{\min }}{1-a_{\min }} $ | (9) |
| $ \dot{a}=\frac{u-\hat{a}}{T} $ | (10) |
| $ T=\left\{\begin{array}{c} T_{\text {act }}(0.5+1.5 \hat{a}) \\ \frac{T_{\text {deact }}}{0.5+1.5 \hat{a}} \end{array}\right. $ | (11) |
式中:Tact、Tdeact分别表示肌肉激活程度的上升和下降时间常数,Tact减小,由于低效钙的释放和扩散会使激活度增加,类似地,Tdeact减小,由于供肌浆网吸收的钙离子不足会使激活度减小[16];amin表示肌肉激活程度的最小值。为了避免肌肉腱数值计算的奇异性,需要通过修正传统的肌肉激活度状态方程[16]使激活度可以光滑变化。
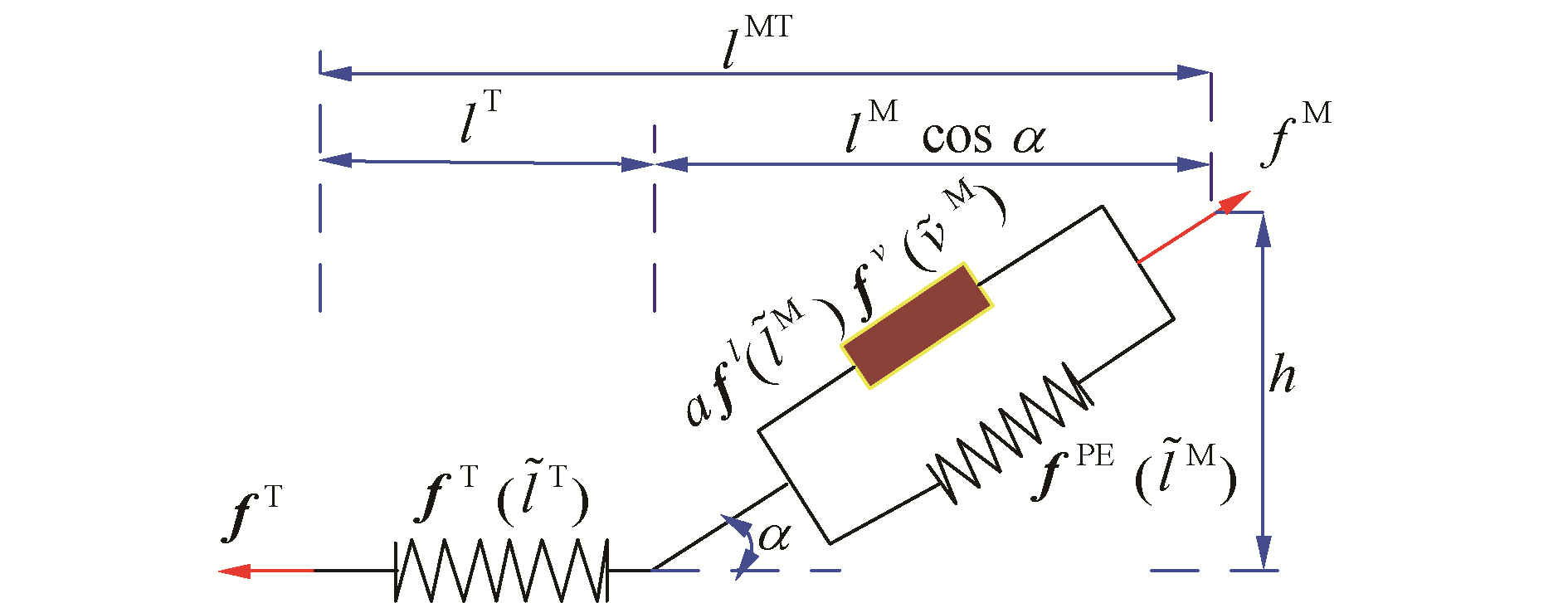
1.3.2 肌肉腱力平衡方程肌肉腱驱动包含主收缩元、被动弹性元件和弹性肌腱,如图 4所示,其中被动弹性元件的力和归一化肌纤维长度之间的关系可以表示为:
| $ f^{\mathrm{PE}}\left(\tilde{l}{}^{\mathrm{M}}\right)= \begin{cases}0, & l^{\mathrm{M}}<l_{0}^{\mathrm{M}} \\ b\left(\tilde{l}{}^{\mathrm{M}}\right)^{2}+c \tilde{l}{}^{\mathrm{M}}+d, & l^{\mathrm{M}} \geqslant l_{0}^{\mathrm{M}}\end{cases} $ | (12) |
|
Download:
|
| 图 4 肌肉腱力学简化模型 Fig. 4 Simplified model of musculo-tendon contraction mechanics | |
式中:l0M为肌肉产生最大等长收缩力时的肌肉纤维的长度;b、c、d为常数,与力-长度变化曲线相关[17]。
主收缩力和归一化的肌纤维长度之间的关系表示为高斯函数的形式:
| $ \boldsymbol{f}^{l}\left(\tilde{l}{}^{\mathrm{M}}\right)=\mathrm{e}^{-\left(\tilde{l}{}^{\mathrm{M}}-1\right)^{2} / \nu} $ | (13) |
式中ν表示力-速度曲线变异系数。
肌肉力fM可以表示为[17]:
| $ f^{\mathrm{M}}=f_{0}^{\mathrm{M}}\left(a \boldsymbol{f}^{l}\left(\tilde{l}{}^{\mathrm{M}}\right) \boldsymbol{f}^{v}\left(\tilde{v}{}^{\mathrm{M}}\right)+\boldsymbol{f}^{\mathrm{PE}}\left(\tilde{l}{}^{\mathrm{M}}\right)\right) $ | (14) |
式中:f0M为最大等长收缩力;激活度a的取值范围为amin~1。
肌纤维和肌腱连接在一起,且羽状角α,
| $ f_{0}^{\mathrm{M}}\left(a \boldsymbol{f}^{l}\left(\tilde{l}{}^{\mathrm{M}}\right) \boldsymbol{f}^{v}\left(\tilde{v}{}^{\mathrm{M}}\right)+\boldsymbol{f}^{\mathrm{PE}}\left(\tilde{l}{}^{\mathrm{M}}\right)\right) \cos \alpha-f_{0}^{\mathrm{M}} \boldsymbol{f}^{\mathrm{T}}\left(\tilde{l}{}^{\mathrm{T}}\right)=0 $ | (15) |
方程式(14)、(15)表示了肌肉力和肌腱力与肌肉纤维长度、速度和力之间的关系。
由方程式(15)是无法计算出肌肉力的,因为需要肌肉力长度和速度所满足方程式,但通过方程式(15)可以唯一的求得归一化速度
| $ \tilde{v}{}^{\mathrm{M}}=f_{\operatorname{inv}}^{v}\left(\frac{\boldsymbol{f}^{\mathrm{T}}\left(\tilde{l}{}^{\mathrm{T}}\right) / \cos \alpha-\boldsymbol{f}^{\mathrm{PE}}\left(\tilde{l}{}^{\mathrm{M}}\right)}{a \boldsymbol{f}^{l}\left(\tilde{l}{}^{\mathrm{M}}\right)}\right) $ | (16) |
式中finvv(·)表示收缩力-速度函数的反函数。
肌肉长度和速度与肌肉腱长度之间存在运动学关系:
| $ l^{\mathrm{MT}}=l^{\mathrm{T}}+l^{\mathrm{M}} \cos \alpha $ | (17) |
对式(17)两边分别对时间求导数,可以得到肌肉、肌腱和肌肉腱驱动速度之间的关系:
| $ v^{\mathrm{MT}}=v^{\mathrm{T}}+v^{\mathrm{M}} \cos \alpha-l^{\mathrm{M}} \dot{\alpha} \sin \alpha $ | (18) |
通过联立式(16)、(18)可以得到主动收缩力和肌纤维速度之间的关系fv(
上面建立了下肢的肌肉骨骼模型和肌肉力学模型,但还要通过约束优化解决冗余肌肉力的问题,对肌肉力的优化应用最广泛的方法为静态优化。选取式(19)的静态优化目标函数:
| $ \begin{cases}\min & J=\sum\limits_{i=1}^{N}\left(a_{i}\right)^{n} \\ \text { s. t. } & f_{0}^{\mathrm{M}}\left(a_{i} \boldsymbol{f}^{l}\left(\tilde{l}{}^{\mathrm{M}}\right) \boldsymbol{f}^{v}\left(\tilde{v}{}^{\mathrm{M}}\right)+\boldsymbol{f}^{\mathrm{PE}}\left(\tilde{l}{}^{\mathrm{M}}\right)\right) \cos \alpha- \\ & f_{0}^{\mathrm{M}} \boldsymbol{f}^{\mathrm{T}}\left(\tilde{l}{}^{\mathrm{T}}\right)=0, \quad 0<f_{i}^{\mathrm{M}}<f_{0}^{\mathrm{M}}\end{cases} $ | (19) |
式中:N为肌肉数量;ai为第i块肌肉的激活度;n的选取要根据不同的要求进行选择,本文选取n=2,选取肌肉激活度平方和最小函数J作为优化目标,可使人体运动感到很好的舒适性。
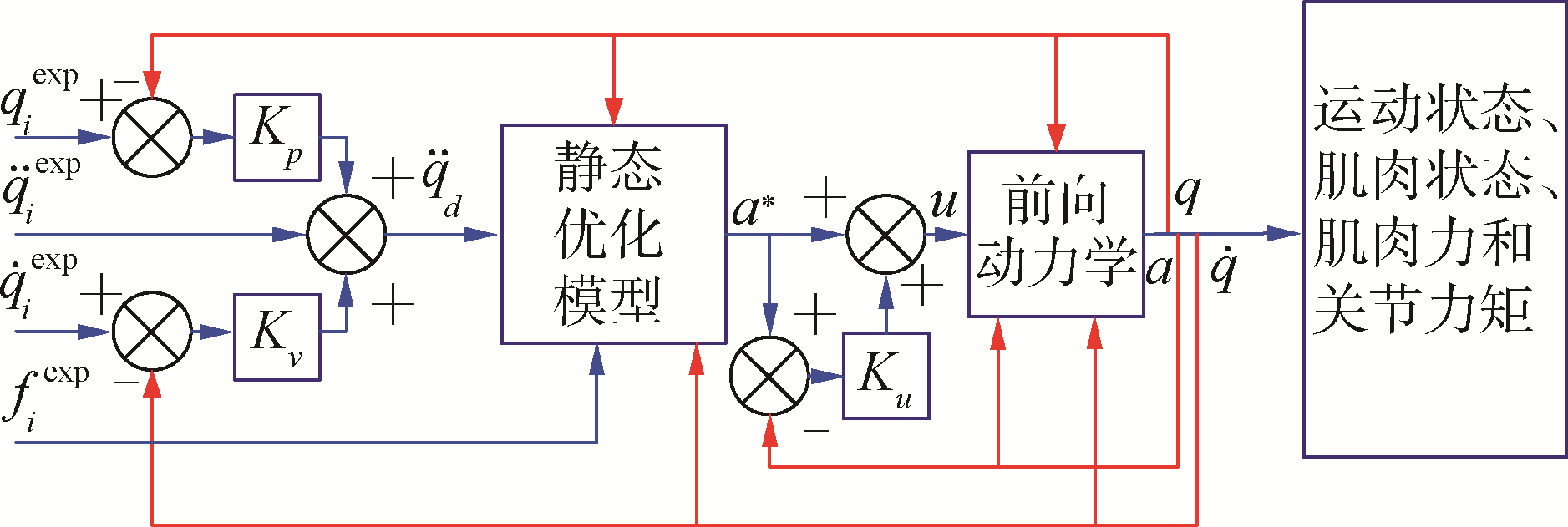
肌肉激活度a的规划可以通过计算肌肉控制模型(CMC)实现[16],在CMC中采用了PD控制方法实现肌肉激活度a的闭环控制,如图 5所示,其中qiexp、
|
Download:
|
| 图 5 CMC算法框图 Fig. 5 Schematic of CMC algorithm applied to gait | |
因此,第i个模型坐标的期望加速度
| $ \ddot{q}_{d}=\ddot{q}{}_{i}^{\text {exp }}+K_{v}\left(\dot{q}{}_{i}^{\text {exp }}-\dot{q}_{i}\right)+K_{p}\left(q_{i}^{\text {exp }}-q_{i}\right) $ | (20) |
且线性反馈控制器所计算得到的肌肉激励为:
| $ u=a^{*}+K_{u}\left(a^{*}-a\right) $ | (21) |
通过合理设置PD控制参数,可以实现下肢生物力学参数的最优化和下肢运动障碍患者的运动学、生物力学等参数的仿真,为下肢运动障碍患者的康复训练模式提供依据。
2 人体下肢运动数据采集为了分析和比较单屈膝行走步态与正常行走步态的下肢运动生物特性差异及对主要肌肉的疲劳损伤的影响,需要对2种行走步态的运动学进行测量(在无任何外界干扰的情况下),将测量髋关节、膝关节和踝关节的运动数据进行函数拟合,并将拟合函数作为在OpenSim建立的3-D人体肌骨模型的运动驱动,最后通过仿真2种行走步态,对下肢肌肉收缩量等问题进行分析。
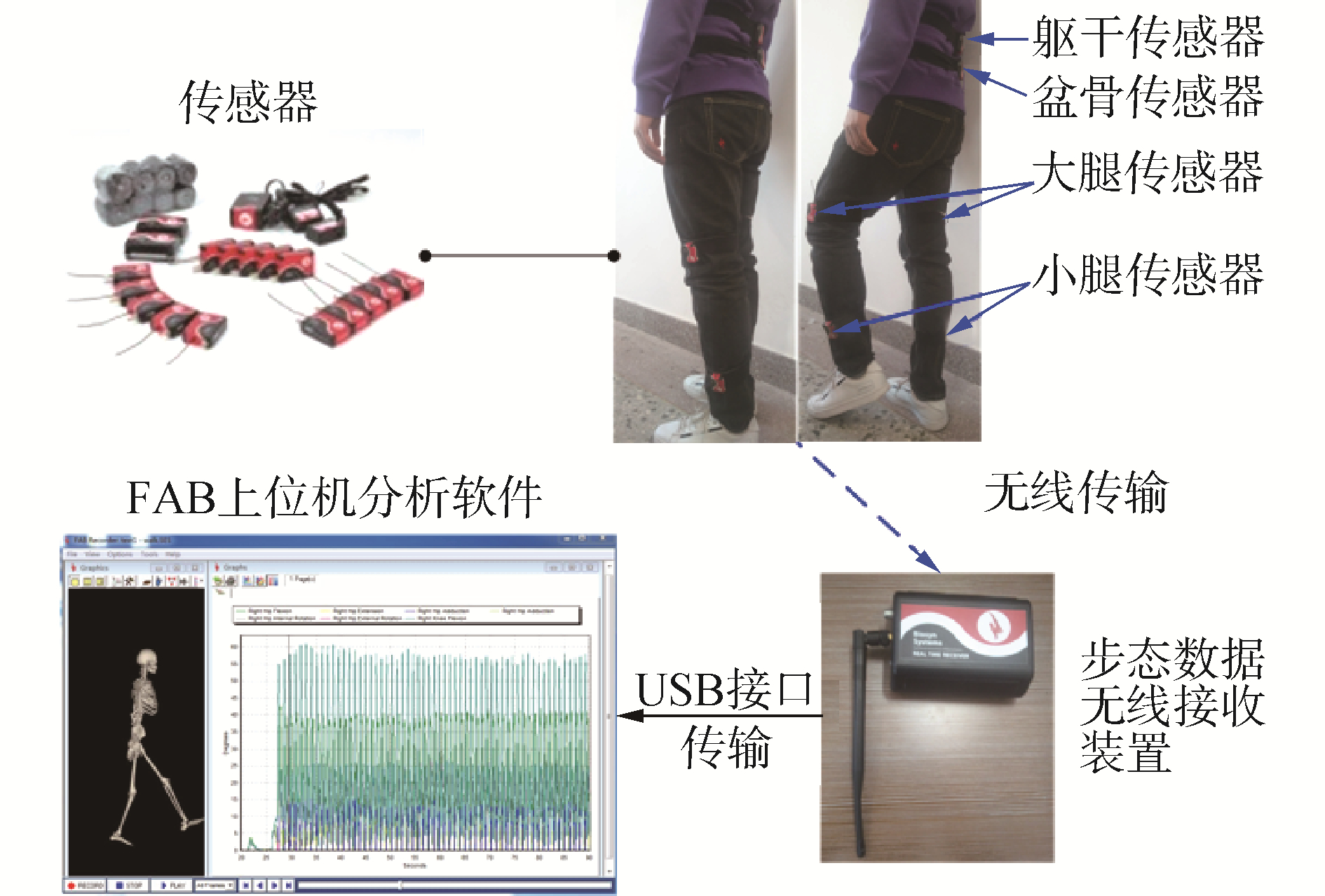
本文以8名男性青年(身高165±10 cm,体重60±5 kg,年龄24±1岁) 作为受试对象,通过FAB采集所需的人体运动数据,FAB系统的惯性传感器结合了加速度传感器、方位传感器和足底力传感器,将各部位的惯性传感器安装在受试者身体相应的位置上,受试者分别按2种步态行走,FAB会通过实时无线步态检测系统的无线步态数据接收端检测和接收人体运动相关的数据,步态数据接收端会通过USB接口将数据传输到计算机分析软件中,软件就可以实时记录人体运动相关的所有运动学和动力学数据,且采样频率为100 Hz。传感器在人体上的安装和FAB采集系统如图 6所示。
|
Download:
|
| 图 6 传感器安装和FAB采集系统 Fig. 6 Installation positions of sensors and FAB collection system | |
受试者行走100 s,在单曲膝行走步态行走过程中,右腿受伤屈膝行走,左腿正常,因此,只研究右腿的运动生物力学特性,忽略膝关节和踝关节的内翻/外翻和内旋/外旋的现象,对记录的下肢运动参数以步态周期为步长取运动参数的平均值,并利用傅里叶级数对关节运动数据进行拟合,傅里叶级数的拟合函数表达式为:
| $ \theta(t)=a_{0}+\sum\limits_{i=1}^{n}\left(a_{i} \cos (\mathrm{i} \omega t)+b_{i} \sin (i \omega t)\right) $ | (22) |
式中:θ(t)为关节运动角度;t为时间;a0、ai、bi和ω均为傅里叶级数方程的系数,n∈Z+的大小取决于拟合度的大小,本研究中拟合度要求不低于99.4%。
针对2种行走步态在步态周期内的关节角度由FAB系统采集记录,通过傅里叶级数进行拟合,其傅里叶级数拟合函数的参数如表 1所示。
| 表 1 傅里叶级数拟合函数的参数 Table 1 The parameters of Fourier series fitted function |
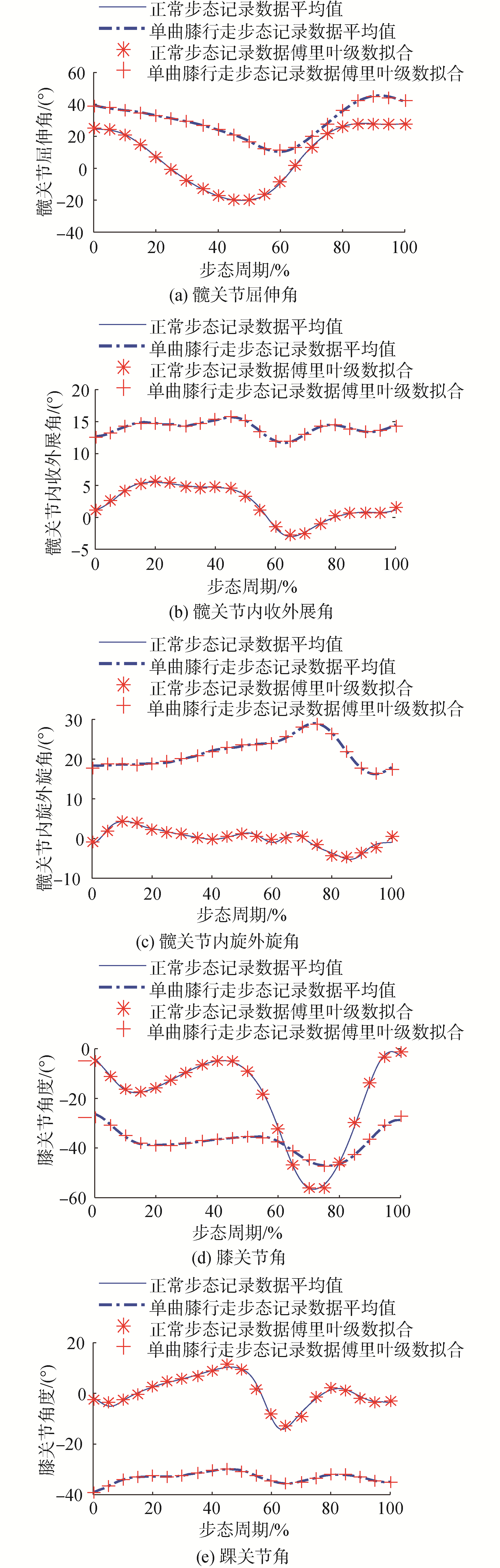
由表 1中参数构成函数的拟合度均大于99.4%,FAB采集到的下肢关节运动角度和傅里叶级数拟合角度的变化曲线如图 7所示,结果表明拟合函数具有很高的跟踪性能,可以直接作为3-D人体肌骨模型关节运动的驱动函数。其中NWG为正常行走步态数据,SCWG为单曲膝行走步态数据。
|
Download:
|
| 图 7 下肢关节角度变化曲线 Fig. 7 Joint angle change curves of lower extremity | |
由图 7可知:人体正常步态行走时,髋关节的屈伸角变化范围为[-21.046°, 21.534°],内收外展角变化范围为[-6.9.5°, 6.991°],内旋外旋角变化范围为[-10.572°, 6.325°],膝关节变化角度变化范围为[-69.27°, 0.647°],踝关节的屈伸角度变化范围为[-6.85°, 16.05°],角度变化速度较大,且髋关节的屈伸角和膝关节角度的变化范围很大;而在单屈膝步态行走时,髋关节的屈伸角变化范围[9.891°, 45.812°],内收外展角变化范围为[11.935°, 14.956°],内旋外旋角变化范围为[16.335°, 20.089°],膝关节变化角度变化范围为[-47.223°, -28.911°],踝关节的屈伸角度变化范围为[-35.595°, -3.391°],角度变化速度较小,因此,在下肢单曲膝步态行走时,关节角度变化范围较小,变化速度较小。从变化规律来看,髋关节内旋/外旋角的变化规律和正常步态由较大差别,其他关节角度变化规律和正常步态基本一致。
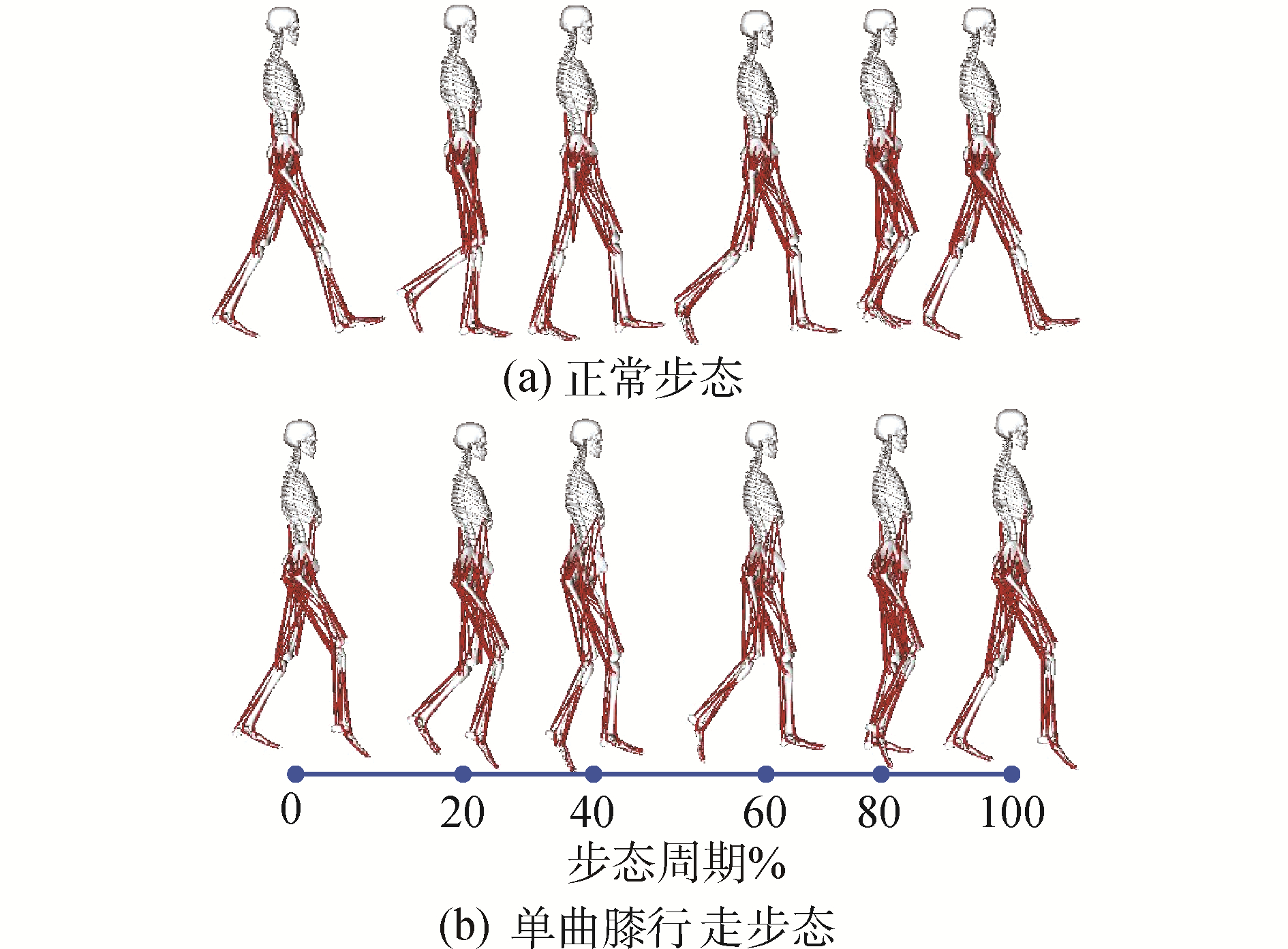
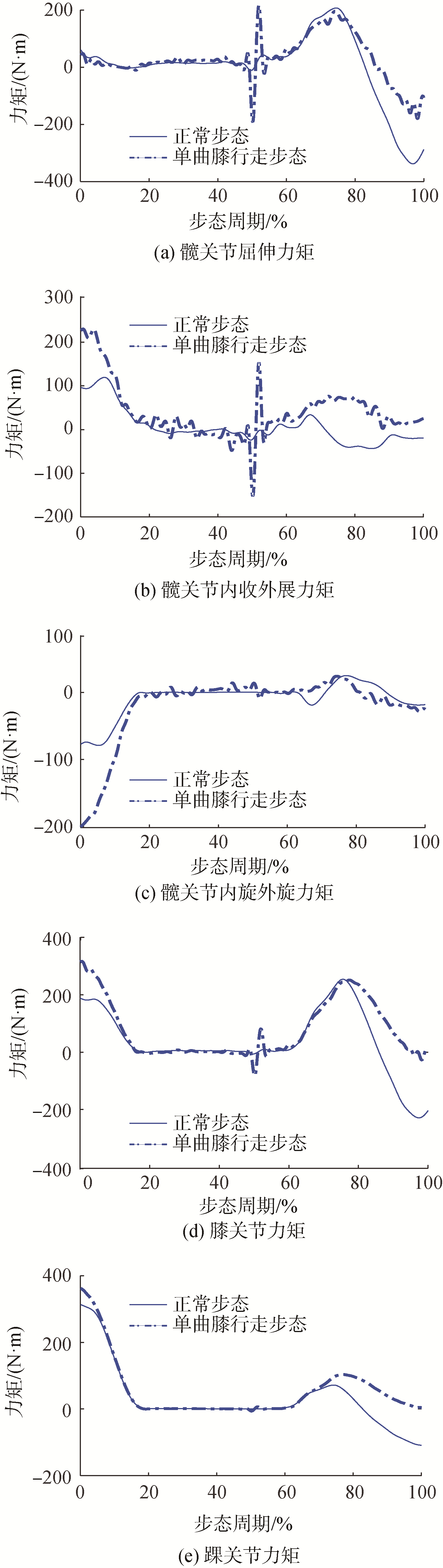
3 单曲膝行走步态对下肢肌肉的影响根据受试者身高、体重,在OpenSim软件中进行SCALE人体3-D模型设置,以图 7所示的关节角度变化数据驱动人体下下肢运动,对下肢运动的动力学模型进行仿真,图 8所示为下肢在NWG和SCWG步态下人体3-D模型的周期运动模型,由图可知:在SCWG行走时,2条腿的运动学特征均有变化,但受伤的右腿变化更为明显。图 9所示为下肢关节驱动力矩的变化曲线,其中实线表示正常步态,点划线表示单曲膝行走步态。
|
Download:
|
| 图 8 NWG和SCWG的人体3-D运动模型对比 Fig. 8 Comparison of human 3-D movement models of NWG and SCWG | |
|
Download:
|
| 图 9 下肢关节驱动力矩 Fig. 9 Joint torque change curves of lower extremity | |
下肢各关节运动对应驱动力矩如图 9所示,和正常行走步态相比,按SCWG行走时,下肢各关节运动驱动力矩波动较大,且在步态周期的48.7%~53.6%,髋关节屈伸运动力矩、髋关节内收外展运动力矩和膝关节运动力矩出现的波动很大,波动范围分别为[-197, 211]N ·m、[-149, 161]N ·m和[-80, 75] N ·m。在步态周期的0~15.9%之间,SCWG的下肢各关节的驱动力矩明显大于正常行走步态的驱动力矩(髋关节屈伸力矩除外),在步态周期的78.2%~100%,SCWG的下肢膝关节和踝关节的驱动力矩明显小于正常行走步态的驱动力矩。因此,当人体下肢受伤后以SCWG行走时,在步态周期的48.7%~53.6%和0~15.9%会产生明显的不舒适感,对该类患者的康复治疗和训练过程中需要考虑这点。
在CMC计算,参数设置为Kp=100,Kv=20和Ku=1。在行走步态周期中,下肢运动主要的12块肌肉力变化如图 10所示,其中实线表示正常步态,点划线表示单曲膝行走步态。总的来看,SCWG行走时,半膜肌、半腱肌、股二头肌、长收肌、臀大肌、髂肌、腰肌、股四头肌、股直肌和胫骨前肌的肌肉力明显大于NWG下的肌肉力,而比目鱼肌和胫骨后肌的肌肉力小于NWG下的肌肉力,SCWG行走的12块肌肉的肌肉力的波动幅度均大于NWG的肌肉力的波动幅度,主要是由于步态的不稳定引起的。这表明:SCWG行走时,半膜肌、半腱肌、股二头肌、长收肌、臀大肌、髂肌、腰肌、股四头肌、股直肌和胫骨前肌均起到了主要作用,而比目鱼肌和胫骨后肌起到辅助的作用。

|
Download:
|
| 图 10 下肢肌肉力变化曲线 Fig. 10 The change curves of muscle forces of lower extremity | |
和NWG相比,SCWG在步态周期后期86.1%~100%,半膜肌、半腱肌和股二头肌的肌肉力减小大约一半,在步态后期63.8%~100%,胫骨前肌的肌肉力为NWG的2倍,在步态周期前期0~14%,长收肌、臀大肌、髂肌、腰肌和股四头肌的肌肉力较小。
图 11给出了下肢运动过程中肌肉激活度的变化情况,其中实线表示正常步态,点划线表示单曲膝行走步态,由图可知肌肉激活度的变化情况和肌肉力的变化趋势基本一致,激活度的变化情况此处不再赘述。

|
Download:
|
| 图 11 下肢肌肉激活度 Fig. 11 The change curves of muscle activation of lower extremity | |
在SCWG行走时,下肢关节力矩的增加和大幅度波动,会导致关节运动不稳定,增加关节的损伤和肌肉的负担,肌肉活性的增强同样会导致肌肉的疲劳损伤等问题的出现,因此,研究结果为下肢损伤的患者康复和康复设备的研发提供了数据基础。
4 结论1) 在单曲膝行走步态下,下肢各关节角度的变化范围小,特别是髋关节和膝关节的变化范围尤为明显。
2) 在步态周期的初期,单曲膝行走步态的下肢关节驱动力矩的波动明显增加,并且下肢关节驱动力矩明显大于正常行走步态下的关节驱动力矩(髋关节屈伸运动的驱动力矩除外);在步态周期的后期,膝关节和踝关节的驱动扭矩明显小于正常行走步态下的关节驱动力矩。
3) 在单曲膝行走步态下,半膜肌、半腱肌、股二头肌、前胫骨肌、臀大肌、股四头肌,股直肌和胫骨的肌肉力和激活度明显增加,其波动值和频率也明显增加。
| [1] |
DESCHAMPS K, EERDEKENS M, GEENTJENS J, et al. A novel approach for the detection and exploration of joint coupling patterns in the lower limb kinetic chain[J]. Gait & posture, 2018, 62: 372-377. (  0) 0)
|
| [2] |
HUME D R, NAVACCHIA A, RULLKOETTER P J, et al. A lower extremity model for muscle-driven simulation of activity using explicit finite element modeling[J]. Journal of biomechanics, 2019, 84: 153-160. DOI:10.1016/j.jbiomech.2018.12.040 (  0) 0)
|
| [3] |
BAILEY J P, SILVERNAIL J F, DUFEK J S, et al. Effects of treadmill running velocity on lower extremity coordination variability in healthy runners[J]. Human movement science, 2018, 61: 144-150. DOI:10.1016/j.humov.2018.07.013 (  0) 0)
|
| [4] |
CHUANG T D, ACKER S M. Comparing functional dynamic normalization methods to maximal voluntary isometric contractions for lower limb EMG from walking, Cycling and running[J]. Journal of electromyography and kinesiology, 2019, 44: 86-93. DOI:10.1016/j.jelekin.2018.11.014 (  0) 0)
|
| [5] |
ALEXANDER N, SCHWAMEDER H. Effect of sloped walking on lower limb muscle forces[J]. Gait & posture, 2016, 47: 62-67. (  0) 0)
|
| [6] |
LIM Y P, LIN Y C, PANDY M G. Effects of step length and step Frequency on lower-limb muscle function in human gait[J]. Journal of biomechanics, 2017, 57: 1-7. DOI:10.1016/j.jbiomech.2017.03.004 (  0) 0)
|
| [7] |
VARRECCHIA T, RINALDI M, SERRAO M, et al. Global lower limb muscle coactivation during walking at different speeds: Relationship between spatio-temporal, kinematic, kinetic, and energetic parameters[J]. Journal of electromyography and kinesiology, 2018, 43: 148-157. DOI:10.1016/j.jelekin.2018.09.012 (  0) 0)
|
| [8] |
MENTIPLAY B F, BANKY M, CLARK R A. Lower limb angular velocity during walking at various speeds[J]. Gait & posture, 2018, 65: 190-196. (  0) 0)
|
| [9] |
LENTON G K, DOYLE T L A, LLOYD D G, et al. Lower-limb joint work and power are modulated during load carriage based on load configuration and walking speed[J]. Journal of biomechanics, 2019, 83: 174-180. DOI:10.1016/j.jbiomech.2018.11.036 (  0) 0)
|
| [10] |
ZHAO Lingyan, MA Xiaohao, ZHANG Bingzao, et al. Biomechanical research of knee joint during the process of running[J]. Journal of Southeast University (English Edition), 2017, 33(1): 27-32. (  0) 0)
|
| [11] |
RESENDE R A, DELUZIO K J, KIRKWOOD R N, et al. Increased unilateral foot pronation affects lower limbs and pelvic biomechanics during walking[J]. Gait & posture, 2015, 41(2): 395-401. (  0) 0)
|
| [12] |
CHENG Y Y, WEI S H, CHEN P Y, et al. Can sit-to-stand lower limb muscle power predict fall status?[J]. Gait & posture, 2014, 40(3): 403-407. (  0) 0)
|
| [13] |
KOYAMA K, YAMAUCHI J. Comparison of lower limb kinetics, kinematics and muscle activation during drop jumping under shod and barefoot conditions[J]. Journal of biomechanics, 2018, 69: 47-53. DOI:10.1016/j.jbiomech.2018.01.011 (  0) 0)
|
| [14] |
DE SOUSA A C C, FREIRE J P C D, BO A P L. Integrating hip exosuit and FES for lower limb rehabilitation in a simulation environment[J]. International federation of automatic control, 2019, 51(34): 302-307. (  0) 0)
|
| [15] |
郭超, 何育民, 孙朝阳, 等. OpenSim环境下人体下肢行走生物力学特性研究[J]. 机械科学与技术, 2020. GUO Chao, HE Yumin, SUN Zhaoyang, et al. Research of biomechanical characteristics of human lower limb walking using the OpenSim technology[J]. Mechanical science and technology for aerospace engineering, 2020. DOI:10.13433/j.cnki.1003-8728.20200225 (  0) 0)
|
| [16] |
MILLARD M, UCHIDA T, SETH A, et al. Flexing computational muscle: modeling and simulation of musculotendon dynamics[J]. Journal of biomechanical engineering, 2013, 135(2): 021005. DOI:10.1115/1.4023390 (  0) 0)
|
| [17] |
THELEN D G, ANDERSON F C. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data[J]. Journal of biomechanics, 2006, 39(6): 1107-1115. DOI:10.1016/j.jbiomech.2005.02.010 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


