2. 黑龙江科技大学 计算机与信息工程学院, 黑龙江 哈尔滨 150022
2. College of Computer Science and Technology, Heilongjiang University of Science and Technology, Harbin 150022, China
深度学习广泛用于处理模式识别问题的实际场景,并且向着结构更深、规模更大、设计更精巧的方向发展,由此带来越来越多的模型参数及越来越长的模型训练时间。深度学习的模型训练过程是一个复杂的、需要综合考量的问题,其优化过程涉及到参数、结构以及方法等各个方面。有研究人员从不同的解读角度入手,提出了不同的解决方法,但这些方面多与模型结构相关,存在无法泛化的弊端。研究证明,传统的深度学习的模型训练过程之所以耗费大量的训练时间,其原因在于模型因寻找全局最优解的过程中陷入到的低学习率区域。与传统的训练方法相比,使用先验知识的引导,可以认为神经网络已知了一个或多个可以通往全局最优解的方向,这类方向的数量由先验知识的数量决定。而在实际应用中,损失平面上鞍点的数量远大于局部极小值区域的数量,正是由于在鞍点处可以存在数十亿个可能的梯度下降方向[1],所以能否尽快的寻找到一条通往全局最优解的方向将决定神经网络训练速度的快慢。近几年,由于应用的需求,如何解决模型的优化问题逐渐成为研究模型解释性与模型优化方法的研究重点之一。
HINTON等[2]提出了深度神经网络的概念。神经网络的训练过程优化方法通常采用更平均的初始化参数、更快的梯度下降算法或更精炼的网络结构来实现的。He等[3]提出的he-normal初始化,与之前比较通用的Xavier方法[4]相比提供了更低的初始loss值和更快的loss值下降速度,从而降低模型训练时间;Kingma等[5]提出了自适应性矩估计(adaptive moment estimation,Adam)优化器,融合了自适应梯度算法(adaptive gradient algorithm,Adagrad)[6]和均方根传递算法(root mean square prop,RMSprop)[7]的优点,在非凸优化问题上有很优秀的性能;Ioffe等[8]提出的批标准化(batch normalization,BN)层,解决了神经网络随着网络深度加深而带来的训练困难、收敛缓慢的问题。这些优化方法有效地提高了神经网络的性能,减少了训练时间,但是在最近的5年里,随着神经网络在各个领域的智能信息处理方面所占据的比重越来越大、待解决的实际问题复杂性越来越高,而目前神经网络的算法和结构优化的发展又较为缓慢,仅仅依靠神经网络来处理这些问题,就会在时间效率等方面稍显不足了。
就目前的深度学习模型应用来说,大量的模型已成功的应用到相似的场景中[9],相似的场景中的现场数据投影到空间内也可以说是同构同模,对迁移学习的研究也早已指出模型的移植性来自于数据的同构[10]。在这样的理论基础上,若神经网络结构中存在不变性,则可以直接将模型参数作为先验知识应用于网络设计中,从而提高网络的训练效率。对网络参数变化趋势的总结,正是基于神经网络的这种本质特性而制定的。因此,利用先验数据来进行模型训练的指导是一个可行的方案。
本文基于参数同构的思想结合深度学习的模型设计理念,提出了一种基于先验知识改进神经网络训练过程的模型训练优化方法。方法通过累积模型训练中的卷积层参数构建数据集,并以此数据集训练反应卷积层参数变化趋势的回归模型,将该模型作为参数变化的先验知识参与到神经网络模型的训练过程中。通过引入先验知识的指导,模型可以根据参数收敛趋势越过训练数据集中的局部极小值或鞍点,降低随机梯度下降算法(stochastic gradient descent,SGD)在训练过程中陷入停滞的风险,提高训练效率。
1 基于先验知识的深度学习训练优化在神经网络模型训练过程中引入先验知识是一种针对复杂任务进行时间优化的方法,这类方法的基础实现方式可以简单的与相机的自动对焦过程类比。在相机的自动对焦过程中,系统将图像送到图像处理器,同时对焦算法库将得到的图像信息结合硬件规范计算出镜头的动作。经过几次循环收敛,对焦成功。由于对焦算法库的干预,使得相机的对焦过程不需要多次迭代就能达到收敛状态。
与该过程类似, 本文所介绍的基于先验知识的优化方法利用回归模型构建了对焦库,并将其嵌入到神经网络的训练过程中,达到了加速网络训练的效果。
1.1 参数先验知识的构建在传统的神经网络结构中,模型参数的训练遵循“差值-梯度-参数”规则,即根据每次迭代输出的标签值与实际值进行对比得到差值,利用差值输出梯度,并按照梯度修改神经网络网络参数。单层神经网络的参数训练过程为:
| $ {\rm{loss}}\left( {w, b} \right) = \frac{1}{N}\sum\limits_{i = 0}^N {{{(w{x_i} + b - {y_i})}^2}} $ | (1) |
| $ {\rm{grad}}\left( w \right) = \frac{{\partial {\rm{loss}}\left( {w, b} \right)}}{{\partial w}} = \frac{1}{N}\sum\limits_{i = 0}^N {(w{x_i} + b - {y_i}){x_i}} $ | (2) |
| ${\rm{grad}}\left( b \right) = \frac{{\partial {\rm{loss}}\left( {w, b} \right)}}{{\partial b}} = \frac{1}{N}\sum\limits_{i = 0}^N {(w{x_i} + b - {y_i})} $ | (3) |
式中:w为权值;b为偏置;N为样本总数。
本文提出的基于先验知识的神经网络优化方法将先验知识应用到了神经网络训练过程中,其先验知识的构建步骤:
1) 需要构建网络在类似数据集上进行预训练时得到的参数矩阵和梯度矩阵。卷积层在每一次迭代的正向传播过程中都可以得到权值、偏置与其分别的梯度所构成的4种矩阵。将网络参数整理成可训练的数据矩阵,同时将对应的梯度矩阵作为标签,就可以形成“权值-梯度”、“偏置-梯度”2种数据集;
2) 构建回归模型用以拟合网络参数与梯度之间的关系。根据上文构建的2种数据集,在卷积层分别构建grad(w)和grad(b)2种回归模型。由于在神经网络的卷积层中,层与层之间的参数变化是离散关系,所以需要分别对每一层的参数构建不同的回归模型来拟合变化规律。一个由n层全连接网络形成的回归模型构建过程为:
| $ {\rm{grad}}\left( w \right) = {w_0}{x_0} + {w_1}{x_1} + \ldots + {w_n}{x_n} = \sum {\mathit{\boldsymbol{w}}_i}{x_i} $ | (4) |
| $ {\rm{grad}}\left( b \right) = {b_0}{y_0} + {b_1}{y_1} + \ldots + {b_n}{y_n} = \sum {\mathit{\boldsymbol{b}}_j}{y_j} $ | (5) |
式中wi、bj分别为回归模型中每一层的权值、偏置矩阵。
由于这样构建的回归模型具有根据网络参数的数值直接拟合下一步更新的梯度、进而指导网络参数变化的性质,同时具有使神经网络在训练时得以跳过对数据集进行迭代求解差值、计算梯度、更新网络参数的正向传播过程的能力,所以称这种回归模型为对焦库。同样地,可以将这种替代梯度下降算法求导过程、修改网络正向传播方式的模型训练方法称为对焦算法。
1.2 基于先验知识回归的参数更新方法在应用梯度下降算法的神经网络训练过程中,每一次迭代都需要运行训练与测试2个模块,如图 1所示,训练模块又包含4个步骤:1)在神经网络中运行训练集,记录训练得到的标签y′;2)对比训练标签y′与相应的数据集标签y,得到差值损失;3)根据差值损失计算神经网络中相应参数的梯度;4)利用梯度梯度更新神经网络参数。

|
Download:
|
| 图 1 神经网络参数更新方法 Fig. 1 Neural network parameter update method | |
网络模型的训练过程中,训练模块占据了每一次迭代中大部分的时间。训练模块所消耗的时间主要集中在分批量训练数据和根据损失计算梯度的过程中。本文在不同深度的VGGNet[11]上进行测试,分析了训练步骤占单次迭代总时间的比例。以本文构建的16层卷积的神经网络模型为例,训练模块约占训练总时间的92%;测试模块约占训练总时间的8%。在此基础上对训练模块进行细分,各步骤占比分别为:
步骤1 训练数据约占训练模块总时间的58%,占单次迭代总时间的53%;
步骤2 计算loss约占训练模块总时间的3%,占单次迭代总时间的3%;
步骤3 计算grad约占训练模块总时间的32%,占单次迭代总时间的30%;
步骤4 更新参数约占训练模块总时间的7%,占单次迭代总时间的6%。
通过对训练模块中不同步骤消耗时间占比数据的分析可以得出,针对神经网络训练方法的优化应该首先考虑对训练模块进行修改。当待处理的数据量持平时,利用回归模型拟合输出数据所消耗的时间远小于利用梯度下降算法计算输出数据的时间,因此,本文提出的通过使用对焦库来替换训练模块的方法将有效地减少训练时间。
将对焦库调入到神经网络结构中形成改进模型后,在单次调用时,参数的更新过程为:1)屏蔽梯度下降算法的正向与反向传播过程,只保留梯度更新过程;2)截取卷积层的权值和偏置矩阵,经过对焦库拟合得到梯度;3)调用梯度更新卷积层参数。这种模型的迭代方法,缩短了梯度下降算法不断迭代并计算差值的过程,从而形成了“参数获取-回归拟合-梯度更新”的神经网络对焦算法。
在实际应用中,改进的神经网络将默认调用梯度下降算法,同时采用对焦算法与梯度下降算法交叉调用的方式。这种交叉调用的方式需要设定一个转换2种训练方式的阈值,本文选择模型训练中2次迭代之间分类正确率增幅小于1%时,即认为模型已经陷入低学习率区域,此时模型将在下一次训练开始前停止当前调用的训练方法,转而使用另一种方法进行训练。这样的交叉调用方法可以使得模型主动跳出由局部极小值和鞍点带来的低学习率区域,从而有效的的提高神经网络训练速度。
2 实验设计与优化结果对比分析 2.1 实验背景设计本实验选取Tiny Images数据中的Cifar10数据集用于神经网络的训练和测试,该数据集为50 000个训练样本和10 000个测试样本组成的32×32×3的图片数据集。同时,网络结构基础框架采用了多个不同的VGG卷积神经网络,其中卷积层深度分别为8、10、13和16层,表 1显示了具体的网络结构配置。此外,实验套用了he-normal正态分布初始化方法用来指导网络参数的初始化。
| 表 1 卷积网络结构配置 Table 1 Convolutional network structure configuration |
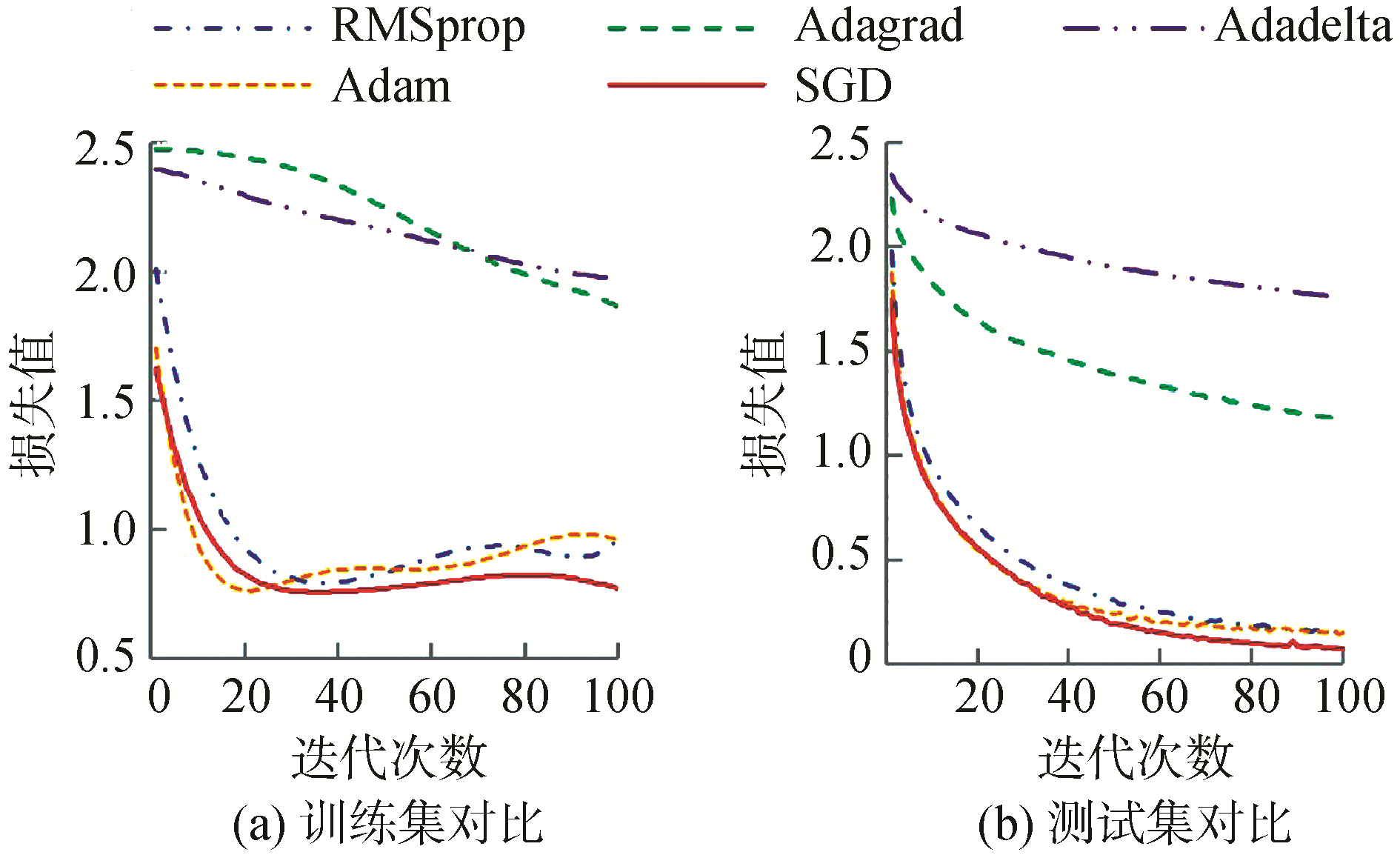
在优化器的选择上,为了排除其他方面对模型训练带来的影响,实验首先在Cifar10数据集中对多种优化器进行对比,各优化器具体变化趋势如图 2所示。可以看出,在训练集上,SGD能够得到最低loss值;在测试集上,SGD前期迭代速度虽然不及Adam,但是后期仍然是较突出的。这样的结果也同文献[12]在论文中得到的实验结果相同,出现这样的现象,主要是由于面对同样的一个优化问题,不同的优化算法可能会找到不同的答案,但自适应学习率的算法往往找到非常差的答案。通过特定的数据例子说明,自适应学习率算法可能会对前期出现的特征过拟合,后期才出现的特征很难纠正前期的拟合效果[13]。同样的,文献[14]进一步的在Cifar10数据集上进行测试,发现Adam的收敛速度比SGD要快,但最终收敛的结果不如SGD有效。
|
Download:
|
| 图 2 不同优化器的函数损失变化 Fig. 2 Loss changes of different optimizers | |
就卷积层单次迭代所消耗的时间而言,传统的梯度下降算法中一次迭代的时间复杂度为o(n),其中n代表batch-size;而在应用了先验知识指导的卷积层中,一次迭代所消耗的时间复杂度仅为o(1)。即要处理的数据量复杂度越高,在模型中引入先验知识所带来的时间优势就越明显。
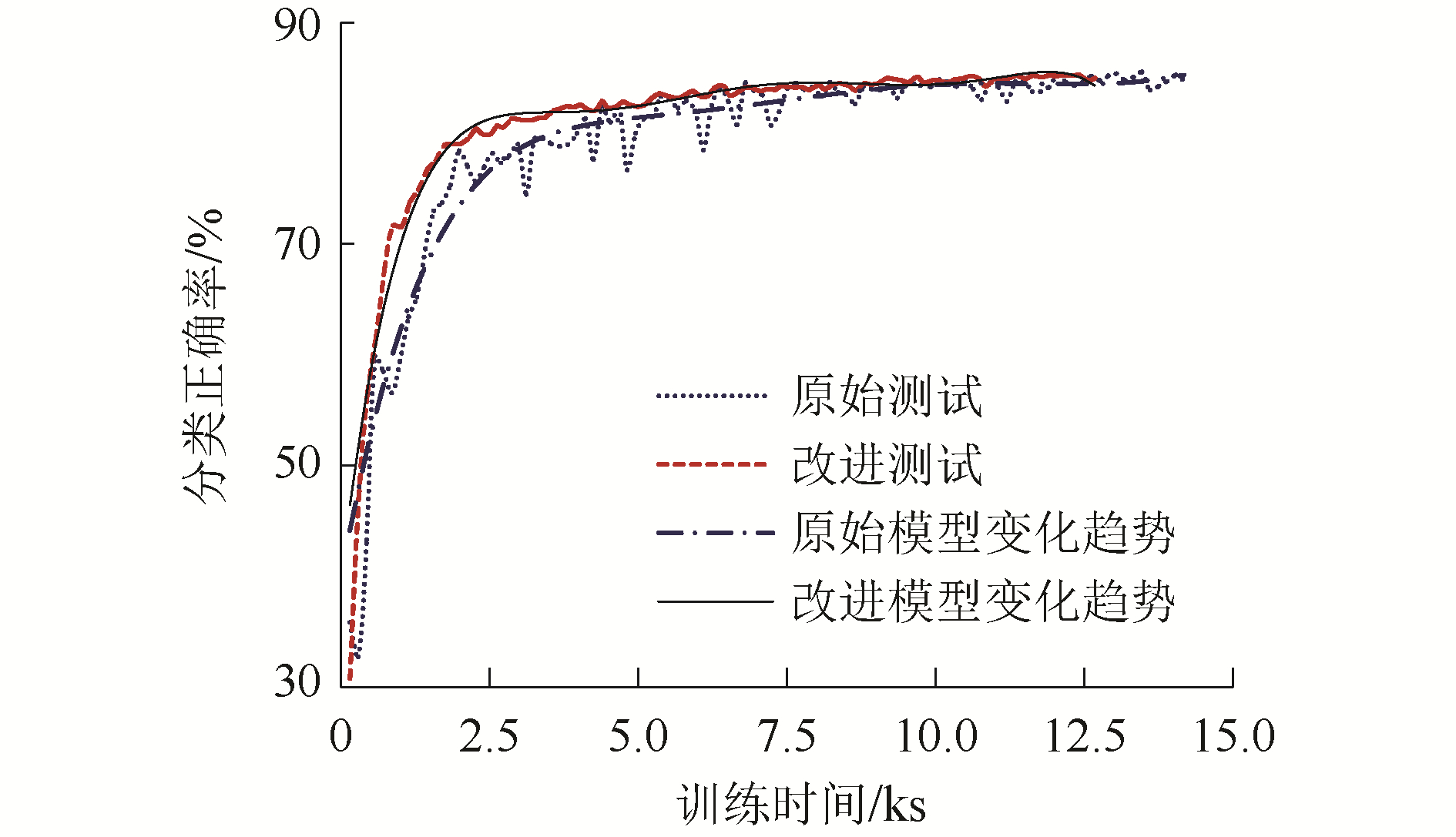
图 3为原始模型和改进模型分别在VGG网络结构中对Cifar10进行训练的“时间-正确率”的平均变化规律折线图,实验记录了应用交叉调用方法的改进模型与应用梯度下降算法的原始模型在训练时产生的迭代次数、正确率和消耗时间等数值。其中圆、方散点分别为原始模型和改进模型的测试集正确率,单点线、实线为分别为原始模型和改进模型的正确率变化趋势。原始模型在10 000 s、改进模型在7 500 s时,两者的变化趋势曲线几乎不再变化,可以认为模型的训练已经结束。在这样的前提条件下,从时间角度来看,不论是模型前期训练的增长速度还是达到最高分类正确率的时间,应用了先验知识指导的神经网络一直领先于原始模型,且达到最高正确率的时间相对提前了约25%,同时两者所能达到的最高分类正确率几乎吻合,误差平均不超过0.5%。
|
Download:
|
| 图 3 正确率变化对比 Fig. 3 Comparison of accuracy changes | |
在实际应用中,为了解决一些复杂问题,会构建出更深层的卷积神经网络,而随着网络层数的增加,训练时间也会越来越长。为了验证这种由先验知识指导的神经网络训练方法在更深层的网络结构中也能起到优化作用,本文分别在VGG11、VGG13、VGG16和VGG19这4个不同卷积层深度的神经网络结构上进行实验,并控制训练时间以模拟实际应用时对模型训练时间的限制。表 2为数据集Cifar10不同深度的神经网络中训练时间的对比,可以看到,当卷积层从8层逐步扩大到16层时,模型训练时间的提升由10.6%扩大为15.4%,与此同时,原始模型和改进模型在全部迭代中所能达到的最高分类正确率差值一直保持在0.5%以下。这说明改进模型在图像特征提取和分类能力上与原始模型没有差别,并且在二者正确率相似的情况下,随着卷积层的不断加深,应用改进模型所能带来的时间优势会越来越大。
| 表 2 卷积层数增加时的时间优势对比 Table 2 Comparison of time advantages when the number of convolutional layers increases |
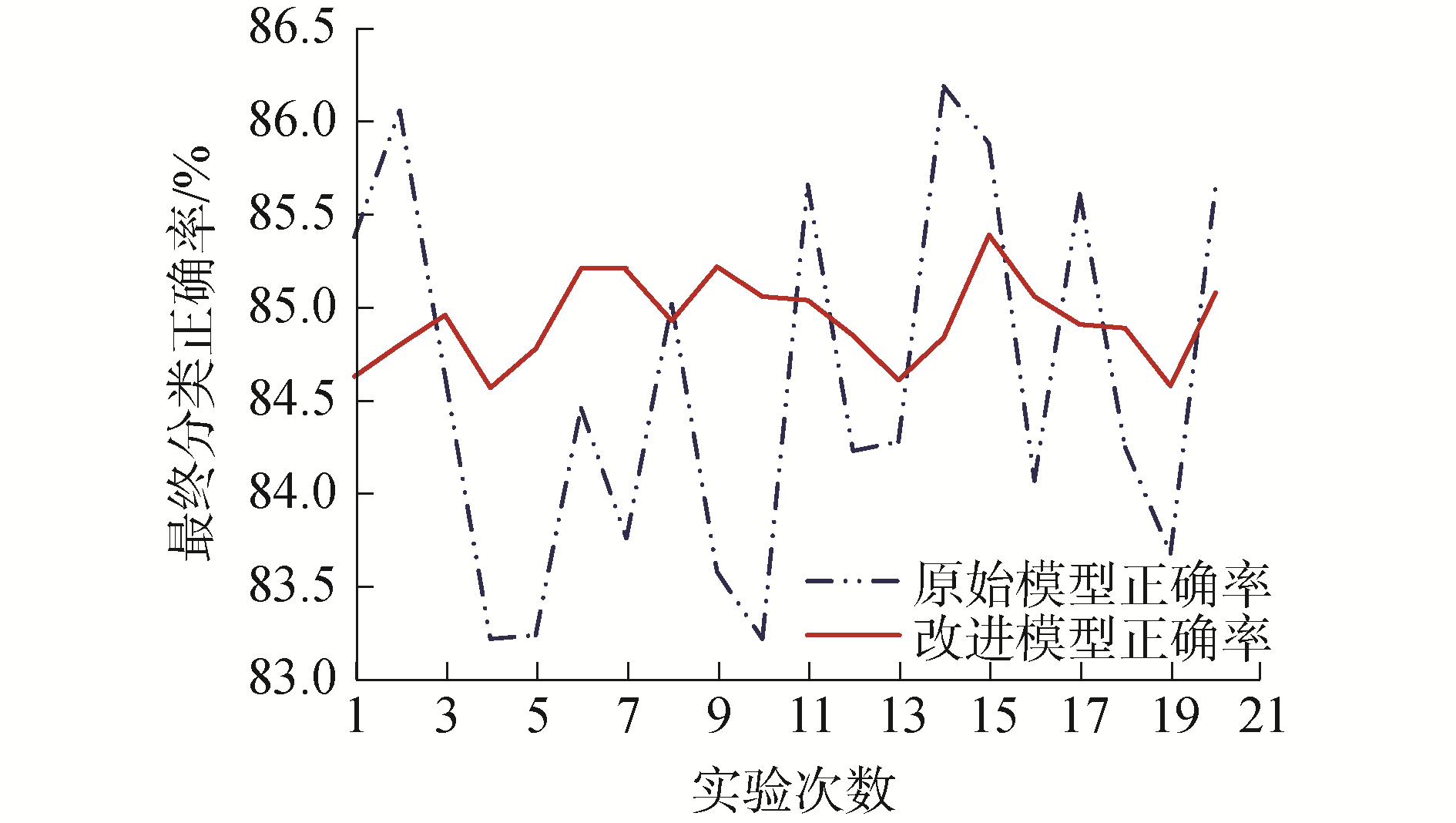
除了时间优势之外,在处理一些复杂的多维度的数据时,没有先验知识指导的神经网络最终很可能会陷入到局部最优解或停滞在鞍点上,使得最终的训练结果存在严重的震荡。在本实验中,为了更贴近实际应用的习惯,引入了5次冗余的早停以标记模型结束训练时的正确率。在这种限制条件下,由于梯度下降算法无法预知优化路径上的低学习率区域,也无法在多次训练时保持梯度下降方向相同,所以在原始模型训练结束时,测试集分类正确率变得非常不稳定,如图 4所示。
|
Download:
|
| 图 4 重复实验中模型的最终分类正确率对比 Fig. 4 Comparison of the final classification accuracy of the model in repeated experiments | |
图 4显示了2组数据集在20次随机训练时停止标记处的最终分类正确率,由于这种不稳定的震荡的影响,在多次进行的训练结果记录中,原始模型的测试集最高分类正确率的最大值与最小值之间的差值达到了5%;而引入了先验知识指导的改进模型在多次试验中训练得到的结果则十分稳定,只有不到1%的震荡。同时,改进模型在停止标记处的测试集分类正确率与原始模型所能达到的最高值只有不到0.5%的差距。
3 结论1) 本文提出的基于先验知识的深度学习模型快速训练方法,利用模型训练过程中积累的先验知识指导网络参数的训练,使网络有效地学习到在相似数据集中训练时遇到的局部最优解与鞍点区域,从而在训练过程中主动跳出低学习率区域,极大地缩短了训练时间。
2) 在使用对焦库指导神经网络的参数选取过程中,为了保持先验知识的有效性,生成的拟合结果会具有极高的拟合优度,所以改进模型的分类结果会趋向于先验知识所能够得到的最高分类正确率,这种特性会减小训练结果的震荡幅度,显著地提高了神经网络的稳定性,但同时也提高了对先验知识质量的需求。所以,选用高分类正确率的先验知识,并扩大数量,是一种能够提高回归模型正确指导参数变化趋势能力的方法。
下一步可以进行验证先验知识在循环神经网络等网络结构上的适用性的分析,并对利用先验知识指导的神经网络结构搜索算法进行研究。
| [1] |
DAUPHIN Y N, PASCANU R, GULCEHRE C, et al. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 2933-2941.
(  0) 0)
|
| [2] |
HINTON G E, OSINDERO S, THE Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 (  0) 0)
|
| [3] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 1026-1034.
(  0) 0)
|
| [4] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the 13th International Conference on Artificial Intelligence and Statistics. Sardinia, Italy, 2010: 249-256.
(  0) 0)
|
| [5] |
KINGMA D P, BA J L. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations. San Diego, CA, USA, 2015.
(  0) 0)
|
| [6] |
DUCHI J, HAZAN E, SINGER Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. The Journal of machine learning research, 2011, 12(7): 2121-2159. (  0) 0)
|
| [7] |
GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge, USA: MIT Press, 2016.
(  0) 0)
|
| [8] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille, France, 2015: 448-456.
(  0) 0)
|
| [9] |
邱宁佳, 王晓霞, 王鹏, 等. 结合迁移学习模型的卷积神经网络算法研究[J]. 计算机工程与应用, 2020, 56(5): 43-48. QIU Jianing, WANG Xiaoxia, WANG Peng, et al. Research on convolutional neural network algorithm combined with transfer learning model[J]. Computer engineering and applications, 2020, 56(5): 43-48. (  0) 0)
|
| [10] |
李茂莹, 杨柳, 胡清华. 同构迁移学习理论和算法研究进展[J]. 南京信息工程大学学报(自然科学版), 2019, 11(3): 269-277. LI Maoying, YANG Liu, HU Qinghua. A survey on theories and algorithms about homogeneous transfer learning[J]. Journal of Nanjing University of Information Science and Technology (natural science edition), 2019, 11(3): 269-277. (  0) 0)
|
| [11] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]//Proceedings of the 3rd International Conference on Learning Representations. San Diego, CA, USA, 2015.
(  0) 0)
|
| [12] |
WILSON A C, ROELOFS R, STERN M, et al. The marginal value of adaptive gradient methods in machine learning[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, CA, USA, 2017: 4148-4158.
(  0) 0)
|
| [13] |
蒋文斌, 彭晶, 叶阁焰. 深度学习自适应学习率算法研究[J]. 华中科技大学学报(自然科学版), 2019, 47(5): 79-83. JIANG Wenbin, PENG Jing, YE Geyan. Research on adaptive learning rate algorithm in deep learning[J]. Journal of Huazhong University of Science & Technology (nature science edition), 2019, 47(5): 79-83. (  0) 0)
|
| [14] |
KESKAR N S, SOCHER R. Improving generalization performance by switching from Adam to SGD[J]. arXiv preprint arXiv: 1712.07628, 2017.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


