2. 清华大学 摩擦学国家重点实验室, 北京 100084;
3. 广州大学 广州大学-淡江大学工程结构灾害与控制联合研究中心, 广东 广州 510006;
4. 中铁大桥科学研究院有限公司, 湖北 武汉 430034;
5. 桥梁结构健康与安全国家重点实验室, 湖北 武汉 430034
2. State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China;
3. Guangzhou University-Tamkang University Joint Research Center for Engineering Structure Disaster Prevention and Control, Guangzhou University, Guangzhou 510006, China;
4. China Railway Bridge Science Research Institute, Ltd., Wuhan 430034, China;
5. State Key Laboratory for Health and Safety of Bridge Structures, Wuhan 430034, China
转体施工法在跨越沟壑、峡谷等复杂地形条件下具有独特的优势[1]。其主要工作原理是将位于不利地形上的桥梁分成2个半跨,每个半跨结构均在河流的两岸,或在与跨越的障碍物平行的位置处施工,施工完成后再通过转动,将2个半跨结构同时旋转到位。转体施工法的出现,突破了传统桥梁建设技术的地理局限,使得桥梁建设可以挑战更加复杂的地形。此外,转体施工法在跨越已运营线路时能够安全、快速进行施工,避免对既有线路的运营造成影响,节省人力物力,产生更好的社会经济效益。转体装置是转体施工中的核心组成部分,该装置的接触面在安装和转动过程处于高应力状态。接触面中的高应力状态有可能使材料出现磨损,在转动过程中出现锁死现象,导致转动失败,甚至有可能在转动过程偏移原位引起倾覆[2]。因此,接触面的应力分析及接触界面设计是转体施工成功的关键工作。转体装置一般采用球铰,其接触属于协调接触。协调接触应用广泛,一直是工程界和学术界的研究重点。Ciavarella等[3]推导了圆柱形协调接触的理论解,Hu等[4]提出了圆柱面协调接触的弹塑性模型,Fang等[5]给出了协调和非协调接触面的半解析解。文献[2-5]利用有限元技术对协调接触进行数值研究。为了在转动过程减小摩擦阻力,转动装置在接触面引入了摩擦系数较低的滑块,然而现有研究忽略了接触面上嵌入的滑块[6-7],难以体现接触面上的真实应力分布。
本文以转体装置的接触面为研究对象,在考虑了滑块的影响下,提炼出简化的接触力学模型,分析接触面的应力分布规律,并对滑块的空间分布作进一步的优化,旨在控制其在安装、转动过程中的应力状态,为接触界面的设计提供理论基础。
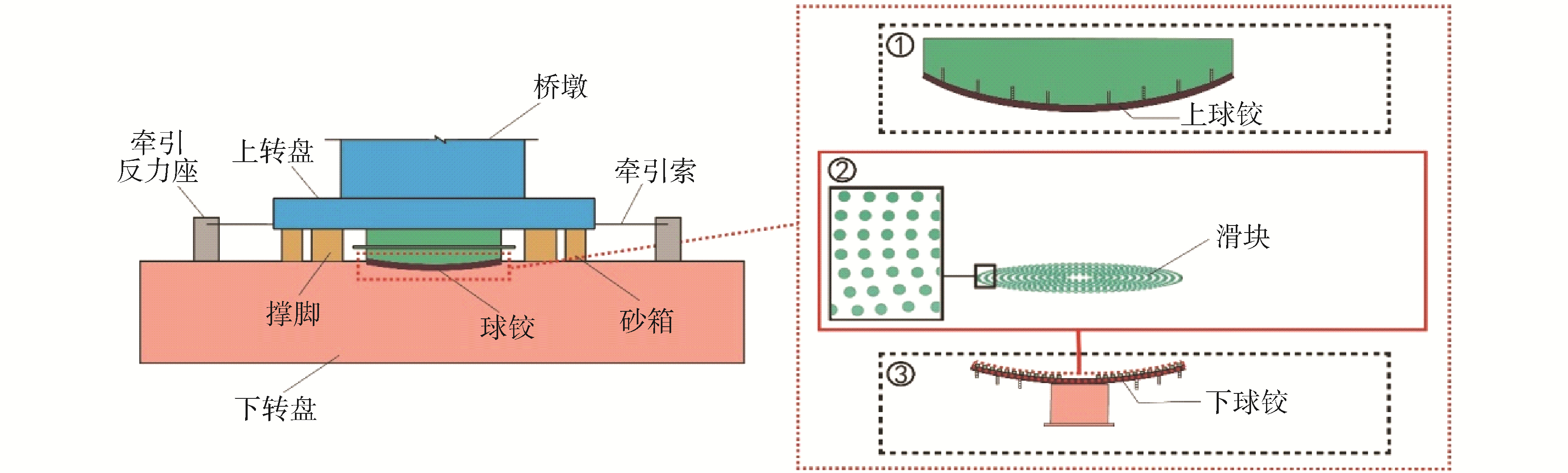
1 转体装置接触模型简化及应力分析 1.1 转体装置构造转体施工法的关键技术问题是对转体系统受力状态的控制,其实质是大型接触体在高压状态下的接触问题。典型转体系统构造如图 1所示,其由上转盘、下转盘和牵引系统组成。嵌固于下转盘的凹球面与上转盘的凸球面相互配合,共同组成一对接触面,下转盘的凹球面由内到外嵌入环形布置的若干聚四氟乙烯(PTFE)滑块,聚四氟乙烯是摩擦系数(0.05~0.1)极低的材料,能显著降低转体过程中的摩擦阻力。
|
Download:
|
| 图 1 转体系统构造 Fig. 1 The construction of rotating system | |
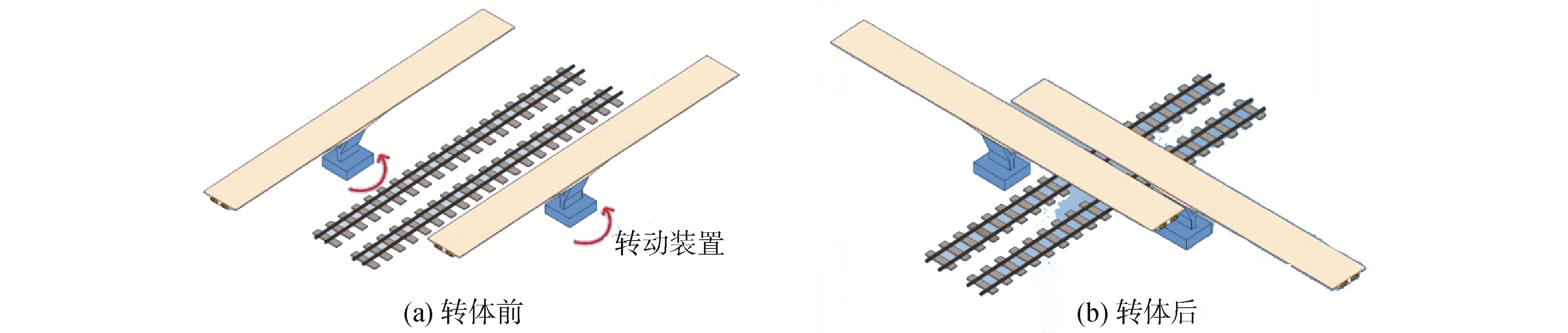
本文以茂湛铁路跨线桥为例,该桥全长2 037.5 m,主桥采用双幅(75 m+75 m)T型刚构桥,分左右2幅。为减少工程施工对既有铁路运营的影响,采用转体施工方法。2幅桥分别在铁路两侧平行于铁路预制,转体施工时双幅同步转动,转体角度为83.6°,如图 2所示。其中,单幅桥转体重量约10 500 t,每个球铰布置12环共634片半径为3 cm的PTFE滑块,滑块的设计抗压强度为100 MPa。滑块现场布置情况如图 3所示。
|
Download:
|
| 图 2 转体施工法示意 Fig. 2 Illustration of the rotation superstructure construction method | |

|
Download:
|
| 图 3 聚四氧乙烯滑块现场布置 Fig. 3 The layout of the PTFE slide plates on site | |
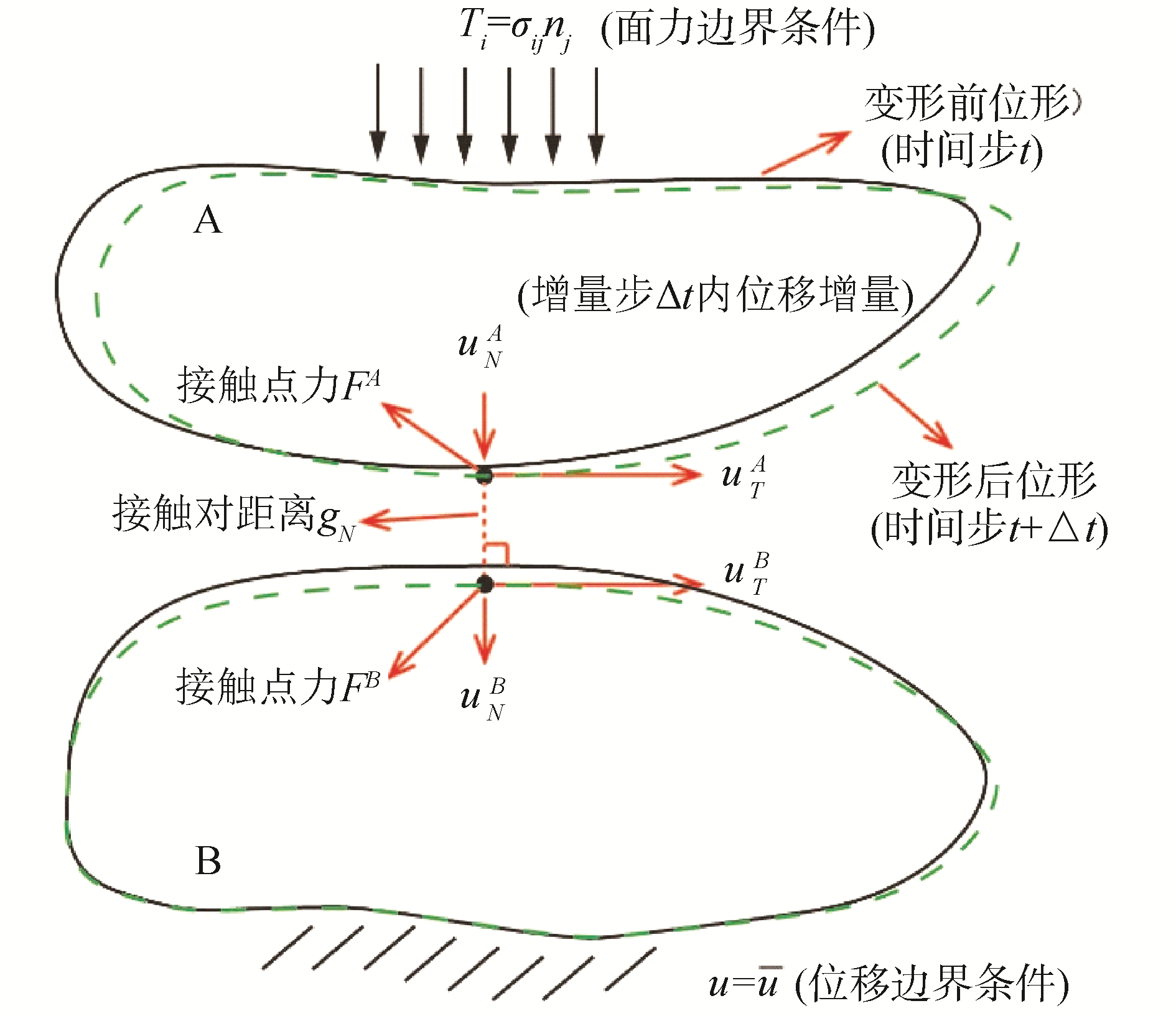
从复杂的转体装置中提炼出接触模型,不仅可以节省大量的建模工作,还为后续有限元模型的求解节省了大量计算时间。本文对上述复杂的接触问题进行简化。接触问题(如图 4所示)区别于一般固体力学问题之处,在于其有独特的附加约束,即接触约束条件。由于接触过程中接触约束条件不断发生变化,计算接触力学一般采用增量法。基于有限元的计算接触力学与一般有限单元法的差异,在于对附加约束的处理。粘结状态下接触问题的接触约束条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {u_N^A - u_N^B + {g_N} = 0}\\ {u_T^A - u_T^B = 0} \end{array}} \right. $ | (1) |
|
Download:
|
| 图 4 典型的接触问题及边界条件 Fig. 4 Typical contact problems and boundary conditions | |
式中:uNA、uNB分别表示接触体A、B在接触面上的法线方向位移增量;gN为接触点间的距离。uTA、uTB分别表示接触体A、B在接触面上的切线位移增量。基于拉格朗日格式的增量法接触问题虚功方程可表示为[8]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{r = }^{A,B} {\left[ {\int_{t + \Delta {t_V}r} {^{t + \Delta t}\tau _{ij}^r{\delta _{t + \Delta t}}e{{_{ij}^r}^{t + \Delta t}}{\rm{d}}V} } \right]} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{r = }^{A,B} {\left[ {\int_{t + \Delta {t_{S_\sigma ^r}}} {_{t + \Delta t}^{t + \Delta t}\mathit{\boldsymbol{T}}_i^r\delta u{{_i^r}^{t + \Delta t}}{\rm{d}}S} } \right]} + \\ \int_{t + \Delta {t_{{S_c}}}} {^{t + \Delta t}\mathit{\boldsymbol{F}}_J^A{{(\delta u_J^A - {\rm{ }}\delta u_J^B)}^{t + \Delta t}}{\rm{d}}S} = 0 \end{array} $ | (2) |
式中:J是接触面的2个垂直方向,J=1, 2;Tir左上标(t+Δt)为用时间表示的增量步,左下标为参考时间;等式第1项是虚应变能;第2项是面力产生的外虚功;第3项是接触面上接触力产生的虚功。引入拉格朗日乘子法考虑附加约束条件,相应的修正泛函对位移增量的变分为[8]:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{r = }^{A,B} {\left[ {\int_{t + \Delta t{V^r}} {^{t + \Delta t}\tau _{ij}^r{\delta _{t + \Delta t}}e{{_{ij}^r}^{t + \Delta t}}{\rm{d}}V} } \right]} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{r = }^{A,B} {\left[ {\int_{t + \Delta {t_{S_\sigma ^r}}} {_{t + \Delta t}^{t + \Delta t}\mathit{\boldsymbol{T}}_i^r\delta u{{_i^r}^{t + \Delta t}}{\rm{d}}S} } \right]} + \\ \int_{t + \Delta {t_{{S_c}}}} {^{t + \Delta t}\lambda _J^A{{(\delta u_J^A - {\rm{ }}\delta u_J^B)}^{t + \Delta t}}{\rm{d}}S} = 0 \end{array} $ | (3) |
式中:第1项是虚应变能;第2项是面力产生的外虚功;第3项是约束变量λ(拉格朗日乘子变量)产生的“虚功”。式(2)和(3)是等价的,同时包含了接触界面上等效结点力和拉格朗日乘子变量间的关系。若对整个区域进行离散化,用结点位移作为形函数的基本变量,其最终有限元求解方程为[8]:
| $ \left[ {\begin{array}{*{20}{c}} {_0^t{K_L} + _0^t{K_{NL}}}&{{K_{c\lambda }}}\\ {K_{c\lambda }^T}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u\\ {^{t + \varDelta t}\lambda } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {^{t + \Delta t}{Q_L} - _0^tF}\\ {{ - ^t}\bar g} \end{array}} \right] $ | (4) |
式中:KL是接触体整体刚度矩阵的线性项;KNL是相应的非线性项; Kcλ是界面约束刚度;QL为等效结点载荷向量。式(4)中第1项等式实质是式(3)的离散化形式,第2项是约束条件(1)的离散化形式。由式(1)~(4)可见,在求解接触方程之前,首先需要在离散化后(即接触界面离散成单元结点)的接触边界中,搜寻满足接触约束条件的接触结点,即判断2个接触点的最短距离gN是否满足接触约束条件。要获得潜在的接触点,需要在每个增量步中根据位移增量重新调整接触体A、B的坐标,然后根据式(1)进行计算。研究表明,接触对的搜寻通常占总分析时间的40%~50%[8]。本文提出简化接触面的思路,即根据现有接触理论[9-12],把2个弹性接触体的接触,简化成1个刚体和1个弹性体的接触。由于刚体仅有刚体位移增量,不存在弹性位移增量,因此在每个增量步中仅需要迭代新弹性体的位移增量,这将大大减小搜索时间。
本文把2个弹性体简化成1个等效曲面刚体和1个水平光滑弹性体接触。等效刚体的表面形状函数,即高度函数为H(x, y),系2个等效前弹性体的复合高度之和[11]:
| $ H(x,y) = {\rm{ }}{H_1}(x,y) + {\rm{ }}{H_2}(x,y) $ | (5) |
式中:H1为等效前弹性体1的表面形状函数,H2为等效前弹性体2的表面形状函数。等效后的光滑弹性体的材料参数为:
| $ \frac{{1 - {v^2}}}{E} = \frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}} $ | (6) |
式中:E1、v1为等效前弹性体1的弹性模量和泊松比;E2、v2为等效前弹性体2的弹性模量和泊松比。根据接触力学理论,对转体装置的接触问题进行简化,旨在降低转体接触面分析的建模成本,提高接触模型计算效率,同时为后续优化转体接触面有限元分析提供支持。
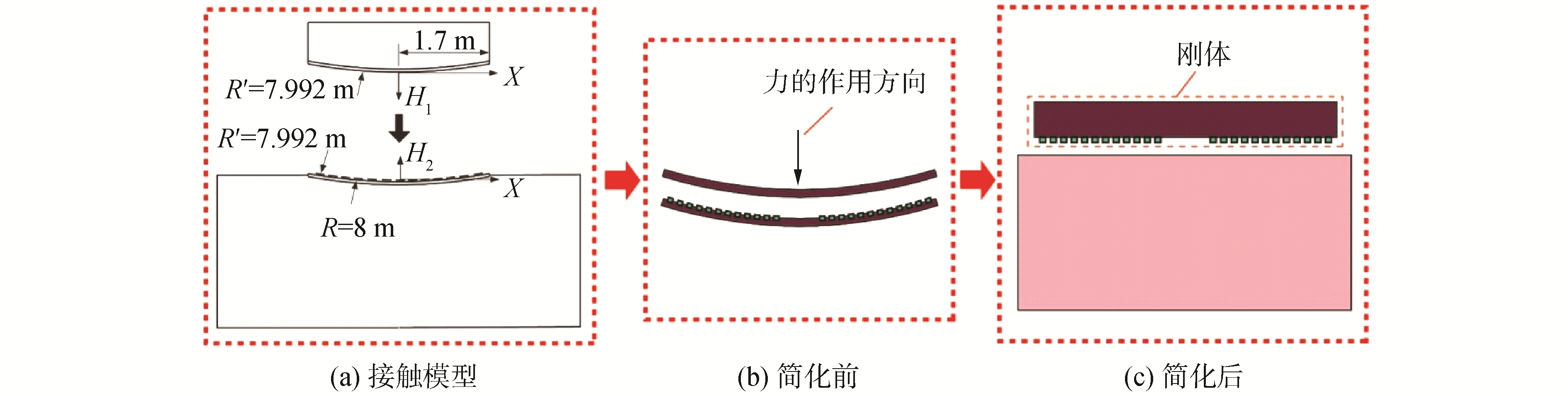
转体施工的接触模型实际为上球铰(钢材)与下球铰所嵌入的PTFE滑块之间的弹性接触,接触模型如图 5(a)所示。以茂湛铁路跨线桥为例,下球铰的球面半径R为8 m,上球铰的球面半径R′为7.992 m。滑块上表面所形成的球面半径与上球铰球面半径相同,其凸出下球铰上表面的高度h,等于下球铰球面半径R与上球铰球面半径R′之差,即0.008 m。由于转体装置的旋转对称性,可将三维空间问题转化为二维平面问题,即只需考虑x方向,高度函数H(x, y)可简化为H(x)。以上球铰和滑块上表面所成球面中心接触点作为原点,分别建立上、下转盘结构局部坐标系,坐标轴方向如图 5(a)所示。
|
Download:
|
| 图 5 接触模型示意 Fig. 5 Illustration of the contact model | |
对于上转盘结构,几何关系为:
| $ {x^2} + {({H_1} + {\rm{ }}{R^\prime })^2} = {\rm{ }}{R^{\prime 2}} $ | (7) |
由此可得高度函数H1为:
| $ {H_1} = - {R^\prime } \pm \sqrt {{R^{\prime 2}} - {x^2}} $ | (8) |
由图 5中几何关系,易知上式第2项应取“+”号,即:
| $ {H_1} = - {R^\prime } + \sqrt {{R^{\prime 2}} - {x^2}} $ | (9) |
对于下转盘结构,由于PTFE滑块的存在,使得下转盘表面分成2种不同的形式,在局部坐标系下,滑块、下球铰分别由几何关系可得:
| $ {{x^2} + {{({H_2} - {R^\prime })}^2} = {R^{\prime 2}}} $ | (10) |
| $ {{x_2}^2 + {{({H_2} - {R^\prime })}^2} = {R^2}} $ | (11) |
可得高度函数H2为:
| $ {{\rm{滑块}}:{H_2} = {R^\prime } \pm \sqrt {{R^{\prime 2}} - {x^2}} } $ | (12) |
| $ {{\rm{下球铰}}:{H_2} = {R^\prime } \pm \sqrt {{R^2} - {x^2}} } $ | (13) |
综合以上2式及几何关系,可得下转盘高度函数H2的综合表达式为:
| $ {{H_2} = \left\{ \begin{array}{l} {R^\prime } - \sqrt {{R^{\prime 2}} - {x^2}} ,{\rm{有滑块区域}}\\ {R^\prime } - \sqrt {{R^2} - {x^2}} ,{\rm{无滑块区域}} \end{array} \right.} $ | (14) |
综上,复合刚性曲面高度函数H的表达式为:
| $ \begin{array}{*{20}{l}} {H = {H_1} + {H_2} = }\\ {\left\{ {\begin{array}{*{20}{l}} {0,}&{{\rm{有滑块区域}}}\\ {\sqrt {{R^{\prime 2}} - {x^2}} - \sqrt {{R^2} - {x^2}} ,}&{{\rm{无滑块区域}}} \end{array}} \right.} \end{array} $ | (15) |
由于
| $ {H = {H_1} + {H_2} = \left\{ {\begin{array}{*{20}{l}} {0,}&{{\rm{有滑块区域}}}\\ { - h,}&{{\rm{无滑块区域}}} \end{array}} \right.} $ | (16) |
分析式(16)的几何意义可知,接触模型经过简化,等效为平面内分布的滑块与圆柱体(半径与球铰投影半径相等)共同构成的刚体,和1个表面水平的弹性体之间的接触模型,其中滑块的高度为h。接触模型的简化过程如图 5(b)、(c)所示。
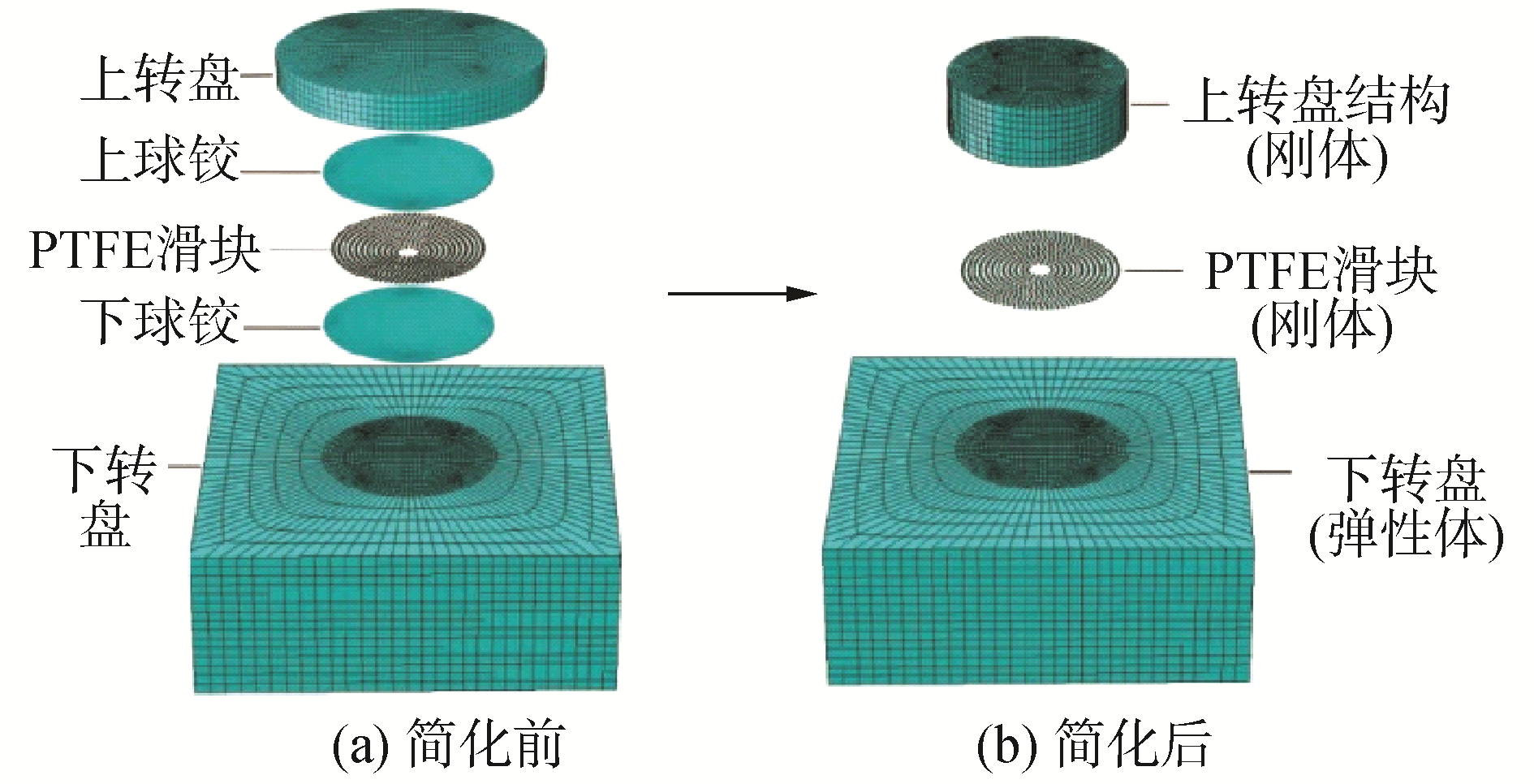
1.3 简化模型在有限元分析的应用本节以茂湛铁路跨线桥为工程背景,验证本文提出的简化理论在有限元分析[8, 13]时的优势及正确性。根据表 1中的参数,采用ABAQUS有限元软件分别建立简化前的接触模型和简化后的接触模型[14-17],单元类型均为C3D8R,如图 6所示。简化前的接触模型为上球铰与下球铰所嵌入的PTFE滑块之间的弹性接触,简化后的模型则变为刚体和弹性体间的接触。
| 表 1 有限元模型参数 Table 1 Parameters of the FE model |
|
Download:
|
| 图 6 转体系统有限元模型示意 Fig. 6 The model of rotating system | |
根据式(6)的理论,选定简化模型的下转盘弹性体材料泊松比为0.35 (即下球铰泊松比和PTFE滑块泊松比的算术平均值),弹性模量由式(6)确定。实际工程中,考虑到转体系统配重后,梁体偏心距较小,因此可视上转盘结构处于中心承重状态,将10 500 t的转体重量转化为均匀面荷载施加于上转盘结构上表面。下转盘底面施加固结边界条件。
由于球铰和滑块是最为关键的部件,应当划分较细的网格。通过对网格尺寸效应进行对比分析[18],最终采用的网格尺寸如下。简化前的模型:球铰网格尺寸为40 mm,单个球铰单元数量为14 336;滑块网格尺寸为6 mm,单个滑块单元数量为186;对于上、下转盘,与球铰接触区域混凝土采用较细网格,网格尺寸为60 mm,外围混凝土采用较粗网格,网格尺寸为200 mm,下转盘单元数为19 484,上转盘单元数为13 658;简化后的模型:对于滑块和上、下转盘,其简化后的网格尺寸与简化前保持一致。简化前的总单元个数为179 738,简化后的总单元个数为139 352。简化前后,由于单元个数及接触类型发生变化,且接触对搜索效率增加了近1倍,总的分析时间减少了近90%。可见,简化模型在有限元分析时有巨大优势。
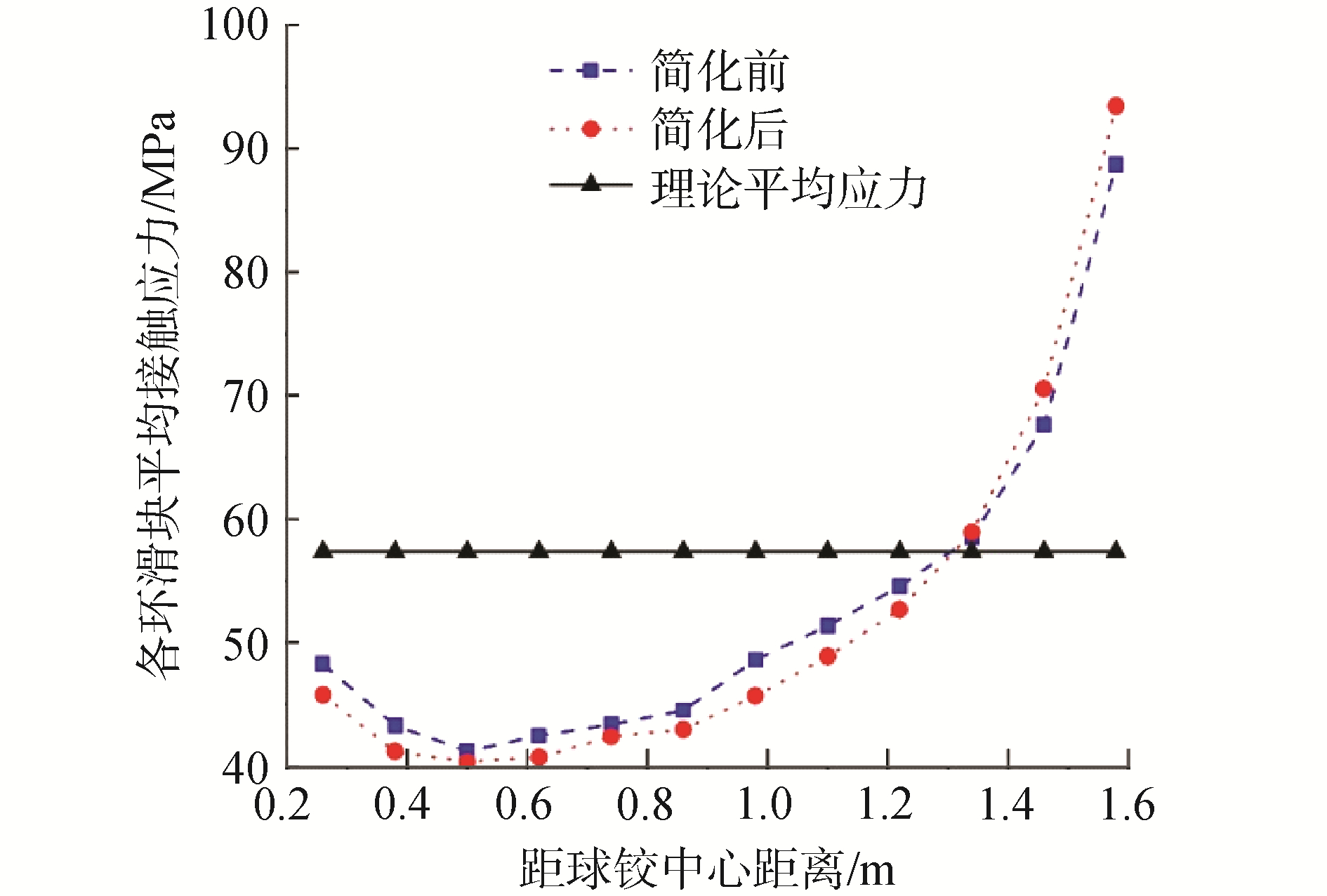
图 7展示了每环滑块(共12环,634个)的平均接触应力,即各环滑块法向接触合力与其总接触面积的比值。可见,简化模型和原模型接触面压应力结果基本吻合,最大相对误差仅为5%。两者无法完全重合的原因为:简化前后的几何模型已经改变,两者自然无法获得完全一样的网格分布,因此应力存在部分差异是合理的。由此可见,本文提出的简化模型是正确的。
|
Download:
|
| 图 7 简化前后各环平均接触应力对比 Fig. 7 Comparison of the average contact stress for different rings of slide plates before and after simplification | |
由图 7可见,各环滑块的平均接触应力极不均匀:滑块平均接触应力的大小总体上随距球铰中心距离的增大而不断增大,最小值出现在第3环滑块,其平均接触应力值为40.40 MPa;最大值出现在最外环滑块,对应93.50 MPa。因此,各滑块的空间分布有待进一步优化。例如,第1环至第9环滑块的平均接触应力在理论平均应力曲线下方,说明前9环滑块的安全度有富余,因而个数可以适当减少;第10环至第12环滑块的平均接触应力在理论平均应力曲线上方,说明后3环滑块的应力较均值偏大,因而个数可以适当增加。各环滑块的平均接触应力与理论平均应力的差值,一定程度上反映了接触面积的盈缺量,进而体现了滑块个数的富余或不足。其中,理论平均应力为简化后模型转体总重量与所有滑块下表面面积总和的比值。通过以上分析,提出本文的优化目标为:在单个滑块的平均接触应力不超过其设计抗压强度,且每环滑块的平均接触应力趋于均匀的情况下,让滑块的总个数N尽可能小。具体的优化方法思路如下:1)在滑块总接触面积不变的情况下,使每环滑块的平均接触应力趋于均匀,通过每环滑块应力与理论平均应力的差值来调节该环滑块的数量;2)在保证各环滑块平均接触应力分布均匀的情况下,按照优化后的最大应力与优化前的最大应力比值,相应地逐环减少冗余滑块数。
优化设计是在初步设计的基础上进行的,初始滑块的数量取决于转体的总重及单个滑块的承载力,单个滑块的尺寸及承载力往往由制造商提供,取决于制造的难度和施工的便利。初始参数一般由经验给出,本文优化设计的初始参数来自上述茂湛铁路跨线桥,其中滑块的半径为30 mm,总高18 mm,凸出下球铰上表面的高度为8 mm,设计抗压强度为100 MPa,共12环,各环滑块个数的初始值如表 2所示。具体的优化步骤为:
| 表 2 滑块应力及个数分配 Table 2 The contact stress and number of the slide plates |
1) 计算理论平均应力P0:
| $ {P_0} = \frac{G}{{N \cdot {\rm{ \mathsf{ π} }} \cdot {r^2}}} $ | (17) |
式中:G为转体总重;r和N分别为滑块半径及总个数。
2) 通过有限元方法计算简化模型得到各环平均接触应力Pi,相应地增减各环滑块的数量Δni:
| $ \Delta {n_i} = \left[ {\frac{{{P_i} - {P_0}}}{{{P_0}}} \cdot {n_i}} \right] $ | (18) |
式中:“[ ]”为取整符号;ni和Pi分别对应各环滑块的个数及平均接触应力。
3) 调整后的各环滑块个数为:
| $ n_i^j = {\rm{ }}{n_i} + {\rm{ }}\varDelta {n_i} $ | (19) |
式中上标j表示迭代的次数。
4) 重复步骤2)、3),进行迭代计算,直到获得趋于均匀的应力。
5) 按最终迭代后滑块中的最大平均接触应力Pjmax与优化前滑块中的最大平均接触应力Pmax的比例逐环减少滑块个数:
| $ {n_{{\rm{end}},i}} = n_i^j \cdot \frac{{P_{{\rm{max}}}^j}}{{{P_{{\rm{max}}}}}} $ | (20) |
通过上述步骤,便可得到最终调整后的每环滑块个数nend,i。
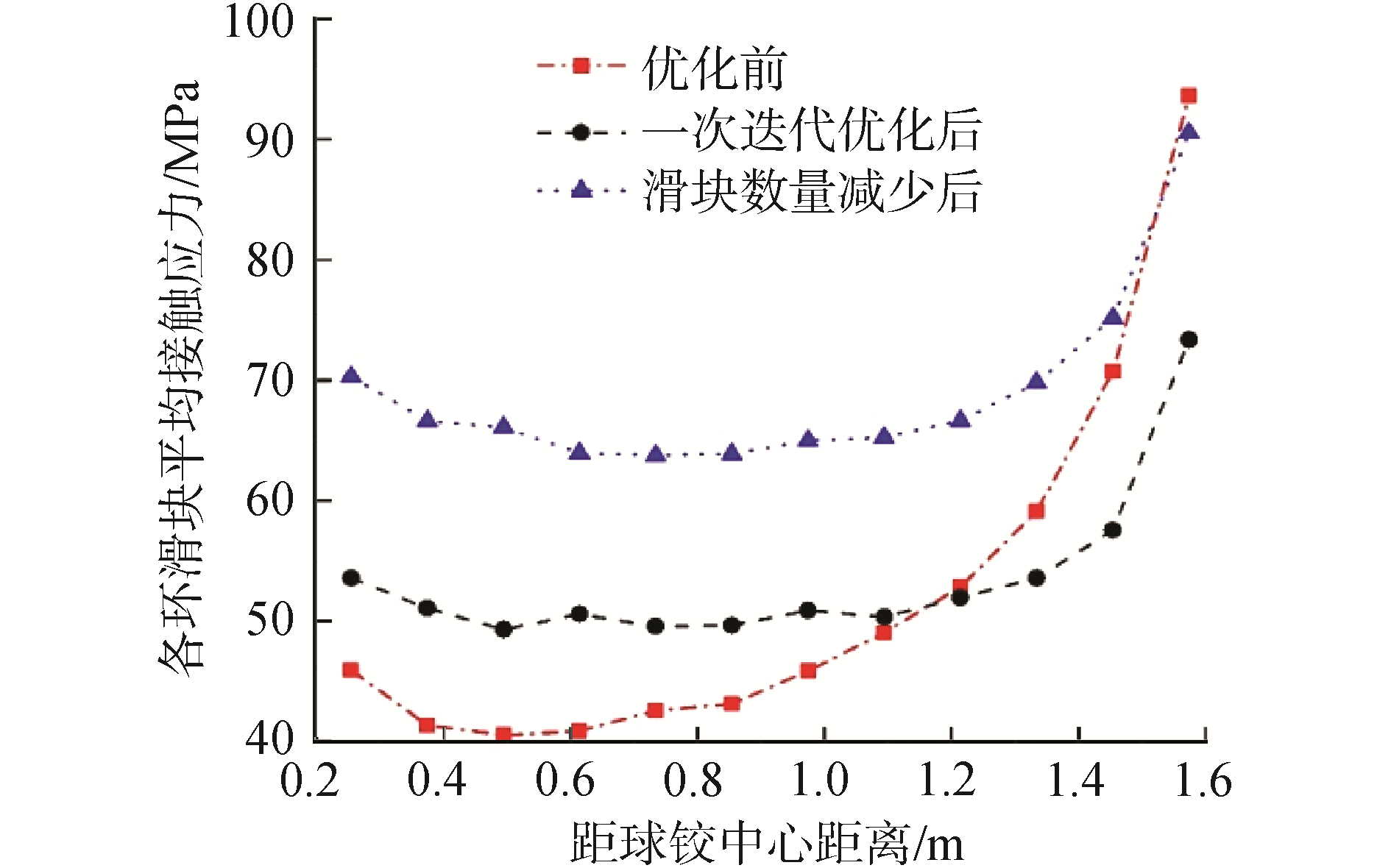
2.2 结果分析图 8是经过一次迭代后的茂湛铁路跨线桥各环滑块的平均接触应力结果。
|
Download:
|
| 图 8 优化前后PTFE滑块应力分布情况 Fig. 8 Stress distribution at each PTFE slide plate for the original model and the optimal model | |
如图显示,经过一次迭代优化后,滑块的平均接触应力明显比优化前均匀。最外侧滑块的平均接触应力由原来的93.50 MPa降低至73.23 MPa,其余各环滑块的平均接触应力约为52 MPa,应力分布已经趋于均匀。并且内侧滑块的平均接触应力相比优化前有所增加,提高了内侧滑块的材料利用率。可利用同样的方法,对滑块的分布进行二次迭代优化。然而二次迭代后,最外环滑块的个数已经超出球铰所能容纳的范围,故不再进行下一次迭代。
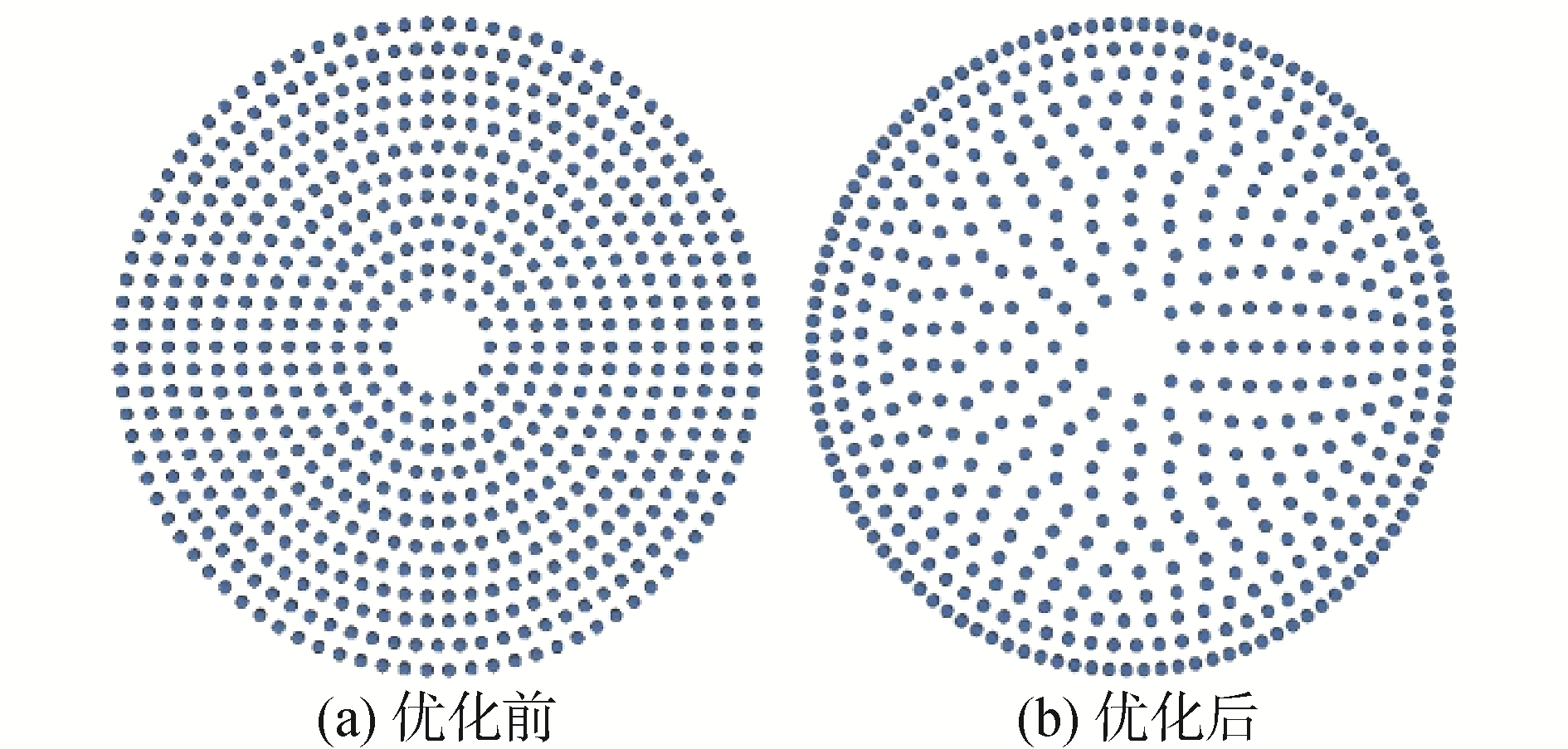
由于优化后滑块的最大平均接触应力为73.23 MPa,远小于优化前的93.50 MPa,因此可以考虑减少滑块的数量。根据前面所述方法,按照优化前后的最大应力比值,相应地减少每环的滑块个数,即在1次迭代后每环滑块个数的基础上,对每环的滑块个数相应地乘以应力比例系数73.23/93.50,得到每环最终优化后的数量。优化后的数量仅为优化前的78%,大幅减少了滑块数量。通过有限元软件验算,由图 8可见,按应力比例减少滑块个数后的应力曲线,大致等于一次迭代后的曲线整体往上平移16 MPa,且接触应力分布的均匀程度与一次迭代后的结果保持较好的一致性。最终优化后的滑块分布与优化前的对比如图 9所示。相应地,表 2为优化前后对应每环的滑块个数及平均接触应力。由此可见,本文提出的优化方法有效。
|
Download:
|
| 图 9 优化前后滑块分布 Fig. 9 The slide plates distribution for the original model and the optimal model | |
1) 常规接触模型经简化后,可等效为平面内分布的滑块与圆柱体共同构成的刚体和1个表面水平的弹性体之间的接触模型;相比常规接触力学模型,简化后的计算效率提高了近10倍;简化前后接触面压应力结果基本吻合,最大相对误差仅为5%。
2) 利用简化后的接触力学模型对滑块的空间分布进行优化。优化后,滑块的数量减少了22%,其应力分布较优化前明显均匀化,边缘应力集中效应大大降低,使材料的力学性能得以充分发挥,为转体施工桥梁往大跨度、大吨位的方向进一步发展提供方法。
| [1] |
ZHANG J, EL-DIRABY T E. Constructability analysis of the bridge superstructure rotation construction method in China[J]. Journal of construction engineering and management, 2006, 132(4): 353-362. (  0) 0)
|
| [2] |
钱桂枫, 程飞, 王景全, 等. 沪杭高铁超大吨位转体施工拱桥建造技术[M]. 北京: 中国铁道出版社, 2012: 15-16. QIAN Guifeng, CHENG Fei, WANG Jingquan, et al. Construction technology of super large tonnage rotating superstructure construction arch bridge of Shanghai Hangzhou high speed railway[M]. Beijing: China Railway Press, 2012: 15-16. (  0) 0)
|
| [3] |
CIAVARELLA M, DECUZZI P. The state of stress induced by the plane frictionless cylindrical contact. I. The case of elastic similarity[J]. International journal of solids and structures, 2001, 38(26/27): 4507-4523. (  0) 0)
|
| [4] |
HU Jianqiao, GAO Fuhai, LIU Xiaoming, et al. An elasto-plastic contact model for conformal contacts between cylinders[J]. Proceedings of the institution of mechanical engineers part J:journal of engineering tribology, 2019, 234(12): 1837-1845. (  0) 0)
|
| [5] |
FANG Xin, ZHANG Chunhua, CHEN Xun, et al. A new universal approximate model for conformal contact and non-conformal contact of spherical surfaces[J]. Acta mechanica, 2015, 226(6): 1657-1672. (  0) 0)
|
| [6] |
车晓军.平转法施工桥梁转动球铰受力精细化分析及平衡控制研究[D].武汉: 武汉理工大学, 2015: 20-39. CHE Xiaojun. Refined analysis of rotating spherical hinge and balance control of parallel swivel construction bridge[D]. Wuhan: Wuhan University of Technology, 2015: 20-39. (  0) 0)
|
| [7] |
刘建.平转法施工球铰受力分析及不平衡力矩预估[D].济南: 山东大学, 2019: 7-19. LIU Jian. Force analysis and unbalanced torque prediction of spherical hinge in parallel swivel bridge construction[D]. Ji'nan: Shandong University, 2019: 7-19. (  0) 0)
|
| [8] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003: 666-695. WANG Xucheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 666-695. (  0) 0)
|
| [9] |
JOHNSON K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985: 104-106.
(  0) 0)
|
| [10] |
MISRA A, HUANG Shiping. Micromechanical stress-displacement model for rough interfaces:effect of asperity contact orientation on closure and shear behavior[J]. International journal of solids and structures, 2012, 49(1): 111-120. (  0) 0)
|
| [11] |
PERSSON B N J. Relation between interfacial separation and load:a general theory of contact mechanics[J]. Physical review letters, 2007, 99(12): 125502. DOI:10.1103/PhysRevLett.99.125502 (  0) 0)
|
| [12] |
瓦伦丁L.波波夫.接触力学与摩擦学的原理及其应用[M].李强, 雒建斌, 译.北京: 清华大学出版社, 2011: 43-62. POPOV L L. Contact mechanics and friction physical principles and applications[M]. LI Qiang, LUO Jianbin, trans. Beijing: Tsinghua University Press, 2011: 43-62. (  0) 0)
|
| [13] |
WRIGGERS P. Computational contact mechanics[M]. New York: Wiley, 2002: 195-221.
(  0) 0)
|
| [14] |
MAZURKIEWICZ M, OSTACHOWICZ W. Theory of finite element method for elastic contact problems of solid bodies[J]. Computers & structures, 1983, 17(1): 51-59. (  0) 0)
|
| [15] |
SACHDEVA T D, RAMAKRISHNAN C V. A finite element solution for the two-dimensional elastic contact problems with friction[J]. International journal for numerical methods in engineering, 1981, 17(8): 1257-1271. DOI:10.1002/nme.1620170809 (  0) 0)
|
| [16] |
PERSSON B N J, BUCHER F, CHIAIA B. Elastic contact between randomly rough surfaces:comparison of theory with numerical results[J]. Physical review B, 2002, 65(18): 184106. (  0) 0)
|
| [17] |
YAMADA K, TAKEDA N, KAGAMI J, et al. Mechanisms of elastic contact and friction between rough surfaces[J]. Wear, 1978, 48(1): 15-34. (  0) 0)
|
| [18] |
HUANG Shiping, HU Mengyu, HUANG Yonghui, et al. A new model for optimal mechanical and thermal performance of cement-based partition wall[J]. Materials, 2018, 11(4): 615. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


