2. 天津大学 天津大学建筑工程学院, 天津 300350;
3. 江苏科技大学 海洋装备研究院, 江苏 镇江 212003;
4. 上海市船舶工程重点实验室, 上海 200011;
5. 中国船舶及海洋工程设计研究院, 上海 200011
2. School of Civil Engineering, Tianjin University, Tianjin 300350, China;
3. Marine Equipment and Technology Institute, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
4. Shanghai Key Laboratory of Ship Engineering, Shanghai 200011, China;
5. Marine Design & Research Institute of China, Shanghai 200011, China
船舶骑浪运动是船舶第二代完整稳性中的5种失效模式之一[1],其非线性动力学特性最为显著。船舶骑浪运动失稳模式,是指船舶在特定的波浪中航行时,船舶推进控制系统失去对船的控制,并使船舶随着波浪前进的现象。即船舶在随浪条件下航行时会被前进的波浪所捕获,并与波浪一起运动,使船舶的航速与波速相同。通常使船舶发生骑浪运动的波长约为船长的1.0~3.0倍,波浪足够陡峭,且船速与波速相当,船速约为波速的75%[2]。
陶醉等[3-4]建立随浪条件下船舶的单自由度纵荡运动方程,通过将船舶骑浪运动与单摆运动同宿分岔现象进行类比,研究船舶纵荡非线性系统中所存在的同宿分岔现象,并预报船舶是否发生骑浪运动。储纪龙等[5]建立船舶骑浪运动方程,将其简化为哈密顿系统,求出其对应的异宿轨道方程,计算船舶发生骑浪运动的螺旋桨临界转速。顾民等[6]以内倾船型为例,开展随浪和尾斜浪中的船舶骑浪/横甩试验,分析了内倾船型在不同波浪条件下的运动特性。
Kan等[7]通过模型试验和数值模拟结果相对比,给出一种获得临界航速和临界波高的简便方法,判断船舶是否发生骑浪运动:当船体的速度低于第一临界速度时,船舶在纵荡方向上作往复的周期运动,并不会发生骑浪运动;在第二临界速度下船舶被波浪捕获,与波浪之间的相对速度为零,发生骑浪运动。Spyrou等[8]研究在大波陡随浪条件下船舶纵荡运动的强非线性特性,研究表明在船舶骑浪条件的边缘,船舶会发生大幅纵荡运动。
本文基于非线性动力学理论,研究船舶骑浪运动特性。建立纵浪条件下船舶纵荡运动方程,分别采用梅林科夫方法和龙格库塔方法对该方程进行求解。通过解析分析方法,得到发生骑浪的临界值,给出梅林科夫函数阈值图。在数值计算中,分别绘制船舶骑浪时和未骑浪时的时历曲线和运动相图,并分析其非线性特性。以螺旋桨转速为分岔参数画出船舶骑浪运动分岔图,分析了船舶骑浪的失稳条件。
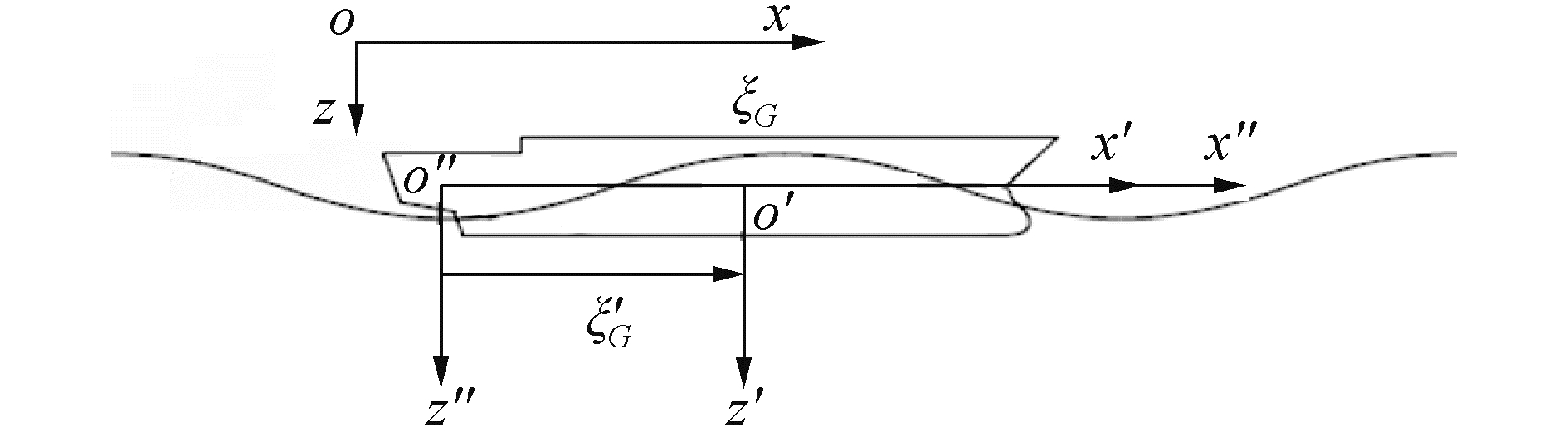
1 纵荡运动方程建立船舶在波浪上航行的坐标系如图 1所示。O(x, y, z)为大地固定坐标系,O′(x′, y′, z′)定义为随船坐标系,其中以船舶的重心G为随船坐标系坐标原点,O″(x″, y″, z″)为波浪坐标系,其原点固定于波浪的一个波谷处,并以波速c在大地坐标系中移动。
|
Download:
|
| 图 1 船舶运动坐标系 Fig. 1 The motion coordinate system of ship motion | |
船舶在规则波波浪激励下纵荡方向的经典的运动方程为[9]:
| $ \left(m+m_{x}\right) \ddot{\xi}_{G}+[R(u)-T(u, n)]+X_{w}\left(\xi_{G}, t\right)=0 $ | (1) |
式中:m为船舶的质量;mx为纵荡附连水质量;ξG为大地坐标系下船舶重心的纵坐标;R(u)为船舶的纵向阻力,其表达式为:
| $ R(u)=r_{1} u+r_{2} u^{2}+r_{3} u^{3} $ |
式中:r1、r2、r3为阻力系数;u为纵荡瞬时速度。
T(u, n)为纵荡方向螺旋桨推力,其表达式为:
| $ T(u, n)=\left(1-t_{p}\right) \rho n^{2} D_{p}^{4} K_{T}(u, n) $ |
式中:tp表示为螺旋桨推力减额系数;ρ为海水密度;n为螺旋桨转速;Dp为螺旋桨桨叶直径;KT表示为螺旋桨推力系数,其表达式为:
| $ K_{T}(u, n)=k_{1}(u, n)+k_{2}(u, n)+k_{3}(u, n) $ |
式中:k1、k2、k3为螺旋桨性能参数,代表螺旋桨敞水特性曲线的回归系数;JP为螺旋桨进速系数,表达式为:
| $ J_{P}=u\left(1-\omega_{p}\right) /\left(n D_{P}\right) $ |
式中ωp为螺旋桨性能参数中的伴流系数。
Xw(ξG, t)为船舶在纵荡方向上受到的波浪力,按切片理论计算[10]:
| $ \left\{\begin{array}{l} X_{w}\left(\xi_{G}, \chi\right)=-\alpha \rho g A k \cos \chi H \\ H=\int_{A E}^{F E} C_{1}(x) S(x) \mathrm{e}^{-k d(x) / 2} \sin \left[k\left(\xi_{G}+x \cos \chi\right] \mathrm{d} x\right. \end{array}\right. $ | (2) |
| $ C_{1}(x)=\frac{\sin (k \sin \chi \cdot B(x) / 2)}{k \sin \chi \cdot B(x) / 2} $ |
式中;g表示重力加速度;A代表波浪幅值;k为波数;χ为船舶航向角;S(x)为船舶横剖面浸水面积;d(x)为各站对应吃水;B(x)为各站船宽;dx为站距; α为考虑绕射效应的波浪力修正系数,按照下式进行计算:
| $ \alpha=\left\{\begin{array}{ll} 1.46 C_{b}-0.05, & C_{m} \leqslant 0.86 \\ \left(5.76-5 C_{m}\right) C_{b}-0.05, & 0.86<C_{m}<0.94 \\ 1.06 C_{b}-0.05, & C_{m} \geqslant 0.94 \end{array}\right. $ |
式中:Cb为船体方形系数;Cm为船体中横剖面系数。
考虑规则波条件计算船体受到的波浪力,波浪力随时间正弦变化。由于各时刻波浪力大小与船-波相对位置有关,因此将波浪力写作波浪力幅值乘以船舶与波浪之间相对位置的正弦函数的形式:
| $ X_{\omega}=F \sin \left(2 {\rm{ \mathsf{ π} }} \frac{\xi_{G}^{\prime \prime}}{\lambda}\right)=F \sin \left(k \xi_{G}^{\prime \prime}\right) $ | (3) |
式中:F表示为纵荡波浪力的幅值;ξ″G为波浪坐标系中船舶的位置。
2 梅林科夫方法梅林科夫(Melnikov)方法始于20世纪60年代,通过度量庞加莱(Poincare)映射的双曲不动点的稳定与不稳定流形之间的距离来确定非线性动力系统是否存在横截同(异)宿点,从而判断动力系统是否发生运动的突变,在确定性系统和随机系统中都有大量应用[11-12]。
首先假设动力系统的参数:
| $ x=f(x)+\varepsilon g(x, t ; \mu) $ | (4) |
其中:f: R2→R2是系统对应的哈密顿矢量场,εg: R2×R×R→R2代表作用在系统上的一个小扰动,μ是系统参数。此后计算系统的梅林可夫积分函数:
| $ M(\theta)=\int\limits_{-\infty}^{\infty} f\left(x^{h}(t)\right) \wedge g(x, t+\theta ; \mu) \mathrm{d} t $ | (5) |
式中xh(t)表示动力系统的异宿轨道方程。
在梅林可夫函数表达式中隐含时间t,可通过求解梅林可夫函数的零点来找到船舶纵荡运动系统失稳时的参数阈值,从而得到船舶发生骑浪失稳的条件。
在纵荡运动方程中,船舶重心在大地固定坐标系中的位置为ξG,所以在大地固定坐标系中船舶纵荡速度为
| $ \left\{\begin{array}{l} c=\frac{\lambda \omega}{2 {\rm{ \mathsf{ π} }}} \\ \omega=\sqrt{g k\left(1+k^{2} A^{2} / 4\right)} \end{array}\right. $ | (6) |
将大地坐标系中的船速u转换为船舶相对速度
| $ \begin{aligned} \left(m+m_{x}\right) \dot{\xi}_{G}^{\prime \prime}+& \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} c_{i}\left[\begin{array}{l} i \\ j \end{array}\right] \dot{\xi}_{G}^{\prime \prime j} c^{i-j}+F \sin \left(k \xi_{G}^{\prime \prime}\right)=\\ & T(c ; n)-R(c) \end{aligned} $ | (7) |
其中:
| $ c_{i}=-\frac{\left(1-t_{p}\right)\left(1-w_{p}\right)^{i} \rho k_{i}}{n^{i-2} D^{i-4}}+r_{i} $ |
对纵荡运动方程(7)进行无量纲化,令y=kξ″G,
| $ \ddot{y}+\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} C_{i j} \dot{y}^{j}+\sin y=\frac{T(c ; n)-R(c)}{F} $ | (8) |
其中:
| $ C_{i j}=\frac{c_{i}}{F k^{j}}[i] \frac{(F k)^{j / 2}}{\left(m+m_{x}\right)^{j / 2}} c^{i-j} $ |
引入小参数ε,其中0<ε≪1,则式(8)转化为:
| $ \ddot{y}+\sin y=\varepsilon\left(\frac{T(c ; n)-R(c)}{F}-\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} C_{i j} \dot{y}^{j}\right) $ | (9) |
当小参数ε=0时,式(9)退化为没有外激励作用,没有阻尼的哈密顿系统:
| $ \ddot{y}+\sin y=0 $ | (10) |
设
| $ \left\{\begin{array}{l} \dot{y}=z \\ \dot{z}=-\sin y \end{array}\right. $ | (11) |
将哈密顿系统式(11)中的右端项取不定积分,并由第1项减去第2项,则得到哈密顿系统(11)对应的Hamilton量H(y, z):
| $ H(y, z)=\frac{z^{2}}{2}-\cos y $ | (12) |
令哈密顿系统中的
当Hamilton量H(±π, 0)=1时,整个哈密顿系统存在着连接(π, 0)和(-π, 0)这2个鞍点的2条异宿轨道,在异宿轨道之间,存在着几条围绕着(0, 0)中心的同宿轨道,从同宿轨道变换成的第1条的异宿轨道则表示此纵荡运动系统中的船舶是否发生骑浪失稳运动的分界线。其中系统的异宿轨道方程为:
| $ z=\pm 2 \cos (y / 2) $ | (13) |
图 2中,虚线为本系统的异宿轨道线,虚线内部的实线则表示系统的同宿轨道方程。

|
Download:
|
| 图 2 异宿轨道示意 Fig. 2 Diagram of heteroclinic orbit | |
省略式(9)右端项中的小参数,并将其沿着异宿轨道方程进行积分,得到纵荡运动方程的梅林可夫函数为:
| $ M=\int_{-\infty}^{+\infty} z\left(\frac{T(c ; n)-R(c)}{F}-\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} C_{i j} \dot{y}^{j}\right) \mathrm{d} \tau $ | (14) |
| $ M=\int_{-\infty}^{+\infty} \frac{T(c ; n)-R(c)}{F} \frac{\mathrm{d} y}{\mathrm{~d} \tau} \mathrm{d} \tau-\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} C_{i j} \int_{-\infty}^{+\infty} \dot{y}^{j} \frac{\mathrm{d} y}{\mathrm{~d} \tau} \mathrm{d} \tau $ | (15) |
改变函数的积分路线,使梅林可夫函数沿着式(13)所示的异宿轨道进行积分,并使积分后的结果M=0,则:
| $ 2 {\rm{ \mathsf{ π} }} \frac{T(c ; n)-R(c)}{F}=\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{i} C_{i j}(-2)^{j} I_{j} $ | (16) |
| $ I_{j}=\int_{-{\rm{ \mathsf{ π} }}}^{{\rm{ \mathsf{ π} }}} \cos ^{j}(y / 2) \mathrm{d} y $ | (17) |
对式(17)进行积分,得到I1=4,I2=π,I3=8/3,代入式(16)得:
| $ \begin{gathered} \frac{T(c ; n)-R(c)}{F}=-\frac{4\left(c_{1}+2 c_{2} c+3 c_{3} c^{2}\right)}{{\rm{ \mathsf{ π} }} \sqrt{F k\left(m+m_{x}\right)}}+ \\ \frac{2\left(c_{2}+3 c_{3} c\right)}{k\left(m+m_{x}\right)}-\frac{32 c_{3} \sqrt{F}}{3 {\rm{ \mathsf{ π} }}\left[k\left(m+m_{x}\right)\right]^{3 / 2}} \end{gathered} $ | (18) |
由此,根据式(18)可求出使等式成立的临界螺旋桨转速n。再根据船舶在波浪中前行时的阻力和推力相等的关系式,求出船舶在波浪中行驶时的螺旋桨临界船速,便确定了船舶骑浪失稳的条件。
3 某内倾船算例以某内倾船为例,分别采用解析方法和数值方法计算内倾船的纵荡运动响应,并判断其是否发生骑浪运动,给出内倾船发生骑浪运动的临界值条件,并通过2种方法结果的比较,验证解析方法的正确性。内倾船垂线间长为112 m,吃水为3.865 m,排水体积为2 789.72 m3,水线宽为13.399 m,水线长为111.997 m,湿表面积为1 518.31 m2,浮心纵向位置距舯后-2.456 m,重心垂向位置距基线5.785 m,中横剖面系数为0.794 6。内倾船的纵荡运动方程中的推力系数和阻力系数由模型试验的数据给出。
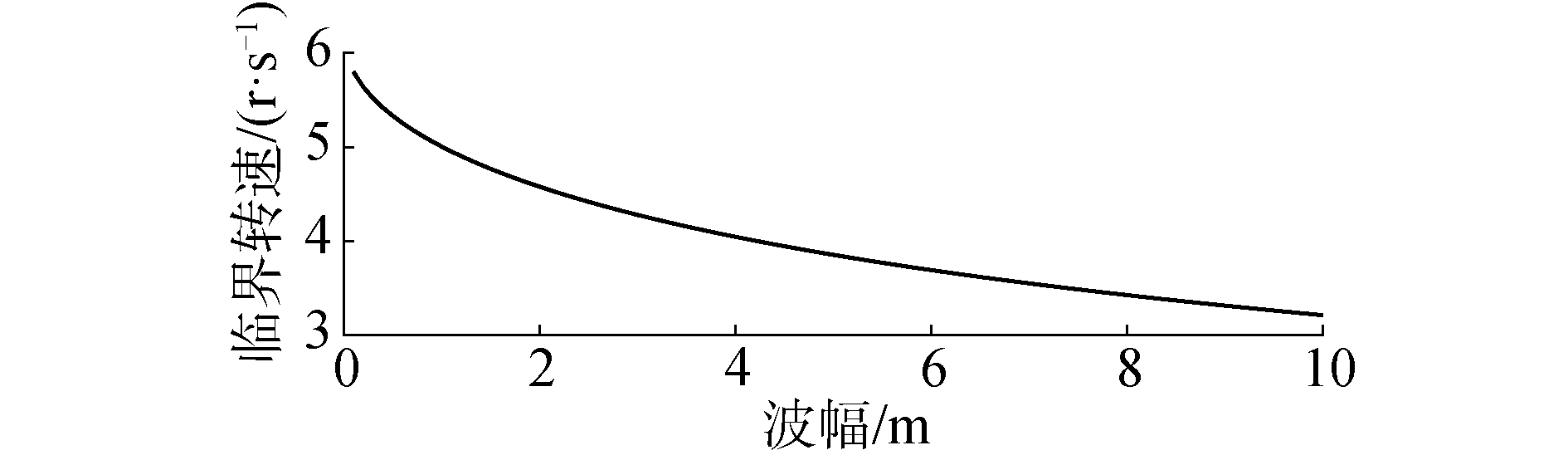
3.1 临界转速与临界船速计算结果选取波浪条件为λ/Lpp=1.5,航向角χ=0°。考虑波幅为渐变量,采用解析方法求解船舶发生骑浪运动时螺旋桨临界转速与波幅之间的关系,采用梅林科夫方法计算得到的临界螺旋桨转速阈值曲线如图 3所示。由图 3可以看出当波长保持不变、波幅增加时,梅林科夫方法得出的螺旋桨临界转速逐渐减低。即在波幅较大时,螺旋桨临界转速较小,船舶易于发生骑浪现象。相反,当波幅较小时,螺旋桨临界转速则更高,骑浪现象更难发生。
|
Download:
|
| 图 3 螺旋桨临界转速随波幅变化曲线 Fig. 3 Critical rotational speed of the propeller against wave amplitude | |
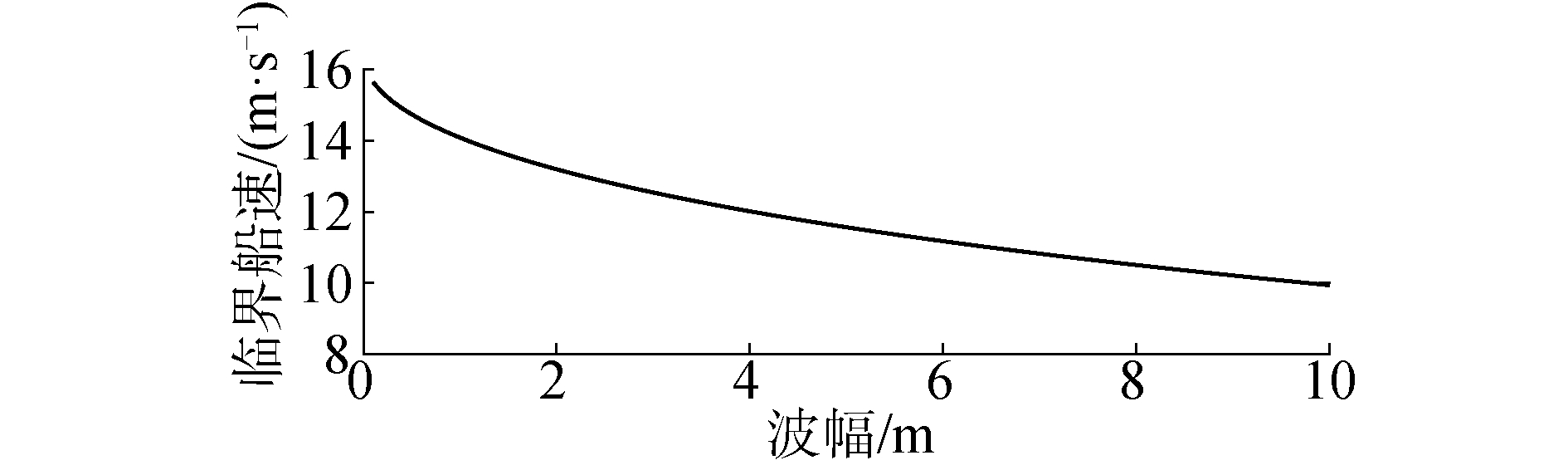
根据船舶的推力和阻力相等条件,可以进一步求出发生骑浪的临界船速。船舶临界船速随波幅变化的关系图如图 4所示。由图 4可以看出,船舶临界船速随波幅变化趋势与船舶螺旋桨临界转速随波幅的变化趋势相同。即当波幅值增加时,梅林科夫方法得出船舶临界航速逐渐减低。这一结果说明,在波幅较大时,船舶临界航速较小,船舶就会易于发生骑浪现象。相反,当波幅较小时,船舶临界航速则更高,不易发生骑浪。
|
Download:
|
| 图 4 船舶临界船速随波幅变化曲线 Fig. 4 Critical ship speed against wave amplitude | |
采用龙格库塔方法对船舶纵荡运动进行数值求解,计算不同螺旋桨转速下船舶纵荡运动,通过对比纵荡运动的数值解形式,判断螺旋桨的临界转速。
选取波浪条件为:λ/Lpp=1.5,航向角χ=0°。H/λ=1/10。在此波浪条件下,由梅林科夫方法得到的螺旋桨临界转速为3.38 r/s,对应临界航速为10.38 m/s,采用龙格库塔方法得出的螺旋桨临界转速为3.5 r/s,对应的临界船速为10.69 m/s。将2种方法得出的结果进行对比,得出2种算法预报的螺旋桨临界转速误差为3.43%,临界船速误差为2.90%,均在5%以内,验证了解析方法的准确性。
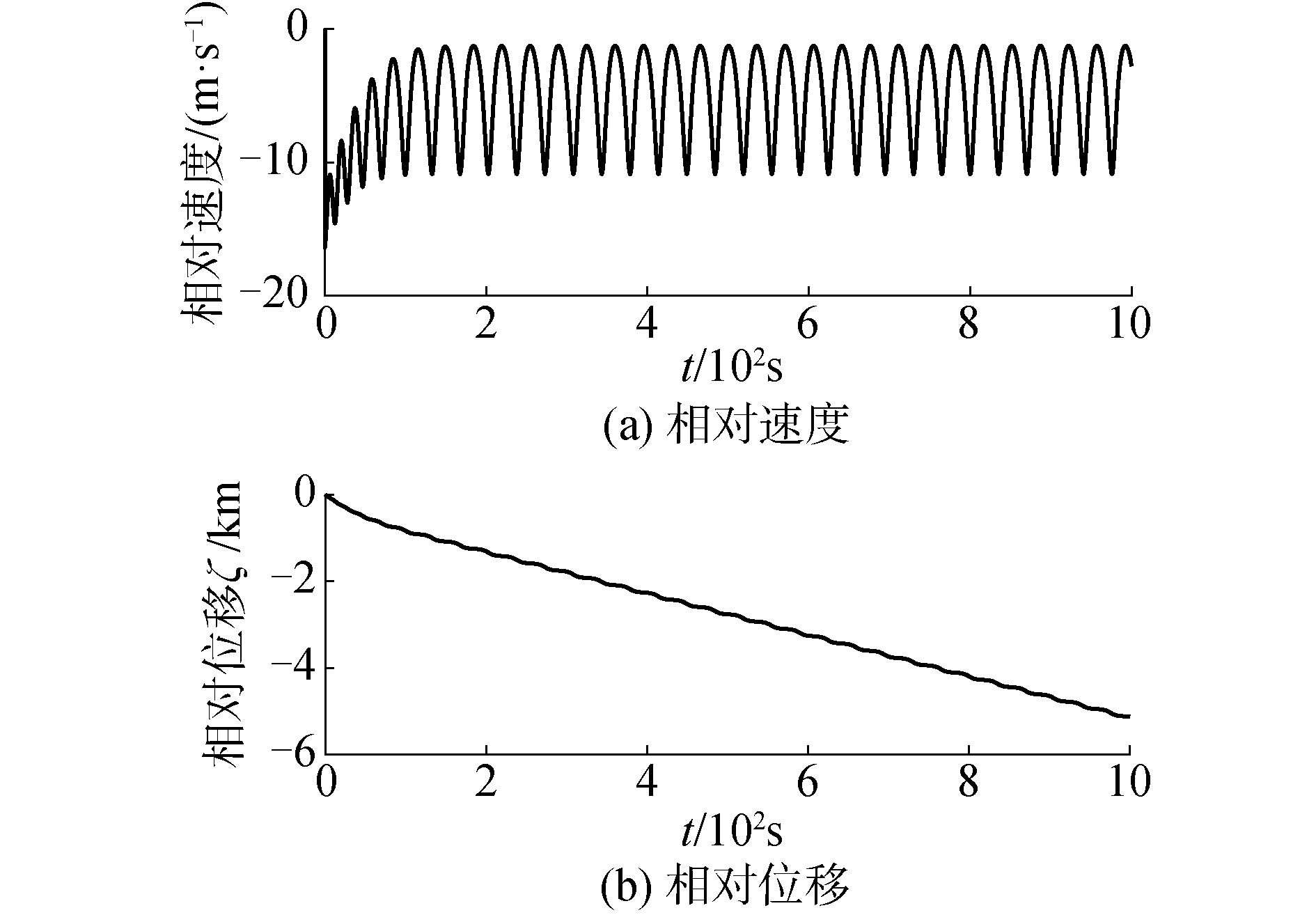
当螺旋桨转速为3.3 r/s时,船舶与波浪间的相对速度如图 5(a)所示,与波浪的相对位移图 5(b)所示。从2个时间历程曲线图中可以看出,当螺旋桨转速为3.3 r/s时,船舶的纵荡速度相对于波浪速度是周期变化的,同时船舶与波浪的相对位移随时间是逐步增大的。此时船由螺旋桨进行推进,并未被波浪所捕获,所以在螺旋桨转速为3.3 r/s时,船舶未发生骑浪现象。
|
Download:
|
| 图 5 转速3.3 r/s时船舶纵荡运动响应 Fig. 5 Surge motion response when the revolution speed of propeller is 3.3 r/s | |
当螺旋桨转速增加到3.5 r/s时,船与波的相对速度及相对位移如图 6(a)和图 6(b)所示。由2个时间历程曲线图中可以看出,当螺旋桨转速为3.5 r/s时,船舶在波浪中运动约200 s后,船舶与波浪之间的相对速度变为零,同时船舶与波浪之间的相对位移也保持不变。从这2个时历曲线图中可以看出,当螺旋桨转速为3.5 r/s时,船舶在运动一段时间后会以波浪速度前进,即船舶被波浪所捕获。此时船的螺旋桨推力系统失去对船舶的控制,发生了船舶骑浪运动现象。

|
Download:
|
| 图 6 转速3.3 r/s时船舶纵荡运动响应 Fig. 6 Surge motion response when the revolution speed of propeller is 3.5 r/s | |
为了更加准确判断船舶骑浪运动的非线性特性,分别给出螺旋桨转速为3.3 r/s和3.5 r/s时,船舶运动的相图。相图的横坐标为cos(2πξ″G/λ),其物理意义代表船舶与波浪的相对位置以波长为周期变化,纵坐标为船的绝对速度,即为船舶在固定坐标系中的速度。从图 7(a)的相图中可以看出,当螺旋桨转速为3.3 r/s时,船舶纵荡运动的相图为封闭环,所以此时船舶运动是稳定的,未发生骑浪现象;而图 7(b)的结果表明,当螺旋桨转速为3.5 r/s时,船舶纵荡运动的相图是一个半环,此时船舶的纵荡运动丧失稳定性,发生了船舶骑浪现象,即船舶被波浪所捕获。

|
Download:
|
| 图 7 船舶运动相图 Fig. 7 Phase diagram of the surf-riding ship | |
取波浪条件为λ/Lpp=1.5,航向角χ=0°,H/λ=1/10。给定不同的螺旋桨转速n,求船舶纵荡运动的时间历程。船舶相对速度随螺旋桨转速变化的分岔图如图 8所示。从图 8中看出,此波浪条件下,当螺旋桨转速低于3.4 r/s时,系统发生的是稳定的周期运动,在分岔图的表现上表示为一个点,即一个圆圈。当螺旋桨转速为3.5 r/s时。分岔图上不能画出点,此处用点集区域示意船舶骑浪的非稳定区域的范围,不再是稳定的往复周期性运动,此时船舶与波浪之间的相对速度为0。所以此条件下船舶纵荡运动丧失稳定性,即船舶发生骑浪失稳运动。

|
Download:
|
| 图 8 船舶相对速度随螺旋桨转速变化分岔图 Fig. 8 The bifurcation diagram of the ship relative speed against rotational speed of the propelle | |
1) 基于非线性动力学方法得到的骑浪条件和骑浪失稳域,与数值方法得到的结论基本吻合,表明非线性动力学方法分析船舶骑浪运动的可行性。
2) 当船舶在规则波中未发生骑浪运动时,船速相对于波速呈周期性变化的规律;当船舶发生骑浪运动时,船舶被波浪捕获,相对速度为零。
3) 当波幅较大,螺旋桨临界转速较小时,船舶容易发生骑浪运动,并且易发生骑浪失稳导致横甩。
| [1] |
封培元, 陆志妹, 余滋红, 等. 船型参数对骑浪/横甩薄弱性衡准影响研究[C]//纪念《船舶力学》创刊二十周年学术会议论文集. 舟山, 中国, 2017. FENG Peiyuan, LU Zhimei, YU Zihong, et al. Influence of ship main particulars on surf-riding/broaching vulnerability criteria[C]//The Academic Conference for Commemorating the Twentieth Anniversary of Journal of Ship Mechanics. Zhoushan, China, 2017. (  0) 0)
|
| [2] |
BEGOVIC E, BERTORELLO C, BOCCADAMO G, et al. Application of surf-riding and broaching criteria for the systematic series D models[J]. Ocean engineering, 2018, 170: 246-265. DOI:10.1016/j.oceaneng.2018.08.062 (  0) 0)
|
| [3] |
陶醉, 张纬康. 船舶骑浪运动的分叉研究[J]. 船舶力学, 2004, 8(2): 29-33. TAO Zui, ZHANG Weikang. Bifurcation research of surf-riding[J]. Journal of ship mechanics, 2004, 8(2): 29-33. (  0) 0)
|
| [4] |
高占胜, 陶醉, 石侃. 舰艇纵荡自由度上非线性动力分析[C]//2006中国大连国际海事论坛论文集. 大连, 中国, 2006: 365-369. GAO Zhansheng, TAO Zui, SHI Kan. Nonlinear dynamic analysis in the surge of ship[C]//Proceedings of The International Marine Tech Forum Dalian China. Dalian, China, 2016: 365-369. (  0) 0)
|
| [5] |
储纪龙, 鲁江, 韩阳, 等. 基于Melnikov方法的船舶骑浪临界值预报研究[J]. 中国造船, 2015, 56(S1): 89-96. CHU Jilong, LU Jiang, HAN Yang, et al. Study on predicting surf-riding threshold based on Melnikov's method[J]. Shipbuilding of China, 2015, 56(S1): 89-96. (  0) 0)
|
| [6] |
顾民, 储纪龙, 韩阳, 等. 内倾船型骑浪/横甩薄弱性衡准和模型试验研究[C]//2017年中国造船工程学会优秀学术论文集. 北京, 中国, 2018. GU Min, CHU Jilong, HAN Yang, et al, Study on the surf-riding/broaching vulnerablitiy criteria and model test of a tumblehome ship[C]//The proceedings of the 2017 best papers in China's Society of Naval Architecture and Marine Engineering. Beijing, China, 2018. (  0) 0)
|
| [7] |
KAN N. A guideline to avoid the dangerous surf-riding[C]//4th International Conference on Stability of Ships and Ocean Vehicles. Naples, Italy, 1990.
(  0) 0)
|
| [8] |
SPYROU K J. Asymmetric surging of ships in following seas and its repercussions for safety[J]. Nonlinear dynamics, 2006, 43(1): 149-172. DOI:10.1007/s11071-006-0758-6 (  0) 0)
|
| [9] |
刘亚柳. 随浪中船舶骑浪横甩非线性运动特性及骑浪概率研究[D]. 天津: 天津大学, 2019. LIU Yaliu. Research on nonlinear motion characteristics of surf-riding/broaching and surf-riding probability of a ship in following waves[D]. Tianjin: Tianjin University, 2019. (  0) 0)
|
| [10] |
吴小平. 基于切片理论的波浪载荷直接计算[J]. 上海造船, 2010(4): 21-25. WU Xiaoping. The direct caculation of wave load based on the strip theory[J]. Shanghai shipbuilding, 2010(4): 21-25. DOI:10.3969/j.issn.1005-9962.2010.04.005 (  0) 0)
|
| [11] |
刘峥. 船舶骑浪横甩及纯稳性丧失状态非线性动力学特性研究[D]. 天津: 天津大学, 2019. LIU Zheng. Research on nonlinear dynamics characteristics of ship's surf-riding, broaching and pure loss of stability[D]. Tianjin: Tianjin University, 2019. (  0) 0)
|
| [12] |
王丽元. 船舶纵浪航行非线性随机运动响应预报方法研究[D]. 天津: 天津大学, 2020. WANG Liyuan. The research on predicting method on ship nonlinear stochastic motion response in longitude wave[D]. Tianjin: Tianjin University, 2020. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


