2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 741852;
3. 赫瑞瓦特大学 基础设施与环境研究所, 爱丁堡 EH144AS
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 741852, China;
3. The Lyell Centre for Earth and Marine Science and Technology, Institute for Infrastructure and Environment, Heriot-Watt University, Edinburgh, EH144AS, UK
随着海岸及近海工程的深水化,兼具观赏性和水体交换功能的潜体结构逐渐得到推广。波浪越过潜体时会出现流体分离和漩涡泄放现象,引起波压脉动和局部冲刷。因此,深入研究潜体附近的紊流结构对于理解其工作机理有重要意义。
近年来快速发展的非接触式光电测流技术已具备量测波生紊流场的能力。Ting等[1]采用单点激光多普勒流速仪(laser-doppler anemometer,LDA)研究了规则波越过矩形潜体的流体分离效应对反射和透射性能的影响。Lin等[2]联合粒子图像测速技术(particle image velocimetry,PIV)和质点追踪技术(particle tracing,PT)捕捉了孤立波越过水下立板过程中的速度场,清晰展示出边界层分离、涡旋生成和泄放、垂向射流、垂向射流与自由表面掺混等涡旋演化现象。李雪临[3]借助PIV技术研究了透空式建筑物浪溅区部位波浪冲击过程中的瞬时流场变化,应用概率分析法探讨了瞬时冲击波压峰值与水质点瞬时速度之间的关系。Poupardin等[4]运用PIV技术分析了水下平板周围波浪振荡流形成的环流系统,观测到平板下游涡对产生的强烈向下射流可能引起底床冲淤,上游涡对则表现为水平对流,对底床无影响。Athanassios等[5]在块石护面的粗糙陡坡上方安设了水下2D-PIV观测系统,获取了斜坡上波浪破碎点海侧的瞬时速度场,分析认为不规则护面块石的流体分离效应和护面层孔隙处的局部水流吐吸增强了波生紊流的强度,并探讨了顺流、横流和垂向流速脉动对平均紊流动能的贡献。蒋学炼等[6]对比了椭圆余弦波作用下矩形潜堤周围波生流场的黏性数值波浪水槽计算值和Chang等[7]的PIV实验值,证明了粒子图像测速技术的准确性。Chang[8]采用光纤反射技术(fibre optic reflectometry,FOR)量测了平底床面上崩破波内的气泡形态,结合PIV技术考查了气液两相掺混区的紊流结构。
以往研究多针对矩形潜体,随着海岸工程深水化对低反射结构的需求,近年来出现了多种流线型的断面,如半圆体和弧形体等。有关这些低反射结构的水力特性研究较多[9-12],但其后的机理探究较少,需要从微观流场的角度开展研究。本文以不同流线型的3种潜体为研究对象,采用PIV技术获取了规则波作用下抛石基床上的瞬时速度场,分析比较了不同潜体波生紊流场的结构。
1 粒子图像测速技术试验方法与验证试验在大连理工大学海岸和近海工程国家重点实验室开展,波浪水槽尺寸为30 m×0.4 m×0.65 m(长×宽×高),水槽一端安装有液压推板式造波机,另一端设有斜坡式消能坡(图 1)。模型段水槽的底部和两侧均为透明玻璃制成,槽底下方设有地下仪器室,安放激光器。

|
Download:
|
| 图 1 试验布置(以半圆体为例) Fig. 1 Experiment configuration | |
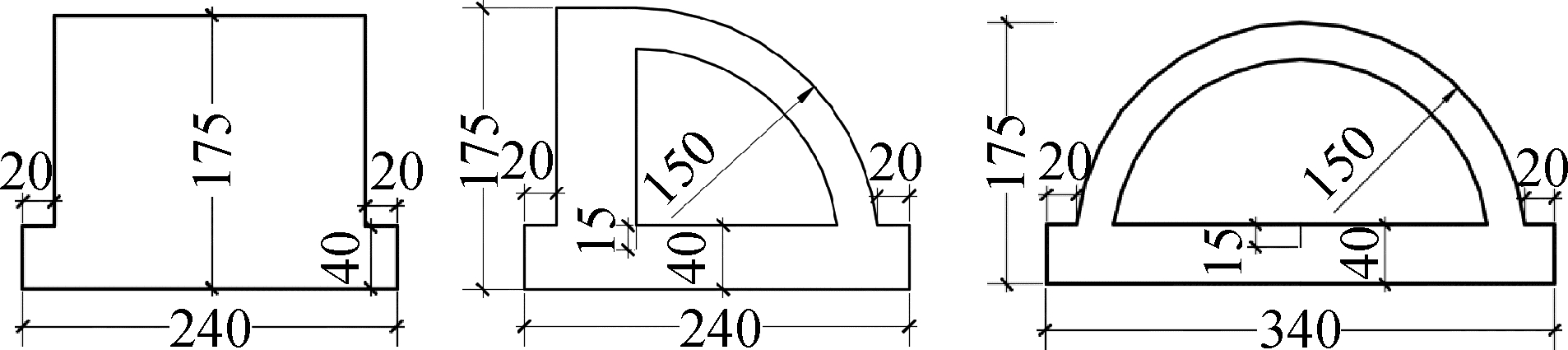
模型堤体采用丙烯酸有机玻璃制成,内部以铅块配重,高度相同,包括3种线型(图 2):矩形(钝体)、弧形(半流线型)、半圆(流线型)。
|
Download:
|
| 图 2 模型堤体几何尺寸 Fig. 2 Geometry of model structures | |
PIV测速系统由5个部分组成:激光器、图像采集系统、图像采集卡、信号同步器、图像分析系统。在抛石基床中心线位置用丙烯酸有机玻璃支护一条宽度约1.5 mm的狭缝作为片光源通道(图 3)。光源由安装在地下仪器室的双头钇铝柘榴石晶体谐波激光器产生,脉冲延迟400 ms,经柱面镜散射后透过玻璃槽底形成垂向二维双倍频片光点亮测速区域。

|
Download:
|
| 图 3 抛石基床开缝处的片光源 Fig. 3 Light sheet plane via a slot in the rubble mound | |
图像采集系统由8位数字电荷耦合摄像机(CCD)和图像采集卡(Coreco Cameralink)构成。CCD相机的分辨率为1 600 pixels×1 192 pixels。采样区域分别设置在堤前和堤后的基肩上方(图 1中的FOV1和FOV2,FOV-Field of View),区域范围均为25.5 cm×18.5 cm(宽度×高度),对应的分辨率为57 pixel/cm。同步器(LaserPulse)用于激光器触发信号和CCD相机采集信号的同步控制。堤前和堤后的采样区域内各布置1支浪高仪。
借助INSIGHT-3G软件(TSI公司)对PIV系统采集的连续图像序列进行多通道互相关分析,在x方向和z方向分别设置48个和35个速度矢量点,采样精度为1.6个/cm速度点,每次采样获取1 680个网格点的瞬时速度矢量值。互相关算法为快速傅里叶变换(FFT),初始通道的平滑窗口尺寸取32 pixels×32 pixels,最后通道的平滑窗口尺寸取64 pixels×64 pixels,相邻窗口的重叠率取50%,对应的空间分辨率为0.6 cm×0.6 cm。
每种线型的潜体重复试验3次,每次试验前均须调整激光脉冲频率、CCD相机的光圈焦距等,再在水槽内采样区域放置标定尺,对相机成像平面尺寸(pixel)和片光平面尺寸(cm)之间的比例进行标定,将标定参数存入INSIGHT-3G软件,以通过图像分析获取水质点的瞬时速度值。为了提高速度场识别的灵敏度,在水槽模型段均匀掺混平均粒径10 μm、密度1 100 kg/m3的聚氯乙烯粉末,作为PIV图像采集的示踪粒子。
由于试验的目的是考查不同流线型潜体抛石基床上的波生紊流分布及发展规律,不研究波面或波能的变化,因此只选择一种代表性的水力条件(即堤顶始终淹没于水中),即:d=0.33 m,H=0.09 m,T=1.0 s,L=1.4 m。对应的水质点运动轨迹幅值
| $ \begin{array}{l} {U_0} = \frac{{{\rm{ \mathsf{ π} }}H}}{T}\frac{{\cosh \left[ {\frac{{2{\rm{ \mathsf{ π} }}\left( {d - {d_i}} \right)}}{L}} \right]}}{{\sinh \left( {\frac{{2{\rm{ \mathsf{ π} }}d}}{L}} \right)}} + \\ \frac{3}{4}\frac{{{{\rm{ \mathsf{ π} }}^2}H}}{T}\left( {\frac{H}{L}} \right)\frac{{\cosh \left[ {\frac{{4{\rm{ \mathsf{ π} }}\left( {d - {d_i}} \right)}}{L}} \right]}}{{{{\sinh }^4}\left( {\frac{{2{\rm{ \mathsf{ π} }}d}}{L}} \right)}} = 0.25\;{\rm{m}}/{\rm{s}} \end{array} $ |
相应地,参考涡量ωref=U0/S =5.79 s-1,参考环量Γref=2U0D =0.08 m2/s,雷诺数Re=U0di/ν =1.98×104,Keulegan-Carpenter数Kc=U0T/D =1.54,厄塞尔数Ur=HL2/d3 =4.94,其中运动黏滞系数取ν=1.01×10-6 m2/s。
基于可靠性考虑,试验中自第5个稳定波峰通过各采样区域中心位置时开始PIV采样,采样频率15 Hz,每次采样的2帧图像之间的时间延迟为600 ms,采集时长6 s,包含6个完整波浪周期。
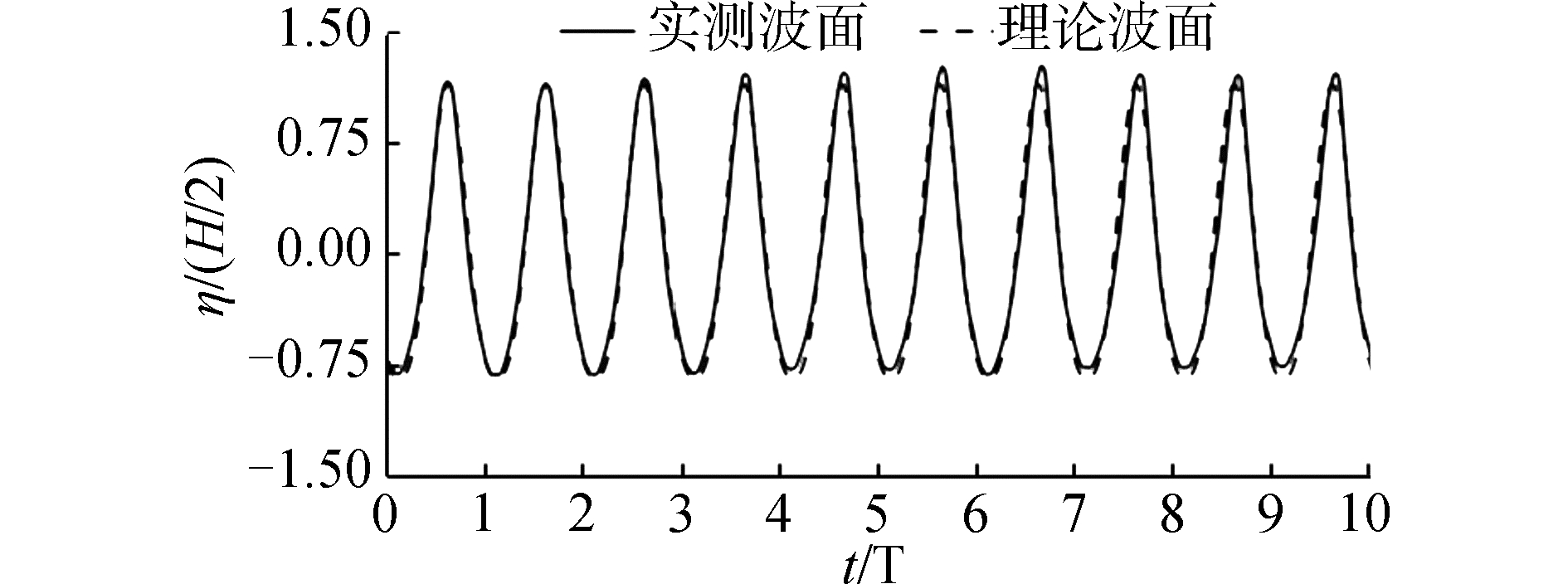
根据Le Méhauté[13]的波浪理论适用范围判断,本次试验的工况对应二阶斯托克斯波形。图 4比较了预备试验中空槽建筑物位置处的实测波面与二阶斯托克斯理论波形,两者吻合良好。实测波高和波周期的均方根偏差平均值分别为0.21和0.90%,说明造波效果良好,试验波形稳定。
|
Download:
|
| 图 4 实测波面与理论波面对比 Fig. 4 Comparison of the measured and theoretical profiles | |
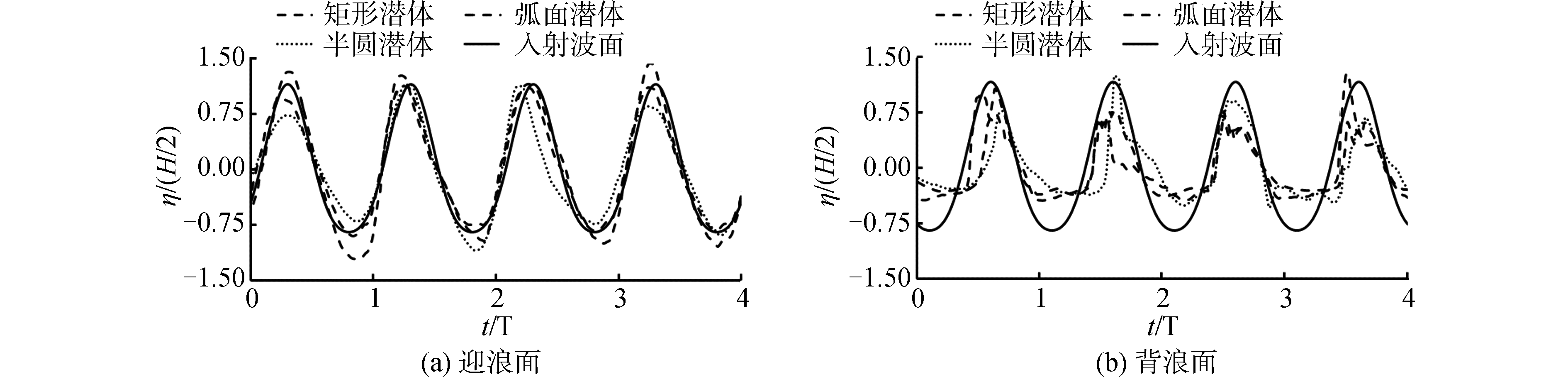
图 5展示了波浪越过3种潜体过程中的波面变化。可以看出,潜体前后的波面均未发生明显的破碎。采用表征波面相对水平轴不对称性的偏度来衡量[14]:
| $ S = {\rm{E}}\left[ {{{\left( {{\eta _i} - {{\bar \eta }_i}} \right)}^3}} \right]/{\sigma ^3} $ |
|
Download:
|
| 图 5 不同线型潜体的波面过程比较 Fig. 5 Comparison of the surface elevations at the weather- and lee-side of the immersed structures with different shapes | |
式中:ηi为波面高程;σ为标准差。与入射波面比较,迎浪面的波形变化幅度较小,3种潜体迎浪面波形的偏度分别为0.25(矩形)、0.41(弧形)、0.27(半圆),与入射波面的偏度0.32接近。背浪面的波高减小幅度较大,说明部分波能在越过潜体的过程中损耗。同时,波峰变陡,波谷变平,且出现多个次生峰谷,表明部分波能从低频向高频转换。3种潜体背浪波面的偏度分别为1.10(矩形)、0.88(弧形)、0.95(半圆),与入射波面比,相对水平轴表现出明显的不对称性。波形的这种非线性变化与潜体附近的流场紊动有关,接下来将从涡动力学角度进行分析。
2 周期平均速度场分析Peng等[15]发现波生漩涡和射流是引起海堤前底床冲刷的直接原因。为了考查抛石基床上部波生紊流场的时均效应,本节采用周期平均速度进行分析,其计算公式为[5]:
| $ {U_{ij}} = \frac{1}{{N{N_p}}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{N_p}} {{u_{ij}}} } $ | (1) |
式中:uij为第i周期中第j相位的瞬时速度值;N =6为周期数;Np为相位数(即采样频率15)。
图 6给出了3种潜体建筑迎浪和背浪基床上的周期平均速度场。可以看出,由于潜体对流场的干扰,周期平均速度场非零且不对称。

|
Download:
|
| 图 6 潜体抛石基床上的周期平均速度场和涡量场 Fig. 6 Period-averaged velocity and vorticity fields above the rubble mound of immersed structures | |
在迎浪基床上方,3种潜体的迎浪堤脚处均存在一个小型环流系统(图 6中的A点),其影响范围大约一个水质点运动轨迹(S =0.043 m),变动范围很小,有可能引起较强烈的局部冲刷,此处需加强防护。与弧形和半圆潜体不同的是,矩形潜体在迎浪堤角附近额外存在一个较强的环流系统(图 6(a)中的C点),其核心距离迎浪堤面大约0.075 m(≈1.75S),因直立迎浪堤面的阻流效应形成。由于位置较高,这一环流系统不会直接对基床形成冲淤,但会引起迎浪堤角较强的压力脉动。
在背浪基床上方,从采样区域的右下方有一股强烈射流冲向左上方,在驻点处(图 6中的B点)分解为一对反向的环流,同时,背浪基肩上的速度很小,存在一个波隐区。这一速度分布特点预示着背浪面底床悬起的泥沙会部分向堤背传递,在B点处分别向离岸和向岸2个方向输移,还有部分泥沙会淤积于背浪基肩处。3种潜体背浪面的周期平均环流系统表现出不同的分布特点。矩形潜体为钝形结构,堤后速度场变化剧烈且靠近堤背,形成一对强烈的反向涡对。半圆潜体为流线型结构,拱形墙背引导水流向后方和下部传递,顺时针负涡显著强于逆时针正涡,涡核位于采样区域右下方。弧形潜体的环流分布介于矩形潜体和半圆潜体之间,堤角附近存在一对较小范围的反向涡对,涡旋主要沿水平方向传递,在B点右上方与堤顶齐平位置有一强环流。
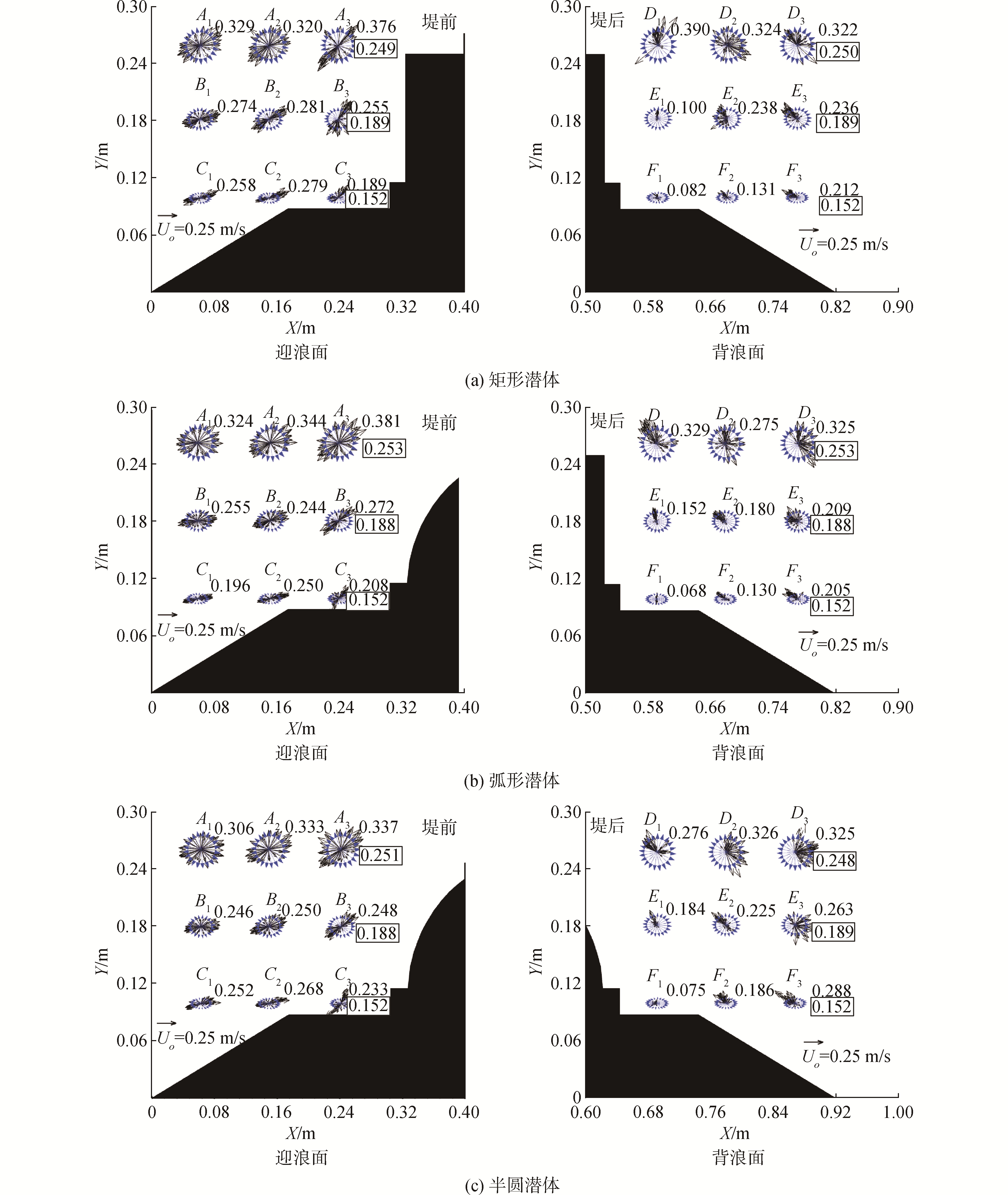
图 6表明,3种线型潜体周围的周期平均速度场与无潜体存在时的势波速度场存在很大偏差。为了探究其原因,图 7比较了潜体前后各9个固定位置的实测瞬时速度值和二阶斯托克斯波速度值的矢端曲线。可以看出,实测值与理论值处于同一量级,这一定程度上证明了实验数据的可靠性。
|
Download:
|
| 图 7 抛石基床上的实测瞬时速度值和理论速度值 Fig. 7 Measured instantaneous and theoretical velocities above the rubble mound 注:A为波峰时刻,B为下跨波中时刻,C为波谷时刻,D为上跨波中时刻,图中正体数字为实测速度最大值,加框数字为斯托克斯波速度最大值;单位:m/s | |
在波浪与潜体相互作用的流场中,实测水质点的运动轨迹与二阶斯托克斯波明显不同,表现为强非对称性,某些方向上的运动减弱,另一些方向的运动则增强。分区域看,迎浪采样区域各点的实测瞬时速度最大值约为同深度二阶斯托克斯波理论最大值的1.2~1.5倍,水质点运动轨迹由上游椭圆形转变为潜体前的斜向运动为主,尤其在矩形潜体迎浪堤角附近的点A3,大部分速度沿45°角斜线方向,这正是图 6(a)中C点较强环流的形成原因。在背浪采样区域,点F3的水质点主要向左上方运动,实测瞬时速度最大值约为同深度二阶斯托克斯波理论最大值的1.3~1.9倍,对应图 6中右下方的射流。在点D2和点D3,弧形潜体和半圆潜体向下游的速度更强,而矩形潜体则有很大部分的速度值指向上游。在点E3,半圆潜体的速度主要指向下游和下方,其他两种潜体的速度则主要指向上游。背浪基肩上的点F1处于波隐区,速度值减小为同深度二阶斯托克斯波理论值的约0.5倍。上述背浪采样区域各点的速度变化均与图 6背浪面的周期平均环流分布特点一致。
从图 7可以推断,由于斯托克斯波来自于势流理论,不会主动生成涡旋,因此,实测瞬时速度值与理论速度值的偏差主要是涡旋在不同位置水体间的对流、扩散、耗散等动量交换现象引起的。
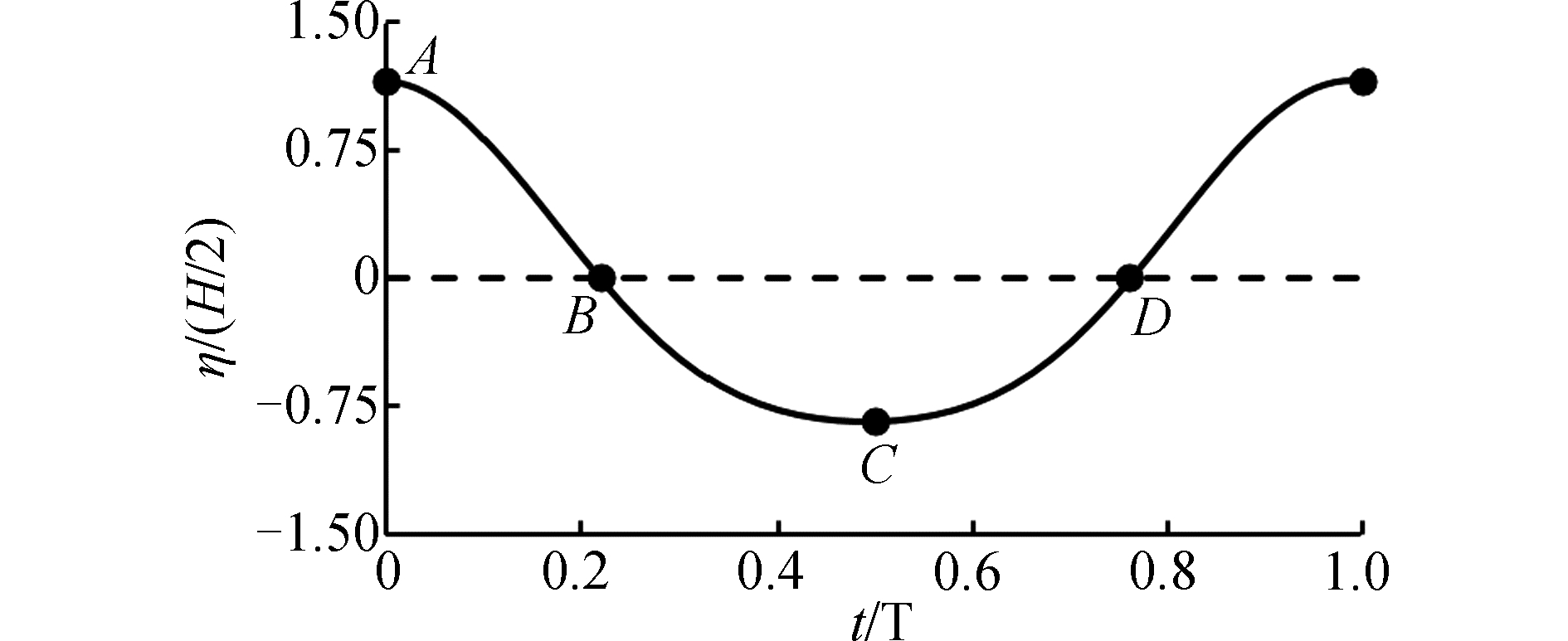
3 相平均涡量场的演变本节分析波浪越过潜体的涡流演化过程。以波面通过采样区域的中心位置定义特征相位时刻(图 8)。
|
Download:
|
| 图 8 一个周期内波面的相位时刻定义 Fig. 8 Sketch indicating the characteristic phases of the surface elevation within a wave period | |
图 9和图 10分别呈现了一个波周期内迎浪面和背浪面各相位时刻的相平均涡量场。相平均涡量场由相平均速度场得到,其计算式为:
| $ {U_{xj}} = \frac{1}{N}\sum\limits_{i = 1}^N {{u_{xij}}} {\bar U_{yj}} = \frac{1}{N}\sum\limits_{i = 1}^N {{u_{yij}}} {\bar \omega _j} = \frac{{\partial {{\bar U}_{xj}}}}{{\partial y}} - \frac{{\partial {{\bar U}_{yj}}}}{{\partial x}} $ | (2) |

|
Download:
|
| 图 9 迎浪基床上方的相平均涡量场 Fig. 9 Phase-averaged vorticity fields at different phases above the weather-side rubble mound | |

|
Download:
|
| 图 10 背浪基床上方的相平均涡量场 Fig. 10 Phase-averaged vorticity fields at different phases above the leeside rubble mound | |
式中:Uxj、Uyj、ωj分别为第j相位的相平均水平速度、垂向速度、涡量。
由图 9可见,迎浪采样区域的涡旋主要生成于波谷过程,水流由下游向上游运动时,3种潜体的迎浪堤脚处边界层速度剪切发生流体分离,生成逆时针正涡(相位C),并诱导出一个顺时针负涡,随后在上升水流(相位D)和正向水流(相位A)作用下,这一反向涡对向上和向下游对流扩散,逐渐分解破碎,在相位B时刻已脱离基肩进入水体。但在一个周期内这一反向涡对并不能充分发展,随着水流转向(相位C),迎浪堤脚处又有新的涡对生成。与图 6(a)对应,矩形潜体的迎浪堤角处存在一对较强的反向涡对,同样生成于波谷过程中(相位C),经历相位D~相位B后三维失稳逐渐耗散。由于迎浪面为流线型,弧形和半圆潜体的迎浪堤角处流体分离不显著,并未生成强烈的反向涡对。
图 10则显示,背浪采样区域的涡旋主要生成于波峰过程,水流通过背浪堤角发生流体分离,生成顺时针负涡(相位A),随后在平均水流(相位B~D)的作用下对流扩散,逐渐分解破碎。3种潜体的涡旋演变过程明显不同。矩形潜体的涡旋靠近堤背,顺时针负涡生成后向下游扩散,相位C时刻的反向水流增强了顺时针负涡诱导出的逆时针正涡,并向底部传递,到相位D时刻,这一强反向涡对主要分解耗散于堤背附近约3倍水质点运动轨迹范围内(3S =0.129 m)。弧形潜体和半圆潜体流线型的迎浪面使得更多波能透射到堤后,两者背浪面涡旋大致水平向下游对流。由于弧形潜体背浪面为直立墙背,生成的顺时针负涡较半圆潜体强度和范围更大,一个周期后采样区域的右侧仍有较强的涡旋运动(相位D),而此时半圆潜体的涡旋已基本消散。在波谷时刻(相位C),反向水流同样增强了半圆潜体背浪面的逆时针正涡,并向底部传递,但其强度和范围弱于矩形潜体。与图 6和图 7一致,除弧形潜体在背浪基肩上存在较弱的涡旋运动外,此处受涡旋影响很小,为紊流遮蔽区,存在淤积可能。
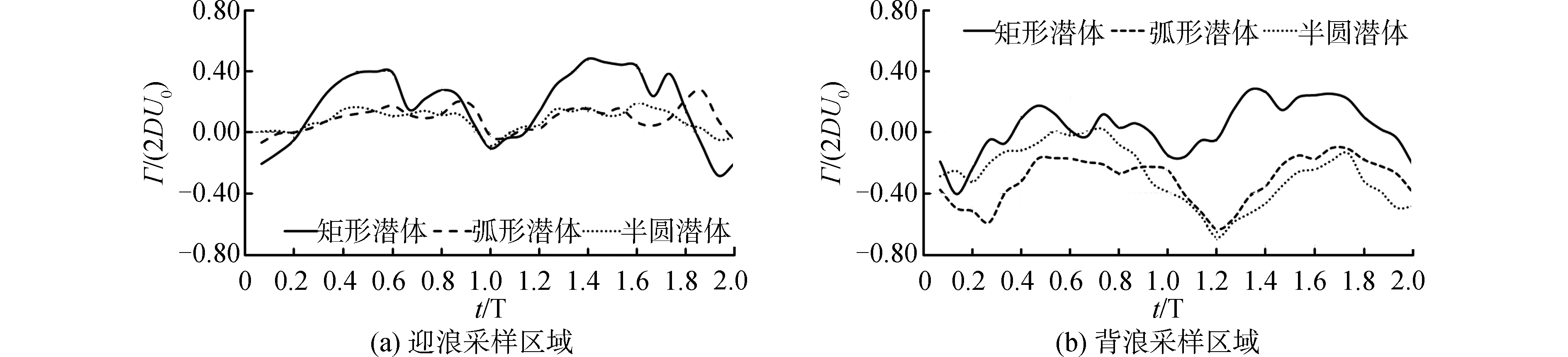
由上可见,波峰和波谷转换过程中,水流变向叠加与不同外形潜体的交互作用,导致迎浪基床(图 9)和背浪基床(图 10)上方的相平均流速场和涡量场强烈非对称,这还可以从表征涡旋场强度的环量的演变进一步证实(图 11)。其中,环量Γ通过积分采样区域内的涡量得到:
| $ \mathit{\Gamma } = \int {\int {\left( {\frac{{\partial {u_y}}}{{{\partial _x}}} - \frac{{\partial {u_x}}}{{\partial y}}} \right){\rm{d}}x{\rm{d}}y} } = \int {\int {\omega {\rm{d}}x{\rm{d}}y} } $ | (3) |
|
Download:
|
| 图 11 抛石基床上的实测环量过程 Fig. 11 Evolution of the circulation above the rubble mound calculated from the measurements | |
式中ω为各采样单元的涡量。
由图 11可见,迎浪区域和背浪区域的环量表现为周期性振荡,其周期大致与波浪周期相等,预示着作用于潜体上的波压脉动。同时,潜体的存在破坏了波生流场的速度连续性,使得周期平均的环量非零。3种潜体的迎浪区域环量均以正值居多,无量纲环量Γ/(2U0D) 的周期平均值分别为0.17(矩形)、0.09(弧形)、0.08(半圆),说明逆时针涡旋居于主导地位,其中矩形潜体的环量最大值约为其他两种潜体的两倍。而背浪区域由于潜体外形的不同出现分化,无量纲环量周期平均值分别为0.03(矩形)、-0.31(弧形)、-0.28(半圆)。弧形潜体和半圆潜体的环量基本为负值,矩形潜体的环量则在波峰和波谷交替过程中变换符号,说明正向和反向水流对矩形潜体的作用相当,而弧形潜体和半圆潜体有更多波能透射到堤后,使得顺时针涡旋始终居于主导地位。
4 结论1) 在堤顶始终淹没的情况下,潜体前后的波面均未发生明显的破碎。由于迎浪区域的紊流较弱,波能损耗小,波形变化幅度较小,而背浪面出现了较强的紊动,波高显著减小,部分波能从低频向高频转换,表现出明显的不对称性。
2) 3种潜体的迎浪堤脚处均存在一个小型周期时均环流系统,有可能引起较强烈的局部冲刷。矩形潜体迎浪堤角附近的环流系统会引起堤面压力脉动。3种潜体背浪面形成的周期时均反向环流,会将悬起的泥沙部分向离岸和向岸2个方向输移,另有部分泥沙会淤积于背浪基肩上的遮蔽区。
3) 3种潜体的迎浪区域涡旋演变过程接近,主要生成于波谷过程,在迎浪堤脚处有一反向涡对,1个周期内未能充分发展。矩形潜体的迎浪堤角处还存在一对较强的反向涡对。背浪区域的涡旋主要生成于波峰过程,首先生成顺时针负涡,随后在平均水流的作用下对流扩散,并诱导出逆时针正涡,逐渐分解破碎。背浪基肩上的涡旋强度很弱,为紊流遮蔽区,存在淤积可能。断面形状对潜体背浪区域的涡旋分布和传递有显著影响,矩形潜体的涡旋靠近堤背,弧形潜体和半圆潜体的涡旋则大致水平向下游对流,其中前者的涡旋强度和范围大于后者,耗散时间更长。
4) 由于潜体对流场的干扰,涡旋在迎浪面和背浪面周期性地生成、泄放和传递,改变了潜体周围的平均流动,速度场变得非零且不对称。涡旋的脱落、对流和扩散对于局部冲淤和结构受力均有影响。因此,下一步的工作应拓展到参数分析,探讨潜体相对尺度(宽度/波长)、相对淹没深度(淹没深度/水深)、相对波高(波高/水深)和相对周期(波陡)等对潜体涡动力学的影响,为深水潜体工程的优化设计提供参考。
| [1] |
TING F C K, KIM Y K. Vortex generation in water waves propagating over a submerged obstacle[J]. Coastal engineering, 1994, 24(1/2): 23-49. (  0) 0)
|
| [2] |
LIN Chang, HO T C, CHANG S C, et al. Vortex shedding induced by a solitary wave propagating over a submerged vertical plate[J]. International journal of heat and fluid flow, 2005, 26(6): 894-904. DOI:10.1016/j.ijheatfluidflow.2005.10.009 (  0) 0)
|
| [3] |
李雪临. 波浪冲击过程的流场变化特性研究[D]. 大连: 大连理工大学, 2009. LI Xuelin. The study on the characteristics of flow field in the process of wave impact[D]. Dalian: Dalian University of Technology, 2009. (  0) 0)
|
| [4] |
POUPARDIN A, PERRET G, PINON G, et al. Vortex kinematic around a submerged plate under water waves. Part Ⅰ: experimental analysis[J]. European journal of mechanics-B/fluids, 2012, 34: 47-55. DOI:10.1016/j.euromechflu.2012.02.003 (  0) 0)
|
| [5] |
DIMAS A A, GALANI K A. Turbulent flow induced by regular and irregular waves above a steep rock-armored slope[J]. Journal of waterway, port, coastal, and ocean engineering, 2016, 142(5): 4016004. DOI:10.1061/(ASCE)WW.1943-5460.0000340 (  0) 0)
|
| [6] |
蒋学炼, 郝敏霞, 杨天, 等. 波浪场中弧面潜堤与矩形潜堤的涡流结构[J]. 哈尔滨工程大学学报, 2019, 40(3): 614-622. JIANG Xuelian, HAO Minxia, YANG Tian, et al. Vortex evolution around submerged quartercircular and rectangular breakwaters due to water waves[J]. Journal of Harbin Engineering University, 2019, 40(3): 614-622. (  0) 0)
|
| [7] |
CHANG Kuang'an, HSU T J, LIU P L F. Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle: Part Ⅱ: Cnoidal waves[J]. Coastal engineering, 2005, 52(3): 257-283. DOI:10.1016/j.coastaleng.2004.11.006 (  0) 0)
|
| [8] |
NA B, CHANG Kuang'an, LIM H J. Flow kinematics and air entrainment under laboratory spilling breaking waves[J]. Journal of fluid mechanics, 2020, 882(A15): 1-36. (  0) 0)
|
| [9] |
DHINAKARAN G, SUNDAR V, SUNDARAVADIVELU R, et al. Effect of perforations and rubble mound height on wave transformation characteristics of surface piercing semicircular breakwaters[J]. Ocean engineering, 2009, 36(15/16): 1182-1198. (  0) 0)
|
| [10] |
LIU Yong, LI Huajun. Analysis of wave interaction with submerged perforated semi-circular breakwaters through multipole method[J]. Applied ocean research, 2012, 34: 164-172. DOI:10.1016/j.apor.2011.08.003 (  0) 0)
|
| [11] |
BINUMOL S, RAO S, HEGDE A V. Runup and rundown characteristics of an emerged seaside perforated quarter circle breakwater[J]. Aquatic procedia, 2015, 4: 234-239. DOI:10.1016/j.aqpro.2015.02.032 (  0) 0)
|
| [12] |
JIANG Xuelian, ZOU Qingping, ZHANG Na. Wave load on submerged quarter-circular and semicircular breakwaters under irregular waves[J]. Coastal engineering, 2017, 121: 265-277. DOI:10.1016/j.coastaleng.2016.11.006 (  0) 0)
|
| [13] |
LE MÉHAUTÉ B. An Introduction to hydrodynamics and water waves[M]. Berlin, Heidelberg: Springer-Verlag, 1976.
(  0) 0)
|
| [14] |
ZOU Qingping, PENG Zhong. Evolution of wave shape over a low-crested structure[J]. Coastal engineering, 2011, 58(6): 478-488. DOI:10.1016/j.coastaleng.2011.01.001 (  0) 0)
|
| [15] |
PENG Zhong, ZOU Qingping, LIN Pengzhi. A partial cell technique for modeling the morphological change and scour[J]. Coastal engineering, 2018, 131: 88-105. DOI:10.1016/j.coastaleng.2017.09.006 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


